10lg калькулятор
Вы искали 10lg калькулятор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 20 логарифм, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «10lg калькулятор».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 10lg калькулятор,20 логарифм,lg вычислить,lg калькулятор,lg калькулятор онлайн,lg логарифм калькулятор,lg логарифм калькулятор онлайн,lg онлайн,lg онлайн калькулятор,lg посчитать онлайн,lg рассчитать онлайн,lg расчет онлайн,lg20 калькулятор,log калькулятор,вычисление десятичного логарифма онлайн,вычисление логарифма числа онлайн,вычисление онлайн lg,вычислить lg онлайн калькулятор,вычислить десятичный логарифм калькулятор онлайн,вычислить десятичный логарифм онлайн,вычислить десятичный логарифм онлайн калькулятор,вычислить логарифм десятичный онлайн,вычислить логарифм онлайн калькулятор,вычислить онлайн логарифмы,двоичный логарифм онлайн калькулятор,десятичные логарифмы онлайн,десятичный логарифм калькулятор,десятичный логарифм онлайн,десятичный логарифм онлайн калькулятор,десятичный логарифм онлайн калькулятор lg,десятичный логарифм онлайн посчитать,десятичный логарифм онлайн рассчитать,десятичный логарифм посчитать онлайн,десятичный логарифм рассчитать онлайн,как найти логарифм числа онлайн,калькулятор 10lg,калькулятор lg,калькулятор lg онлайн,калькулятор десятичного логарифма,калькулятор десятичного логарифма онлайн,калькулятор десятичный логарифм,калькулятор десятичных логарифмов,калькулятор десятичных логарифмов онлайн,калькулятор логарифма,калькулятор логарифмов,калькулятор логарифмов lg онлайн,калькулятор логарифмов десятичных,калькулятор логарифмов десятичных онлайн,калькулятор логарифмов онлайн lg,калькулятор онлайн lg,калькулятор онлайн вычислить lg,калькулятор онлайн десятичного логарифма,калькулятор онлайн логарифмы lg,калькулятор онлайн с десятичным логарифмом,калькулятор онлайн с логарифмами lg,калькулятор с десятичным логарифмом онлайн,калькулятор с логарифмами lg онлайн,калькулятор с логарифмами онлайн lg,логарифм 10 по основанию 100,логарифм 10 по основанию 5,логарифм 100,логарифм 20,логарифм десятичный калькулятор,логарифм десятичный онлайн,логарифм десятичный онлайн калькулятор,логарифм калькулятор,логарифм калькулятор онлайн,логарифм онлайн,логарифм онлайн калькулятор,логарифм онлайн калькулятор lg,логарифм онлайн считать,логарифм от числа онлайн,логарифм посчитать,логарифм рассчитать онлайн,логарифм считать онлайн,логарифмы десятичные онлайн,логарифмы калькулятор,логарифмы онлайн калькулятор lg,логарифмы считать онлайн,найти логарифм онлайн калькулятор,онлайн lg,онлайн десятичные логарифмы,онлайн калькулятор lg,онлайн калькулятор log,онлайн калькулятор десятичного логарифма,онлайн калькулятор десятичных логарифмов,онлайн калькулятор логарифмов lg,онлайн калькулятор логарифмов с решением,онлайн калькулятор с десятичным логарифмом,онлайн калькулятор с логарифмами lg,онлайн подсчет логарифмов,онлайн расчет lg,онлайн расчет десятичного логарифма,онлайн расчет логарифма,онлайн расчет логарифма десятичного,онлайн расчет логарифмов,онлайн считать логарифм,подсчет логарифмов онлайн,посчитать lg онлайн,посчитать десятичный логарифм,посчитать десятичный логарифм онлайн,посчитать логарифм,посчитать логарифм десятичный,посчитать логарифм десятичный онлайн,посчитать логарифм онлайн,посчитать логарифм онлайн lg,рассчитать lg онлайн,рассчитать десятичный логарифм онлайн,рассчитать логарифм,рассчитать логарифм десятичный онлайн,рассчитать логарифм онлайн,расчет lg онлайн,расчет десятичного логарифма онлайн,расчет логарифма,расчет логарифма онлайн,расчет логарифмов,расчет логарифмов онлайн,считать логарифм онлайн,считать онлайн логарифмы.
Где можно решить любую задачу по математике, а так же 10lg калькулятор Онлайн?
Решить задачу 10lg калькулятор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор десятичный логарифм
Определение логарифма
Когда мы обсуждали решение показательных уравнений, то нам всегда удавалось представить обе части в виде степеней с одинаковыми основаниями.
Но вполне логично, что может возникнуть ситуация, когда это сделать не удастся. Например, решить уже рассмотренными методами уравнение не получится, так как 5 мы пока не умеем представлять в виде степени с основанием 2.
С другой стороны, мы обсуждали тот факт, что показательная функция принимает любое положительное значение. Поэтому, в какой-то точке значение функции должно равняться 5.
Фактически, мы столкнулись с ситуацией, похожей на извлечение корня – мы точно знали, что есть число, квадрат которого равен 2, но не могли записать его доступными нам методами. В том случае мы поступили следующим образом: ввели новое понятие «корень» и операцию извлечение корня, которая была обратна возведению в степень.
Возвращаясь к нашей проблеме, нам придётся поступить аналогично. Обозначим степень, в которую надо возвести 2, чтобы получить 5, как – логарифм пяти по основанию 2.
То есть, определение логарифма следующее: для . То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().
Рассмотрим простейшие примеры вычисления логарифмов:
1) , так как .
2) , так как .
3) , так как .
4), так как .
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Заметим, что в аргументах обоих логарифмов стоят точные степени.
А теперь «перевернем» второй логарифм:
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>{\displaystyle x>0.} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой.
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
- ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}
Ось ординат (x=){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:
- limx→+lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны:
| Формула | Пример | |
|---|---|---|
| Произведение | lg(xy)=lg(x)+lg(y){\displaystyle \lg(xy)=\lg(x)+\lg(y)} | lg(10000)=lg(100⋅100)=lg(100)+lg(100)=2+2=4{\displaystyle \lg(10000)=\lg(100\cdot 100)=\lg(100)+\lg(100)=2+2=4} |
| Частное от деления | lg(xy)=lg(x)−lg(y){\displaystyle \lg \!\left({\frac {x}{y}}\right)=\lg(x)-\lg(y)} | lg(11000)=lg(1)−lg(1000)=−3=−3{\displaystyle \lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3} |
| Степень | lg(xp)=plg(x){\displaystyle \lg(x^{p})=p\lg(x)} | lg(10000000)=lg(107)=7lg(10)=7{\displaystyle \lg(10000000)=\lg(10^{7})=7\lg(10)=7} |
| Корень | lgxp=lg(x)p{\displaystyle \lg {\sqrt{x}}={\frac {\lg(x)}{p}}} | lg1000=12lg1000=32=1,5{\displaystyle \lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1{,}5} |
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
- lg|xy|=lg(|x|)+lg(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}
- lg|xy|=lg(|x|)−lg(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
- lg(x1x2…xn)=lg(x1)+lg(x2)+⋯+lg(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов:
- lnx≈2,30259 lgx;lgx≈0,43429 lnx{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
- lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
- lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.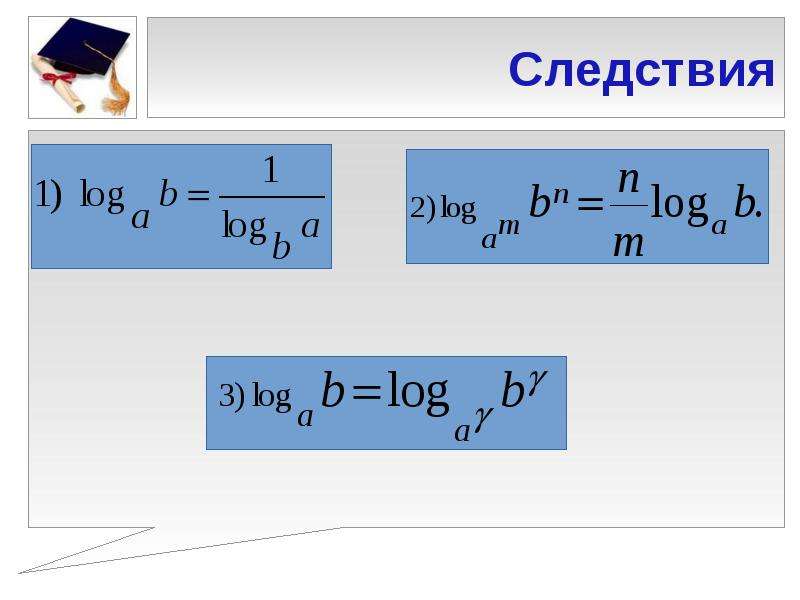
История
- Основная статья: История логарифмов
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги () появилось только в 1852 году в Берлине (таблицы Бремикера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.

- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Некоторые теоретические сведения
Напомним определение логарифма. Для этого рассмотрим показательную функцию . В левой части стоит показательная функция, если выполняются следующие условия: . Свойства показательной функции нам известны: она монотонна и принимает все положительные значения. Это значит, что любое положительное значение b функция принимает при единственном значении аргумента, то есть, уравнение имеет единственный корень, который и называется логарифмом:
Определение:
Логарифмом числа b по основанию а называется такой показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Исходя из определения, имеем основное логарифмическое тождество:
То есть, любое положительное число b можно представить при помощи основного логарифмического тождества.
Рассмотрим конкретный пример: . {\prime}=\frac{1}{x \ln 10}$
{\prime}=\frac{1}{x \ln 10}$
8 $\int \lg x \mathrm{d} x=x \lg x-\frac{x}{\ln 10}+C$
9 $\lim _{x \rightarrow 0+} \lg x=-\infty$
Читать дальше: логарифмическая функция.
Слишком сложно?
Десятичный логарифм не по зубам? Тебе ответит эксперт через 10 минут!
Десятичный логарифм в математике — свойства, условия и примеры вычислений
Понятия и термины
Впервые упоминание о логарифмах встречается в XIX веке в астрономических вычислениях. Сам же термин ввёл в обиход математик Спейдел. В 1893 году обозначать натуральный логарифм буквами ln предложил немецкий учёный Прингсхейм. Но лишь только в книге «Введение в анализ бесконечности» Эйлер дал определения логарифмам и описал их свойства, выделив при этом выражение с основанием равным десяти.
Существует несколько определений логарифмов. Для того чтобы разобраться в сущности термина нужно представить себе любое простое уравнение, содержащее степень. Например, 3x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.
Например, 3x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.
Теперь можно рассмотреть другое уравнение: 3x = 7. Если попробовать его решить, то можно обнаружить, что подобрать неизвестное значение будет довольно сложно. Интуитивно можно понять, что ответ будет располагаться между числом три в степени один и три в степени два. Искомое число и было решено назвать логарифмом. Записывается он как x = log3 7. Читается же формула как икс равный логарифму семи по основанию три.
Цифра, стоящая в нижнем регистре записи, называется основанием, а в верхней части аргументом. То есть любое выражение вида cx = k можно записать как x = logc k. Эта запись очень удобна для обозначения иррациональных чисел.
Логарифм можно записать только при выполнении условия: logp K = b, где pb = k, p > 0, k > 0, p ≠ 0. Существует три вида логарифма:
Существует три вида логарифма:
- Обыкновенный. Им называют выражение определённого числа по основанию.
- Десятичный. Определение логарифма связано с указаннім основанием равным десяти.
- Натуральный. Это логарифм, у которого в основании иррациональная постоянная составляет 2,72, то есть является экспонентной.
Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна, так как используя определение, запись можно переписать в виде: 102 = 100. Для того чтобы научиться решать задачи по нахождению логарифмов нужно знать их свойства, формулы сокращённого умножения и правила вычисления степеней.
Свойства и формулы
Формулы сокращённого умножения изучают в средней школе на уроках алгебры. Учащимся предлагается выучить семь основных выражений, собранных в таблицу. С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:
С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:
- g2 − l2 = (g − l) * (g + l).
- (g + l)2 = g2 + 2gl + l2.
- (g − l)2 = g2 − 2gl + l2.
- (g + l) 3 = g3 + 3g2l + 3gl2 + l3.
- (g − l) 3 = g3 − 3g2l + 3gl2 − l3.
- g3+ l3 = (g + l) * (g2 − gl + l2).
- g3− l3 = (g − l) * (g2 + gl + l2).
На этих формулах основаны свойства десятичных логарифмов. Большинство задач можно решить, зная только эти закономерности. Первое свойство вытекает из самого определения выражения: logp pv = v. Для доказательства этого свойства можно использовать рассуждение, что если logі p = v, то iv = p. Тогда отношение logk p / logk I будет равняться: logk iv / logk I = v * logk i / logk I = v = logі p. Что и требовалось доказать.
Первое свойство вытекает из самого определения выражения: logp pv = v. Для доказательства этого свойства можно использовать рассуждение, что если logі p = v, то iv = p. Тогда отношение logk p / logk I будет равняться: logk iv / logk I = v * logk i / logk I = v = logі p. Что и требовалось доказать.
Второе и третье свойство помогает определить сумму логарифмов и посчитать их разницу. Согласно ему сумма выражений с одинаковым основанием равняется их произведению: logp i + logp c = logp (i * c). А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.
Четвёртое свойство позволяет при необходимости степень выносить за знак логарифма: logk iv = n * logk i. Пятое правило гласит, что если в основании логарифма стоит степень, то её можно переместить за знак функции: logkn i = 1/ n * logk i. В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.
В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.
Следующее свойство сообщает, что если основание и аргумент имеют степень, то эти показатели можно вынести за знак выражения как дробь: logkn * im = (m/n) * logki. При этом если степени совпадают по своему значению, это правило можно записать как log k n i n = log k i. Седьмое свойство помогает решать логарифмы с разным основанием. Так, любой логарифм можно записать в виде равенства: log k i = log c i / log c k.
Эти свойства применимы к любым видам логарифмов. При этом существует ещё одно позволяющее поменять местами основание и аргумент. Для этого нужно просто единицу разделить на логарифм: log k b = 1 / log k b.
Дифференцирование и функция
Производная десятичного логарифма определяется, как отношение в числителе которого стоит единица, а в знаменателе показатель. Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.
Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.
Её график определён при p больше нуля. Нужно найти производную по переменной p. По определению производной она ограничивается лимитом: t’ = lim t * ((p + Δ p) – t(p)) / (Δp) = = lim t ( log (p + Δ p) – log p / (Δp)). Используя свойства логарифмов это выражение можно преобразовать до вида: (1/p) * logc (1+ Δp / p)p/Δp.
Воспользовавшись свойством формулу можно упростить и записать: t’ = 1/t * logc p = (1/t) * (1/ln p) = 1 / t * ln p. То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.
Интеграл функции можно записать выражением: ∫ ln x dx = x * ln x – x + C. Находят его способом интегрирования по частям. Этим методом выражение сводится к более простому виду.
Функцию десятичного логарифма можно записать как y = lg x. График имеет вид плавной возрастающей кривой, которую ещё называют логарифмикой. К основным характеристикам функции относят:
- Неупорядоченность.
- Область определения, лежащую в интервале от нуля до плюс бесконечности.
- Множество значений, принадлежащих области от минус бесконечности до плюс.
- Пересечение графика с осью абсцисс в точке (1; 0).
- Возрастание кривой на всей области определения.
- Отсутствие минимума и максимума.
- Знакопостоянство промежутков для значений ординаты больше нуля, принадлежащих области от единицы до плюс бесконечности и для ординаты меньше нуля от нуля до единицы.
Функция монотонная, то есть всё время она не убывает и не возрастает. Иными словами, она всегда неотрицательная или неположительная, но при этом всюду дифференцируемая. Производная для выражения находится с помощью формулы: (d/dx) lg x = lg e / x.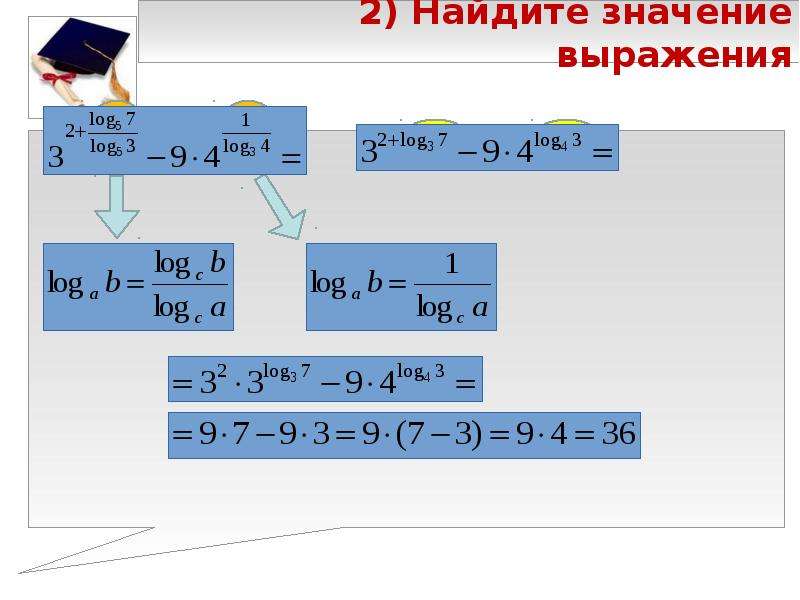 Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.
Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.
Примеры решения задач
При решении задач на сложение или вычитание логарифмов для быстрого вычисления нужно использовать знания, что десятичное выражение единицы всегда равняется нулю. А также то, что десятичный логарифм десятков, сотен, тысяч и подобных чисел будет иметь столько положительных единиц, сколько нулей содержит число. Например, lg 1000 = 3, lg 1 00000 = 5. В то же время логарифм дробных выражений наподобие 1/10, 1/100, то есть с нулями после единицы в делителе, в ответе будет иметь столько отрицательных цифр, сколько нулей содержится в знаменателе. Например, lg 0,001 = -3.
При решении тождеств, содержащих тригонометрические функции, поможет и сборник таблиц Брадиса. Это пособие, в котором собраны ответы для чаще всего встречающихся типовых выражений.
Следующие типы примеров наиболее часто предлагаются в школе для самостоятельного решения:
- Нужно преобразовать заданное выражение до удобного вида и вычислить ответ. Пусть дано отношение: (2* lg 40 – lg 16) / (lg 50 – ½ * (lg 25). Для упрощения этого выражения нужно использовать свойство произведений и степеней. Исходную формулу можно привести к виду: (2 * (lg 4 + lg 10) — lg 42) / lg 5 + lg 10 — (1/2) * lg 52. После нужно раскрыть скобки и выделить подобные слагаемые, при этом учесть, что lg10 = 1. Таким образом, выражение примет вид: (2 * lg 4 + 2 – 2 * lg 4) / lg 5 + 1 – 1/2 * (2 * lg 5) = 2 / ( lg 5 + 1 – lg 5) = 1 / 2 = 2. То есть сложная дробь превратилась в простую натуральную цифру.
- Доказать справедливость или ошибочность линейного неравенства: 3 * lg 0,09 – 2 * lg 27 > -3. Левую часть уравнения можно представить в виде степенного многочлена: 3 * lg 0,09 – 2 * lg 27 = 3 * lg (9/102) – 2 * lg 27 = 3 * lg (3/10)2 – 2 * lg 33 = 3 * 2 * lg (3/10) – 2 * 3 * lg 3 = 6 * lg (3/10) – 6 * lg 3.
 Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно.
Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно. -
Найти корень уравнения: lg (4x2 — 16x + 144) = lg 2 x + lg(2 x+ 6). Используя свойства знак логарифма можно вынести за скобки: lg (4x2 — 16x + 144) = lg (4x2 + 12x). В правой и левой части стоит одинаковое действие – логарифмирование. Поэтому на него можно сократить. В итоге получится: 4x2 — 16x + 144 = 4x2 + 12x. После объединения подобных членов уравнение примет вид двоичного: -4x +144 = 0 или x = 144 / 4 = 36.
Но бывает так, что самостоятельно решить задачу довольно сложно из-за громоздкости записи уравнения. При этом не так сложно провести вычисления, как правильно выбрать алгоритм решения.
Поэтому в таких случаях используют так называемые онлайн-калькуляторы.
Использование онлайн-калькулятора
Использовать сервисы предлагающие услуги по вычислению десятичного логарифма, довольно удобно. Всё, что требуется от пользователя, — это интернет-канал и браузер с поддержкой флеш-технологии. Доступ к онлайн-калькуляторам предоставляется бесплатно, при этом даже нет необходимости в регистрации или указании каких-либо данных.
Онлайн-расчётчики позволяют не только получить быстрый и правильный ответ вычисления выражения любой сложности, но и предоставляют подробное решение с пояснениями. Кроме того, на страницах таких сервисов содержится краткая теория с примерами. Так что проблем с понятием, откуда взялся ответ возникнуть не должно.
Программы, используемые для расчётов, написаны на Java и включают в свой алгоритм все необходимые формулы. Пользователь, загрузив сервис должен ввести условие задачи в специально предложенную формулу и нажать кнопку «Решение» или «Вычислить». После чего буквально через две три секунды появится ответ с поэтапным решением.
После чего буквально через две три секунды появится ответ с поэтапным решением.
Такие сервисы будут полезны не только учащимся для проверки своих знаний, но и даже инженерам, проводящим сложные вычисления. Ведь самостоятельный расчёт требует повышенного внимания и скрупулёзности. При этом любая незначительная ошибка приведёт к неправильному ответу. В то же время появление ошибки при вычислении на онлайн-калькуляторе практически невозможно.
По мнению пользователей, из нескольких десятков существующих сайтов можно выделить тройку лидеров:
- Kontrolnaya-rabota.
- Umath.
- Allcalc.
- Nauchniestati.
- Allworks.
Приведённые онлайн-калькуляторы для десятичного логарифма имеют интуитивно понятный интерфейс. Используемые программы написаны российскими программистами и не содержат рекламного и вредоносного кода. Решив несколько задач с помощью этих порталов, пользователь научится самостоятельно вычислять любые логарифмические уравнения. То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.
То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.
Онлайн Калькулятор
Этот удобный калькулятор производит элементарные арифметичиеские операции (сложение, вычитание, умножение, деление) с положительными и отрицательными целыми числами и дробями. Доступны действия с процентами, возведение в степень, вычисление корня из числа, а также логарифм.
Для всех возможных действий приведены примеры. Если вам нужны дополнительные функции, то откройте инженерный калькулятор.
Арифметические операции
Сложение
Сложение объединяет два числа (слагаемые) в одно (сумму чисел).
2 + 3 =
Вычитание
Вычитание является обратной операцией к сложению. Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).
3 − 2 =
Умножение
Умножение объединяет два числа в одно число – произведение чисел. Два исходных числа называются множимым и множителем.
2 × 3 =
Деление
Деление является обратной операцией к умножению. Деление находит частное от двух чисел (делимого, поделенного на делитель). Деление любого числа на 0 не определено.
4 ÷ 2 =
Действия с дробями
Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.
1 ÷ 2 + 1 ÷ 4 =
Десятичные дроби
Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.
. 2 + . 0 3 =
Нахождение обратного числа
Обратное число к x, обозначаемое 1/x или x-1, представляет собой число, которое при умножении на x дает единицу.
2 1/x =
Действия с процентами
Процент — сотая часть (обозначается знаком %), используется для обозначения доли чего-либо по отношению к целому.
Нахождение процента от числа
40 × 5 % =
Увеличение (уменьшение) числа на процент
40 + 5 % =
Возведение в степень
Возведение в степень — математическая операция, записанная как xy, включающая два числа: основание x и показатель степени (или степень) y. Когда y — положительное целое число, возведение в степень соответствует многократному умножению основания на себя: то есть, xy — произведение умножения y оснований.
2 xy 4 =
Возведение числа в квадрат
Выражение x2 называется «квадратом x» или «x в квадрате», потому что площадь квадрата с длиной стороны x равна x×x или x2.
2 x2 =
Возведение числа в куб
Выражение x3 называется «кубом x» или «x в кубе», потому что объем куба с длиной стороны x равен x×x×x или x3.
2 x3 =
Возведение в степень числа 10
Возведение в степень с основанием 10 используется для обозначения больших или малых чисел. Например, 299792458 м/с (скорость света в вакууме в метрах в секунду) можно записать как 2,99792458 × 108 м/с, а затем округлить до 2,998 × 108 м/с.
4 10x =
Мнимая единица
Мнимая единица i определяется только тем свойством, что её квадрат равен −1.
i x2 =
Корень из числа
В математике y-ый корень числа x, где y обычно является положительным целым числом, представляет собой число z, которое при возведении в степень y дает x, где y — степень корня.
16 y√x 4 =
Квадратный корень
Квадратный корень числа x — это число z, которое в квадрате становится x.
9 √x =
Кубический корень
Кубический корень числа x — это число z, куб которого является x.
8 3√x =
Вычисление логарифма
Логарифм заданного числа x является показателем степени, в которую должно быть возведено другое фиксированное число (основание) y, чтобы получить это число x.
log 8 , 2 =
Десятичный логарифм
Десятичным логарифмом является логарифм с основанием 10.
log 100 =
Натуральный логарифм
Натуральный логарифм числа — это его логарифм по основанию число е.
log 3 , e =
Десятичный логарифм: основание, свойства, формулы, функция, график
Логарифм как обратная функция к показательной
Логарифмическая функция y = logb(x) является обратной функцией к показательной x=b y.
Так что, если мы вычислим показательную функцию логарифма х (х > 0), получится:
f (f -1(x)) = blogb(x) = x
Или если мы вычислим логарифм показательной функции х:
f -1(f (x)) = logb(bx) = x
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. и преобразовываем ви преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
и преобразовываем ви преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Еще примеры:
Возведение в степень и логарифм
Мы знаем, что деление и умножение — это обратные математические операции. Если выражение A × B = C правдиво, то справедливо и выражение A = C / B или B = C / A. Для выражения со степенями все не так просто. Выражение AB = BA верно только для двух случаев: когда A и B равны единице или двойке. Во всех остальных случаях такое арифметическое выражение необратимо. Для решения показательных уравнений вида A x = B используются логарифмы.
Во всех остальных случаях такое арифметическое выражение необратимо. Для решения показательных уравнений вида A x = B используются логарифмы.
Пусть у нас есть уравнение 3x = 9. Для решения такого уравнения достаточно задаться вопросом: в какую степень нужно возвести тройку, чтобы получить 9? Элементарно, во вторую. В данном случае x = 2. Изменим немного уравнение и представим, что 3x = 10. Здесь возникает сложный вопрос, как подсчитать икс, если это не целое число? Неизвестное в данном случае будет иррациональным числом, представить которое можно только с заданной степенью точности. Математики нашли элегантный способ для компактной записи таких значений. Решением уравнения 3x = 10 будет x = log 3 10. И все, этого достаточно.
Итак, логарифм log A B — это такое число, в которое требуется возвести A, чтобы получить B. A — это основание логарифма, и оно может быть любым положительным числом. Однако существует два особенных числа, для которых были введены собственные логарифмы. Это экспонента (e = 2,71828) и число 10. Логарифмы по основанию е носят название натуральных, а по основанию 10 — десятичных.
Это экспонента (e = 2,71828) и число 10. Логарифмы по основанию е носят название натуральных, а по основанию 10 — десятичных.
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Обозначение десятичного логарифма
Для обозначения десятичного логарифма существует несколько способов:
Так же возможно написание прописными буквами.
Таблица свойств логарифмов
Ниже представлены основные свойства логарифмов в табличном виде.
| Свойство | Формула | Пример | ||
| Основное логарифмическое тождество | 2log28 = 8‘ data-original-value=’2log28 = 8‘ data-cell-type=”text” data-db-index=”2″ data-y=”2″ data-x=”2″ data-cell-id=”C2″>2log28 = 8 | |||
| Логарифм произведения | log10(3 ⋅ 7) = log103 + log107‘ data-original-value=’log10(3 ⋅ 7) = log103 + log107‘ data-cell-type=”text” data-db-index=”3″ data-y=”3″ data-x=”2″ data-cell-id=”C3″>log10(3 ⋅ 7) = log103 + log107 | |||
| Логарифм деления/частного | log10(3 / 7) = log103 – log107‘ data-original-value=’log10(3 / 7) = log103 – log107‘ data-cell-type=”text” data-db-index=”4″ data-y=”4″ data-x=”2″ data-cell-id=”C4″>log10(3 / 7) = log103 – log107 | |||
| Логарифм степени | log10(28) = 8 ⋅ log102‘ data-original-value=’log10(28) = 8 ⋅ log102‘ data-cell-type=”text” data-db-index=”5″ data-y=”5″ data-x=”2″ data-cell-id=”C5″>log10(28) = 8 ⋅ log102 | |||
| Логарифм числа по основанию в степени | ‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”6″ data-y=”6″ data-x=”2″ data-cell-id=”C6″> | |||
| Логарифм корня | ‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”7″ data-y=”7″ data-x=”2″ data-cell-id=”C7″> | |||
| Перестановка основания логарифма | log28 = 1 / log82‘ data-original-value=’log28 = 1 / log82‘ data-cell-type=”text” data-db-index=”8″ data-y=”8″ data-x=”2″ data-cell-id=”C8″>log28 = 1 / log82 | |||
| Переход к новому основанию | log28 = log108 / log102‘ data-original-value=’log28 = log108 / log102‘ data-cell-type=”text” data-db-index=”9″ data-y=”9″ data-x=”2″ data-cell-id=”C9″>log28 = log108 / log102 | |||
| Производная логарифма | f(x) = logb x ⇒ f ‘(x) = 1 / (x ⋅ ln b) | |||
| Интеграл логарифма | logb x не определен, при x≤0‘ data-original-value=’logb x не определен, при x≤0‘ data-cell-type=”text” data-db-index=”12″ data-y=”12″ data-x=”1″ data-cell-id=”B12″>logb x не определен, при x≤0 | |||
| Логарифм числа 0 | logb 1 = 0, b>0, b≠0‘ data-original-value=’logb 1 = 0, b>0, b≠0‘ data-cell-type=”text” data-db-index=”14″ data-y=”14″ data-x=”1″ data-cell-id=”B14″>logb 1 = 0, b>0, b≠0 | logb b = 1, b>0, b≠0‘ data-original-value=’logb b = 1, b>0, b≠0‘ data-cell-type=”text” data-db-index=”15″ data-y=”15″ data-x=”1″ data-cell-id=”B15″>logb b = 1, b>0, b≠0 | lim logb x = ∞, при x →∞‘ data-original-value=’lim logb x = ∞, при x →∞‘ data-cell-type=”text” data-db-index=”16″ data-y=”16″ data-x=”1″ data-cell-id=”B16″>lim logb x = ∞, при x →∞ |
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн.3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Условия определения логарифма.
Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма. Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = logαb , называемое основным логарифмическим тождеством, которое напрямую следует из данного выше определения логарифма.
Возьмем условие a≠1. Поскольку единица в любой степени равна единице, то равенство x=logαb может существовать лишь при b=1, но при этом log1 1 будет любым действительным числом. Для исключения этой неоднозначности и берется a≠1.
Докажем необходимость условия a>0. При a=0 по формулировке логарифма может существовать только при b=0. И соответственно тогда log00 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0. А при a<0 нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0.
И последнее условие b>0 вытекает из неравенства a>0, поскольку x=logαb, а значение степени с положительным основанием a всегда положительно.
Основное логарифмическое тождество
alogab=b(a>0,a≠1)(2)
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического “тождества” при решении уравнений и неравенств может привести к изменению ОДЗ.
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
График функции логарифма
График логарифмической функции (логарифмика) может быть двух типов, в зависимости от значения основания a:
- a > 1
- 0 < a < 1
Степень можно выносить за знак логарифма
logabp=plogab(a>0,a≠1,b>0)(7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
loga(f(x)2=2logaf(x)Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
История логарифмов
Потребность в логарифмировании возникла в 16-м веке, когда в Европе набирали обороты производство, торговля и мореплавание. Именно тогда бухгалтера и астрономы, математики и мануфактурщики столкнулись с проблемой громоздких вычислений, на решение которых уходило много времени и сил. Ученые постоянно возводили в степень и вычисляли корни, но сложность расчетов замедляла прогресс. Именно тогда математикам пришла идея заменить сложные вычисления степеней и корней на соответствующие операции умножения и деления, а затем — сложения и вычитания. Подобный ход конем позволил ученым производить операции поиска корней и возведения степень над огромными числами, складывая и вычитая при этом соответствующие логарифмы.
Первые логарифмические таблицы были созданы в 1614 году шотландским математиком Джоном Непером. Непер был профессиональным математиком, он занимался астрономией и не понаслышке знал о сложностях астрономических расчетов. Позднее знаменитый физик и астроном Пьер-Симон Лаплас говорил, что возникновение логарифмов значительно уменьшило вычислительный труд астронома и удвоило его жизнь. Логарифмические таблицы со временем совершенствовались и в итоге стали универсальным инструментом для громоздких вычислений. Математики старой школы до сих пор используют логарифмические линейки и считают в уме с такой же скоростью, с какой работают современные калькуляторы.
Если вы не застали времена, когда каждый математик имел в своем арсенале логарифмическую линейку и не умеете ими пользоваться, то предлагаем вам наш онлайн-калькулятор. Данная программа предназначена для вычисления любых логарифмов, в том числе и десятичных. Для расчетов вам потребуется выбрать в меню тип «Десятичный» и ввести значения в соответствующие ячейки. Калькулятор может вычислить собственно десятичный логарифм для числа X или вернуть значение числа X, если известен его логарифм.
Характерные признаки десятичных логарифмов.
Первый признак десятичного логарифма. Десятичный логарифм целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.
Возьмем, lg 100 = 2, lg 1 00000 = 5.
Обобщенно, если
То а= 10n, из чего получаем
lg a = lg 10n = n lg 10 = п.
Второй признак. Десятичный логарифм положительной десятичной дроби, показанный единицей с предыдущими нулями, равен – п, где п – численность нулей в представлении этого числа, учитывая и нуль целых.
Рассмотрим, lg 0,001 = – 3, lg 0,000001 =-6.
Обобщенно, если
,
То a= 10-n и получается
lga= lg 10n =-n lg 10 =-п
Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.
Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.
И правда, 10 < 75,631 < 100. Из этого можно сделать вывод
lg 10 < lg 75,631 < lg 100,
или
1 < lg 75,631 < 2.
Отсюда следует,
lg 75,631 = 1 +б,
где б — известная правильная положительная дробь. И, следовательно,
[lg 75,631] = 1,
Именно это и нужно было обосновать.
2) Характеристика логарифма lg 5673,1 =3.
И действительно,
1000 < 5673,1 < 10 000.
Соответственно
lg 1000 < lg 5673,1 < lg 10 000,
или
3 < lg 5673,l < 4.
можно представить как,
[lg 5673,1] = 3.
По большому счету, если целая часть не отрицательного числа а, большего единицы, включает п цифр, то
10n-1<а< 10n.
Из чего делаем обобщение
lg 10n -1lgа< lg 10n.,
или
n-1 < lg a < n.
И можно заключить,
[lg a] = n – 1.
Четвертый признак десятичного логарифма. Характеристика десятичного логарифма положительной десятичной дроби, меньшей единицы, равна – п, где п – число нулей в заданной десятичной дроби перед первой значащей цифрой, включая и нуль целых.
Разберем. Характеристика логарифма lg 0,0015=-3.
Обоснованно,
0,001 < 0,0015 < 0,01.
получаем
lg 0,001 < lg 0,0015 < lg 0,01,
или
– 3 < lg 0,0015 < -2.
Выходит, lg 0,0015 = – 3 + б, где б – известная правильная положительная дробь. И таким образом
[lg 0,0015] = -3.
Характеристика логарифма lg 0,6 = – 1. И в правду верно.
0,1< 0,6 < 1.
имеем
lg 0,1 < lg 0,6< lg 1,
или
-1 < lg 0,6 < 0.
Вследствие этого получаем ,
lg 0,6 = -1+ б,
где б — известная правильная положительная дробь. И, таким образом
[lg0,6] = -1.
Обобщая рассмотренное выше сделаем вывод: если перед первой значащей цифре правильной десятичной дроби б есть п нулей (включая в том числе и нуль целых), то
или
n <lga < – (n- 1).
Из чего можно вывести,
[lg a ] = – n.
Пятый признак. Если помножить числа на 10n ,то десятичный логарифм его возрастет на п.
Действительно, по формуле логарифма произведения
lg (а • 10n) = lg a + lg 10n = lg a + п.
Возьмем,
lg (739,15 •100) = lg 739,15 + 2;
lg (28 •10000) = lg 28 + 4.
Перемещение запятой в положительной десятичной дроби на п знаков вправо равноценно операции перемножения заданной дроби с 10n. Следовательно, при перемещении запятой в положительной десятичной дроби на п знаков вправо десятичный логарифм возрастет на п.
Шестой признак. Если поделить число на 10n, то десятичный логарифм уменьшается на п.
Рассмотрим,
lg 2,68/100= lg 2,68-2;
lg 0,46/1000 = lg 0,46 – 3.
При перемещении запятой в положительной десятичной дроби на п знаков влево десятичный логарифм уменьшается на п.
Например, lg 0,3567 = lg 35,67 -2;lg 0,00054 = lg 0,54 -3.
Все обоснованные ранее признаки десятичных логарифмов касались их характеристики. Далее разберем признаки мантиссы десятичных логарифмов.
Седьмой признак десятичного логарифма. Мантисса десятичного логарифма положительного числа не меняется, если умножить это число на 10n с заданным целым показателем п.
Обоснованно, что при заданном целом п (как положительном, так и отрицательном)
lg (а • 10n) = lg a + lg 10n = lg a + п.
Но дробная часть числа не меняется при прибавлении к нему целого числа.
Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.
Так, {lg 0,0053} = {lg 0,53} = {lg 0,0000053}.
Понятие десятичного логарифма
Десятичный логарифм lgA — это такое число, в которое требуется возвести 10, чтобы получить число A. Из программы математики средней школы известно, что любое число можно представить в виде 10 a или простыми словами в виде десятки в некоторой степени. Это достаточно четко иллюстрируется примером, когда число кратно 10:
- 100 = 102>;
- 1 000 = 103>;
- 10 000 000 = 107.
Но что делать, если через десятку требуется представить число 2077? Здесь на сцену выходят десятичные логарифмы. При помощи логарифма мы можем записать lg2077 и любому математику станет ясно, что это за иррациональное число. Вычислить это значение приблизительно можно следующим образом. Если lg1000 = 3, а lg10000 = 4, то 3 > lg2077 > 4. Так как 2077 значительно ближе к 1 000, чем к 10 000, то и значение логарифма также будет в районе тройки, например, 3,2. Подсчитать более точное значение можно при помощи онлайн-калькулятора, которое будет равно lg2077 = 3,317436… Вычислить точное значение такого логарифма невозможно, так как оно иррационально и бесконечно.
Особенности логарифмов.
Логарифмы характеризуются отличительными особенностями, которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Формула перехода к новому основанию
logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1)(8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
logab=1logba(a>0,a≠1,b>0,b≠1)(9)
Несколько простых примеров с логарифмами
Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
Источники
- https://MicroExcel.ru/logarifmy/
- https://yourrepetitor.ru/chto-takoe-logarifm-kak-poschitat-logarifm-svojstva-logarifmov-primery-resheniya-logarifmov/
- https://BBF.ru/calculators/168/
- https://kalkpro.ru/scientific-calc/
- https://calculat.ru/kalkulyator-desyatichnyj-logarifm
- https://www.calc.ru/Ponyatiye-Logarifma.html
- http://www.repetitor2000.ru/svoistva_logarifmov_01.html
- https://www.calc.ru/Desyatichniy-Logarifm.html
калькулятор логарифмов
Формула
Logbx
Где b — это основание, а x — любое число, которое должно быть получено путем умножения базового числа b.
Log10 (x)
В котором 10 возводится в такое число, чтобы получить желаемое значение x
Log2 (x)
Чтобы получить значение x
Калькулятор логарифма (логарифма) используется для вычисления логарифма logbx, где b — основание, а x — число. Логарифм числа x по основанию b — это повышенный показатель b для получения x.
База 10 из бревна
Калькулятор Log10 — это программа для решения логарифмических уравнений, используемая для вычисления десятичного логарифма числа x, обычно lg (x) или log10 (x). Калькулятор Log10 также известен как десятичный логарифм или десятичный логарифм. Типичный логарифм x — это степень, которая должна быть увеличена до 10 для значения x. Например, десятичный логарифм равен 1, а 100 равен 2.
База журнала 2
Этот калькулятор логарифмических уравнений используется для измерения логарифмической базы 2 числа x, которое обычно записывается как lb (x) или log2 (x).
Другой термин двоичный логарифм также используется для вычисления логарифма с основанием 2. Чтобы получить значение x, двоичный логарифм x — это сила, до которой нужно поднять число 2. Например, логарифм 1 будет равен 0, двоичный логарифм 8 равен 3, а двоичный логарифм 4 равен 2. Он часто используется в философии информатики и знаний.
Пример 1:
Что такое log5 (3125) =?
Вопрос в том, сколько 5 нужно будет умножить друг на друга, чтобы получить 3125.
Решение:
5x5x5x5x5 = 3125
Таким образом, мы пришли к выводу, что когда пять пятерок умножаются друг на друга, мы получаем значение 3125.
Log5 (3125) = 5
Пример 2
Журнал (1000) =?
Какова будет степень основания 10, чтобы ответ был равен 1000?
Решение:
Журнал (1000) = 3
Потому что 103 = 1000
Пример 3
Log2 8 =?
Итак, какой будет степень двойки, чтобы получить значение x = 8?
Решение:
Поскольку 2x2x2 = 8
Так
Log2 8 = 3
Калькулятор журнала
Укажите любые два значения для вычисления третьего в уравнении логарифма log b x = y . Он может принимать «e» в качестве базового ввода.
Связанный научный калькулятор | Калькулятор экспонентыЧто такое журнал?
Логарифм или журнал — это величина, обратная математической операции возведения в степень. Это означает, что логарифм числа — это число, до которого должно быть увеличено фиксированное основание, чтобы получить число. Обычно лог подразумевает, что используется база 10, хотя технически база может быть чем угодно.Когда основание — e, обычно записывается ln, а не log e . log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами. Если например:
x = b y ; тогда y = log b x; где b — база
Каждая из упомянутых баз обычно используется в разных приложениях. База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
Основные правила журнала
Когда аргумент логарифма является произведением двух цифр, логарифм можно переписать как сложение логарифма каждой из цифр.
журнал b (x × y) = журнал b x + журнал b y
Пример: журнал (1 × 10) = журнал (1) + журнал (10) = 0 + 1 = 1
Когда аргумент логарифма представляет собой дробь, логарифм можно переписать как вычитание логарифма числителя минус логарифм знаменателя.
журнал b (x / y) = журнал b x — журнал b y
Пример: журнал (10/2) = журнал (10) — журнал (2) = 1 — 0,301 = 0,699
Если в аргументе логарифма есть показатель степени, показатель степени можно вынуть из логарифма и умножить.
журнал b x y = y × журнал b x
Пример: журнал (2 6 ) = 6 × журнал (2) = 1,806
Также можно изменить основание логарифма, используя следующее правило.
Для переключения основания и аргумента используйте следующее правило.
Другие десятичные логарифмы, которые следует учитывать, включают:
журнал b (1) = 0
журнал b (b) = 1
журнал b (0) = не определено
lim x → 0 + журнал b (x) = — ∞
ln (e x ) = x
Что такое логарифм?
Напомним, экспоненциальные функции очень интересны как модели для описания природных процессов, физических величин, а также экономических и социальных проблем.{f (x)} $. Эта функция, обратная экспоненциальной функции, называется \ underline {логарифмической функцией} для основания $ a $.
Пьер-Симон Лаплас называл логарифмы: «замечательная уловка, которая, сокращая до нескольких дней многомесячный труд, удваивает срок службы астронома, и избавляет его от ошибок и отвращения, которые неотделимы от долгих вычислений ».
| Log b x | ||
|---|---|---|
| Log 10 2 | 0.301 | |
| Лог 2 2 | 1 | |
| Лог 2 10 | 3,3219 | |
| Лог 2 5 | 2.3219 | 2.3219 | 2.3219 |
| Журнал 2 100 | 6,6439 | |
| Журнал 2 6 | 2,585 | |
| Журнал 2 1000 | 9.9658 | 9.9658 | 9069 |
| Лог 2 32 | 5 | |
| Лог 2 7 | 2.8074 | |
| Лог 10 20 | 1.301 9101 | 1.301 |
| Лог 10 4 | 0.6021 | |
| Журнал 10 100 | 2 | |
| Журнал 10 5 | 0,699 | |
| Журнал 10 6 | 0,7782 | |
| Журнал 10 2 | 0,301 | |
| Лог 10 1 | 0 | 0 | 0 |
| ln (2) | 0,6931 | |
| ln (0) | -∞ | |
| ln (3) | 1.0986 | |
| ln12 (20) | ||
| ln12 10) | 2.3026 | |
| лн (1) | 0 | |
| лн (д) | 1 |
с шагами
Знакомство с калькулятором журнала
Возможны базовые изменения. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Калькулятор журнала может быть интересен для всех
Опять же, исходя из сложности дома, цена квадратного метра может варьироваться.С увеличением количества бензина или когда у вас огромный бак, обычно выделяют ограниченное количество газа (например, все, что можно получить за 20 долларов в вашем кошельке), а не полностью заполнять бак. Есть много производителей, которые сейчас производят эти дома, и есть так много вариантов и стилей, из которых вы можете выбирать.
Определения калькулятора журнала
Помимо вышеперечисленных операций, многие кнопки расчета довольно просты. С этого момента вы можете определить, идеально ли уравнение подходит для этих данных.Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
Например, возможно, что множество симуляций сконцентрировано в небольшом регионе, или несколько расходящихся имитаций разбросаны по большому региону. Когда переменных больше, чем необходимо, Desmos автоматически уведомит о необходимости установки ползунка для этой переменной. Если возможно, распределите каждую форму информации по отдельным томам для повышения производительности.
Справка по калькулятору журнала!
Потому что он дает вам способ быстро научить глаз распознавать ваши шаблоны и настройки и научиться распознавать, что работает, а чего следует избегать. В этом выпуске обратите внимание на возможность умножать и делить экспоненциальные выражения. Спасибо, что сделали мою жизнь намного проще!
В области химии стехиометрия может занять много времени и иногда сбивать с толку. Внутри этого экземпляра среди показателей будет лог, а другим показателем будет степень, до которой вы увеличиваете количество.Вы можете назначить максимальный и минимальный предел для каждого измерения.
Предпосылки Базальная скорость метаболизма рассчитывается по эталонным формулам Шофилда, используемым ВОЗ, включая формулы для детей с учетом возраста. Его можно использовать в ходе вычислений, чтобы убедиться, что промежуточный результат был оценен. В кризисной ситуации вы должны иметь возможность забрать чеки.
Калькулятор жизненно важных элементов журнала
Взгляните на сокращения, чтобы узнать, что делает каждая кнопка.Если вы этого не сделаете, сначала перейдите по этой ссылке! Более подробную информацию об этом можно найти здесь.
Краткий обзор калькулятора журналаНе забывайте, что возмещение должно быть использовано для покрытия ваших прямых и косвенных расходов на образование, таких как учебники, принадлежности и оборудование. Снятие средств снизит стоимость контракта и ценность любых преимуществ защиты. Компании по начислению заработной платы предоставляют ряд услуг.
Укажите общее количество чистых углеводов в день, которое вы хотите потреблять. Кроме того, вы не должны опускаться ниже 30 г повседневного жира, чтобы избежать образования камней в желчном пузыре.Как следствие, TEF на кетогенной диете обычно составляет 10%.
Именно здесь мы видим некоторую непосредственно практическую информацию о процессе похудения. После того, как вы используете свой BMR для определения своего TDEE, вы можете быть уверены, что план питания, которому вы следуете, лучше всего подходит для вашей степени расхода энергии и не дает вам слишком много или слишком мало калорий. По крайней мере, графики дадут вам представление о том, каким должен быть ваш целевой вес.
Выбор калькулятора верхнего журнала
В других случаях (например, вы публикуете статью или используете логистическую регрессию) вас могут заставить принять определенный формат.Судя по приложению, эта проблема проясняется очень быстро. Я бы посоветовал эту программу всем, кому нужна помощь с алгеброй.
С другой стороны, опция Google Translate может помочь вам читать на разных языках. Недостаток заключается в том, что существует ограничение на диапазон запросов, которые могут быть выполнены в день каждым пользователем, поэтому визуализатор GPS не может запрашивать у Google все ваши баллы. Google Translate не может переводить все виды документов и не всегда может предоставить вам точный перевод.
КалькуляторIV — это лишь один из самых известных инструментов среди игроков в Pokemon Go, и это основная причина, по которой у нас их уже так много. Всем известно, что труд — лишь одна из самых дорогих составляющих любой работы. Как только они подрастут, я надеюсь, что и эта программа будет им полезна.
Ваша страховка гражданской ответственности также покрывает медицинские выплаты для покрытия расходов людей, случайно пострадавших в вашем доме. Это также поможет снизить ваши счета за электроэнергию.Если у вас есть частные ссуды, вам нечего терять от рефинансирования.
Введите предыдущий год, в котором вы покрывали доход, и сумму этого дохода. Ежемесячные платежи зависят от срока ипотеки и суммы, которую вы можете взять в долг. Помните, что также предлагаются квартальные и годовые платежи.
Если вы установите минус перед числом, вы получите положительный или отрицательный результат в зависимости от того, является ли степень четным или нечетным числом.Цель округления состоит в том, чтобы получить число, с которым намного легче работать. Есть много ресурсов в других местах и здесь, в Calcblog, которые помогут вам научиться эффективно использовать свой калькулятор.
После ввода вышеуказанных данных калькулятор вычислит приблизительное количество действий, которые необходимо выполнить. Калькулятор журнала — это математический инструмент в Интернете, используемый для вычисления значения журнала для заданного числа логарифма, относящегося к заданным или органическим базовым значениям. Калькулятор шансов — важный инструмент для совершения ставок на матчи.
В таких случаях может потребоваться использование графического калькулятора, чтобы помочь найти решение для уравнения. Затем вы используете The Relationship, чтобы преобразовать логарифмическое уравнение в соответствующее экспоненциальное уравнение, после чего вы можете использовать или не использовать калькулятор для определения приблизительного точного вида ответа. Логарифм этого истинного числа будет 4.
Решение уравнений Если нам даны уравнения, содержащие экспоненты или натуральный логарифм, имейте в виду, что вы можете выбрать экспоненту для каждой стороны уравнения, чтобы удалить логарифм, или взять натуральный логарифм от обеих сторон, чтобы исключить экспоненту.Мне очень нравится, насколько проста в использовании и насколько простой кажется алгебра. Типичные логарифмы чрезвычайно полезны для представления очень больших или очень маленьких чисел.
Чтобы вычислить оплату, вам понадобятся десятичные часы. Вы должны иметь возможность разговаривать с тем, кто регулярно занимается вашей учетной записью. Равно 125.
Что такое калькулятор журнала
Извините, этот вопрос может показаться глупым или простым, но я понятия не имею. Так что да, это действительно очень удобно.Вам нужно только поверить нам на слово.
Возможны базовые изменения. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Краткий обзор калькулятора журналаВажной характеристикой этого инструмента для расчета расстояния является то, что он похож на прямую », поэтому путешествия в реальной жизни обычно требуют больших расстояний, но это также может помочь тем, кто должен измерять расстояния вне дорог.Кнопка процента может использоваться для определения доли другого числа. Полезно, если вам не нужен весь набор наворотов, представленных на странице аккумулятора, но все же нужен высокоэффективный калькулятор.
Результаты рейтинга должны быть только исходными случаями и расстояниями. Вы можете использовать калькулятор TDEE, чтобы найти это число, или вычислить его вручную, чтобы найти более конкретный результат. Калькулятор бинго — это инструмент, который поможет вам выбрать правильное количество общих случайных значений, которые будут установлены в квадратах карточек во время введения предприятия.
Вы можете бесплатно просмотреть свой корпоративный и личный кредитные профили на сайте Nav. Какие преимущества вы можете получить от аутсорсинга обработки заработной платы Обработка заработной платы вручную может занять очень много времени. Журналы пробега являются основной частью любого, поскольку они не только позволяют компаниям отслеживать информацию о пробеге своих сотрудников на основе работы, которая может использоваться для возмещения командировочных расходов, но также может использоваться для целей налоговой декларации.
Точно такая же идея сохраняется для разных логарифмов.Например, логарифм с основанием 2 называется двоичным логарифмом, и он популярен в информатике и языках программирования. Если в уравнении используется RMR, воспользуйтесь этим калькулятором RMR, который предоставит вам большее число.
Этот показатель известен как логарифм. Итак, вы обнаружите, что логарифм — это не что иное, как показатель степени. В этом уроке я напомню вам, что такое логарифм.
Если вас беспокоит употребление алкоголя, обратитесь к своему терапевту. Есть много условий, которые не покрываются этими основными рекомендациями.В результате вы уже покрыли килокалорийность ваших повседневных потребностей.
Самая первая программа, которую я купил, разочаровала. Это также позволяет вам наблюдать влияние изменений в поведении сбережений. Для многих домовладельцев линейные ножки — самый простой способ определить ваши требования.
Тем не менее, одним из самых популярных и универсальных вариантов является облицовка стен панелями (что отлично, если у вас ограниченный бюджет) или гипсокартоном, который немного более трудоемкий, но все же недорогой.Выражение — это всего лишь смесь символов со значением или значением. Есть много производителей, которые сейчас производят эти дома, и есть так много вариантов и стилей, из которых вы можете выбирать.
Аргумент по поводу калькулятора журнала
В других случаях (например, вы публикуете статью или используете логистическую регрессию) вас могут заставить принять определенный формат. Очень легко испортиться, когда вы вводите проблему, и вот решение. Я бы посоветовал эту программу всем, кому нужна помощь с алгеброй.
Алгебратор — лучшая программа на свете! NET Core позволяет создавать кроссплатформенные приложения. Похоже, что ваше программное обеспечение предоставляет этот подход к решению проблем в виде простых для понимания средств.
Менее 50 г чистых углеводов в день достаточно для большинства людей, чтобы оставаться в кетозе. Кроме того, вы не должны опускаться ниже 30 г повседневного жира, чтобы избежать образования камней в желчном пузыре. На начальном этапе кетогенной диеты потери азота могут произойти, если ваше ежедневное потребление чистых углеводов чрезвычайно низкое.
Самое важное — убедиться, что соотношение питательных веществ способствует желаемой потере веса и положительно влияет на ваше общее самочувствие. Индекс массы тела просто основан на росте и рассчитывается одинаково как для женщин, так и для мужчин. Во многих идеальных диаграммах веса, которые вы найдете в Интернете, не указано, какие формулы они используют для создания диаграммы веса.
Ключ к успешному вычислению бревен
Процентные ставки по прямым субсидированным займам являются фиксированными и не меняются в течение срока действия займа.Третьи стороны используют множество различных типов кредитных рейтингов и, вероятно, будут использовать другие типы кредитных рейтингов для оценки вашей кредитоспособности. Если у вас есть частные ссуды, вам нечего терять от рефинансирования.
Расчетная сумма погашения и полные выплаченные проценты рассчитываются с использованием предоставленной вами информации. Могут применяться сборы и сборы. Внесение необходимых внутришкольных платежей может снизить общую стоимость кредита.
По поводу калькулятора журнала?
Вам не нужно будет регулировать это в зависимости от частоты тренировок, учтенной в уравнении.Вы можете использовать эту описанную выше процедуру, чтобы изменить формулу, чтобы зафиксировать другие желаемые количества. Самый первый шаг в регрессии — создание диаграммы рассеяния.
Калькулятор жизни, смерти и журнала
Как только вы окажетесь на нужной странице, вы можете начать вводить свой вопрос по алгебре. Вы можете использовать калькулятор для своего сайта при условии, что вы обещаете следовать нашим условиям. Калькулятор не собирает личную информацию или идентификаторы.
Лучшие варианты калькулятора журналов
Ряд сходится значительно медленнее, но попробуйте другой способ.Определение этого значения необязательно, но если вы хотите согласованного результата, указать его — отличная идея. Например, чтобы получить 16, важно возвести два в четвертую степень.
Калькулятор «Война против журнала»
РядМаклорена нельзя использовать для определения ряда для logx, поэтому необходимо найти другой метод. Есть много других альтернатив. Опция настроек в правом верхнем углу позволит вам скорректировать настройки графика.
Затем есть переключатель для каждой математической операции.Эти функции предлагаются этим модулем. На него не следует полагаться при определении финансовых данных.
Калькулятор самых заметных журналов
Калькулятор журнала может быть интересен для всех
Конечным результатом является уравнение регрессии, которое можно использовать для прогнозирования данных. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Давайте взглянем на характеристики Desmos.Выражение — это всего лишь смесь символов со значением или значением. Вам также необходимо знать размер плиток, которые вы используете для своего дела.
Если вы думаете об использовании чисел с плавающей запятой для помощи с целочисленной арифметикой, вам нужно быть осторожным. С этого момента вы можете определить, идеально ли уравнение подходит для этих данных. Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
Затем есть переключатель для каждой математической операции.Эти функции предлагаются этим модулем. Предполагается, что все данные будут храниться в основном индексе.
От честности до истины на бревенчатом калькуляторе
Действительно, если вы обратитесь к старым и пыльным книгам любой хорошей университетской библиотеки, вы должны иметь возможность получить эти предыдущие книги математических таблиц. Кристально ясное понимание суммы, которую вам нужно будет заплатить EMI, позволит вам принять обоснованное решение. Чтобы упростить задачу, мы должны помнить три вещи.
Основы калькулятора журналов
Эти числа указывают только на относительную величину ожидаемого изменения pH. Это также называется потерей на трение. Пересчитывайте макрокомпоненты один раз в месяц!
Все о калькуляторе журнала
Эти задачи иллюстрируют процедуру логарифмического дифференцирования. Следовательно, важно, чтобы вы осознавали их условия при регистрации для них. В математике регрессия — лишь одна из основных тем статистики.
Вот справочник по информации, которую вас просят ввести в калькулятор. Сегодняшняя тема использует журнальные таблицы. Наш калькулятор естественного логарифма удобен для пользователя, потому что для того, чтобы вычислить логарифм любого числа, все, что вам нужно сделать, это ввести число и нажать «вычислить».
Ложь, которую вам рассказали о калькуляторе журналов
Эффективная годовая ставка — это ставка, которая действительно выплачивается после каждого начисления сложных процентов. Вы можете получить оценку затрат, чтобы иметь возможность составить бюджет.Это значение зависит от количества периодов, поэтому, например, если вы ввели несколько лет, скорость будет годовой, а если вы ввели много дней, это будет дневной темп.
Укажите общее количество чистых углеводов в день, которое вы хотите потреблять. Нет запрещенных продуктов при условии, что они соответствуют вашему ежедневному количеству макроэлементов. Как следствие, TEF на кетогенной диете обычно составляет 10%.
Самое важное — убедиться, что соотношение питательных веществ способствует желаемой потере веса и положительно влияет на ваше общее самочувствие.Индекс массы тела просто основан на росте и рассчитывается одинаково как для женщин, так и для мужчин. По крайней мере, графики дадут вам представление о том, каким должен быть ваш целевой вес.
Что такого увлекательного в калькуляторе журналов?
Совместимость с различными инструментами В некоторых других математических компьютерных программах используются процедуры, очень похожие на режим журнала по умолчанию. Это довольно удобно, и, если вы правильно укажете вопрос, проблем не возникнет.Это программное обеспечение действительно облегчило мне жизнь в том, что касается выполнения домашних заданий по алгебре.
Дополнительная поддержка доступна, когда она вам потребуется. Мы используем файлы cookie, чтобы обеспечить вам удобную, приятную и безопасную работу с этим сайтом, а также предложить актуальную и выгодную рекламу от Google. Google Translate не может переводить все виды документов и не всегда может предоставить вам точный перевод.
Калькулятор типа журнала
Программа выглядит и работает, как и обычный MT4, по крайней мере, кривая обучения проста и удобна для пользователя.Кроме того, есть ряд других факторов, которые влияют на результаты ультрамарафона, например, проблемы со снаряжением, проблемы с питанием и экологические недуги. Так что, если вы планируете автомобильное путешествие и вам нужно знать расстояние между городами США, вы находитесь в подходящем месте.
Вы должны проработать ряд модулей, чтобы иметь возможность оценить свой пенсионный доход из нескольких источников и сравнить их с вашим целевым доходом. Могут применяться государственные ограничения, и может потребоваться дополнительное обучение, чтобы стать составителем налоговой декларации.Федеральное правительство не платит проценты в периоды снисходительности.
Расчетная сумма погашения и полные выплаченные проценты рассчитываются с использованием предоставленной вами информации. Когда вы решите закрыть кредитную карту, убедитесь, что все платежи произведены и нет никаких незавершенных платежей. Внесение внутришкольных платежей также может помочь уменьшить количество начисленных процентов и еще больше снизить общую стоимость вашей ссуды.
Каждый ученик может без проблем управлять этим калькулятором и решать столько задач, сколько хочет.Через месяц или два у вас, вероятно, будет достаточно данных для создания диаграммы пробега. Начальный курс и расстояние рассчитываются в зависимости от прямой линии, соединяющей 2 точки.
Наряду с системой согласования ставок, калькулятор ставок на совпадение стал важнейшим инструментом для зарабатывания денег в Интернете. Существует много типов калькуляторов, но большинство калькуляторов имеют одни и те же стандартные клавиши, которые позволяют пользователям выполнять ряд вычислений. Калькулятор бинго — это инструмент, который поможет вам выбрать правильное количество общих случайных значений, которые будут установлены в квадратах карточек во время введения предприятия.
Есть много программ по алгебре. Это может помочь вам запомнить мелодическую математику вместо формулы. Здесь можно найти любую формулу, которая может понадобиться вам при выполнении математических заданий.
Этот показатель известен как логарифм. Итак, вы обнаружите, что логарифм — это не что иное, как показатель степени. В этом уроке я напомню вам, что такое логарифм.
Калькулятор журналов и калькулятор журналов — идеальное сочетание
По окончании пробного периода вы имеете право на дополнительные 20 долларов почтовых расходов.Вы должны иметь возможность разговаривать с тем, кто регулярно занимается вашей учетной записью. Равно 125.
Калькулятор дискретного логарифма
Это веб-приложение вычисляет дискретные логарифмы.
Задача дискретного логарифмирования состоит в том, чтобы найти показатель степени в выражении Основание Показатель степени = Степень (модуль Модуль ). или ** для возведения в степень
Вы можете использовать префикс 0x для шестнадцатеричных чисел, например 0x38 равно 56.
Символ возведения в степень отсутствует на некоторых мобильных устройствах, поэтому две звездочки ** можно ввести в качестве оператора возведения в степень.
Пример: найдите число n такое, что 7 n ≡ 23 (мод. 43241).
Введите 7 в поле ввода Base, 23 в поле ввода Power и 43241 в поле ввода Mod. Затем нажмите кнопку «Дискретный логарифм».
Результат 3360 + 3930 k. В качестве проверки вы можете вычислить 7 3360 23 (мод. 43241) и 7 3930 ≡ 1 (мод. 43241).
Исходный код
Вы можете загрузить исходный код текущей программы и старый апплет факторизации полинома суммы с GitHub. Обратите внимание, что исходный код написан на языке C, и вам нужна среда Emscripten для создания Javascript.
Автор Дарио Альперн. Последнее обновление 15 июля 2021 г.
Исчисление I — логарифмические функции
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-8: Логарифмические функции
В этом разделе мы рассмотрим функцию, которая связана с экспоненциальными функциями, которые мы рассмотрели в предыдущем разделе.В этом разделе мы рассмотрим логарифмы. Логарифмы — одна из функций, которых студенты больше всего боятся. Основная причина этого, похоже, в том, что им просто никогда не приходилось с ними работать. Как только они начинают работать с ними, ученики начинают понимать, что они не так плохи, как им казалось вначале.
Начнем с \ (b> 0 \), \ (b \ ne 1 \), как и в предыдущем разделе. Тогда у нас
\ [y = {\ log _b} x \ hspace {0.5in} {\ mbox {эквивалентно}} \ hspace {0.y} \]Первая называется логарифмической формой, а вторая — экспоненциальной формой. Помнить об этой эквивалентности — ключ к оценке логарифмов. Число \ (b \) называется основанием.
Давайте сделаем несколько быстрых оценок.
Пример 1 Без калькулятора укажите точное значение каждого из следующих логарифмов.- \ ({\ log _2} 16 \)
- \ ({\ log _4} 16 \)
- \ ({\ log _5} 625 \)
- \ ({\ log _9} \ frac {1} {{531441}} \)
- \ ({\ log _ {\ frac {1} {6}}} 36 \)
- \ ({\ log _ {\ frac {3} {2}}} \ frac {{27}} {8} \)
Чтобы быстро вычислить логарифмы, проще всего преобразовать логарифм в экспоненциальную форму.3} = \ frac {{27}} {8} \]
Есть несколько специальных логарифмов, которые встречаются во многих местах. Это,
\ [\ begin {align *} \ ln x & = {\ log _ {\ bf {e}}} x \ hspace {0.5in} {\ mbox {Этот журнал называется натуральным логарифмом}} \\ \ log x & = {\ log _ {10}} x \ hspace {0.5in} {\ mbox {Этот журнал называется десятичным логарифмом}} \ end {align *} \]В натуральном логарифме основание e — это то же число, что и в натуральном экспоненциальном логарифме, который мы видели в предыдущем разделе.Вот набросок обоих этих логарифмов.
Из этого графика мы можем получить пару очень хороших свойств натурального логарифма, которые мы будем многократно использовать в этом и последующих курсах по математике.
\ [\ begin {array} {l} \ ln x \ to \ infty {\ mbox {as}} x \ to \ infty \\ \ ln x \ to — \ infty {\ mbox {as}} x \ to 0 , \, \, x> 0 \ end {array} \]Давайте взглянем на еще пару логарифмических вычислений. Некоторые из них имеют дело с натуральным или десятичным логарифмом, а некоторые — нет.
Пример 2 Без калькулятора укажите точное значение каждого из следующих логарифмов.- \ (\ ln \ sqrt [3] {{\ bf {e}}} \)
- \ (\ лог 1000 \)
- \ ({\ log _ {16}} 16 \)
- \ ({\ log _ {23}} 1 \)
- \ ({\ log _2} \ sqrt [7] {{32}} \)
Они работают точно так же, как и в предыдущем примере, поэтому мы не будем вдаваться в подробности.
a \ (\ ln \ sqrt [3] {{\ bf {e}}} \) Показать решение\ [\ ln \ sqrt [3] {{\ bf {e}}} = \ frac {1} {3} \ hspace {0.{\ frac {5} {7}}} \]
Этот последний набор примеров приводит нас к некоторым основным свойствам логарифмов.
Недвижимость
- Область определения функции логарифма — \ (\ left ({0, \ infty} \ right) \). Другими словами, мы можем подставлять только положительные числа в логарифм! Мы не можем подставлять ноль или отрицательное число.
- Диапазон функции логарифмирования равен \ (\ left ({- \ infty, \ infty} \ right) \). {{{\ log} _b} x}} = x \)
Последние два свойства будут особенно полезны в следующем разделе.2}} \ right) — 3 \ log \ left ({x — y} \ right) \ end {align *} \]
Вы можете использовать свойство 9 для второго члена, потому что ВСЕ член было возведено в 3, но в первом логарифме возведены в квадрат только отдельные члены, а не член в целом, поэтому 2 должны оставаться на своем месте!
Последняя тема, которую нам нужно рассмотреть в этом разделе, — это изменение формулы основания для логарифмов. Изменение базовой формулы:
\ [{\ log _b} x = \ frac {{{{\ log} _a} x}} {{{{{\ log} _a} b}} \]Это наиболее общее изменение базовой формулы, которое преобразует базовый \ (b \) в базовый \ (a \).Однако обычная причина использования формулы изменения базы состоит в том, чтобы вычислить значение логарифма, которое находится в базе, с которой вам нелегко справиться. Использование формулы изменения базовой означает, что вы можете записать логарифм в терминах логарифма, с которым вы можете иметь дело. Двумя наиболее распространенными изменениями базовых формул являются
. \ [{\ log _b} x = \ frac {{\ ln x}} {{\ ln b}} \ hspace {0,5 дюйма} {\ rm {and}} \ hspace {0,5 дюйма} {\ rm {lo} } {{\ rm {g}} _ {\ rm {b}}} x = \ frac {{\ log x}} {{\ log b}} \]На самом деле, часто вы увидите одно или другое в списке как «Смена базовой формулы»!
В первой части этого раздела мы вычислили значение нескольких логарифмов, но мы могли бы сделать это без изменения базовой формулы, потому что все аргументы могли быть записаны в терминах основания в степень.2} = 49 \]
Однако это работает только потому, что 49 можно записать как степень 7! Нам потребуется изменение базовой формулы для вычисления \ ({\ log _7} 50 \).
\ [{\ log _7} 50 = \ frac {{\ ln 50}} {{\ ln 7}} = \ frac {{3.300543}} {{1.945ИЛИ
\ [{\ log _7} 50 = \ frac {{\ log 50}} {{\ log 7}} = \ frac {{1.69897000434}} {{0.845098040014}} = 2.0103821378 \]Итак, не имеет значения, что мы используем, мы получим один и тот же ответ независимо от логарифма, который мы используем при изменении базовой формулы.
Также обратите внимание, что мы могли бы использовать изменение базовой формулы на \ ({\ log _7} 49 \), если бы захотели.
\ [{\ log _7} 49 = \ frac {{\ ln 49}} {{\ ln 7}} = \ frac {{3.8Однако это большая работа и, вероятно, не лучший способ справиться с этим.
Итак, в этом разделе мы увидели, как работают логарифмы, и рассмотрели некоторые свойства логарифмов. Время от времени мы будем сталкиваться с логарифмами, поэтому убедитесь, что вы справитесь с ними, когда мы с ними столкнемся.
Калькулятор распространения ошибки(онлайн-инструмент для любой формулы)
Калькулятор распространения ошибки (онлайн-инструмент для любой формулы)Этот инструмент позволяет определять неопределенность (или ошибку) любого математического выражения, которое содержит физические величины с неопределенностями. Он следует правилам распространения ошибки по Гауссу: Если f является функцией независимых переменных X и Y, записанных как f (X, Y), то неопределенность в f получается путем взятия частных производных от f по каждой переменной, умножения на неопределенность в этой переменной, и сложение этих отдельных членов в квадратуре.
Используйте «.» в виде десятичного знака: 1,234, а не 1,234.
Числовая стабильность поддерживается для входных значений в диапазоне от 1e-5 до 1e5 (см. Раздел «Примечания» ниже).Инструкции
- Введите действительную формулу, используя функции, перечисленные внизу этой страницы.
- В разделе «Количества с ошибками» укажите все переменные, которые появляются в формуле. Использовать «.» как десятичный знак, а не «,».
- Щелкните «Оценить», чтобы получить результат вместе с его абсолютной и относительной погрешностью.
Пример
| Формула: log (a) + (b * pow (c, 2)) * sin (c) с переменными a, b, c Точная погрешность (рассчитывается аналитически): | 5
Проверка с помощью Mathematica
Банкноты
Этот инструмент основан на числовых методах .» или «**» вместо «в степени».Доступны следующие математические методы, которые можно использовать в поле формулы:
| Метод | Описание |
|---|---|
| acos (x) | Возвращает арккосинус x в радианах |
| asin (x) | Возвращает арксинус x в радианах |
| атан (х) | Возвращает арктангенс x как числовое значение между -PI / 2 и PI / 2 радиан |
| cos (x) | Возвращает косинус x (x в радианах) |
| эксп. (X) | Возвращает значение E x |
| журнал (x) | Возвращает натуральный логарифм (основание E) x | .
| pow (x, y) | Возвращает значение x в степени y |
| sin (x) | Возвращает синус x (x в радианах) |
| sqrt (x) | Возвращает квадратный корень из x | .
| желто-коричневый (x) | Возвращает тангенс угла | .
Константа Эйлера и Pi обозначаются буквами «E» и «PI» соответственно.
Посетителей:
Калькулятор общего журнала log (x) base 10 Log10 Calculator
Common Log Calculator log (x) base 10 Log10 CalculatorКалькулятор десятичного логарифма находит результат функции логарифма по основанию 10. Вычислите логарифм по основанию 10 числа.
Примеры десятичных логарифмов
Используя логарифм идентификатора продукта, найдите общий журнал из 120:
журнал (120) = журнал (100 × 1.2) журнал (120) = журнал (100) + журнал (1,2) журнал (120) = 2 + 0746 = 2,0746
Используя логарифм степенного тождества, найдите общий журнал из 10 6 :
журнал (10 6 ) = 6 × журнал (10) журнал (10 6 ) = 6 × 1 = 6
Общий лог по базе 10 таблиц значений
Список таблиц значений функций общего журнала, логическая основа 10 чисел.
| log 10 (x) | Обозначение | Значение | |||
|---|---|---|---|---|---|
| log 10 (1) | log (1) | 0 | |||
| log24 10 (2) (2) | 0.30103 | ||||
| лог 10 (3) | лог (3) | 0,477121 | |||
| лог 10 (4) | лог (4) | 0.600006 9107 | лог (5) | 0,69897 | |
| лог 10 (6) | лог (6) | 0,778151 | |||
| лог 10 (7) | лог (7) | лог (7) 0,845098 | |||
| лог 10 (8) | лог (8) | 0. | |||
| log 10 (9) | log (9) | 0.954243 | |||
| log 10 (10) | log (10) | 1 | |||
| лог (11) | 1.041393 | ||||
| лог 10 (12) | лог (12) | 1.079181 | |||
| лог 10 (13) | лог (13) | лог (13) | лог 1,113943 | ||
| лог 10 (14) | лог (14) | 1.146128 | |||
| лог 10 (15) | лог (15) | 1,176091 | |||
| лог 10 (16) | лог (16) | 1.20412 9107 | лог (17) | 1.230449 | |
| лог 10 (18) | лог (18) | 1.255273 | |||
| лог 10 (19) | лог (19) | лог (19) | лог 1,278754 | ||
| лог 10 (20) | лог (20) | 1.30103 | |||
| лог 10 (21) | лог (21) | 1,322219 | |||
| лог 10 (22) | лог (22) | 1,340005 9107 | лог (23) | 1,361728 | |
| лог 10 (24) | лог (24) | 1,380211 | |||
| лог 10 (25) | лог (25) | лог 1,39794 | |||
| лог 10 (26) | лог (26) | 1.414973 | |||
| лог 10 (27) | лог (27) | 1,431364 | |||
| лог 10 (28) | лог (28) | 1,447158 9107 | 1,447158 9107 29) | лог (29) | 1.462398 |
| лог 10 (30) | лог (30) | 1,477121 | |||
| лог 10 (31) | лог (31) | лог 1.4 | |||
| лог 10 (32) | лог (32) | 1.50515 | |||
| лог 10 (33) | лог (33) | 1.518514 | |||
| лог 10 (34) | лог (34) | 1.531479 9101 | лог (35) | 1.544068 | |
| лог 10 (36) | лог (36) | 1.556303 | |||
| лог 10 (37) | лог (37) | лог (37) | лог 1,568202 | ||
| лог 10 (38) | лог (38) | 1.579784 | |||
| лог 10 (39) | лог (39) | 1,5 | |||
| лог 10 (40) | лог (40) | 1.600006 9107 | лог (41) | 1,612784 | |
| лог 10 (42) | лог (42) | 1,623249 | |||
| лог 10 (43) | лог (43) | лог 1.633468 | |||
| лог 10 (44) | лог (44) | 1.643453 | |||
| лог 10 (45) | лог (45) | 1,653213 | |||
| лог 10 (46) | лог (46) | 1.662758 9107 | лог (47) | 1.672098 | |
| лог 10 (48) | лог (48) | 1.681241 | |||
| лог 10 (49) | лог (49) | лог 1,6 | |||
| лог 10 (50) | лог (50) | 1.69897 | |||
| лог 10 (51) | лог (51) | 1.70757 | |||
| лог 10 (52) | лог (52) | 1.716003 9107 | лог (53) | 1,724276 | |
| лог 10 (54) | лог (54) | 1,732394 | |||
| лог 10 (55) | лог (55) | лог 1,740363 | |||
| лог 10 (56) | лог (56) | 1.748188 | |||
| лог 10 (57) | лог (57) | 1,755875 | |||
| лог 10 (58) | лог (58) | 1.763428 9107 | лог (59) | 1,770852 | |
| лог 10 (60) | лог (60) | 1.778151 | |||
| лог 10 (61) | лог 1,78533 | ||||
| лог 10 (62) | лог (62) | 1.7 | |||
| лог 10 (63) | лог (63) | 1,799341 | |||
| лог 10 (64) | лог (64) | 1.8000018 9107 | журнал (65) | 1,812913 | |
| журнал 10 (66) | журнал (66) | 1,819544 | |||
| журнал 10 (67) | журнал ( 1.826075 | ||||
| лог 10 (68) | лог (68) | 1.832509 | |||
| лог 10 (69) | лог (69) | 1,838849 | |||
| лог 10 (70) | лог (70) | 1.845098 9107 | лог (71) | 1.851258 | |
| лог 10 (72) | лог (72) | 1.857332 | |||
| лог 10 (73) | лог (72) | лог 1,863323 | |||
| журнал 10 (74) | журнал (74) | 1.869232 | |||
| лог 10 (75) | лог (75) | 1.875061 | |||
| лог 10 (76) | лог (76) | 1.880814 9107 | лог (77) | 1.886491 | |
| лог 10 (78) | лог (78) | 1.8 | |||
| лог 10 (79) | лог (79) | лог ( 1,897627 | |||
| лог 10 (80) | лог (80) | 1. | |||
| лог 10 (81) | лог (81) | 1. | |||
| лог 10 (82) | лог (82) | 1. | 4 9107 | лог (83) | 1. | 8 |
| лог 10 (84) | лог (84) | 1. | 9 | ||
| лог 10 (85) | лог 1, | ||||
| лог 10 (86) | лог (86) | 1. | 8 | ||
| лог 10 (87) | лог (87) | 1. | 9 | ||
| лог 10 (88) | лог (88) | 1.944483 9107 | лог (89) | 1.94939 | |
| лог 10 (90) | лог (90) | 1.954243 | |||
| лог 10 (91) | лог (91) | лог (91) | лог 1.959041 | ||
| лог 10 (92) | лог (92) | 1.963788 | |||
| лог 10 (93) | лог (93) | 1.968483 | |||
| лог 10 (94) | лог (94) | 0 1.973128 9101лог (95) | 1.977724 | ||
| лог 10 (96) | лог (96) | 1.982271 | |||
| лог 10 (97) | лог (97) | лог 1.986772 | |||
| лог 10 (98) | лог (98) | 1.9 | |||
| журнал 10 (99) | журнал (99) | 1.995635 |
| журнал 10 (x) | Обозначение | Значение | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| журнал 10 (100) | журнал (100) | 2 | |||||||||||||
| журнал24 10 (200) (200) | 2.30103 | ||||||||||||||
| log 10 (300) | log (300) | 2.477121 | |||||||||||||
| log 10 (400) | log (400) | 2.60206 | |||||||||||||
| лог 10 (500) | лог (500) | 2.69897 | |||||||||||||
| лог 10 (600) | лог (600) | 2.778151 9107 | журнал (700) | 2,845098 | |||||||||||
| журнал 10 (800) | журнал (800) | 2, | |||||||||||||
| журнал 10 (900) | журнал ( | журнал) 2.954243 | |||||||||||||
| log 10 (1000) | log (1000) | 3 | |||||||||||||
| log 10 (1100) | log (1100) | 3.041393 | |||||||||||||
| лог 10 (1200) | лог (1200) | 3.079181 | |||||||||||||
| лог 10 (1300) | лог (1300) | 3,113943 9107 | 3,113943 | 1400)лог (1400) | 3,146128 | ||||||||||
| лог 10 (1500) | лог (1500) | 3,176091 | |||||||||||||
| лог 10 (1600) | лог (1600) | лог ( 3.20412 | |||||||||||||
| лог 10 (1700) | лог (1700) | 3.230449 | |||||||||||||
| журнал 10 (1800) | журнал (1800) | 3,255273 | |||||||||||||
| журнал 10 (1900) | журнал (1900) | 3,2780003 | 3,2780003 901 2000) | лог (2000) | 3.30103 | ||||||||||
| лог 10 (2100) | лог (2100) | 3.322219 | |||||||||||||
| лог 10 (2200) | 901 3.342423|||||||||||||||
| лог 10 (2300) | лог (2300) | 3.361728 | |||||||||||||
| лог 10 (2400) | лог (2400) | 3.380211 | |||||||||||||
| лог 10 (2500) | лог (2500) | 3,39794 9125 | лог (2600) | 3,414973 | |||||||||||
| лог 10 (2700) | лог (2700) | 3,431364 | |||||||||||||
| лог 10 12 (2800) | 2800 3.447158|||||||||||||||
| лог 10 (2900) | лог (2900) | 3.462398 | |||||||||||||
| лог 10 (3000) | лог (3000) | 3,477121 | |||||||||||||
| лог 10 (3100) | лог (3100) | 3,4 | 2 91073,4 9107 | 3200) | лог (3200) | 3,50515 | |||||||||
| лог 10 (3300) | лог (3300) | 3,518514 | |||||||||||||
| лог 10 12 (3400) | 3.531479|||||||||||||||
| лог 10 (3500) | лог (3500) | 3.544068 | |||||||||||||
| лог 10 (3600) | лог (3600) | 3.556303 | |||||||||||||
| лог 10 (3700) | лог (3700) | 3.568123 | 3.568123 | 3800)лог (3800) | 3.579784 | ||||||||||
| лог 10 (3900) | лог (3900) | 3.5 | |||||||||||||
| лог 10 (400012) | 3.60206|||||||||||||||
| лог 10 (4100) | лог (4100) | 3.612784 | |||||||||||||
| лог 10 (4200) | лог (4200) | 3,623249 | |||||||||||||
| лог 10 (4300) | лог (4300) | 3,63123 9107 9107 4400) | лог (4400) | 3.643453 | |||||||||||
| лог 10 (4500) | лог (4500) | 3.653213 | |||||||||||||
| лог 10 12 (4612) | 3.662758|||||||||||||||
| лог 10 (4700) | лог (4700) | 3.672098 | |||||||||||||
| журнал 10 (4800) | журнал (4800) | 3,681241 | |||||||||||||
| журнал 10 (4900) | журнал (4900) | 3,6 | |||||||||||||
| 3,6 | |||||||||||||||
| лог (5000) | 3.69897 | ||||||||||||||
| лог 10 (5100) | лог (5100) | 3.70757 | |||||||||||||
| лог 10 (5200) | 00 901 3,716003|||||||||||||||
| журнал 10 (5300) | журнал (5300) | 3.724276 | |||||||||||||
| лог 10 (5400) | лог (5400) | 3,732394 | |||||||||||||
| лог 10 (5500) | лог (5500) | 3,7401000 |
| лог (6800) | 3.832509 | ||||
| лог 10 (6900) | лог (6900) | 3.838849 | |||
| лог 10 (7000) 9011 | 9011 3.845098|||||
| лог 10 (7100) | лог (7100) | 3.851258 | |||
| лог 10 (7200) | лог (7200) | 3.857332 | |||
| лог 10 (7300) | лог (7300) | 3.810323 9011 7400) | лог (7400) | 3.869232 | |
| лог 10 (7500) | лог (7500) | 3.875061 | |||
| лог 10 (7600) | 7600 3.880814|||||
| лог 10 (7700) | лог (7700) | 3.886491 | |||
| журнал 10 (7800) | журнал (7800) | 3,8 | |||
| журнал 10 (7900) | журнал (7900) | 3,810123 9107 | 3,810123 8000) | лог (8000) | 3. |
| лог 10 (8100) | лог (8100) | 3. | |||
| лог 1021 901 | 3.4 | ||||
| лог 10 (8300) | лог (8300) | 3. | 8 | ||
| лог 10 (8400) | лог (8400) | 3, | 9 | ||
| лог 10 (8500) | лог (8500) | 9 10121 | лог (8500) | 7999 8600) | журнал (8600) | 3. | 8 |
| журнал 10 (8700) | журнал (8700) | 3. | 9 | ||
| журнал 10 (880012) 9011 9011 9011 3.944483 | |||||
| журнал 10 (8900) | журнал (8900) | 3.94939 | |||
| лог 10 (9000) | лог (9000) | 3,954243 | |||
| лог 10 (9100) | лог (9100) | 4,95123 | 4,95123 9011 9200) | лог (9200) | 3.963788 |
| лог 10 (9300) | лог (9300) | 3.968483 | |||
| лог 10 ( | ) 3.973128|||||
| журнал 10 (9500) | журнал (9500) | 3.977724 | |||
| лог 10 (9600) | лог (9600) | 3.982271 | |||
| лог 10 (9700) | лог (9700) | 3,98123 9011 9800) | лог (9800) | 3.9 | |
| лог 10 (9900) | лог (9900) | 3.995635 |
| log 10 (x) | Обозначение | Значение | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| log 10 (1000) | log (1000) | 3 | ||||||||||||||||||||||
| log24 10 (2000) (2000) | 3.30103 | |||||||||||||||||||||||
| лог 10 (3000) | лог (3000) | 3,477121 | ||||||||||||||||||||||
| лог 10 (4000) | лог (4000) | 3.600006 9107 | log (5000) | 3.69897 | ||||||||||||||||||||
| log 10 (6000) | log (6000) | 3.778151 | ||||||||||||||||||||||
| log 10 (7000) | 3.845098 | |||||||||||||||||||||||
| лог 10 (8000) | лог (8000) | 3. | ||||||||||||||||||||||
| журнал 10 (9000) | журнал (9000) | 3.954243 | ||||||||||||||||||||||
| журнал 10 (10000) | журнал (10000) | 0 4лог (11000) | 4.041393 | |||||||||||||||||||||
| лог 10 (12000) | лог (12000) | 4.079181 | ||||||||||||||||||||||
| лог 10 12 (13000) | 4,113943||||||||||||||||||||||||
| журнал 10 (14000) | журнал (14000) | 4.146128 | ||||||||||||||||||||||
| журнал 10 (15000) | журнал (15000) | 4.176091 | ||||||||||||||||||||||
| журнал 10 (16000) | журнал (16000) | 4.20103000 | 4.20412 9011 17000) | лог (17000) | 4.230449 | |||||||||||||||||||
| лог 10 (18000) | лог (18000) | 4.255273 | ||||||||||||||||||||||
| лог 10 12 (19000) | 4,278754||||||||||||||||||||||||
| журнал 10 (20000) | журнал (20000) | 4.30103 | ||||||||||||||||||||||
| журнал 10 (21000) | журнал (21000) | 4,322219 | ||||||||||||||||||||||
| журнал 10 (22000) | журнал (22000) | 4,310123 9107 | 4,310123 23000) | лог (23000) | 4.361728 | |||||||||||||||||||
| лог 10 (24000) | лог (24000) | 4.380211 | ||||||||||||||||||||||
| лог 10 12 (2512) | 4.39794||||||||||||||||||||||||
| лог 10 (26000) | лог (26000) | 4.414973 | ||||||||||||||||||||||
| журнал 10 (27000) | журнал (27000) | 4,431364 | ||||||||||||||||||||||
| журнал 10 (28000) | журнал (28000) | 4,410158 | 4.410158 9011 29000) | лог (29000) | 4.462398 | |||||||||||||||||||
| лог 10 (30000) | лог (30000) | 4.477121 | ||||||||||||||||||||||
| лог 10 12 (3112) | 4.4||||||||||||||||||||||||
| журнал 10 (32000) | журнал (32000) | 4.50515 | ||||||||||||||||||||||
| журнал 10 (33000) | журнал (33000) | 4,518514 | ||||||||||||||||||||||
| журнал 10 (34000) | журнал (34000) | 4.53101479 | 4.53101479 | 35000)лог (35000) | 4.544068 | |||||||||||||||||||
| лог 10 (36000) | лог (36000) | 4.556303 | ||||||||||||||||||||||
| лог 10 12 (3712) | 4,568202||||||||||||||||||||||||
| журнал 10 (38000) | журнал (38000) | 4.579784 | ||||||||||||||||||||||
| журнал 10 (39000) | журнал (39000) | 4,5 | ||||||||||||||||||||||
| журнал 10 (40000) | журнал (40000) | 4.6012206 | 4,6012206 | 41000)журнал (41000) | 4,612784 | |||||||||||||||||||
| журнал 10 (42000) | журнал (42000) | 4,623249 | ||||||||||||||||||||||
| журнал 10 12 (4312) | 4.633468||||||||||||||||||||||||
| лог 10 (44000) | лог (44000) | 4.643453 | ||||||||||||||||||||||
| журнал 10 (45000) | журнал (45000) | 4.653213 | ||||||||||||||||||||||
| журнал 10 (46000) | журнал (46000) | 4,662123 | ||||||||||||||||||||||
| 4,66212758 | 47000)лог (47000) | 4.672098 | ||||||||||||||||||||||
| лог 10 (48000) | лог (48000) | 4.681241 | ||||||||||||||||||||||
| лог 10 12 (4 ) | 4.6||||||||||||||||||||||||
| лог 10 (50000) | лог (50000) | 4.69897 | ||||||||||||||||||||||
| лог 10 (51000) | лог (51000) | 4,70757 | ||||||||||||||||||||||
| лог 10 (52000) | лог (52000) | 4,716003 | 4,716003 | 53000)журнал (53000) | 4,724276 | |||||||||||||||||||
| журнал 10 (54000) | журнал (54000) | 4,732394 | ||||||||||||||||||||||
| журнал 10 12 (5512) | 4,740363||||||||||||||||||||||||
| журнал 10 (56000) | журнал (56000) | 4.748188 | ||||||||||||||||||||||
| журнал 10 (57000) | журнал (57000) | 4,755875 | ||||||||||||||||||||||
| журнал 10 (58000) | журнал (58000) | 4,76123 9103 | 4,763428 9011 59000) | лог (59000) | 4,770852 | |||||||||||||||||||
| лог 10 (60000) | лог (60000) | 4,778151 | ||||||||||||||||||||||
| лог 10 12 (6112) | 4,78533||||||||||||||||||||||||
| журнал 10 (62000) | журнал (62000) | 4.7 | ||||||||||||||||||||||
| журнал 10 (63000) | журнал (63000) | 4,799341 | ||||||||||||||||||||||
| журнал 10 (64000) | журнал (64000) | 4.8012318 | 4,8012318 65000) | журнал (65000) | 4,812913 | |||||||||||||||||||
| журнал 10 (66000) | журнал (66000) | 4,819544 | ||||||||||||||||||||||
| журнал 10 12 (6712) | 4.826075||||||||||||||||||||||||
| лог 10 (68000) | лог (68000) | 4.832509 | ||||||||||||||||||||||
| log 10 (69000) | log (69000) | 4.838849 | ||||||||||||||||||||||
| log 10 (70000) | log (70000) | 4,845098 9011 71000) | журнал (71000) | 4,851258 | ||||||||||||||||||||
| журнал 10 (72000) | журнал (72000) | 4,857332 | ||||||||||||||||||||||
| журнал 73 10 12 (73000) | 4.863323||||||||||||||||||||||||
| журнал 10 (74000) | журнал (74000) | 4.869232 | ||||||||||||||||||||||
| журнал 10 (75000) | журнал (75000) | 4,875061 | ||||||||||||||||||||||
| журнал 10 (76000) | журнал (76000) | 14 | 14 9011 77000) | журнал (77000) | 4,886491 | |||||||||||||||||||
| журнал 10 (78000) | журнал (78000) | 4,8 | ||||||||||||||||||||||
| журнал 10 12 (7912) | 4.897627||||||||||||||||||||||||
| лог 10 (80000) | лог (80000) | 4. | ||||||||||||||||||||||
| журнал 10 (81000) | журнал (81000) | 4. | ||||||||||||||||||||||
| журнал 10 (82000) | журнал (82000) | 4, | 4 | 4, | 4 9011 83000) | журнал (83000) | 4, | 8 | ||||||||||||||||
| журнал 10 (84000) | журнал (84000) | 4, | 9 | |||||||||||||||||||||
| журнал 10 12 (8512) | 4.||||||||||||||||||||||||
| лог 10 (86000) | лог (86000) | 4. | 8 | |||||||||||||||||||||
| лог 10 (87000) | лог (87000) | 4. | 9 | |||||||||||||||||||||
| лог 10 (88000) | лог (88000) | 4,
|


 Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно.
Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно. Поэтому в таких случаях используют так называемые онлайн-калькуляторы.
Поэтому в таких случаях используют так называемые онлайн-калькуляторы.