Квадрат суммы
Квадрат суммыНавигация по странице:
- Квадрат суммы — определение
- Вывод формулы квадрата суммы
- Применение формулы квадрата суммы
- Геометрическая интерпретация квадрата суммы
- Примеры задач на применение формулы квадрата суммы
Определение.
Квадрат суммы двух выражений равен квадрату первого, плюс удвоенное произведение первого и второго, плюс квадрат второго:
Вывод формулы квадрата суммы
Для доказательства справедливости формулы квадрата суммы достаточно перемножить выражения раскрыв скобки:
Применение формулы квадрата суммы
Формулу квадрата суммы удобно использовать:
- для раскрытия скобок
- для упрощения выражений
- для вычисления квадратов больших чисел, не используя калькулятор или умножение в столбик
Геометрическая интерпретация
Формулу квадрата суммы двух положительных чисел a и b можно изобразить геометрически
Рассмотрим квадрат со стороной (a + b), его площадь равна (a + b)2.
В противоположных углах рассматриваемого квадрата построим квадраты со сторонами a и b.
Тогда большой начальный квадрат, будет разделен на четыре части: два квадрата с площадями a2 и b2, а также два прямоугольника с площадями равными ab. Тогда получаем, что
Примеры задач на применение формулы квадрата суммы
Пример 1.
Раскрыть скобки (x + 3)2.
Решение:
Пример 2.
Раскрыть скобки (2x + 3y2)2.
Решение:
Пример 3.
Упростить выражение
9x2 + 6x + 1(3x + 1).
Решение:
Можно заметить, что выражение в числителе — это разложенный квадрат суммы
Заметим, что с помощью формулы квадрата суммы легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик.
Пример 4.
Решение:
Фомулы сокращенного умножения Квадрат суммы Квадрат разности Разность квадратов Куб суммы Куб разности Сумма кубов Разность кубов
Квадрат суммы
Навигация по странице:
- Квадрат суммы — определение
- Вывод формулы квадрата суммы
- Применение формулы квадрата суммы
- Геометрическая интерпретация квадрата суммы
- Примеры задач на применение формулы квадрата суммы
Определение.
Квадрат суммы двух выражений равен квадрату первого, плюс удвоенное произведение первого и второго, плюс квадрат второго:
Вывод формулы квадрата суммы
Для доказательства справедливости формулы квадрата суммы достаточно перемножить выражения раскрыв скобки:
Применение формулы квадрата суммы
Формулу квадрата суммы удобно использовать:
- для раскрытия скобок
- для упрощения выражений
- для вычисления квадратов больших чисел, не используя калькулятор или умножение в столбик
Геометрическая интерпретация
Формулу квадрата суммы двух положительных чисел a и b можно изобразить геометрически
Рассмотрим квадрат со стороной (a + b), его площадь равна (a + b)2.
В противоположных углах рассматриваемого квадрата построим квадраты со сторонами a и b.
Тогда большой начальный квадрат, будет разделен на четыре части: два квадрата с площадями a
Примеры задач на применение формулы квадрата суммы
Пример 1.
Раскрыть скобки (x + 3)2.
Решение:
Пример 2.
Раскрыть скобки (2x + 3y2)2.
Решение:
Пример 3.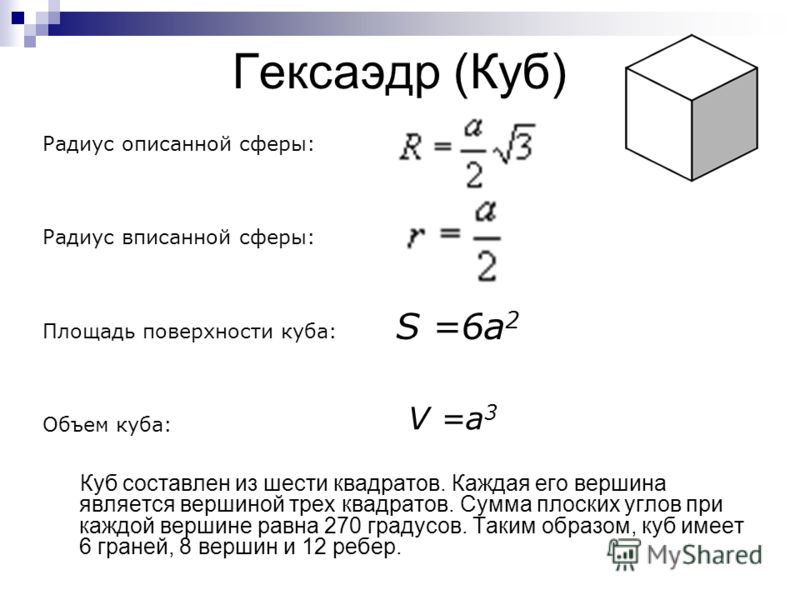
Упростить выражение
9x2 + 6x + 1(3x + 1) .Решение:
Можно заметить, что выражение в числителе — это разложенный квадрат суммы
Заметим, что с помощью формулы квадрата суммы легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик.
Пример 4.
Вычислить 712.
Решение:
Фомулы сокращенного умножения Квадрат суммы Квадрат разности Разность квадратов Куб суммы Куб разности Сумма кубов Разность кубов
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Калькулятор суммы квадратов
Чтобы найти алгебраическую и статистическую сумму квадратов, введите значения, разделенные запятыми, и нажмите кнопку .
Дайте нам отзыв
✎
✉
Калькулятор суммы квадратов
Калькулятор суммы квадратов используется для нахождения алгебраической и статистической суммы квадратов заданных терминов, чисел, последовательностей или наблюдений. Этот калькулятор предоставляет пошаговые решения алгебраической и статистической суммы квадратов.
Какова сумма квадратов?
В алгебре сумма квадратов используется для нахождения суммы двух или более квадратов членов. Например, используйте метод суммы квадратов, если даны два квадрата членов со знаком сложения между ними, например, 2 + б 2 .
В статистике сумма квадратов представляет собой отклонение заданного шага данных от его среднего значения. Он вычитает среднее значение из всех наблюдений и находит квадрат разностей, чтобы найти статистическую сумму квадратов.
The formula of the algebraic sum of squares is:
Algebraic sum of squares = a 1 2 + a 2 2 + a 3 2 + a 4 2 + … + а n 2
Эту формулу можно записать в виде суммирования.
Алгебраическая сумма квадратов = Σ a n 2
Формула статистической суммы квадратов:
Статистическая сумма квадратов = Σ (x — x̄)
5 научиться вычислять алгебраическую и статистическую сумму квадратов.
Пример
Найдите алгебраическую и статистическую сумму квадратов, если данные наблюдения:
2, 3, 6, 7, 8, 10, 13
Решение
Шаг 1: Прежде всего, найдите алгебраическую сумму квадратов, взяв квадрат каждого члена.
Алгебраическая сумма квадратов = (2) 2 + (3) 2 + (6) 2 + (7) 2 + (8) 2 + (10) 2 + 13) 2
= 4 + 9 + 36 + 49 + 64 + 100 + 169
= 431
Шаг 2: Теперь найдите среднее значение данных наблюдений, чтобы найти статистическую сумму квадратов.
Среднее = x̄ = сумма наблюдений / общее число
Среднее = x̄ = (2 + 3 + 6 + 7 + 8 + 10 + 13) / 7 3: Найдите отличия и квадраты отличий каждого члена от среднего.
| (x – x̄) | (x – x̄) 2 |
| 2 -7 = -5 | (-5) 2 = 25 |
| 3 -7 = -4 | (-4) 2 = 16 |
| (-1) 2 = 1 | |
| 7-7 = 0 | (0) 2 = 0 |
| 8-7 = 1 | (1 93131313131311319131 = 2 93131313131 . |
| 10 – 7 = 3 | (3) 2 = 9 |
| 13 – 7 = 6 | (6) 2 = 36 |
Шаг 4: Теперь сложите квадрат разностей, чтобы получить статистическую сумму квадратов.
Статистическая сумма квадратов = 25 + 16 + 1 + 0 + 1 + 9 + 36
Статистическая сумма квадратов = Σ (x — x̄) = 88 Калькулятор суммы квадратов — это онлайн-инструмент, который помогает вычислить сумму квадратов двух чисел. Сумма квадратов в статистике – это инструмент, который используется для оценки дисперсии набора данных. Чтобы оценить это, мы берем сумму квадрата вариации каждой точки данных.
Что такое калькулятор суммы квадратов?
Онлайн-калькулятор суммы квадратов поможет вам вычислить сумму квадратов двух чисел за несколько секунд. Формула суммы квадратов в статистике используется для описания того, насколько хорошо моделируемые данные представлены моделью. Он показывает дисперсию набора данных
Калькулятор суммы квадратов
Как пользоваться калькулятором суммы квадратов?
Выполните следующие шаги, чтобы найти сумму квадратов двух чисел:
- Шаг 1: Введите значения «a» и «b» в соответствующие поля ввода.

- Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти сумму квадратов двух чисел.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поле и ввести новые значения.
Как рассчитать калькулятор суммы квадратов?
Сумма квадратов может быть легко вычислена с помощью следующего тождества:
(a 2 + b 2 ) = (a + b) 2 — 2ab
Хотите находить сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры с помощью калькулятора суммы квадратов0031 2 .Решение:
Учитывая a = 36, b = 23
Используя вышеприведенное тождество, (a 2 + b 2 ) = (a + b) 2 9 3 0-0 2 0-0 23) 2 — 2 × 36 × 23
= 59 2 — 1656
= 3481- 1656
= 1825
С. 2:
2:
Найдите значение 45 2 + 24 2 .
Решение:
Учитывая a = 45, b = 24
Используя вышеприведенное тождество, (a 2 + b 2 ) = (a + b) 2 5 2 5 9 0 2 ab 4 0-0 0-0 24) 2 — 2 × 45 × 24
= 69 2 — 2160
= 4761- 2160
= 2601
Следовательно, сумма примеров примеров приведенных навес 3:
Найдите значение 18 2 + 13 2 .
Учитывая a = 18, b = 13
Используя вышеприведенное тождество, (a 2 + b 2 ) = (a + b) 2 2 9 13) 2 — 2 × 18 × 13
= 31 2 — 468
= 961- 468
= 493
Следовательно, сумма квадратов из данных двух чисел- 493.
Теперь, теперь, теперь, сумма квадратов из двух чисел- 493.
, теперь, теперь сумма квадратов из двух чисел составляет 493.

