Карты Карно для 4-х переменных — Студопедия
Поделись
Как и в обычных таблицах соответствия клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки).
Например, на рис. показана карта Карно для функции, отображение которой дано на 4-х-мерном кубе (см. рис.).
Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
Рис. а) отображение функции четырех переменных;
б) отображение ее минимального покрытия.
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно S-кубу соответствует совокупность 2-х соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике. Поэтому все положения, изложенные ранее, справедливы и для карт Карно. Так на рис. б) показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме
у= , рассматриваемой функции.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие S-куб, дают минитерм (n-S)-го ранга, в который входят те (n-S)-переменные, которые сохраняют одинаковые значения на этом S-кубе, причем значениям “1” соответствуют сами переменные, а значениям “0” их отрицание.
Переменные, которые не сохраняют свои значения на S-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в ДНФ.
у= у=
у=
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае 4-х переменных.
Для отображения функций 5-ти переменных используют две карты Карно на 4-ре переменные, а для функции 6-ти переменных — четыре таких карты.
При дальнейшем увеличении числа переменных карты Карно становятся практически непригодны.
Метод Мак-Класски (алгебраический метод)
Алгебраический метод известен как метод Мак-Класски, модифицировавшего в 1956 году метод Квайна.
Базируется данный метод на следующей теореме.
Теорема. Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.
Элементарную конъюнкцию ранга n будем называть минитермом ранга n.
Элементарная конъюнкция называется импликантой булевой функции , если , то есть булева функция на данном наборе является константной и равна 1.
Минимизация булевой функции по методу Мак-Класски осуществляется согласно следующей последовательности действий:
1. Записать минитермы в виде их двоичных кодов и разбить их на непересекающиеся группы по числу единиц в этих группах. В i-ю группу войдут только те кодовые комбинации, которые в своей двоичной записи содержат ровно i единиц. Группы располагаются по мере роста i.
2. Попарное сравнение минитермов.
2.1. Произвести попарное сравнение двоичных номеров всех членов группы с индексом i с членами только группы с индексом (i+1).
2.2. Если некоторые два минитерма имеют вид axi и , то выписывают конъюнкцию а, которая является минитермом ранга (n-1), то есть если сравниваемы двоичные коды различаются только в одном разряде, то в столбец остатков записывается двоичный код с прочерком “-” на месте этого разряда (этот код соответствует минитерму (n-1)-го ранга.
2.3. Все двоичные коды номеров, участвующих в операции сравнения при условии их склеивания, отмечаются знаком “*”.
2.4. Пункты 2.1-2.3. повторяются для всех групп последовательно в порядке возрастания i. Двоичные коды, не отмеченные знаком “*”, соответствуют простым импликантам.
2.5. После построения всех минитермов (n-1) ранга по пунктам 2.1-2.3, они также сравниваются между собой и получают минитермы ранга (n-2) и т.д. Работа по первому этапу продолжается до тех пор, пока среди двоичных кодов можно будет обнаружить сравнимые, то есть такие укороченные коды, которые содержат прочерки в одних и тех же разрядах и различаются значением одного разряда.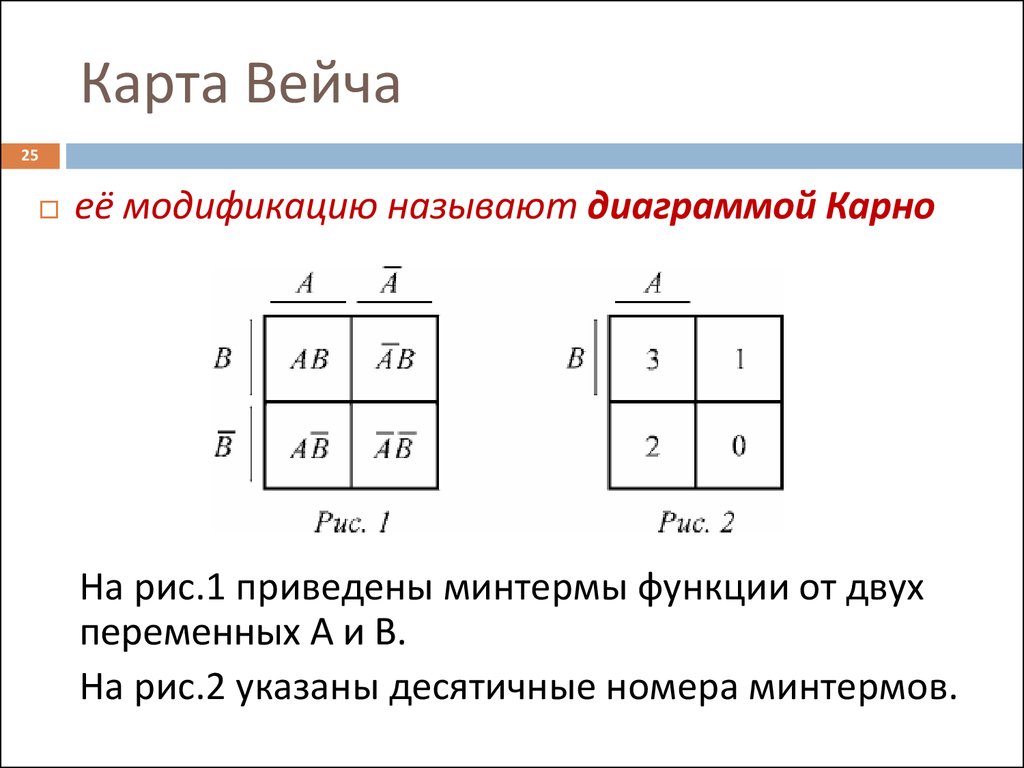
Все неотмеченные минитермы называются первичными или простыми импликантами.
3. Построение импликантной таблицы. Строится таблица, в которой число строк равно числу полученных первичных импликант минимизируемой функции, а число столбцов равно числу минитермов исходной СДНФ. Если в некоторый минитерм исходной СДНФ входит первичная импликанта, то на пересечении строки и столбца ставится метка. Данные импликантной таблицы позволяют определить импликанты, отбросив которые, истинность функции не изменится.
4. Нахождение существенных импликант. Если в каком-либо из столбцов полученной таблицы имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной. Существенная импликанта включается в минимальную ДНФ, а из таблицы исключаются строки, соответствующие существенным импликантам, а также столбцы минитермов, покрываемые этими существенными импликантами. Если в таблице нет столбцов, содержащих только одну метку, то переход на п.
7.
5. Вычеркивание лишних столбцов. Если в таблице после четвертого этапа есть два столбца, в которых стоят метки в одинаковых строках, то один из них вычеркивают, так как покрытие оставшегося столбца будет осуществлять покрытие исключенного минитерма.
6. Вычеркивание лишних первичных импликант. Если на пятом этапе появляются строки, в которых нет меток, то первичная импликанта исключается из дальнейшего рассмотрения.
7. Выбор минимального покрытия. Выбирают наименьшее число строк таких, чтобы для каждого столбца из данной таблицы и каждой метки в этом столбце нашлась бы по крайней мере одна строка из множества выбранных строк, которая содержит эту метку.
Дизъюнкция всех простых импликантов покрытия, в том числе и существенных, образует тупиковую форму функции. Из найденных тупиковых форм выбирают минимальную по наименьшему числу дизъюнкций и элементов переменных.
Пример.
.
1) Получение групп кодовых комбинаций. 0011 0100 0101 0111 1001 1011 1100 1101
1 гр.
0100 2 гр. 0011 3 гр. 0111
0101 1011
1001 1101
2) Попарное сравнение минитермов.
Минитермы 3-го ранга: 010-*, -100, 0-11, -011, -101, 10-1, 1-01, 110-*
Минитермы 2-го ранга: -10-.
3) Построение импликантной таблицы и расстановка меток
| -100 | * | * | ||||||
| 0-11 | * | * | ||||||
| -011 | * | * | ||||||
| -101 | * | * | ||||||
| 10-1 | * | * | ||||||
| 1-01 | * | * | ||||||
| -10- | * | * | * | * |
4) Нахождение существенных импликант.
Столбец, соответствующий кодовой комбинации 0111 содержит единственную метку. Соответствующая этой метке импликанта является существенной, поэтому включаем ее в минимальную ДНФ , а из таблицы согласно п.4 исключаем столбцы и строку, после чего получаем следующую таблицу:
| -100 | * | * | ||||
| -011 | * | |||||
| -101 | * | * | ||||
| 10-1 | * | * | ||||
| 1-01 | * | * | ||||
| -10- | * | * | * | * |
5) и 6) В полученной таблице нет столбцов, в которых стоят метки в одинаковых строках и нет строк, в которых нет меток, поэтому переходим к п.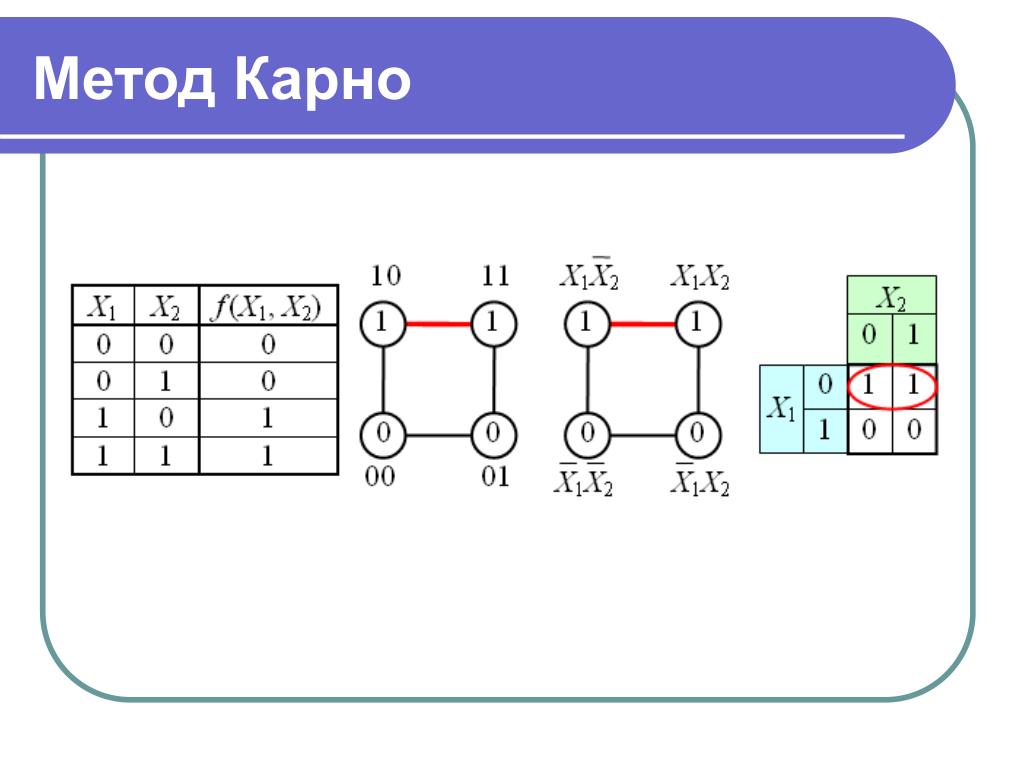
7) Выбор минимального покрытия. Минимальному покрытию соответствует выбор строк -10- и 10-1. Тогда минимизированная ДНФ запишется как .
Метод карт Карно — Студопедия
Поделись
Метод Карно основан на законе склеивания. Склеиваются наборы , отличающиеся друг от друга значением одного разряда. Такие наборы называются соседними. Карно закодировал клетки своей карты так ,что в соседних клетках оказались соседние, а значит, склеивающиеся наборы. Соседними могут быть не только отдельные клетки, которые мы назовем элементарными квадратами Карно, но и целые группы соседних клеток (назовем их прямоугольниками Карно). Под прямоугольником Карно будем понимать некоторую, зачастую разрозненную фигуру покрытия, все соседние клетки которой закодированы соседними наборами.
Например, на вышеприведённом рисунке в поле карты для 4-х переменных изображён прямоугольник Карно P, состоящий из четырёх элементарных квадратов Карно, описываемых наборами x4’x3’x2’x1′ , x4’x3’x2x1′ , x4x3’x2’x1′ , x4x3’x2x1′ .
Если над логической суммой этих четырёх наборов произвести последовательно операции склеивания, то мы аналитически получим результат в виде импликанты (под импликантой будем понимать неполный набор x3’x1′. Карта Карно позволяет получить этот результат графически значительно быстрее и проще. Для решения этой задачи используем алгоритм графической минимизации. Кстати говоря, сам Карно никакого алгоритма не предложил.
Упрощение выражений булевых функций (минимизация) основывается на понятии несущественности переменных. Переменная называется несущественной на паре наборов, если при изменении ее значения на противоположное булева функция сохраняет свое значение.
Например, для булевой функции трех переменных, f (1, 3, 5, 6, 7) = 1 , которая рассматривалась в подразделе 1.3 «Теории переключательных схем», 6-я и 7-я конъюнкции имеют вид : x1x23, x1x2x3.
По дистрибутивному закону :
x1x23 v x1x2x3 = x1x2 ( 3 v x3 ) = x1x2.
Таким образом, две конъюнкции, содержащие несущественную переменную, заменяются одной, в которой несущественная переменная отсутствует.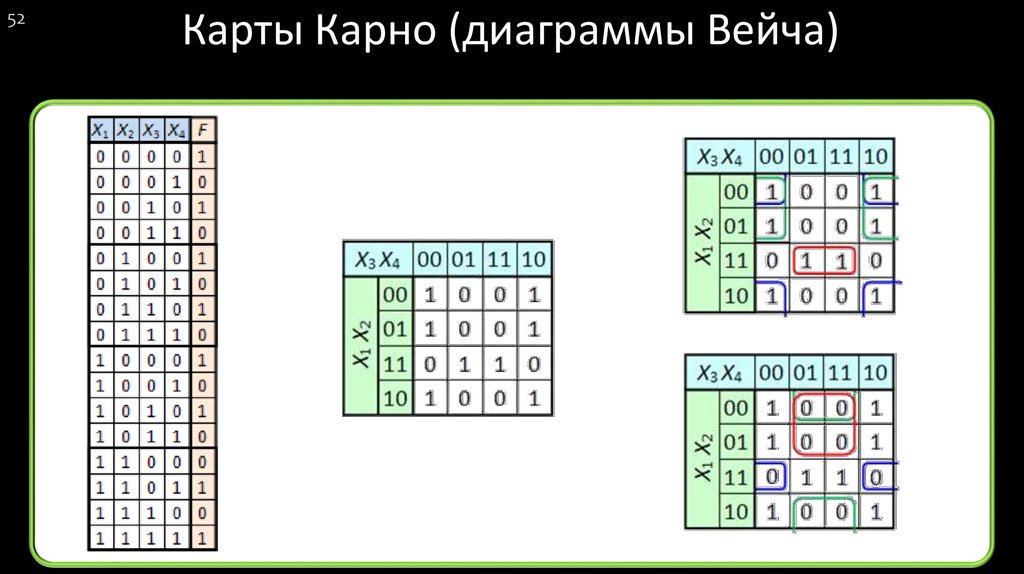
В кубическом виде склеивание имеет следующую интерпретацию : 1 1 0 1 1 1 = 1 1 X , что соответствует конъюнкции x1x2.
Приведем основные определения, используемые при минимизации булевых функций. Данные определения используют понятия нормальных (канонических) форм булевых функций, введенные в подразделе 1.3 .
Число переменных, входящих в элементарную конъюнкцию (для ДНФ) или в элементарную дизъюнкцию (для КНФ) называется ее рангом.
В основе любых методов минимизации лежит операция склеивания. Два элементарных произведения одного ранга (для ДНФ) или элементарных сумм одного ранга (для КНФ) склеиваются, если они различаются только по одной переменной.
Операция Аx v A = A называется полным склеиванием, а операция Аx v A = A v Аx v A — неполным склеиванием (для ДНФ).
Операция ( А v x )· ( A v ) = A называется полным склеиванием, а операция ( А v x )· ( A v ) = A· ( А v x )· ( A v ) — неполным склеиванием (для КНФ).
Например, полное склеивание (x1 v x2 v x3)· (x1 v x2 v 3) = x1 v x2 ;
Неполное склеивание x1x2x3 v x1x23 = x1x2 v x1x2x3 v x1x23 .
Импликантой называется элементарное произведение, равное 1 на одном или нескольких наборах, где данная функция равна 1, и равное 0 на всех наборах, где данная функция равна 0. Импликанта покрывает один или несколько минтермов рассматриваемой булевой функции. Обычно, импликанта — это результат склеивания соответствующих минтермов или импликант.
Простая импликанта — это импликанта, которая содержит хотя бы минтерм функции, но перестает быть импликантой после удаления любого аргумента (иными словами, это импликанта, к которой не нельзя применить операцию склеивания).
Сокращенная ДНФ — это дизъюнкция всех простых импликант.
Существенная импликанта — это простая импликанта, образованная склеиванием таких минтермов, что по крайней мере для одного из них эта операция была единственной. Существенные импликанты образуют ядро функции.
Тупиковая ДНФ — это дизъюнкция простых импликант, из которых ни одна не является лишней.
МДНФ (минимальная ДНФ) — тупиковая ДНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.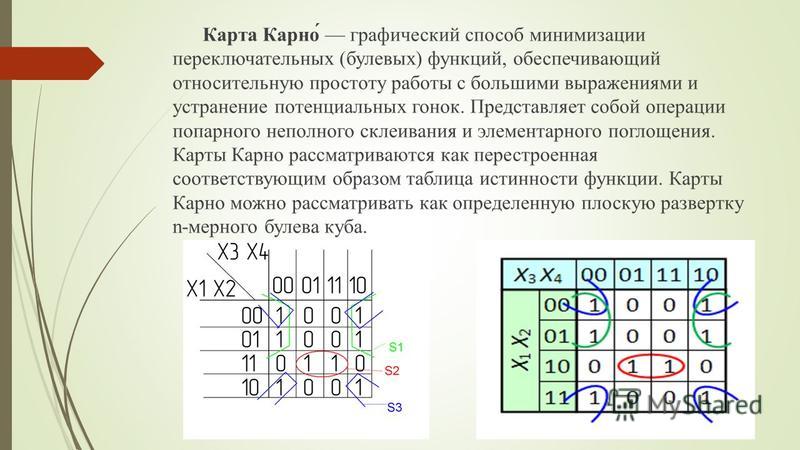
Имплицентой называется элементарная логическая сумма, равная 0 на одном или нескольких наборах, где данная функция равна 0, и равная 1 на всех наборах, где данная функция равна 1. Имплицента покрывает один или несколько макстермов рассматриваемой булевой функции. Обычно, имплицента — это результат склеивания соответствующих макстермов.
Простая имплицента — это имплицента, которая содержит хотя бы макстерм функции, но перестает быть имплицентой после удаления любого аргумента (иными словами, это имплицента, к которой не нельзя применить операцию склеивания).
Сокращенная КНФ — это конъюнкция всех простых имплицент.
Существенная имплицента — это простая имплицента, образованная склеиванием таких макстермов, что по крайней мере для одного из них эта операция была единственной. Существенные имплиценты образуют ядро функции.
Тупиковая КНФ — это конъюнкция простых имплицент, из которых ни одна не является лишней.
МКНФ (минимальная КНФ) — тупиковая КНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.
1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.
2. Количество клеток внути контура должно быть целой степенью двойки (1, 2, 4, 8, 16…).
3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).
4. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.
5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.
6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ).
Целью минимизации является нахождение минимальной из множества тупиковых форм.
7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией — если 0. Для значений булевой функции, равных 0, записываются элементарные дизьюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией — если 1.
Если рассматривать запись результатов минимизации в кубическом виде, то при минимизации булевой функции по единичным значениям, каждой конъюнкции ранга R соответствует куб ранга R, где каждой переменной без инверсии соответствует 1 в кубе, переменной с инверсией — 0, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует единичное покрытие C1 (соответствующее ДНФ).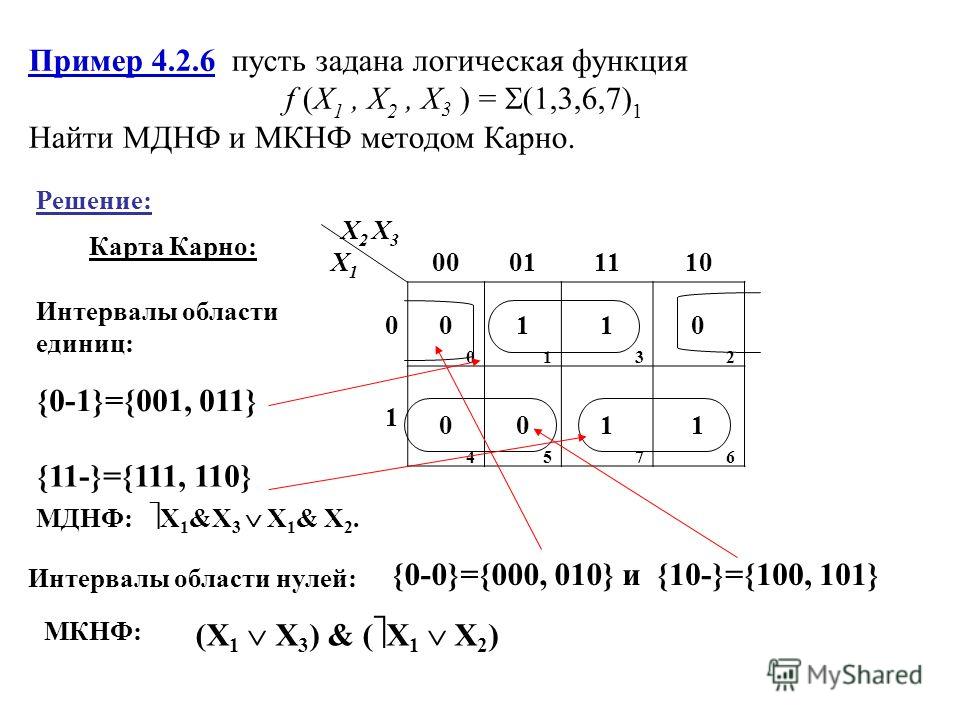
При минимизации булевой функции по нулевым значениям и представлении результатов минимизации в кубическом виде, нулевое покрытие C0 формируется на основе обратной ДНФ , которая является инверсной функцией по отношению к КНФ (способ построения инверсных функций и пример инверсных функций для f ( 1,3,5,6,7 ) = 1 рассмотрен в подразделе 1.3). Отметим, что обратная ДНФ строится на основе КНФ. Таким образом каждой дизъюнкции ранга R (из КНФ) соответствует куб ранга R, где каждой переменной без инверсии соответствует 0 в кубе, переменной с инверсией — 1, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует нулевое покрытие C0.
При данном способе задания таблица истинности функции представляется в виде координатной карты состояний, которая содержит 2n клеток (по числу входных наборов булевой функции n переменных). Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца карты, а другая — координаты строки.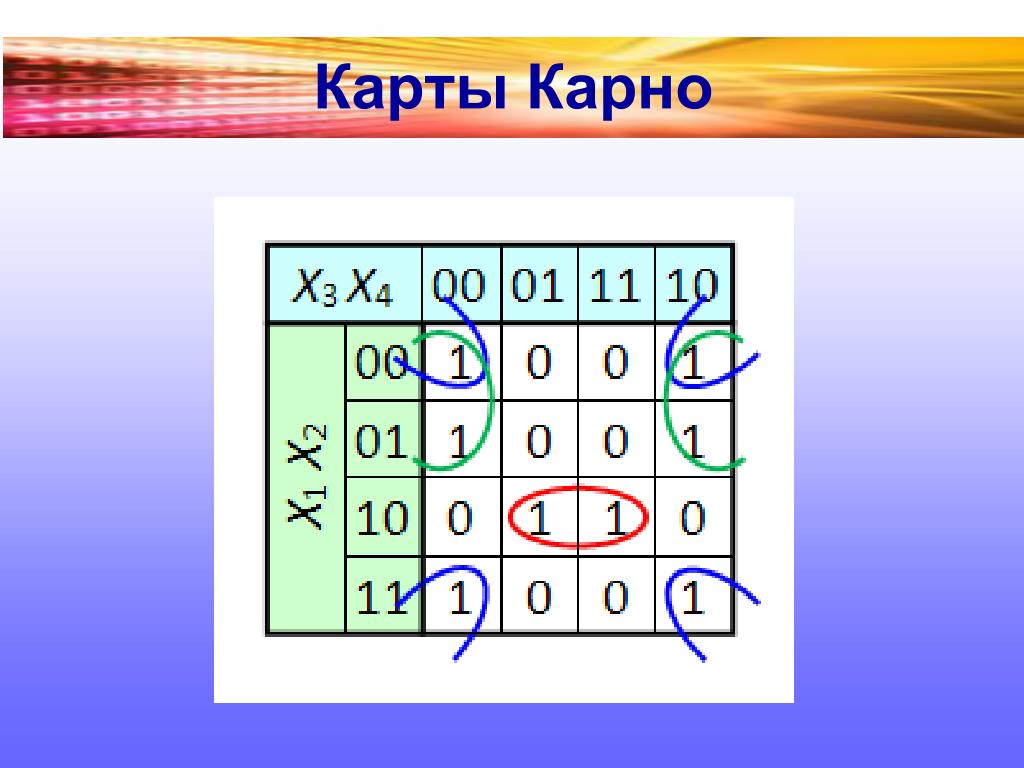
При такoм способе построения каждая клетка определяется значениями переменных, соответствующих определенному двоичному набору. Внутри каждой клетки карты Карно ставится значение функции на данном наборе. Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е. были соседними. Поэтому значения переменных в столбцах и в строках карты образуют соседний код Грея. Такой способ представления очень удобен для наглядности при минимизации булевых функций.
Карты Карно были изобретены в 1952 Эдвардом В. Вейч’ем и усовершенствованы в 1953 Морисом Карно, физиком из «Бэлл Лабс» Метод карт Карно применим к минимизации булевых функций до 6-ти переменных (до 4 переменных на плоскости) и до 6 — в трехмерной интерпретации.
Если требуется получить карту Карно для какой – либо функции, сначала надо записать эту функцию в СДНФ, – в совершенной дизъюнктивно нормальной форме, или в виде таблицы истинности.
Каждое слагаемое булева выражения в СДНФ, или каждая единица в столбце функции таблицы истинности, задается на карте Карно единицей в соответствующей клетке.
Координаты этой клетки содержат те же входные переменные и их инверсии, что и данное слагаемое СДНФ булева выражения ( или данная строка таблицы истинности ).
Taблица истинности для четырех переменных включает 16 строк, следовательно карта Карно должна состоять из 16 клеток, как показано на рисунке:
У карты Карно для четырех переменных клетки крайнего левого столбца должны рассматриваться как соседние для клеток крайнего правого столбца, а клетки верхней строки, – как соседние для клеток нижней строки. Другими словами можно сказать, что эта карта расположена на поверхности цилиндра (склеили правый край карты с левым ), изогнутого и растянутого так, что его верхний срез соединяется с нижним срезом; при этом цилиндр превращается в тор (бублик).
Правила упрощения заполненной карты Карно для четырех переменных заключаются в следующем :
– соседние две, четыре, или восемь единиц обводят общим контуром;
– контур должен быть прямоугольным без изгибов или наклонов;
– каждый контур превращает все входящие в него единицы в одну, т.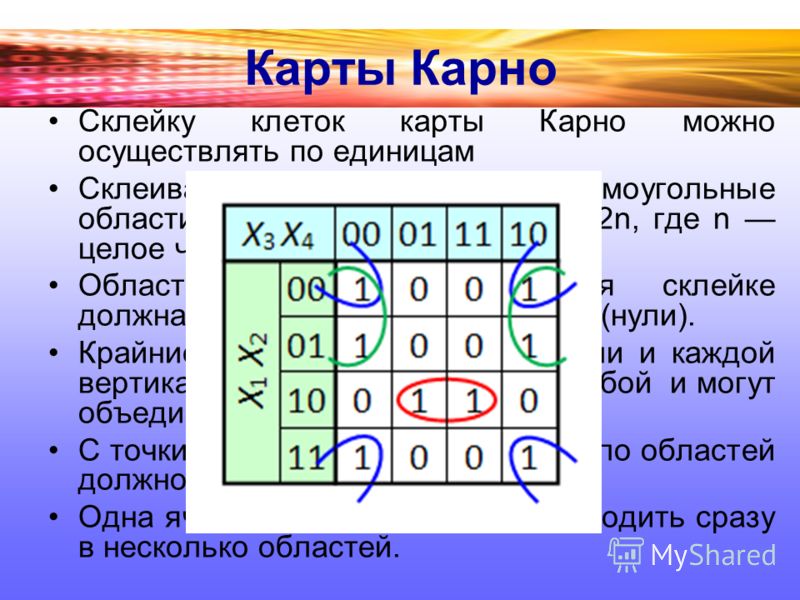
е. объединенные таким образом слагаемые СДНФ булева выражения дают одно слагаемое в упрощенном выражении;
– те входные переменные, которые входят в координаты данного контура совместно со своими инверсиями, исключаются из слагаемого, которое дает этот контур в упрощенное выражение.
Примеры упрощения булевых выражений с помощью карты Карно:
В первом примере минимизации булевой функции F1 нижний контур из двух единиц 15 и 16 , соответствующие пятому и шестому слагаемым в исходном булевом выражении, дает возможность опустить B и`B. После этого в нем остается произведение `A C`D. В верхнем контуре из четырех единиц 11, 12, 13 и 14 , соответствующие первым четырем слагаемым в исходном булевом выражении попарно опускаются A и`A, D и`D, так что в результате этого верхний контур дает произведение B C.
Во втором примере минимизации булевой функции F2 контур из двух единиц 12 и 13 , соответствующие второму и третьему слагаемым в исходном булевом выражении, дает возможность опустить А и`А.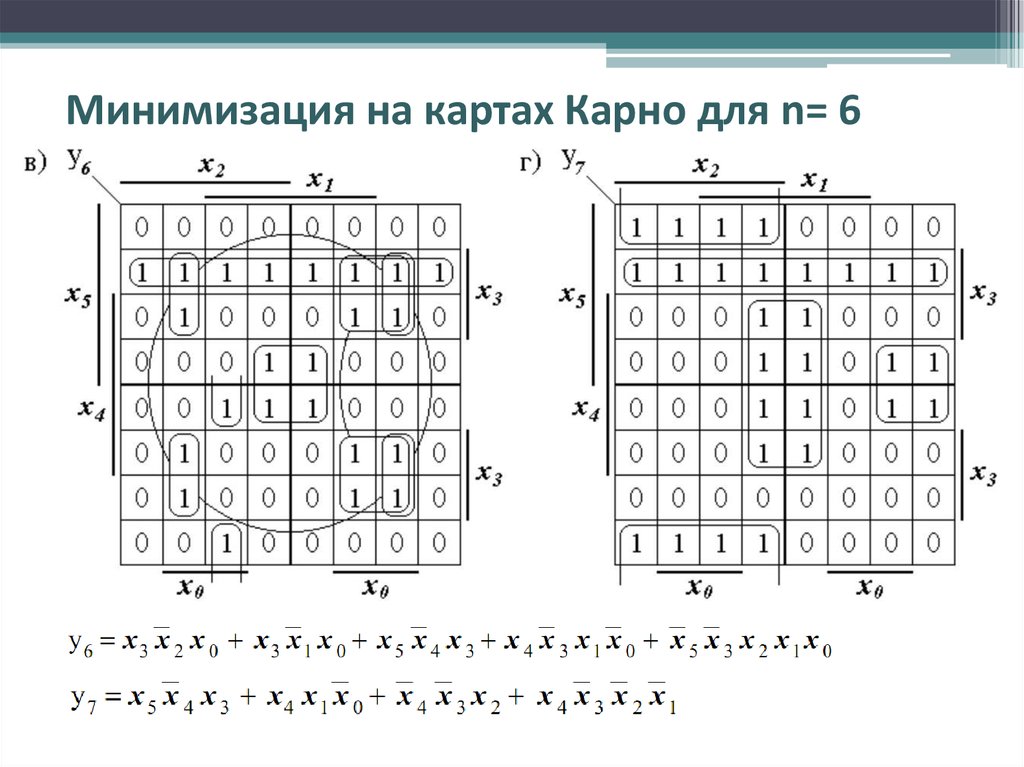
После этого в нем остается произведение B`C`D. В контуре из четырех единиц 11, 12, 14 и 15 , соответствующие другим четырем слагаемым из исходного булева выражения, попарно опускаются В и`В, С и`С, так что в результате этого верхний контур дает произведение `A`D.
Карта Карно представляется в данном случае свернутой в цилиндр, в котором верхний край совмещается с нижним. Этот пример показывает также, что контура могут накладываться друг на друга.
Правило покрытия 1.
Любой области из 2k смежных клеток можно поставить в соответствие конъюнкцию (n-k)-го ранга, состоящую из переменных, которые имеют постоянное значение во всех единичных наборах, соответствующих клеткам области. Причем переменная xi включается в конъюнкции в прямом виде, если эта переменная имеет значение 1 на всех клетках области.
Соответственно переменная xi включается в конъюнкции в инверсном виде, если она имеет значение 0 на всех клетках области. «Покрытая» область на карте обводится контуром.
Дизъюнкция конъюнкции, совместно покрывающих все клетки карты, заполненные единицами, есть одна из ДНФ переключательной функции.
Цель минимизации формулы ПФ по карте Карно — «покрыть» все клетки, содержащие единицы, наименьшим числом конъюнкции наименьшего ранга, т. е. «покрыть» наименьшим числом контуров, каждый из которых охватывает как можно большую область смежных клеток, все клетки, содержащие единицы. Дизъюнкция полученных конъюнкций есть одна из тупиковых (возможно, минимальная) ДНФ функции.
Простым импликантам (минималям) в методе Квайна-Мак-Класки на карте Карно соответствуют области смежных клеток, не являющиеся частью никакой другой области смежных клеток.
Обязательной простой импликанте (экстремали) в методе Квайна-Мак-Класки соответствует область смежных клеток, которая покрывает хотя бы одну единичную клетку, не входящую в состав никакой из других областей смежных клеток.
Правило покрытия 2.
Любой смежной области 2k клеток, заполненных нулями, можно поставить в соответствие дизъюнкцию (n-k)-го ранга, состоящую из переменных, которые имеют постоянное значение во всех нулевых наборах, соответствующих клеткам области, причем переменная xi входит в дизъюнкцию в прямом виде, если имеет значение 0 на всех клетках области, и, соответственно в инверсном виде, если она имеет значение 1 на всех клетках области.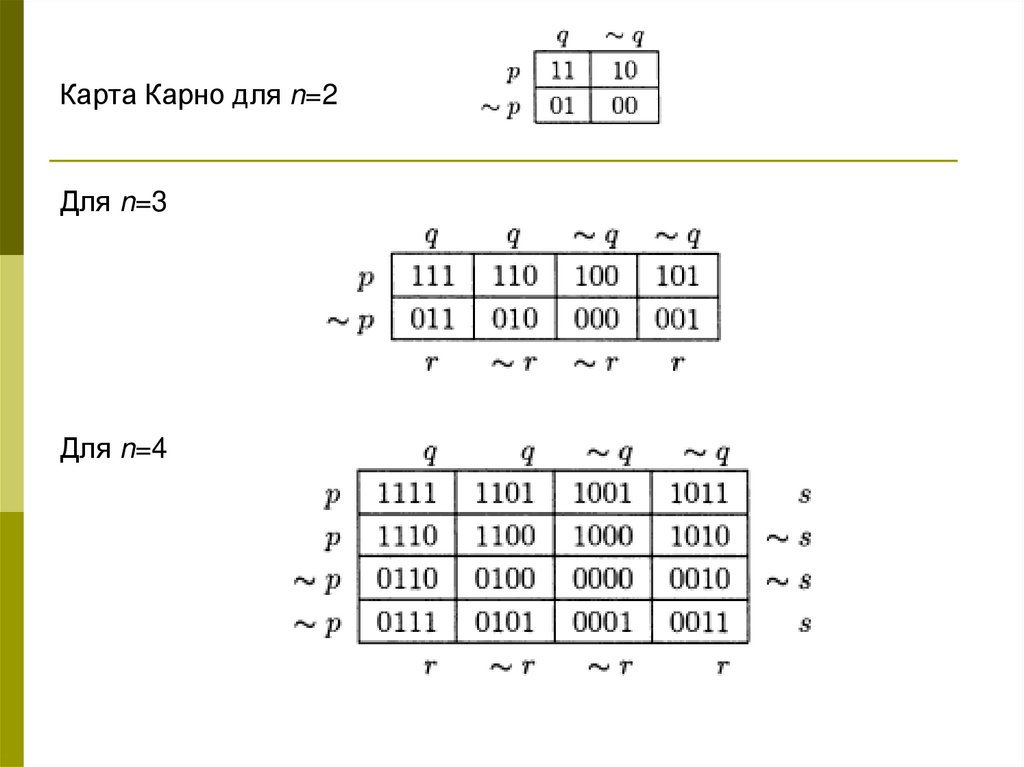
Конъюнкция минимального числа дизъюнкций, совместно покрывающих все клетки карты, заполненные нулями, есть одна из тупиковых (возможно, минимальных) КНФ переключательной функции.
Поздравительные открытки Карно — Fine Art America
Результаты: 53
Результаты: 53
Открытка Сади Карно
5,00 долл. США
4,00 долл. США
Открытка Карно о термодинамике
5,00 долл. США
4,00 долл. США
Портрет Николя Леонарда Сади Карно Открытка
5,00 долл. США
4,00 долл. США
Открытка «Портрет французского инженера Лазара Карно»
5,00 долл. США
4,00 долл. США
Победа Франции объявлена поздравительной открыткой Telegram
Открытка «Второй закон термодинамики»
Открытка Сади Карно
5,00 долл.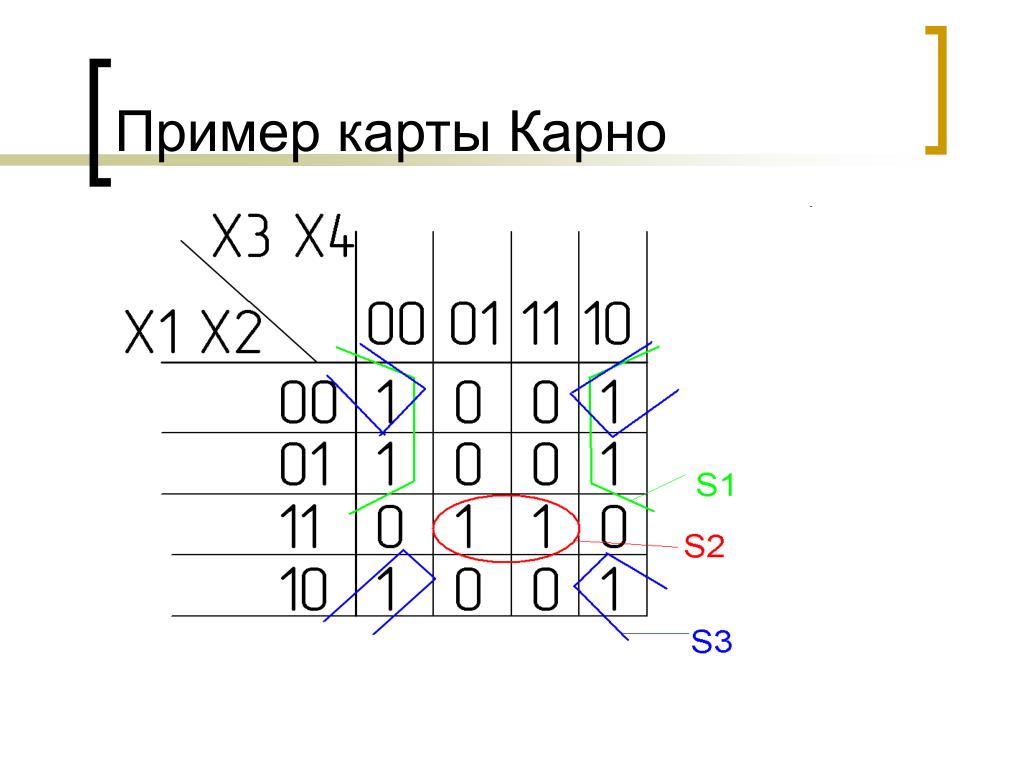
США
4,00 долл. США
Поздравительная открытка «Трактат о термодинамике» Карно 1824 г.
5,00 долл. США
4,00 долл. США
Открытка с портретом Сади Карно
5,00 долл. США
4,00 долл. США
Портрет Николя Леонарда Сади Карно Открытка
$5,00
$4,00
Фонтан с бюстом Нострадамуса Поздравительная открытка
7,00 долл. США
5,60 долл. США
Открытка «Второй закон термодинамики»
Открытка «Второй закон термодинамики»
Открытка «Второй закон термодинамики»
Поздравительная открытка Эмиля Клапейрона
5,00 долл. США
4,00 долл. США
Лазар Николя Маргарита Карно Поздравительная открытка
6,95 долл.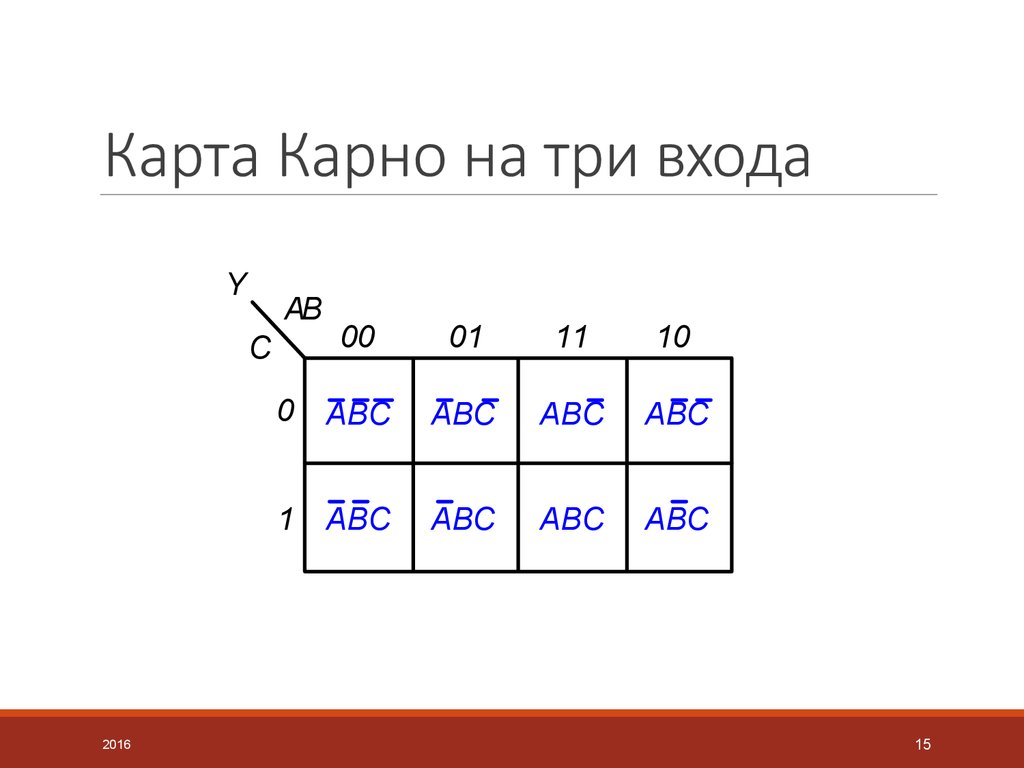
США
5,56 долл. США
Лазар Николя Маргарита Карно Поздравительная открытка
5,95 долл. США
4,76 долл. США
Мари-Франсуа-Сади Карно Французская открытка
5,95 долл. США
4,76 долл. США
Президент Франции Карно с поздравительной открыткой
5,95 долл. США
4,76 долл. США
Лазар Ипполит Карно Французская открытка
5,95 долл. США
4,76 долл. США
Лазар Николя Маргарита Карно Поздравительная открытка
5,95 долл. США
4,76 долл. США
Лазар Николя Маргарита Карно, 1753-1823 гг. Поздравительная открытка французского государственного деятеля
4,45 доллара
3,56 доллара
Николя Леонард Сади Карно, Французская открытка
6,95 долл.
США
5,56 долл. США
Поздравительная открытка Кираса Карно
19 долларов
15 долларов
Открытка с Лазаром Карно, французским математиком
6,95 долл. США
5,56 долл. США
Сади Карно, открытка с французским физиком
6,95 долл. США
5,56 долл. США
Сади Карно, открытка с французским физиком
6,95 $
$5,56
Портрет мадемуазель Карно Поздравительная открытка
8,95 долл. США
7,16 долл. США
Луи-Оскар Роти, Поздравительная открытка с телом президента Сади Карно Борне
4,95 долл. США
3,96 долл. США
Поздравительная открытка Мари Фран
6,95 долл. США
5,56 долл. США
Поздравительная открытка Мари Фран
6,95 долл.
США
5,56 долл. США
Анри де Тулуз-Лотрек, Франция, 1864-1901 гг. Поздравительная открытка
4,95 $
$3,96
Волна, разбивающаяся о скалы. Открытка с мысом Карно
4,95 долл. США
3,96 долл. США
Больной Карно! (Карно Малад!) Поздравительная открытка
4,94 долл. США
3,95 долл. США
Francais Portrait de Lazare Carnot 1753-1823 Поздравительная открытка
5,95 долл. США
4,76 долл. США
Бронзовая статуя «Путешественник» французского художника Бруно Каталано на площади Карно, Бон, Бургундия, Франция Поздравительная открытка
5,45 долл. США
4,36 долл. США
Париж на закате открытка
4,95 долл. США
3,96 долл. США
Открытка на углу площади Белькур и улицы Виктора Гюго
7,95 долл. США
6,36 долл. США
Открытка с эмоциями
4,95 долл. США
3,96 долл. США
Вейнанд Эссер — Открытка с изображением Наполеона Карно, 1815 г.
5,95 долл. США
4,76 долл. США
Карно болен из Les Vieilles Histoires 1893 Поздравительная открытка
8,95 долл. США
7,16 долл. США
Le President Sadi Carnot entoure de personnalites de la IIIeme Republique devant lOpera Поздравительная открытка
5,94 долл. США
4,75 долл. США
Поздравительная открытка Carnot cuirasse d’escadre 1907 года
5,94 долл. США
4,75 долл. США
Поздравительная открытка Президента Сади Карно в окружении персон из IIIeme Republique, devant l’ Opera
4,95 долл. США
3,96 долл. США
Поздравительная открытка тени
5,95 долл. США
4,76 долл. США
Открытка с природой
4,95 долл. США
3,96 долл. США
Поздравительная открытка с горами
4,95 долл. США
3,96 долл. США
Элегантная архитектура в стиле модерн в Каннах на бульваре Greeting Card
6,95 долл. США
5,56 долл. США
Второй закон термодинамики. Открытка
5,95 долл. США
4,76 долл. США
Поздравительная открытка Осада Парижа
5,94 долл. США
4,75 долл. США
Неоновая вывеска Le Cafe Carnot, площадь Карно, Невер, Ньевр, Бургундия, открытка Франции
4,95 доллара
3,96 доллара
Площадь Карно, Невер, Ньевр, Бургундия, Франция Поздравительная открытка
4,95 долл. США
3,96 долл. США
Президент Франции Сади Карно из серии флагов и гербов правителей N126 2, выпущенной W Du Greeting Card
4,95 $
3,96 $
Фильтры применены0003
Home Decor
Throw PillowsFleece BlanketsDuvet CoversShower CurtainsBath TowelsHand TowelsCoffee MugsOrnaments
Apparel
Men’s T-ShirtsMen’s Tank TopsWomen’s T-ShirtsWomen’s Tank TopsLong Sleeve T-ShirtsSweatshirtsKid’s T-ShirtsBaby OnesiesFace Masks
Phone Cases
iPhone CasesGalaxy CasesPortable Battery Chargers
Канцелярские товары
Поздравительные открыткиНоутбукиНаклейки
Lifestyle
Коврики для йогиСумкиСумки-тоут WeekenderСумки Carry-AllCouchКофейные кружкиГоловоломки
Beach
Beach Totelelsround Beach Totelsweekender Tote Bagscarry-All Coutsportable Bagsweekend
Все Картины Фотографии Чертежи Цифровое искусство
Все поздравительные открытки
Мы отправили миллионы товаров по всему миру для более чем миллиона художников.