Численные методы
Численные методы
ОглавлениеГЛАВА I. ЧТО ТАКОЕ ЧИСЛЕННЫЕ МЕТОДЫ? Приближенный анализ Приближенный анализ2. Структура погрешности. 3. Корректность. ГЛАВА II. АППРОКСИМАЦИЯ ФУНКЦИЙ § 1. Интерполирование 2. Линейная интерполяция. 3. Интерполяционный многочлен Ньютона. 4. Погрешность многочлена Ньютона. 5. Применения интерполяции. 6. Интерполяционный многочлен Эрмита. 7. Сходимость интерполяции. 8. Нелинейная интерполяция. 9. Интерполяция сплайнами. 10. Монотонная интерполяция. 11. Многомерная интерполяция. § 2. Среднеквадратичное приближение 2. Линейная аппроксимация. 3. Суммирование рядов Фурье. 4. Метод наименьших квадратов. 5. Нелинейная аппроксимация. § 3. Равномерное приближение 2. Нахождение равномерного приближения. ЗАДАЧИ ГЛАВА III. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ 1. Полиномиальные формулы. 2. Простейшие формулы. 3. Метод Рунге — Ромберга. 4. Квазиравномерные сетки. 5. Быстропеременные функции. 6. Регуляризация дифференцирования. ЗАДАЧИ ГЛАВА IV. 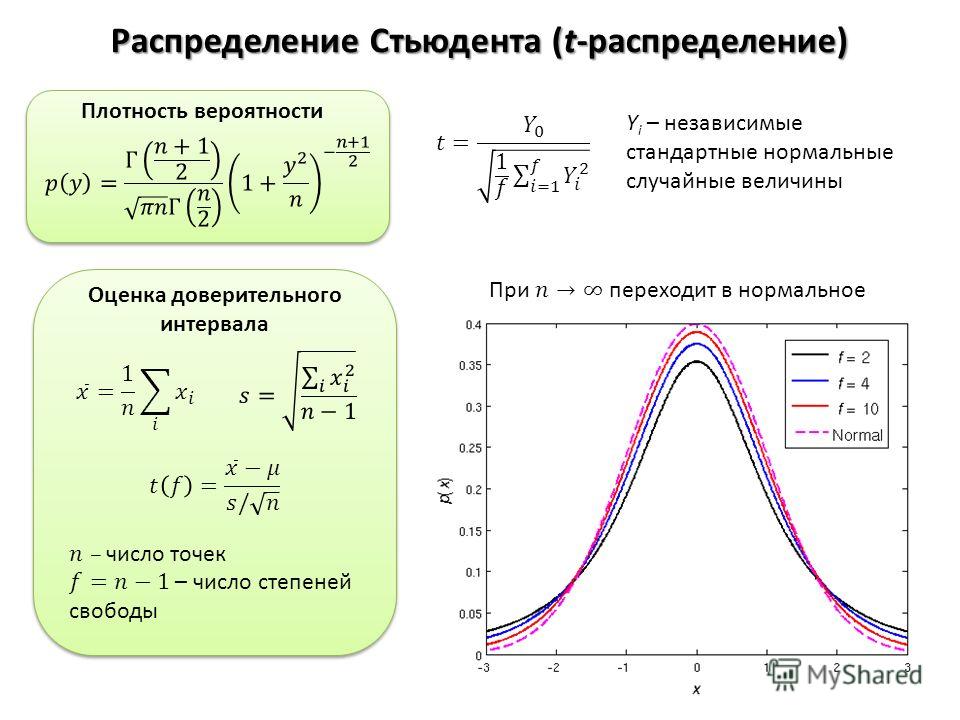 ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ§ 1. Полиномиальная аппроксимация 2. Формула трапеций. 3. Формула Симпсона. 4. Формула средних. 5. Формула Эйлера. 6. Процесс Эйткена. 7. Формулы Гаусса — Кристоффеля. 8. Формулы Маркова. 9. Сходимость квадратурных формул. § 2. Нестандартные формулы 2 Нелинейные формулы. 3. Метод Филона. 4. Переменный предел интегрирования. 5. Несобственные интегралы. § 3. Кратные интегралы 2. Последовательное интегрирование. § 4. Метод статистических испытаний 2. Разыгрывание случайной величины. 3. Вычисление интеграла. 4. Уменьшение дисперсии. 5. Кратные интегралы. ЗАДАЧИ ГЛАВА V. СИСТЕМЫ УРАВНЕНИЙ § 1. Линейные системы 2. Метод исключения Гаусса. 3. Определитель и обратная матрица 4. О других прямых методах. 5. Прогонка. 6. Метод квадратного корня. § 2. Уравнение с одним неизвестным 2. Дихотомия (деление пополам). 3.  Удаление корней. Удаление корней.4. Метод простых итераций. 5. Метод Ньютона. 6. Процессы высоких порядков. 7. Метод секущих [48]. 8. Метод парабол. 9. Метод квадрирования. § 3. Системы нелинейных уравнений 2. Метод Ньютона. 3. Методы спуска. 4. Итерационные методы решения линейных систем ЗАДАЧИ ГЛАВА VI. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ § 1. Проблема и простейшие методы 2. Устойчивость. 3. Метод интерполяции. 4. Трехдиагольные матрицы. 5. Почти треугольные матрицы. 6. Обратные итерации. § 2. Эрмитовы матрицы 2. Прямой метод вращений. 3. Итерационный метод вращений. § 3. Неэрмитовы матрицы 2. Итерационные методы. 3. Некоторые частные случаи. § 4. Частичная проблема собственных значений 2. Метод линеаризации. 3. Степенной метод (счет на установление) 4. Обратные итерации со сдвигом. ЗАДАЧИ ГЛАВА VII. ПОИСК МИНИМУМА § 1. Минимум функции одного переменного 2. Золотое сечение.  3. Метод парабол. 4. Стохастические задачи. § 2. Минимум функции многих переменных 2. Спуск по координатам. 3. Наискорейший спуск. 4. Метод оврагов. 5. Сопряженные направления. 6. Случайный поиск. § 3. Минимум в ограниченной области 2. Метод штрафных функций. 3. Линейное программирование. 4. Симплекс-метод 5. Регуляризация линейного программирования. § 4. Минимизация функционала 2. Метод пробных функций. 3. Метод Ритца. ЗАДАЧИ ГЛАВА VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. Задача Коши 2. Методы решения. 4. Метод малого параметра. 5. Метод ломаных. 7. Метод Адамса. 8. Неявные схемы. 9. Специальные методы. 10. Особые точки. 11. Сгущение сетки. § 2. Краевые задачи 2. Метод стрельбы (называемый также баллистическим). 3. Уравнения высокого порядка 4. Разностный метод; линейные задачи. 5. Разностный метод; нелинейные задачи. 6. Метод Галеркина.  7. Разрывные коэффициенты. § 3. Задачи на собственные значения 2. Метод стрельбы. 3. Фазовый метод. 5. Метод дополненного вектора. 6. Метод Галеркина. ЗАДАЧИ ГЛАВА IX. УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2. Точные методы решения. 3. Автомодельность и подобие. 4. Численные методы. § 2. Аппроксимация 2. Явные и неявные схемы. 3. Невязка. 4. Методы составления схем. 5. Аппроксимация и ее порядок. § 3. Устойчивость 2. Основные понятия. 4. Метод разделения переменных. 5. Метод энергетических неравенств. 6. Операторные неравенства. § 4. Сходимость 2. Оценки точности. 3. Сравнение схем на тестах. ЗАДАЧИ ГЛАВА X. УРАВНЕНИЕ ПЕРЕНОСА 2. Схемы бегущего счета. 3. Геометрическая интерпретация устойчивости. 4. Многомерное уравнение. 5. Перенос с поглощением. 6. Монотонность схем. 7. Диссипативные схемы. § 2. Квазилинейное уравнение 2. Однородные схемы. 3. Псевдовязкость.  4. Ложная сходимость. 5. Консервативные схемы. ЗАДАЧИ ГЛАВА XI. ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ § 1. Одномерные уравнения 3. Асимптотическая устойчивость неявной схемы. 4. Монотонность. 6. Наилучшая схема. 7. Криволинейные координаты. 8. Квазилинейное уравнение. § 2. Многомерное уравнение 2. Продольно-поперечная схема 3. Локально-одномерный метод. 4. Метод Монте-Карло. ЗАДАЧИ ГЛАВА XII. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ § 1. Счет на установление 2. Оптимальный шаг. 3. Чебышевский набор шагов. § 2. Вариационные и вариационно-разностные методы 2. Стационарные разностные схемы. 3. Прямые методы решения. 4. Итерационные методы. ЗАДАЧИ ГЛАВА XIII. ГИПЕРБОЛИЧЕСКИЕ УРАВНЕНИЯ § 1. Волновое уравнение 2. Неявная схема. 3. Двуслойная акустическая схема. 4. Инварианты. 5. Явная многомерная схема. 6. Факторизованные схемы. § 2. Одномерные уравнения газодинамики 2. Псевдовязкость.  3. Схема «крест». 4. Неявная консервативная схема. 5. О других схемах. ЗАДАЧИ ГЛАВА XIV. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ § 1. Корректно поставленные задачи 2. Разностный метод. 5. Метод Галеркина § 2. Некорректные задачи 2. Вариационный метод регуляризации. 3. Уравнение Эйлера. 4. Некоторые приложения. 5. Разностные схемы. ЗАДАЧИ ГЛАВА XV. СТАТИСТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТА 2. Величина и доверительный интервал. 3. Сравнение величин. 4. Нахождение стохастической зависимости. ЗАДАЧИ ПРИЛОЖЕНИЕ. ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ ЛИТЕРАТУРА |
Функция СТЬЮДЕНТ.ОБР.2Х — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще. ..Меньше
..Меньше
Возвращает двустороннее обратное t-распределение Стьюдента.
Синтаксис
СТЬЮДЕНТ.ОБР.2Х(вероятность;степени_свободы)
Аргументы функции СТЬЮДЕНТ.ОБР.2Х описаны ниже.
-
Вероятность Обязательный. Вероятность, соответствующая t-распределению Стьюдента.
-
Степени_свободы Обязательный. Число степеней свободы, характеризующее распределение.
Замечания
-
Если хотя бы один из аргументов не является числом, то Т.
ОV.2Х возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если вероятность <= 0 или вероятность > 1, то Т.ОV.2Х возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значение «степени_свободы» не является целым, оно усекается.
-
Если deg_freedom < 1, то ОКБ.ОV.2Х возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Функция СТЬЮДЕНТ.ОБР.2Х возвращает значение t, для которого P(|X| > t) = вероятность, где X — случайная переменная, соответствующая t-распределению, и P(|X| > t) = P(X < -t или X > t).

-
Одностороннее t-значение может быть получено при замене аргумента «вероятность» на 2*вероятность. Для вероятности 0,05 и 10 степенях свободы двустороннее значение вычисляется по формуле СТЬЮДЕНТ.ОБР.2Х(0,05;10) и равно 2,28139. Одностороннее значение для той же вероятности и числа степеней свободы может быть вычислено по формуле СТЬЮДЕНТ.ОБР.2Х(2*0,05;10), возвращающей значение 1,812462.
Если задано значение вероятности, функция СТЬЮДЕНТ.ОБР.2Х ищет значение x, для которого функция СТЬЮДЕНТ.РАСП.2Х(x, степени_свободы, 2) = вероятность. Поэтому точность функции СТЬЮДЕНТ.ОБР.2Х зависит от точности СТЬЮДЕНТ.РАСП.2Х.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
0,546449 |
Вероятность, соответствующая двустороннему распределению Стьюдента. |
|
|
60 |
Степени свободы |
|
|
Формула |
Описание (результат) |
Результат |
|
=СТЬЮДЕНТ. |
T-значение t-распределения Стьюдента для приведенных выше условий (0,606533076) |
0,606533 |
8.3: Среднее значение одной совокупности с использованием t-распределения Стьюдента
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 20399
- OpenStax
- OpenStax
На практике мы редко знаем стандартное отклонение генеральной совокупности. В прошлом, когда размер выборки был большим, это не представляло проблемы для статистиков. Они использовали стандартное отклонение выборки \(s\) в качестве оценки \(\сигма\) и продолжали, как и прежде, вычислять доверительный интервал с достаточно близкими результатами. Однако статистики столкнулись с проблемами, когда размер выборки был небольшим. Небольшой размер выборки вызвал неточности в доверительном интервале.
Они использовали стандартное отклонение выборки \(s\) в качестве оценки \(\сигма\) и продолжали, как и прежде, вычислять доверительный интервал с достаточно близкими результатами. Однако статистики столкнулись с проблемами, когда размер выборки был небольшим. Небольшой размер выборки вызвал неточности в доверительном интервале.
Уильям С. Госет (1876–1819 гг.)37) пивоварни Guinness в Дублине, Ирландия, столкнулась с этой проблемой. Его эксперименты с хмелем и ячменем дали очень мало образцов. Простая замена \(\sigma\) на \(s\) не дала точных результатов, когда он попытался вычислить доверительный интервал. Он понял, что не может использовать для расчетов нормальное распределение; он обнаружил, что фактическое распределение зависит от размера выборки. Эта проблема привела его к «открытию» так называемого t-распределения Стьюдента. Название происходит от того факта, что Госсет писал под псевдонимом «Студент».
Вплоть до середины 1970-х годов некоторые статистики использовали аппроксимацию нормального распределения для больших размеров выборки и только \(t\)-распределение Стьюдента только для размеров выборки не более 30. С графическими калькуляторами и компьютерами практика теперь использовать t-распределение Стьюдента всякий раз, когда \(s\) используется в качестве оценки для \(\sigma\). Если вы возьмете простую случайную выборку размером \(n\) из совокупности, которая имеет примерно нормальное распределение со средним значением \(\mu\) и неизвестным стандартным отклонением совокупности \(\sigma\), и рассчитаете \(t\ )-оценка
С графическими калькуляторами и компьютерами практика теперь использовать t-распределение Стьюдента всякий раз, когда \(s\) используется в качестве оценки для \(\sigma\). Если вы возьмете простую случайную выборку размером \(n\) из совокупности, которая имеет примерно нормальное распределение со средним значением \(\mu\) и неизвестным стандартным отклонением совокупности \(\sigma\), и рассчитаете \(t\ )-оценка
\[t = \dfrac{\bar{x} — \mu}{\left(\dfrac{s}{\sqrt{n}}\right)},\]
, то \(t\)-показатели следуют t-распределению Стьюдента с \(n – 1\) степенями свободы. \(t\)-оценка имеет ту же интерпретацию, что и z -оценка. Он измеряет, насколько далеко \(\bar{x}\) от своего среднего значения \(\mu\). Для каждого размера выборки \(n\) существует разное t-распределение Стьюдента.
Степени свободы, \(n – 1\), получены из расчета выборочного стандартного отклонения \(s\). В 2.8 мы использовали \(n\) отклонений (\(x — \bar{x}\)) значений) для вычисления \(s\). Поскольку сумма отклонений равна нулю, мы можем найти последнее отклонение, зная остальные \(n – 1\) отклонений. Остальные \(n – 1\) отклонения могут изменяться или варьироваться свободно. Мы называем число \(n – 1\) степенями свободы (df).
Поскольку сумма отклонений равна нулю, мы можем найти последнее отклонение, зная остальные \(n – 1\) отклонений. Остальные \(n – 1\) отклонения могут изменяться или варьироваться свободно. Мы называем число \(n – 1\) степенями свободы (df).
Для каждого размера выборки \(n\) существует разное t-распределение Стьюдента.
Свойства \(t\)-распределения Стьюдента
- График для \(t\)-распределения Стьюдента подобен стандартной нормальной кривой.
- Среднее значение \(t\)-распределения Стьюдента равно нулю, и распределение симметрично относительно нуля.
- \(t\)-распределение Стьюдента имеет большую вероятность в своих хвостах, чем стандартное нормальное распределение, потому что распространение \(t\)-распределения больше, чем распространение стандартного нормального. Таким образом, график распределения Стьюдента \(t\)-распределения будет толще в хвостах и короче в центре, чем график стандартного нормального распределения.

- Точный вид \(t\)-распределения Стьюдента зависит от степеней свободы. По мере увеличения степеней свободы график \(t\)-распределения Стьюдента становится все более похожим на график стандартного нормального распределения.
- Предполагается, что основная совокупность отдельных наблюдений имеет нормальное распределение с неизвестным средним значением совокупности \(\mu\) и неизвестным стандартным отклонением совокупности \(\sigma\). Размер основной популяции, как правило, не имеет значения, если только он не очень мал. Если он имеет форму колокола (нормальный), то предположение выполняется и не нуждается в обсуждении. Предполагается случайная выборка, но это совершенно отличное от нормальности предположение.
Визуально сравните распределение \(t\) Стьюдента с нормальным распределением
На приведенных ниже графиках стандартное нормальное распределение показано черным цветом, а распределение Стьюдента — красным. Переместите ползунок, чтобы увидеть, как изменение размера выборки и, следовательно, степеней свободы изменяет распределение \(t\) студента.
n = 10, df = 9
Калькуляторы и компьютеры могут легко вычислить \(t\) -вероятностей любого Стьюдента.
Обозначение для t-распределения Стьюдента (с использованием T в качестве случайной величины):
- \(T \sim t_{df}\), где \(df = n – 1\).
- Например, если у нас есть выборка размером \(n = 20\) единиц, то мы вычисляем степени свободы как \(df = n — 1 = 20 — 1 = 19\) и записываем распределение как \ (Т \sim t_{19}\).
Если стандартное отклонение генеральной совокупности неизвестно , предельная ошибка для среднего значения генеральной совокупности составляет:
- \(E = \left(t_{\alpha/2}\right)\left(\frac{s}{\sqrt{n}}\right)\),
- \(t_{\alpha/2}\) — это \(t\)-показатель с площадью справа, равной \(\frac{\alpha}{2}\),
- используют \(df = n – 1\) степеней свободы, а
- \(s =\) стандартное отклонение выборки.

Формат доверительного интервала:
\[(\бар{х} — Е, \бар{х} + Е).\]
Пример \(\PageIndex{1}\): Иглоукалывание
Предположим, вы изучаете акупунктуру, чтобы определить, насколько она эффективна в облегчении боли. Вы измеряете сенсорные скорости для 15 субъектов с предоставленными результатами. Используйте выборочные данные, чтобы построить 95% доверительный интервал для средней сенсорной скорости для популяции (предполагаемой нормальной), из которой вы взяли данные.
8,6; 9,4; 7,9; 6,8; 8,3; 7,3; 9,2; 9,6; 8,7; 11,4; 10,3; 5,4; 8.1; 5,5; 6.9
Ответ
Используйте доверительный интервал для среднего значения с данными.
Введите данные, разделенные запятыми (точки с запятой необходимо заменить запятыми).
Введите 0,95 для CL.
Hit Calculate
95% доверительный интервал составляет (7,3006, 9,1527)
При 95% достоверности средний уровень сенсорной чувствительности для людей, получающих иглоукалывание, составляет от 7,3006 до 9,1527.
Калькулятор доверительного интервала со статистикой (сигма неизвестна)
Введите размер выборки (n), среднее значение выборки (\(\bar{x}\)), стандартное отклонение выборки (s) и доверительный уровень (CL ). Запишите уровень достоверности в виде десятичной дроби. Например, для 9Уровень достоверности 5%, введите 0,95 для CL. Затем нажмите «Вычислить» и, предполагая, что население распределено нормально, доверительный интервал будет рассчитан для вас.
| н: | \(\ полоса {х}\): | с: | Класс: |
| Нижняя граница | Верхняя граница |
Калькулятор ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ДАННЫМИ (сигма неизвестна)
Введите значения из набора данных, разделенные запятыми, например, 2,4,5,8,11,2. Затем введите уровень достоверности, CL, и нажмите «Рассчитать». Запишите уровень достоверности в виде десятичной дроби. Например, для доверительного уровня 95% введите 0,95 для CL.
Затем введите уровень достоверности, CL, и нажмите «Рассчитать». Запишите уровень достоверности в виде десятичной дроби. Например, для доверительного уровня 95% введите 0,95 для CL.
Данные:
| CL: | \(\ полоса {х}\): | с: | Нижняя граница | Верхняя граница |
Упражнение \(\PageIndex{2}\)
Вы изучаете гипнотерапию, чтобы определить, насколько она эффективна в увеличении количества часов сна субъектов каждую ночь. Вы измеряете количество часов сна для 12 испытуемых со следующими результатами. Постройте 95% доверительный интервал для среднего количества часов сна для популяции (предполагаемой нормальной), из которой вы взяли данные.
8.2; 9.1; 7,7; 8,6; 6,9; 11,2; 10,1; 9,9; 8,9; 9,2; 7,5; 10.5
Ответ
(8.1634, 9.8032)
Пример \(\PageIndex{2}\): Проект Human Toxome Project
Проект Human Toxome Project (HTP) направлен на изучение масштабов промышленного загрязнения человеческого организма. Промышленные химикаты могут попасть в организм через загрязнение или в составе потребительских товаров. В октябре 2008 года ученые из ПВТ протестировали образцы пуповинной крови 20 новорожденных в США. Пуповинная кровь группы «In utero/newborn» была проверена на наличие 430 промышленных соединений, загрязняющих веществ и других химических веществ, включая химические вещества, связанные с токсичностью для мозга и нервной системы, токсичностью для иммунной системы, репродуктивной токсичностью и проблемами с фертильностью. Есть опасения по поводу воздействия некоторых химических веществ на мозг и нервную систему. В таблице ниже показано, сколько целевых химических веществ было обнаружено в пуповинной крови каждого младенца.
Промышленные химикаты могут попасть в организм через загрязнение или в составе потребительских товаров. В октябре 2008 года ученые из ПВТ протестировали образцы пуповинной крови 20 новорожденных в США. Пуповинная кровь группы «In utero/newborn» была проверена на наличие 430 промышленных соединений, загрязняющих веществ и других химических веществ, включая химические вещества, связанные с токсичностью для мозга и нервной системы, токсичностью для иммунной системы, репродуктивной токсичностью и проблемами с фертильностью. Есть опасения по поводу воздействия некоторых химических веществ на мозг и нервную систему. В таблице ниже показано, сколько целевых химических веществ было обнаружено в пуповинной крови каждого младенца.
| 79 | 145 | 147 | 160 | 116 | 100 | 159 | 151 | 156 | 126 |
| 137 | 83 | 156 | 94 | 121 | 144 | 123 | 114 | 139 | 99 |
Используйте эти выборочные данные для построения 90% доверительного интервала для среднего количества целевых промышленных химикатов, обнаруженных в крови младенца.
Ответ
Используйте доверительный интервал для среднего значения с данными.
Введите данные, разделенные запятыми (точки с запятой необходимо заменить запятыми.)
Введите 0,90 для КЛ.
Hit Calculate
90% доверительный интервал составляет (7,3006, 9,1527)
Мы оцениваем с 90% достоверностью, что среднее количество всех целевых промышленных химикатов, обнаруженных в пуповинной крови в США, составляет от 117,412 до 137,488.
Упражнение \(\PageIndex{2}\)
Случайную выборку статистических данных студентов попросили оценить общее количество часов, которые они тратят на просмотр телевизора в среднем в неделю. Ответы заносятся в табл. Используйте этот образец данных, чтобы построить 98% доверительный интервал для среднего количества часов, которое учащиеся статистики проводят за просмотром телевизора в течение одной недели.
| 0 | 3 | 1 | 20 | 9 |
| 5 | 10 | 1 | 10 | 4 |
| 14 | 2 | 4 | 4 | 5 |
Ответ
Используйте доверительный интервал для среднего значения с данными.
Введите данные, разделенные запятыми (точки с запятой необходимо заменить запятыми).
Введите 0,98 для CL.
Hit Calculate
98% доверительный интервал равен (2,397, 9,869)
Мы оцениваем с 98% достоверностью, что среднее количество всех часов, которые студенты-статистики тратят на просмотр телевизора в неделю, составляет от 2,397 и 9.869.
- «Лучшие малые компании Америки». Forbes, 2013. Доступно на сайте http://www.forbes.com/best-small-companies/list/ (по состоянию на 2 июля 2013 г.).
- Данные из Microsoft Bookshelf .
- Данные с сайта http://www.businessweek.com/.
- Данные с сайта http://www.forbes.com/.
- «Каталог раскрытия данных: отчет руководства PAC и спонсоров, 2012 г.». Федеральная избирательная комиссия. Доступно на сайте http://www.fec.gov/data/index.jsp (по состоянию на 2 июля 2013 г.).
- «Проект Human Toxome: картирование загрязнения у людей».
 Экологическая рабочая группа. Доступно на сайте http://www.ewg.org/sites/humantoxome…tero%2Fnewborn (по состоянию на 2 июля 2013 г.).
Экологическая рабочая группа. Доступно на сайте http://www.ewg.org/sites/humantoxome…tero%2Fnewborn (по состоянию на 2 июля 2013 г.). - «Описание метаданных списка лидеров PAC». Федеральная избирательная комиссия. Доступно на сайте http://www.fec.gov/finance/disclosur…pPacList.shtml (по состоянию на 2 июля 2013 г.).
- Степени свободы (\(df\))
- количество объектов в выборке, которые могут свободно варьироваться 9{2}}\), где \(\mu\) — среднее значение распределения, а \(\sigma\) — стандартное отклонение, обозначение: \(X \sim N(\mu,\sigma)\). Если \(\mu = 0\) и \(\sigma = 1\), RV называется стандартным нормальным распределением .
- Стандартное отклонение
- число, равное квадратному корню из дисперсии и измеряющее, насколько далеко значения данных от их среднего значения; обозначение: \(s\) для стандартного отклонения выборки и \(\sigma\) для стандартного отклонения совокупности
- Студенческая т -Раздача
- исследовано и сообщено Уильямом С.
 Госсеттом в 1908 году и опубликовано под псевдонимом Студент; основные характеристики случайной величины (RV):
Госсеттом в 1908 году и опубликовано под псевдонимом Студент; основные характеристики случайной величины (RV): - Непрерывен и принимает любые действительные значения.
- PDF симметричен относительно своего среднего значения, равного нулю. Однако оно более распространено и более плоско на вершине, чем при нормальном распределении.
- Оно приближается к стандартному нормальному распределению по мере увеличения \(n\).
- Имеется «семейство \(t\)-распределений: каждый представитель семейства полностью определяется числом степеней свободы, которое на единицу меньше числа данных.
Барбара Илловски и Сьюзан Дин (Колледж Де Анза) со многими другими авторами. Контент, созданный OpenStax College, находится под лицензией Creative Commons Attribution License 4.0. Скачать бесплатно на http://cnx.org/contents/30189442-699…[email protected].
Эта страница под названием 8. 3: Среднее значение одной совокупности с использованием студенческого t-распределения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
3: Среднее значение одной совокупности с использованием студенческого t-распределения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- источник@https://openstax.
 org/details/books/introductory-statistics
org/details/books/introductory-statistics - источник[1]-stats-6953
- источник[1]-stats-765
- источник[2]-stats-6953
- t-распределение Стьюдента
- источник@https://openstax.
t-распределение и степени свободы — AnalystPrep
t-распределение Стьюдента представляет собой колоколообразное распределение вероятностей, симметричное относительно своего среднего значения. Это распределение считается наиболее подходящим для построения доверительных интервалов в следующих случаях:
- При работе с небольшими выборками из менее 30 элементов.
- Когда дисперсия населения неизвестна.
- Когда задействованное распределение либо нормальное, либо приблизительно нормальное.
Помимо использования при построении доверительных интервалов, t-распределение используется для проверки следующего:
- Среднее значение отдельной совокупности.

- Различия между двумя средними значениями генеральной совокупности.
- Средняя разница между парными (зависимыми) популяциями.
- Коэффициент корреляции населения.
При отсутствии явной нормальности данного распределения t-распределение все же может быть пригодным для использования, если размер выборки достаточно велик для применения центральной предельной теоремы. В таком случае распределение считается приблизительно нормальным.
t-статистика, также называемая t-оценкой, определяется по формуле:
$$ t = \cfrac {(x – \mu)}{\left(\cfrac {S}{\sqrt n} \right )} $$
Где:
\(x\) = выборочное среднее.
\(μ\) = Среднее значение населения.
\(S\) = стандартное отклонение выборки.
\(n\) = размер выборки.
Связь между t-распределением и нормальным распределением
t-распределение позволяет нам анализировать распределения, которые не являются совершенно нормальными. У t-распределения более толстые хвосты по сравнению с нормальным распределением.
Форма t-распределения зависит от числа степеней свободы. Отсюда следует, что как число ф.р. увеличивается, распределение становится более «шипообразным», а его хвосты становятся тоньше, приближаясь к хвостам нормального распределения.
Стьюдентное распределение обладает следующими свойствами:
- Стьюдентное распределение симметрично. Это колоколообразное распределение, которое принимает форму нормального распределения и имеет нулевое среднее значение.
- t-распределение определяется одним параметром, то есть степенями свободы (df) \(v= n – 1\), где \(n\) – размер выборки. Его \(\text {дисперсия} = \frac {v}{ \left(\frac {v}{2} \right) }\), где \(v\) представляет число степеней свободы, а \(v ≥ 2\).
- Дисперсия всегда больше 1. Обратите внимание, однако, что она становится очень близкой к единице, когда имеется много степеней свободы. При большом числе степеней свободы t-распределение напоминает нормальное распределение.
- Хвосты t-распределения толще и менее остроконечные, чем у нормального распределения, что указывает на большую вероятность хвостов.

- Форма t-распределения меняется с изменением степеней свободы. Чем больше ф.р. увеличивается, тем больше форма t-распределения похожа на стандартное нормальное распределение.
У t-распределения, как и у некоторых других распределений, есть только один параметр: Степени свободы (d.f.). Количество степеней свободы относится к количеству независимых наблюдений (общее количество наблюдений меньше 1):
$$ v = n-1 $$
Следовательно, выборка из 10 наблюдений или элементов будет проанализирована с использованием t-распределения с 9 степенями свободы. Точно так же 6 ф.р. распределение будет использоваться для размера выборки из 7 наблюдений.
Обозначения Стандартной практикой статистиков является использование \(t_α\) для представления t-показателя с кумулятивной вероятностью \((1 – α)\). Следовательно, если бы нас интересовал t-показатель с кумулятивной вероятностью 0,9, α был бы равен 1–0,9. = 0,1. Мы бы обозначили статистику как \(t_0.1\).
= 0,1. Мы бы обозначили статистику как \(t_0.1\).
Однако значение \(t_α\) зависит от числа степеней свободы и часто записывается как \(t_{α,n-1}\). Например, мы могли бы написать \(t_{0,05,2}= 2,92\), где второй нижний индекс (2) представляет число ф.р.
Важные соотношенияКак и нормальное распределение, t-распределение симметрично относительно среднего. Таким образом,
$$ t_{\alpha}= -t_{1 — \alpha} \text{ и } t_{1 — \alpha} = -t_{\alpha} $$
В таблице ниже представлены односторонние доверительные интервалы и различные вероятности для диапазона степеней свободы.
ВопросКакое из следующих утверждений о t-распределении наиболее вероятно верно?
- Распределение At менее разбросано, чем стандартное нормальное распределение.
- t-распределение симметрично относительно нуля.
- По мере увеличения степеней свободы t-распределение становится более широким и плоским.



 ОБР.2Х(A2;A3)
ОБР.2Х(A2;A3)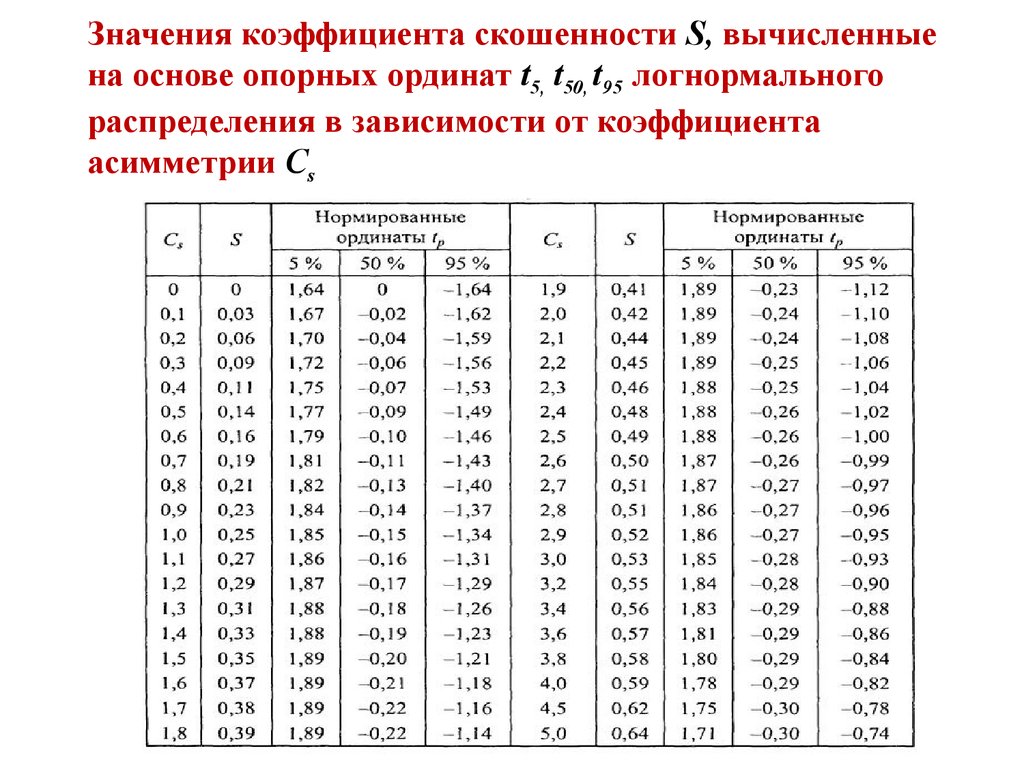

 Экологическая рабочая группа. Доступно на сайте http://www.ewg.org/sites/humantoxome…tero%2Fnewborn (по состоянию на 2 июля 2013 г.).
Экологическая рабочая группа. Доступно на сайте http://www.ewg.org/sites/humantoxome…tero%2Fnewborn (по состоянию на 2 июля 2013 г.). Госсеттом в 1908 году и опубликовано под псевдонимом Студент; основные характеристики случайной величины (RV):
Госсеттом в 1908 году и опубликовано под псевдонимом Студент; основные характеристики случайной величины (RV):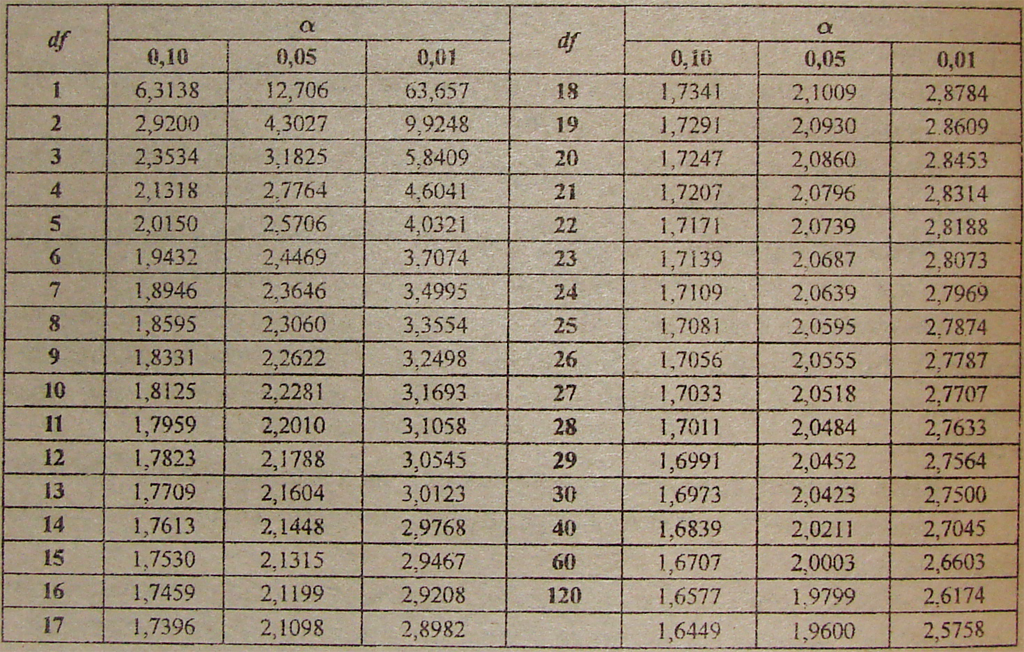 org/details/books/introductory-statistics
org/details/books/introductory-statistics