Составить уравнение касательной к графику функции в точке: Уравнение касательной к графику функции — урок. Алгебра, 10 класс.

№ 29.12 ГДЗ Алгебра 10-11 класс Мордкович. Помогите составить уравнение касательной – Рамблер/класс

№ 29.12 ГДЗ Алгебра 10-11 класс Мордкович. Помогите составить уравнение касательной – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Составьте уравнение касательной к графику функции у = f(x) в точке с абсциссой х = а, если:

а) f(x) = х² , а = 3;
б) f(x) = 2 — х — х³, а = 0;
в) f(x) = х³, а = 1;
г) f(x) = х³ — 3х + 5, а = -1.
 

ответы

Вот такое уравнение:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х — 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)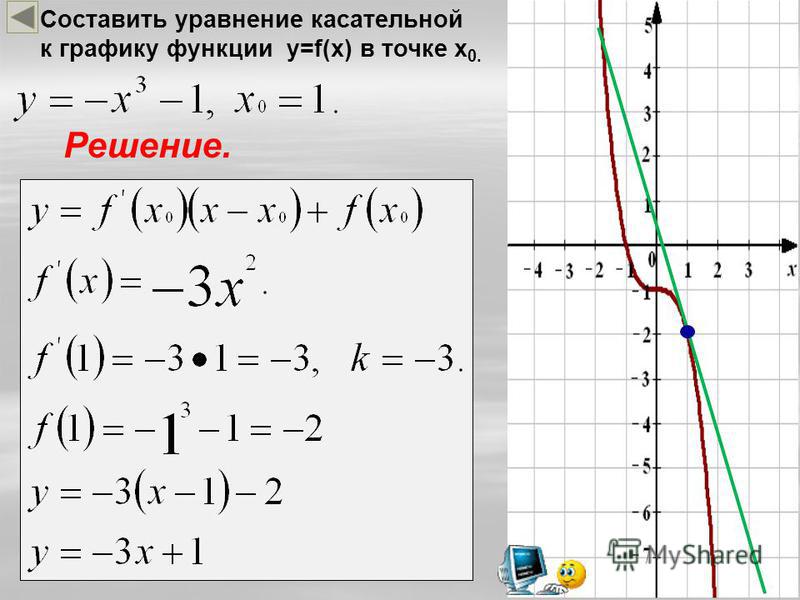

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

Касательная к графику

 

Касательная к эллипсу.

Эллипс с центром  в точке   с полуосями a и b задается уравнением  .

Эллипс также  как и окружность можно задать объединением двух функций — верхнего и нижнего полуэллипса: 

Касательные в вершинах эллипса параллельны либо оси  абсцисс (на рисунке ниже изображены синими прямыми), либо оси ординат (на рисунке ниже изображены красными прямыми).

Пример.

Написать уравнения  касательных к эллипсу   в точках с абсциссамиx=2.

Решение.

Найдем сначала  ординаты точек касания, соответствующих  абсциссам x=2. Для этого подставим значение x=2 в уравнение эллипса и решим полученное уравнение относительно y: 

Таким образом, получаем две точки касания   и  , принадлежащие верхнему и нижнему полуэллипсу соответственно.

Найдем уравнения  полуэллипсов, для этого разрешим уравнение эллипса относительноy: 

То есть, верхний  полуэллипс задается функцией  , а нижний —  .

Теперь можем  действовать по стандартному алгоритму  для составления уравнения касательной  к графику функции в точке.

Первая касательная  в точке  : 

Вторая касательная  в точке  : 

Графическая иллюстрация.

 

Касательная к гиперболе.

Гипербола с центром  в точке   и вершинами   и  задается равенством  (рисунок ниже слева), а с вершинами   и   — равенством   (рисунок ниже справа).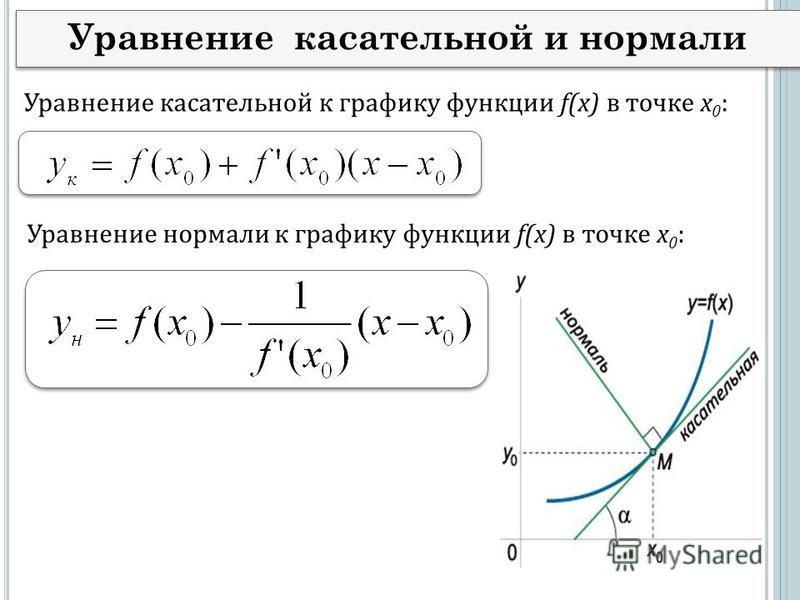

В виде объединения  двух функций гипербола представима  как 
 
 или  .

В вершинах гиперболы  касательные параллельны оси Оу

 для первого случая и параллельны оси Ох для второго.

Таким образом, для  нахождения уравнения касательной  к гиперболе, выясняем какой функции принадлежит точка касания, и действуем обычным образом.

Возникает логичный вопрос, как определить какой из функций принадлежит точка. Для  ответа на него подставляем координаты в каждое уравнение и смотрим, какое из равенств обращается в тождество. Рассмотрим это на примере.

Пример.

Составьте уравнение  касательной к гиперболе   в точке  .

 

Решение.

Запишем гиперболу  в виде двух функций: 

Выясним к какой функции принадлежит точка касания  .

Для первой функции  , следовательно, точка не принадлежит графику этой функции.

Для второй функции  , следовательно, точка принадлежит графику этой функции.

Находим угловой  коэффициент касательной: 

Таким образом, уравнение  касательной имеет вид  .

Графическая иллюстрация.

Касательная к параболе.

Для составления  уравнения касательной к параболе вида   в точке  пользуемся стандартной схемой, и уравнение касательной записываем как  . Касательная к графику такой параболы в вершине параллельна осиОх.

Параболу   сначала зададим объединением двух функций. Для этого разрешим это уравнение относительно y: 

Теперь выясняем к какой из функций принадлежит точка касания   и действуем по стандартной схеме.

Касательная к графику  такой параболы в вершине параллельна  оси Оу.

Пример.

Написать уравнение  касательной к графику параболы  , если угол наклона касательной равен  .

Решение.

Представим параболу через две функции: 

Мы знаем, что  угловой коэффициент 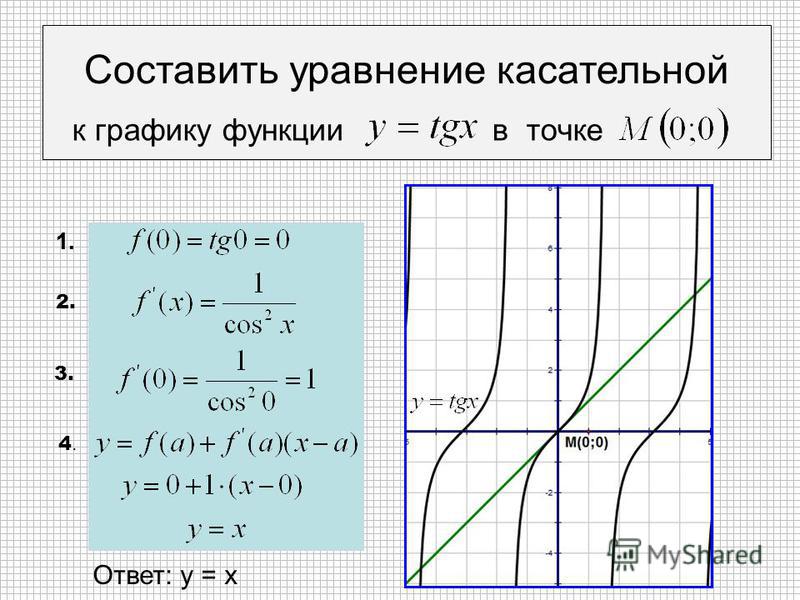касательной  равен значению производной функции  в точке   и равен тангенсу угла наклона:  .

Из этого равенства мы можем найти абсциссу точки касания.

Для первой функции: 

Полученное уравнение  действительных корней не имеет, следовательно, к этой функции не существует касательной  с углом наклона  .

Для второй функции: 

Получаем точку  касания  .

Таким образом, уравнение  искомой касательной имеет вид  .

Графическая иллюстрация.

Модуль 13. Неявное дифференцирование

В этом уроке обсуждаются неявное дифференцирование, частные производные, горизонтальные касательные и решение нелинейных систем.

---

Рассмотрим лист x ³ + y ³ 9 xy = 0 из урока 13.1. Как бы вы нашли наклон этой кривой в данной точке? Как и прежде, для нахождения наклона будет использоваться производная.

Неявное дифференцирование

Один из способов найти наклон — взять производную от обеих частей уравнения по отношению к

x .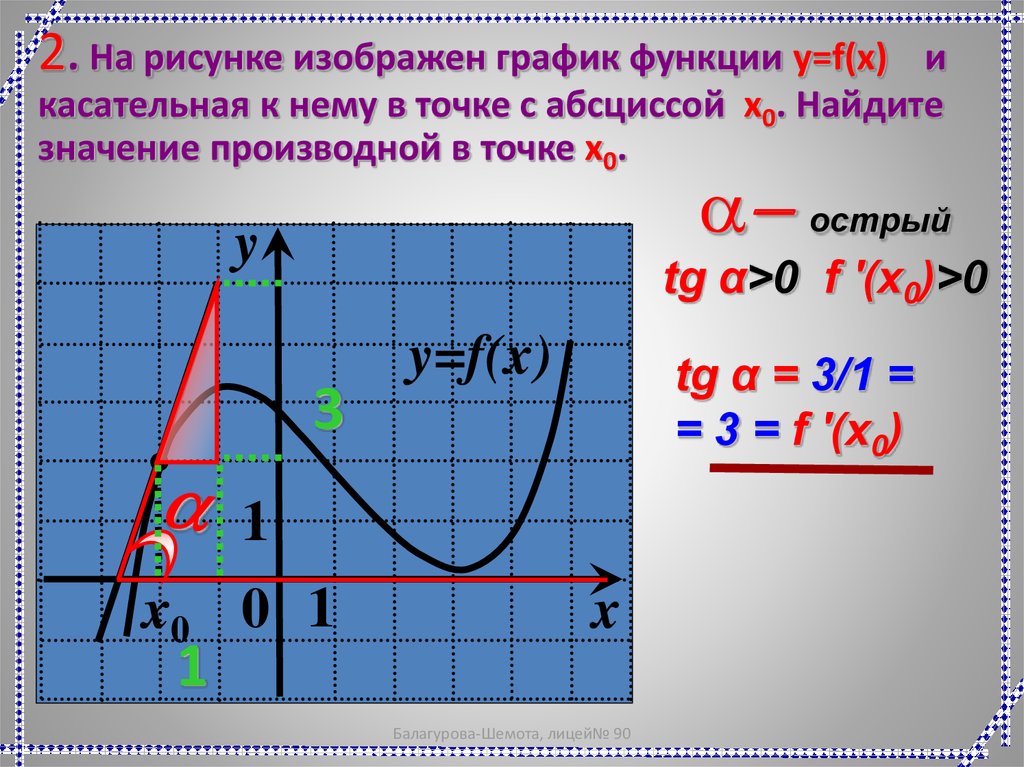 При получении производной от выражения, содержащего y , вы должны рассматривать y как функцию x . Этот метод называется неявным дифференцированием и проиллюстрирован ниже.

Неявное дифференцирование листа x ³ + y ³ 9 xy = 0 выход .

Обратите внимание, что термин -9 xy считается произведением двух функций, и правило произведения используется для нахождения его производной, .

Решение для

Решение выражения для дает производную:

Обратите внимание, что производная содержит как x , так и y . Это характерно для неявной дифференциации.

Использование TI-89 для неявного дифференцирования

Другой метод, используемый для поиска с вашим TI-89 и следующей теоремой из исчисления:

Если з — это дифференцируемая функция x и y , такая, что z ( x , y ) = 0 определяет y неявно как дифференцируемую функцию от

4 x 90, тогда

Символ называется частной производной z относительно х . Это значит взять производную от z по x при обработке y как константы. Сходным образом, является частной производной z относительно y . Чтобы найти эту частную производную, возьмите производную х по отношению к y , рассматривая х как константу.

Нахождение частных производных

С z 1= x ³ + у ³ 9 ху , можно найти на TI-89 с производной командой.

Обратите внимание, что скобки используются для обозначения переменных x и y функции z1.

• Введите — d (z1(x,y),x)/ d (z1(x,y),y)

13.2.1 Используя приведенное выше выражение, найдите наклон линии, касательной к листу в точке (4,2). Щелкните здесь, чтобы получить ответ.

График z 1, показанный в уроке 13.1, предполагает, что одна ветвь кривой имеет касательную по горизонтали в точке (0, 0), а другая ветвь имеет касательную по вертикали в точке (0, 0).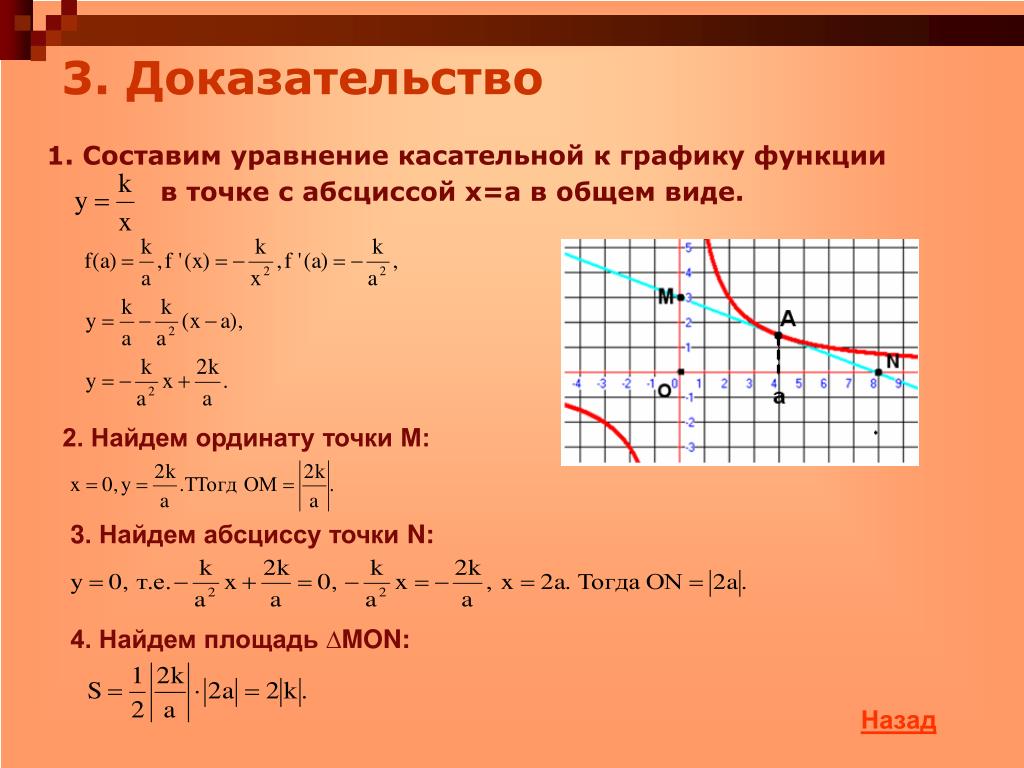 Формула для dy / dx принимает вид 0/0 в точке (0, 0).

Горизонтальные и вертикальные касательные Если и числитель, и знаменатель формулы dy / dx равны нулю, касательная(и) в этой точке может быть горизонтальной, вертикальной или ни той, ни другой, и единственный способ определить это – посмотреть на предел.

Нахождение горизонтальных касательных

Если наклон равен нулю, касательная горизонтальна, что происходит, когда числитель равен нулю, а знаменатель не равен нулю.

Решение нелинейных систем уравнений

В этом случае вы можете найти координаты точек на листе, найдя решения нелинейной системы уравнений, где одно уравнение определяет множество точек на графике, а второе уравнение определяет множество точек, где производная равна нулю. Решения системы ниже — это точки на x ³ + y ³ 9 xy = 0, где касательная может быть горизонтальной.

x ³ + y ³ 9 xy = 0 и 3 y x ² =

Решения системы можно найти, используя команду «Решить» для поиска значений двух переменных x и y , которые делают оба уравнения верными. Обратите внимание, что круглые скобки используются для обозначения того, что z1( x , y ) является функцией x и y и что искомые переменные x и y заключены в фигурные скобки.

Одно из двух решений . Вам нужно будет прокрутить вправо в области истории, чтобы увидеть другую точку (0, 0). Мы можем отбросить (0, 0), потому что это делает знаменатель dy / dx равным нулю.

13.2.2 Покажите, что касательная горизонтальна в найденной выше точке. Щелкните здесь, чтобы получить ответ.

Посмотрите на график фолиума, чтобы увидеть, кажется ли это разумным.

Нахождение вертикальных касательных

Если знаменатель равна нулю, а числитель не равен нулю, то касательная вертикальна.

Точки, которые удовлетворяют системе x ³ + y ³ xy = 0 и y ² 3 x = 0 — точки народного быть вертикальным.

13.2.3 Найдите координаты точек листа, удовлетворяющих системе выше. Щелкните здесь, чтобы получить ответ.

На рисунке ниже показано, что dy / dx не определен в

Нам нужно знать, что производная бесконечна при иметь вертикальную касательную. Мы можем видеть это на графике, поэтому у нас есть вертикальная касательная в точке . Обратите внимание, что производная имеет вид 0/0 в точке (0, 0).

Что происходит в (0, 0)?

Из графика видно, что есть касательная по горизонтали и касательная по вертикали в точке (0, 0).

Изучение нового неявного отношения

Процедура, используемая при исследовании листа, будет использоваться для исследования неявно определенного отношения y ⁴ = y ² x ² .

График отношения

Соберите все члены в левой части уравнения: 92

Установите следующие значения куба просмотра:

глаз = 90	хмин = 1,5	умин = 1	zмин = 10
глаз = 0	хмакс = 1,5	умакс = 1	zmax = 10
глаз = 0	xрешетка = 14	сетка = 14	nконтур = 5

13.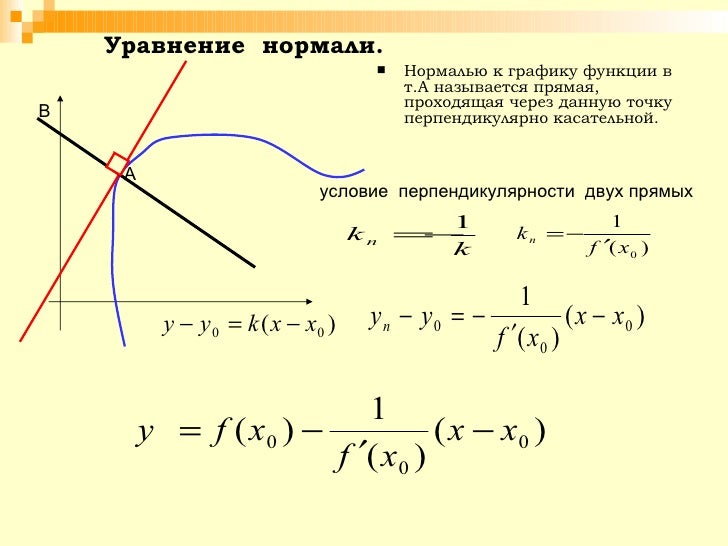 2.4 Отображение графика зависимости. Щелкните здесь, чтобы получить ответ.

13.2.5 Найдите наклон y ⁴ y ² + x ² = 0 в точке . Дифференцируйте вручную, а затем используйте свой TI-89, чтобы проверить результат. Нажмите здесь, чтобы проверить свой ответ.

13.2.6 Где находится касательная к y ⁴ y ² + x ² = 0 по вертикали? Используйте свой TI-89, чтобы просмотреть график и определить, кажутся ли ответы разумными. Щелкните здесь, чтобы получить ответ.

Tan-Line-Calculator-Google Suce

ALLBILDERVIDEOSSHOPPINGMAPSNEWSBücher

SUCOOPTION

Entält Auch Ergebniss www.symbolab.com › … › Derivative Applications

Бесплатный калькулятор касательной — найдите уравнение касательной по заданной точке или отрезку шаг за шагом.

калькулятор касательной — Wolfram|Alpha

www. wolframalpha.com › input › i=tangent+line+ca…

калькулятор касательной. естественный язык; Математический ввод. Используйте режим математического ввода, чтобы напрямую вводить математические обозначения из учебника.

Калькулятор касательной — Mathway

www.mathway.com › Калькулятор › калькулятор касательной

Свободный калькулятор касательной — пошаговые решения, помогающие найти уравнение касательной к заданной кривой в заданной точке.

Калькулятор касательной — eMathHelp

www.emathhelp.net › калькуляторы › calculus-1 › tang…

Калькулятор найдет касательную к явной, полярной, параметрической и неявной кривой в заданной точке , с показанными шагами.

Другой фрагмент или

Как рассчитать касательную?

Что такое касательная кривой?

Что такое уравнение касательной?

Какова формула для наклона касательной?

Калькулятор свободной касательной — Mathepower

www. mathepower.com › tangent

Этот калькулятор прямой находит касательную через точку заданной функции.

Найти наклон и уравнение касательной — онлайн калькулятор данной кривой в данной точке.

Калькулятор касательной — Бесплатный онлайн калькулятор — Byju’s

byjus.com › Калькуляторы › Математические калькуляторы

19.10.2020 · Узнайте, как использовать калькулятор касательной с пошаговой процедурой на BYJU’S. Кроме того, изучите стандартное уравнение и ответы на часто задаваемые вопросы в Интернете.

Найти уравнение касательной — Калькулятор — Solumaths

www.solumaths.com › калькулятор › вычислить › уравнение…

Калькулятор уравнения касательной используется для расчета уравнения касательной к кривой при заданная точка абсцисс с расчетом этапов.

Калькулятор уравнения касательной — Онлайн-поиск линии касательной — dCode

www.dcode.fr › tangent-equation

Инструмент для вычисления касательной к кривой, к функции, в заданной точке (бесконечность вблизи этой точки ) и найти уравнение касательной как функцию.