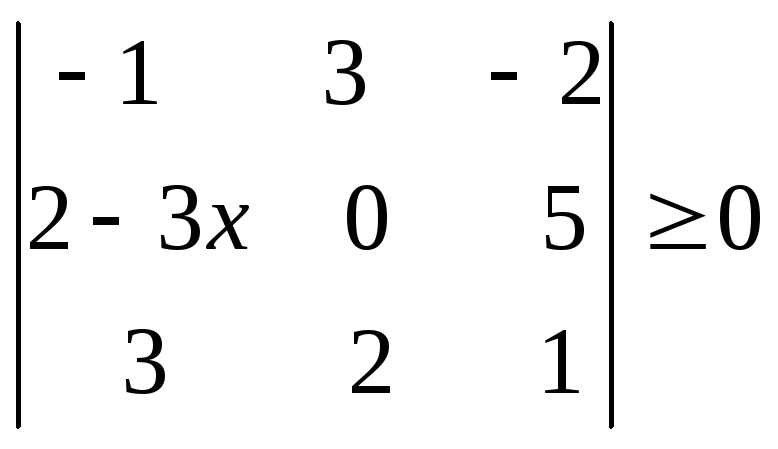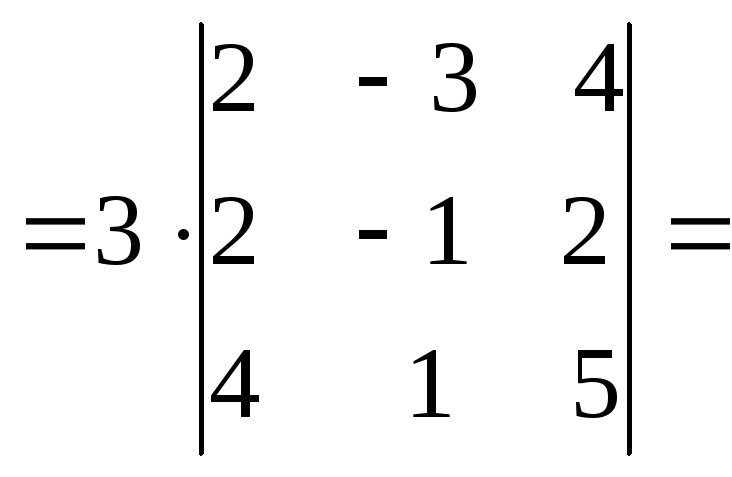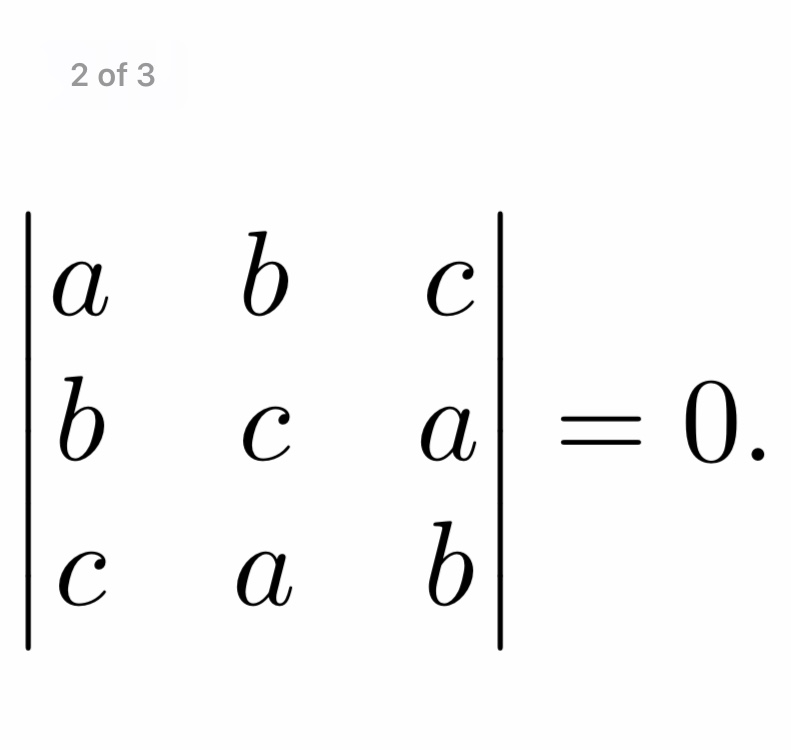Свойства определителей
Билет 1. Матрицы. Основные понятия
Определение. Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов. Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i — номер строки, j — номер столбца.
3) Нулевая матрица: ;
4) Квадратная матрица – если
5) Диагональная матрица (напр. 3-го порядка, где любые числа ):
6) Единичная матрица, где все элементы, кроме главной диаг=0, а эл-ты глав диаг=1
7) Треугольная матрица – квадратн матр, у которой все элементы, расположенные по одну сторону от главной диагонали = 0. Бывают верхние и нижние 3угольные матрицы.
8)
Матрицы произвольного размера называют
квази3угольной, ступенчатой или
трапециевидной.
9) Матрицы равны, если имеют одинаковые размер.
Билет 2. Действия над матрицами. Их св-ва.
1.Умножение матрицы на число.
Произведением матрицы A на число λ называется матрица B= λ *A ,элементы которой bij= λ*Aijдля i=1,2..m, j=1,2..n. Если λ=0, то A*0=0 (нулевая матрица того же размера).
2.Сложение матриц.
Суммой матриц A и B одинакового размера m*n называется матрица C=A+B, элементы которой cij=aij+bij для i=1,2..m, j=1,2..n.
3.Вычитание матриц.
Разность матриц одинакового размера определяется как A-B=A+(-1)*B.
4.Умножение матриц.
Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц A m*k*Bk*nназывается матрица C, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:
, где
Свойства операций сложения и умножения матриц
.
 5)
.
5)
.. 6) .
. 7) .
.
8) (в общем случае). Кроме того, если существует, то может вообще не существовать.
9) , где — единичная квадратная матрица.
10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если , то не следует, что или .
5.Возведение в степень.
Целой положительной степенью квадратной матрицы называют произведение матриц, равных , т.е. .
6.Транспонирование матриц.
Транспонирование матрицы есть переход матрицы к матрице , в которой строки и столбцы поменялись местами с сохранением порядка. т.е. если имеет размер , то имеет размер .
Свойства операции транспонирования.
., , .,
Билет 3. Определители 2-го и 3-го порядков. Определения. Свойства.
Опред-ль 2-го порядка=минор, опред-ль 3-го пор-ка=алгебр дополн
Понятие определителя — число, характеризующее квадратную
матрицу
,
необходимо для решения систем линейных
алгебраических уравнений.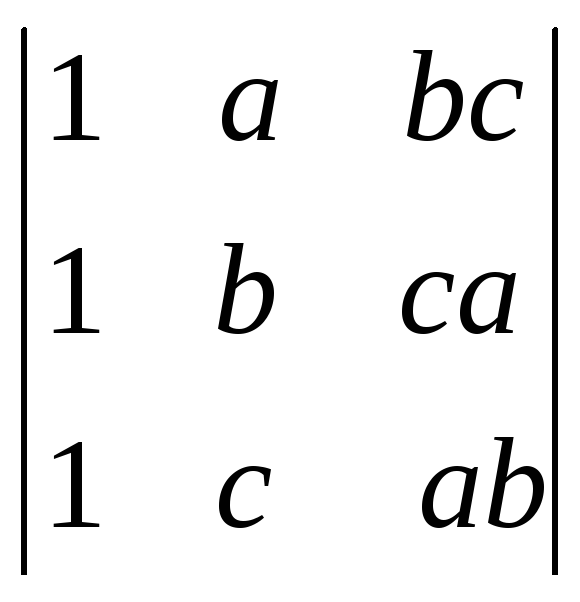
Определитель матрицы обозначают , дельта (треугольник) ,det A.
1) Определителем матицы
1-го порядка , называется элемент : ;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
. Произведения называются членами определителя 2-го порядка.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
Данная формула получила название правила треугольников или правило Сарруса.
При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:п
.
Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.

Если все элементы какой-либо строки (столбца) матрицы умножить на число ,то ее определитель умножится на это число .
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
При транспонировании матрицы ее определитель не изменяется: .
При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.

Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Если каждый элемент какого-либо столбца (строки) определителя – есть сумма двух слагаемых, то этот определитель – сумма двух определителей, причем в первом из них соответственно столбец (строка) состоит из первого слагаемого, а в другой – из второго.
Если элементы какого-либо столбца (строки) = 0, за исключением одного, то такой определитель равен этому, неравному 0, элементу, умноженному на его алгебраическое дополнение.
Сумма произведений произвольных чисел на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .
12. Определитель произведения двух
квадратных матриц равен произведению
их определителей:
,
где
,
а
и
— матрицы
-го
порядка.
Определитель произведения двух
квадратных матриц равен произведению
их определителей:
,
где
,
а
и
— матрицы
-го
порядка.
Перечисленные свойства определителей позволяют существенно упростить их вычисления для определителей высоких порядков. При этом с помощью свойств 1-9 желательно преобразовать исходную матрицу таким образом, чтобы она имела строку (столбец), содержащую как можно больше нулей, а потом вычислить определитель, разложенный по этой строке (столбцу).
Билет 4. Определители n-ного порядка. Вычисление. Свойства.
По той же формуле, что и определители 3-го определителя. 2 Метода: как и опред 3-го порядка, продолжая понижать///или приведение к треугольному виду: в этом случае опред-ль = произведению чисел на главн диагонали.Билет 5. Обратная матрица. Определение. Вычисление.
Для
каждого числа
существует обратное число
такое, что произведение
. Для квадратных матриц тоже вводится
аналогичное понятие.
Для квадратных матриц тоже вводится
аналогичное понятие.
Определение. Матрица называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: А-1*А=А* А-1=Е.Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.
Определение. Матрица является
Теорема (необходимое
и достаточное условие существования
обратной матрицы). Обратная матрица существует (и единственна) тогда и
только тогда, когда исходная матрица
является невырожденной (неособенной)
и вычисляется по формуле: А-1=1/|A|
*A^,
где A^
— присоединенная матрица, состоящая из
алгебраических дополнений элементов
транспонированной матрицы, т. е.
.
е.
.
Сингулярная матрица — определение, свойства, примеры, значение
Мы определяем, является ли матрица сингулярной матрицей или невырожденной матрицей в зависимости от ее определителя. Определитель матрицы ‘A’ обозначается как ‘det A’ или ‘|A|’. Если определитель матрицы равен 0, то она называется вырожденной матрицей. Зачем нам нужно специальное имя для матриц с определителем 0? Покажи нам.
Давайте узнаем больше о сингулярной матрице, а также о ее определении, формуле, свойствах и примерах.
| 1. | Что такое сингулярная матрица? |
| 2. | Идентификация сингулярной матрицы |
| 3. | Свойства сингулярной матрицы |
| 4 | Сингулярная матрица и невырожденная матрица |
| 5. | Теорема для генерации сингулярных матриц |
| 6. | Часто задаваемые вопросы о сингулярной матрице |
Что такое сингулярная матрица?
A сингулярная матрица является квадратной матрицей, если ее определитель равен 0.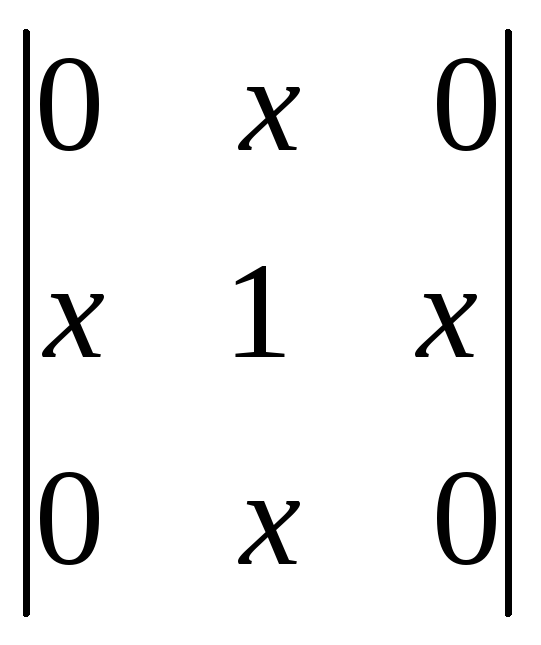 т. е. квадратная матрица A является сингулярной тогда и только тогда, когда det A = 0. Мы знаем, что обратная матрица A находится по формуле А -1 = (прил А) / (прил А). Здесь det A (определитель A) стоит в знаменателе. Мы знаем, что дробь НЕ определена, если ее знаменатель равен 0. Следовательно, A -1 НЕ определено, когда det A = 0. т. е. обратная сингулярная матрица НЕ определена. т. е. не существует такой матрицы B, что AB = BA = I (где I — единичная матрица).
т. е. квадратная матрица A является сингулярной тогда и только тогда, когда det A = 0. Мы знаем, что обратная матрица A находится по формуле А -1 = (прил А) / (прил А). Здесь det A (определитель A) стоит в знаменателе. Мы знаем, что дробь НЕ определена, если ее знаменатель равен 0. Следовательно, A -1 НЕ определено, когда det A = 0. т. е. обратная сингулярная матрица НЕ определена. т. е. не существует такой матрицы B, что AB = BA = I (где I — единичная матрица).
Исходя из приведенного выше объяснения, квадратная матрица ‘A’ называется сингулярной, если
- det A = 0 (что также записывается как |A| = 0) (или)
- A -1 НЕ определено (т. е. A необратимо).
Идентификация сингулярной матрицы
Чтобы определить/идентифицировать, является ли данная матрица вырожденной, нам нужно проверить два условия:
- проверить, является ли A квадратной матрицей.

- проверить, что det A = 0.
Вот несколько примеров, чтобы определить, является ли данная матрица вырожденной.
- A = \(\left[\begin{array}{rr}3 & 6 \\ \\ 2 & 4 \end{array}\right]\) является сингулярной матрицей, потому что
это квадратная матрица (порядка 2 × 2) и
det A (или) |A| = 3 × 4 — 6 × 2 = 12 — 12 = 0, - A = \(\left[\begin{array}{rr}1 & 2 & 2 \\ 1 & 2 & 2\\ 3 & 2&-1 \end{array}\right]\) является сингулярной матрицей, потому что
это квадратная матрица (порядка 3 × 3) и
как det A (или) |A| = 0 (поскольку первые две строки равны).
Свойства сингулярной матрицы
Вот некоторые свойства сингулярной матрицы, основанные на ее определении.
- Каждая сингулярная матрица является квадратной матрицей.
- Определитель сингулярной матрицы равен 0.
- Обратная сингулярная матрица НЕ определена и, следовательно, необратима.
- По свойствам определителей в матрице
* если любые две строки или любые два столбца одинаковы, то ее определитель равен 0 и, следовательно, это сингулярная матрица.
* если все элементы строки или столбца нули, то ее определитель равен 0 и, следовательно, это сингулярная матрица.
* если одна из строк (столбцов) кратна другой строке (столбцу), то определитель равен 0 и, следовательно, это сингулярная матрица. - Нулевая матрица любого порядка является сингулярной матрицей.
- Ранг сингулярной матрицы заведомо меньше порядка матрицы. Например, ранг матрицы 3×3 меньше 3.
- Все строки и столбцы сингулярной матрицы НЕ являются линейно независимыми.
Сингулярная матрица и невырожденная матрица
Несингулярная матрица, как следует из ее названия, НЕ является сингулярной матрицей. Таким образом, определитель невырожденной матрицы есть ненулевое число. т. е. квадратная матрица A называется невырожденной матрицей тогда и только тогда, когда det A ≠ 0. Тогда очевидно, что A -1 определено. т. е. неособая матрица всегда имеет мультипликативную обратную. Таким образом, мы можем резюмировать различия между сингулярной матрицей и невырожденной матрицей следующим образом:
Таким образом, мы можем резюмировать различия между сингулярной матрицей и невырожденной матрицей следующим образом:
| Сингулярная матрица | Несингулярная матрица |
|---|---|
| Матрица A является сингулярной, если det (A) = 0. | Матрица A невырожденна, если det (A) ≠ 0. |
| Если ‘A’ в единственном числе, то A -1 НЕ определено. | Если ‘A’ не единственное число, то определяется A -1 . |
| Ранг А < Орден А. | Ранг А = Орден А. |
| Некоторые строки и столбцы линейно зависимы. | Все строки и столбцы линейно независимы. |
| Если ‘A’ сингулярно, то система одновременных уравнений AX = B либо не имеет решения, либо имеет бесконечно много решений. | Если ‘A’ невырождена, то система уравнений AX = B имеет единственное решение. |
| Пример: \(\left[\begin{array}{rr}3 & 6 \\ \\ 1 & 2 \end{array}\right]\) в единственном числе как \(\left|\begin{array}{rr}3 & 6 \\ \\ 1 & 2 \end{array}\right|\) = 3 × 2 — 1 × 6 = 6 — 6 = 0, | Пример: \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & -2 \end{array}\right]\) не единственное число, как \(\left|\begin{array}{rr}3 & 2\\ \\ 1 & -2 \end{array}\right|\) = 3 × -2 — 1 × 2 = -6 — 2 = — 8 ≠ 0, |
Теорема для генерации сингулярных матриц
Существует одна важная теорема о сингулярной матрице, которую можно использовать для создания сингулярной матрицы, и эта теорема гласит: «Произведение двух матриц A = [A] n × k и B = [B] k × n (где n > k) является матрицей AB порядка n × n и всегда сингулярна». По этой теореме:
По этой теореме:
- Произведение AB двух матриц A порядка n × 1 и B порядка 1 × n всегда сингулярно.
- Произведение AB двух матриц A порядка n × 2 и B порядка 2 × n также вырождено и т. д.
Используя эту теорему, можно сгенерировать сингулярную матрицу, перемножив две случайно сгенерированные матрицы порядков n × k и k × n, где n > k.
☛ Связанные темы:
- Диагональная матрица
- Ортогональная матрица
- Обратная матрица 3×3
- Симметричная матрица
Примеры сингулярных матриц
Пример 1: Определите, какие из следующих матриц являются сингулярными. (a) \(\left[\begin{array}{rr}-7 & 4 \\ \\ 12 & 4 \end{array}\right]\) (b) \(\left[\begin{array} {rr}2 & -1 & 3 \\ 1 & 0 & 2\\ -6 & 3&1 \end{массив}\right]\).
Решение:
Найдем определители каждой из заданных матриц.
(a) \(\left|\begin{array}{rr}-7 & 2 \\ \\ -14 & 4 \end{array}\right|\) = -7 × 4 — 2 × -14 = -28 + 28 = 0,
Таким образом, данная матрица является сингулярной матрицей.

(b) \(\left|\begin{array}{rr}2 & -1 & 3 \\ 1 & 0 & 2\\ -6 & 3&1 \end{array}\right|\)
= 2 \(\left|\begin{array}{rr}0 & 2 \\ \\ 3 & 1 \end{array}\right|\) — (-1) \(\left|\begin{array}{ rr}2 & 3 \\ \\ -6 & 1 \end{массив}\right|\) + 3 \(\left|\begin{массив}{rr} 1 & 0 \\ \\ -6 & 3 \ конец {массив}\право|\)
= 2 (0 — 6) + 1 (1 + 12) + 3 (3 — 0)
= -12 + 13 + 9
= 10 ≠ 0
Таким образом, данная матрица невырожденная.
Ответ: (а) Сингулярная матрица (б) Несингулярная матрица.
Пример 2: Найти x, если A = \(\left[\begin{array}{rr}x+1 & x & 2 \\ 1 & 0 & 1\\ 4 & 1&x+3 \end{array} \right]\) — сингулярная матрица.
Решение:
Поскольку A сингулярна, ее определитель равен 0, т. е.
\(\left|\begin{array}{rr}x+1 & x & 2 \\ 1 & 0 & 1\ \ 4 & 1&x+3 \end{массив}\right|\) = 0
(х + 1) (0 — 1) — х (х + 3 — 4) + 2 (1 — 0) = 0
-х — 1 — х 2 + х + 2 = 0
— x 2 + 1 = 0
x 2 = 1
x = ± 1
Ответ: x = 1 или -1, если A единственное число.

Пример 3: Определите, имеет ли следующая система единственное решение: 2x + y + 2z = 3, x + z = 5, 4x + y + 4z = 7.
Решение:
Если мы запишем данную систему в матричной форме, то соответствующее матричное уравнение будет AX = B, тогда матрица коэффициентов будет A = \(\left[\begin{array}{rr}2 & 1 & 2 \\ 1 & 0 & 1\\ 4 & 1&4 \end{массив}\right]\).
Если определитель A НЕ равен нулю (т. е. если A неособо), то только система имеет единственное решение (по правилу Крамера)
|A| = \(\left|\begin{array}{rr}2 & 1 & 2 \\ 1 & 0 & 1\\ 4 & 1&4 \end{array}\right|\)
= 2 (0 — 1) — 1 (4 — 4) + 2 (1 — 0)
= -2 + 0 + 2
= 0
Ответ: Система НЕ имеет единственного решения . Она либо имеет бесконечное число решений, либо не имеет решений.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по сингулярной матрице
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о сингулярной матрице
Что означает сингулярная матрица?
Сингулярная матрица означает квадратную матрицу, определитель которой равен 0 (или) это матрица, НЕ имеющая обратной мультипликативной матрицы.
Как узнать, является ли матрица сингулярной матрицей?
Можно сказать, что матрица ‘A’ является сингулярной, если выполняется одно из следующих условий.
- Если определитель A = 0 (или)
- Если A необратим.
Что такое формула сингулярной матрицы?
Мы знаем, что определитель сингулярной матрицы равен 0. Таким образом, формула для сингулярной матрицы такова: «A сингулярна тогда и только тогда, когда det(A) = 0».
Почему матрица называется сингулярной?
Слово «сингулярный» означает «исключительный» (или) «замечательный». Сингулярная матрица специально используется для определения того, имеет ли матрица обратную, ранг матрицы, уникальность решения системы уравнений и т. Д. Она также используется для различных целей в линейной алгебре и, следовательно, название.
Что такое сингулярная матрица 3×3?
Определитель сингулярной матрицы равен 0. Примером сингулярной матрицы 3×3 является \(\left[\begin{array}{rr}2 & 1 & -1 \\ 1 & 0 & 1\\ 2 & 1& -1 \end{array}\right]\) вырожден, так как его определитель равен нулю (так как его первая и третья строки равны).
Что делает матрицу А сингулярной матрицей?
Если определитель A равен 0, то A сингулярна. Если не существует такой матрицы B, что AB = BA = I, то это означает, что A не имеет обратной, и в этом случае также говорят, что A является вырожденной.
Каков ранг сингулярной матрицы?
Если A — сингулярная матрица порядка n, то это означает, что det A = 0. Тогда ранг матрицы заведомо меньше порядка матрицы. т. е. rank(A) < n.
Тогда ранг матрицы заведомо меньше порядка матрицы. т. е. rank(A) < n.
Что такое сингулярные и невырожденные матрицы?
Сингулярная матрица — это матрица, определитель которой равен 0 и, следовательно, не имеет обратной. С другой стороны, невырожденная матрица — это матрица, определитель которой НЕ равен 0, и, следовательно, она имеет обратную.
Что такое определитель сингулярной матрицы?
Сингулярная матрица не имеет обратной. Мы знаем, что обратная матрица A равна (adj A)/(det A), и она НЕ существует, когда det A = 0. Следовательно, определитель сингулярной матрицы равен 0.
Download FREE Study Materials
SHEETS
Что значит иметь определитель равный нулю? | by Alfredo Maussa
Определитель, равный нулю, означает , что матрица является сингулярной матрицей. Матрица является вырожденной, если она не имеет обратной, что означает, что ее нельзя использовать для решения систем линейных уравнений.
Это может быть проблемой при попытке решить систему линейных уравнений с помощью обратной матрицы и обнаружить, что обратная сингулярная матрица не определена. Вы можете заключить, что «решения нет» , и на этом остановиться.
Вы можете заключить, что «решения нет» , и на этом остановиться.
Однако можно найти другой способ решения системы уравнений, когда определитель равен нулю, без прямого использования обратной матрицы.
Почему нельзя найти обратную матрицу, если определитель равен нулю?
Напомним, что определитель матрицы представляет собой числовое значение, которое можно вычислить из элементов матрицы. Определитель матрицы используется в различных областях математики и физики для решения задач, связанных с матрицами. Его отношение к обратной матрице зависит от следующей эквивалентности, где обратная матрица существует только в том случае, если определитель отличен от нуля, поскольку это означает деление на ноль:
Геометрически мы могли бы интерпретировать определитель матрицы как площадь (для матриц 2×2) или объем (для 3×3 и т. д.) между всеми векторами. Если один вектор равен нулю или компланарен другим, то он не будет вносить вклад в «высоту» объема, и определитель будет равен нулю.
Аналогичным примером зависимой переменной может быть стол с четырьмя ножками, который может стоять, даже если отсутствует одна ножка. Хотя технически возможно, чтобы зависимый вектор вносил некоторый вклад, в этом нет необходимости, поскольку его можно заменить линейной комбинацией других векторов. Каждая нога может быть смоделирована как сила в линейном уравнении, а уравнения основаны на законах Ньютона.
Преобразование
Матрица обычно преобразует один набор характеристик в другой. Это происходит плавно, когда существует однозначное соответствие, также известное как биективное отображение. Однако если определитель матрицы равен нулю, это означает, что биективного отображения нет.
При биективном отображении информация преобразуется из одного пространства в другое, аналогично переводу между языками. Исходное преобразование можно отменить с помощью взаимно-однозначного сопоставления, аналогичного кодированию и декодированию сообщения, путем отслеживания исходного преобразования во внешней таблице (например, Розеттский камень преобразования).
В этом случае определитель отличен от нуля.
В системах уравнений каждая строка представляет собой уравнение или ограничение, а каждый столбец представляет переменную, которую необходимо отобразить. Для каждой переменной нам нужно одно уравнение. Если уравнений больше, чем переменных, мы не сможем удовлетворить их все одновременно. С другой стороны, если переменных больше, чем уравнений, у нас не будет достаточно уравнений, чтобы свести переменные к однозначному результату.
Проблемы возникают при отображении «многие к одному» или «один ко многим», так как в этих случаях определитель равен нулю.
Это связано с тем, что может быть невозможно однозначно определить исходный набор характеристик из преобразованного набора или наоборот. Другими словами, информация может быть не сохранена или необратима при преобразовании.
От многих к одному, может быть интерпретировано как проекция, кодировщик или суммирование, это процесс конвергенции. Это может дать вам корреляцию с вектором.
Это может дать вам корреляцию с вектором.
> Решение. В этом случае, чтобы найти решение, нам необходимо определить дополнительные ограничения, в основном функцию стоимости для оптимизации наилучшего решения.
От одного ко многим, можно интерпретировать как генератор или декодер. это расходящийся процесс. Мы могли бы сгенерировать множество художественных рисунков, имеющих одинаковый стиль, поскольку степень свободы вывода не выше, чем входная, по крайней мере, в детерминированном процессе.
> Решение. В этом случае нам нужно не лучшее решение для данных, а лучшая система или модель для описания основного поведения для правильного создания данных с помощью этой модели.
Чтобы найти желаемое решение на техническом уровне, вы можете применить инверсию Мура-Пенроуза. Этот метод представляет собой процесс оптимизации, который минимизирует среднеквадратичную ошибку/значение за счет сокращения «многих» вариантов до одного. Для этого вам в основном нужно будет умножить обе части уравнения на транспонированную матрицу, а затем решить как обычно.
Для этого вам в основном нужно будет умножить обе части уравнения на транспонированную матрицу, а затем решить как обычно.
Эта концепция может быть трудной для понимания , но ее легко реализовать . Вот почему я даю больше контекста и объяснений, а не просто пишу формулы. Я надеюсь, что некоторые из ключевых идей останутся с вами.
Почему этот трюк с умножением на транспонированную матрицу работает? Короче говоря, это проекция, которая избавляется от неортогонального направления, и поскольку ближайшая точка к исходной точке содержится в ортогональной линии к нулевому пространству, вы получаете минимизацию.
Далее я приведу пример того, как обрабатывать определитель, равный нулю, в ситуации, когда столбцов больше, чем строк. Так как конкретный пример с реальным приложением мог бы быть пока этот рассказ я напишу отдельно.
Спойлер: Это связано с тросовыми роботами и статическим равновесием.

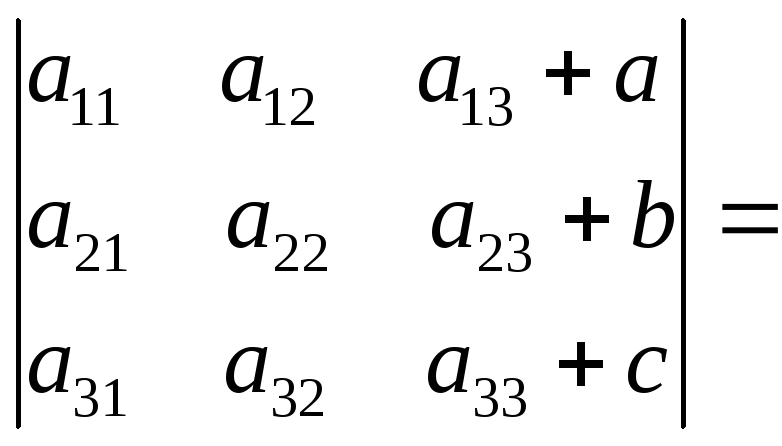 5)
.
5)
.