15. Перестановки, размещения и сочетания. Бином Ньютона и иллюстративные примеры
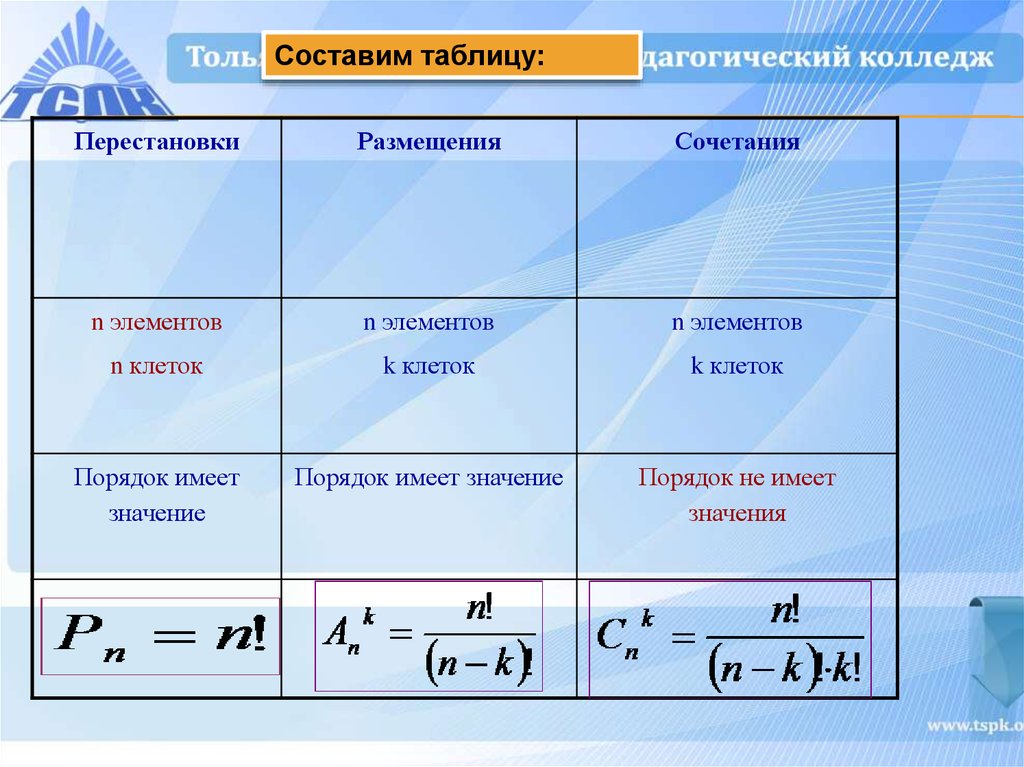
Пусть — какое-либо конечное множество; Соединением элеметов из множе-ства называется любой набор, составленный из элементов множества . Если в этом на-боре какой-либо элемент встречается больше, чем один раз то говорят о Соединении с повто-рениями; если же в наборе каждый элемент появляется лишь один раз, то говорят о Соединении без повторений. В дальнейшем мы будем говорить именно о соединениях без повторений и по-этому будем обозначать такие наборы просто термином Соединение.
Перестановкой элементов множества называется всякое соединение элементов мно-жества , в котором обязательно присутствуют все элементы из и в котором учитывается порядок следования элементов друг за другом. Например, если , то и явля — ются разными подстановками. Нетрудно доказать, что При произвольном количество все-возможных перестановок множества Равно ( — это традиционное обозна-чение для произведения чисел ; читается «эн факториал»).
Всякое соединение из элементов множества , в котором учитывается по-рядок следования элементов друг за другом, называется Размещением из по . При — это перестановка; при таких соединений нет; при Нетрудно получить следующую формулу для количества размещений из по :
.
Очевидно, .
Всякое соединение из элементов множества , где , в котором по-рядок следования элементов друг за другом не учитывается, называется Сочетанием Из по . Например, при Соединения и являются различными размещениями из 4
По 3, но как сочетания они равны. Количество Сочетаний из по Определяется следующей формулой:
.
Числа часто называют Биномиальными коеффициентами по следующей причине: если в выражении раскрыть скобки и привести подобные члены, то возникнет следующее равенство, которое называется Биномом Ньютона:
.
Если договориться, что символ обозначает число 1, то бином Ньютона можно записать короче с помощью знака суммы:
.
Биномиальные коэффициенты обладают многочисленными свойствами, которым уделяли внимание математики самых разных поколений. Отметим три простейших из них.
Свойство первое. Всегда .
Свойство второе. .
Свойство третье. .
Первое свойство устанавливается просто сравнением формул, а последние два свойства возникают просто из бинома Ньютона, в котором переменным придают значения .
Пример. В выражении раскрыли скобки и привели подобные члены; какой коэффициент будет стоять около выражения ?
Для ответа рассмотрим бином Ньютона:
.
Искомое число равно
=
=.
| < Предыдущая | Следующая > |
|---|
1. Элементы комбинаторики. Перестановки. Размещения. Сочетания (без повторений).
Элементы комбинаторики используются для подсчета элементарных исходов.
Правило произведения: если объект А можно выбрать k способами, а объект В можно выбрать (независимо от выбора объекта А) m способами, то пары объектов А и В можно выбрать k·m способами.
Теория соединений — это теория составления групп из n различных элементов по m элементов.
Виды соединений:
Размещения – соединения из n различных элементов по m элементов, отличающихся друг от друга либо составом, либо порядком своих элементов.
Пример: В группе из 20 человек нужно выбрать старосту, профорга, физорга. Сколькими способами это можно сделать?
Перестановки — все возможные соединения из n различных элементов, отличающиеся только порядком элементов.
Пример. Сколько трехзначных чисел можно составить из цифр 2,3,5
Р3 = 3! = 1* 2* 3 = 6
Сочетания — соединения из n различных элементов по m элементов, отличающихся друг от друга хотя бы одним элементом.
Пример. Группа спортсменов из 10 человек должна выставить на соревнования команду из 4 человек. Сколькими способами это можно сделать?
2. Случайные события. Классификация случайных событий. Действия над случайными событиями.
Случайное событие
Среди случайных событий различают:
1. Равновозможные.
2. Единственно возможные.
3. Несовместные.
4. Полная система событий.
5.
Противоположные
события.
Равновозможными называются события, если нет оснований считать, что одно из них наступит чаще, чем другое.
Единственно возможные – это события, если наступает одно из них и никакое другое.
Несовместными называются события, если появление одного из них исключает появление другого.
Полной системой событий называются события, единственно возможные и несовместные.
Два события называются противоположными, если они образуют полную систему.
Действия над случайными событиями.
Суммой двух случайных событий А и В называют новое случайное событие А+В, которое происходит, если происходят либо А, либо В, либо А и В одновременно. Событию А+В соответствует объединение (сумма) множеств исходов, соответствующих событиям А и В.
Произведением
двух случайных событий А и В называется новое случайное событие
АxВ, которое происходит только тогда,
когда происходят события А и В одновременно.
Событию АxВ соответствует пересечение
множеств исходов, соответствующих
событиям А и В.
3. Классическое определение вероятности случайного события. Свойства вероятности.
Вероятностью события А называется отношение количества благоприятствующих событию А элементарных исходов к общему числу равновозможных элементарных исходов: ,
где n – общее количество равновозможных элементарных исходов, m – количество благоприятствующих событию А исходов.
Вероятность — Комбинаторика
Комбинаторика состоит из трех частей: Перестановок , Вариаций и Комбинаций .
Перестановки
Перестановки представляют собой количество различных возможных способов расположения набора элементов.
Пример: есть шесть уникальных способов, которыми 3 гонщика могут разделить медали (золото, серебро и бронза).
Математическая формула :
P n = n * (n — 1) * (n — 2) * … * 1 = n!н! : n факториал
Когда мы определяем доступные варианты для каждой позиции в перестановке, можем ли мы начать со среднего элемента?
Да, выбор заказа полностью зависит от нас.
Имея дело с перестановкой, мы можем начать с любой позиции в пространстве выборки. Условие диктует, что мы обычно начинаем с первого, но мы можем начать с любого элемента, который пожелаем.
Факториалы
n!: произведение натуральных чисел от 1 до n
или:
n! = 1 * 2 * 3 * … * nФакториальные важные свойства:
n! = (n — 1)! * п (п + 1)! = п! * (n + 1) (n + k)! = п! * (n + 1) * (n + 2) * . . . * (н + к) (н — к)! = п! / (n — k + 1) * (n — k + 2) * … * n n! / к! = (к + 1) * (к + 2) * … * пВарианты
Варианты — это общее количество способов, которыми мы можем выбрать и расположить некоторые элементы данного набора.
Variations with repetition:Math formula:
V n p = n pn — общее количество элементов, которые у нас есть в наличии
p — количество позиций, которые нам нужно заполнить
Пример: у нас есть комбинация из двух букв кода доступа с A, B и C.
Всего элементов будет 3 — A, B и C. И всего позиций будет 2. Таким образом, у нас будут варианты этой комбинации: n p = 3 2 = 9
В случае комбинации со всеми буквами 2 26 букв, у нас будет 26 2 = 676 вариантов.
Когда мы используем вариации вместо перестановок?
Когда мы не размещаем все элементы в пространстве выборки. Мы используем вариации, когда нам нужно сначала выбрать, а затем расположить некоторые (но не все) элементы семплового пространства.
Возвращаясь к примеру с кодовым замком из лекции, представьте, что правильный код состоит из одного слова из 4 букв. Однако на этот раз пароль может состоять только из букв, содержащихся в слове «пароль». Сколько существует возможных кодов доступа?
7 4 — Несмотря на то, что слово «пароль» состоит из 8 букв, оно состоит только из 7 различных букв. Это означает, что у нас есть 7 вариантов для каждой позиции, поэтому существует 7 4 различных возможных паролей.
Вариации без повторения:
Количество вариаций без повторения при организации P Элементы из общего числа N
Math Formula: V : v : v 9006 9000 n p = n! /(н — р)!Пример: нам нужно выбрать 4 участников в команде из 5 человек для запуска эстафеты. Всего людей n = 5 , и нам нужно выбрать p = 4 участников при организации.
У нас будет В 5 4 = 5! / (5 — 4)! = 5! / 1! = 120
Из приведенного выше примера, что, если бы вместо 5 человек в команде у нас было 7. Нам все равно пришлось бы выбрать 4 из них и расположить их в каком порядке для запуска, но сколькими способами мы можем выполнить это?
7! / (7 — 4)! = 7! / 3!
Что, если бы вместо 5 человек в команде было 7.
Кроме того, на этот раз нам также нужно выбрать запасного игрока, который будет наготове. (Значит нам нужно выбрать 5 участников)
н! / (п — р)!=7! / (7-5)! или просто 7! / 2!.
Представьте, что вас попросили заказать трехъярусный торт на свадьбу лучшего друга. Они попросили вас купить торт с разными вкусами, поэтому вы решили заказать разные виды теста (вкусы торта) для каждого яруса. Кондитерская, в которую вы обратились, предлагает 5 разных видов теста, поэтому вы хотите знать, сколько различных вариантов торта у вас есть.
Нам нужно выбрать и расставить 3 из 5 доступных вкусов. Применяя формулу, о которой мы говорили ранее, получаем 5! / (5 — 3)! или 5! / 2! разных тортов.
Комбинации
Комбинации — это количество различных способов выбора определенных элементов набора.
Каково количество комбинаций для выбора p-любых элементов из выборки из n элементов?
Количество комбинаций равно количеству вариаций над количеством перестановок:
C n P = V N P / P P .
/ р!(п — р)! Пример: нам нужно разыграть 3 человека в группе из 10 человек -> n = 10 и P = 3
.0006 10 3 = 10! / 3!(10 — 3)! = 10! / 3!7! = 120
Связь между перестановками, вариациями и сочетаниями без повторения?
C = V / P — каждая перестановка комбинации представляет собой другую вариацию. Следовательно, вариаций в P раз больше, чем комбинаций.
Представьте, что вы путешествуете по Парижу и решили попробовать их знаменитое миндальное печенье. Пекарня, в которую вы идете, предлагает «разнообразные» пакеты разного размера, где вы можете выбрать 3, 5 или 8 миндальных печенья. Единственное требование – все они должны быть разных вкусов.
Сколько разных упаковок по 3 миндальных печенья вы можете получить, учитывая, что существует 8 различных вкусов.
Есть 8 различных вкусов, но мы получаем только 3 макарон. Тогда n равно 8, а p равно 3, поэтому мы подставляем эти значения в формулу из этой лекции, чтобы получить n! / р!(п — р)! = 8! / 3!5!.
Теперь представьте, что вы хотите получить среднюю упаковку, содержащую 5 миндальных печенья вместо 3. Сколько различных возможных упаковок вы можете сделать?
Есть 8 различных вкусов, но мы получаем только 5 миндальных печенья. Тогда n равно 8, а p равно 5, поэтому мы подставляем эти значения в формулу из этой лекции, чтобы получить n! / р!(н-р)! = 8! / (5!3!)
Теперь представьте тот же сценарий, но на этот раз вам нужна большая коробка с 8 миндальными печеньями. Сколько различных наборов разнообразия вы можете получить?
Если мы подставим 8 вместо n и p, мы получим n! / р!(н-р)! = 8! / (8!0!) различные наборы из 8 макронов. С 0! = 1, 8! / (8!0!) = 8! / 8! , то есть всего 1. Потому что у нас есть только 1 способ получить 8 макронов с разными вкусами, учитывая, что у нас есть только 8 разных начинок.
Симметрия комбинаций
Выбор большего количества элементов может привести к меньшему количеству комбинаций. Мы можем выбрать p-множество элементов сколькими способами мы можем выбрать n минус p-множество элементов.
C n p = C n n — pExample: From the example выше, что, если мы выберем 7 человек в группе из 10 человек? n = 10 и p = 7
C 10 7 = 10! / 7!(10 — 7)! = 10! / 7!3! = 120
Мы имеем тот же результат, как если бы мы выбрали группу из 3 из 10. Это симметрия комбинаций.
Что такое интуиция за симметрией комбинаций?
Примечание. Мы ищем утверждение, которое точно объясняет математические симметрия вид (т.
е. объекты, находящиеся на одинаковом расстоянии друг от друга, имеют одинаковые характеристики)
Выбор p-многих элементов из n аналогичен исключению (n-p)-многих элементов
5 Комбинации с отдельными пространствами для проб
Комбинация может представлять собой смесь различных более мелких отдельных событий.
Расчет общего количества комбинаций осуществляется путем умножения количества вариантов, доступных для каждого отдельного события.
Сколько различных меню гамбургеров мы можем заказать в ресторане McDonald’s, если у нас есть выбор из 8 гамбургеров, 3 размеров картофеля фри и 5 различных напитков, при условии, что меню состоит из гамбургера, небольшого количества картофеля фри и напитка?
У нас есть 3 позиции, и у нас есть места для образцов разного размера для каждой из них. Мы относимся к различным частям меню как к позициям. Для каждой из 3 позиций у нас есть различное количество возможных вариантов: 8 для гамбургеров, 3 для картофеля фри и 5 для напитков.
Таким образом, у нас есть 8×3×5 или 120 различных возможных меню на выбор.
Хотите купить лотерею? Смотрите комбинаторику в реальной жизни: лотерея из 365 профессий
Резюме комбинаторики
Мы используем перестановки с вариациями, когда мы должны упорядочить набор объектов в таких случаях порядка.
Перестановки отличаются от вариаций тем, что мы всегда размещаем весь набор элементов в пространстве выборки.
Пример:
- Если нам нужно собрать 4 участников в команду из 4 человек, мы будем использовать Перестановки.
- Если мы выберем и расположим 4 элемента из 6 элементов, нам нужно использовать варианты
- В то время как Комбинации помогают нам выбрать группу из 4 членов в 6 членов
Снова и снова смотрите видео «Практический пример комбинаторики». «для тренировки нашего аналитического ума.
Примечания к курсу от 365 Careers.
Перестановка и комбинация – формула, вопросы, значение, определение, примеры
← Список тем
Уровень: базовый
Ветвь: Комбинаторика
Основная цель изучения математики — умение считать и получать ответы.
Для этого мы просто используем определенные методы подсчета. Раздел математики, связанный с различными методами счета, известен как Комбинаторика . Перестановка и комбинация используют эти методы и избавляют нас от необходимости вручную перечислять желаемые результаты один за другим. Эти понятия не только помогают нам отличить один набор вещей от другого, но также позволяют нам понять, как элементы любой отдельной группы могут быть расположены между собой по многочисленным шаблонам.
Основной принцип подсчета:
Правило продукта:Если определенное действие может быть выполнено в ‘ a ‘ количеством способов, а другое, ‘ b числом способов’ , то оба эти действия могут быть выполнены a x b числом способов.
Обратите внимание, что правило произведения можно распространить и на более чем два фактора. Давайте посмотрим на пример, где есть 3 фактора.
На представленном ниже виде города с высоты птичьего полета зеленая точка слева отмечает въезд в город.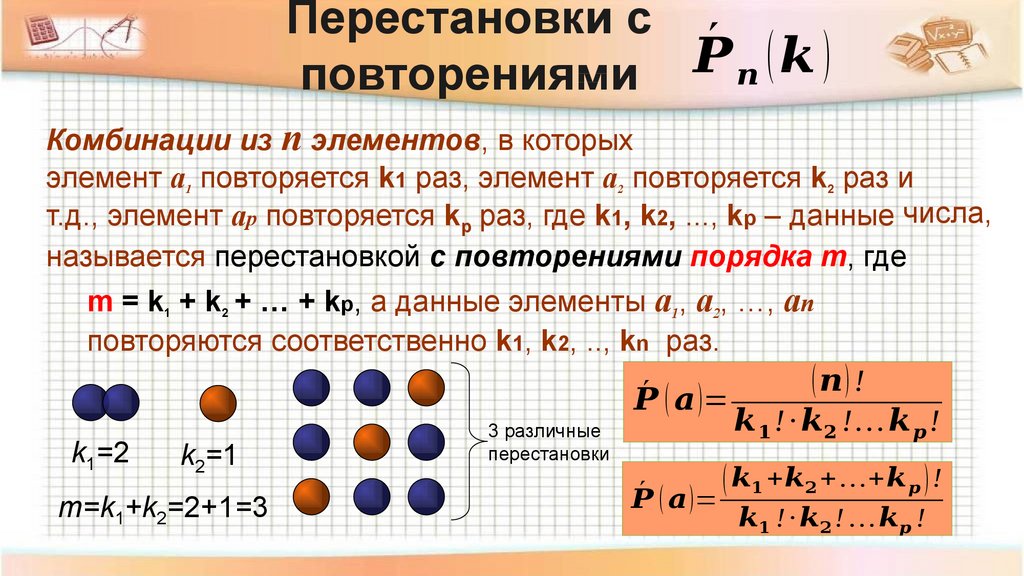
Затем у нас есть путь к ряду из 3 кафе, C1, C2 и C3. Путь от кафе ведет к ряду из 2-х банков, B1 и B2. От ряда 2 банков берет начало общий путь к последнему ряду зданий библиотеки, L1 и L2. Наконец, дороги от библиотек сходятся в тропе с красной точкой, обозначающей конец города.
Чтобы найти способы пересечь этот город и добраться до его конца, вы можете вручную начать подсчет и построение маршрутов случайным образом. Например, можно войти в город, пройти в кафе C1, затем в банк B1, а затем пройти через библиотеку L1 и выйти из города. Этот подход является трудоемким и занимает много времени. Хотя это число конечно, вам понадобится некоторое время, чтобы вычислить общее количество способов, которыми это можно сделать.
Обратите внимание, что вся сделка будет происходить поэтапно, первая задача — выбор 1 из 3 кафе, вторая — выбор 1 из 2 банков и третья — выбор 1 из 2 библиотек.
1. Есть 3 варианта для кафе
2. Есть 2 варианта для банков
3. Есть 2 варианта для библиотек
∴ Согласно правилу произведения количество возможных способов пересечь город = 3 X 2 X 2 = 12 способов
их нельзя делать вместе одновременно, то их m + n способов сделать одну из этих вещей.
Обратите внимание, что правило суммы можно распространить и на более чем два фактора. Давайте рассмотрим пример, где есть два фактора.
Ниже приведены блюда в двух магазинах, A и B. Магазин A продает картофель фри, пиццу и гамбургер, а магазин B продает вафли и пирожные. Когда нам нужно купить одно блюдо в любом из магазинов, мы применяем правило суммы и вычисляем общее количество способов, которыми мы можем это сделать. Мы можем купить либо 1 из 3 блюд в магазине A, либо 1 из 2 блюд в магазине B.
Есть 3 варианта для магазина А, если мы его выбрали, или есть 2 варианта для магазина Б, если мы его выбрали.
∴ По правилу суммы количество возможных способов, которыми можно выбрать и купить только блюдо = 3 + 2 = 5 способов Положительное целое число получается путем умножения на него каждого положительного целого числа, меньшего соответствующего числа. Функция факториала обозначается восклицательным знаком.
Например, факториал 7 обозначается как 7! и его математическое значение равно 7 х 6 х 5 х 4 х 3 х 2 х 1 = 5040.
Очень важно, чтобы мы знали функцию факториала, поскольку комбинаторика в значительной степени опирается на нее. Функция факториала существует только для неотрицательных целых чисел.
н! = n (n-1)! = n x (n – 1) x (n – 2 ) x (n – 3)… 2 x 1
По правилу:
1! = 0! = 1
Давайте разберемся, почему 0! = 1
Мы знаем n! = n (n-1)!
Пусть n=1
Тогда мы получим 1! = 1(1-1)!
1! = 1*0!
1 = 0!
Так как отказ от выбора предмета или элемента (который в идеале может быть представлен в числовом выражении как 0!) также является формальным выбором, 0! = 1. 1 означает выбор ничего не выбирать.
Перестановка
Когда все или некоторые элементы данного набора предметов располагаются в определенном порядке или порядке, или когда уже существующее расположение одних и тех же предметов переставляется в другом порядке, различные перестановки создаются. Другими словами, в перестановке последовательность или выбор объектов действительно имеет значение и имеет все значение.
Поскольку перестановки так сильно связаны с закономерностями и порядком, они имеют первостепенное значение в нашей реальной жизни. Например, если код доступа нашего телефона 1234, очень важно, чтобы мы ввели его и только его, поскольку наш телефон не примет никаких других перестановок, таких как 3421, 1243 и т. д. Слова в английском языке в конечном счете представляют собой перестановки алфавитов и отклонений. из предполагаемого порядка любого слова либо полностью изменит его значение, либо создаст бессмысленное слово. Например, оба слова «забота» и «раса» были созданы с использованием одних и тех же букв, но имеют совершенно разные значения, опять же потому, что они представляют собой две разные перестановки одних и тех же четырех букв а, с, е и г.
1. Перестановки n различных элементов, взятых одновременно = n!
Рассмотрим случай, когда 4 разных элемента нужно расположить между собой в ряд. Начнем выяснять количество перестановок, обозначив четыре места черточками.
Поскольку 1 из 4 отдельных элементов может быть на первом месте, первое место имеет 4 варианта:
4 x __ x __ x __
Поскольку 1 из 4 отдельных элементов уже размещен, на втором месте остается 3 варианта:
4 x 3 x __ x __
Поскольку первые два элемента уже размещены, на третье место остается 2 варианта:
4 x 3 x 2 x __
Поскольку первые три элемента уже размещены, у последнего, естественно, останется 1 вариант:
4 x 3 x 2 x 1 = 4! = п! (n = 4)
Следовательно, перестановки 4 различных элементов, взятые одновременно, = 4! = 24
Перестановка и комбинация — решено Пример:
Q.1) На приведенной выше диаграмме есть 3 конуса мороженого. Сколькими способами эти 3 разных сорта мороженого, а именно клубнику, манго и гуаву, можно распределить между 3 друзьями X, Y и Z, если все 3 друга любят разные рожки?
Решение: Мы должны раздать все 3 вида мороженого среди 3 человек, и у каждого должен быть свой рожок.
∴ Количество способов, которыми эти 3 вида мороженого можно распределить между 3 людьми = 3! = 3 x 2 x 1 = 6
Следовательно, 3 разных конуса можно распределить между 3 людьми 6 различными способами.
2. Перестановки n различных элементов, взятых по r за раз (повторение не допускается) = P(n,r) = n P r = n!/(n-r)!
Рассмотрим случай, когда 2 из 4 различных элементов должны быть расположены между собой. Начнем выяснять число перестановок с обозначения двух мест черточками, так как нам нужно расположить только два, а не все четыре заданных предмета.
Поскольку 1 из 4 отдельных элементов может быть на первом месте, первое место имеет 4 варианта:
4 x __
Поскольку 1 из 4 отдельных элементов уже размещен, на втором и последнем месте останется 3 варианта.
4 x 3 = 12
Теперь давайте проверим это с помощью формулы, здесь n = 4 и r = 2
n P r = n!/(n-r)! = 4!/(4 – 2)! = 4!/2! = (4 х 3 х 2!)/2! = 4 x 3 = 12
Следовательно, перестановки 4 отдельных элементов, взятые по 2 за раз (повторение не допускается) = 4 x 3 = 12
Перестановка и комбинация — решено Пример:
Q.
2) В На приведенной выше диаграмме есть пять разных напитков. Сколькими способами можно подать эти 5 напитков 2 клиентам, если обоим нельзя дать один и тот же напиток?
Решение: Мы знаем, что не можем подавать два одинаковых напитка двум клиентам.
∴ Количество способов, которыми эти 2 клиента могут быть обслужены 5 напитков = 5 P 2
= 5!/(5 – 2)!
= 5!/3!
=5 х 4 х 3!/3!
= 5 x 4
= 20
Следовательно, 5 напитков можно подать 2 клиентам 20 различными способами.
3. Перестановки n отдельных элементов по r за раз (повторение разрешено) = n r
Рассмотрим случай перестановки любых 2-х из 4-х элементов, где допускается повторение элементов. Перестановки должны производиться с учетом того факта, что элементы могут повторяться и что количество вариантов выбора не уменьшится после размещения любого из доступных элементов, поскольку все элементы можно использовать более одного раза.
Так как 1 из 4 различных элементов может быть на первом месте, у первого места есть 4 варианта:
4 x __
Поскольку любой из элементов, стоящих на первом месте, может быть повторен во второй раз, у второго места снова будет четыре варианта :
4 x 4 = n x n = n 2 = n r (n = 4, r = 2)
Следовательно, перестановки 4 отдельных элементов, взятых по 2 за раз (повторение разрешено) = 4 x 4 = 16
Перестановка и комбинация — решено Пример:
Q.3) Эдна хочет купить букет из 3 цветов. Каждый цветок доступен в трех цветах: красном, желтом и синем. Сколькими способами можно купить букет из этих трех цветов?
Решение: Мы знаем, что каждый цветок доступен в трех цветах.
Так как цвета цветов могут повторяться, количество способов, которыми Эдна может купить эти 3 букета цветов = 3 3
= 3 x 3 x 3 (∵ есть 3 варианта выбора для каждого цветка и всего 3 цветка)
= 27
Следовательно, букет цветов можно купить 27 способами.
второго рода и одинаковые, а r третьего рода и одинаковые = n!/p!q!r!
Давайте изучим случай слова «ОЧКИ», которое состоит из букв G, O, L, E и S, из которых G — 3 одинаковых и одинаковых, а остальные буквы O, L, E и S существуют индивидуально.
Давайте временно назовем буквы G как G1, G2 и G3 и будем рассматривать их как 3 отдельные буквы или сущности. Благодаря этой модификации у нас есть буквы G1, G2, G3, O, L, E и S, встречающиеся по отдельности. Общее количество перестановок этих 7 различных букв без повторения будет равно 7! . Когда мы рассматриваем различные буквы G1, G2 и G3, число способов, которыми эти 3 различные буквы могут быть расположены между собой, равно 3! = 6 способов:
G1, G2, G3
G1, G3, G2
G2, G1, G3
G2, G3, G1
G3, G1, G2
G3, G2, G1
родительское слово в форме 3! . Проще говоря, 7! (аранжировки всего 7 букв) включительно 3! (расположение 3 различных букв G, G1, G2 и G3)
Однако, когда мы рассматриваем исходное слово «ОЧКИ», мы понимаем, что буква G просто повторяется трижды, и независимо от того, как расположены три G , можно было бы получить только 1 их перестановку или только 1 способ их расположить: G, G, G
Следовательно, чтобы узнать истинное количество перестановок исходного слова «ОЧКИ», мы просто берем факториал количества элементов, присутствующих в слове, а затем делим его на факториал повторяющихся элементов:
7!/3 ! = 7 х 6 х 5 х 4 х 3!/3! = 7 x 6 x 5 x 4 = 840 = n!/p! (n = 7, p = 3)
Это обеспечивает избавление от лишних расположений и сохраняет только одну перестановку, которой в данном случае является G, G, G.
Следовательно, перестановки 7 предметов, из которых 3 предмета одного добрый и похожий = 840
Перестановка и комбинация — решено Пример:
Q.4) Сколькими способами можно произвести перестановку слова «острость»?
Решение: Мы знаем, что слово «острость» состоит из 8 букв, из которых e повторяется трижды, n, s повторяются дважды, а k встречается только один раз.
∴ Количество перестановок букв слова «проницательность» = 8!/3!2!2!
= 8 х 7 х 6 х 5 х 4 х 3 х 2 х 1/ 3 х 2 х 2 х 2
= 1680
Следовательно, буквы слова «проницательность» можно расположить 1680 способами.
Комбинация
Когда определенное количество вещей выбирается из набора отдельных/отдельных вещей или предметов без учета порядка их выбора, создается комбинация . Другими словами, в комбинации последовательность выбора не имеет значения или не имеет значения.
Например, в случае выбора 3-х видов фруктов из 4-х доступных фруктов – клубники, манго, гуавы и яблока, комбинации могут быть составлены таким образом, что получается группа из 3-х выбранных сортов одновременно:
1) яблоко + манго + гуава [отказ от клубники]
2) яблоко + клубника + гуава [отказ от манго]
3) яблоко + клубника + манго [отказ от гуавы]
4) клубника + манго + гуава [отказ от яблока]
It также выполняется путем простого отказа от одного фрукта за раз, и по умолчанию у нас останется 4 комбинации из оставшихся 3 фруктов.
Таким образом, в любом случае мы получаем 4 комбинации, перечисленные выше.
После того, как вы выберете любой из этих трех фруктов, последовательность покупки не будет иметь значения. Что, однако, имеет значение, так это то, что вы придерживаетесь одних и тех же фруктов. В этом суть комбинации. В комбинации положение или порядок элементов не имеет значения. Такие слова, как «набор» и «группа» являются синонимами слова «комбинация» .
5. Комбинации из n элементов, взятых по r за раз (без повторений) = C(n, r) = n C r = n C n-r = n!/r!(n – р)!
Возьмем случай выбора 2 элементов из 4 элементов, A, B, C и D, без повторения. Прежде чем мы углубимся в способы выбора этих двух элементов, давайте сначала узнаем количество перестановок любых 2 элементов, выбранных из 4 элементов. Мы знаем, что перестановки 4 различных элементов, взятых по 2 за раз (повторение запрещено) = 4 P 2 = 4!/(4 –2)! = 4!/2! = 4 x 3 = 12
.
Возьмем две из двенадцати перестановок и изучим их. Например, одна перестановка — это AB, а другая — BA. Заметим, что эти перестановки состоят из одних и тех же двух элементов, А и В. Можно заключить, что еще десять перестановок должны состоять из таких пар. Любые два отдельных элемента можно расположить по 2! = 2 пути. В идеале на каждые два элемента приходится одна комбинация. Другими словами, 2! перестановки есть для 1 комбинации. Следовательно, для 12 перестановок комбинаций будет:
2 декабря! = 6
Теперь давайте проверим это с помощью формулы, здесь n = 4 и r = 2
n!/r!(n –r)! = 4!/(2!)(4-2)! = 4!/(2!2!) = 6
Простым перекрестным умножением, если есть 1 комбинация на 2! или 2 перестановки, будет 6 комбинаций для 12 перестановок.
Следовательно, комбинации из 4 предметов, взятых по 2 за раз (без повторения) = 6
Перестановка и комбинация — решены Пример:
Q.5) В школе есть группа из 5 мальчиков и 4 девочек. Должна быть сформирована команда из четырех человек, в которой равное количество мальчиков и девочек.