Сочетания и их свойства примеры. Элементы комбинаторики
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов;
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных
предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.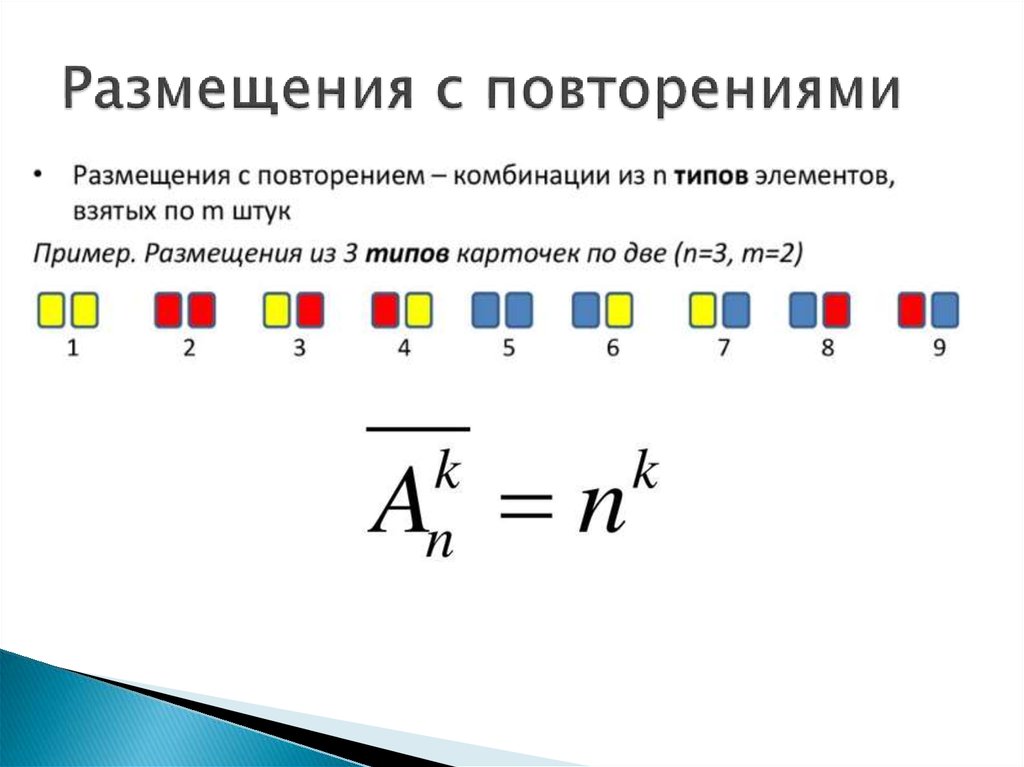
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог.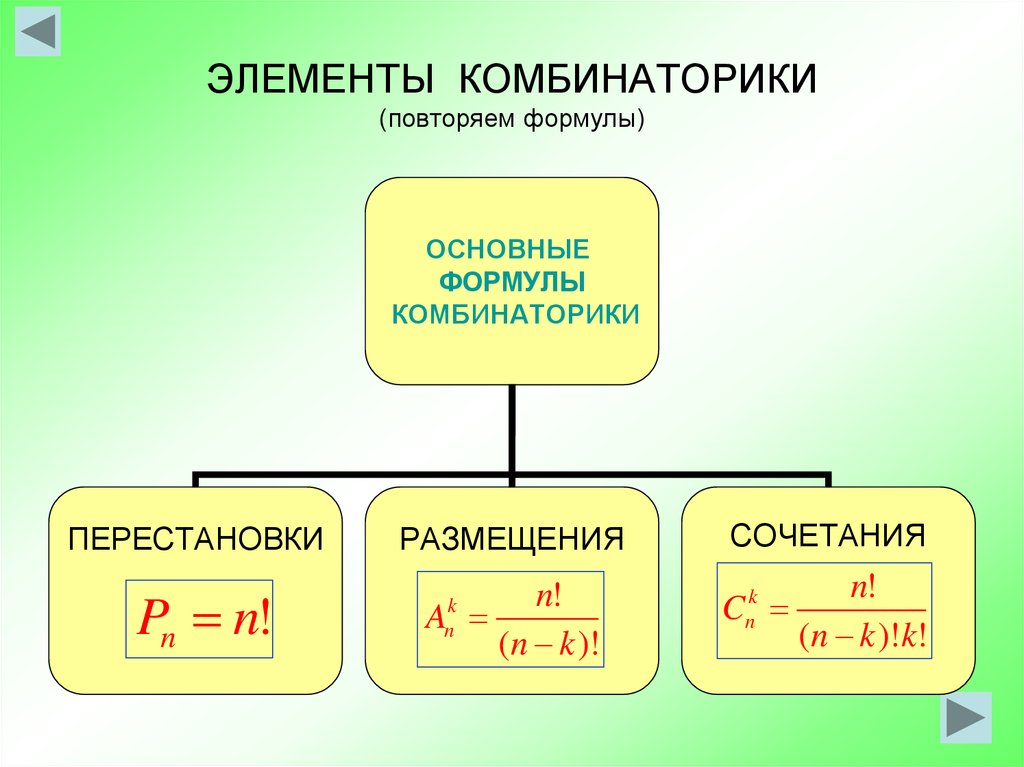 Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных
местах?Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Правило умножения (основная формула комбинаторики)
Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:
Пример 1
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет альтернативы – либо орел, либо решка. Для второй монеты также есть альтернативы и т.д., т.е. .
Искомое количество способов:
Правило сложения
Если любые две группы
и
не имеют общих элементов, то выбор одного
элемента или из
,
или из
,
…или из
можно осуществить
способами.
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана способами, экономическая — способами.
По правилу суммы существует способа выбора математической или экономической книги.
Размещения и перестановки
Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.
Размещения без повторений , когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .
Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:
Пример 3
Расписание дня состоит из 5 различных уроков.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
Размещения с повторениями , когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат — размещением с повторениями из элементов по .
Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно
Пример 5
Лифт останавливается на 7
этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров,
находящихся в кабине лифта?
Сколькими способами могут выйти на этих этажах 6 пассажиров,
находящихся в кабине лифта?
Решение
Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:
Сочетания
Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.
Пусть из генеральной совокупности берется сразу несколько элементов
(либо элементы берут последовательно, но порядок их появления не учитывается).
В результате такого одновременного неупорядоченного выбора
элементов из генеральной совокупности объема
получаются комбинации, которые называются сочетаниями без повторений из
элементов по
.
Число сочетаний из элементов по равно:
Пример 6
В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:
Количество способов, которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из элементов по .
Число сочетаний с повторениями из элементов по :
Пример 7
На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?
Это задача на отыскание числа сочетаний с повторениями из 3 по 6:
Разбиение множества на группы
Пусть множество из
различных элементов разбивается на
групп так, то в первую группу попадают
элементов, во вторую —
элементов, в
-ю
группу —
элементов, причем
. Такую ситуацию называют разбиением множества на группы.
Такую ситуацию называют разбиением множества на группы.
Число разбиений на групп, когда в первую попадают элементов, во вторую — элементов, в k-ю группу — элементов, равно:
Пример 8
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
Основные правила комбинаторики.
Комбинаторика —
это раздел математики, изучающий способы
расположения объектов в соответствии
со специальными правилами и методы
подсчета числа всех возможных
способов. Правило
умножения. Если
некоторый выбор A можно осуществить m
способами, а для каждого из них некоторый
другой выбор B можно осуществить n
способами, то выбор A и B (в указанном
порядке) можно осуществить m×n
способами. Пример
1. На
гору ведут 6 дорог. Сколькими способами
можно подняться на гору и спуститься с
горы, если подъем и спуск должен быть
по разным дорогам?
Решение.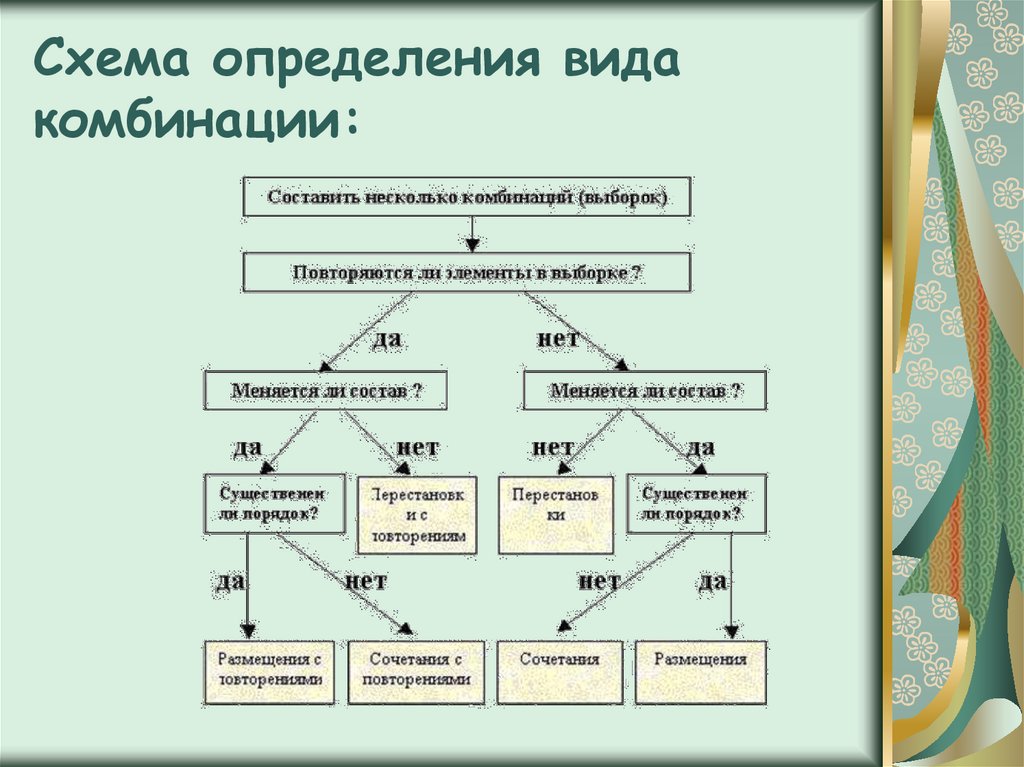 Дорогу на
гору можно выбрать 6-ю способами, так
как подъем и спуск должны быть по разным
дорогам, то выбрать дорогу для спуска
можно 5-ю способами. Тогда по правилу
умножения число способов выбора дороги
для подъема и спуска равно 6×5=30. Правило
сложения. Если
некоторый выбор A можно осуществить m
способами, а выбор B можно осуществить
n способами, то выбор A или B можно
осуществить m+n способами. Пример
2. В
ящике имеется 6 красных карандашей, 5
синих и 3 простых карандаша. Сколькими
способами можно выбрать цветной
карандаш?
Решение. Цветной карандаш
— это красный или синий, следовательно,
по правилу сложения число способов
выбора цветного карандаша равно
6+5=11.
Замечание. Данные правила можно
обобщить на большее число
выборов. Вопрос. Сколько
основных правил комбинаторики существует?
Дорогу на
гору можно выбрать 6-ю способами, так
как подъем и спуск должны быть по разным
дорогам, то выбрать дорогу для спуска
можно 5-ю способами. Тогда по правилу
умножения число способов выбора дороги
для подъема и спуска равно 6×5=30. Правило
сложения. Если
некоторый выбор A можно осуществить m
способами, а выбор B можно осуществить
n способами, то выбор A или B можно
осуществить m+n способами. Пример
2. В
ящике имеется 6 красных карандашей, 5
синих и 3 простых карандаша. Сколькими
способами можно выбрать цветной
карандаш?
Решение. Цветной карандаш
— это красный или синий, следовательно,
по правилу сложения число способов
выбора цветного карандаша равно
6+5=11.
Замечание. Данные правила можно
обобщить на большее число
выборов. Вопрос. Сколько
основных правил комбинаторики существует?
Перестановки.
Определение
1. Множество
называется упорядоченным,
если каждому элементу этого множества
поставлено в соответствие некоторое
натуральное число от 1 до n, где n — это
число элементов данного множества,
причем разным элементам поставлены в
соответствие разные числа.
Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком. Определение 2. Различные упорядоченные множества, составленные из элементов данного множества, отличающиеся лишь порядком элементов, называются его перестановками. Пример 3. Рассмотрим множество M={a,b,c}. Это множество из трех элементов. Составим его различные перестановки: (a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a). Получили 6 перестановок. P n — число всех перестановок множества из n элементов.
P n =n! (1), где
n!=1·2·3·…·n (читается «н факториал»).
Замечание.
0!=1; (n+1)!=n!·(n+1) . Пример
4. Сколько
шестизначных чисел, кратных пяти, можно
составить из цифр 0,1,2,3,4,5, при условии,
что в числе нет одинаковых цифр?
Решение.
Числа, кратные пяти(делящиеся на пять),
оканчиваются либо на 0, либо на 5. Если
последняя цифра числа 0, то остальные
цифры можно располагать в любом порядке,
получим перестановки из пяти элементов,
их P 5 =5!=120. Если на конце 5, то остальные можно
расположить P 5 =120
способами, но среди них не подходят те,
которые начинаются на 0, так как это
будут не шестизначные числа. а пятизначные,
данных чисел P 4 =4!=24.Тогда
требуемых чисел будет 120+120-24=216.
Если на конце 5, то остальные можно
расположить P 5 =120
способами, но среди них не подходят те,
которые начинаются на 0, так как это
будут не шестизначные числа. а пятизначные,
данных чисел P 4 =4!=24.Тогда
требуемых чисел будет 120+120-24=216.
Вопрос. Сколько существует перестановок из шести элементов?
Ваш ответ : 720
Перестановки с повторениями.
Если взять цифры 1, 2, 3, 4, то из них можно составить 24 перестановки. Но если взять четыре цифры 1, 1, 2, 2, то можно получить только следующие различные перестановки: (1,1,2,2),(1,2,1,2),(1,2,2,1),((2,2,1,1),(2,1,2,1),(2,1,1,2), то есть шесть перестановок, их в 4 раза меньше, чем перестановок из четырех различных чисел, так как перестановки, в которых меняются местами одинаковые числа — это не новые перестановки, их 2!·2!=4. Рассмотрим задачу в общем виде:пусть имеется множество из элементов, в котором элементы встречаются раз, элементы встречаются раз,…, элементы встречаются раз, причем .
Определение
3. Перестановки
с повторениями —
это перестановки из элементов данного
множества, в которых элементы
повторяются.
—
число всех перестановок с повторениями.
Число
перестановок, не меняющих данную
перестановку с повторениями равно ,
а чисел
можно переставлять способами,
поэтому получаем следующую формулу для
вычисления числа перестановок с
повторениями:
Перестановки
с повторениями —
это перестановки из элементов данного
множества, в которых элементы
повторяются.
—
число всех перестановок с повторениями.
Число
перестановок, не меняющих данную
перестановку с повторениями равно ,
а чисел
можно переставлять способами,
поэтому получаем следующую формулу для
вычисления числа перестановок с
повторениями:
Пример 4. Сколькими способами можно расселить 8 студентов по трем комнатам: одноместной, трехместной и четырехместной? Решение. Различныеспособы расселения студентов по комнатам являются перестановками с повторениями, так как внутри, например, трехместной комнаты выбранные студенты могут занимать спальные места по-разному, но эти варианты не будут являться новыми перестановками, поэтому получаем: То есть всего 280 способов расселения студентов. Вопрос. Вычислить
Сочетания.
Пусть некоторое множество содержит n элементов.
Определение
4. Всякое
m- элементное подмножество n- элементного
множества называется
сочетанием из
n элементов по m. —
число всех сочетаний.
—
число всех сочетаний.
(3)
Пример 5. Для соревнований из 30 спортсменов надо выбрать трех человек. Сколькими способами это можно сделать? Решение. Команда из 3 спортсменов — это подмножество из трех элементов, то есть сочетание из 30 по 3, поэтому количество способов выбора таких команд вычисляется по формуле (3): .
Свойства сочетаний.
1. 2. . Из данных свойств следует, что , тогда , далее , , и так далее. Можно расположить эти числа в виде таблицы:
……………………………………………..
…………………..
Эта таблица в виде треугольника называется треугольником Паскаля.
Определение 5. Выражение a+b называется биномом.
Формула (4) называется биномиальной формулой Ньютона, а коэффициенты называются биномиальными коэффициентами. Из данной формулы вытекает следующее свойство числа сочетаний
Вопрос. .
Сочетания с повторениями
Пусть
имеется множество, содержащее n видов
элементов, поэтому есть взять какое-то
подмножество
этого множества, то
в нем могут быть одинаковые
элементы. Определение
6. Сочетание
с повторениями —
это m- элементное подмножество множества,
содержащего n видов
элементов, в котором
элементы повторяются.
—
число всех сочетаний с повторениями из
n по m. Состав m- элементного подмножества
имеет вид
,
где .
Заменяя каждое из чисел соответствующим
количеством единиц
и разделяя единицы
нулями, получаем набор, состоящий из m
единиц и n-1 нулей. Каждому составу
отвечает
только одна запись из нулей
и единиц, а каждая запись задает только
один состав, следовательно, число
различных составов равно числу
перестановок с повторениями из n-1 нулей
и m единиц. Получаем формулу для вычисления
всех сочетаний с повторениями.
Определение
6. Сочетание
с повторениями —
это m- элементное подмножество множества,
содержащего n видов
элементов, в котором
элементы повторяются.
—
число всех сочетаний с повторениями из
n по m. Состав m- элементного подмножества
имеет вид
,
где .
Заменяя каждое из чисел соответствующим
количеством единиц
и разделяя единицы
нулями, получаем набор, состоящий из m
единиц и n-1 нулей. Каждому составу
отвечает
только одна запись из нулей
и единиц, а каждая запись задает только
один состав, следовательно, число
различных составов равно числу
перестановок с повторениями из n-1 нулей
и m единиц. Получаем формулу для вычисления
всех сочетаний с повторениями.
(5)
Пример 6. В
кондитерском магазине продаются пирожные
четырех видов: наполеоны, эклеры, песочные
и бисквитные. Сколькими способами можно
купить 7 пирожных? Решение. Любая
покупка — это подмножество, в котором
могут быть одинаковые элементы,
поэтому
это сочетание с повторениями.
Число всех возможных покупок находим
по формуле (5):
. Вопрос. В
формуле (5) m может быть больше n.
Вопрос. В
формуле (5) m может быть больше n.
Размещения
Определение 7. Упорядоченное m — элементное подмножество n- элементного множества называется размещением. — число всех размещений из n элементов по m. Число всех размещений из n по m больше числа всех сочетаний из n по m, так как из каждого подмножества из m элементов с помощью перестановок можно получить m! упорядоченных подмножеств, получаем формулу для числа размещений
(6)
Пример 7. В группе 25 человек. Нужно выбрать актив группы: старосту, заместителя старосты и профорга. Сколькими способами это можно сделать? Решение. Актив группы — это упорядоченное подмножество из трех элементов, так как надо выбрать не только трех человек, но и распределить между ними должности, значит актив группы — это размещение, число всех размещений вычисляем по формуле (6): . Вопрос. Во сколько раз число сочетаний из 20 по 4 меньше числа размещений из 20 по 4?
Размещения с повторениями
Пусть дано
множество из n элементов, в котором есть
одинаковые элементы, тогда его подмножества
тоже могут
содержать одинаковые
элементы. Определение
8. Упорядоченные
m- элементные подмножества n- элементного
множества, в которых элементы могут
повторяться, называются размещениями
с повторениями.
—
число всех размещений из n по m. В
подмножестве из m элементов первый
элемент можно
выбрать n способами(то есть любой элемент множества) , так
как элементы могут повторяться, то
второй
элемент тоже можно выбрать n способами,
аналогично остальные элементы подмножества
можно выбрать n способами, если
воспользоваться правилом умножения,
получим формулу для вычисления числа
размещений с повторениями:
Определение
8. Упорядоченные
m- элементные подмножества n- элементного
множества, в которых элементы могут
повторяться, называются размещениями
с повторениями.
—
число всех размещений из n по m. В
подмножестве из m элементов первый
элемент можно
выбрать n способами(то есть любой элемент множества) , так
как элементы могут повторяться, то
второй
элемент тоже можно выбрать n способами,
аналогично остальные элементы подмножества
можно выбрать n способами, если
воспользоваться правилом умножения,
получим формулу для вычисления числа
размещений с повторениями:
Пример 8. В
лифт десятиэтажного дома вошли 5 человек.
Каждый из них может выйти на любом
этаже,
начиная со второго. Сколькими
способами они могут это сделать? Решение. Так
как каждый человек может выйти на любом
этаже, начиная со второго, то этажей для
выхода 9.
Надо выбрать этажи для
возможности выхода каждого человека:
для первого человека — можно выбрать
любой из девяти этажей, аналогично для
остальных пассажиров, тогда по формуле
(7):
способов. Вопрос. Вычислить .
Вопрос. Вычислить .
При решении многих практических задач приходится использовать комбинации элементов, выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными . Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina» , что в переводе на русский язык означает – «сочетать», «соединять».
Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.
Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения .
Задача 1.
В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?
Решение .
Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).
Ответ: 24.
Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.
Рассмотрим решение нескольких задач на разные виды соединений без повторений.
Задача 2.
Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.
Решение.
Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.
Ответ: 210.
Задача 3.
Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?
Решение.
На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:
A 10 7 – A 9 6 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.
Ответ: 544 320.
Задача 4.
Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?
Решение.
Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.
Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.
Ответ: 8! · 5!
Задача 5 .
В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?
Решение.
Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:
С 16 4 · С 12 3 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.
Ответ: 400 400.
Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.
Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания / Хабр
В комбинаторике сочетанием из по называют набор элементов, выбранных из элементов. В отличие от размещений, число сочетаний не учитывает последовательность размещения элементов, например: «Сколько групп из 4 человек, можно получить, если всего в классе 20 человек?». Хотя удобные способы подсчёта давно известны, на ещё два стоит взглянуть.
Обозначается сочетание из по так: . В литературе они чаще обозначаются (но мне больше нравится первый вариант, чтобы не путать с матрицами).
В литературе они чаще обозначаются (но мне больше нравится первый вариант, чтобы не путать с матрицами).
В комбинаторике известны несколько способов подсчёта:
Где — эн факториал, произведение всех целых чисел от 1 до n (например: ), а считается равным единице. Для вышесказанной задачи получается:
Или так:
Вторая формула сочетаний выводится очень просто. Есть понятие числа размещений из по , когда последовательность элементов имеет значение (то есть набор «первый со вторым с пятым» это не тоже самое, что «первый с пятым со вторым»), обозначается .
Например все размещения из 3 по 2 выглядят так:
12 21
13 31
23 32
Первый элемент можно выбрать способами, второй — способами, последний — способами. Поэтому число размещений из по равно , всего множителей.
Для подсчёта сочетаний получившиеся число нужно разделить на , поскольку есть способов разместить элементов. В данном случае — способа (первый со вторым и второй с первым — это одно и тоже сочетание).
В данном случае — способа (первый со вторым и второй с первым — это одно и тоже сочетание).
Вспомним, как идет счёт в шашках по круговой системе (когда все играют со всеми). Для этого пишут обычную таблицу:
По горизонтали и вертикали идут номера игроков. Диагональ можно закрасить — игрок не может играть сам с собой. Результат каждой партии записывают в таблицу два раза. Как сыграл второй с пятым и как сыграл пятый со вторым. Таким образом, количество партий в турнире — и есть число сочетаний по 2.
Число вычеркнутых клеток равно , а число всех клеток — это . Стало быть, число сочетаний по 2 можно посчитать так:
Когда я это заметил, не сразу увидел что это равно . Решил сделать также для , с трёхмерной таблицей:
На каждом её слое, кроме диагонали исключаются еще клетки. Например, клетка 161 исключается, потому что единица повторилась два раза.
Всего на каждом слое исключается клеток.
Итак, на каждом слое исключается клетки. Всего слоёв, поэтому общее число исключившихся ячеек:
Всего слоёв, поэтому общее число исключившихся ячеек:
А вся таблица — . Значит, число сочетаний по 3 можно посчитать так:
Как уже сказано выше, это и есть общая формула, в которой просто раскрыли скобки:
И тут возник вопрос, можно ли посчитать сочетания, так же представив их через таблицы, не используя факториалы вообще? К слову, в комбинаторике уже известна рекуррентная формула для числа сочетаний: (число сочетаний по 0 равно 1, из любого количества элементов можно получить только одну группу в которой 0 элементов). Итак, я попробовал посмотреть, какие еще клетки исключаются в трёхмерной таблице, когда мы делим число оставшихся клеток на .
Клетки ниже диагонали дублируют клетки, которые выше диагонали — вычеркнем их (ячейка 431 — то же самое, что и 341). Для того, чтобы получить такое же количество клеток, просто поделим число размещений на 2.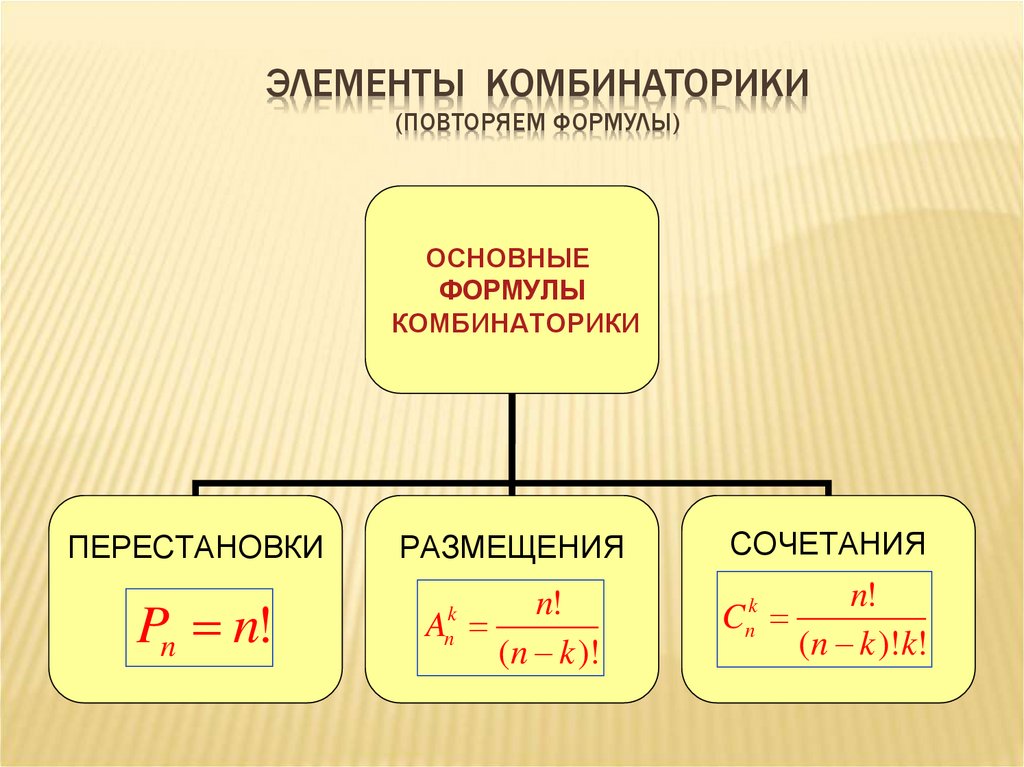 Цифрами в самой таблице я отметил, в какой строке встретилось данное сочетание. Например, сочетание 251 впервые встретилось здесь во второй строке, поэтому отмечено цифрой 2. Посмотрим на следующий слой:
Цифрами в самой таблице я отметил, в какой строке встретилось данное сочетание. Например, сочетание 251 впервые встретилось здесь во второй строке, поэтому отмечено цифрой 2. Посмотрим на следующий слой:
Закрашенные клетки с цифрой означают, что данное сочетание уже встречалось. Например, комбинация 152 уже встречалась во второй строке (в виде 251), поэтому отмечена цифрой 2 в закрашенной клетке.
Итак, на втором слое исключается ещё клетки (кроме тех, которые вычеркнуты из-за повторяющихся чисел в них, и тех, которые вычеркнуты ниже диагонали, из-за того что дублируют верхние). Перебрав так всю таблицу, я получил следующее. На третьем слое исключается ещё клеток:
На четвертом слое вычеркивается ещё клеток:
На пятом — :
На шестом, по видимому, :
Получается, что для подсчёта сочетаний по 3, из числа нужно вычесть такую сумму:
Это можно переписать в таком виде:
Ещё можно переписать эту сумму так:
То есть:
Значит, число сочетаний по 3 можно вычислить так:
Например число сочетаний из 8 по 3:
На этом этапе вряд ли видна какая-либо зависимость, посмотрим то же самое с четырёхмерной таблицей. Изобразить её можно в виде нескольких трёхмерных (у трёхмерной таблицы слои двухмерные, у четырёхмерной — трёхмерные). То есть, первый фрагмент четырёхмерной таблицы будет выглядеть так (первая ячейка будет иметь координаты 1111):
Изобразить её можно в виде нескольких трёхмерных (у трёхмерной таблицы слои двухмерные, у четырёхмерной — трёхмерные). То есть, первый фрагмент четырёхмерной таблицы будет выглядеть так (первая ячейка будет иметь координаты 1111):
Весь первый двухмерный слой этого слоя исключается (на нем единица везде повторяется). В итоге на первом трёхмерном слое вычитается такая сумма:
Слагаемые в столбик записаны лишь для наглядности. Прочерком я отметил первый двухмерный слой, который итак исключился весь. Посмотрим следующий «слой» четырёхмерной таблицы:
Значит, на втором слое исключается такая сумма:
Посмотрим на третий:
На третьем исключается сумма:
Уже здесь видно, что общая сумма, которая будет вычитаться будет такой:
её можно переписать в таком виде:
4(n-3)+3(n-4)+2(n-5)+1(n-n)+
5(n-3)+4(n-4)+3(n-5)+2(n-n)+
5(n-3)+5(n-4)+4(n-5)+3(n-n)+
5(n-3)+5(n-4)+5(n-5)+4(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)
Получаем:
Видно, что коэффициенты перед скобками уменьшаются на число, которое возрастает на единицу. Поэтому можем записать:
Поэтому можем записать:
Однако, получившаяся формула будет работать только для , ведь для других коэффициенты будут другие. И, поскольку я не увидел зависимости от и здесь, решил посмотреть тоже самое для , через пятимерную таблицу, весь её первый трёхмерный «слой» исключается, поскольку единица здесь повторяется во всех ячейках:
Для наглядности запишем это так:
Смотрим дальше:
Тут, как видно, вычитается такая сумма:
Третий:
Тут вычитается:
Затем, шестой фрагмент:
На этом первый четырёхмерный слой заканчивается. Не сложно понять, что трёхмерный «слой» 21 будет дублировать слой 12, а слой 22 исключится весь, также как 11.
Перейдем к «слою» 23:
Здесь встретилось последнее сочетание из 6 по 5 — 56423 (клетки, которые встретились впервые отмечены белым, если кто забыл)). Напишем, какую в итоге надо вычесть сумму из , чтобы получить число сочетаний из по 5. На первом четырёхмерном слое исключилось:
Напишем, какую в итоге надо вычесть сумму из , чтобы получить число сочетаний из по 5. На первом четырёхмерном слое исключилось:
На втором:
Получается что каждая сумма в скобке обозначает исключившиеся ячейки на трёхмерных слоях. Всего четырёхмерных слоёв. Запишем это в виде суммы:
Получается, что последняя сумма суммирует исключившиеся ячейки на одномерных слоях, образуя исключения на двухмерных. Предпоследняя сумма складывает исключившиеся ячейки на двухмерных слоях, образуя исключившиеся ячейки на трёхмерных и т.д.
Индекс второй суммы берем до , поскольку она «образует» исключения на четырёхмерных слоях, суммируя вычеркнутые ячейки на трёхмерных, как мы могли видеть выше, у пятимерной таблицы на каждом четырёхмерном слое исключается один трёхмерный, то есть для , на каждом четырёхмерном остается пять трёхмерных слоёв, .
Для , шестимерную таблицу можно не смотреть, достаточно выписать индексы её последних трёх измерений:
111 121 131 141 151 161112 122 132 142 152 162113 123 133 143 153 163114 124 134 144 154 164115 125 135 145 155 165116 126 136 146 156 166
211 …212 …
…
Опять же, вычеркнули мы те слои, где хоть одна цифра повторилась. Уже по первому пятимерному слою видно, что на пятимерных слоях для шестимерной таблицы останется на один четырёхмерный слой меньше. Количество оставшихся четырёхмерных слоёв равно . А трёхмерных слоёв на каждом четырёхмерном остается все также (по 4 в данном случае: ). Запись в виде сумм получилась такой:
Уже по первому пятимерному слою видно, что на пятимерных слоях для шестимерной таблицы останется на один четырёхмерный слой меньше. Количество оставшихся четырёхмерных слоёв равно . А трёхмерных слоёв на каждом четырёхмерном остается все также (по 4 в данном случае: ). Запись в виде сумм получилась такой:
Запись для можно переписать так:
Для получается:
Для :
В общем виде запись для получается такой (сумма, которую мы вычитаем вычисляется рекуррентно):
Второй способ
Как я уже писал выше, число сочетаний по 3 можно записать через одну сумму:
А число сочетаний из 6 по 4 можно записать так:
Оказывается, что 30 во вторых скобках, это (логического обоснования этому я так и не смог найти).
Вторые скобки здесь представляют собой коэффициент, который умножается на . Для этот коэффициент просто уменьшается на 1 с каждым слагаемым первой суммы. Для — число, на которое уменьшается этот коэффициент возрастает на 1. Затем я просто посчитал количество слагаемых , и в сумме которая вычитается для :
Число, на которое увеличивается число, на которое уменьшается коэффициент, возрастает на 1. Этот коэффициент можно записать через две суммы:
Зависимость ясна — для эта формула будет выглядеть так:
А в общем виде (опять же, для ) получилось так:
Под конец скажу, что метод действительно получился неоптимальный, хотя мне и было интересно найти его. Фактически, деление на факториал здесь просто заменяется вычитанием, но думаю лишним не будет.
Открытые видеолекции учебных курсов МГУ
Список всех тем лекций
Лекция 1. Введение в комбинаторику. Часть 1.
Введение в комбинаторику. Часть 1.
Список литературы
Общие слова о комбинаторике
Правила комбинаторики
Принцип Дирихле
Сочетания, размещения, перестановки
Лекция 2. Введение в комбинаторику. Часть 2.
Формула сочетаний с повторениями
Бином Ньютона
Первое тождество
Второе тождество (треугольник Паскаля)
Третье тождество
Лекция 3. Комбинаторные тождества. Часть 1.
Четвертое тождество
Полиномиальная формула
Пятое тождество
Лекция 4. Комбинаторные тождества. Часть 2.
Часть 2.
Шестое тождество
Формула включений и исключений
Седьмое тождество
Восьмое (знакопеременное) тождество
Лекция 5. Формула обращения Мёбиуса.
Перечисление циклических последовательностей
Формула обращения Мёбиуса
Теорема (формула обращения Мёбиуса)
Лекция 6. Циклические последовательности.
Формула обращения Мёбиуса
Циклические последовательности
Подсчет количества циклических последовательностей
Лекция 7. Оценки и асимптотики для факториалов и чисел сочетания.
Теорема 1
Теорема 2
(оценка факториала)
Понятие асимптотики
(формула Стирлинга)
Рекуррентные соотношения в комбинаторике
Разбиение чисел на слагаемые
Теорема об упорядоченных разбиениях
Лекция 8. Рекуррентные соотношения.
Рекуррентные соотношения.
Теорема
Теорема (рекуррентное соотношение)
Диаграммная техника работы с неупорядоченными разбиениями
Теорема 1
Теорема 2
Лекция 9. Числа Фибоначчи.
(о количестве разбиений числа на слагаемые)
Задача Эйлера
Теорема Эйлера
Числа Фибоначчи
Линейные рекуррентные соотношения с постоянными коэффициентами
Соотношения второго порядка
Лекция 10. Линейные рекуррентные соотношения.
(общая формула для разных корней характеристического уравнения)
(общая формула для совпадающих корней характеристического уравнения)
Линейные рекуррентные соотношения с постоянными коэффициентами произвольного порядка k
Теорема
Лекция 11. Отношения эквивалентности.
Отношения эквивалентности.
Выравнивание последовательностей
Теорема о количестве выравниваний
Отношение эквивалентности
«Основная теорема математики»
Отношение эквивалентности на множестве выравниваний
Теорема о числе классов эквивалентности выравнивания
Лекция 12. Формальные степенные ряды.
Следствие из теоремы о числе классов эквивалентности выравниваний
Пример
Пример
Лекция 13. Графы. Введение.
Определение графа и примеры
Маршруты в графах
Степень вершины
Изоморфные графы
Лекция 14. Эйлеровы графы. Деревья.
Эйлеровы графы. Деревья.
Эйлеровы графы и эйлеровы циклы
Теорема об эквивалентности определений эйлерового графа
Деревья
Теорема об эквивалентности определений дерева
Лекция 15. Теорема об эквивалентности определений дерева.
Теорема об эквивалентности определений дерева
Некоторые определения графов
Доказательство Прюфера
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375469 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Образовательная платформа московских колледжей
Образовательная платформа московских колледжейРесурсы колледжей
- Главная
- Курсы
- Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика
Пройти курс
Раздел 1. Теория вероятностей. Тема 1. 1. Комбинаторика
1. Комбинаторика
Правила комбинаторики. Сочетания. Размещения. Перестановки Практическое занятие №1. Сочетания. Размещения. Перестановки
Раздел 1. Теория вероятностей. Тема 1.2. Основные понятия и теоремы теории вероятностей. Вероятность случайного события
Случайные события. Виды случайных событий. Вероятность случайного события. Классическое, статистическое и геометрическое определения вероятности события. Вероятность суммы событий. Вероятность произведения событий. Условная вероятность. Формула полной вероятности события. Формула Байеса
Практическое занятие №2. Классическое определение вероятности событий
Практическое занятие №3. Операции над вероятностями
Практическое занятие №4. Формула полной вероятности события. Формула Байеса
Формула Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли. Формула Пуассона. Формула Муавра-Лапласа. Интегральная формула Лапласа
Практическое занятие №5. Формула Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли
Практическое занятие №6. Формула Пуассона
Практическое занятие №7.
Операции над вероятностями
Практическое занятие №4. Формула полной вероятности события. Формула Байеса
Формула Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли. Формула Пуассона. Формула Муавра-Лапласа. Интегральная формула Лапласа
Практическое занятие №5. Формула Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли
Практическое занятие №6. Формула Пуассона
Практическое занятие №7. Формула Муавра-Лапласа. Интегральная формула Лапласа
Формула Муавра-Лапласа. Интегральная формула Лапласа
Раздел 1. Теория вероятностей. Тема 1.3. Случайные величины
Дискретные случайные величины. Закон распределения. Числовые характеристики дискретной случайной величины: мода, медиана, математическое ожидание, дисперсия, среднеквадратическое отклонение
Практическое занятие №8. Числовые характеристики ДСВ
Виды распределений: биноминальное, геометрическое. Распределение Пуассона. Нормальное, равномерное распределение непрерывной случайной величины
Практическое занятие №9. Виды распределений ДСВ. Числовые характеристики
Виды распределений ДСВ. Числовые характеристики
Раздел 2. Математическая статистика. Тема 2.1. Дискретный и интервальный вариационные ряды
Дискретный вариационный ряд. Интервальный вариационный ряд. Числовые характеристики вариационных рядов. Полигон и гистограмма Практическое занятие №10. Полигон и гистограмма. Числовые характеристики
Раздел 2. Математическая статистика. Тема 2.2. Проверка статистических гипотез
Практическое занятие №11. Проверка гипотезы о статистической значимости различий между величинами
Итоговое тестирование
Тест
Модуль
Теория вероятностей и математическая статистика
Занятие
Правила комбинаторики. Сочетания. Размещения. Перестановки
Сочетания. Размещения. Перестановки
Материалы
Презентация по теме «Правила комбинаторики. Сочетания. Размещения. Перестановки»
Скачать
Вопросы для самоконтроля
Скачать
Math.ru
Наум Яковлевич Виленкин
М.: Наука, 1969. 328 с.
Тираж 100000 экз.
| |||||||||||
Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой . В данной книге о комбинаторных проблемах рассказывается в занимательной, популярной форме. Тем не менее в ней разбираются и некоторые довольно сложные задачи, дается понятие о методах рекуррентных соотношений и производящих функций.
В данной книге о комбинаторных проблемах рассказывается в занимательной, популярной форме. Тем не менее в ней разбираются и некоторые довольно сложные задачи, дается понятие о методах рекуррентных соотношений и производящих функций.
Первая глава книги посвящена общим правилам комбинаторики — правилам суммы и произведения. Во второй главе изучаются размещения, перестановки и сочетания. В главе 3 изучаются задачи, в которых на рассматриваемые комбинации налагаются те или иные ограничения. В главе 4 рассмотрены задачи на разбиения чисел и рассказано о геометрических методах в комбинаторике. Глава 5 посвящена задачам о случайных блужданиях и различным модификациям арифметического треугольника. В главе 6 рассказано о рекуррентных соотношениях, а в главе 7 — о производящих функциях, и в частности о биномиальной формуле.
Содержание
Предисловие
Глава I. Общие правила комбинаторики
Суеверные велосипедисты
Размещения с повторениями
Системы счисления
Секретный замок
Код Морзе
Морской семафор
Электронная цифровая вычислительная машина
Генетический код
Общие правила комбинаторики
Задача о домино
Команда космического корабля
Задача о шашках
Сколько человек не знают иностранных языков?
Формула включений и исключений
В чем ошибка?
Решето Эратосфена
Глава II. Размещения, перестановки и сочетания
Размещения, перестановки и сочетания
Футбольное первенство
Размещения без повторений
Научное общество
Перестановки
Задача о ладьях
Лингвистические проблемы
Хоровод
Перестановки с повторениями
Анаграммы
Сочетания
Генуэзская лотерея
Покупка пирожных
Сочетания с повторениями
Снова футбольное первенство
Свойства сочетаний
Частный случай формулы включений и исключений
Знакопеременные суммы сочетаний
Глава III. Комбинаторные задачи с ограничениями
Львы и тигры
Постройка лестницы
Книжная полка
Рыцари короля Артура
Девушка спешит на свидание
Сеанс телепатии
Общая задача о смещении
Субфакториалы
Караван в пустыне
Катание на карусели
Очередь в кассу
Задача о двух шеренгах
Новые свойства сочетаний
Глава IV. Комбинаторика разбиений
Комбинаторика разбиений
Игра в домино
Раскладка по ящикам
Букет цветов
Задача о числе делителей
Сбор яблок
Сбор грибов
Посылка фотографий
Флаги на мачтах
Полное число сигналов
Разные статистики
Разбиения чисел
Отправка бандероли
Общая задача о наклейке марок
Комбинаторные задачи теории информации
Проблема абитуриента
Уплата денег
Покупка конфет
Как разменять гривенник?
Разбиение чисел на слагаемые
Диаграммная техника
Двойственные диаграммы
Формула Эйлера
Глава V. Комбинаторика на шахматной доске
Человек бродит по городу
Арифметический квадрат
Фигурные числа
Арифметический треугольник
Расширенный арифметический треугольник
Шахматный король
Обобщенный арифметический треугольник
Обобщенные арифметические треугольники и m-ичная система счисления
Некоторые свойства чисел Cm(k,n)
Шашка в углу
Арифметический пятиугольник
Геометрический способ доказательства свойств сочетаний
Случайные блуждания
Броуновское движение
У Шемаханской царицы
Поглощающая стенка
Блуждания по бесконечной плоскости
Общая задача о ладьях
Симметричные расстановки
Два коня
Глава VI. Рекуррентные соотношения
Рекуррентные соотношения
Числа Фибоначчи
Другой метод доказательства
Процесс последовательных разбиений
Умножение и деление чисел
Задачи о многоугольниках
Затруднение мажордома
Счастливые троллейбусные билеты
Рекуррентные таблицы
Другое решение проблемы мажордома
Решение рекуррентных соотношений
Линейные рекуррентные соотношения с постоянными коэффициентами
Случай равных корней характеристического уравнения
Третье решение задачи мажордома
Глава VII. Комбинаторика и ряды
Деление многочленов
Алгебраические дроби и степенные ряды
Действия над степенными рядами
Применение степенных рядов для доказательства тождеств
Производящие функции
Бином Ньютона
Полиномиальная формула
Ряд Ньютона
Извлечение квадратных корней
Производящие функции и рекуррентные соотношения
Разложение на элементарные дроби
Об едином нелинейном рекуррентном соотношении
Производящие функции и разбиения чисел
Сводка результатов по комбинаторике разбиений
Задачи по комбинаторике
Решения и ответы
| |||||||||||
Постоянный адрес этой страницы: http://math.ru/lib/363
Комбинаторика: перестановки, комбинации и диспозиции | Валентина Альто
Комбинаторика — это область математики, в основном занимающаяся подсчетом элементов из одного или нескольких наборов. Это может помочь нам подсчитать количество заказов из , в которых что-то может произойти.
В этой статье я собираюсь остановиться на трех различных типах методов:
- перестановок
- диспозиций
- комбинаций
Их проще всего вычислить. Представьте, что у нас есть n объектов, отличающихся друг от друга. Что ж, перестановка — это любое возможное расположение этих объектов.
Рассмотрим следующий пример. У нас есть коробка с несколькими шарами внутри (каждый разного цвета), и мы хотим вычислить, сколько способов мы можем расположить эти шары. Мы можем сделать это с помощью двух разных подходов: с повторением (каждый шар снова вставляется в коробку после того, как его взяли) или без повторения.
Мы можем сделать это с помощью двух разных подходов: с повторением (каждый шар снова вставляется в коробку после того, как его взяли) или без повторения.
- С повторением : идея состоит в том, что после извлечения каждого шара мы можем снова брать его столько раз, сколько захотим. Давайте начнем с простого и рассмотрим коробку={g,b}, где g=’зеленый шар’ и b=’синий шар’: что ж, в этом случае мы можем расположить эти шары так: ‘gg’, «бг», «гб», «бб». Мы также можем вычислить его с помощью Python:
box_1=['g','b']
perm=[]
для p в itertools.product(listA, repeat=2):
perm.append(p)perm
Вывод:
[( 'g', 'g'), ('g', 'b'), ('b', 'g'), ('b', 'b')]
Вместо этого сделаем то же самое с 3 мячами :
box_2 = ['g','b','y']
perm=[]
for p в itertools.product(box_2, repeat=3):
perm.append(p)perm
Вывод:
[('г', 'г', 'г'),
('г', 'г', 'б'),
('г', 'г', 'у'),
('г ', 'б', 'г'),
('г', 'б', 'б'),
('г', 'б', 'у'),
('г', 'у', 'г'),
('г' , 'у', 'б'),
('г', 'у', 'у'),
('б', 'ж', 'г'),
('б', 'г', 'б'),
('б', 'ж', 'у'),
('б', 'б', 'г'),
('б', 'б', 'б'),
('б', 'б', 'у'),
('б', 'у', 'г'),
('б', 'у', 'б'),
('б' , 'у', 'у'),
('у', 'ж', 'ж'),
('у', 'ж', 'б'),
('у', 'ж', 'у'),
('у', 'б', 'ж'),
('у', 'б', 'б'),
('у', 'б', 'у'),
('у', 'у', 'г'),
('у', 'у', 'б'),
('y', 'y', 'y')]
Теперь у нас есть 27 возможных результатов наших экспериментов. Если мы хотим обобщить, когда у нас есть n объектов и мы хотим увидеть, сколькими способами мы можем их расположить, мы имеем:
Если мы хотим обобщить, когда у нас есть n объектов и мы хотим увидеть, сколькими способами мы можем их расположить, мы имеем:
- Без повторения: в этом случае, как только вы выбрали один мяч, его нельзя использовать. больше. Таким образом, каждое расположение шаров будет иметь уникальные значения. В этом случае, возвращаясь к нашему box={g,b}, две возможные перестановки — это «gb» и «bg»:
import itertoolsbox_1 = ['g','b']
perm = itertools.permutations(box_1)для i в списке(perm):
print(i)Вывод:
('g', 'b')
('b', 'g')
Снова рассмотрим большую коробку ={g,b,y}, где y=’желтый шар’:
box_2 = ['g','b', 'y']
perm = itertools.permutations(box_2)for i in list(perm):
print(i)Вывод:
('g', 'b', 'y')
('g ', 'у', 'б')
('б', 'ж', 'у')
('б', 'у', 'г')
('у', 'ж', 'б ')
('y', 'b', 'g')
В этом случае мы должны учитывать, что после каждого извлечения количество доступных элементов на один меньше. Итак, если у нас есть n элементов в нашем наборе, перестановки будут:
Итак, если у нас есть n элементов в нашем наборе, перестановки будут:
Чтобы вы могли оценить разницу между перестановками с повторением и без него, давайте визуализируем приведенный выше пример. У нас есть коробка, содержащая 4 шара разных цветов:
Мы хотим посчитать количество возможных перестановок этих шаров, то есть: сколькими способами я могу расставить эти шары, вынимая из коробки по одному шару?
Если после каждого извлечения не будет замены, мы получим, что на первом этапе есть 4 способа, которыми мы можем установить наш первый элемент (желтый, зеленый, оранжевый и синий):
Затем мы выбираем один на один, остальные шары, и на каждом этапе способы расстановки оставшихся шаров уменьшаются:
Следовательно, в итоге у нас есть 24 возможных способа расстановки этих предметов, так как:
С другой стороны, если на на втором этапе (и на последующих) вставляем извлеченный шар обратно:
Что равно 256.
Расстановки — это не что иное, как перестановки, в которых количество объектов, которые мы хотим выбрать, меньше, чем общее количество объектов n. Давайте просто вернемся к приведенному выше примеру и предположим, что из трех шаров мы хотим расположить только первую и вторую позиции. Давайте используем box={g,b,y} и начнем со случая повторения:
Давайте просто вернемся к приведенному выше примеру и предположим, что из трех шаров мы хотим расположить только первую и вторую позиции. Давайте используем box={g,b,y} и начнем со случая повторения:
- С повторением : мы хотим выбрать два шара (k=2) из трех (n=3) и вычислить количество возможных перестановок:
box_2 = ['g','b','y']
perm=[]
for p в itertools.product(box_2, repeat=2):
perm.append(p)perm
Вывод :
[('g', 'g'),
('g', 'b'),
('g', 'y'),
('b', 'g'),
('b ', 'b'),
('b', 'y'),
('y', 'g'),
('y', 'b'),
('y', 'y') ]
В этом случае 9 возможных перестановок, а не 27. Как и в предыдущем случае, есть n возможностей для первого выбора, затем снова есть n возможностей для второго выбора, и так далее, умножая каждый раз . Но на этот раз они будут умножаться не на общее количество объектов (n), а просто на количество интересующих нас объектов (k). Итак, имеем:
Итак, имеем:
- Без повторения : то же рассуждение верно, если нет повторений. Действительно:
box_2 = ['g','b','y']
perm = itertools.permutations(box_2,2)для i в списке(perm):
print(i)Вывод:
('g', 'b')
('g', 'y')
('b', 'g')
('b', 'y')
('y', 'g')
('y', 'b')
В этом случае у нас есть:
Опять же, давайте визуализируем это, рассматривая коробку с 4 шарами и что мы хотим расположить только два из них. Для диспозиции с повторением имеем:
В то время как для диспозиции без повторения имеем:
Комбинации — это диспозиции (или перестановки, если k=n), порядок которых не имеет значения. По сути, мы используем комбинации всякий раз, когда хотим вычислить, сколькими способами из n объектов мы можем извлечь k из них, независимо от порядка их выбора .
А именно, если вспомнить рассмотренную нами в самом начале перестановку без повторения, выходами которой были ‘gb’ и ‘bg’, эквивалентной комбинацией будет только ‘gb’ (или только ‘bg’), так как порядок не не имеет значения, следовательно, они представляют один и тот же объект.
Давайте посмотрим на Python, всегда рассматривая отдельно два случая повторения и отсутствия повторения:
- С повторением:
комбинации_с_заменой (коробка_1, 2)для i в списке (гребенка):
печать (i)Вывод:
('g', 'g')
('g', 'b')
('b ', 'b')
Как видите, четвертой перестановки ‘bg’ среди этих комбинаций нет, так как она эквивалентна ‘gb’.
То же самое с 3-мя шарами (сочетаем только два из них):
из itertools импортировать комбинации_с_заменойbox_2=['g','b','y']
comb = комбинации_с_заменой(box_2, 2)для i в списке (comb):
print(i)Вывод:
('g', 'g')
('g', 'b')
('g', 'y')
( 'b', 'b')
('b', 'y')
('y', 'y')
- Без повторения:
из комбинаций импорта itertoolsгребенка = комбинации (коробка_1, 2)
для i в списке (гребенка):
print(i)Вывод:
('g', 'b')
И с тремя шарами:
из itertools импортирует комбинацииcomb = комбинации (box_2, 2)
для i в списке (comb):
print(i)Вывод:
('g', 'b')
('g', 'y' )
('b', 'y')
Количество возможных комбинаций (без повторения) определяется как:
Который известен как биномиальный коэффициент и используется в биномиальном распределении вероятностей, чтобы вычислить, сколько способами, которыми мы можем добиться наших k успехов в n испытаниях. С другой стороны, если мы допускаем повторения, биномиальный коэффициент становится:
С другой стороны, если мы допускаем повторения, биномиальный коэффициент становится:
Опять же, давайте визуализируем это с помощью нашей коробки с шариками, с повторением:
И без повторения:
Первоначально опубликовано по адресу http://datasciencechalktalk.com 7 сентября 2019 года.
5
5 Комбинации С повторениями — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 28730
- Харрис Квонг
- Государственный университет Нью-Йорка во Фредонии через OpenSUNY
Рассмотрим наш выбор \(3\) человек из \(20\) дискретных студентов.
Перестановки включают в себя все различные договоренности, поэтому мы говорим «порядок имеет значение», и есть \(P(20,3)\) способов выбрать \(3\) людей из \(20\) на пост президента, вице- президент и дворник. Steve, Ahmet, Liz (SAL) и Liz, Ahmet, Steve (LAS) — две разные аранжировки.
Steve, Ahmet, Liz (SAL) и Liz, Ahmet, Steve (LAS) — две разные аранжировки.
Для комбинаций мы выбрали \(3\) человек из \(20\), чтобы получить пятерку за курс, поэтому порядок не имеет значения. Это «\(20\) выберите \(3\)», количество наборов из 3, где порядок не имеет значения. SAL и LAS — это одно и то же. Это \(\binom{20}{3}\).
Как в перестановках, так и в комбинациях повторение не допускается. LLA – это не выбор.
Теперь переходим к комбинациям с повторениями. Здесь мы выбираем \(3\) человек из \(20\) дискретных студентов, но допускаем повторяющихся людей. Это комбинации, поэтому SAL и LAS по-прежнему являются одним и тем же выбором, но у нас есть другие различные варианты, такие как LLA, SSS, WAW, SWW и многие другие!
Пример \(\PageIndex{1}\) Первый пример
Определите количество способов выбрать 3 чайных пакетика и положить их в чайник. У вас есть по 100 штук каждого из этих шести видов чая: черный чай, ромашковый, Эрл Грей, зеленый, жасминовый и роза. (По сути, у вас есть неограниченное количество каждого вида чая.). Вы можете повторить виды чая.
(По сути, у вас есть неограниченное количество каждого вида чая.). Вы можете повторить виды чая.
Например, некоторые варианты: CEJ, CEE, JJJ, GGR и т. д.
| тип чая: | Черный | Ромашка | Эрл Грей | Зеленый | Жасмин | Роза |
|---|---|---|---|---|---|---|
| на выбор: | х | хх | ||||
| # вариантов: | 1 | 0 | 2 | 0 | 0 | 0 |
Это соглашение BEE.
| тип чая: | Черный | Ромашка | Эрл Грей | Зеленый | Жасмин | Роза |
|---|---|---|---|---|---|---|
| выбор: | хх | х | ||||
| # вариантов: | 0 | 0 | 0 | 2 | 0 | 1 |
Это соглашение GGR.
Сократите эту таблицу следующим образом: Черный | Ромашка | Эрл Грей | Зеленый | Жасмин | Роза
только разделители: | | | | |
Наши 6 видов чая дают нам 5 делителей.
Мы выбираем 3 чайных пакетика, поэтому нам нужны 3 крестика и 5 разделителей.
Вот два варианта в приведенных выше таблицах: x | | х х | | | и | | | х х | | Икс.
Какие буквы обозначают эти два варианта? | | | | xx|x и x| | х | х | | .
- Ответ
JJR и BEG
Мы расставляем 8 предметов (5 разделителей и 3 варианта чайных пакетиков), поэтому у нас есть 8 мест для размещения 3 чайных пакетиков.
______ ______ ______ ______ ______ ______ ______ ______
После того, как мы поместим 3 чайных пакетика, размещение 5 разделителей будет определено автоматически.
Есть \(\binom{8}{3}\) способы собрать 3 чайных пакетика.
Откуда взялись \(8\) и \(3\)? См. следующую теорему.
следующую теорему.
Комбинация с формулой повторения
Теорема \(\PageIndex{1}\label{thm:combin}\)
Если мы выберем набор \(r\) элементов из \(n\) типов элементов, где повторение разрешено, и количество элементов, из которых мы выбираем, практически не ограничено, возможное количество вариантов:
\[\binom{n+r-1}{r}.\]
Пример \(\PageIndex{2}\ ) Пример с ограничениями
Из неограниченного выбора из пяти видов газированных напитков, одним из которых является Dr. Pepper, вы ставите на стол 25 банок.
(a) Определите, сколькими способами вы можете выбрать 25 банок газировки.
- Раствор
Это случай без ограничений. \(\binom{5+25-1}{25}=\binom{29}{25}=23751\)
Существует 23751 способ выбрать 25 банок газировки пяти видов.
(b) Определите, сколькими способами вы можете выбрать 25 банок содовой, если вы должны включить не менее семи напитков Dr. Peppers.
- Раствор
Здесь цифра семь Dr.
 Peppers уже выбрана, так что вы действительно выбираете \(25-7=18\) банок. \(\binom{5+18-1}{18}=\binom{22}{18}=7315\)
Peppers уже выбрана, так что вы действительно выбираете \(25-7=18\) банок. \(\binom{5+18-1}{18}=\binom{22}{18}=7315\)
Есть 7315 способов выбрать 25 банок содовой пяти типов, по крайней мере, семь банок одного определенного типа.
(c) Определите количество способов, которыми вы можете выбрать 25 банок газировки, если окажется, что в наличии только три Dr. Peppers.
- Раствор
Это сложнее сделать напрямую и проще использовать дополнение. Дополнение — «четыре или более Dr. Peppers», что составляет как минимум четыре Dr. Peppers.
Следуя нашим рассуждениям в (b), количество способов выбрать 25 банок как минимум с четырьмя Dr. Peppers равно \(\binom{5+21-1}{21}=\binom{25}{21}=12650 .\)
Итак, есть 12650 способов получить четыре или более Dr. Peppers. Нам нужно вычесть это из общего количества, чтобы получить количество трех или менее Dr. Peppers.
\(\binom{5+25-1}{25}-\binom{5+21-1}{21}=\binom{29}{25}-\binom{25}{21}=23751-12650 =11101. \)
\)
Существует 11101 способ выбрать 25 банок газировки пяти видов, но не более трех одного определенного типа.
Резюме и обзор
- Перестановки: порядок имеет значение, повторы не допускаются.
- (обычный) Комбинации: порядок НЕ имеет значения, повторы не допускаются.
- Комбинации С повторениями: порядок НЕ имеет значения, повторы РАЗРЕШЕНЫ.
Упражнения
Упражнения \(\PageIndex{1}\label{ex:combin-01}\)
На ферме Lollypop есть кошки, собаки, козы, утки и лошади. Сколькими способами вы можете выбрать трех питомцев, чтобы забрать их домой?
- Раствор
\(\бином{7}{3}=35\)
Упражнение \(\PageIndex{2}\label{ex:combin-02}\)
Вы собираетесь принести на вечеринку два пакета чипсов. В отделе с чипсами вы видите обычные картофельные чипсы, картофельные чипсы барбекю, картофельные чипсы со сметаной и луком, кукурузные чипсы и кукурузные чипсы, которые можно зачерпывать. Сколько выборов вы можете сделать?
Сколько выборов вы можете сделать?
Упражнение \(\PageIndex{3}\label{ex:combin-03}\)
(a) Вычислить \(\binom{5+7-1}{7}\) (до целого числа).
(b) Если бы вам пришлось вычислять \(\binom{5+7-1}{7}\) без калькулятора, как бы вы могли упростить вычисления?
(c) Заполните пропуски, чтобы создать задачу, решением которой является формула в (a):
Вы сидите с несколькими друзьями и идете за ____________ банок газировки для своего стола. Есть __________ видов газировки. Сколько выборов вы можете сделать?
- Раствор
(a) 330
(b) \(\binom{5+7-1}{7}=\binom{11}{7} =\binom{11}{4}=\frac{11 \cdot 10 \ cdot 9 \cdot 8}{4 \cdot 3 \cdot 2 \cdot 1}=\frac{11 \cdot 10 \cdot 9}{3}=11 \cdot 10 \cdot 3=110 \cdot 3=330\)
(c) получить 7 банок газировки; 5 видов соды
Упражнение \(\PageIndex{4}\label{ex:combin-04}\)
Вы расставляете 30 банок напитков. Есть шесть видов напитков, и один тип — сельтерская.
(a) Сколькими способами можно выбрать напитки для похода?
(b) Сколькими способами вы можете выбрать напитки, которые включают не менее 8 банок газированной воды?
(c) Сколькими способами можно выбрать напитки, если в наличии только 5 банок газировки?
Упражнение \(\PageIndex{5}\label{ex:combin-05}\)
На дисплей будет установлено двадцать батареек. Типы батарей: AAA, AA, C, D и 9-вольтовые.
а) Сколькими способами мы можем выбрать двадцать батареек?
(b) Сколькими способами мы можем выбрать двадцать батарей, но быть уверенными, что по крайней мере четыре батареи являются 9-вольтовыми?
(c) Сколькими способами мы можем выбрать двадцать батарей, но иметь при этом не более двух 9-вольтовых батарей?
- Решение
(a) \(\binom{24}{20}=10626\)
(b) \(\binom{20}{16}=4845\)
(c) \(\binom{24}{ 20}-\бином{21}{17}=4641\)
Упражнение \(\PageIndex{6}\label{ex:combin-06}\)
Используйте чайные пакетики из примера 7. 5.1: черный, ромашковый, Эрл Грей, зеленый, жасминовый и розовый для ответа на эти вопросы.
5.1: черный, ромашковый, Эрл Грей, зеленый, жасминовый и розовый для ответа на эти вопросы.
(a) Вы готовите чашку чая для проректора, профессора математики и студентки. Сколько способов вы можете сделать это?
(b) Вы готовите чай для Провоста, профессора математики и студентки. У каждого человека будет свой вкус. Сколько способов вы можете сделать это?
(c) Вы завариваете чайник из четырех чайных пакетиков. Сколько способов вы можете сделать это?
(d) Вы завариваете чай из четырех чайных пакетиков разного вкуса. Сколько способов вы можете сделать это?
(e) Вы раскладываете 30 чайных пакетиков. Сколько способов вы можете сделать это?
(f) Вы раскладываете 30 чайных пакетиков, но в наличии только 5 розовых чайных пакетиков. Сколько способов вы можете сделать это?
(ж) Вы раскладываете 30 чайных пакетиков, среди которых будет как минимум 10 Эрл Грей. Сколько способов вы можете сделать это?
Упражнение \(\PageIndex{7}\label{ex:combin-07}\)
Сколько целых неотрицательных решений есть у этого уравнения: \[x_1+x_2+x_3+x_4=18?\]
- Раствор
\(\binom{21}{18}=1330\)
Упражнение \(\PageIndex{8}\label{ex:combin-08}\)
Сколько неотрицательных решений есть у этого уравнения: \[x_1+x_2+x_3+x_4+x_5=26?\ ]
Эта страница под заголовком 7. 5: Комбинации с повторениями распространяется под лицензией CC BY-NC-SA, ее автор, ремикс и/или куратор — Харрис Квонг (OpenSUNY) .
5: Комбинации с повторениями распространяется под лицензией CC BY-NC-SA, ее автор, ремикс и/или куратор — Харрис Квонг (OpenSUNY) .
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Харрис Квонг
- Лицензия
- CC BY-NC-SA
- Показать страницу Содержание
- да
- Теги
- Комбинации
комбинаций и перестановок.
 Мы бросаемся термином «комбинация»… | Бретт Берри | Математические лайфхаки
Мы бросаемся термином «комбинация»… | Бретт Берри | Математические лайфхакиВведение в комбинаторику
Мы используем термин «комбинация » неточно и обычно неправильно. Мы говорим что-то вроде: «Эй, какой у тебя код от шкафчика?» но на самом деле мы должны говорить: «Эй, какой у тебя шкафчик перестановка ?»
Так какая разница? А что такое перестановка? Смотрите или читайте дальше 🙂
Нажмите здесь, чтобы подписаться на Math HacksРазница между комбинациями и перестановками заключается в порядке. При перестановках нам важен порядок элементов, а при комбинациях — нет.
Например, предположим, что «комбо» вашего шкафчика — 5432. Если вы введете 4325 в свой шкафчик, он не откроется, потому что это другой порядок (также известный как перестановка).
The permutations of 2, 3, 4, 5 are:
- 5432, 5423, 5324, 5342, 5234, 5243, 4532, 4523, 4325, 4352, 4253, 4235, 3542, 3524, 3425 , 3452, 3254, 3245, 2543, 2534, 2435, 2453, 2354, 2345
«Комбо» вашего шкафчика представляет собой определенную комбинацию 2, 3, 4 и 5. Если бы ваш шкафчик действительно работал комбинацией, вы могли бы ввести любую из вышеперечисленных комбинаций, и она открылась бы!
Если бы ваш шкафчик действительно работал комбинацией, вы могли бы ввести любую из вышеперечисленных комбинаций, и она открылась бы!
Предположим, вы хотите узнать, сколько существует перестановок чисел 2, 3, 4, 5, не перечисляя их, как я сделал выше. Как бы вы это сделали?
Давайте воспользуемся линейной диаграммой, чтобы визуализировать проблему.
Мы хотим найти, сколько возможных 4-значных перестановок можно составить из четырех различных чисел. Начните с рисования четырех линий, представляющих 4 цифры.
Первая цифра может быть любой из 4 цифр, поэтому поставьте «4» в первый пробел.
Теперь осталось 3 варианта для второго пробела, потому что вы уже использовали одно из чисел в первом пробеле. Поставьте «3» в следующем месте.
Для третьей позиции у вас осталось два числа.
И на последнюю позицию осталось одно число, поэтому поставьте там «1».
Принцип умножения
Использование комбинаторного принципа умножения , мы знаем, что если существует x способов сделать одно и y способов сделать другое, то общее количество способов сделать оба действия равно x•y . Это означает, что нам нужно умножить, чтобы найти общее количество перестановок.
Это означает, что нам нужно умножить, чтобы найти общее количество перестановок.
Это отличная возможность использовать сокращенную запись факториала (!) :
Есть 24 перестановки, что соответствует списку, который мы сделали в начале этого поста.
Что, если я хочу найти общее количество перестановок, включающих числа 2, 3, 4 и 5, но хочу включить такие порядки, как 5555 или 2234, где не все числа используются, а некоторые используются более одного раза? ?
Сколько существует этих перестановок?
Это простой расчет. Снова мы составляем 4-значное число, поэтому нарисуйте 4 линии, чтобы обозначить цифры.
В первой позиции у нас есть 4 варианта чисел, поэтому, как и раньше, поставьте «4» в первый пробел. Поскольку нам разрешено повторно использовать числа, теперь у нас есть 4 варианта номеров для второй, третьей и четвертой цифр.
Это то же самое, что:
Допустив повторение чисел, мы получим 256 перестановок!
Давайте попробуем решить более сложную задачу:
Сколько различных комбинаций из 5 карт можно составить из стандартной колоды карт?
В этой задаче порядок не имеет значения, так как не имеет значения, в каком порядке мы выбираем карты.
Мы начнем с пяти строк, представляющих нашу комбинацию из 5 карт.
Предполагая, что никто другой не берет карты из колоды, в первом розыгрыше доступно 52 карты, поэтому поставьте «52» в первый пробел.
После того, как вы выберете карту, в следующем розыгрыше будет на одну карту меньше. Таким образом, вторая заготовка будет иметь 51 вариант. В следующем розыгрыше в колоде будет на две карты меньше, так что теперь есть 50 вариантов и так далее.
Это 311 875 200 перестановок .
Это перестановки, а не комбинации. Чтобы исправить это, нам нужно разделить на количество рук, которые представляют собой разные перестановки, но одну и ту же комбинацию.
Это то же самое, что сказать , сколько различных способов я могу расположить 5 карт?
Примечание. Математически это похоже на нахождение различных комбинаций нашей комбинации шкафчиков.Таким образом, число комбинаций из пяти карт равно:
Приложив немного изобретательности, мы можем переписать приведенный выше расчет, используя факториалы.
Мы знаем 52! = 52•51•50•…•3•2•1, но нам нужны только произведения целых чисел от 52 до 48. Как мы можем выделить только эти целые числа?
Мы хотим разделить все целые числа, кроме от 48 до 52. Для этого разделим на 47! так как это произведение целых чисел от 47 до 1,
Не забудьте разделить на 5! , чтобы избавиться от лишних перестановок:
Вот так!
Самое интересное → мы вывели формулу для комбинаций.
Если у нас есть n объектов и мы хотим выбрать k из них , , мы можем найти общее количество комбинаций, используя следующую формулу:
читать: «n выбрать k»Например, мы у нас есть 52 карты (n=52) и мы хотим узнать, сколько рук из 5 карт (k=5) мы можем собрать.
Подставляем значения получаем:
примечание: (52–5)! = 47!Именно это мы и нашли выше!
Часто вы увидите эту формулу, написанную в скобках, как показано выше, но в некоторых книгах она пишется с гигантской буквой C:
Различные обозначения для формулы комбинацийФормула для перестановок аналогична формуле комбинаций, за исключением того, не делим перестановки, поэтому мы можем удалить k! из знаменателя:
читать: n перестановок k элементов Ну вот! Краткое изложение основ комбинаторики. Надеюсь, это поможет вам 🙂
Надеюсь, это поможет вам 🙂
❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤
Будьте в курсе всех новостей Math Hacks!
Инстаграм | Фейсбук | Twitter
Math Hacks на YouTube
Добро пожаловать во второй сезон Math Hacks! В этом сезоне мы рассмотрим темы из алгебры и тригонометрии, а также…
www.youtube.com
Больше математических материалов →
10 главных секретов треугольника Паскаля
Биномиальная теорема, последовательность Фибоначчи и треугольник Серпинского Еще
medium.com
Объяснение «правила нулевой мощности»
Показатели кажутся довольно простыми, не так ли? Возведение числа в степень 1 означает, что у вас есть одно из этих чисел, поднимите…
medium.com
Как «заполнить квадрат»
и проблемы с запоминанием
medium.com
Введение к модульной арифметике
и классам эквивалентности
medium. com
com
Перестановки и комбинации | Комбинаторика: очень краткое введение
Фильтр поиска панели навигации Oxford AcademicCombinatorics: A Very Short IntroductionVery Short IntroductionCombinatorics and Graph TheoryBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicCombinatorics: A Very Short IntroductionVery Short IntroductionCombinatorics and Graph TheoryBooksJournals Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Cite
Wilson, Robin,
‘Permutations and combinations’
,
Combinatorics: A Very Short Introduction
, Very Short Introductions
(
Oxford,
2016;
online edn,
Oxford Academic
, 28 апреля 2016 г.
), https://doi.org/10.1093/actrade/9780198723493.003.0003,
, по состоянию на 24 сентября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicCombinatorics: A Very Short IntroductionVery Short IntroductionCombinatorics and Graph TheoryBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicCombinatorics: A Very Short IntroductionVery Short IntroductionCombinatorics and Graph TheoryBooksJournals Термин поиска на микросайте
Advanced Search
Abstract
Перестановки и комбинации изучаются уже тысячи лет. «Перестановки и комбинации» предполагают выбор объектов из коллекции либо в определенном порядке (например, при ранжировании сухих завтраков), либо без учета порядка (например, при раздаче бриджа). Он описывает и исследует четыре типа выбора — упорядоченный выбор с повторением, упорядоченный выбор без повторения, неупорядоченный выбор без повторения и неупорядоченный выбор с повторением — и показывает, как они связаны с перестановками, комбинациями, тремя правилами комбинаций, факториалами, треугольником Паскаля. , биномиальная теорема, биномиальные коэффициенты и распределения.
«Перестановки и комбинации» предполагают выбор объектов из коллекции либо в определенном порядке (например, при ранжировании сухих завтраков), либо без учета порядка (например, при раздаче бриджа). Он описывает и исследует четыре типа выбора — упорядоченный выбор с повторением, упорядоченный выбор без повторения, неупорядоченный выбор без повторения и неупорядоченный выбор с повторением — и показывает, как они связаны с перестановками, комбинациями, тремя правилами комбинаций, факториалами, треугольником Паскаля. , биномиальная теорема, биномиальные коэффициенты и распределения.
Ключевые слова: биномиальная теорема, факториал, лотерея, парадокс, Блез Паскаль, перестановка, треугольное число, Варахамихира
Предмет
Комбинаторика и теория графов
Серия
Краткие введения
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Вход через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
комбинаций с повторением | Superprof
Что такое комбинаторика?
Раздел математики , который занимается подсчетом , комбинацией и перестановками элементов в наборе, известен как комбинаторика . Мы используем термин комбинаторика для описания огромного подмножества дискретной математики, которое также охватывает теорию графов . Комбинаторика — это все о счете, поэтому при решении задач, связанных с комбинаторикой, вы будете иметь дело с перечислением вещей. Другими словами, мы можем сказать, что речь идет о подсчете количества аранжировок, в которых что-то может произойти.
Индийские, арабские и греческие математики являются пионерами комбинаторики. Интерес к этому предмету достиг своего пика в 19 и 20 веках. Некоторые известные математики, работавшие в этой области, — Блез Паскаль, Леонард Эйлер и Якоб Бернулли.
Интерес к этому предмету достиг своего пика в 19 и 20 веках. Некоторые известные математики, работавшие в этой области, — Блез Паскаль, Леонард Эйлер и Якоб Бернулли.
В комбинаторике есть два основных понятия — комбинация и перестановка. Оба эти понятия используются для перечисления количества порядков, в которых могут произойти вещи. Однако между этими двумя терминами есть одно различие: комбинация имеет дело с подсчетом количества аранжировок, в которых может произойти событие, при условии, что порядок аранжировок не имеет значения. Принимая во внимание, что порядок расположения имеет значение в перестановке. Подобно перестановке, комбинация бывает двух типов:
- Комбинация с повторением
- Комбинация без повторения
В этой статье мы обсудим только комбинацию с повторением.
Лучшие репетиторы по математике
Поехали
Комбинация с повторением
Предположим, что в наборе A есть p элементов. Нас просят выбрать q элементов из этого набора, учитывая, что каждый элемент может быть выбран несколько раз. Это известно как комбинация с повторением 9.0023 . Например, мы можем составить комбинации из трех элементов множества {p, q, r, s} таким образом:
Это известно как комбинация с повторением 9.0023 . Например, мы можем составить комбинации из трех элементов множества {p, q, r, s} таким образом:
ppp, ppq, ppr, pps, pqq, pqr, pqs, prr, prs, pss, qqq, qqr, qqs, qrr, qrs, qss, rrr, rrs,rss, sss
Как видите, большинство алфавитов повторяются более одного раза.
Рассмотрим другой пример:
В кафе-мороженом доступны три вида мороженого. Это шоколад, ваниль и ананас. У человека может быть только два шарика мороженого. Какие будут вариации в этом случае?
Ну, если человек может выбрать две мерные ложки за раз, то он может есть один вкус два раза. При этом примерами вариаций могут быть:
шоколадный, шоколадный, ванильный шоколадный, шоколадно-ананасовый и т.д.
Порядок не имеет значения, вкусы могут повторяться.
Комбинации с повторениями Формула
Вы можете использовать приведенную ниже формулу, чтобы узнать количество комбинаций, когда разрешено повторение.
Здесь n = общее количество элементов в наборе
r = количество элементов, которые можно выбрать из набора
Теперь мы решим некоторые примеры, связанные с комбинациями с повторением, что сделает всю концепцию более понятной.
Пример 1
В пуле пять цветных шаров. Все шарики разного цвета. Сколькими способами мы можем выбрать четыре шара для пула?
Решение
Порядок выбора шаров в данном случае не имеет значения. Подбор шаров можно повторить.
Общее количество шаров в пуле = n = 5
Количество шаров, которые нужно выбрать = r = 4
Используйте следующую формулу, чтобы получить количество расстановок, в которых можно выбрать четыре шара пула.
Подставьте эти значения в приведенную выше формулу:
Следовательно, шары для пула можно выбирать 70 различными способами.
Пример 2
В магазине мороженого есть восемь разных вкусов мороженого. Сколькими способами мы можем выбрать пять вкусов из этих восьми?
Сколькими способами мы можем выбрать пять вкусов из этих восьми?
Решение
Порядок выбора ароматов в данном случае не имеет значения. Один вкус мороженого можно выбрать несколько раз.
Общее количество вкусов мороженого = n = 8
Количество выбираемых вкусов мороженого = r = 5 быть выбранным.
Подставьте эти значения в приведенную выше формулу:
Следовательно, вкусы мороженого можно выбрать 792 способами.
Пример 3
У Гарри шесть рубашек разного цвета. Сколькими способами он может повесить четыре рубашки в шкафу?
Решение
Порядок, в котором можно выбирать рубашки, в данном случае не имеет значения. Рубашки можно повторить.
Общее количество рубашек = n = 6
Количество выбираемых рубашек = r = 4
Используйте следующую формулу, чтобы получить количество аранжировок, в которых можно выбрать четыре рубашки.
Подставьте эти значения в приведенную выше формулу:
Таким образом, рубашки могут отображаться 126 различными способами.
Пример 4
У Алисы семь разных шоколадок. Сколькими способами можно выбрать пять шоколадок?
Решение
Порядок, в котором можно выбирать конфеты, в данном случае не имеет значения. Ароматы могут повторяться.
Общее количество шоколадных конфет = n = 7
Количество шоколадных конфет, которые нужно выбрать = r = 5
Используйте следующую формулу, чтобы получить количество расстановок, в которых можно выбрать четыре рубашки.
Подставьте эти значения в приведенную выше формулу:
Следовательно, конфеты можно выбирать 462 способами.
Пример 5
У Сэма есть пять цветных карандашей. Сколькими способами он может выбрать три карандаша?
Решение
Порядок, в котором можно выбирать карандаши, в данном случае не имеет значения. Карандаши можно повторить.
Общее количество карандашей = n = 5
Количество карандашей, которые нужно выбрать = r = 3
Используйте следующую формулу, чтобы получить количество расстановок, в которых можно выбрать пять карандашей.
Подставьте эти значения в приведенную выше формулу:
Следовательно, карандаши можно выбирать 35 различными способами.
Пример 6
У Мэрайи десять разных конфет. Сколькими способами можно выбрать шесть конфет?
Решение
Порядок выбора конфет в данном случае не имеет значения. Конфеты можно повторять.
Общее количество конфет = n = 10
Количество выбираемых конфет = r = 6
Используйте следующую формулу, чтобы получить количество композиций, в которых можно выбрать шесть конфет.
Подставьте эти значения в приведенную выше формулу:
Следовательно, конфеты можно выбирать 5005 различными способами.
Блестящая вики по математике и естественным наукам
Энди Хейс, Хуа Чжи Ви, Цезарь Тариган, а также
способствовал
Содержимое
- Правило произведения и суммы
- Перестановки и комбинации
- Биномиальная теорема
- Принцип включения и исключения
- Раскраски
- Теория графов
- Рекурсия
- Распределение объектов по корзинам
- Раздел целого числа
- Принцип сортировки
- Ходьба по сетке
- Смотрите также
Основные статьи: правило произведения и правило суммы
Комбинаторика часто занимается изучением устройства вещей. В этом контексте расположение представляет собой способ группировки объектов. Самыми основными правилами, касающимися договоренностей, являются правило произведения и правило суммы. Эти правила определяют, как подсчитывать аранжировки с использованием операций умножения и сложения соответственно.
В этом контексте расположение представляет собой способ группировки объектов. Самыми основными правилами, касающимися договоренностей, являются правило произведения и правило суммы. Эти правила определяют, как подсчитывать аранжировки с использованием операций умножения и сложения соответственно.
Правило произведения определяет порядок подсчета аранжировок с помощью умножения.
Правило продукта
Если есть mmm способов упорядочить что-то, а затем nnn способов упорядочить что-то еще, то количество способов упорядочить обе эти вещи равно m×n,m \times n,m×n.
Правило суммы определяет порядок подсчета аранжировок с помощью сложения. Язык этих правил может показаться похожим. Основное отличие состоит в том, что договоренности, учитываемые по правилу произведения, происходят последовательно или одновременно, в то время как договоренности, учитываемые по правилу суммы 9.0003 не может произойти последовательно или одновременно.
Правило суммы
Если есть mmm способов упорядочить что-то и есть nnn способов упорядочить что-то еще, и эти расположения не могут произойти одновременно, то количество способов упорядочить любую из этих вещей равно m+n.m + n.m+n.
Какой процент от первых 100100100 целых положительных чисел не содержит четных цифр?
Многие задачи комбинаторики можно решить, применяя эти простые правила. На самом деле более продвинутые формулы комбинаторики являются просто расширениями этих правил. Одной из потенциальных ловушек в задачах подсчета является концепция двойного подсчета. Двойной учет — это ошибка, при которой один и тот же объект или расположение учитываются более одного раза.
Сколько целых чисел от 1 до 100 делятся на 7 или 13?
Количество целых чисел от 1 до 100, которые делятся на 7, равно ⌊1007⌋=14.\left\lfloor \frac{100}{7} \right\rfloor=14.⌊7100⌋=14.

Количество целых чисел от 1 до 100, которые делятся на 13, равно ⌊10013⌋=7.\left\lfloor \frac{100}{13} \right\rfloor=7.⌊13100⌋=7.Может показаться, что здесь применимо правило суммы, и ответ будет 7+14=21,7+14=21,7+14=21. Однако это было бы ошибкой в двойной счет . Нужно учитывать, что целое число может делиться и на 7, и на 13.
Количество целых чисел от 1 до 100, которые делятся на 7 и 13 равно ⌊1007×13⌋=1.\left\lfloor \frac{100}{7\times 13} \right\rfloor=1.⌊ 7×13100⌋=1.
Чтобы учесть двойной счет, эта сумма вычитается из исходного ответа 21. Таким образом, существует 202020 целых чисел от 1 до 100, которые делятся на 7 или 13. □_\квадрат□
Процесс «удаления» элементов, которые учитываются дважды, формализован по принципу включения и исключения.
12 14 16 18 20
Начиная с буквы «J» и двигаясь вниз по диагонали влево или вправо каждый шаг, как показано, сколько существует способов написать слово «ПРЫЖКИ»?
Примечание : В последнем ряду всего три буквы S, поэтому крайняя правая и левая буквы P имеют только одно направление.
Основные статьи: перестановки и комбинации
См. также: Биномиальный коэффициент
Перестановка — это расположение объектов по порядку. В комбинаторике основное внимание обычно уделяется подсчету количества элементов в наборе перестановок.
Сколько существует перестановок букв ABC?\text{ABC}?ABC?
Перестановки
ABCACBBACBCACABCBA.\begin{массив}{lll} \text{ABC} и \text{ACB} и \text{BAC} \\ \text{BCA} & \text{CAB} & \text{CBA.} \end{массив}ABCBCAACBCABBACCBA.
Есть 6\boxed{6}6 перестановок. □_\квадрат□
Пусть задан набор из nnn различных объектов, пусть набор перестановок этих объектов равен P.P.P. Тогда
∣P∣=n!,|P|=n!,∣P∣=n!,
где!!! является факториальным оператором.
Существует nnn способов выбрать первый объект в порядке. Тогда есть n−1n-1n−1 способов выбрать второй объект в порядке.
.Это продолжается до тех пор, пока не останется 111 способов выбрать последний объект в порядке. По правилу произведения число перестановок объектов nnn равно
n×(n−1)×(n−2)×⋯×2×1=n!. □n \times (n-1) \times (n-2) \times \cdots \times 2 \times 1=n!.\ _\squaren×(n−1)×(n−2)×⋯×2 ×1=n!. □
Также можно учитывать перестановки подмножества объектов.
Сколько существует перестановок двух букв из ABCD?\text{ABCD}?ABCD?
Перестановки
ABADBDBADADBACBCCDCACBDC.\begin{массив}{lll} \text{AB} & \text{AD} & \text{BD} \\ \text{BA} & \text{DA} & \text{DB} \\ \text{AC} & \text{BC} & \text{CD} \\ \text{CA} & \text{CB} & \text{DC.} \end{array}ABBAACCAADDABCCBBDDBCDDC.
Имеется 12\упакован{12}12 перестановок. □_\квадрат□
Пусть задан набор объектов nnn, пусть набор перестановок kkk этих объектов равен S.S.S. Затем
∣S∣=n!(n−k)!.|S|=\frac{n!}{(n-k)!}.∣S∣=(n−k)!n!.
Если на железнодорожной линии имеется 25 железнодорожных станций, сколько типов разовых билетов второго класса необходимо напечатать, чтобы пассажир мог проехать с одной станции на другую?
Комбинация — это расположение объектов без учета порядка.
Дан набор nnn различных объектов, пусть CCC будет набором комбинаций kkk этих объектов. Тогда
∣C∣=(nk)=n!k!(n−k)!,|C|=\binom{n}{k}=\frac{n!}{k!(n-k)!},∣C ∣=(kn)=k!(n−k)!n!,
, где (⋅⋅)\binom{\cdot}{\cdot}(⋅⋅) — оператор биномиального коэффициента.
Количество перестановок kkk объектов из набора nnn объектов равно n!(n−k)!.\frac{n!}{(n-k)!}.(n−k)!n!. Для каждого подмножества объектов kkk из набора объектов nnn имеется k!k!k! перестановки этого подмножества. Следовательно, количество комбинаций объектов kkk из набора объектов nnn равно
.n!(n−k)!÷k!=n!k!(n−k)!=(nk). □\frac{n!}{(n-k)!} \div k!=\frac{n!}{k!(n-k)!}=\binom{n}{k}.\ _\square(n−k )!n!÷k!=k!(n−k)!n!=(kn). □
Оператор биномиального коэффициента получил свое название из-за его применения к биномиальной теореме ниже. Однако этот оператор имеет широкое применение для подсчета количества комбинаций.
Сколько различных треугольников можно составить из 10 точек на плоскости, никакие 3 из которых не лежат на одной прямой?
Комбинации можно использовать для подсчета результатов в вероятностном эксперименте. Это особенно полезно, когда вероятностный эксперимент однороден. В этом случае вероятность — это просто отношение количества комбинаций.
Это особенно полезно, когда вероятностный эксперимент однороден. В этом случае вероятность — это просто отношение количества комбинаций.
Мешок содержит по 4 шарика каждого цвета: красного, оранжевого, зеленого, синего и фиолетового. Из мешка достают 3 шарика (без возврата). Если ab\frac{a}{b}ba — это вероятность того, что вытащенные шарики разного цвета, где aaa и bbb — взаимно простые положительные целые числа, то что такое a+b?a+b?a+b?
Основная статья: Биномиальная теорема
Биномиальная теорема дает полиномиальное разложение бинома, возведенного в положительную целую степень.
94\\ &\vdots& \end{выровнено} (x+y)0(x+y)1(x+y)2(x+y)3(x+y)4=====⋮1x+yx2+2xy+y2x3+3x2y+3xy2+ y3x4+4x3y+6x2y2+4xy3+y4Когда мы смотрим на коэффициенты в выражениях выше, мы находим следующую закономерность:
11112113311464115101051⋯1\\ 1\четверка 1\\ 1\четверка 2 \четверка 1\\ 1\четверка 3 \четверка 3 \четверка 1\\ 1\четверка 4 \четверка 6 \четверка 4 \четверка 1\\ 1 \четверка 5 \четверка 10 \четверка 10 \четверка 5 \четверка 1\\ \cdots11112113311464115101051⋯
Это называется треугольником Паскаля. {16}?(x+y)16? 96?(х+у+г)6?
{16}?(x+y)16? 96?(х+у+г)6?
Основная статья: Принцип включения и исключения
Принцип включения и исключения описывает, как вычислить количество элементов в пересечениях и объединениях множеств.
Сколько целых чисел от 1 до 1000 (включительно) делятся на 3, 5 или 7?
Количество целых чисел, делящихся на 3, равно ⌊10003⌋=333. \left\lfloor \frac{1000}{3} \right\rfloor = 333.⌊31000⌋=333.
Количество целых чисел, делящихся на 5, равно ⌊10005⌋=200. \left\lfloor \frac{1000}{5} \right\rfloor = 200.⌊51000⌋=200.
Количество целых чисел, делящихся на 7, равно ⌊10007⌋=142. \left\lfloor \frac{1000}{7} \right\rfloor = 142.⌊71000⌋=142.Целые числа, которые делятся на 3 и 5, делятся на 15. Число целых чисел, делящихся на 15, равно ⌊100015⌋=66. \left\lfloor \frac{1000}{15} \right\rfloor = 66.⌊151000⌋=66.
Целые числа, которые делятся на 3 и 7, делятся на 21. Число целых чисел, делящихся на 21, равно ⌊100021⌋=47.\left\lfloor \frac{1000}{21} \right\rfloor = 47.⌊211000⌋=47.
Целые числа, которые делятся на 5 и 7, делятся на 35. Число целых чисел, делящихся на 35, равно ⌊100035⌋=28. \left\lfloor \frac{1000}{35} \right\rfloor = 28.⌊351000⌋=28.Целые числа, которые делятся на 3, 5 и 7, делятся на 105. Число целых чисел, делящихся на 105, равно ⌊1000105⌋=9. \left\lfloor \frac{1000}{105} \right\rfloor = 9.⌊1051000⌋=9.
Принцип включения и исключения дает размер множества, который делится на 3, 5 или 7:
333+200+142−66−47−28+9=543,333+200+142-66-47-28+9=543,333+200+142−66−47−28+9=543.
Существует 543\в коробках{543}543 целых чисел от 1 до 1000 (включительно), которые делятся на 3, 5 или 7. □_\квадрат□
Два целых положительных числа xxx и yyy выбираются случайным образом из первых 100 целых положительных чисел с заменой. Вероятность того, что xyxyxy делится на 6, равна η\etaη.
Рассчитать ⌊1000η⌋\lэтаж 1000\эта\rэтаж⌊1000η⌋.
Бонус: Возможно, вы захотите посчитать вероятность без замены для развлечения.
Основная статья: Раскраска (аргументы четности)
См. также: Теорема Холла о браке.
Окраска — это стратегия, используемая для определения возможности мозаичного расположения. Вместо исчерпывающего поиска аранжировки, отвечающей требованиям задачи, иногда может быть более эффективно проверить цветовой паритет всех аранжировок. Цветовой паритет — это концепция, согласно которой цветовая схема для всех возможных аранжировок должна совпадать с цветовой схемой желаемой аранжировки.
Можно ли замостить фигуру ниже костяшками домино 1 × 21 \× 21 × 2?
Если бы кто-то попытался найти расположение, которое полностью замостило бы фигуру домино, то показалось бы, что это невозможно. Однако проверить каждую возможную схему было бы сложно. Вместо этого рассмотрите схему раскраски в виде шахматной доски.
Домино размером 1 × 21 × 21 × 2 будет иметь аналогичную расцветку — 1 черную и 1 белую кости. Чтобы замостить фигуру домино, должно быть равное количество черных и белых полей. Однако на рисунке справа 11 черных плиток и 13 белых плиток. Таким образом, плитка невозможна. □_\квадрат□
Основная статья: Теория графов
Теория графов — это изучение графов , которые представляют собой совокупность связанных узлов.
Базовый граф с 3 циклами
В комбинаторике можно изучать обходы графа и перестановки графа.
Докажите, что следующий граф невозможно пройти, пройдя по каждому пути ровно один раз. Любая из вершин может быть выбрана в качестве начальной или конечной вершины, и вершины могут быть пройдены более одного раза.
Предположим, что можно обойти граф, пройдя по каждому пути ровно один раз.
Подумайте, сколько раз будет пройдена каждая вершина. При каждом входе в вершину происходит и выход из нее. Следовательно, если каждый путь пройден ровно один раз, то из каждой вершины должно выходить четное количество путей. Существует исключение, если наш граф имеет разные начальную вершину и конечную вершину. Эти вершины должны иметь нечетное количество путей, исходящих из них. Может быть только одна начальная вершина и одна конечная вершина. Однако в приведенном выше графе есть 4 вершины, из которых выходит нечетное количество путей.
Таким образом, невозможно пройти указанный выше граф, пройдя по каждому пути ровно один раз. □_\квадрат□
1720\dfrac{1}{720}7201 112\dfrac{1}{12}121 16\dfrac{1}{6}61 13\dfrac{1}{3}31
Игрушка внизу представляет собой твердый шестиугольник с цветным кругом в каждой вершине. В настоящее время он находится в своем держателе, у каждой вершины которого есть соответствующие цветные кружки.
В настоящее время он находится в своем держателе, у каждой вершины которого есть соответствующие цветные кружки.
Игрушка вынимается из держателя, перебрасывается случайным образом, а затем снова помещается в держатель. Какова вероятность того, что цвета теперь совпадают с держателем?
Примечание : шестигранную игрушку можно перевернуть вверх дном. Те же цвета находятся на противоположной стороне.
Основная статья: Рекурсия
См. также: Линейные рекуррентные соотношения
Рекурсия формализует процесс распознавания того, как можно слой за слоем создавать решения для небольших случаев проблемы, чтобы решить любой случай проблемы, независимо от того, насколько он велик. Рекурсия особенно важна для разработки формул в комбинаторике.
Приведите выражение для Sn (n=1,2,3,…),S_n \, (n=1, 2, 3, \ldots),Sn(n=1,2,3,…), которое обозначает количество строк из nnn символов, состоящих только из A,B,\text{A}, \text{B},A,B и/или C,\text{C},C, которые не содержат последовательных символов, одинаковый.
Сначала рассмотрим строки длиной 1:
ABC.\begin{array}{ccc} \text{A} & \text{B} & \text{C}. \end{массив}ABC.
Итак, S1=3.S_1=3.S1=3. Теперь рассмотрим строки длины 2:
ABACBABCCACB.\begin{массив}{ll} \текст{АВ} и \текст{АС} \\ \text{BA} и \text{BC} \\ \text{CA} и \text{CB.} \end{массив}ABBACAACBCCB.
Итак, S2=6.S_2=6.S2=6. Теперь рассмотрим строки длины 3:
.ABCABAACAACBBABBACBCABCBCABCACCBACBC.\begin{массив}{llll} \text{ABC} & \text{ABA} & \text{ACA} & \text{ACB} \\ \text{BAB} & \text{BAC} & \text{BCA} & \text{BCB}\\ \text{CAB} & \text{CAC} & \text{CBA} & \text{CBC.} \end{массив}ABBCBABCABABABACCACACABBCACBAACBBCBCBC. 9{n-1}.\ _\squareSn=3⋅2n−1. □
Gn=3Gn−1−1G_n=3G_{n-1}-1Gn=3Gn−1−1 Gn=3Gn−1−Gn−2G_n=3G_{n-1}-G_{n-2}Gn=3Gn−1−Gn−2 Gn=3Gn−1G_n=3G_{n-1}Gn=3Gn−1 Gn=Gn−1+Gn−2G_n=G_{n-1}+G_{n-2}Gn=Gn−1+Gn−2
Строка символов nnn состоит из символов A\text {A}A, B\text{B}B и C\text{C}C.
Пусть GnG_nGn будет количеством таких строк из nnn символов, которые не содержат экземпляров AB\text{AB}AB (в указанном порядке).
Напишите рекуррентное соотношение для GnG_nGn.
Артикул:
Отдельные объекты в разные ячейки
Разные объекты в одинаковые корзины
Одинаковые объекты в разные ячейки
Одинаковые предметы в одинаковые контейнеры
Распределение объектов по ячейкам — это тип расположения, при котором каждый объект в наборе группируется в ячейку.
Распределение отдельных объектов учитывает, какие объекты сгруппированы вместе в каждом бине. Напротив, распределения идентичных объектов не учитывают, какие объекты сгруппированы вместе, а только то, сколько объектов находится в каждой ячейке.
Распределения по различным ячейкам учитывают порядок ячеек. Напротив, распределения по идентичным бинам не учитывают порядок бинов, а только то, как сгруппированы объекты.
Напротив, распределения по идентичным бинам не учитывают порядок бинов, а только то, как сгруппированы объекты.
Эти различия создают четыре типа проблем с распределением по корзинам. Как и в других задачах комбинаторики, обычно проблема заключается в подсчете количества возможных распределений.
В аквариуме есть цихлида, тетра, золотая рыбка и данио. В аквариум бросают 14 кормовых гранул. Если все гранулы съедены, то сколько существует возможных распределений гранул?
В этом примере «контейнеры» — это рыба, а «объекты» — гранулы. Каждая ячейка уникальна, потому что важно, какая рыба получит гранулы. Каждый объект идентичен, потому что не имеет значения, какие гранулы потребляются, важно только, сколько их потребляется. Обратите внимание, что рыба может получить 0 гранул. Эффективный способ решения проблемы с одинаковыми объектами в разных ячейках — применить стратегию звезд и полос.
⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆⋆{\color{#D61F06}\star \star} \mid {\color{#3D99F6}\star \star \star \star} \mid {\ color{#EC7300}\star \star \star \star} \mid {\color{#20A900}\star \star \star \star} ⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆ ⋆
Приведенная выше схема представляет собой распределение 2 гранул для цихлид (обозначены красным), 4 гранул для тетр (синие), 4 гранул для золотых рыбок (оранжевые) и 4 гранулы для данио (зеленые).
.В представлении 14 звезд и 3 полосы, что дает всего 17 объектов. Можно получить представление для любое распределение гранул, выбрав 3 места размещения стержней из 17 возможных мест размещения. Таким образом, количество раздач пеллет составляет
(173)=680. □\бином{17}{3}=680.\ _\квадрат(317)=680. □
Основная статья: Раздел целого числа
Раздел целого числа , иногда называемый просто разделом , представляет собой сумму положительных целых чисел, которая равна заданному целому числу. В комбинаторике проблема заключается в подсчете количества разделов целого числа.
Сколько разделов из 8 есть?
Разделы 8 следующие:
87+16+25+34+46+1+15+2+14+3+14+2+23+3+25+1+1+14+2+1+13+3+1+13+2 +2+12+2+2+24+1+1+1+13+2+1+1+12+2+2+1+13+1+1+1+1+12+2+1+1 +1+12+1+1+1+1+1+11+1+1+1+1+1+1+1\begin{массив}{cccc} 8 и 7+1 и 6+2 и 5+3 \\ 4+4 и 6+1+1 и 5+2+1 и 4+3+1 \\ 4+2+2 и 3+3+2 и 5+1+1+1 и 4+2+1+1 \\ 3+3+1+1 и 3+2+2+1 и 2+2+2+2 и 4+1+1+1+1 \\ 3+2+1+1+1 и 2+2+2+1+1 и \hspace{5мм} 3+1+1+1+1+1\hspace{5мм} &\hspace{5мм} 2+2 +1+1+1+1\hпробел{5мм} \\ \hspace{5мм} 2+1+1+1+1+1+1 \hspace{5мм} и \hspace{5мм} 1+1+1+1+1+1+1+1\hspace{5мм} \end{массив}84+44+2+23+3+1+13+2+1+1+12+1+1+1+1+1+17+16+1+13+3+23 +2+2+12+2+2+1+11+1+1+1+1+1+1+16+25+2+15+1+1+12+2+2+23+1 +1+1+1+15+34+3+14+2+1+14+1+1+1+12+2+1+1+1+1
Имеется 22\упакованные{22}22 разделов по 8.
□_\квадрат□
Перечисление всех возможных разделов может оказаться непростой задачей. Не существует известного выражения в закрытой форме для числа разделов целого числа n.n.n. К счастью, существует биекция между разделами и распределениями одинаковых объектов по одинаковым корзинам. Можно использовать тот же подход к решению проблемы.
Основная статья: Принцип сортировки
Принцип классификации описывает, как при заданном количестве ячеек и большем количестве объектов, помещенных в эти ячейки, по крайней мере в одной ячейке должно быть более одного объекта.
5 точек расположены внутри единичного равностороннего треугольника. Докажите, что две из этих точек должны находиться на максимальном расстоянии 12\frac{1}{2}21 друг от друга.
Предположим, что для любой пары точек из 5 расстояние между точками больше 12\frac{1}{2}21.
Теперь рассмотрим разбиение треугольника на 4 меньших равносторонних треугольника. 9\text{th}5-я точка (красная) должна быть помещена в тот же треугольник, что и другая точка.
Таким образом, если 5 точек расположены внутри единичного равностороннего треугольника, две из этих точек должны быть удалены друг от друга не более чем на 12\frac{1}{2}21. □_\квадрат□
Основная статья: Прогулка по прямоугольной сетке
Проход по сетке — это путь, проходящий по графу от начального узла к конечному узлу. В задаче обхода по сетке цель состоит в том, чтобы найти количество возможных путей.
Двигаясь только вверх или вправо, сколько возможных путей ведет от начального узла к конечному узлу?
Для любого пути от начального узла к конечному узлу потребуется 3 хода вверх и 5 ходов вправо. Считайте 8 ходов набором различных объектов.

 RU
RU
 58)
58) Peppers уже выбрана, так что вы действительно выбираете \(25-7=18\) банок. \(\binom{5+18-1}{18}=\binom{22}{18}=7315\)
Peppers уже выбрана, так что вы действительно выбираете \(25-7=18\) банок. \(\binom{5+18-1}{18}=\binom{22}{18}=7315\)  \)
\) 
 Это продолжается до тех пор, пока не останется 111 способов выбрать последний объект в порядке. По правилу произведения число перестановок объектов nnn равно
Это продолжается до тех пор, пока не останется 111 способов выбрать последний объект в порядке. По правилу произведения число перестановок объектов nnn равно \left\lfloor \frac{1000}{21} \right\rfloor = 47.⌊211000⌋=47.
\left\lfloor \frac{1000}{21} \right\rfloor = 47.⌊211000⌋=47. 
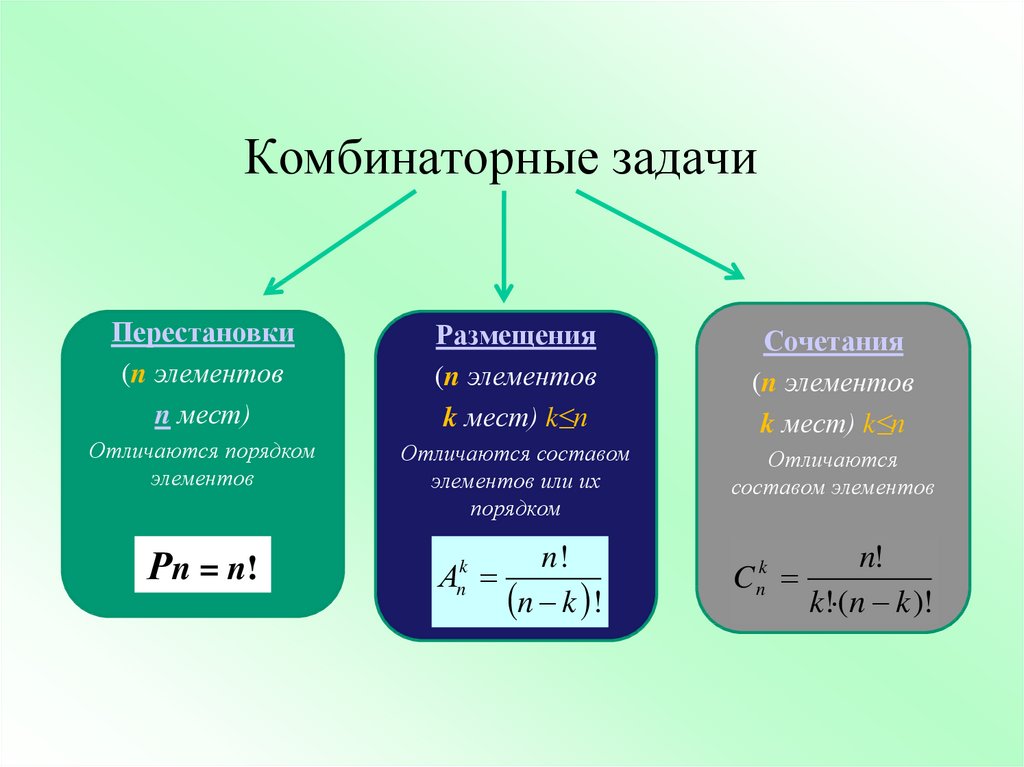 Подумайте, сколько раз будет пройдена каждая вершина. При каждом входе в вершину происходит и выход из нее. Следовательно, если каждый путь пройден ровно один раз, то из каждой вершины должно выходить четное количество путей. Существует исключение, если наш граф имеет разные начальную вершину и конечную вершину. Эти вершины должны иметь нечетное количество путей, исходящих из них. Может быть только одна начальная вершина и одна конечная вершина. Однако в приведенном выше графе есть 4 вершины, из которых выходит нечетное количество путей.
Подумайте, сколько раз будет пройдена каждая вершина. При каждом входе в вершину происходит и выход из нее. Следовательно, если каждый путь пройден ровно один раз, то из каждой вершины должно выходить четное количество путей. Существует исключение, если наш граф имеет разные начальную вершину и конечную вершину. Эти вершины должны иметь нечетное количество путей, исходящих из них. Может быть только одна начальная вершина и одна конечная вершина. Однако в приведенном выше графе есть 4 вершины, из которых выходит нечетное количество путей.
 В представлении 14 звезд и 3 полосы, что дает всего 17 объектов. Можно получить представление для любое распределение гранул, выбрав 3 места размещения стержней из 17 возможных мест размещения. Таким образом, количество раздач пеллет составляет
В представлении 14 звезд и 3 полосы, что дает всего 17 объектов. Можно получить представление для любое распределение гранул, выбрав 3 места размещения стержней из 17 возможных мест размещения. Таким образом, количество раздач пеллет составляет □_\квадрат□
□_\квадрат□ Теперь рассмотрим разбиение треугольника на 4 меньших равносторонних треугольника. 9\text{th}5-я точка (красная) должна быть помещена в тот же треугольник, что и другая точка.
Теперь рассмотрим разбиение треугольника на 4 меньших равносторонних треугольника. 9\text{th}5-я точка (красная) должна быть помещена в тот же треугольник, что и другая точка.