Определение вектора по двум точкам — онлайн калькулятор
Чтобы найти вектор по двум точкам онлайн, нужно:
- Задать размерность вектора (двумерный или трехмерный).
- Ввести в поля координаты соответственно начальной и конечной точек.
- Нажать «рассчитать».
Определение вектора по двум точкам
Чтобы задать (определить вектор), нужно знать его начальную и конечную точки. Как определить вектор по двум точкам с помощью онлайн-калькулятора? Вот последовательность действий:
- Указываем размерность вектора. Можно выбрать вектор на плоскости (2), или вектор в пространстве (3):
Для наглядности, выберем вектор в пространстве (размерность=3)
- Задаем координаты соответственно начальной и конечно точек вектора:
- Введем произвольные координаты и нажмем «Рассчитать»:
После этого можно получить ответ и ознакомиться с решением:
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Операции над векторами и их свойства: сложение и умножение
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение координат вектора через координаты точек
- Операции над векторами в прямоугольной системе координат
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Сложение и вычитание двух векторов
- Скалярное произведение векторов
- Разложение вектора по базису
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Проекция вектора на вектор
- Площадь треугольника, построенного на векторах
- Площадь параллелограмма, построенного на векторах
Нахождение вектора по двум точкам онлайн
Нахождение координат вектора по двум точкам онлайн будет полезно тем, кто хочет сократить время на расчеты или проверить правильность своего решения. Онлайн-калькулятор выдает ответ, а также поясняет использование формул, наглядно иллюстрируя ход решения.
Онлайн-калькулятор выдает ответ, а также поясняет использование формул, наглядно иллюстрируя ход решения.
Данный сервис рекомендован студентам и школьникам при самостоятельной подготовке. Также онлайн-калькулятор может быть полезен преподавателям и просто любителям математической науки.
Понравился калькулятор? Поделись с друзьями!
Координаты вектора по двум точкам. Онлайн калькулятор.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор нахождения координат вектора по двум точками найдет координаты вектора плоскости и пространства, а так же даст подробное решение.

Укажите размерность пространства 23
Задайте координаты точек
Координаты начальной точки
А:
(
;
)
Координаты конечной точки
В:
(
;
)
Как найти координаты вектора плоскости и пространства по двум точкам
Для того чтобы вычислить координаты вектора по двум точкам необходимо воспользоваться одной из формул:
AB = {Bx — Ax ; By — Ay } — для вычисления координат вектора плоскости
AB = {Bx — Ax ; By — Ay ; Bz — Az} — для вычисления координат вектора пространства
Примеры вычисления координат вектора по двум точкам
Дан вектор AB с концами в точках A(A x; Ay) и B(Bx; By)
Координаты точки A равны: A(5 ; 9).
Координаты точки B равны: B(1 ; 4).
Тогда, AB = {Bx — Ax; By — Ay} = {1 — 5 ; 4 — 9} = {-4 ; -5}
Вычислим координаты вектора пространства:
Дан вектор AB с концами в точках A(Ax; Ay; Az) и B(Bx; By; Bz)
Координаты точки A равны: A(2; 4; -5).
Координаты точки B равны: B(3; 6; 8).
Тогда, AB = {Bx — Ax ; By — Ay; Bz — Az} = {3 — 2 ; 6 — 4 ; 8 — (-5)} = {1 ; 2 ; 13}
| Вам могут также быть полезны следующие сервисы |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Скалярное произведение векторов через координаты. Онлайн калькулятор.
Укажите размерность пространства 23
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
}
Задайте координаты вектора b
b̅ =
{
;
}
Как вычислить скалярное произведение векторов через координаты
Скалярным произведением двух векторов a и b – называется сумма произведений координат данных векторов:
Если
a = {ax; ay} и b = {bx; by}, тогда:
a ⋅ b = axbx + ayby
Если
a = {ax; ay; az} и b = {bx; by; bz}, тогда:
a ⋅ b = axbx + ayby + azbz
Если координаты векторов a и b заданы точками, а именно:
Вектор a задан точками A и B, где
A = {Ax; Ay}
B = {Bx; By}
Вектор b задан точками C и D, где
C = {Cx; Cy}
D = {Dx; Dy}
то скалярное произведение определяется как:
a ⋅ b = (Bx — Ax)(Dx — Cx) +
(By — Ay)(Dy — Cy)
Если координаты векторов a и b заданы точками, а именно:
Вектор a задан точками A и B, где
A = {Ax; Ay; Az}
B = {Bx; By; Bz}
Вектор b задан точками C и D, где
C = {Cx; Cy; Cz}
D = {Dx; Dy; Dz}
то скалярное произведение определяется как:
a ⋅ b = (Bx — Ax)(Dx — Cx) +
(By — Ay)(Dy — Cy) +
(Bz — Az)(Dz — Cz)
Примеры вычисления скалярного произведения векторов по координатам
Пример 1. Найдем скалярное произведение векторов плоскости.
Найдем скалярное произведение векторов плоскости.
a ⋅ b = axbx + ayby = -2 ⋅ 3 + 6 ⋅ 5 = -6 + 30 = 24
a ⋅ b = 24
Пример 2. Найдем скалярное произведение векторов пространства.
Координаты вектора a: (5; 1; 7)
Координаты вектора b: (2; 4; 6)
a ⋅ b = axbx + ayby + azbz = 5 ⋅ 2 + 1 ⋅ 4 + 7 ⋅ 6 = 10 + 4 + 42 = 56
a ⋅ b = 56
Пример 3. Найдем скалярное произведение векторов плоскости, координаты которых заданы точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)
Воспользуемся формулой: a ⋅ b = (Bx — Ax)(Dx — Cx) + (By — Ay)(Dy — Cy) тогда,
AB ⋅ CD = (-2 — 5) ⋅ (-3 — 0) + (11 — 9) ⋅ (1 — 12) = -1
Этот пример можно решить по-другому, вычислив сначала координаты векторов по точкам, а затем зная координаты вычислить скалярное произведение:
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx— Ax; By— Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
Вектор ABВычислим координаты второго вектора по двум точкам C и D:
CD = {Dx— Cx; Dy— Cy} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
Вектор CDНайдем скалярное произведение векторов: AB и CD, воспользуемся формулой a ⋅ b = axbx + ayby
AB ⋅ CD = ABxCDx + AByCDy = -7 ⋅ (-3) + 2 ⋅ (-11) = 21 + (-22) = -1
Пример 4. Найдем скалярное произведение векторов пространства. Координаты обоих векторов заданны точками.
Найдем скалярное произведение векторов пространства. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Воспользуемся формулой: a ⋅ b = (Bx — Ax)(Dx — Cx) + (By — Ay)(Dy — Cy) + (Bz — Az)(Dz — Cz) тогда,
AB ⋅ CD = (-1 — 7) ⋅ (3 — (-4)) + (0 — 0.2) ⋅ (0 — (-6)) + ((2/8) — 69) ⋅ (9 — 2) = -538.45
Как в предыдущем примере решим пример иначе, сначала вычислив координаты векторов по точкам:
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx— Ax;By— Ay;Bz— Az} = {-1 — 7 ; 0 — 0. 2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx— Cx;Dy— Cy;Dz— Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
Найдем скалярное произведение векторов: AB и CD
AB ⋅ CD = ABxCDx + AByCDy + ABzCDz = -8 ⋅ 7 + (-1/5) ⋅ 6 + (-275/4) ⋅ 7 = -56 + (-6/5) + (-1925/4) = -10769/20 = -538.45
Онлайн калькуляторы векторов
Данный раздел содержит калькуляторы, позволяющие выполнять все основные действия над
векторами. В частности, с помощью данных калькуляторов можно вычислять скалярное, векторное и смешанное произведения векторов, раскладывать вектора по базису, проверять их ортогональность, компланарность и др. Всего представлено 19 калькуляторов и для каждого предусмотрено подробное решение соответствующей задачи.
Сложение векторов Калькулятор позволяет складывать вектора, заданные в координатной форме.
Разность векторов Калькулятор позволяет вычитать вектора, заданные в координатной форме.
Умножение вектора на скаляр Калькулятор находит произведение вектора на скаляр.
Скалярное произведение векторов Калькулятор позволяет найти скалярное произведение двух векторов.
Векторное произведение векторов
Калькулятор позволяет найти векторное произведение двух векторов.
Смешанное произведение векторов Калькулятор находит смешанное произведение трех векторов.
Модуль (длина) вектора Калькулятор находит модуль (длину) вектора с описанием подробного решения на русском языке.
Угол между векторами Калькулятор позволяет найти угол между векторами. Подробное решение также имеется.
Направляющие косинусы вектора Калькулятор позволяет найти направляющие косинусы вектора с подробным решением на русском языке.
Проекция вектора
Калькулятор вычисляет проекцию вектора на ось или на другой вектор.
Площадь треугольника, построенного на векторах Калькулятор вычисляет площадь треугольника, построенного на векторах с описанием подробного решения на русском языке.
Площадь параллелограмма, построенного на векторах Калькулятор позволяет вычислить площадь параллелограмма, построенного на векторах с описанием подробного решения на русском языке.
Объём параллелепипеда, построенного на векторах Калькулятор позволяет найти объём параллелепипеда, который построен на трёх векторах.
Объём треугольной пирамиды (тетраэдра), построенного на векторах
Калькулятор находит объём тетраэдра, построенного на трёх векторах.
Проверить ортогональность векторов Калькулятор позволяет проверить ортогональность векторов с описанием подробного решения на русском языке.
Проверить коллинеарность векторов Калькулятор позволяет проверить коллинеарность двух векторов.
Проверить компланарность векторов Калькулятор предназначен для проверки компланарности трёх векторов.
Проверить образует ли система векторов базис Калькулятор позволяет проверить образует ли система векторов базис.
Разложить вектор по базису
Калькулятор позволяет разложить вектор по базису с описанием подробного решения на русском языке.
Произведение трех векторов онлайн калькулятор. Векторное произведение векторов. Смешанное произведение векторов
Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение b x c , т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc .
Назначение . Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word . Дополнительно создается шаблон решения в Excel .
a (; ; )b (; ; )
c (; ; )
При вычислении определителя использовать правило треугольников
Признаки компланарности векторов
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.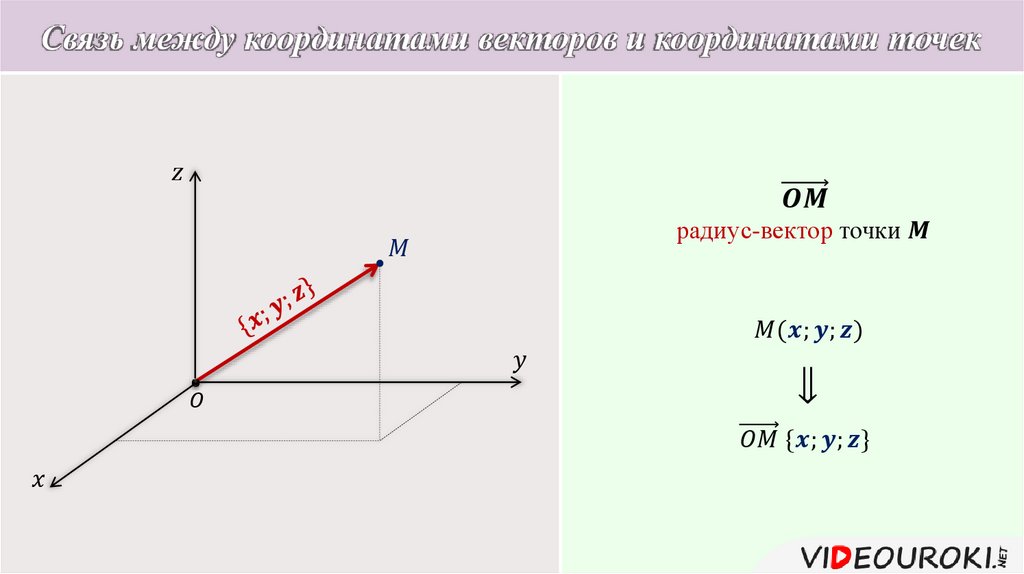
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.
Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая.
Свойства смешанного произведения
- При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
Вытекает из геометрического смысла. - (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
Вытекает из определения смешанного произведения. - (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. - Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0 .
Пример №1 . Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc .
Пример №2 . (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca . Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc .
Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k .
Решение . Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а».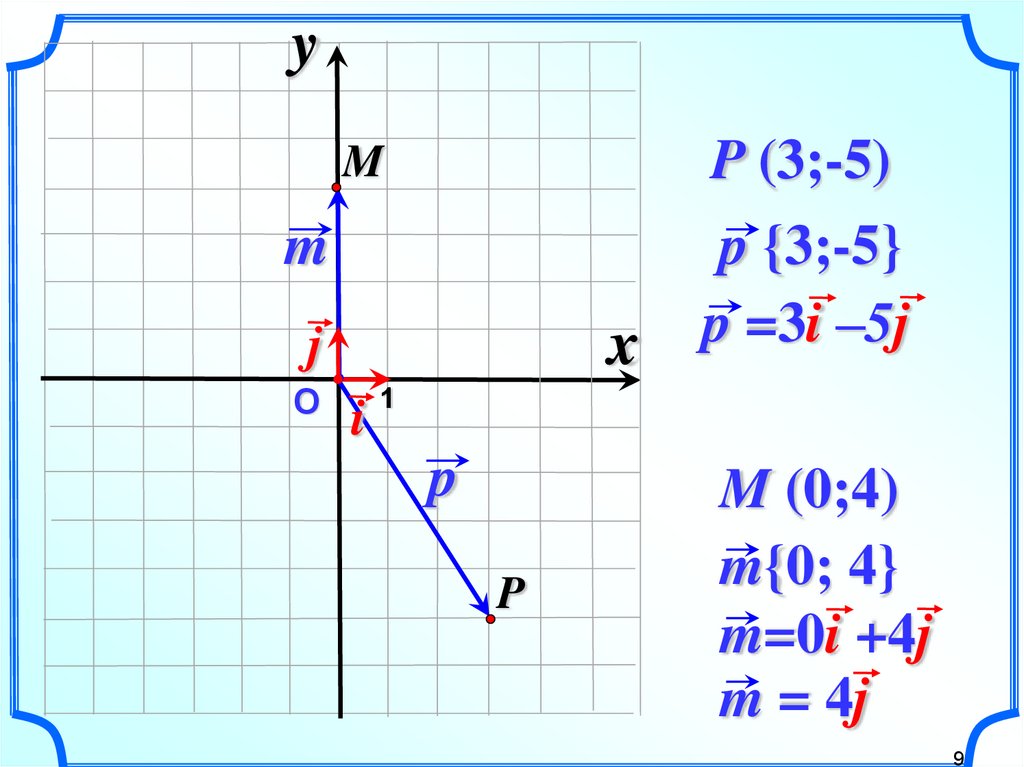 Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе .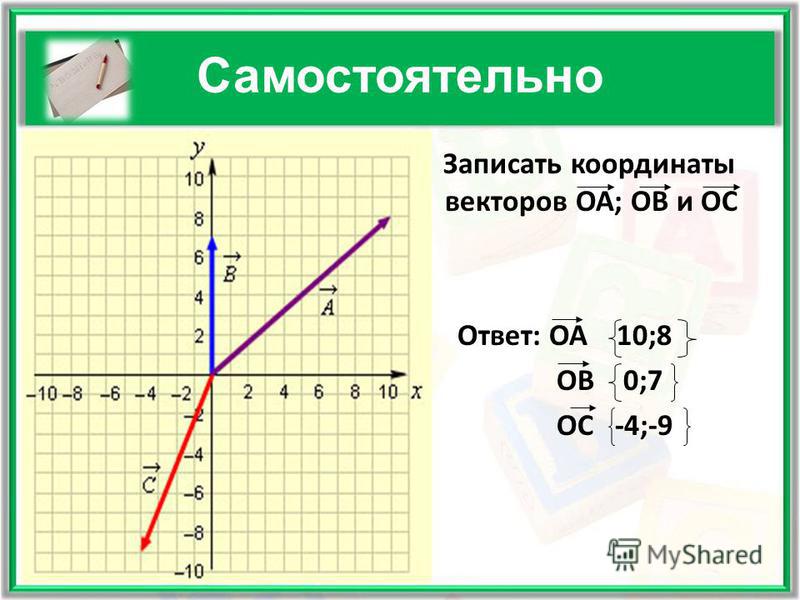 Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони.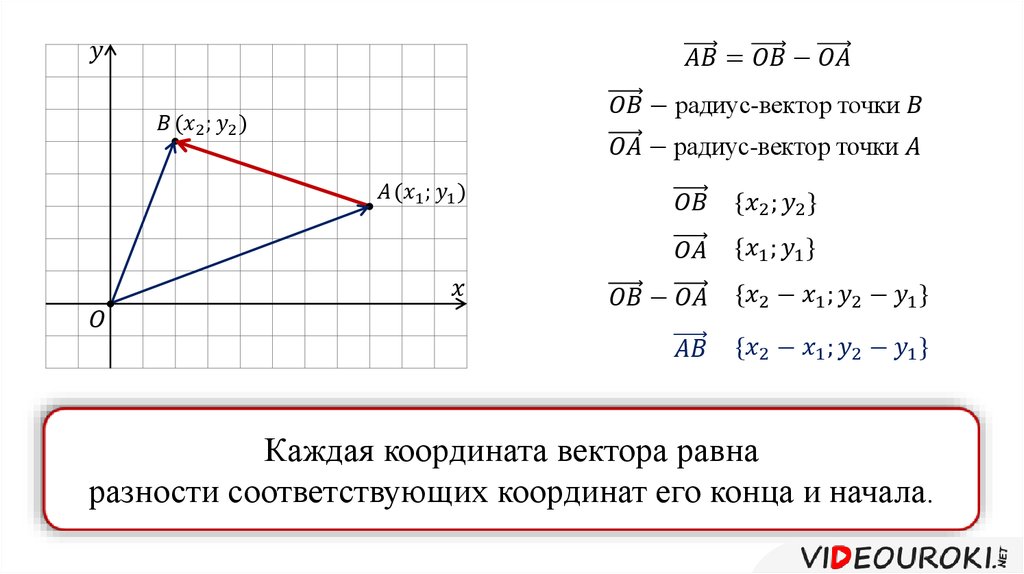 В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .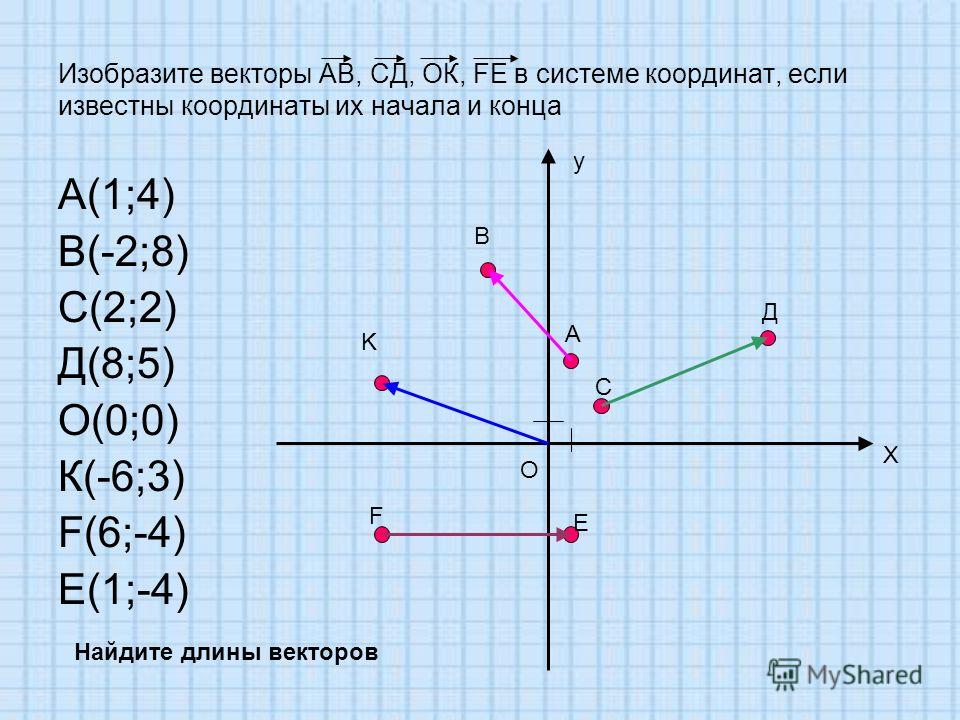
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Yandex.RTB R-A-339285-1
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Определение 1
Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = (a → × b → , d →) .
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i → , j → , k →
Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Определение 2
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Из этого следует:
a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a → × b → = (a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k →) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z
Таким образом, можно сделать вывод, что:
a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z
Определение 3
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z .
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.
Ниже мы приведем основные свойства.
- (λ · a →) · b → · d → = a → · (λ · b →) · d → = a → · b → · (λ · d →) = λ · a → · b → · d → λ ∈ R ;
- a → · b → · d → = d → · a → · b → = b → · d → · a → ; a → · d → · b → = b → · a → · d → = d → · b → · a → ;
- (a (1) → + a (2) →) · b → · d → = a (1) → · b → · d → + a (2) → · b → · d → a → · (b (1) → + b (2) →) · d → = a → · b (1) → · d → + a → · b (2) → · d → a → · b → · (d (1) → + d (2) →) = a → · b → · d (2) → + a → · b → · d (2) →
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ([ a → × b → ] , d →) = (0 → , d →) = 0 .
Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Пример 1
Докажите равенство ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) , где λ — некоторое действительное число.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →)
Мы разобрали, что (([ a → × b → ] , b →) = 0 . Из этого следует, что
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →) = = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + 0 = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →)
Согласно первому свойству ([ a ⇀ × b ⇀ ] , λ · a →) = λ · ([ a ⇀ × b ⇀ ] , a →) , а ([ a ⇀ × b ⇀ ] , a →) = 0 .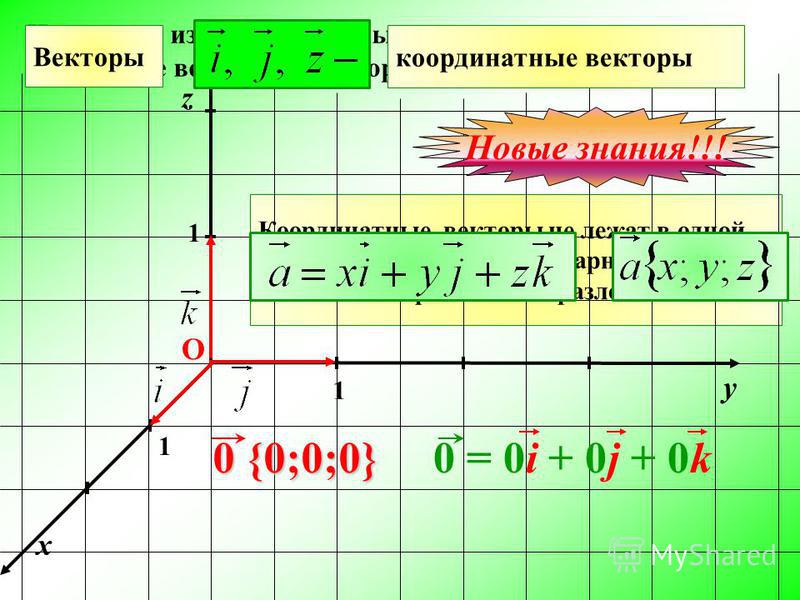 , d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
, d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
Неравенство доказано.
Разбор типовых задач
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z .
Пример 3
В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = (1 , — 2 , 3) , b → (- 2 , 2 , 1) , d → = (3 , — 2 , 5) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → .
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + (- 1) · 1 · 3 + 3 · (- 2) · (- 2) — 3 · 2 · 3 — (- 1) · (- 2) · 5 — 1 · 1 · (- 2) = — 7
Пример 4
Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = (1 , 1 , 0) i → + j → — k → = (1 , 1 , — 1) i → + j → + 2 · k → = (1 , 1 , 2)
Используем формулу, которая использовалась выше
i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 1 1 0 1 1 — 1 1 1 2 = 0 i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
Пример 5
В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора.
Обозначим c → = a → × b → .
Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a → · b → · d → = ([ a → × b → ] , d →) = c → , d → = c → · d → · cos (c → , d → ^) . ) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → .
Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → .
Определение 4
Абсолютная величина векторного произведения является объемом параллелепипеда : V п а р а л л е л е п и п и д а = a → · b → · d → .
Данная формула и является геометрическим смыслом.
Определение 5
Объем тетраэдра , который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → .
Для того, чтобы закрепить знания, разберем несколько типичных примеров
Пример 6
Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = (3 , 6 , 3) , A C → = (1 , 3 , — 2) , A A 1 → = (2 , 2 , 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · (- 2) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · (- 2) · 2 = — 18
Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 .
V п а р а л л е л е п и п и д а = 18
Пример 7
В системе координат заданы точки A (0 , 1 , 0) , B (3 , — 1 , 5) , C (1 , 0 , 3) , D (- 2 , 3 , 1) . Следует определить объем тетраэдра, который расположен на этих точках.
Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = (3 — 0 , — 1 — 1 , 5 — 0) = (3 , — 2 , 5) A C → = (1 — 0 , 0 — 1 , 3 — 0) = (1 , — 1 , 3) A D → = (- 2 — 0 , 3 — 1 , 1 — 0) = (- 2 , 2 , 1)
Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · (- 1) · 1 + (- 2) · 3 · (- 2) + 5 · 1 · 2 — 5 · (- 1) · (- 2) — (- 2) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 .
V т э т р а э д р а = 7 6 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение
трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c .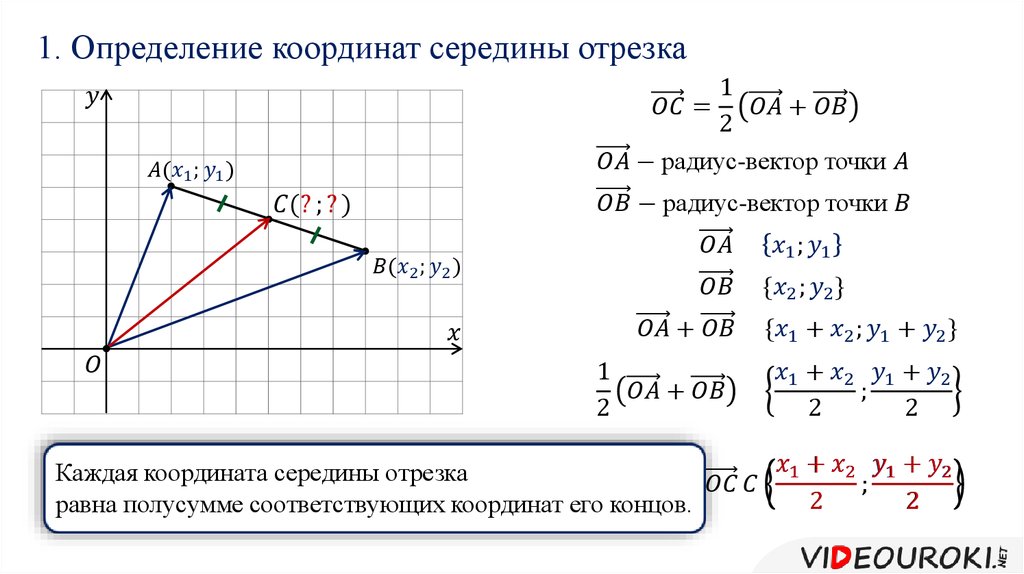
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать:
| abc =([ab ],c ) |
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю.
Следствие 1. Имеет место следующее равенство:
Следовательно нам достаточно доказать, что
| ([ab ],c )=([bc ],a ) | (3) |
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда.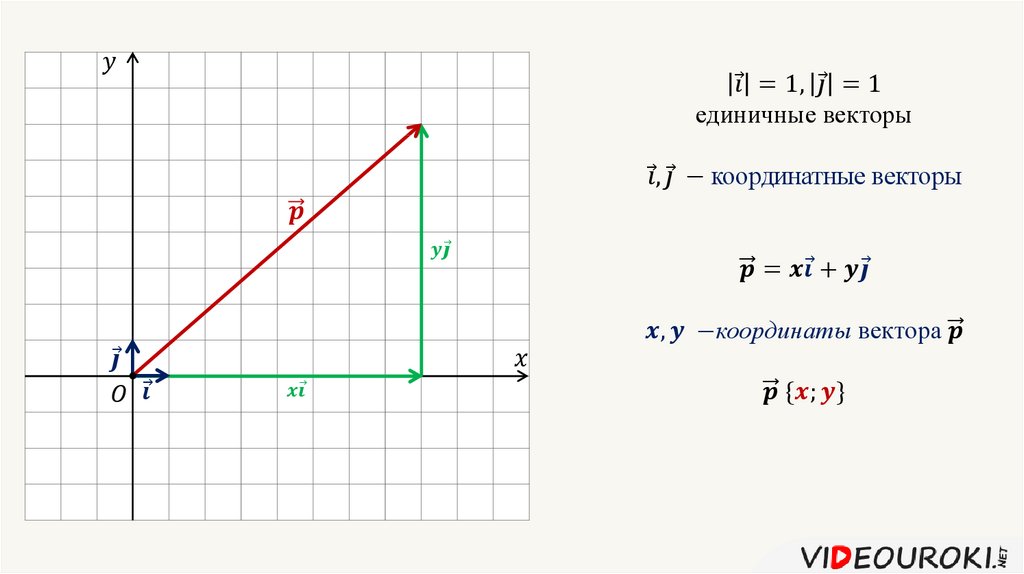 Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Последнее выражение можно записать, используя определители второго порядка:
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
| . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс , где
Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1:
Конечная точка вектора a .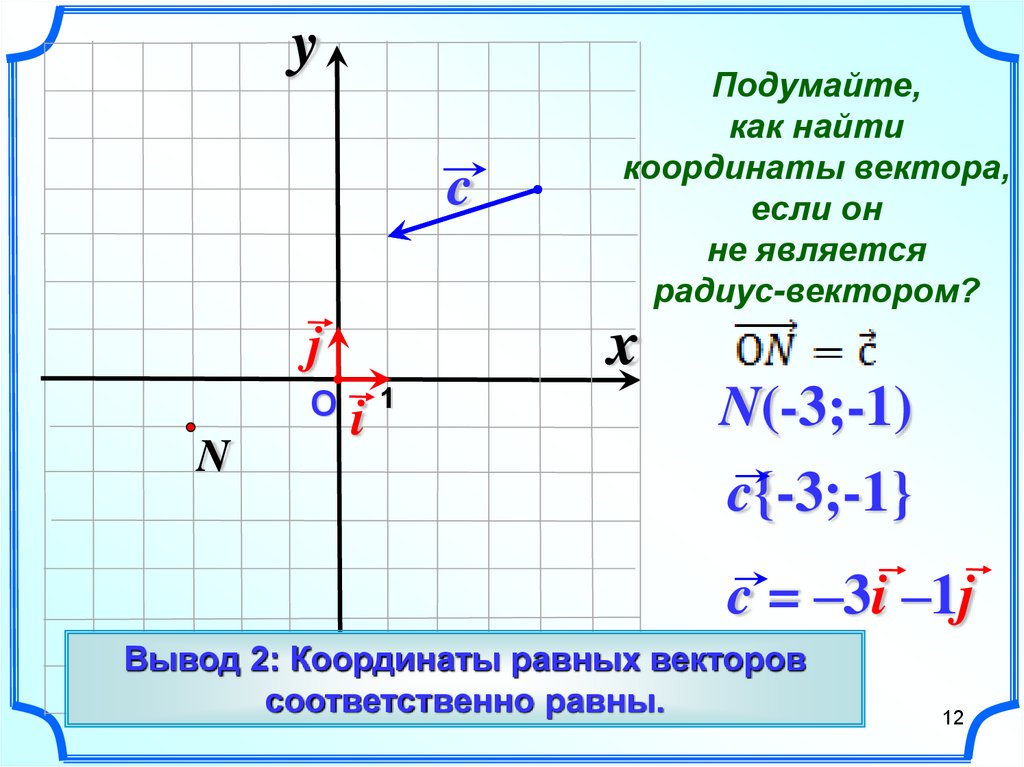
Уравнение прямой по двум точкам онлайн калькулятор. Уравнение прямой на плоскости
Рубрика: Косички
Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.
Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:
.
Приведённые выше уравнения и есть канонические уравнения прямой.
Числа m , n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m , n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:
,
которая означает, что проекции вектора на оси Oy и Oz равны нулю.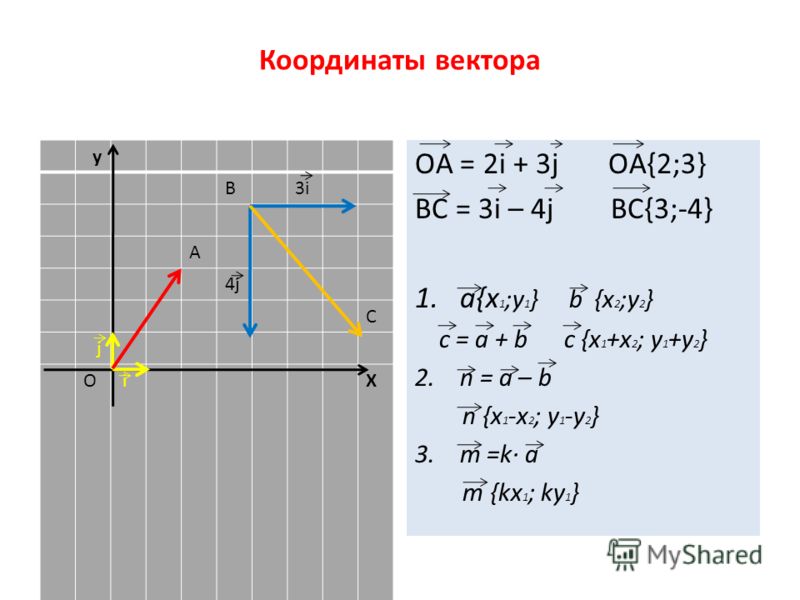 Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz , т. е. плоскости yOz .
Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz , т. е. плоскости yOz .
Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz .
Решение. Найдём точку пересечения данной плоскости с осью Oz . Так как любая точка, лежащая на оси Oz , имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0 , получим 4z — 8 = 0 или z = 2 . Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2) . Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.
Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :
Уравнения прямой, проходящей через две данные точки
Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид
Тогда канонические уравнения прямой примут вид
.
Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.
Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .
Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:
.
Так как , то искомая прямая перпендикулярна оси Oy .
Прямая как линия пересечения плоскостей
Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений
Уравнения системы называются также общими уравнениями прямой в пространстве.
Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями
Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой.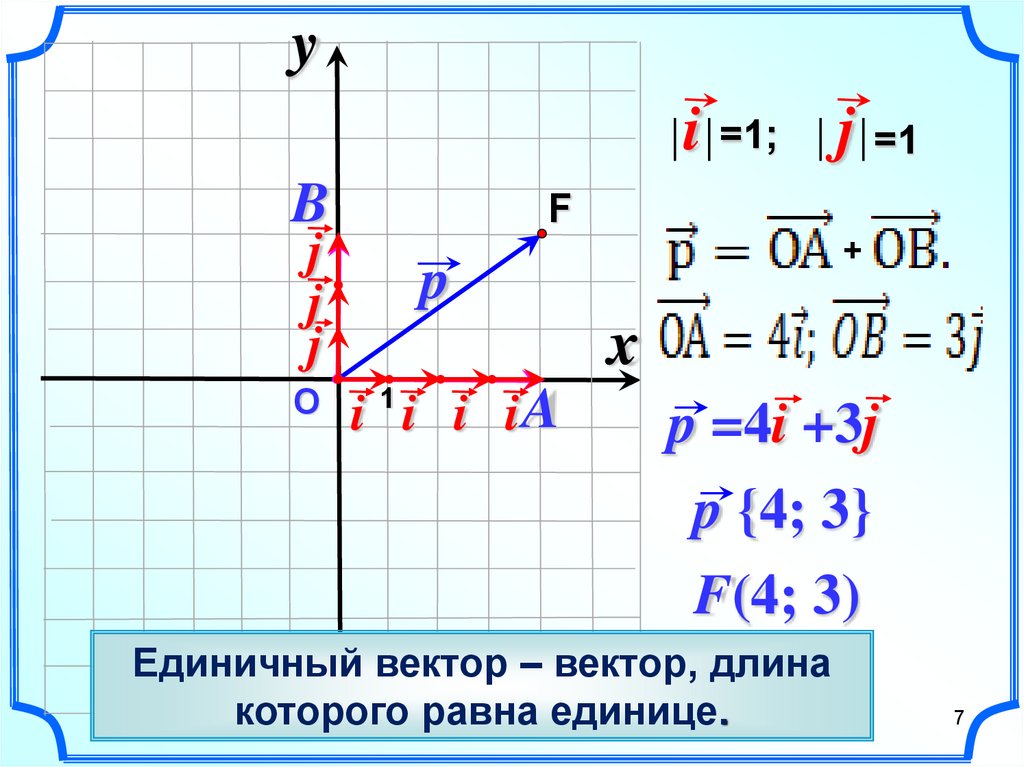 Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz .
Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz .
Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0 . Поэтому, полагая в данной системе уравнений x = 0 , получим систему с двумя переменными:
Её решение y = 2 , z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0 , получим систему
Её решение x = -2 , z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz .
Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0) :
,
или после деления знаменателей на -2:
,
Общее уравнение прямой:
Частные случаи общего уравнения прямой:
а) Если C = 0, уравнение (2) будет иметь вид
Ax + By = 0,
и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.
б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид
Ax + С = 0, или .
Уравнение не содержит переменной y , а определяемая этим уравнением прямая параллельна оси Oy .
в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид
By + С = 0, или ;
уравнение не содержит переменной x , а определяемая им прямая параллельна оси Ox .
Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.
г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.
Это уравнение оси Ox .
д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.
Это уравнение оси Oy .
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости.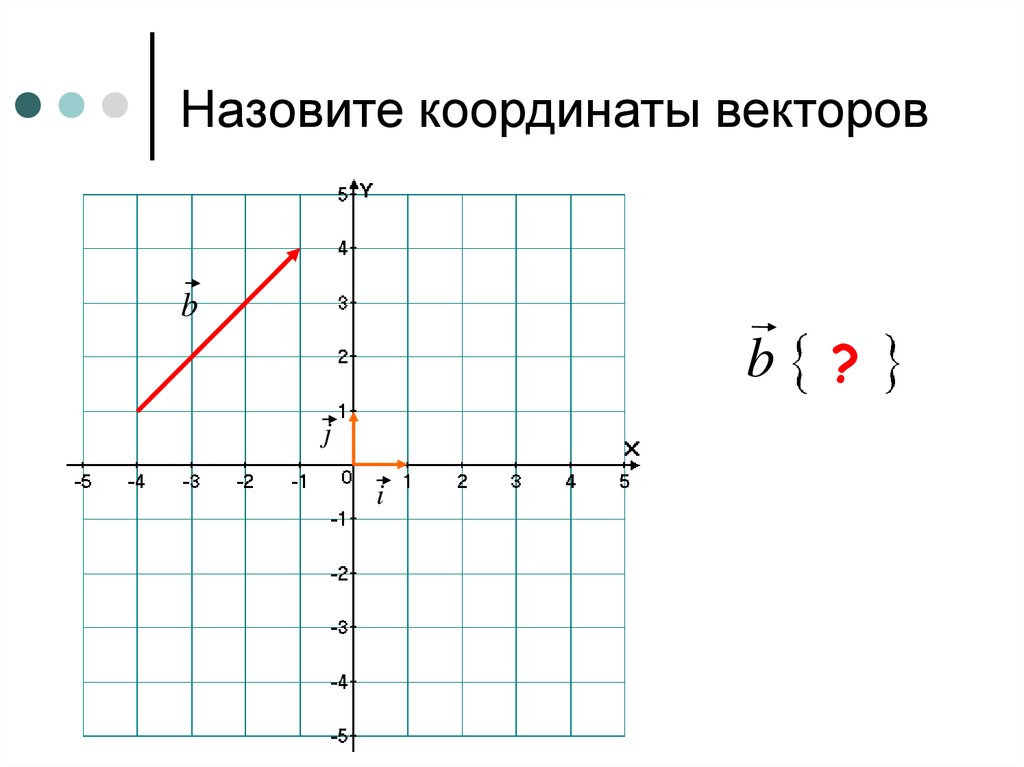 Условие параллельности прямых. Условие перпендикулярности прямых.
Условие параллельности прямых. Условие перпендикулярности прямых.
l 1 l 2 l 1: A 1 x + B 1 y + C 1 = 0
l 2: A 2 x + B 2 y + C 2 = 0
S 2 S 1 Вектора S 1 и S 2 называются направляющими для своих прямых.
Угол между прямыми l 1 и l 2 определяется углом между направляющими векторами.
Теорема 1: cos угла между l 1 и l 2 = cos(l 1 ; l 2) =
Теорема 2: Для того, чтобы 2 прямые были равны необходимо и достаточно:
Теорема 3: чтобы 2 прямые были перпендикулярны необходимо и достаточно:
L 1 l 2 ó A 1 A 2 + B 1 B 2 = 0
Общее уравнение плоскости и его частные случаи. Уравнение плоскости в отрезках.
Общее уравнение плоскости:
Ax + By + Cz + D = 0
Частные случаи:
1. D=0 Ax+By+Cz = 0 – плоскость проходит через начало координат
2. С=0 Ax+By+D = 0 – плоскость || OZ
3. В=0 Ax+Cz+d = 0 – плоскость || OY
4. A=0 By+Cz+D = 0 – плоскость || OX
5. A=0 и D=0 By+Cz = 0 – плоскость проходит через OX
A=0 и D=0 By+Cz = 0 – плоскость проходит через OX
6. В=0 и D=0 Ax+Cz = 0 – плоскость проходит через OY
7. C=0 и D=0 Ax+By = 0 – плоскость проходит через OZ
Взаимное расположение плоскостей и прямых линий в пространстве:
1. Углом между прямыми в пространстве называется угол между их направляющими векторами.
Cos (l 1 ; l 2) = cos(S 1 ; S 2) = =
2. Углом между плоскостями определяется через угол между их нормальными векторами.
Cos (l 1 ; l 2) = cos(N 1 ; N 2) = =
3. Косинус угла между прямой и плоскостью можно найти через sin угла между направляющим вектором прямой и нормальным вектором плоскости.
4. 2 прямые || в пространстве, когда их || направляющие вектора
5. 2 плоскости || когда || нормальные вектора
6. Аналогично вводятся понятия перпендикулярности прямых и плоскостей.
Вопрос №14
Различные виды уравнения прямой линии на плоскости(уравнение прямой в отрезках, с угловым коэффициентом и др. )
)
Уравнение прямой в отрезках:
Допустим, что в общем уравнении прямой:
1. С = 0 Ах + Ву = 0 – прямая проходит через начало координат.
2. а = 0 Ву + С = 0 у =
3. в = 0 Ах + С = 0 х =
4. в=С=0 Ах = 0 х = 0
5. а=С=0 Ву = 0 у = 0
Уравнение прямой с угловым коэффициентом:
Любая прямая, не равная оси ОУ (В не=0), может быть записана в след. виде:
k = tgα α – угол между прямой и положительно направленной линией ОХ
b – точка пересечения прямой с осью ОУ
Док-во:
Ах+Ву+С = 0
Ву= -Ах-С |:В
Уравнение прямой по двум точкам:
Вопрос №16
Конечный предел функции в точке и при x→∞
Конечный предел в точке х 0:
Число А называется пределом функции y = f(x) при x→х 0 , если для любого Е > 0 существует б > 0 такое, что при х ≠x 0 , удовлетворяющее неравенству |х – х 0 |
Предел обозначается: = A
Конечный предел в точке +∞:
Число А называется пределом функции y = f(x) при x→ + ∞ , если для любого Е > 0 существует С > 0, такое что при x > C выполняется неравенство |f(x) — A|
Предел обозначается: = A
Конечный предел в точке -∞:
Число А называется пределом функции y = f(x) при x→-∞, если для любого Е
В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.
Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.
Пусть задана произвольная декартова прямоугольная система координат Oxy . Рассмотрим уравнение первой степени или линейное уравнение:
| Ax+By+C =0, | (1) |
где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.
Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.
Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.
Доказательство.
Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.
Пусть на плоскости задана прямая L . Выберем систему координат так, чтобы ось Ox совпадал с прямой L , а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:
| y=0. | (2) |
Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.
Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M (x 0 ,y 0). (Например, при A ≠0, точка M 0 (−C/A , 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество
Ax 0 +By 0 +C =0.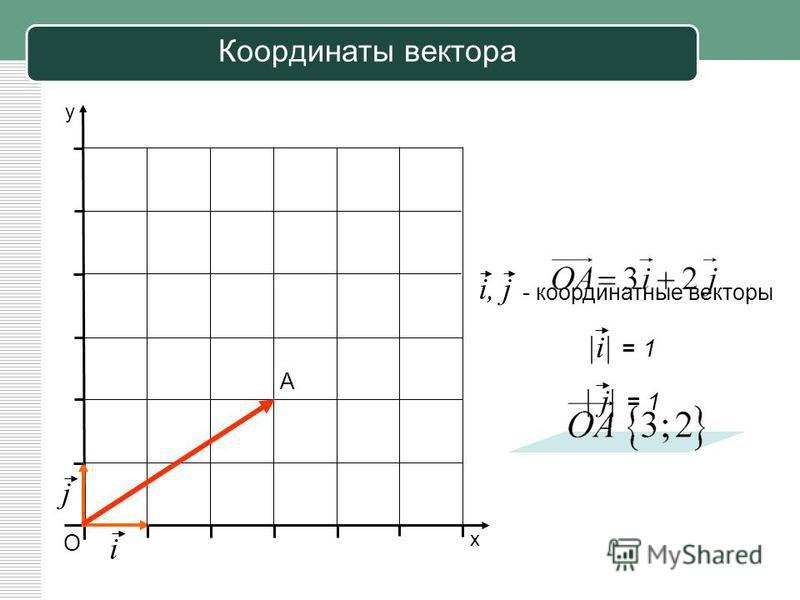 | (3) |
Вычтем из (1) тождество (3):
| A (x −x 0)+B (y −y 0)=0. | (4) |
Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую.
Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами {x−x 0 , y−y 0 } ортогонален вектору n с координатами {A,B }.
Рассмотрим некоторую прямую L , проходящую через точку M 0 (x 0 , y 0) и перпендикулярной вектору n (Рис.1). Пусть точка M (x ,y) принадлежит прямой L . Тогда вектор с координатами x−x 0 , y−y 0 перпендикулярен n и уравнение (4) удовлетворено (скалярное произведение векторов n и равно нулю). Обратно, если точка M (x ,y) не лежит на прямой L , то вектор с координатами x−x 0 , y−y 0 не ортогонален вектору n и уравнение (4) не удовлетворено. Теорема доказана.
Теорема доказана.
Доказательство. Так как прямые (5) и (6) определяют одну и ту же прямую, то нормальные векторы n 1 ={A 1 ,B 1 } и n 2 ={A 2 ,B 2 } коллинеарны. Так как векторы n 1 ≠0, n 2 ≠0, то существует такое число λ , что n 2 =n 1 λ . Отсюда имеем: A 2 =A 1 λ , B 2 =B 1 λ . Докажем, что C 2 =C 1 λ . Очевидно, что совпадающие прямые имеют общую точку M 0 (x 0 , y 0). Умножая уравнение (5) на λ и вычитая из него уравнение (6) получим:
Так как выполнены первые два равенства из выражений (7), то C 1 λ −C 2 =0. Т.е. C 2 =C 1 λ . Замечание доказано.
Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M 0 (x 0 , y 0) и имеющий нормальный вектор n ={A,B }. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).
Пример 1. Прямая проходит через точку M =(4,−1) и имеет нормальный вектор n ={3, 5}. Построить общее уравнение прямой.
Решение. Имеем: x 0 =4, y 0 =−1, A =3, B =5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):
Ответ:
Вектор параллелен прямой L и, следовательно, перпердикулярен нормальному вектору прямой L . Построим нормальный вектор прямой L , учитывая, что скалярное произведение векторов n и равно нулю. Можем записать, например, n ={1,−3}.
Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M 1 (можем взять также координаты точки M 2) и нормального вектора n :
Подставляя координаты точек M 1 и M 2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.
Ответ:
Вычтем (10) из (1):
Мы получили каноническое уравнение прямой. Вектор q ={−B , A } является направляющим вектором прямой (12).
Вектор q ={−B , A } является направляющим вектором прямой (12).
Обратное преобразование смотрите .
Пример 3. Прямая на плоскости представлена следующим общим уравнением:
Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5.
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы начнем изучать алгоритмы, связанные с геометрией. Дело в том, что олимпиадных задач по информатике, связанных с вычислительной геометрией, достаточно много и решение таких задач часто вызывают затруднения.
За несколько уроков мы рассмотрим ряд элементарных подзадач, на которые опирается решение большинства задач вычислительной геометрии.
На этом уроке мы составим программу для нахождения уравнения прямой , проходящей через заданные две точки . Для решения геометрических задач нам понадобятся некоторые знания из вычислительной геометрии. Часть урока мы посвятим знакомству с ними.
Сведения из вычислительной геометрии
Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач.
Исходными данными для таких задач могут быть множество точек на плоскости, набор отрезков, многоугольник (заданный например, списком своих вершин в порядке движения по часовой стрелке) и т.п.
Результатом может быть либо ответ на какой то вопрос (типа принадлежит ли точка отрезку, пересекаются ли два отрезка, …), либо какой-то геометрический объект (например, наименьший выпуклый многоугольник, соединяющий заданные точки, площадь многоугольника, и т.п.).
Мы будем рассматривать задачи вычислительной геометрии только на плоскости и только в декартовой системе координат.
Векторы и координаты
Чтобы применять методы вычислительной геометрии, необходимо геометрические образы перевести на язык чисел. Будем считать, что на плоскости задана декартова система координат, в которой направление поворота против часовой стрелки называется положительным.
Теперь геометрические объекты получают аналитическое выражение. Так, чтобы задать точку, достаточно указать её координаты: пару чисел (x; y). Отрезок можно задать, указав координаты его концов, прямую можно задать, указав координаты пары ее точек.
Но основным инструментом при решении задач у нас будут векторы. Напомню поэтому некоторые сведения о них.
Отрезок АВ , у которого точку А считают началом (точкой приложения), а точку В – концом, называют вектором АВ и обозначают либо , либо жирной строчной буквой, например а .
Для обозначения длины вектора (то есть длины соответствующего отрезка) будем пользоваться символом модуля (например, ).
Произвольный вектор будет иметь координаты, равные разности соответствующих координат его конца и начала:
,
здесь точки A и B имеют координаты соответственно.
Для вычислений мы будем использовать понятие ориентированного угла , то есть угла, учитывающего взаимное расположение векторов.
Ориентированный угол между векторами a и b положительный, если поворот от вектора a к вектору b совершается в положительном направлении (против часовой стрелки) и отрицательный – в другом случае. См рис.1а, рис.1б. Говорят также, что пара векторов a и b положительно (отрицательно) ориентирована.
Таким образом, величина ориентированного угла зависит от порядка перечисления векторов и может принимать значения в интервале .
Многие задачи вычислительной геометрии используют понятие векторного (косого или псевдоскалярного) произведений векторов.
Векторным произведением векторов a и b будем называть произведение длин этих векторов на синус угла между ними:
.
Векторное произведение векторов в координатах:
Выражение справа – определитель второго порядка:
В отличии от определения, которое дается в аналитической геометрии, это скаляр.
Знак векторного произведения определяет положение векторов друг относительно друга:
a и b положительно ориентирована.
Если величина , то пара векторов a и b отрицательно ориентирована.
Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда они коллинеарны (). Это значит, что они лежат на одной прямой или на параллельных прямых.
Рассмотрим несколько простейших задач, необходимых при решении более сложных.
Определим уравнение прямой по координатам двух точек.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки: с координатами (x1;y1) и с координатами (x2; y2). Соответственно вектор с началом в точке и концом в точке имеет координаты (x2-x1, y2-y1). Если P(x, y) – произвольная точка на нашей прямой, то координаты вектора равны (x-x1, y – y1).
С помощью векторного произведения условие коллинеарности векторов и можно записать так:
Т. е. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
е. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
Последнее уравнение перепишем следующим образом:
ax + by + c = 0, (1)
c = x1(y1-y2) + y1(x2-x1)
Итак, прямую можно задать уравнением вида (1).
Задача 1. Заданы координаты двух точек. Найти её представление в виде ax + by + c = 0.
На этом уроке мы познакомились с некоторыми сведениями из вычислительной геометрии. Решили задачу по нахождению уравнения линии по координатам двух точек.
На следующем уроке составим программу для нахождения точки пересечения двух линий, заданных своими уравнениями.
Пусть прямая проходит через точки М 1 (х 1 ; у 1) и М 2 (х 2 ; у 2). Уравнение прямой, проходящей через точку М 1 , имеет вид у- у 1 = k (х — х 1), (10.6)
где k — пока неизвестный коэффициент.
Так
как прямая проходит через точку М 2 (х 2
у 2),
то координаты этой точки должны
удовлетворять уравнению (10.6): у 2 -у 1
= k (х 2 -х 1).
Отсюда
находим
Подставляя найденное значениеk в уравнение (10.6), получим уравнение
прямой, проходящей через точки М 1
и М 2:
Предполагается, что в этом уравнении х 1 ≠ х 2 , у 1 ≠ у 2
Если х 1 = х 2 , то прямая, проходящая через точки М 1 (х 1 ,у I) и М 2 (х 2 ,у 2) параллельна оси ординат. Ее уравнение имеет вид х = х 1 .
Если у 2 = у I , то уравнение прямой может быть записано в виде у = у 1 , прямая М 1 М 2 параллельна оси абсцисс.
Уравнение прямой в отрезках
Пусть
прямая пересекает ось Ох в точке М 1 (а;0),
а ось Оу – в точке М 2 (0;b).
Уравнение примет вид:
т.е.
.
Это уравнение называетсяуравнением
прямой в отрезках, т.к. числа а и b
указывают, какие отрезки отсекает прямая
на осях координат .
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем
уравнение прямой, проходящей через
заданную точку Мо (х О;
у о)
перпендикулярно данному ненулевому
вектор n = (А; В).
Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М 0 М (х — х 0 ; у — у о) (см. рис.1). Поскольку векторы n и М о М перпендикулярны, то их скалярное произведение равно нулю: то есть
А(х — хо) + В(у — уо) = 0. (10.8)
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору .
Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой .
Уравнение (10.8) можно переписать в виде Ах + Ву + С =0 , (10.9)
где А и В координаты нормального вектора, С = -Ах о — Ву о — свободный член. Уравнение (10.9) есть общее уравнение прямой (см. рис.2).
Рис.1 Рис.2
Канонические уравнения прямой
,
Где
— координаты точки, через которую проходит
прямая, а
— направляющий вектор.
Кривые второго порядка Окружность
Окружностью
называется множество всех точек
плоскости, равноотстоящих от данной
точки, которая называется центром.
Каноническое
уравнение круга радиуса R с
центром в точке
:
В частности, если
центр кола совпадает с началом координат,
то уравнение будет иметь вид:
Эллипс
Эллипсом
называется множество точек плоскости,
сумма расстояний от каждой из которых
до двух заданных точек и,
которые называются фокусами, есть
величина постоянная
,
большая чем расстояние между фокусами
.
Каноническое уравнение эллипса,
фокусы которого лежат на оси Ох, а начало
координат посредине между фокусами
имеет вид
где a длина большой полуоси; b– длина
малой полуоси (рис. 2).
Расчет координат вектора онлайн
Векторные координаты, расчет онлайн
Сводка:
Векторный калькулятор позволяет вычислить координаты вектора из координат двух точек в режиме онлайн.
vector_coordinates онлайн
Описание:
Векторный калькулятор позволяет определить координаты вектора по двум точкам , это относится к
точки на плоскости и в пространстве. Векторный калькулятор возвращает шаги расчета.
Векторный калькулятор возвращает шаги расчета.
- Вычисление координат вектора по двум точкам на плоскости
- Вычислить координаты вектора по двум точкам в пространстве
- Вычислить координаты вектора по 2 точкам в системе любой размерности Векторный калькулятор используется по тому же принципу для любой размерности систем.
Пусть (O, `vec (i)`, `vec (j)`) система, A и B две точки, которые являются соответствующими координатами (`x_a`,`y_(a)`) и (`x_(b)` ,`y_(b)`) в система (O,`vec(i)`,`vec(j)`) .
Координаты вектора `vec(AB)` равны (`x_(b)`-`x_(a)`,`y_(b)`-`y_(a)`) в системе (O,`vec (i)`,`vec(j)`).
Векторный калькулятор может вычислять числовые координаты или символьные координаты.
Пусть A(1;2) B(3;5) для вычисления координат вектора `vec(AB)`, введите vector_coordinates(`[1;2];[3;5]`).
Пусть A(a;b) B(2*a;`b/2`) для вычисления координат вектора `vec(AB)`, введите vector_coordinates(`[a;b];[2*a;b/2]`).
Пусть (O,`vec(i)`,`vec(j)`,`vec(k)`) система, A и B две точки, которые являются соответствующими координатами (`x_a`,`y_(a)`,` z_(а)`)
и (`x_(b)`,`y_(b)`,`z_(a)`) в системе (O,`vec(i)`,`vec(j)`,`vec(k)`) .
Координаты вектора vec(AB) равны (`x_(b)`-`x_(a)`,`y_(b)`-`y_(a)`,`z_(b)`-`z_ (a)`) в системе (O,`vec(i)`,`vec(j)`,`vec(k)`).
Векторный калькулятор позволяет вычислять числовые координаты или символьные координаты.
Пусть A(1;2;1) B(3;5;2) для вычисления координат вектора `vec(AB)`, введите vector_coordinates(`[1;2;1];[3;5;2]`) , возвращаются результаты [2;3;1].
Пусть A(a;b,c) B(2*a;2-b,c+1) для вычисления координат вектора `vec(AB)`, введите vector_coordinates(`[a;b;c];[2*a;2-b;c+1]`) , возвращается результат [a;2-2*b;1].
Синтаксис:
vector_coordinates(point;point)
Примеры:
vector_coordinates(`[1;2;1];[5;5;6]`) возвращает [4;3;5]
Расчет онлайн с помощью vector_coordinates (расчет координаты вектора из двух точек.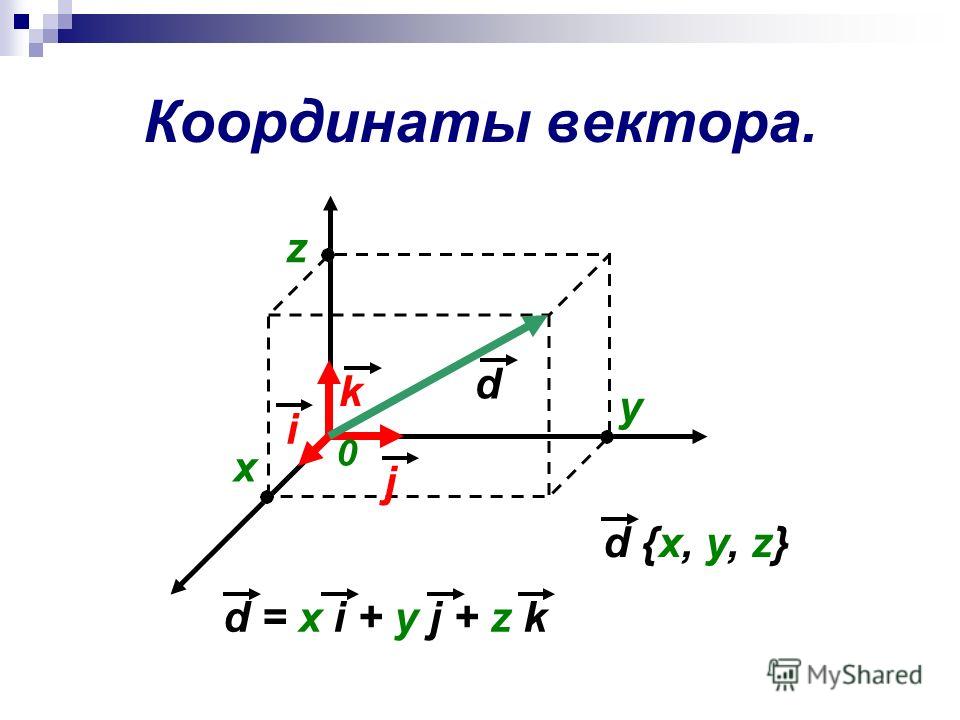 )
)
См. также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Список связанных упражнений:
- Координаты вектора по координатам двух точек : Целью этого исправленного упражнения является вычисление координат вектора по координатам двух точек.
Векторы
Векторный калькулятор — со всеми шагами
- Калькуляторы
- ::
- Матрицы и векторы
- ::
- Векторный калькулятор
Этот калькулятор выполняет все векторные операции в двух- и трехмерном пространстве. Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов.
Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов.
К каждой операции калькулятор выводит пошаговое, простое для понимания объяснение того, как была выполнена работа.
Векторы 2D Векторы 3D
Входные векторы $V_1$ и $V_2$ В 1 = ( , ) В 2 = ( , ) Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r8 } = \sqrt{8}} ~ \right) $. Примеры: Выберите, что вычислить| Величина (длина) $ V_1 $ | |
| $ v_1 \cdot v_2 $ ( скалярное произведение ) | |
| $ v_1 + v_2 $ | $ v_1 — v_2 $ |
| Угол между $v_1$ и $v_2$ | |
| Проверить, являются ли $v_1$ и $v_2$ линейно зависимыми | |
| Найдите проекцию $v_1$ на $v_2$ | |
 «> Скрыть шаги Входные векторы $V_1$, $V_2$ и $V_3$
В 1 =
(
,
,
)
В 2 =
(
,
,
)
В 3 =
(
,
,
)
Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r8 } = \sqrt{8}} ~ \right) $.
Пример:
Выберите, что вычислить
«> Скрыть шаги Входные векторы $V_1$, $V_2$ и $V_3$
В 1 =
(
,
,
)
В 2 =
(
,
,
)
В 3 =
(
,
,
)
Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r8 } = \sqrt{8}} ~ \right) $.
Пример:
Выберите, что вычислить| Величина (длина) $ V_1 $ | |
| $ v_1 \cdot v_2 $ ( скалярное произведение ) | $ v_1 \times v_2 $ ( перекрестное произведение ) |
| $ v_1 + v_2 $ | $ v_1 — v_2 $ |
| Угол между $v_1$ и $v_2$ | |
| Проверить, являются ли $v_1$, $v_2$ и $v_3$ линейно зависимыми | |
| Найдите проекцию $v_1$ на $v_2$ | |
работающий…
Полиномиальные калькуляторы
Факторные полиномы
- Полиномиальные корни
- Синтетический отдел
- Полиномиальные операции
- Графические полиномы
- Расширить и упростить
- Генерировать из корней
Рациональные выражения
Упрощение
- Умножение/деление
- Сложение/вычитание
Подкоренные выражения
Рационализировать знаменатель
- Упрощение
Решение уравнений
Квадратные уравнения (с шагами)
- Полиномиальные уравнения
- Решение уравнений — с шагами
Квадратное уравнение
Решение (с шагами)
- Квадратичный плоттер
- Факторинг трехчленов
Геометрия
Равносторонний треугольник
- Прямоугольный треугольник
- Косой треугольник
- Калькулятор площади
- Калькулятор прямоугольника
- Калькулятор круга
Калькулятор шестиугольника
- Калькулятор ромба
Комплексные номера
Модуль, обратный, полярная форма
- Подразделение
- Упростить выражение
Системы уравнений
Система 2х2
- Система 3х3
- Система 4×4
Матрицы
Векторы (2D и 3D)
- Сложить, вычесть, умножить
- Калькулятор определителя
- Матрица обратная
- Характеристический полином
- собственные значения
- Собственные векторы
- Разложение матрицы
Расчетные калькуляторы
Калькулятор лимита
- Калькулятор производных
- Интегральный калькулятор
Последовательности и серии
Арифметические последовательности
- Геометрические последовательности
- Найти n й Срок
Аналитическая геометрия
Расстояние и середина
- Калькулятор треугольника
- Графические линии
- Пересечение линий
- Двухточечная форма
- Расстояние от линии до точки
- Параллельно/Перпендикулярно
- Уравнение окружности
- Круг из 3 точек
- Пересечение круговой линии
Тригонометрия
Градусов в Радиан
- Триггер Уравнения
Номера
Длинная дивизия
- Вычислить выражения
- Калькулятор дробей
- Наибольший общий делитель НОД
- Наименее распространенный кратный LCM
- Простые множители
- Научная нотация
- Калькулятор процентов
- Dec / Bin / Hex
- Калькулятор вероятности
- Распределения вероятностей
Описательная статистика
- Стандартное отклонение
- Z — Калькулятор очков
- Нормальное распределение
- Калькулятор Т-теста
- Корреляция и регрессия
Финансовые калькуляторы
Простые проценты
- Сложные проценты
- Калькулятор амортизации
- Калькулятор ренты
Прочие калькуляторы
Наборы
Проблемы с работой
ПРИМЕРЫ
пример 1:ex 1:
По заданному вектору $v_1 = (8, -4)$ вычислить величину.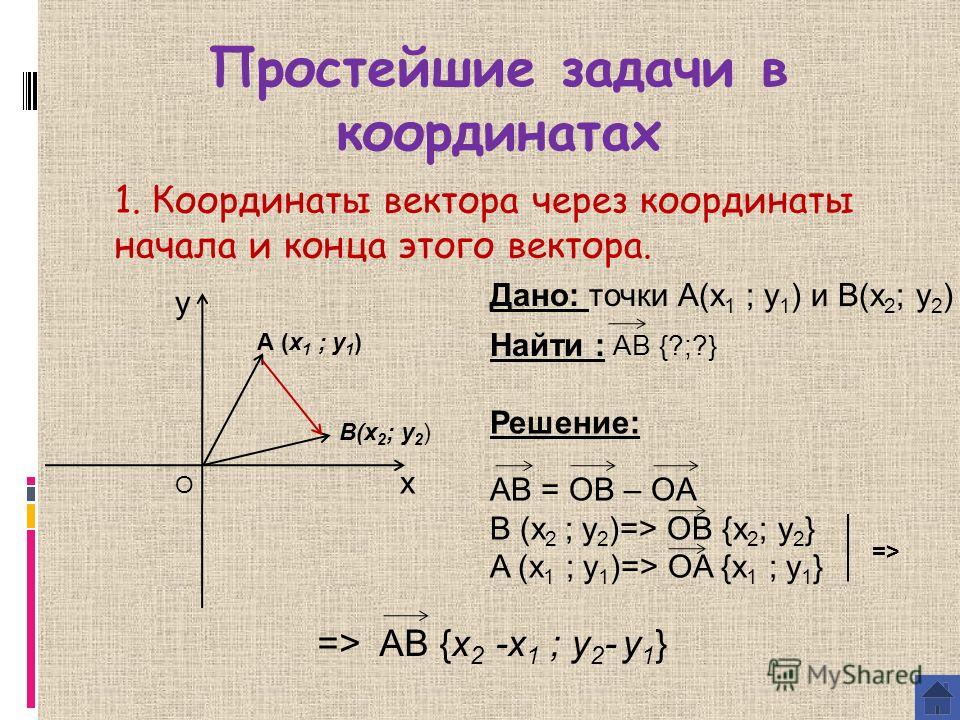
пример 2:ex 2:
Вычислить разность векторов $v_1 = \left(\dfrac{3}{4}, 2\right)$ и $v_2 = (3, -2)$.
пример 3:ex 3:
Вычислить скалярное произведение векторов $v_1 = \left(-\dfrac{1}{4}, \dfrac{2}{5}\right)$ и $v_2 = \left (-5, -\dfrac{5}{4}\right)$.
пример 4:ex 4:
Найдите угол между векторами $v_1 = (3, 5, −7)$ и $v_2 = (-3, 4, -2)$.
пример 5:ex 5:
Найдите векторное произведение $v_1 = \left(-2, \dfrac{2}{3}, −3 \right)$ и $v_2 = \left(4, 0, -\dfrac{1}{2} \right)$.
пример 6:ex 6:
Определите, является ли линейно независимым набор векторов: $v_1 = (3, -2, 4)$ , $v_2 = (1, -2, 3)$ и $v_3 = (3, 2, -1)$.
ТУТОРИАЛ
Операции с векторами
В этом уроке мы научимся находить: величину , скалярное произведение , угол между двумя векторами 92} = \sqrt{20} = 2\sqrt{5} $$
Пример 02: Найдите модуль вектора $ \vec{v} = \left(\dfrac{2}{3}, \sqrt{3}, 2\right) $.
Решение
2 : Скалярное произведение
Формула скалярного произведения векторов $ \vec{v} = (v_1, v_2) $ и $ \vec{w} = (w_1, w_2) $ равна
$$ \vec{v} \cdot \vec{w}= v_1 \cdot w_1 + v_2 \cdot w_2 $$
Два вектора ортогональны друг другу, если их скалярное произведение равно нулю.
Пример 03: Вычислить скалярное произведение $ \vec{v} = \left(4, 1 \right) $ и $ \vec{w} = \left(-1, 5 \right) $. Проверьте, взаимно ортогональны ли векторы.
Чтобы найти скалярный продукт, мы используем формулу компонента:
$$ \begin{выровнено} \vec{v} \cdot \vec{w} &= \left(4, 1 \right) \cdot \left(-1, 5 \right) = \\[1 em] &= 4 \cdot (-1) + 1 \cdot 5 = -4 + 5 = 1 \end{выровнено} $$
Поскольку скалярное произведение не равно нулю, мы можем заключить, что векторы НЕ ортогональны.
Пример 04: Найдите скалярное произведение векторов $ \vec{v_1} = \left(\dfrac{1}{2}, \sqrt{3}, 5 \right) $ и $ \vec{v_2 } = \left( 4, -\sqrt{3}, 10 \right) $.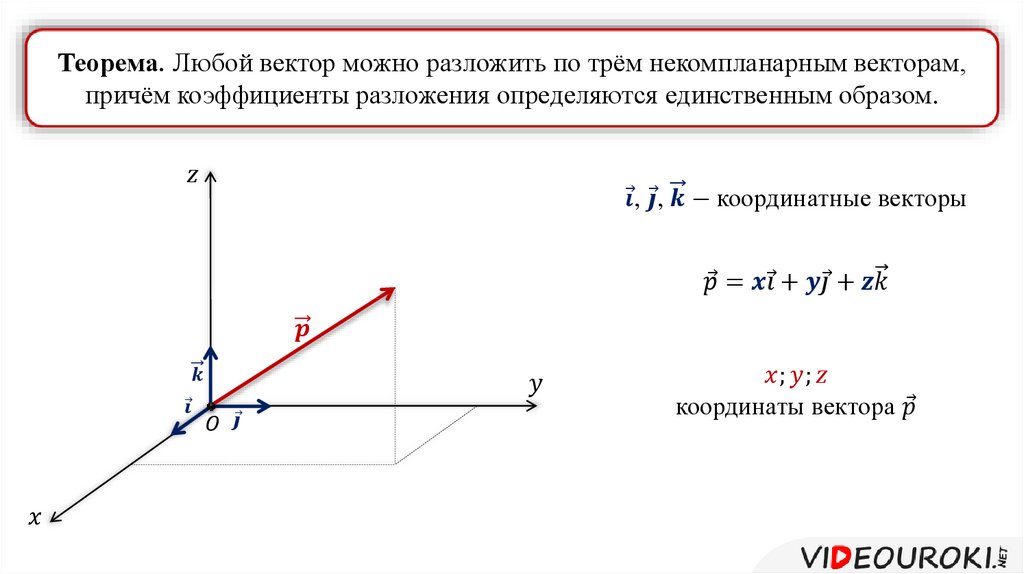
Решение
3 : Угол между двумя векторами
Чтобы найти угол $ \alpha $ между векторами $ \vec{a} $ и $ \vec{b} $, мы используем следующую формулу:
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} $$
Обратите внимание, что $ \vec{a} \cdot \vec{b} $ — скалярное произведение, а $\|\vec{a}\|$ и $\|\vec{b}\|$ — величины векторов $\vec{a}$ и $\vec{b}$. 9{о} $$
Пример 06: Найдите угол между векторами $ \vec{v_1} = \left(2, 1, -4 \right) $ и $ \vec{v_2} = \left( 3, -5, 2 \ правильно) $.
Решение
4 : Перекрестное произведение
Перекрестное произведение векторов $ \vec{v} = (v_1,v_2,v_3) $ и $ \vec{w} = (w_1,w_2,w_3)$ определяется выражением формула:
$$ \vec{v} \times \vec{w} = \left( v_2 w_3 — v_3 w_2, v_3 w_1 — v_1 w_3, v_1 w_2 — v_2 w_1 \right) $$
Обратите внимание, что векторное произведение требует, чтобы оба вектора были трехмерными.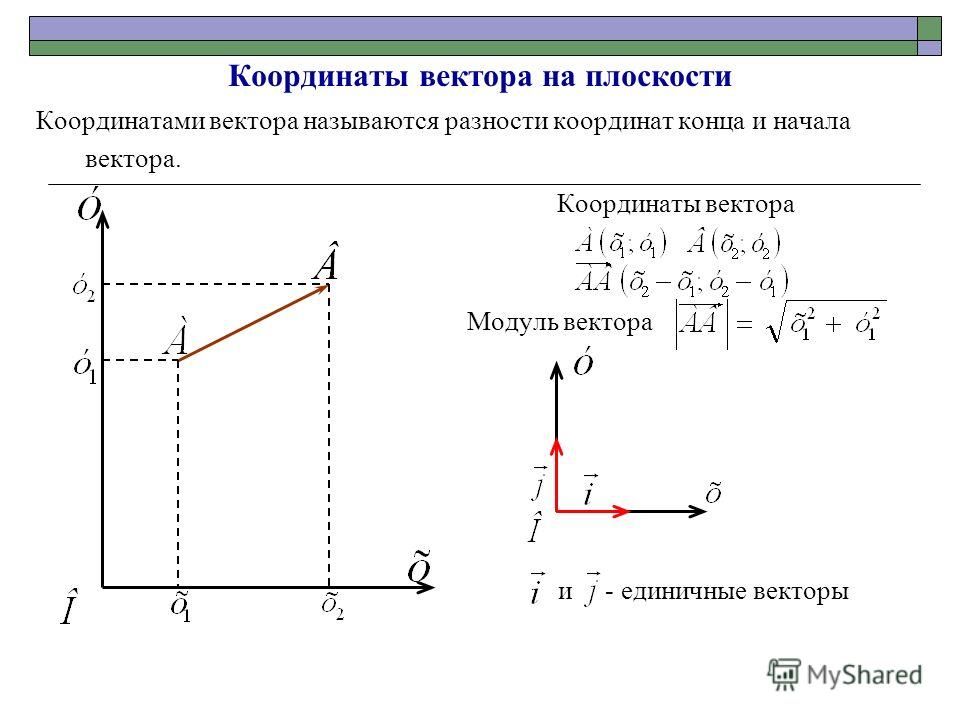
Если два вектора параллельны, то векторное произведение равно нулю.
Пример 07: Найдите векторные произведения векторов $ \vec{v} = (-2, 3 , 1) $ и $ \vec{w} = (4, -6, -2) $. Проверьте, параллельны ли векторы.
Мы найдем векторное произведение, используя приведенную выше формулу
$$ \begin{выровнено} \vec{v} \times \vec{w} &= \left( 3 \cdot (-2) — 1 \cdot (-6), 1 \cdot 4 — (-2) \cdot (-2), — 2 \cdot (-6) — 3 \cdot 4 \right) = \\[1 em] &= \влево(-6-(-6), 4-4,12 — 12 \вправо) = (0, 0, 0) \end{выровнено} $$
Поскольку векторное произведение равно нулю, мы заключаем, что векторы параллельны.
Пример 08: Найдите векторные произведения векторов $ \vec{v_1} = \left(4, 2, -\dfrac{3}{2} \right) $ и $ \vec{v_2} = \ влево(\dfrac{1}{2}, 0, 2 \вправо) $.
Решение
Найдите в нашей базе данных более 200 калькуляторов
227 654 730 решенных задач
Калькулятор векторного произведения (вектор)
Вы ищете онлайн-калькулятор выполняет быстрые вычисления и отображает результаты перекрестного произведения за доли секунды? Тогда наш бесплатный калькулятор точно поможет вам найти векторное произведение двух векторов.
| i | и | к |
|---|---|---|
| х1 | у1 | z1 |
| x2 | у2 | z2 |
| у1 | z1 |
| у2 | z2 |
| x1 | z1 |
| x2 | z2 |
| x1 | у1 |
| x2 | у2 |
на разложении x * y = i (y1.z2 – z1.y2) — j (x1.z2 – z1.x2) + k (x1.y2 – y1.x2)
Калькулятор векторного векторного произведения довольно прост в использовании. Чтобы узнать векторное произведение, выполните следующие действия:
Чтобы узнать векторное произведение, выполните следующие действия:
- Шаг 2 : Нажмите кнопку «Получить расчет» , чтобы получить значение перекрестного произведения.
- Шаг 3 : Наконец, вы получите значение векторного произведения двух векторов вместе с подробным пошаговым решением.
Шаг 1 : Введите заданные коэффициенты векторов X и Y в поля ввода.
Что еще? Вы можете использовать его для академических или личных целей, что обычно занимает довольно много времени при выполнении вручную.
Прочтите эту статью, чтобы лучше понять, как пользоваться калькулятором.
Что такое ПЕРЕКРЕСТНОЕ ПРОИЗВЕДЕНИЕ?
Произведение между двумя векторами, a и b, , называется «Перекрестное произведение ». Оно может быть выражено только в трехмерном пространстве, а не в двухмерном. Он представлен ‘ a ⨯ b ’ (сказал крестик b).
Он представлен ‘ a ⨯ b ’ (сказал крестик b).
Результат двух векторов обозначается как « c », который перпендикулярен обоим векторам, a и b , где θ — угол между двумя векторами. Его направление определяется правилом правой руки , а величина определяется площадью параллелограмма.
ФОРМУЛА ПЕРЕКРЕСТНОГО ПРОИЗВЕДЕНИЯ
а ⨯ б = |а| |б| sin (θ) n
- | а | и | б | — длина двух векторов.
- θ это угол между двумя векторами a и b (в диапазоне от 0° до 180°).
- n — единичный вектор, перпендикулярный обоим векторам a и b.
Если векторы a и b параллельны, то их векторное произведение равно нулю .
Направление вектора c можно просто узнать по правилу большого пальца правой руки, где-
Указательный палец должен быть в направлении а.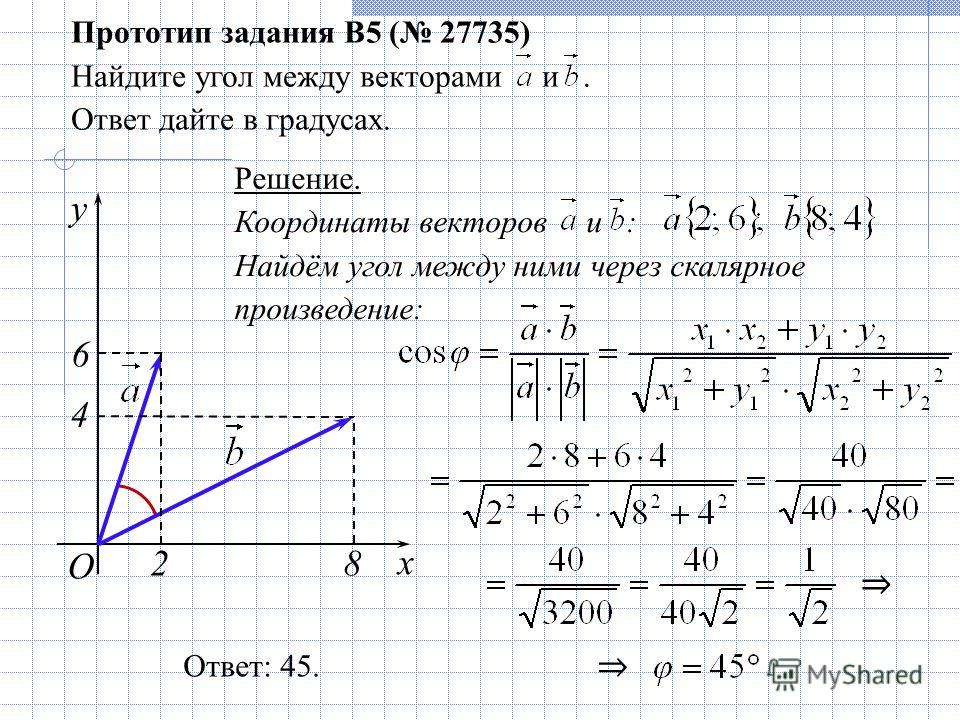
Средний палец должен быть в направлении b.
Формула перекрестного произведения немного сложнее, чем обычные формулы. Требуется немного больше концентрации и открытый, ясный ум. Сосредоточение внимания на основах поможет вам лучше понять концепцию.
Мы можем найти направление единичного вектора, принимая во внимание Правило правой руки для перекрестного произведения . Чтобы определить правильное перекрестное произведение, у нас есть правило правой руки.
Чтобы воспользоваться этим правилом, вы поднимаете правую руку вверх, затем поднимаете указательный палец и направляетесь к первому вектору, а теперь указываете средним пальцем в направлении второго вектора. При этом большой палец правой руки будет показывать направление единичного вектора.
Решенный пример перекрестного произведения
Два вектора даны как:
Найдите векторное произведение.
Решение:
Дано –
Представление двух приведенных выше векторов с использованием метода матрицы перекрестного произведения дается следующим образом: –
При расширении,
больше проблем с перекрестным продуктом.
Что такое вектор?
Это измерение одной точки пространства относительно другой точки пространства . Он имеет две составляющие – величину и направление. Векторы помогают узнать положение, смещение, скорость и ускорение объекта.
Величина — это значение длины вектора. Он обозначается ‘||a||.’
Направление – это угол поворота вектора относительно востока, запада, севера и юга. Обозначается ‘ → ’ , который имеет два конца: хвост и головку . Направление стрелки зависит от вектора, т.е. вперед, назад, вверх или вниз (обычно только вперед и назад).
Типы векторов
Существует два типа векторов:
1. Параллельные векторы
2. Перпендикулярные векторы
1. Параллельные векторы:
Два вектора, a и b , параллельны , когда их скалярные кратные равны нулю.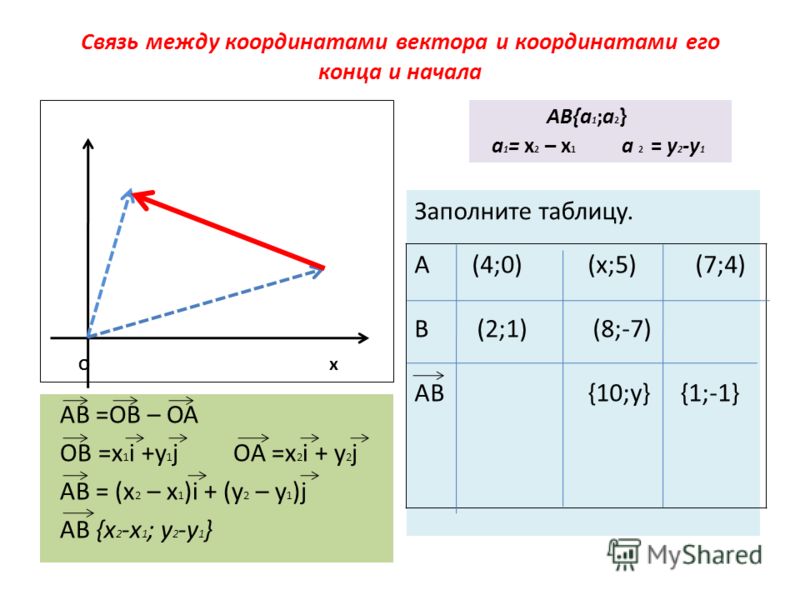
a = k b , где «k» — константа, которая означает, что она не равна нулю.
Пусть a = (ax , ay) и b = (bx , by) a и b параллельны тогда и только тогда
если
а = к б (ах, ау) = к (Ьх, бай) = (ках, кбай)
2. Перпендикулярные векторы:
Два вектора, a и b, перпендикулярны , когда их скалярные произведения равны нулю .
a = k b , где «k» — константа, что означает, что она не равна нулю.
Пусть a = (ax , ay) и b = (bx , by) a и b перпендикулярны тогда и только тогда, когда
и . б = 0
(топор , ай). (bx, by) = ax bx + ay по
Типы продуктов
Нужно знать произведение двух векторов, чтобы найти, какой из них перпендикулярен обоим векторам.
Существует два способа вычисления произведения двух векторов:
- 1. Скалярное произведение
- 2. Перекрестное произведение
- 1. Скалярное произведение (также называемое скалярным произведением):
Дает уровень, на котором два вектора указывают в одном направлении.
Он представлен и . б = ||а|| ||б|| cos (θ)
Где a и b два вектора
и θ является углом между двумя векторами, a, и b.
- 2. Перекрестное произведение (также называемое векторным произведением):
Это операция между двумя векторами.
Он представлен a ⨯ b = ||a|| ||b||sin (θ)n
Где a и b — два вектора
и θ — угол между двумя векторами, a и б.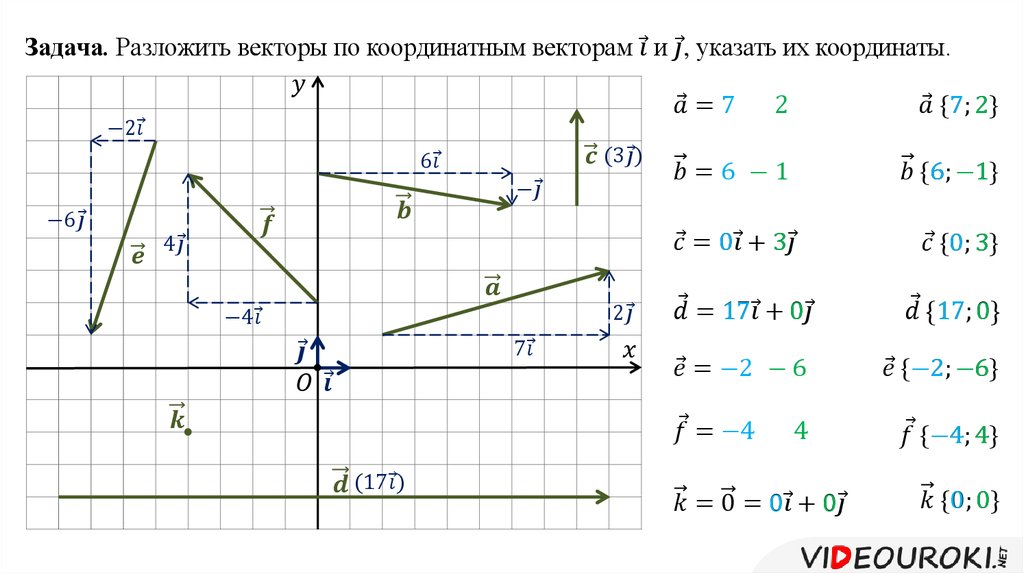
- 1. Число определяется скалярным произведением, а вектор определяется перекрестным произведением.
- 2. В любом количестве измерений можно использовать скалярные произведения, но перекрестное произведение только для трех измерений.
- 3. Результатом скалярного произведения является скалярная величина, а результатом перекрестного произведения является векторная величина.
4. Сходство направлений двух векторов измеряется скалярным произведением, тогда как различие направлений двух векторов измеряется перекрестным произведением.Также проверьте это: Разница между перекрестным произведением и скалярным произведением
ОБОЗНАЧЕНИЕ КООРДИНАТ: СТАНДАРТНЫЙ МЕТОД
Рассмотрим два вектора A и B , где,
A = A I + B J + C K
B = x K
B = x K
B = x k
B = x k
+ + y + .
Здесь i — единичный вектор по оси x
j — единичный вектор по оси Y
K — единичный вектор по оси Z
i × j = k and j × i = – k
j × k = i and k × j = – i
к × i = j и i × k = – j
can say that –
i × i = j × j = k × k = 0
So,
A × B = (a i + b j + c k ) × (x i + Y J + Z K )
= AX ( I × I ) + AY ( I × J ) + AZ ( I × J ) + AZ ( I × J ) + AZ ( I × J ) + AZ ( I × J ) + AZ ( I × ) + AZ ( I × J ) + AZ ( I × J ). j × i ) + by( j × j ) + bz( j × k ) + cx( k × i ) + cy( k × j ) + cz( k × k )
j × i ) + by( j × j ) + bz( j × k ) + cx( k × i ) + cy( k × j ) + cz( k × k )
Используя приведенные выше равенства,
A × B = ax(0) + ay( k ) + az(- j ) + bx(- k ) + by(0) + bz( i ) + cx( j ) + cy (- i ) + cz(0)
= (bz – cy) i + (cx – az) j + (ay – bx) k
МАТРИЦА ПЕРЕКРЕСТНЫХ ПРОИЗВЕДИЙ: АЛЬТЕРНАТИВНЫЙ МЕТОД
Помимо стандартного метода, другой альтернативой, применимой для применения, является метод «матрицы перекрестного произведения ».
Разница между стандартным методом и методом матрицы перекрестного произведения заключается в том, что определители не используются в первом, но во втором .
Рассмотрим два вектора A и B , где,
A = A I + B J + C K
B = C K
B = C K
. k
k
Здесь i — единичный вектор по оси X
j — единичный вектор по оси Y
K — единичный вектор по оси Z
5
0123 матрица перекрестного произведения
метод представляет собой –Где,
A × B = (bz – cy) i – (az – cx) j + (ay – bx) k
= (bz – cy) i + (cx – az) j + (ay – bx) k
ИЛИ Они также называются – « Формальные детерминанты » и приведены ниже –
Применение правила разложения кофакторов Сарура,
Расширение приводит к –
Свойства перекрестного произведения
Свойства играют большую роль в поиске перекрестных произведений различных заданных векторов, которые определяют рекомендации в определенных условиях. Они связывают растворы полученных перекрестных произведений. Есть четыре свойства, из которых два верхних являются наиболее важными. Это –
Это –
- 1. Антикоммутативное свойство
Это свойство имеет преимущественно отрицательные знаки.
Представлено как –
антикоммутативность принимает участие в способе записи координат, поэтому равенства i, j и k становятся соответственно -i, -j, и -k, .
2. Распределяющее свойство
Оно показывает нам, как найти решение таких выражений, как a (b + c). Его также называют «Распределительный закон умножения и деления».
Представлено как –
Обычно, решая выражение приведенного выше шаблона, мы сначала решаем уравнение в скобках. Тем не менее, когда дело доходит до распределительное свойство , мы должны сначала умножить числа вне скобок с числами внутри него в правильном порядке.
Пример:
В приведенном выше примере мы наблюдаем, что 2 умножается на 4 , затем 8 , а затем складывается их результат, и мы получаем ответ 24 .
Если мы воспользуемся упомянутым ранее стандартным методом, мы все равно получим ответ равный 24. Тогда почему мы используем распределительное свойство? Когда речь идет о векторах, часто вместо чисел присутствуют переменные в виде коэффициентов. Когда присутствуют переменные, мы должны использовать дистрибутивное свойство , а не стандартный метод; в противном случае мы получим неверные ответы.
- 3. Свойство Якоби
Названо в честь немецкого математика Карла Густава Якоба Якоби.
Представлено как –
Это свойство контролирует порядок, в котором предполагается вычислять выражения, и положение скобок в выражении множественного порядка. Это необходимо для сохранения единообразия в решении однотипных выражений во всем мире.
Имеет различные формы в зависимости от предмета использования.
- 4. Свойство нулевого вектора
Представлено как –
Имеет три определяющих подсвойства. Это –
Это –
(i) Аддитивная идентичность, означающая a + 0 = a.
(ii) Ноль, умноженный на любой вектор в пространстве, дает это свойство, что означает 0 ( a ) = 0.
(iii) Прямые углы (ортогональные) к каждому вектору в пространстве, что означает и . 0 = 0,
Решенный пример
Вопрос: Найдите угол между a и b: учитывая, что a = (-4, 3,0) и b = (2, 0,0)
Решение:
a= 5
б = 2 ; a × b = (0, 0, -6)
a × b = 6
Итак, 1/sin(6/(5*2)) = 1/sin(⅗) = 36,87°
Часто задаваемые вопросы!
Что такое векторный векторный калькулятор? Калькулятор векторного умножения для нахождения векторного произведения двух векторов.
Калькулятор довольно прост в использовании, нужен ли он вам для академических или личных целей, вы можете просто ввести цифры и нажать Enter, чтобы найти ответ.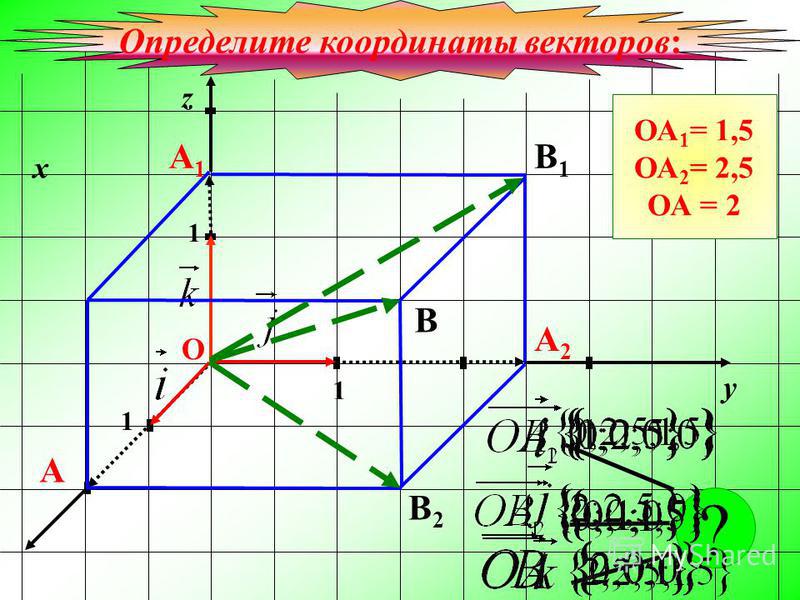 Наш калькулятор также предоставляет подробное пошаговое решение вместе с прямым ответом.
Наш калькулятор также предоставляет подробное пошаговое решение вместе с прямым ответом.
Существует два типа калькуляторов, которые используются соответственно для 2D- и 3D-векторов, т. е. на основе количества измерений векторов, которое может быть два или три. Например, если пользователь использует векторы только с двумя измерениями, то калькулятор перекрестного произведения 2×2 можно использовать для двух векторов. Здесь пользователь заполняет только поля «i» и «j», поэтому оставляет третье поле «k» пустым. Если пользователь использует калькулятор для трехмерного вектора, как в случае калькулятора перекрестного произведения 3×3, то пользователь должен ввести все поля. Здесь есть значения, введенные для всех трех измерений в соответствующих полях i, j и k, которые перемножаются, а затем складываются, чтобы получить общий результат.
Как работает этот калькулятор? Без калькулятора векторного векторного произведения трудно вычислить векторное произведение двух векторов. Академически или нет, вы, возможно, уже знаете формулу векторного произведения двух векторов. К счастью, этот калькулятор является таким инструментом, который поможет вам понять формулу. Вдобавок, есть целый список практических приемов, таких как правило правой руки, с помощью которого вы можете освоить трюк, как сделать перекрестное произведение двух или трех векторов.
Академически или нет, вы, возможно, уже знаете формулу векторного произведения двух векторов. К счастью, этот калькулятор является таким инструментом, который поможет вам понять формулу. Вдобавок, есть целый список практических приемов, таких как правило правой руки, с помощью которого вы можете освоить трюк, как сделать перекрестное произведение двух или трех векторов.
Калькулятор векторных координат по двум точкам
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор векторных координат по двум точкам вычисляет векторные координаты в двухмерном и трехмерном пространстве и дает подробное решение.

Размер помещения 23
Координаты точки
Координаты первой точки
A:
(
;
)
Координаты второй точки
B:
(
;
)
Как найти векторные координаты из двух точек в двухмерном и трехмерном пространстве
Для того чтобы вычислить координаты вектора по двум точкам, необходимо воспользоваться одной из формул.
AB = {x B — x A ;
у Б — у А }
— для вычисления координат вектора в двумерном пространстве
AB = {x B — x A ; у В — у А ; z B — z A } — вычислять координаты вектора в трехмерном пространстве
Пример вычисления координат вектора по двум точкам.
Вам дан вектор AB с концами в точках A(x A ; y A ) и B(x B ; y B ).
Координаты точки А: А (5; 9).
Координаты точки B: A (1; 4).
Результат:
AB = {-4 ; -5}
Пошаговое решение:
AB = {x B — x A ; у B — y A } =
{1 — 5; 4 — 9} =
{-4; -5}
| You may also find the following calculators helpful | |
| Linear Algebra and Analytical Geometers Calculators | |
| Matrix Addition and Subtraction Calculator | |
| Matrix Multiplication Calculator | |
| Matrix Transpose Calculator | |
| Калькулятор определителя матрицы | |
| Калькулятор обратной матрицы | |
| Длина сегмента линии. Онлайн-калькулятор расстояния между точками. | |
| Калькулятор векторных координат по двум точкам | |
| Калькулятор векторного модуля (длины) | |
| Калькулятор векторного сложения и вычитания |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. |
| Калькулятор векторного произведения. Используя векторные координаты. |
| Vector Triple Product Calculator |
| Vector Multiplication by Number Calculator |
| Angle Between Vectors Calculator |
| Vector Collinearity Check Calculator |
| Vector Coplanarity Calculator |
| Combinatorics Calculators |
| Калькулятор перестановок N элементов |
| Combinations of N Elements by M Calculator |
| Permutations of N Elements by M Calculator |
| Numeral Systems Calculators |
| Roman Numeral Calculator |
| Roman Numerals From 1 to 3999 |
| Калькулятор систем счисления |
Двоичный калькулятор. Сложение, вычитание, умножение и деление двоичных чисел. Сложение, вычитание, умножение и деление двоичных чисел. |
| Fraction Calculators |
| Simplifying Fractions Calculator |
| Improper to Mixed Fraction Calculator |
| Mixed Fraction to Improper Calculator |
| Fractions Calculator With Step by Step Solution |
| Raising a Fraction to a Power . Онлайн калькулятор. |
| Преобразование десятичной дроби в дробь |
| Преобразование дроби в десятичную дробь |
| Compare Fractions Calculator |
| Common Denominator Calculator |
| Trigonometers Calculators |
| Sine Calculator |
| Cosine Calculator |
| Tangent Calculator |
| Cotangent Calculator |
| Secant Калькулятор |
| Калькулятор косеканса |
| Калькулятор арксинуса |
| Arccosine Calculator |
| Arctangent Calculator |
| Arccotangent Calculator |
| Arcsecant Calculator |
| Arccosecant Calculator |
| Calculators (Number theory) |
| Mathematical Expressions Calculator |
| Калькулятор в скобках |
| Калькулятор простой факторизации |
| Gcd and Lcm Calculator With Steps |
| Gcd and Lcm calculator using Euclidean algorithm |
| Gcd and Lcm Calculator for Any Number of Numbers |
| Break Down the Number Into Its Place Value |
Разделить число на отношение. Онлайн-калькулятор с шагами Онлайн-калькулятор с шагами |
| Калькулятор процентов с шагами |
| Калькулятор преобразования научной записи в десятичную |
| Scientific Notation Converter |
| Factorial Calculator With Steps |
| Logarithm Calculator |
| Quadratic Equations Calculator With Steps |
| Remainder Calculator |
| Root Calculator |
| Decimal Period Calculator |
| Калькулятор больших чисел |
| Калькулятор округления чисел |
| Properties of Roots and Exponents Calculator |
| Complex Number Calculator |
| Area Calculators |
| Area of a Square Calculator |
| Area of a Rectangle Calculator |
| Math Trainers |
| Математический тренажер сложения |
| Математический тренажер вычитания |
| Математический тренажер умножения |
| Дивизион Математический тренажер |
| Математический тренажер таблицы умножения |
| Онлайн-тренажер счета для дошкольников |
| Онлайн-тренажер внимательности для дошкольников | 6 | 6 | Найдите правильный ответ. |
| Онлайн-тренажер числовых выражений |
| Преобразователи |
| Преобразователь длины |
| Speed Converter |
| Acceleration Converter |
| Physics Calculators |
Mechanics |
| Speed Time Distance Calculator |
| Acceleration Speed Distance Calculator |
| Displacement Time Calculator |
| Time Калькулятор |
| Калькулятор второго закона Ньютона |
| Калькулятор гравитационной силы |
| Momentum Calculator |
| Impulse Calculator |
| Object Weight Calculator |
Optics |
| Light Reflection and Refraction Calculator |
Electricity and Magnetism |
| Ohm’s Law Калькулятор |
| Калькулятор закона Кулона |
| Калькулятор напряженности электрического поля |
| Point Electric Charge Calculator Q |
| Force Acting on Charge Calculator |
| Distance From Charge Calculator |
| Potential Charge Energy Calculator |
| Electric Field Potential Calculator |
| Conductor and Sphere Capacitance Калькулятор |
Конденсаторы |
| Калькулятор емкости параллельных пластинчатых, цилиндрических и сферических конденсаторов |
| Electric Field Strength in Parallel Plate, Cylindrical and Spherical Capacitors Calculator |
| Voltage (Potential Difference) of Parallel Plate, Cylindrical and Spherical Capacitors Calculator |
| Distance Between Plates in Parallel Plate Capacitor Calculator |
| Калькулятор площади пластины в параллельном пластинчатом конденсаторе |
| Калькулятор запасенной энергии в заряженном конденсаторе |
| Калькулятор энергии, накопленной в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов |
| Астрономические калькуляторы |
| Вес объекта на других планетах |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор случайных чисел |
| Генератор паролей |
Векторный калькулятор физики | iCalculator™
★ ★ ★ ★ ★ [ 68 Votes ]
The Vector Calculator is provided in support of our Physics Tutorials on Vectors and Scalars which explores addition and subtraction of vectors, multiplication of вектор скалярным, точечным (скалярным) произведением двух векторов и векторным произведением двух векторов с практическими рабочими примерами и формулой. Список вспомогательных учебных пособий по векторной и скалярной физике доступен внизу этой страницы. Этот калькулятор посчитает:
Список вспомогательных учебных пособий по векторной и скалярной физике доступен внизу этой страницы. Этот калькулятор посчитает:
- Величина каждого вектора при заданных координатах
- Сумма двух векторов
- Разность двух векторов
- Скалярное произведение двух векторов
- Величина векторного произведения двух векторов
- Угол между двумя векторами
Эти результаты будут использованы для нахождения следующих физических величин:
- Равнодействующая двух векторных величин
- Работа, совершаемая силой при перемещении объекта на определенное линейное расстояние
- Момент силы
- Угол между силой и линейным расстоянием, на которое система движется линейно или вращается вокруг фиксированной точки (оси)
Точность (десятичных мест) 012345678
|
| X-координата вектора U ⃗ (U x ) |
| y-coordinit0128 |
| z-coordinate of vector u ⃗ (u z ) |
| x-coordinate of vector v ⃗ (v x ) |
| y-coordinate of vector v ⃗ (v y ) |
| z-coordinate of vector v ⃗ (v z ) |
| Magnitude of Вектор и ⃗ 7 (| U ⃗ |) | |
| величина вектора v ⃗ (| V ⃗ |) | |
| Difference of Vectors u ⃗ and v ⃗ (u ⃗ -v ⃗ ) | |
| Dot Product of Vectors u ⃗ и v ⃗ (u ⃗ ∙v ⃗ ) | |
| Синусная формула угла и расчет (SIN θ) | |
| ТАН КОНСКА ты ⃗ Формула и расчет | |
| |u ⃗ | = √ U 2 x + U 2 Y + U 2 Z 9 2 Z 79 2 Z 774 4 9 9 9 9 9 9 9 9 9 9 2 2 9 2 9077 = √ 2 + 2 + 2 |u ⃗ | = √ + + |u ⃗ | = | |
| Величина вектора v ⃗ Формула и расчет | |
|---|---|
| |v ⃗ | = √ V 2 x + V 2 Y + V 2 Z 9 2 Z 79 2 Z 779 2 77777 2 Z | |
| Сумма векторов u ⃗ и V ⃗ Формула и расчет | |
| U ⃗ + V ⃗ = U x + U y , U + Z u ⃗ + v ⃗ = + , + , + u ⃗ + v ⃗ = | |
| Difference of Vectors u ⃗ and v ⃗ Формула и расчет | |
| U ⃗ — V ⃗ = U x — U Y , U Z — V x , V Y -V Z x , V Y -V Z . ⃗ = — , — , — u ⃗ — v ⃗ = | |
| Dot Product of Vectors u ⃗ and v ⃗ Formula and Calculation | |
| и ⃗ ∙v ⃗ = (и x ∙ V x ) + (U Y ∙ V Y ) + (U Z ∙ V Z ) U ⃗ 7 ∙ V ⃗ = (6999999999999 года.  + 9). + 79 ∙ ∙ v ⃗ = (669 ∙ 7779 ∙ ∙ v ⃗ 9077 = (69 ⃗ 7 ∙ v ). ∙ ) + ( ∙ ) + 9). + 79 ∙ ∙ v ⃗ = (669 ∙ 7779 ∙ ∙ v ⃗ 9077 = (69 ⃗ 7 ∙ v ). ∙ ) + ( ∙ ) U ⃗ ∙ v ⃗ = | |
| Масштабирование поперечного продукта u ⃗ | поперечного продукта |
| . и ⃗ ∙v ⃗ | х = и у ∙ v z — и z ∙ v y |u ⃗ ∙v ⃗ | x = ∙ — ∙ |u ⃗ ∙v ⃗ | x = |u ⃗ ∙v ⃗ | y = u z ∙ v x — u x ∙ v y |u ⃗ ∙v ⃗ ⃗ | y = ∙ — ∙ |u ⃗ ∙v ⃗ | y = |u ⃗ ∙в ⃗ | z = u x ∙ v y — u y ∙ v x |u ⃗ ∙v ⃗ | z = ∙ — ∙ |u ⃗ ∙v ⃗ | z = |u ⃗ ∙v ⃗ | = √ / |u ⃗ ∙v ⃗ | 2 x + |u ⃗ ∙v ⃗ | 2 у + |u ⃗ ∙v ⃗ | 2 z |u ⃗ ∙v ⃗ | = √ / + + |u ⃗ ∙v ⃗ | = | |
| Формула косинуса угла и вычисление | |
| cos θ = u ⃗ ∙ v ⃗ 7 7 977 907 | 76 |у ⃗ | ∙ |v ⃗ | cos θ = / ∙ cos θ = |
| Sine of Angle Formula and Calculation | |
| sin θ = |u ⃗ ∙ v ⃗ | / |u ⃗ | ∙ |v ⃗ | sin θ = / ∙ sin θ = | |
| Tan of Angle Formula and Calculation | |
| tan θ = sin θ / cos θ tan θ = / TAN θ = | |
| Угол θ Формула и расчет | |
| Угол θ = Арктан (TAN θ) Угол θ = ARCTAN () Угол θ) θ = ARCTAN () Угол θ).  0005 0005Обратите внимание, что формулы для каждого расчета вместе с подробными расчетами показаны ниже на этой странице. Когда вы вводите конкретные коэффициенты для каждого векторного расчета, векторный калькулятор автоматически вычисляет результаты и обновляет элементы формулы с каждым элементом векторного расчета. Затем вы можете отправить по электронной почте или распечатать этот векторный расчет для дальнейшего использования. Мы надеемся, что векторный калькулятор был вам полезен. Если это так, просим вас оценить этот калькулятор и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. ★ ★ ★ ★ ★ [ 68 голосов ] Калькуляторы физики9000
Графический калькулятор векторных функций + онлайн-решатель с бесплатными шагамиA Графический калькулятор векторных функций область фундаментальных значений и набор векторов. Используя этот калькулятор, вы можете последовательно продемонстрировать разброс векторной функции. Что такое калькулятор векторных функций? Графический калькулятор векторных функций — это онлайн-калькулятор, который обеспечивает визуальное представление векторной функции в каждый момент времени. A Векторная функция , часто известная как Функция векторного значения , представляет собой функцию с областью определения всех действительных чисел (R) и широким набором векторов. Векторные функции ‘r’ с трехмерными (3D) векторными значениями особенно важны для нас. Это указывает на то, что для каждого числа (t) в диапазоне r(t) существует отдельный вектор в V3 с символом «r». Если функции ‘f(t)’ , ‘g(t)’ и ‘h(t)’ являются вещественными функциями, известными как функции-компоненты ‘r’ , то они являются составляющими вектора ‘r(t)’ , и мы можем записать их как: \[ r(t) = 〈f(t), g(t), h(t)〉 = f (t) i + g(t) j + h(t) k \] Поскольку время обычно представляется символом ‘t’ в приложениях векторных функций, мы используем эту букву для обозначения независимой переменной. Как пользоваться калькулятором векторных функций? Вы можете использовать калькулятор векторных функций , следуя приведенным подробным пошаговым инструкциям; калькулятор обязательно даст вам желаемые результаты. Шаг 1Введите параметрических уравнений вектора в соответствующие поля ввода. Шаг 2Нажмите кнопку «Отправить» , чтобы рассчитать График векторной функции для заданных параметрических уравнений и просмотреть подробное пошаговое решение для Расчет графика векторной функции . Как работает калькулятор векторных функций?Графический калькулятор векторных функций работает, вычитая путевые точки начальной точки из координат конечной точки. Помните, что величина и ориентация плоского вектора — это два элемента. В конечном итоге мы определяем второе местоположение, если идем в определенной ориентации на определенное расстояние от любой точки плоскости (исходной точки). Это представление конечной точки вектора. Вычитая путевые точки начального положения из значений координат конечной точки, мы можем получить составляющие вектора. Если начальная точка вектора находится в центре, считается, что он находится в стандартном положении. Чтобы обеспечить четкость графика при построении вектор-функции, мы обычно строим векторы в диапазоне функции в нормальном положении. Графики трехмерных (3D) вектор-функций также следуют этому подходу. График векторнозначной функции следующего вида \[ r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}} \] — это путь, состоящий из набора всех конечных точек (f(t),g(t)) , и этот путь известен как плоская кривая . График векторнозначной функции следующего вида \[ r(t)=f(t)\hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t ) \hat{\mathbf{k}} \] включает в себя набор всех координат f (t), g(t) и h(t) , а траектория, по которой он движется, называется пространственной кривой . Векторная математическая модель кривой изображает плоскую или пространственную кривую с помощью векторнозначной функции. Каждая плоская кривая и пространственная кривая имеет направление, которое по мере увеличения величины параметра t указывает направление движения по кривой. Эта ориентация обозначена стрелками, нанесенными на кривую. Параметр подлежит ограничению, если диапазон значений t ограничен константами в интервале [a,b]. Тогда график параметризованной функции и график векторной функции будут согласованы, а векторный график будет представлять векторы вместо точек. Решенные примерыДавайте рассмотрим несколько примеров, чтобы лучше понять работу графического калькулятора векторных функций. Пример 1Создайте график для каждой из перечисленных ниже векторных функций.\[ \vec r ( t ) = \langle {t,1} \rangle \] РешениеИтак, наша первая задача — ввести несколько значений t, чтобы получить векторы положения. Вот пара \[ \vec r ({ – 3}) = \langle { – 3,1} \rangle \; \; \; \; \vec r ( { – 1} ) = \langle { – 1,1} \rangle \; \; \; \; \vec r ( 2 ) = \langle {2,1} \rangle \; \; \; \; \vec r ( 5) = \langle {5,1} \rangle \] 93} – 10t + 7}\rangle \] Решение Вот несколько примеров вычисления этой векторной функции. |

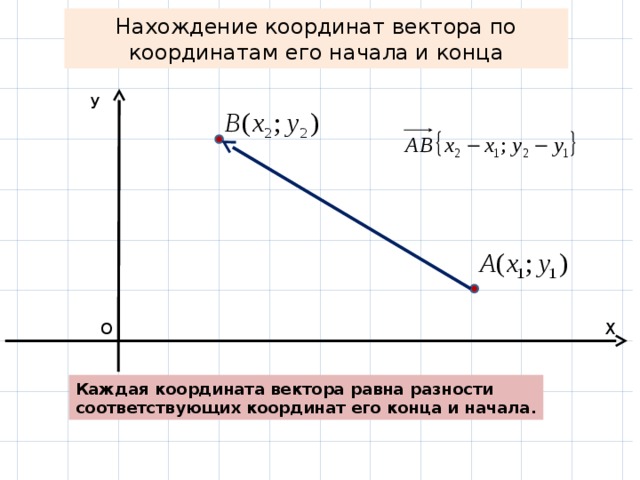 Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.