| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |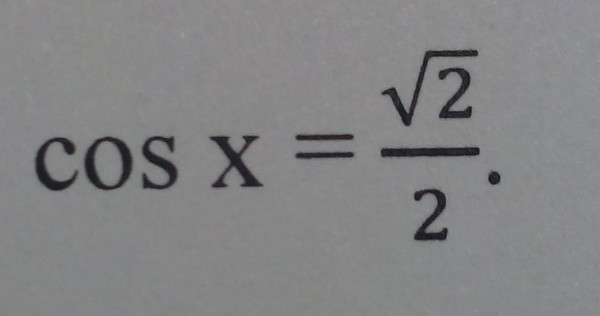
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Тест, 10 класс
Итоговый контроль по алгебре и началам анализа
Тест 10 класс
Учитель Н.П.Грызина МБОУ школа №3 ,г.Озёры.
Bариант 1.
Часть первая.
1. Упростить выражение: (2sin2x – 2cos2x)tg2x
1. –cos2x. 2. 2. 3. – 4. 4. – 2sin2x
2. Найти значение выражения: 6tg2x – 2, если cos2x = 0,5
– 2. 2. – 5. 3. 22. 4. 4.
3. Вычислите: sin550 cos350 + cos550 sin350.
1. 1. 2. 0. 3. Sin200 . 4. — 2
4. Найти множество значений функции у = 3cos28x – 2.
2. 3. 4.
5. Решить уравнение: sinx — = 0
1. +2πn, nZ. 2. (- 1)n + , nZ
3. +n, nZ. 4. ± +πn, nZ.
6. Решить неравенство: ≥0
[2;+). 2. (- ; — 4)
3. ( — 4; — ] [2; +). 4. (-;
7. Функция задана графиком на промежутке . Укажите те значения х, при которых функция отрицательна.
2. 3. (-1; 2).
4. [-4; -3) (-1; 2).
8. Найти производную функции у = 4×3– 2cosx
1. 12×2 + 2sinx. 2. 12×3 + 2sinx. 3. 7×2 – 2sinx. 4. 3×2 – 2cosx.
9. Указать чётную функцию.
1. y=sinx – x2. 2. Y=x2 + x + cosx. 3. Y=sin2x + x3. 4. Y=7×2 +cos3x.
10. Найти угловой коэффициент касательной, проведённой к графику функции у =x2 в точке с абсциссой х0= 1.
1. 1. 2. 2. 3. 3. 4. 0,5.
В 1. Найти значение выражения: tg(π+α)sin( – α)cos( +α) при α=–
В 2. Точка движется прямолинейно по закону х(t) = 2t3 – 1,5t2 + 5 (где t – время в секундах, х – расстояние в метрах). Вычислите скорость движения точки в момент времени t = 2c.
B 3. Сколько целых чисел входит в область определения функции
F(x) = ?
Часть вторая.
В 4. Функция определена на отрезке .
На рисунке изображён график её производной. Укажите количество точек минимума функции у = f(x).
B 5. Найдите наибольшую длину промежутка убывания функции
y= x3– 4×2 + 6x +3.
B 6. Определите количество корней уравнения 2sin2x – 3sinx – 2 = 0 на отрезке .
В 7. Найдите f(x0), если f(x) = (3x–5)2 + , x0= 2.
C 1. Найти множество значений функции f(x) = x+cos2x, заданной на промежутке .
С 2. Найдите все решения системы уравнений
удовлетворяющие условию (х – у) .
С 3. Найдите все значения параметра p, при которых заданное уравнение не имеет корней:
4sin3x+3cos2x+p=0.
Тест 10 класс
Вариант 2.
Часть первая.
А 1. Упростить выражение: sin22x.
1. –1. 2. 2. 3. 0. 4. 4.
A 2. Найти значение выражения: 7 – 3cos2x, если tg2x = 2.
1. 1. 2. 6. 3. 5,5. 4. 4.
A 3. Вычислить: cos 700 cos 200– sin 700sin 200 .
1. –1. 2. Sin500. 3. Cos500. 4. 0.
A 4. Найдите множество значений функции у = 6 + sin2x.
1. . 2. . 3. . 4. .
A 5. Решить уравнение: sin =.
1. (–1)n2. ±. 3. (–1)n 4. ±
A 6. Решить неравенство:
1. ( –4;2][4;+). 2. (–3. (–4. [–4;2]
A 7. Функция задана графиком на промежутке . Укажите те значения х , при которых функция положительна.
1. (–3;–1)2. (0;3]. 3.[–3;–1]. 4. (3;4).
A 8. Найти производную функции: y= 6х4 – 3
1. 10x+3cosx. 2. 24×4– 3cosx. 3. 24×3- 3cosx. 4. 4×3+3sinx.
A 9. Укажите нечётную функцию.
1. y=x7+cosx.
2. Y=x5+2sinx. 3. Y=2×3–cos2x. 4. Y=x4+sinx.
A 10. Найдите угловой коэффициент касательной, проведённой к графику функции у= 5х3–7х в точке с абсциссой х0=2.
1. 23. 2. 67. 3. 8. 4. 53.
В 1. Найдите значение выражения: tgsin(2π-α)cos(π+α), при α=.
В 2. Тело движется прямолинейно по закону x(t)=3t3 – 2t2 – t ( где t –время в секундах, х – расстояние в метрах). Вычислить скорость тела в момент t=2c.
B 3. Сколько целых чисел входит в область определения функции
F(x)=.
Часть вторая.
В 4. Функция определена на отрезке [-5;3]. На рисунке изображён график её производной. укажите количество точек максимума функции y=f(x).
В 5. Найдите наибольшую длину промежутка возрастания функции
F(x)=–.
В 6. Определите количество корней уравнения на заданном промежутке:
2cos2x–5cosx+2=0, [0;π].
B 7. Найдите f’(x0), если f(x)=.
C 1. Найдите множество значений функции f(x)= x – , заданной на промежутке .
С 2. Найдите все решения системы уравнений удовлетворяющие условию (х+у).
С 3. Найдите все значения параметра р, при которых данное уравнение имеет хотя бы один корень pctg2x+2sinx+p=3.
Тест 8 класс
Вариант 1.
Часть первая.
1. Представить число – 0,125 в виде квадрата или куба.
А. (–0,25)2. Б. (–0,5)3. В. (–0,25)3. Г. Представить нельзя.
2. Даны выражения: 1) ; 2) ; 3) Какие из этих выражений не имеют смысла при х=3?
А. только 2. Б. только 1. В. 1 и3. Г. 1 и 2.
3. Упростить выражение:
Ответ:____________
4. Чему равно значение выражения ?
А.
5. Решите уравнение: 7х2+9х+2=0.
А.
корней нет. Б. 7; –2. В. –1;. Г. ; 1.
6. Найти значение выражения:
Ответ:_______________
7. Решить неравенство: 5х+1
А. (–Б. (2;+. В. (–Г. (–2;+
8. Решить уравнение: х2+3х=0.
А. 0;3. Б. 0;–3. В. 0. Г. –3.
9. Расположить числа ,в порядке возрастания.
Ответ:________________
10. Решить систему неравенств:
Ответ:_________________
11. Какое из нижеприведённых высказываний является верным относительно уравнения:
-3х2=2–х?
А. Уравнение имеет один корень. Б. Уравнение не имеет корней.
В. имеет два корня различных знаков. Г. имеет два корня одного знака.
12. Для каждого графика укажите соответствующую ему функцию:
А) у=х2; Б) у=–1,5х2; В) у=–2х+2; Г) у=
Часть вторая.
1. (2 балла) Решите уравнение:
.
2. (4 балла) Решить систему неравенств:
3. (6 баллов) Катер проплывает 8 км против течения и ещё 30 км по течению за то же время, за которое плот может проплыть по этой реке 4 км. Скорость катера в стоячей воде равна 18 км/ч. Найдите скорость течения реки.
Тест 8 класс
Вариант 2.
Часть первая.
1. Представьте число 0,0027 в виде квадрата или куба.
А. (0,09)2. Б. 0,33. В. (0,03)2. Г. Представить нельзя.
2. Даны выражения: 1) ; 2) Какие из этих выражений не имеют смысла при х=–3.
А. Только 1. Б. 1 и 2. В. 2 и 3. Г. 1 и 3.
3. Упростить выражение:
Ответ:__________
4. Чему равно значение выражения ?
А. . Б. . В. –25. Г. 25.
5. Решить уравнение: 5х2–7х+2=0.
А. 1,6; –. Б. 1; . В. –1;–0,4. Г. Корней нет.
6. Чему равно значение выражения
Ответ___________
7. Решить неравенство: 2х+5.
А. (–Б. (–В. (–1;+Г. (4;+
8. Решить уравнение: х2– 9х=0.
А. –9. Б. 0; 9. В. 0. Г. 0;–9.
9. Расположить числа 2,5; и в порядке возрастания.
Ответ:____________
10. Решить систему неравенств:
Ответ:____________
11.
Какое из нижеприведённых высказываний является верным относительно уравнения 3х2=4–х?
А. Уравнение имеет единственный положительный корень.
Б. Уравнение имеет единственный отрицательный корень.
В. Уравнение имеет два корня различных знаков.
Г. Уравнение имеет два корня одинакового знака.
12. Для каждого графика укажите соответствующую ему функцию.
А. у=1,5х2; Б. у=; В. У=2х; Г. У=–х3;
Часть вторая.
1. (2 балла) Решите уравнение: – =.
2. (4 балла) Решите систему уравнений:
3.
(6 баллов) Мотоциклист проехал расстояние от пункта М до пункта N за 5 ч. На обратном пути он первые 36 км ехал с той же скоростью, а остальную часть пути со скоростью на 3 км/ч большей. С какой скоростью ехал мотоциклист первоначально, если на обратный путь он затратил на 15 мин меньше, чем на путь из М в N?
sinx + cosx = sqrt(2) cos2x
ПУБЛИКАЦИЯ CHHAYA-ОБЩИЕ РЕШЕНИЯ ТРИГНОМЕТРИЧЕСКИХ УРАВНЕНИЙ — Вопросы с коротким ответом
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
ки рукаават ке!
Обновлено на: 27-06-2022
Текстовое решение
Решение
Nπ-π4,2nπ+π12,2nπ-7π12
Связанные видео
∫SINX+SIN2X√COSX+COS2XDX
∫SINX+SIN2X√COSX+COS2XDX.0003
8491692
11:17
∫cos2x(sinx+cosx)2dx is equal to
53803847
01:49
∫cos2x(sinx+cosx)2dx बराबर है :
94832207
04:44
General solution of cos2x=√2(cosx−sinx) is
121601159
04:29
x के सापेक्ष समाकलन कीजिए —
cos2x(sinx+cosx)2
124631255
03:37
cosx +sinx=cos2x+sin2x
127291042
07:59
Найти интегралы функций
COS2X (COSX+SINX) 2
515792598
02:43
Найдите интегралы функций
COS2X (COSX+SINX) 2
5175666987
04:52
517566987
04:52
517566987 9000 2 9000 2 5175666987 9000.
9000 2
517566987 9000.
9000 2
517566987 9000. 9000 2
5175666987 9000. 9000 2
A=[cosxsinx−sinxcosx], покажите, что A2=[cos2xsin2x−sin2xcos2x] и A1A=1.642796754
09:48
∫COS2X (SINX+COSX) 2DX равен
642977033
02:52
∫ (COS2X (SINX+COSX) 2) DX ਬਰਾਬਰ ਹੈ ਬਰਾਬਰ ਹੈ ਬਰਾਬਰ ਹੈ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ ਬਰਾਬਰ
000306:36
∫cos2x (sinx+cosx) 2dx равен
644365336
03:18
If F (x) = Beg | {vmatrix} cos2x & cos2x & sin2x \ –cosx & cosxx & cosxx & cosxx & sinx & sinx & sinx & sinx & sinx & cosxx & cosxx & cosxx & cosxx & cosxx & sinx & sinx & sinx & cosxx & sinonx \ \ o jatrix} then
644545331
05:26
Integrate the functionscos2x(cosx+sinx)2
644861887
03:13
Find the integrals of the function: cos2x(cosx+sinx)2
644870942
03 :16
РЕКЛАМА 9(@))
05:53
COT2X = COSX + SINX
07:21
SINX + COSX = SQRT (2) COS2X
06:11
06:11
29
.
04:21
COSX + COS2X + COS3X = 0
03:16
SIN2X + SIN4X + SIN6X = 0
04:26
COSX -3x2x2x2x 2
. 18
sin theta +sin 2theta+sin3theta+sin4theta=0 92x_1`
`sinx_1=sqrt(2)`
Если вы попытаетесь вычислить `arcsinsqrt2` в своем калькуляторе, вы получите ошибку. Это потому, что его не существует. Значения, которые существуют для arcsin, находятся в диапазоне от -1 до 1, и `sqrt(2)>1`
Значение `sin((3pi)/4)` равно `sqrt(2)/2`; следовательно, это не может быть решением для `arcsinsqrt2` . Скорее, это произведение одного существующего корня `pi/4`.
Также обратите внимание на график функции, что график не пересекает ось x в точке sqrt(2), что еще раз подтверждает, что корня не существует. Скорее, все корни этой функции кратны 1 существующему корню, пи/4, поскольку это бесконечно повторяющаяся функция. 92x_2`
Поскольку вы не можете извлечь квадратный корень из отрицательного числа, x2 не существует.
См. eNotes без рекламы
Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступаУже зарегистрирован? Войдите здесь.
Утверждено редакцией eNotes
Задайте вопрос
Похожие вопросы
Просмотреть всеМатематика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
математика
Последний ответ опубликован 07 октября 2013 г.
в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 ответа учителя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г. в 14:12:01.
Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a.