Корень из 2 плюс 1: 1/корень из 2 это тоже самое что и корень из 2, деленный на 2?

Почему квадратный корень из 2 равен 1,414? — Фактические вопросы

Доска объявлений Straight Dope

Данмерри 10 января 2003 г., 10:30

1

Я знаю, что квадрат числа — это число, умноженное само на себя. Я знаю, что квадратный корень — это число, которое при умножении само на себя даст вам это число.
Я не понимаю, почему квадратный корень из 2 не равен 1.
Но 1×1=1. Квадратный корень из 2 равен 1,4142135623 с точностью до 10 знаков после запятой. Следовательно, 1,4142135623 x 1,4142135623 должно быть 2, а это 1,9.9999999979325598129
Если квадратный корень из 2 разделить на 31 знак после запятой, то получится 1,9999999999999999, а не 2.
Почему 1,4, которое при умножении само на себя равно 2,8, является квадратным корнем из 2? Почему 1,414 х 1,414 равно 1,999999?

Субсвет

10 января 2003 г. , 10:38

2

Я оставлю более полное объяснение для более крепких сердец, чем я, но для начала 1,4, умноженное само на себя, равно 1,9.6, а не 2,8

амансет 10 января 2003 г., 10:41

3

Проще говоря, вы не можете записать квадратный корень из 2 в виде десятичной дроби. Фактическое значение имеет бесконечный список чисел после запятой. Для простоты использования квадратный корень укорачивается при выполнении простых вычислений.

Что касается 31 знака после запятой, то 1,99999999999 может быть не 2, а 1,9999999999 (т.е. список из 9s никогда не кончается) может быть больше или меньше 2, но использовать части Анализа, которые я никогда не понимал, когда занимался этим в университете 10 лет назад, не говоря уже сейчас.

Десмостил 10 января 2003 г., 10:44

4

Квадратный корень из 2 равен всего приблизительно 1,4142.

1,4142 x 1,4142 = 1,99996164, то есть приблизительно равно 2.

Откуда вы взяли другие сведения о том, что квадратный корень из 2 равен 1? Или 1,4, умноженное само на себя, равно 2,8?

Дандерман 10 января 2003 г., 10:44

5

Во-первых, 1,4х1,4 — это 1,96, а не 2,8.

Во-вторых, квадратный корень из 2 не равен 1, потому что 1 умножить на 1 не равно 2. Это и есть определение квадратного корня.

В-третьих, 1,414×1,414 равно 1,999396, потому что это то, что вы получите, если умножите 1,414 на себя.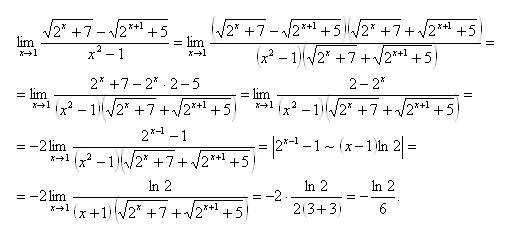

И в-четвертых, я не уверен, что понял ваш вопрос. Наверняка вы понимаете, что некоторые числа нельзя точно выразить десятичными знаками, например, пи или 1/3. Я не уверен, что квадратный корень из 2 является таким числом, но в любом случае, как вы показываете, в нем много десятичных знаков. Поскольку вы точно не выразили квадратный корень из 2, у вас есть только приближение, и квадрат этого приближения, очевидно, не будет равен 2.

Если я совсем не понял, пожалуйста, поясните. Я чувствую, что что-то упускаю.

Caught_Work 10 января 2003 г., 10:55

6

Бедный парень, вероятно, нажал + вместо x, чтобы получить от 1,4 до 2,8
Дайте ему немного передохнуть.
Мечтать, мечтать.

Манжеут 10 января 2003 г. , 11:09

7

Людей может застать врасплох тот факт, что произведение умножения числа само на себя (квадрата) меньше, чем произведение сложения числа само на себя, для чисел меньше 2; это потому, что формула сложения является линейной, а квадрат — нет.

Манжеут 10 января 2003 г., 11:17

8

Конечно, более простое объяснение состоит в том, что, добавляя число к самому себе, вы удваиваете его, а умножая меньше чем на два, вы получаете 9.0039 меньше, чем , удвоив его.

Фридо 10 января 2003 г., 12:44

9

Отличное объяснение Mangetout — это то же самое, что почему-то заставило мою учительницу математики в четвертом классе подумать, что я какой-то гений, когда объяснял ей это.

Я трижды провалил исчисление.

Дж. Р. Делириус 10 января 2003 г., 1:09вечера

10

Priceguy , вы поняли, SQRT(2) не только не может быть выражена как конечное десятичное число, но в отличие от (1/3) это также «иррациональное» число, которое не может быть выражено как отношение из двух целых чисел, A/B. Я считаю, что Пифагор разработал доказательство этого.

На занятиях по теоретической математике я обычно НЕ умножаю его при получении ответа на расчет, а оставляю его выраженным в виде Sqrt(2) (используя знак sqrt, который я не знаю, как здесь кодировать). Например:

косинус 45[sup]o[/sup] = [Sqrt(2)]/2

В практической инженерии вы просто выводите его на сколько угодно значащих цифр, чтобы то, что вы проектируете, работало и соответствовало указанные допуски, и как только вы будете удовлетворены, все будет работать правильно, вы двигаетесь дальше.

MC_Master_of_Ceremonies 10 января 2003 г., 13:16

11

Относительно 31 знака после запятой, 1,99999999999 может не быть 2, но 1,9999999999 повторяющихся (т. е. список девяток никогда не заканчивается) может быть более или менее 2, но использовать фрагменты анализа, которые я никогда не понимал, когда делал это в университете 10 лет назад, неважно сейчас.

Это простое доказательство:

1,9999…*10 = 19,9999… =>

9*1,9999… = 19,9999… — 1,9999… = 18 = 2

QED

Хари_Селдон 10 января 2003 г., 14:34

12

К сказанному выше добавить нечего, кроме как подтвердить, что sqrt(2) не является повторяющимся десятичным числом (как, скажем, 1/7 = . 142857142857…), а просто продолжается бесконечно без какой-либо очевидной закономерности. Это было обнаружено пифагорейцами по крайней мере 2500 лет назад (и их доказательство используется до сих пор), и это как бы разрушило их философию, что все можно сделать с целыми числами и их дробями. Интересно, что sqrt(2), как и все квадратные корни, может быть выражен в виде периодической цепной дроби, но я не буду пытаться иллюстрировать непрерывную дробь в этой среде. Однажды я это сделал, но форматер полностью уничтожил его, удалив все символы возврата каретки и пробелы, которые я так тщательно ввел. Другими словами, квадратный корень из 2 равен 1 плюс 1 больше (2 плюс 1 больше (1 плюс 2 больше (1 плюс 2 больше 1 (плюс…)))…), где 1 и 2, не говоря уже о скобках, идут навсегда.

Гэри_Т 10 января 2003 г., 15:43

13

Я знаю, что квадрат числа — это число, умноженное само на себя. Я знаю, что квадратный корень — это число, которое при умножении само на себя даст вам это число.
Я не понимаю, почему квадратный корень из 2 не равен 1.

Давайте начнем с того, что вы знаете, и немного подумаем. Из ваших первых двух утверждений и базовой арифметики вы знаете, что 1×1=1. Это означает, что квадрат 1 равен единице, а квадратный корень из единицы равен 1. Вы также знаете, что 2×2=4, а это значит, что квадрат 2 равен четырем, а квадратный корень из четырех равен 2.

Итак, два находится где-то в между один и четыре, поэтому вполне логично, что если квадратный корень из единицы равен 1, а квадратный корень из четырех равен 2, то квадратный корень из двух должен быть где-то между 1 и 2. Учитывая это и тот факт, что мы уже знаем, что квадратный корень из из одного равен 1, нет смысла думать, что квадратный корень из из двух может быть равен 1. Конечно, если вы на мгновение задумаетесь об этом вы поймете почему квадратный корень из двух не равен 1.

*Почему 1,4, которое при умножении само на себя равно 2,8, является квадратным корнем из 2? *

Очевидная ошибка здесь в том, что 1,4 , добавленное к (не умноженное на), само по себе равно 2,8. Это и ваше мнение о том, что квадратный корень из двух должен быть равен 1, предполагает, что вы путаете сложение и умножение. Вы, кажется, понимаете, как умножать, и я предполагаю, что вы понимаете, как складывать. Похоже, вам нужно приложить некоторые усилия, чтобы подумать о , когда нужно умножить, и о , когда добавить.

Что касается остальной части ОП, вы наверняка понимаете концепцию приближения. Квадратный корень из двух до 7 знаков после запятой равен 1,4142136, что, умноженное само на себя, равно 2,00000010642496. Всякий раз, когда вы имеете дело с приближением, вы будете немного выше или немного ниже точного значения. Разве ты этого не знал?

ультрафильтр 10 января 2003 г. , 16:07

14

* Первоначально опубликовано MC Master of Cermonies *
** Это простое доказательство:

1,9999…*10 = 19,9999… =>

9*1,9999… = 19,9999… — 1,9999… = 18

=> 1,9999… = 18/9 = 2 =>

1,9999… = 2

КЭД**

Почему-то многим это доказательство не нравится. Я видел пару тем здесь, которые занимают четыре страницы, пока люди обсуждают, является ли .9… действительно равным 1.

Uncommon_Sense 10 января 2003 г., 16:46

15

Давайте здесь ПЯТЬ страниц!!!

Уильям_Эшблесс 10 января 2003 г. , 17:02

16

Да, ультрафильтр, видимо были огромные темы о бесконечностях и пределах, которые, кажется, бушуют без конца. Задача примерно аналогична: предел

, когда k стремится к бесконечности

1 +
k
——/ 9
\ —
/ 10i
——
i=0

= 2
(простите, я недостаточно хорошо разбираюсь в умных тегах, чтобы делать это, кроме asciiart).

Или,

предел, когда k приближается к бесконечности

2 — 1/k
Сводит людей с ума. Весьма парадоксально, но необходимо для различных типов математики, не последним из которых является исчисление. Однако это захват исходного сообщения…

William_Ashbless 10 января 2003 г., 17:03

17

Драт. Этот первый asciiart должен был быть

1+ сумма (я идет от 1 до k) 9/10i

Ну ладно.

smile_bandit 10 января 2003 г., 17:06

18

Не верь калькулятору!

кальмар 10 января 2003 г., 17:59

19

* Первоначально опубликовано Caught@Work *
** Бедный парень, вероятно, нажал + вместо x, чтобы получить от 1,4 до 2,8
Дайте ему немного передохнуть.
Мечтать, мечтать. **

Дать ему передохнуть?

Я думаю, вы упомянули «Дайте ему немного передохнуть».

Запретный фруктовый салат 10 января 2003 г. , 18:29

20

* Первоначально опубликовано JRDelirious *
знак sqrt, который я не знаю как здесь закодировать

Можно сделать так: √2 (то есть √)

К сожалению, здесь такие трюки не будут надежно работать, т.к. в SDMB нет явной кодировки символов (она должна быть). Поэтому писать sqrt(2) лучше.

Исходное сообщение от ultrafilter
По какой-то причине многим людям не нравится это доказательство.

У меня нет доказательств, но я обнаружил, что многие люди найдут такое объяснение удовлетворительным:

1 = 1/3 + 1/3 + 1/3 = 0,333… + 0,333… + 0,333… = 0,999…

следующая страница →

Правило выборки «Квадратный корень из N плюс один»

98 Dr Wayne A. Taylor

Лучшее, что я могу сказать, это то, что это правило, вероятно, возникло в Министерстве сельского хозяйства США в 1920-30-х годах. Но никаких подтверждающих документов нет. На самом деле существует три версии правила:

1. Возьмите квадратный корень из размера партии, чтобы получить размер выборки. Принять при нулевых дефектах. Эта версия правил определяет используемый план выборочного контроля.
2. Возьмите квадратный корень из числа коробок, откройте это количество коробок и выберите из них необходимое количество образцов. В этом случае план выборочного контроля, включая количество проб, уже определен. Например, если размер выборки равен 20 и существует 50 коробок, необходимо открыть SQRT(50)+1=8 коробок. Выберите 3 образца из 4 коробок и 2 из оставшихся 4. Квадратный корень из n плюс один используется для получения репрезентативной выборки.
3. Возьмите квадратный корень из числа бочек, возьмите образец из этого количества бочек и скомпонуйте образцы вместе, чтобы выполнить один тест. Например, если получено 50 барабанов, возьмите образцы из SQRT(50)+1=8 барабанов, скомпонуйте их вместе и измерьте интересующую характеристику. Правило снова используется для получения репрезентативной выборки.

Большинство дискуссий, похоже, путают эти разные варианты использования. Никогда не следует использовать правило 1. Планы выборочного контроля следует выбирать на основе операционных характеристик, таких как AQL и LTPD, с использованием таблиц планов выборочного контроля, подобных приведенным в моей книге «Руководство по приемочному выборочному контролю», или одного из многих стандартов, таких как ANSI Z1.4. Операционная характеристика не зависит от размера лота, как описано в статье «Влияние размера лота». Поэтому такие планы можно выбирать независимо от размера лота. Одна ссылка, которая может представлять интерес:

Кит Борланд (1950), «Заблуждение правила выборки квадратного корня», Журнал Американской фармацевтической ассоциации, 39, № 7, стр. 373–377.

В этом справочнике описывается, почему правило квадратного корня из n плюс один не следует использовать для выбора плана выборочного контроля.

Правила 2 и 3 во многих случаях представляют собой разумный компромисс между стоимостью тестирования и точностью результатов. Однако, безусловно, есть ситуации, когда правило 2 и 3 не следует использовать. Например, дефекты печати, когда процесс может произвести 100 последовательных бракованных единиц, упакованных в одну коробку, а затем исправить себя.

Несмотря на отсутствие обоснования и документации, это правило широко используется. Например:

РУКОВОДСТВО ПО ПРОВЕРКАМ ПРОИЗВОДИТЕЛЕЙ РАЗЛИЧНЫХ ПИЩЕВЫХ ПРОДУКТОВ – ТОМ 1

«На наличие микроскопических загрязнений, излишков скорлупы и т. д. возьмите квадратный корень из количества пакетов в партии. Соберите не менее шести и не более восемнадцати пачек весом 900 граммов (2 фунта) по 340 граммов (2/3 фунта) из каждого из трех мешков. Соберите подписки в двух экземплярах для части 702(b)».

«Для контейнеров розничного размера возьмите квадратный корень из количества контейнеров в партии, взяв не менее шести и не более 18–900 г (2 фунта) подложек».