Направление вектора это: направление вектора | Перевод направление вектора?

НОУ ИНТУИТ | Лекция | Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства

< Лекция 10 || Лекция 7: 123

Аннотация: В лекции рассматриваются линейные операции над векторами, и дается практическое использование этих операций при решении различных задач

Ключевые слова: операции, вектор, длина, модуль, компланарность, коллинеарность, Произведение, базисными векторами, ПО, Главная диагональ, произведение вектора, равенство, векторное произведение, антисимметричность, координаты, разность, направляющие косинусы, аргумент, площадь

Умножение

Различают несколько видов операции умножения.

1. Умножение вектора на скалярную величину. При умножении вектора на скаляр получают новый вектор , длина (модуль) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если , или противоположно исходному вектору, если . В координатной форме, если a = (a_x;a_y;a_z), то b = a= . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.

Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е.

1Модуль вектора можно обозначать |\overrightarrow{b}| или просто b. Из последнего равенства следует, что . Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности: , а также свойством дистрибутивности: .

2. Скалярное произведение векторов.

Определение 14. Скалярным произведением двух векторов и называется число S, равное . Эта операция обозначается или

В частности, скалярный квадрат вектора равен квадрату его длины, т.е.

Если один из перемножаемых векторов единичный, то:

В этом случае результат представляет собой проекцию вектора на направление единичного вектора . Следовательно, любой вектор можно представить как , где a

x,a_y,a_z — проекции вектора соответственно на оси 0х, 0у и 0z.

Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора на эти оси. Из этого же рисунка следует, что модуль вектора численно будет равен .

Рис. 6.1.

Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:

где , и есть скалярное произведение вектора с ортами осей координат. Тогда из последнего равенства имеем

где , и — углы, которые составляет вектор соответственно с осями 0х, 0у и 0z.

Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е. и . Можно убедиться самостоятельно в том, что всегда выполняется равенство

Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда

intuit.ru/2010/edi»>

Замечание 2. , где — единичные векторы (орты) осей координат ^{2При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).}

Замечание 3. .

Замечание 4. Скалярное произведение векторов в координатной форме

Замечание 5. Используя формулу скалярного произведения векторов и , можно найти выражение косинуса угла между этими векторами через их проекции на орты:

Если , то это значит, что угол между векторами больше 90 , т.е. тупой, а если , то угол острый.

Замечание 6. Механический смысл скалярного произведения векторов.

Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.

Дальше >>

< Лекция 10 || Лекция 7: 123

Урок 2. Координаты вектора | Уроки математики и физики для школьников и родителей

Для введения понятия координат вектора следует рассмотреть возможность разложения вектора по осям координат. Каждый вектор задаётся парой чисел – проекциями этого вектора на оси координат. При таком подходе действия над векторами можно свести к действиям с парами чисел.

Определим проекцию вектора на координатную ось. Пусть задана координатная ось  Ох. Единичный отрезок 

ОЕ  будем считать единичным вектором

то есть вектором, длина которого равна  1.

Возьмём любой вектор

и отложим его от некоторой точки  А:

Спроектируем точки  А  и  В  на ось  Ох. Получим точки  А₁, В₁  и составляющую  А₁В₁  вектора

по оси  Ох.

Её длину со знаком <<плюс>> или <<минус>> и называют проекцией вектора

на ось  Ох.

Проекцией  а_х  вектора

на ось  Ох  называют длину его составляющей

по этой оси, взятую со знаком <<плюс>> или <<минус>>.

При этом берётся знак <<плюс>>, если направление вектора

совпадает с направлением оси  Ох, и знак  <<минус>>, если эти направления противоположны.
Если

то есть  А₁ = В₁, то  а_х = 0.

Прежде чем ввести понятие координат вектора, рассмотрим следующий пример.

ПРИМЕР:

Пусть на плоскости введена прямоугольная система координат с единичными векторамикоординатных осей  Ох  и  Оу.
Пусть – некоторый вектор, а  а_х  и  а_у – его проекции на оси координат. Тогда вектор

единственным образом представляется в видеПолученная формула применяется для разложения вектора

по векторам

Пару чисел  а_х  и  а_у  называют координатами вектора

в данной системе координат.
Любой вектор является свободным, поэтому при необходимости можно отложить его от какой-нибудь другой точки плоско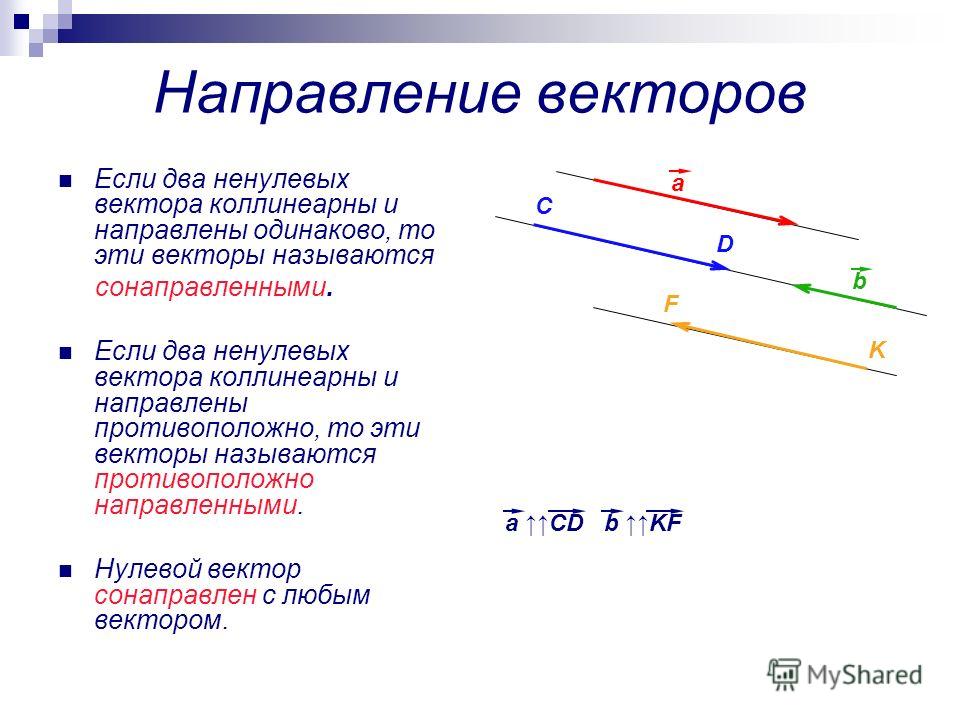сти. Для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости

ПРИМЕР:

Разложить векторпо базисным векторамРЕШЕНИЕ:

Составим векторное уравнение:

которое можно записать в виде системы линейных уравненийИз первого уравнения выражаем  х.

Подставим  х  во второе уравнение.ОТВЕТ:Записи координат точек и координат вектора вроде бы схожи:

                                   А(2; 1), В(–2; 3),

а смысл координат абсолютно разный, и надо хорошо понимать эту разницу.
Вектор

получается из коллинеарного ему единичного вектора

умножением на

При этом, если

сонаправлен с

Если же

противоположно направлен

Следовательно, имеет место равенство

Проекция точки – точка, проекция отрезка – отрезок (или точка), а проекция вектора – число.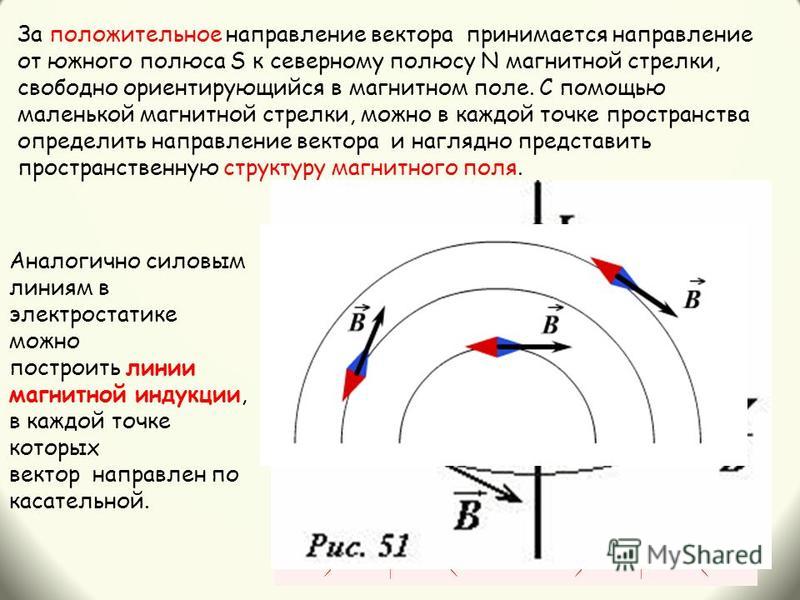

Обязательно нужно понимать различие между координатами точек и координатами векторов.

Координаты точек – это обычные координаты в прямоугольной системе координат. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.

Координаты вектора – это его разложение по базису

Координаты вектора – это коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Рассмотрим рисунок.

 Если точка  А  не лежит на координатных осях, то треугольник  ОАА₁  прямоугольный.
Тогда

по теореме Пифагора.
Так как  А₁А = ОА₂, то получим, что

Но

поэтому

то есть

Формула справедлива и в тех случаях, когда точка  А  лежит на какой-то оси координат.

Координаты равных векторов соответственно равны.

Векторы, имеющие соответственно равные координаты, равны.

Координаты вектора связаны с координатами точки по следующему правилу:

Чтобы найти координаты вектора, нужно от координат конца вектора отнять координаты начала вектора.

В частности, если вектор отложен от начала координат, то координаты вектора равны координатам его конца.

Проекция вектора на заданное направление.

Пусть заданы два вектора

Приведём эти векторы к одному началу  О.

Угол, образованный лучами, исходящими из точки  О  и направленными вдоль векторов

называют углом между векторами

Обозначим это угол через  α.
Число

a_b = a cos α

называется проекцией вектора

на направление вектора

Проекция вектора

получается, если из его конца опустить перпендикуляр на направление вектора

Тогда расстояние от общего начала векторов – точки  О – до точки пересечения указанного перпендикуляра с прямой, на которой лежит вектор

будет равно модулю проекции вектора

на направление вектора

Угол  α  может принимать различные значения, поэтому в зависимости от знака  cos α  проекция может принимать положительные, отрицательные значения или нуль.
Проекция равна нулю, если направления векторов

взаимно перпендикулярны. Проекции равных векторов равны. Проекции противоположных векторов отличаются знаком.

На координатной плоскости будем откладывать векторы от начала координат:

Каждому вектору будет отвечать полностью определенная точка  А, каждой точке  А  плоскости – полностью определенный вектор

Точку  А  называть будем концом вектора

Координатами вектора называют координаты его конца,

которые обозначим

Координаты нулевого вектора

равны

Если вектор

ненулевой, то он имеет определённое направление. Направление вектора

– это не что иное, как направление, заданное лучом  ОА. Этот луч можно получить из луча  Ох (положительного луча оси абсцисс) в результате поворота  R^α.

Если ограничить угол  α  условием

–180⁰ < α ≤ 180⁰,

то угол  α  определяется вектором

однозначно. Говорят, что вектор

образует угол  α  с положительным направлением оси абсцисс. Ненулевой вектор полностью определяется заданием его длины

и углом  α, который образует вектор с положительным направлением оси абсцисс. Вектор единичной длины называется единичным вектором. Конец единичного вектора лежит на единичном кругу. Поэтому единичный вектор, который образует угол  α  с осью абсцисс, записывают в виде

Его координаты равны

Возьмём единичный вектор

того же самого направления, что и вектор

Отношение

будут равными между собою при произвольном угле  α.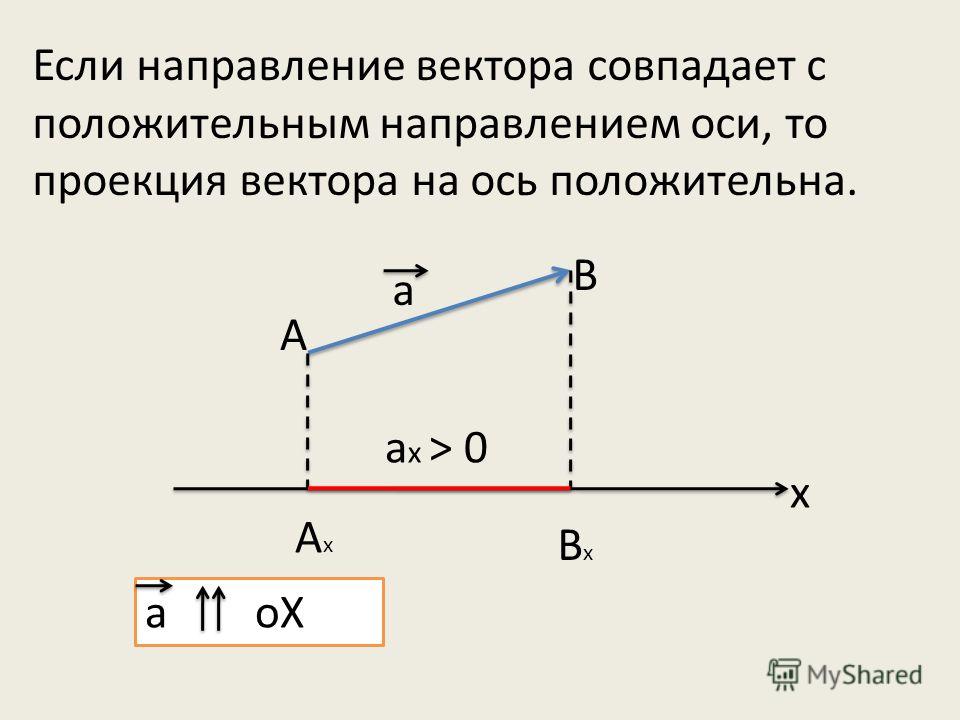 Равенство абсолютных величин этих отношений выплывает из подобия треугольника  OAN  и  OEM.

Знаки ординат

одинаковые. Но

Поэтому

откуда

Аналогично получим:

Равенство абсолютных величин этих отношений выплывает из подобия треугольников  OAN  и  OEM.

Знаки абсцисс

одинаковые. Поэтому,

Откуда

Таким образом, вектор

который образует угол  α  с положительным направлением оси абсцисс, имеет координаты

Координаты вектора на плоскости.

Координаты вектора

который имеет начало в точке  А и  конец в точке  В, равняются разности соответствующих координат точек  В  и  А. Если началом вектора является точка  А(х_А; у_А), а концом – точка  В(х_В; у_В), то

Записывают вектор

указывая его координаты так:

Например:

ПРИМЕР: 

Найдите вектор

если  А(4; 1), В(2; –5).

РЕШЕНИЕ:

то есть

Длина вектора на плоскости

Если есть вектор

ПРИМЕР:

Найдите модуль вектораРЕШЕНИЕ:
ПРИМЕР:

Модуль вектора

ПРИМЕР:

Найти длину векторов, если одна клетка имеет площадь  1 см².

РЕШЕНИЕ:

Так как клетка имеет площадь  1 см², то очевидно что

Длину вектора

найдём с помощью теоремы Пифагора. Получим:

ОТВЕТ:

ПРИМЕР: 

Найдите модуль вектора

РЕШЕНИЕ:

ПРИМЕР:

Модуль вектора

равен  10. Найдите  х.

РЕШЕНИЕ:

По условию

Равенство векторов на плоскости.

Равные векторы имеют равные координаты. Если координаты векторов равны, то векторы равны.

Если

Если

Равные векторы имеют соответственно равные координаты. И наоборот: если у векторов соответствующие координаты равны, то векторы равны.

ПРИМЕР:

Даны точки 

А(–2; 3), B(4; –1), C(x; –2), D(0; y).

Найдите  х  и  у. Если

РЕШЕНИЕ:

то есть  АВ = (6; –4).

то есть  CD = (–x; y + 2). Поскольку

то  –х = 6  і  у + 2 = –4.
Откуда  х = –6; у = –6.

Определение коллинеарности векторов с помощью координат вектора.

Если векторы коллинеарные, то их соответствующие координаты пропорциональные. И наоборот, если соответствующие координаты двух векторов пропорциональны, то эти векторы коллинеарные.

Если есть векторы

и они коллинеарные, то

Если есть векторы

– коллинеарные векторы.

Противоположные векторы имеют противоположные соответствующие координаты.

Если соответствующие координаты двух векторов противоположны, то векторы противоположны.

Если имеем

Если имеем

ПРИМЕР:

Какие из векторовколлинеарны ?

РЕШЕНИЕ:

Так как вектора не содержат компоненты равные нулю, то воспользуемся условием коллинеарности следующего вида:

Вектораколлинеарны, так какВекторане коллинеарны, так какВекторане коллинеарны, так как

Сравнение двух векторов

Математика и наука были изобретены людьми для описания и понимать окружающий мир. Заметим, что существуют некоторые величины и процессы в наш мир, которые зависят от направления , в котором они происходят, и есть некоторые величины, которые не зависят по направлению. Математики и ученые называют количество который зависит от направления a количество векторов . Количество которая не зависит от направления, называется скалярной величиной . А векторное количество имеет две характеристики: величина и направление . При сравнении две векторные величины одного и того же типа, вы должны сравнить обе величина и направление. На этом слайде мы показываем три примера, в которых два вектора в сравнении. Векторы обычно обозначаются на рисунках стрелкой. Длина стрелки указывает величину и кончик стрелки указывает направление. Вектор помечены буквой в алфавитном порядке буква с линией сверху, чтобы отличить ее от скаляра. Наши шрифты для веб-печати не поддерживают эту запись, поэтому мы будем использовать жирная буква для вектора. Мы будем сравнивать два вектора, и и б . Это могут быть силы, скорости или ускорения; это действительно не имеет значения. Пример №1: у нас есть два вектора с одинаковым направлением, но величины (или длины векторов) различны. Вектор и не равен вектору b в этом примере. Этот пример кажется довольно просто, потому что то же правило применимо и к скалярам; если величина разная, количества не равны. Объект весом 50 фунтов не равен объекту весом 25 фунтов. Пример №2: Этот пример немного сложнее. В этом случае у нас есть два вектора с одинаковые по величине, но направления разные. Вектор и не равен вектору b в этом примере. Если бы вектор был скорости, это говорит нам о том, что автомобиль, движущийся со скоростью 45 миль в час на северо-восток окажется в другом месте, чем другая машина, также движущаяся со скоростью 45 миль в час строго на восток. За один час они оба пройдут 45 миль, но места будет другим. Через два часа они будут еще дальше друг от друга. Пример №3: В этом примере у нас есть два вектора одинаковой длины. и одинаковое направление. Вектор равен вектору b . Чтобы два вектора были равны, они должны иметь как модуль, так и направления равны. Экскурсии с гидом Векторов: Деятельность: Похожие сайты: Rocket Index Rocket Home Руководство для начинающих Home

от горизонтальных/вертикальных составляющих до направления/величины

Пусть $\,\vec v\,$ — вектор с известным аналитическая форма $\,\langle a\,\,b\rangle\,$:

Как можно использовать эту информацию для определения направления и величины вектора $\,\vec v\,$? 92} = 0\,$.
только способ, которым это может произойти, для и $\,a\,$ и $\,b\,$ равны нулю.
Таким образом, $\,\vec v = \langle 0\,\,0\rangle\,$.
Если вектор имеет нулевую величину, то он должен быть нулевым вектором.

Соединяем оба направления: $\|\vec v\| = 0\,$ если и только если $\,\vec v = \langle 0\,\,0\rangle\,$

Получение (стандарт) направления от горизонтальных и вертикальных компонентов

направление вектора можно описать по-разному. Например, пеленги часто используются в навигации. Условные обозначения углов, используемые для определения тригонометрических функций дают особенно удобный способ определить направление вектора. Для удобства читателя эта схема повторяется ниже: Условные обозначения углов «стандартного направления» Поместите хвост вектора в начале прямоугольной системы координат. Укажите направление вектора, используя отложенный угол $\,\theta\,$ следующее: начало с положительной оси $x$ положительных углов выметаются против часовой стрелки (начните с движения вверх) отрицательные углы сметаются по часовой стрелке (начните с движения вниз) Когда необходимо подчеркнуть, что используется эта схема направления, это будет называться стандартным направлением . Стандартное направление 9\circ\,$ оба описывают вектор, указывающий одинаково. В дальнейшем символ $\,\theta\,$ (theta) всегда относится к стандартному направлению , а используются простые значения $\,\theta\,$.

стандартное направление: положительный угол $\,\theta$ стандартное направление: отрицательный угол $\,\theta$

Стандартное направление для векторов, указывающих вверх/вниз/влево/вправо

Когда хотя бы одна компонента (горизонтальная или вертикальная) вектора равна нулю,
тогда не требуется никакой формулы, чтобы найти стандартное направление.
Вот таблица, в которой суммированы результаты для $\,\vec v = \langle a\,\, b\rangle\,$:

9\циркуляр\,$ 9\циркуляр\,$

горизонтальные/вертикальные компоненты	представление стрелки	стандартное направление, $\,\theta$
нулевой вектор: $\,a = 0\,$ и $\,b = 0\,$	(без стрелки)	нулевой вектор не имеет направления; направление $\,\langle 0,0\rangle\,$ не определено
$\,\vec v = \langle a\,\,0\rangle\,$ с $\,a > 0\,$ 9\циркуляр\,$
$\,\vec v = \langle 0\,\,b\rangle\,$ с $\,b > 0\,$	вектор указывает вверх
$\,\vec v = \langle 0\,\,b\rangle\,$ с $\,b	вектор указывает вниз

Формула стандартного направления векторов в квадрантах I и IV

Для произвольного вектора функция арктангенса дает удобные формулы для стандартное направление . Однако в разных квадрантах нужны разные формулы. 9\circ)\,$, тангенс которого равен $\,x\,$ Это «степенная версия» определения. Воспоминание: если ваш калькулятор находится в режиме градусов, $\,\arctan x\,$ будет в градусах если ваш калькулятор работает в радианном режиме, $\,\arctan x\,$ будет в радианах Для формул в этом разделе предполагается, что $\,\arctan x\,$ выражается в градусах. В квадранте I, где $\,a > 0\,$ и $\,b > 0\,$, все просто: $$ \начать{собирать} \cssId{s83}{\tan\theta = \frac ba}\cr \cssId{s84}{\theta = \arctan\bigl(\frac ba\bigr)} \конец{собрать} $$ Когда $\,\frac ba\,$ положительно, $\,\arctan(\frac ba)\,$ возвращает угол между $\,0^\circ\,$ и $\,9\circ + \arctan(\frac ba) \,$.

Формула для (стандартного) направления вектора $\,\vec v = \langle a\,\,b\rangle\,$ зависит от знаков $\,a\,$ и $\,b\,$, как указано ниже: КВАДРАНТ II КВАДРАНТ I КВАДРАНТ III КВАДРАТ IV

В итоге:

В квадранте I: $\,\theta = \arctan(\frac ba)\,$
(Эта формула всегда дает угол между $\,0^\circ\,$ и $\,9\цирк\,$.

В квадранте II это различных углов :

• (желаемый, положительный) угол направления:   $\,\theta\,$
• (нежелательный, отрицательный) угол:   $\,\arctan(\frac ba)\,$

Обратите внимание, что оба этих углов имеют значение тангенса, равное $\,\frac ba\,$. 9\цирк\,$.

В квадранте III это различных углов :

• (желаемый) угол направления:   $\,\theta\,$
• (нежелательный) угол:   $\,\arctan(\frac ba)\,$

Обратите внимание, что оба этих углов имеют значение тангенса, равное $\,\frac ba\,$.

No related posts.