324 — триста двадцать четыре. натуральное четное число. регулярное число (число хемминга). в ряду натуральных чисел находится между числами 323 и 325. Все о числе триста двадцать четыре.
- Главная
- О числе 324
324 — триста двадцать четыре. Натуральное четное число. Регулярное число (Число Хемминга). В ряду натуральных чисел находится между числами 323 и 325.
Like если 324 твое любимое число!
Изображения числа 324
Склонение числа «324» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 324 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | триста двадцать четыре |
| Родительный | Нет | Кого? Чего? | трёхсот двадцати четырёх |
| Дательный | Дать | Кому? Чему? | трёмстам двадцати четырём |
| Винительный | Видеть | Кого? Что? | триста двадцать четыре |
| Творительный | Доволен | Кем? Чем? | тремястами двадцатью четырьмя |
| Предложный | Думать | О ком? О чём? | трёхстах двадцати четырёх |
Перевод «триста двадцать четыре» на другие языки
- Азербайджанский
- üç yüz iyirmi dörd
- Албанский
- 324
- Английский
- three hundred twenty-four
- Арабский
- 324
- Армянский
- երեք հարյուր քսանչորս
- Белорусский
- 324
- Болгарский
- триста двадесет и четири
- Вьетнамский
- 324
- Голландский
- 324
- Греческий
- τριακόσιες είκοσι τέσσερις
- Грузинский
- სამას ოცდაოთხი
- Иврит
- 324
- Идиш
- 324
- Ирландский
- 324
- Исландский
- 324
- Испанский
- trescientos veinticuatro
- Итальянский
- 324
- Китайский
- 324
- Корейский
- 삼백스물네
- Латынь
- trecenti viginti quatuor:
- Латышский
- 324
- Литовский
- 324
- Монгольский
- гурван зуун хорин дөрвөн
- Немецкий
- 324
- Норвежский
- 324
- Персидский
- 324
- Польский
- trzysta dwadzieścia cztery
- Португальский
- 324
- Румынский
- 324
- Сербский
- три стотине двадесет четири
- Словацкий
- 324
- Словенский
- 324
- Тайский
- 324
- Турецкий
- 324
- Украинский
- триста двадцять чотири
- Финский
- kolmesataakaksikymmentäneljä
- Французский
- 324
- Хорватский
- 324
- Чешский
- 324
- Шведский
- 324
- Эсперанто
- tricent dudek kvar
- Эстонский
- 324
- Японский
- 三百二十から四
Перевод «324» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- CCCXXIV
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ٣٢٤
- Восточно-арабскими цифрами
- ۳۲۴
- Деванагари
- ३२४
- Бенгальскими цифрами
- ৩২৪
- Гурмукхи
- ੩੨੪
- Гуджарати
- ૩૨૪
- Ория
- ୩୨୪
- Тамильскими цифрами
- ௩௨௪
- Телугу
- ౩౨౪
- Каннада
- ೩೨೪
- Малаялам
- ൩൨൪
- Тайскими цифрами
- ๓๒๔
- Лаосскими цифрами
- ໓໒໔
- Тибетскими цифрами
- ༣༢༤
- Бирманскими цифрами
- ၃၂၄
- Кхемерскими цифрами
- ៣២៤
- Монгольскими цифрами
- ᠓᠒᠔
В других системах счисления
- 324 в двоичной системе
- 101000100
- 324 в троичной системе
- 110000
- 324 в восьмеричной системе
- 504
- 324 в десятичной системе
- 324
- 324 в двенадцатеричной системе
- 230
- 324 в тринадцатеричной системе
- 1BC
- 324 в шестнадцатеричной системе
- 144
QR-код, MD5, SHA-1 числа 324
Адрес для вставки QR-кода числа 324, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/324/3a4acbc3dc4158708d5ba496189f70ca.png
- MD2 от 324
- 4b9ab0647ab54bdfbd57f01a928b3c57
- MD4 от 324
- 477529b0f3a5ac0b9d08d53be5d05f7d
- MD5 от 324
- f2fc990265c712c49d51a18a32b39f0c
- SHA1 от 324
- 914127d1002e9938e2e1ee54cd92fd8195a248b0
- SHA256 от 324
- 1038e0b72d98745fac0fb015fd9c56704862adf11392936242a2ff5a65629f50
- SHA384 от 324
- 0b2c831959f171713ec627518c71a8a68887b695c26c9019329215b6c1bb541d42f85e4c3b7b4cc29c940eb02bbede8c
- SHA512 от 324
- 3af08aa730ce419e37e88a96a675c1882dcb94c8618979b43745c899bb8a877755c583df647af2064a10978b964b65dff50e9db75ea84d0d080bac6db7a32e46
- GOST от 324
- 7bdd67f517e62c3706b781817b48f3ec2159371ac30b86cabb30c95eae20e887
- Base64 от 324
- MzI0
324й день в году
324й день в не високосном году — 20 ноября
Всеобщий день детей
324й день в високосном году — 19 ноября
День ракетных войск и артиллерии
День ракетных войск и артиллерии:
День работника стекольной промышленности
Математические свойства числа 324
- Простые множители
- 2 * 2 * 3 * 3 * 3 * 3
- Делители
- 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324
- Количество делителей
- 15
- Сумма делителей
- 847
- Простое число
- Нет
- Предыдущее простое
- 317
- Следующее простое
- 331
- 324е простое число
- 2143
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Нет
- Регулярное число (Число Хемминга)
- Да
- Совершенное число
- Нет
- Полигональное число
- квадрат(18)
- Квадрат
- 104976
- Квадратный корень
- 18
- Натуральный логарифм (ln)
- 5.
 7807435157923
7807435157923 - Десятичный логарифм (lg)
- 2.5105450102066
- Синус (sin)
- -0.40406521945636
- Косинус (cos)
- -0.91473017793538
- Тангенс (tg)
- 0.4417315938656
Комментарии о числе 324
← 323
325 →
- Изображения числа 324
- Склонение числа «324» по падежам
- Перевод «триста двадцать четыре» на другие языки
- Перевод «324» на другие языки и системы
- QR-код, MD5, SHA-1 числа 324
- 324й день в году
- Математические свойства числа 324
- Комментарии о числе 324
324 — перевод на французский | русский-французский
Translate.vc EnglishespañolFrançaisPortuguêsрусскийTürkçe
Английские фразы | Русские фразы | Турецкие фразы
английскийиспанскийфранцузскийпортугальскийрусскийтурецкийанглийскийиспанскийфранцузскийпортугальскийрусскийтурецкийTranslate. vc / русский → французский / [ 3 ] / 324
vc / русский → французский / [ 3 ] / 324
52 параллельный перевод
324, Вормзер!
Wormser 324!
Потсдам 324!
Potsdam 324!
324!
324!
Сердцебиение Сарека поднялось до 324.
Rythme cardiaque de Sarek : 324.
Думал, что получу «5» за прилежность Сегодня мы полетим на 324 м.
J’espère avoir 20 / 20 pour ma peine. Non, on prend le 324 ce soir.
Ты жалок, Кассавиус. Умирающий человек, живущий снами. 254 00 : 31 : 09,333 — — 00 : 31 : 11,324 Ты слеп, дурак.
Vous êtes pathétique, un mourant qui vit en plein délire.
— Вижу прояснение, Кларенс. — Понял, Роджерс.
Vol 209, itinéraire 324 dégagé.
[Skipped item nr. 324]
Désolé d’avoir utilisé ta robe de mariée pour lustrer la voiture.
Поезжайте по 324-му, потом по 666-му, там 65 миль. Быстро доедете.
Suivez la 324 jusqu’à la 66… et Farmington n’est plus qu’à 100 km.
Я не знаю, как ты пьёшь это чёрное говно, Ник. 77 00 : 06 : 20,444 — — 00 : 06 : 23,324 Мне надо добавить молока. Это единственный способ перебить вкус.
Это единственный способ перебить вкус.
Tu le bois noir?
Получается… три сотни и двадцать четыре.
Ce qui fait… 324.
Вы зарезервировали для меня номер 384?
Je suis Bui Kim Ngân. Je voudrais savoir si l’hôtel m’a réservé la chambre 324?
Мне нужно в кабинет 324 на четвёртом этаже.
Je dois aller à la chambre 324 au 3ème étage.
Тут ошибка — ошибка оффлайн 324. Так что я вытащу бумагу.
Il y a une erreur… erreur 324, je crois… alors je vais sortir le papier.
Нет, нет, орентируйся на 5 Сайлонских рейдеров по курсу 324-отметка-110
Non, cinq raiders cylons 324-point-110.
201, 851.
324,778.
201, 851 мили в час.
324,778 km / h.
Это новый рекорд! 201, 851 мили в час!
324,778 km / h!
На борту 324 человека, включая персонал.
324 personnes à bord, y compris l’équipage.
Учитывая малую вероятность успеха спасательной операции, власти официально объявили всех 324 пассажиров погибшими.
L’avion a été retrouvé, mais une mission de sauvetage est peu probable. Au regard des autorités, les 324 passagers sont déclarés morts.
Он был найден в обломках самолета вместе с останками всех 324 пассажиров.
C’était avec l’épave de l’avion, ainsi que les 324 passagers décédés.
Обманом заставить 324 семьи оплакивать своих родных?
Faire endurer le deuil à 324 familles avec un mensonge?
Где они смогли взять 324 трупа?
comment se procure-t-on 324 cadavres?
Свидетельства тому, что же на самом деле случилось с этим злополучным лайнером, может так и остаться погребенной вместе с останками его 324 пассажиров.
La vérité sur ce qui est arrivé à cet avion de ligne a peut-être disparu, tout comme les 324 passagers qu’il transportait.
— Это Сан-Хуан, сектор 324. Приём, остров Харпера.
Ici San Juan secteur 324, continuez Harper’s Island.
Это Сан-Хуан, сектор 324. Вы там, Крис?
Ici San Juan secteur 324, vous êtes là Chris?
— Это Сан-Хуан, сектор 324. Приём.
Приём.
— Ici San Juan secteur 324, terminé.
Остров Харпера, это Сан-Хуан, сектор 324.
Harper’s Island, ici San Juan secteur 324.
Квадратный корень из 2 396 324?
Quelle est la racine carrée de 2396324?
– 324 души.
— Trois cent vingt-quatre âmes.
Деннис сказал, что он следующий.
324, North Oakhurst à Hallendale.
324 Норт Окхаст в Галандейл.
Allez-y avant 17 h.
» олько 324 миллиграмма аспирина, которые € дал ему 1 5 минут назад.
Seulement les 324 milligrammes d’Aspirine que je lui ai donnés tout à l’heure.
У Деймона — 3,24.
Celle de Damon était de 0,324.
Я поцеловал каждую девушку в этой школе, и заработал 324 доллара для Хора.
J’ai embrassé chaque fille de ce lycée, et obtenu 324 dollars pour le Glee Club.
Касл третий сезон финальная серия Нокаут
Mystery Writers 324 Knockout
Поехали!
822 00 : 33 : 15,324 — — 00 : 33 : 16,424 — Est-ce que…
324-Би-21.
C’est 324b21.
324-Би-21?
324b21.
Значит, я — 324-Би-21.
Je suis 324b21.
324-Би-21.
324b21
Квартира 324.
Appartement 324.
На юге Швеции расположено 324 ветряка.
Il y a 324 éoliennes dans le sud de la Suède.
Мы на 324 мегаджоулях и становимся сильнее… опасная территория, сэр.
On est a 324 mégajoules et ça augmente. territoire dangereux, Monsieur.
Мацусима Рэйдзи свернул историю в узел.
324 ) } Celui qui a changé l’histoire est Mastsushima Reiji.
И вот, 324 жизни спасены.
324 vies sauvées.
В посольстве 342 сотрудника.
L’ambassade a 324 employés.
152 998 324 долларов, которые вы потратили в прошлом году, этого не покроют.
Les 152,998,324 dollars que vous avez dépensé l’année passée, ça ne sera juste pas assez.
Хорошо, 324… Гайст. Гайст.
Okay, 324… 322.
Она находится в Саут Луп. восьмая улица, 324.
C’est au 324, 8e rue. C’est dans le South Loop.
368 ) } Nikiola 324 ) } Перевод песен : 368 ) } Lonely _ Enot 368 ) } Nikiola 368 ) } Ksilnew и пытался отнять трон у Его Величества!
Voici la personne qui a enlevé le Prince Gyeong Chang, et prévu de commettre un complot contre Sa Majesté!
- перевод на «324» турецкий
Арифметический квадратный корень | План-конспект урока по алгебре:
05. 12.2019 алгебра, 8 класс
12.2019 алгебра, 8 класс
Учитель: Абайханова К. М.
Тема урока: Арифметический квадратный корень
Цели урока:
- Образовательные:
- обеспечить усвоение учащимися определения квадратного корня и арифметического квадратного корня;
- отработать навыки извлечения арифметического квадратного корня из положительного числа;
- добиться усвоения учащимися понятия «область определения арифметического квадратного корня».
- Воспитательные:
- Воспитание мотивов учения, положительного отношения к получению знаний;
- Воспитание дисциплинированности, внимания, как качеств, помогающих успешному усвоению материала;
- Развивающие:
- Развивать умение выделять существенные признаки и свойства понятия;
- развитие умение делать обобщающие выводы;
- развитие умений применять знания на практике.
Тип урока:
Урок изучения нового учебного материала
Методы ведения урока:
- Диалогический метод
- Исследовательский метод
План урока:
- Организационный момент.
 Объявление темы урока и целей урока.
Объявление темы урока и целей урока. - Устная работа. Актуализация прежних знаний.
- Объяснение нового материала. Формирование новых понятий и способов действия.
- Формирование умений и навыков.
- Домашнее задание.
- Итоги урока.
Ход урока.
- Организационный момент. Объявление темы урока и целей урока.
Девиз нашего урока будут слова: «Зри в корень».
Сообщение темы и целей урока.
- Устная работа. Актуализация прежних знаний.
Выполнение заданий на вычисление квадрата числа.
Вычислите:
72; 0,52; 1,62; (-17)2; 202.
- Объяснение нового материала. Формирование новых понятий и способов действия.
- Введение понятия квадратного корня.
Создание проблемной ситуации: Мы знаем, как вычисляется площадь квадрата по стороне квадрата. Рассмотрим обратную задачу: нахождение стороны квадрата по его площади:
Пусть площадь квадрата равна 64 см2. Чему равна длина стороны этого квадрата?
Чему равна длина стороны этого квадрата?
Учащиеся делают попытку определить значение стороны квадрата известными им действиями с числом 64, однако проверка возведением в квадрат показывает, что ответы неправильные. Делаем вывод, что ответ находится подбором такого значения стороны квадрата, которое при умножении на само себя даст 64.
Обозначим длину стороны квадрата (в сантиметрах) буквой х. Тогда площадь квадрата будет X2 см2. По условию площадь равна 64 см², значит х²=64.
Корнями уравнения х²=64 являются числа: 8 и — 8. Действительно, 8²=64 и (-8)²=64. Так как длина не может выражаться отрицательным числом, то условию задачи удовлетворяет только один из корней — число 8. Итак, длина стороны квадрата равна 8 см.
Корни уравнения х²=64, т.е. Числа, квадраты которых равны 64, называют квадратными корнями из числа 64.
Учитель знакомит с новым знаком – знаком квадратного корня.(√ ).
Задание. Вместо X поставьте числа так, чтобы равенства были верными:
X²=16 X ²=0,25 X ²=100
Решение записать с помощью знака √.
Далее работа с определением (по учебнику).
Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.
Задание: выяснить, является ли число n квадратным корнем из числа m, если:
а) n=5, m=25; в) n=0,3, m=0,9;
б) n= — 7, m=49; г) n=6, m= — 36.
2. Введение понятия арифметического квадратного корня.
Изложение данного материала учитель ведет в форме сообщающей беседы. Учащиеся должны усвоить существенный признак данного понятия — арифметический квадратный корень является неотрицательным числом (то есть необходимо знание того, что равенство √a=b означает одновременно выполнение двух условий: b²=a и b≥0).
Число 8 — неотрицательный корень уравнения х²=64 — называют арифметическим квадратным корнем из 64. Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.
Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а.
√a = b, a≥0, b2=a
Задание: определить, является ли число n арифметическим квадратным корнем из числа m, если:
а) n=8, m=64; в) n=0,2, m=0,4;
б) n= — 3, m=9; г) n=0,4, m=0,16.
- Историческая справка.
Обратим внимание на совпадение в терминах — квадратный корень и корень уравнения. Это совпадение неслучайно. Уравнения вида х²=а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.
Название «радикал» тоже связано с термином «корень»: по-латыни «корень» — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r.
- Основное свойство арифметического квадратного корня.
Учитель ставит проблему: вычислить значения следующих выражений:
(√4)2; (√16)2; (√0,81)2;
Формулируется вывод:
(√a)2=a; , если а≥0.
- Формирование умений и навыков.
- Найдите значение арифметического квадратного корня:
√121; √225; √0,49; √4900; √10000;
- Найдите значение выражения:
√121-√4; √0,25+√0,64; √400*√1,44+8; √9-√0,36.
- Тест с последущей самопроверкой
Уровень 1: за каждый правильный ответ 1 балл
Уровень 2: за каждый правильный ответ 2 балла
Уровень 3: за каждый правильный ответ 3 балла
Уровень 1 Оценка «3» | 1.Какое выражение не имеет смысла? А) В) С) Д) 2. А) 18 В) — 9 С) 36 Д) 324 3.Вычислите √26+в, если в=10 А) 216 В) С) 12 Д) 6 4.Решите уравнение А) 25 В) — 25 С) 25; — 25 Д) не имеет корня 5.Найдите значение выражения — √9 * √121 А) 22 В) 33 С) -33 Д) 0 |
Уровень 2 Оценка «4» | 1.Найдите значение корня А) В) С) Д) 2.Найдите значение выражения — √0,01 — √0,36 А) 0,5 В) -5 С) – 0,5 Д) – 0,7 3.Выполните действия х- 3√х при х=9 А) 0 В) 1 С) -1 Д) 0,5 4.При каких значениях у верно равенство 6√у=6 А) -1 В) 36 С) 1 Д) 0 5. А) 121 В) — 121 С) 121; — 121 Д) не имеет корня |
Уровень 3 Оценка «5» | 1.Найдите значение выражения 2√х – х при х=0,36 А) 7,2 В) -0,84 С) 0,84 Д) 0 2.Найдите значение корня √ А) В) С) Д) нельзя извлечь 3.При каком значении х верно равенство √х – 6 =0 A)1B) 36C) 6Д) -6 4.Найдите значение выражения А) 0 В) 0,7 С) – 0,7 Д) — 3 5.При каких значениях х имеет смысл выражение √7х А) при х>0 В) при х=0 С) при х |
I — 1.В, 2.В, 3 Д, 4.А, 5 С
II — 1.Д, 2. Д, 3. А, 4. С,5. А
III- 1.С, 2. В, 3. В, 4. С, 5. Д
- Домашнее задание. § 20, № 309-312(2, 4, 6)
- Рефлексия.

Диалог учителя и учеников.
Какова связь темы нашего урока с цветком? (Учащиеся говорят, что корень бывает не только у цветка, «корень» — это одно из важнейших понятий алгебры).
- Что называется квадратным корнем из числа а?
- Сколько квадратных корней может быть из числа а?
- Что такое арифметический квадратный корень из числа а?
- Имеет ли смысл запись √-9? Почему?
Вычисление корня. Как высчитать квадратный корень из числа без помощи калькулятора? Извлечение корней из дробных чисел
Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).
Ключевые слова : квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
- Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1. От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
- Киселев А. Элементы алгебры и анализа. Часть первая.-М.-1928 г
Ключевые слова: квадратный корень, извлечение квадратного корня .
Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
В математике вопрос о том, как извлекать корень, считается относительно несложным. Если возвести в квадрат числа из натурального ряда: 1, 2, 3, 4, 5 …n, то у нас получится следующий ряд квадратов: 1, 4, 9, 16 …n 2 . Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.
Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.
Корень из числа: правила вычисления и примеры
Итак, мы возвели число 2 в квадрат, то есть умножили его само на себя и получили 4. А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.
Степень корня – всегда натуральное число, то есть нельзя решить такое уравнение: корень в степени 3,6 из n.
Квадратный корень
Вернемся к вопросу о том, как извлечь корень квадратный из 4. Так как возводили мы число 2 именно в квадрат, то и корень будем извлекать квадратный. Для того чтобы правильно извлечь корень из 4, нужно просто правильно подобрать число, которое при возведении в квадрат дало бы число 4. И это, конечно же, 2. Посмотрите на пример:
- 2 2 =4
- Корень из 4 = 2
Этот пример довольно простой. Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.
Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.
- 8 2 =64
- Корень из 64=8
Кубический корень
Как выше было сказано, корни бывают не только квадратными, на примере попробуем более понятно объяснить, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:
- 3x3x3=27
- Естественно, кубическим корнем из числа 27 будет тройка:
- Корень 3 из 27 = 3
Допустим, необходимо найти кубический корень из 64. Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.
- 4 3 =64
- Корень 3 из 64 = 4
Извлечь корень из числа на калькуляторе
Конечно, лучше всего учиться извлекать квадратные, кубические и корни другой степени на практике, путем решения многих примеров и запоминания таблицы квадратов и кубов небольших чисел. В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.
В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.
Не из каждого числа можно извлечь целый корень, рассмотрим следующий пример:
Корень из 1859 = 43,116122…
Вы можете параллельно попробовать решить этот пример на калькуляторе. Как видите, полученное число не является целым, более того, набор цифр после запятой является не конечным. Более точный результат могут дать специальные инженерные калькуляторы, на дисплее же обычных полный результат просто не умещается. А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.
А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.
Если вам необходимо извлечь корень третьей степени на простом калькуляторе, то необходимо нажать дважды на кнопку со знаком корня. Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:
Корень 3 из 1859 = 6,5662867…
То есть, если число 6,5662867… возвести в третью степень, то мы получим приблизительно 1859. Таким образом, извлекать корни из чисел не сложно, достаточно лишь запомнить выше приведенные алгоритмы.
Что такое квадратный корень?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал «.
Как извлечь корень? Это лучше рассмотреть на примерах .
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры :
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень …
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
В этом и есть сложность извлечения корней . Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24.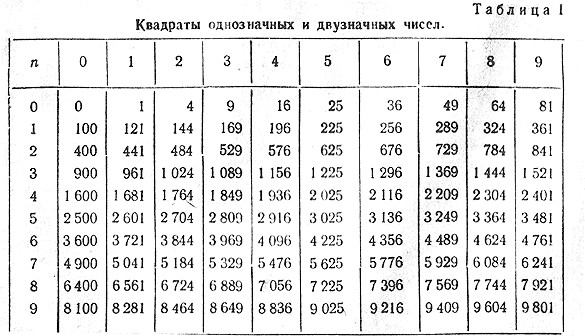 Хотя, не у всех он выплывает, да…
Хотя, не у всех он выплывает, да…
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла ! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных — можно. Например, вполне можно вычислить
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными . Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
Конечно, если корень из числа извлекается ровно , вы обязаны это сделать. Ответ задания в виде, например
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: из числа а — это неотрицательное число, квадрат которого равен а . Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.
В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный ! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня . Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения . Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Потому, что это — арифметический квадратный корень .
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Всё это — в следующих уроках.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.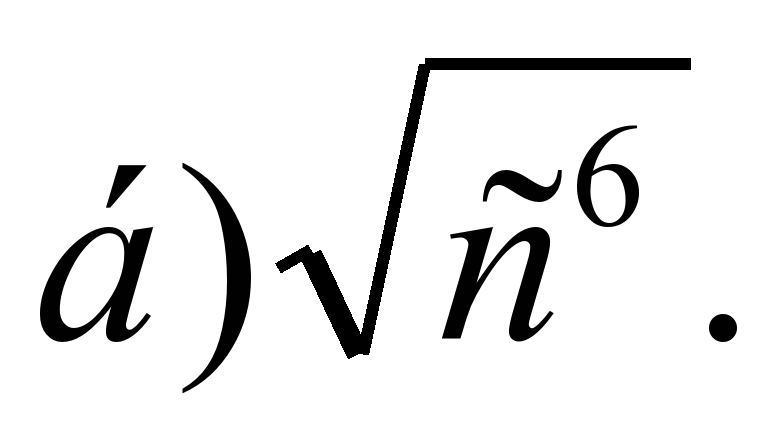
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
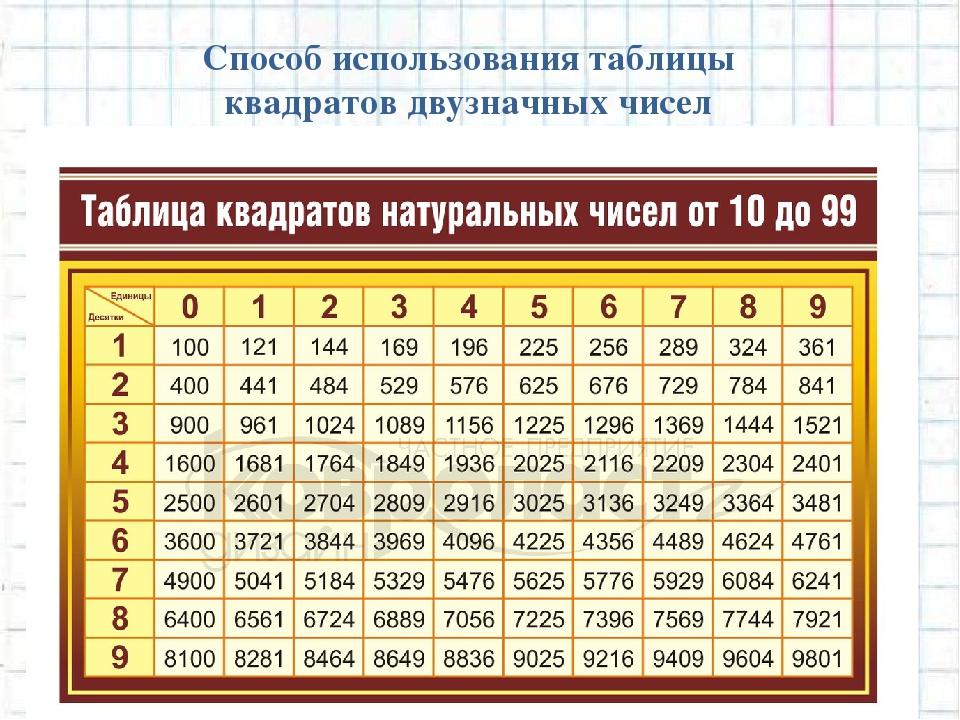
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.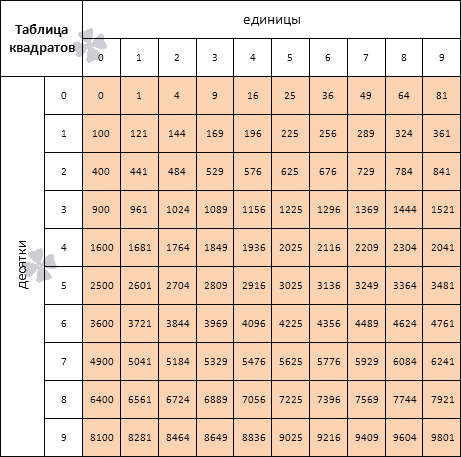 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.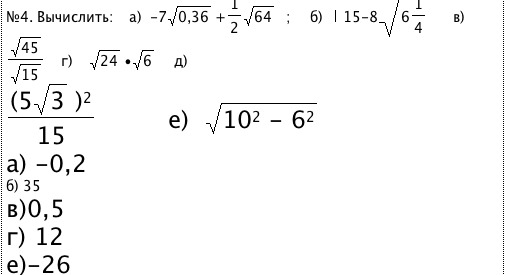 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Урок и презентация на тему:
«Свойства квадратного корня. Формулы. Примеры решений, задачи с ответами»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Интерактивное учебное пособие «Геометрия за 10 минут» для 8 класса
Образовательный комплекс «1С: Школа. Геометрия, 8 класс»
Свойства квадратного корня
Мы продолжаем изучать корни квадратные . 2$. Если квадраты двух неотрицательных чисел равны, то значит и сами числа равны, что и требовалось доказать.
2$. Если квадраты двух неотрицательных чисел равны, то значит и сами числа равны, что и требовалось доказать.
Из нашего свойства следует, что, например, $\sqrt{5}*\sqrt{3}=\sqrt{15}$.
Замечание 1. Свойство справедливо и для случая, когда под корнем более двух неотрицательных множителей.
Свойство 2. Если $а≥0$ и $b>0$, то справедливо следующее равенство: $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
То есть корень из частного равен частному корней.
Доказательство.
Воспользуемся таблицей и кратко докажем наше свойство.
Примеры использования свойств квадратных корней
Пример 1.
Вычислить: $\sqrt{81*25*121}$.
Решение.
Конечно, мы можем взять калькулятор, перемножить все числа под корнем и выполнить операцию извлечения корня квадратного. А если под рукой нет калькулятора, как быть тогда?
$\sqrt{81*25*121}=\sqrt{81}*\sqrt{25}*\sqrt{121}=9*5*11=495$.
Ответ: 495.
Пример 2. 2}$.
2}$.
4. Вычислить:
а) $\sqrt{128*\sqrt{8}}$;
б) $\frac{\sqrt{128}}{\sqrt{8}}$.
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению.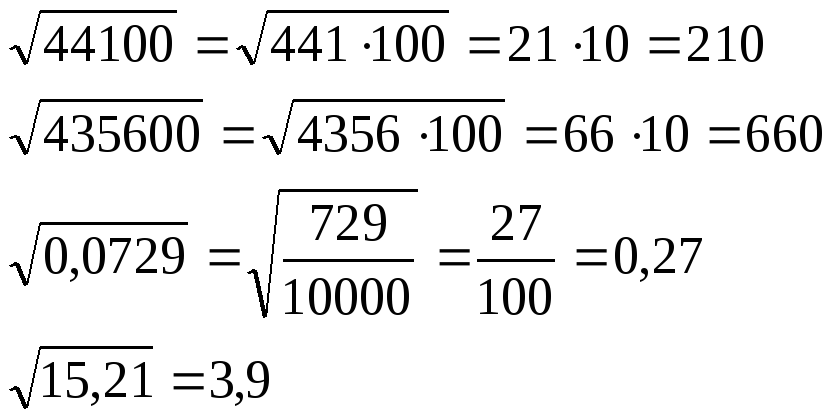 На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным. Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю.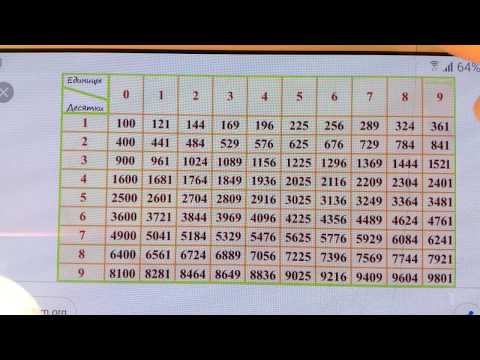 Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Следующее нечетное число — это 11, остаток у нас следующий: 1
Для таких случаев существует разложение в ряд Тейлора:
√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
Как найти квадратный корень из 324?
LearnPracticeDownload
Квадратный корень из 324 — это число, которое при умножении само на себя дает 324. Число 324 является особенным, поскольку представляет собой совершенный квадратный корень. Это указывает на то, что его квадратный корень представляет собой целое число. Теперь мы рассмотрим, как найти значение квадратного корня из 324, и решим некоторые задачи, чтобы лучше понять эту концепцию.
Квадратный корень из 324: √324 = 18
Квадратный корень из 324: 324 2 = 104976
| 1. | Чему равен квадратный корень из 324? |
| 2. | Является ли квадратный корень из 324 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 324? |
| 4. | Часто задаваемые вопросы о квадратном корне из 324 |
Что такое квадратный корень из 324?
Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. В случае 324 число 18 при умножении само на себя дает число 324, что делает 18 полным квадратом. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 5. Мы можем выразить квадратный корень из 324 по-разному.
- Десятичная форма: 18,0
- Радикальная форма: √324
- Форма экспоненты: (324) 1/2
Является ли квадратный корень из 324 рациональным или иррациональным?
- Десятичная часть квадратного корня из 324 заканчивается, так как она равна 18,0; его также можно выразить как отношение p/q, 18/1, что говорит нам о том, что это рациональное число.

- Таким образом, мы можем заключить, что квадратный корень из 324 является рациональным.
Как найти квадратный корень из 324?
Существует два основных метода нахождения квадратного корня из 324:
- Повторное вычитание
- Длинное деление
Щелкните здесь, чтобы узнать о других методах нахождения квадратного корня числа.
Повторное вычитание
Начните с 324 и продолжайте вычитать последовательные нечетные числа, пока не получите ноль. Общее число, которое мы вычитаем, представляет собой квадратный корень из 324.
- 324 — 1 = 323
- 323 — 3 = 320
- 320 — 5 = 315
- 315 — 7 = 308
- 308 — 9 = 299
- 299 — 11 = 288
- 288 — 13 = 275
- 275 — 15 = 260
- 260 — 17 = 243
- 243 — 19 = 224
- 224 — 21 = 203
- 203 — 23 = 180
- 180 — 25 = 155
- 155 — 27 = 128
- 128 — 29 = 99
- 99 — 31 = 68
- 68 — 33 = 35
- 35 — 35 = 0
Так как общее число, которое мы вычитаем, равно 18, квадратный корень из 324 равен 18 .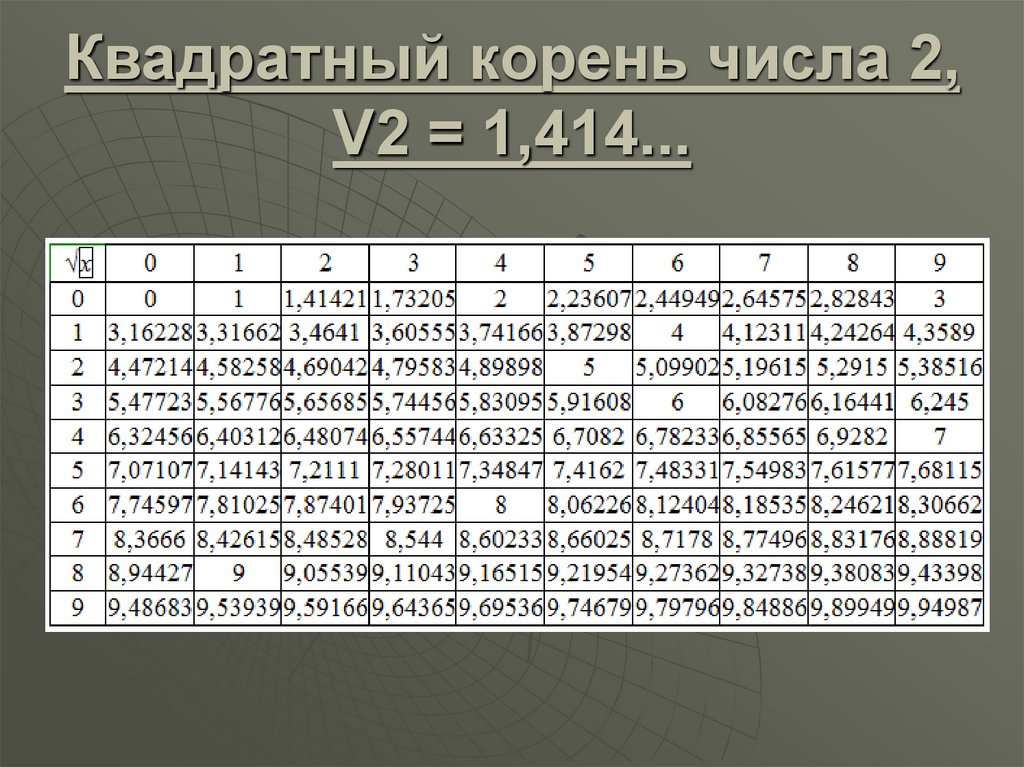
Полное деление
- Шаг 1: Поместите черту над цифрами 03 и 24.
- Шаг 2: Найдите такое число, чтобы при умножении его на себя произведение было меньше или равно 03. Мы знаем, что 1 2 = 1, что меньше 3. Разделив 3 на 1 с частным как 1, получаем 2 в остатке.
- Шаг 3: Не забудьте перетащить следующую пару чисел, то есть 24, что даст следующее делимое 224. Кроме того, добавление 1 дает нам 2, которые становятся начальной цифрой нашего следующего делителя.
- Шаг 4: Теперь у нас есть новый делитель 2X. Нам нужно найти такое значение X, что 2X × X дает нам значение, меньшее или равное 224. 8 заполняет значение X, чтобы дать нам 28 × 8 = 224, в результате чего остаток становится 0,
Таким образом, наше длинное деление теперь выглядит так:
Следовательно, квадратный корень из 324 равен 18.
Исследуйте квадратные корни, используя иллюстрации и интерактивные примеры0048 Квадратный корень из 225 Загадочные вопросы Пример 1: Кевин хочет купить квадратный участок площадью 324 квадратных фута. Решение: Во-первых, чтобы рассчитать стоимость добавления смолы, нам понадобится периметр земли. Чтобы найти периметр, нам нужно сначала найти длину стороны. Длина стороны равна квадратному корню из площади квадрата. Следовательно, длина стороны здесь будет √324 = 18, а периметр в 4 раза больше. Следовательно, общая стоимость добавления смолы = 4 × 18 × 40 = 2880 $ Пример 2: Крис едет на велосипеде в свой офис со скоростью √324 миль/ч. За какое время он проедет 9 км? Решение: Нам нужно использовать формулу Время = Расстояние/Скорость Следовательно, Крису потребуется 30 минут, чтобы добраться до своего офиса. перейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных эффектов. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайдуперейти к слайду  Он хочет построить дорогу вдоль границы. Если стоимость добавления гудрона за фут составляет 40 долларов, найдите стоимость добавления гудрона по всему периметру участка.
Он хочет построить дорогу вдоль границы. Если стоимость добавления гудрона за фут составляет 40 долларов, найдите стоимость добавления гудрона по всему периметру участка.
Скорость = √324 = 18 миль/ч
Расстояние = 9 миль
Используя формулу, Время = 9 / 18 = 0,5 часа или 30 минут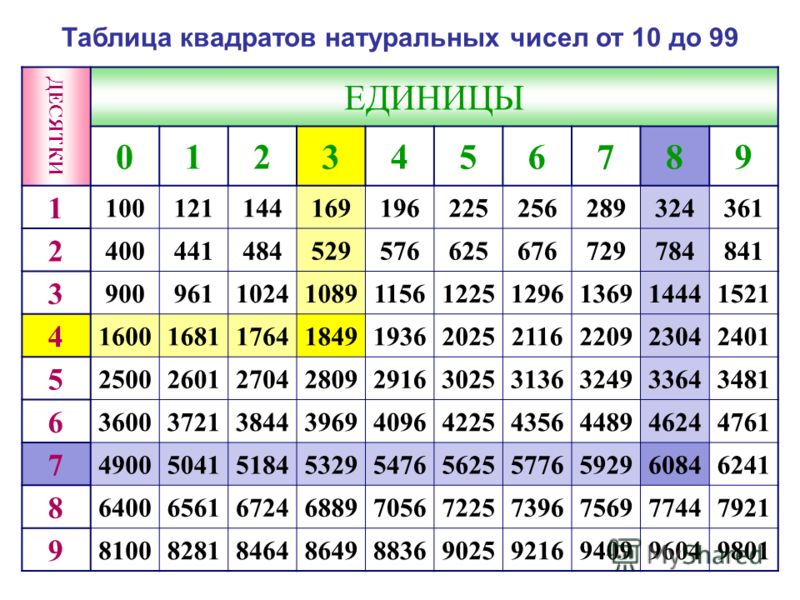
Часто задаваемые вопросы о квадратном корне из 324
Является ли 324 полным квадратным корнем?
Квадратный корень из 324 равен √324 = 18. Следовательно, это полный квадратный корень.
Чему равен квадрат 324?
Квадрат числа 324 равен 324 2 = 104976
Чему равен квадратный корень из 324 в упрощенном виде?
Если разложить 324 на множители, то получится, что 324 = 2 × 2 × 9 × 9 или 18 × 18. Следовательно, упрощенная форма может быть записана как 18 2
Является ли квадратный корень из 324 рациональным числом ?
Квадратный корень из 324 – это рациональное число, поскольку его можно представить в виде p/q (18/1), и оно имеет конечный десятичный разряд.
Какая экспоненциальная форма корня 324? 93-8
Квадратный корень из 324 пошаговое решение
| Пожалуйста, введите реальное число: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: Квадратный корень из 324 пошаговое решение | √324 или чему равен квадратный корень из 324?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа. См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя
Ниже показано, как шаг за шагом вычислить квадратный корень из 324 с помощью вавилонского метода , также известного как Метод Героя .
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 18 — это квадратный корень из 324, потому что 18 2 = 18•18 = 324, -18 — это квадратный корень из 324, потому что (-18) 2 = (-18)•(-18) = 324.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до ближайшей тысячной.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1 | 1. 000 000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4. 243 243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| нет | нет 2 | √ |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5. 745 745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2 401 | 7. 000 000 |
| 50 | 2 500 | 7,071 |
| нет | нет 2 | √ | ||
|---|---|---|---|---|
| 51 | 2,601 | 7.141 | ||
| 52 | 2,704 | 7.211 | ||
| 53 | 2,809 | 7.280 | ||
| 54 | 2,916 | 7.348 | ||
| 55 | 3,025 | 7.416 | ||
| 56 | 3,136 | 7.483 | ||
| 57 | 3,249 | 7.550 | ||
| 58 | 3,364 | 7.616 | ||
| 59 | 3,481 | 7.681 | ||
| 60 | 3,600 | 7.746 | ||
| 61 | 3,721 | 7.810 | ||
| 62 | 3,844 | 7.874 | ||
| 63 | 3,969 | 7.937 | ||
| 64 | 4,096 | 8. 000 000 | ||
| 65 | 4,225 | 8.062 | ||
| 66 | 4,356 | 8.124 | ||
| 67 | 4,489 | 8.185 | ||
| 68 | 4,624 | 8.246 | ||
| 69 | 4,761 | 8.307 | ||
| 70 | 4,900 | 8.367 | ||
| 71 | 5,041 | 8.426 | ||
| 72 | 5,184 | 8.485 | ||
| 73 | 5,329 | 8.544 | ||
| 74 | 5 476 | 8.602 | ||
| 75 | 5 625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.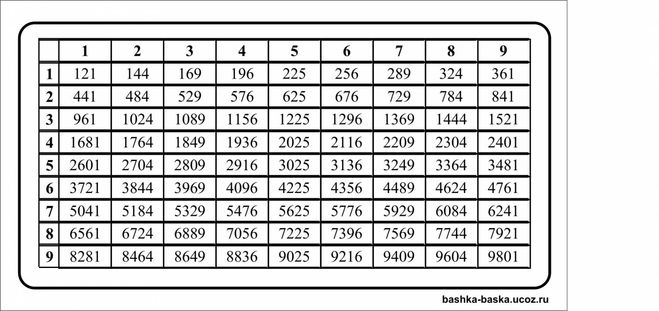 888 888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.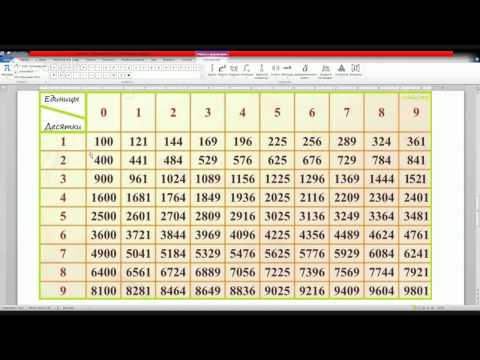 747 747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10,000 | 10.000 |
Найдите квадратный корень из 324 методом многократного вычитания…
Перейти к
- Квадраты и квадратные корни и кубы и кубические корни — Упражнение
- Рациональное число
- Обработка данных
- Квадраты и квадратные корни и кубы и кубические корни
- Линейные уравнения с одной переменной
- Понимание четырехугольников и практической геометрии
- Визуализация твердых фигур
- Алгебраические выражения и тождества и факторизация
- Показатели и силы
- Сравнение количеств
- Прямые и обратные пропорции
- Измерение
- Введение в графики
- Игра с числами
Главная >
Образцовые решения NCERT
Класс 8
Математика
>
Глава 3. Квадраты и квадратные корни, кубы и кубические корни
>
Квадраты и квадратные корни и кубы и кубические корни — Упражнение
>
Вопрос 133
Квадраты и квадратные корни, кубы и кубические корни
>
Квадраты и квадратные корни и кубы и кубические корни — Упражнение
>
Вопрос 133
Вопрос 133 Квадраты и квадратные корни и кубы и кубические корни — Упражнение
Найдите квадратный корень из 324 методом многократного вычитания.
Ответ:
Из вопроса следует, что 324
Теперь последовательно вычитаем нечетные числа, начиная с 1, как:
315 — 7 = 308
308 — 9 = 299
299 — 11 = 288
288 — 13 = 275
275 — 15 = 260
260 — 17 = 243
243 — 19 = 224
— 17 = 243
243 — 19 = 224
0003224 — 21 = 203
203 — 23 = 180
180 — 25 = 155
155 — 27 = 128
128 — 29 = 99
99 — 31 = 68
68 — 33 = 35
35 – 35 = 0
Здесь мы видим, что 324 сводится к 0 после вычитания 18 нечетных чисел.
Следовательно, квадратный корень из 324 равен 18.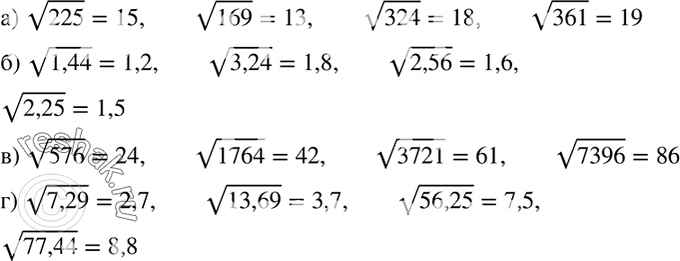 2?(а) 9(б) 10 (в) 11 (г) 12
2?(а) 9(б) 10 (в) 11 (г) 12
Что из следующего не может быть полным квадратом? (a) 841 (b) 529 (c) 198 (d) Все вышеперечисленное
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
квадраты и квадратные корни, кубики и корни куба — упражнение
Главы
Рациональные номера
Обработка данных
Квадраты и квадратные корни и кубики и кубические корни
Линейные уравнения в одном переменном
. Практическая геометрия
Визуализация объемных фигур
Алгебраические выражения, тождества и факторизация
Экспоненты и степени
Сравнение величин
Прямые и обратные пропорции
Измерение
Знакомство с графиками
Игра с числами
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
| 1 | Фактор | х^2-4 93-8 | ||
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Что такое квадратный корень из 324?
В математике квадратный корень из числа, подобного 324, — это число, которое при умножении само на себя равно 324.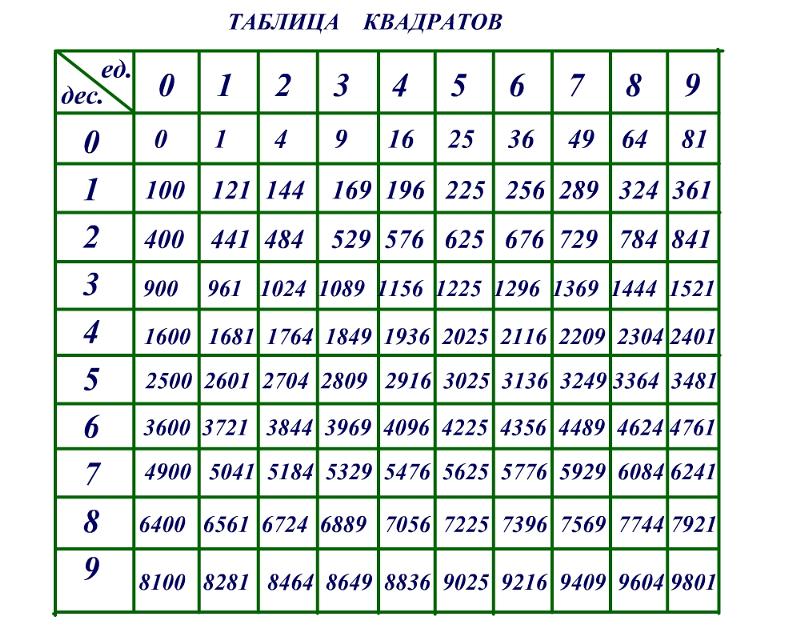 Мы можем показать это в математической форме с помощью символа квадратного корня, который называется подкоренным символом: √
Мы можем показать это в математической форме с помощью символа квадратного корня, который называется подкоренным символом: √
Любое число с подкоренным символом рядом с ним называется подкоренным членом или квадратным корнем из 324 в подкоренной форме.
Чтобы объяснить квадратный корень немного больше, квадратный корень из числа 324 — это величина (которую мы называем q), которая при умножении сама на себя равна 324:
√324 = q × q = q 2
Итак, что такое квадратный корень из 324 и как его вычислить? Хорошо, если у вас есть компьютер или калькулятор, вы можете легко вычислить квадратный корень. Если вам нужно сделать это вручную, то для этого потребуется старое доброе деление в длину с помощью карандаша и листа бумаги.
Для целей этой статьи мы вычислим его за вас (но позже в статье мы покажем вам, как вычислить его самостоятельно с помощью деления в большую сторону). Квадратный корень из 324 равен 18:
18 × 18 = 324
Является ли число 324 идеальным квадратом?
Когда квадратный корень данного числа является целым числом, это называется полным квадратом. Совершенные квадраты важны для многих математических функций и используются во всем, от плотницких работ до более сложных тем, таких как физика и астрономия.
Совершенные квадраты важны для многих математических функций и используются во всем, от плотницких работ до более сложных тем, таких как физика и астрономия.
Если мы посмотрим на число 324, то узнаем, что квадратный корень равен 18, а поскольку это целое число, мы также знаем, что 324 — это полный квадрат 9.0008 .
Если вы хотите узнать больше о числах с идеальным квадратом, у нас есть список идеальных квадратов, который охватывает первые 1000 чисел с идеальным квадратом.
324 — рациональное или иррациональное число?
Еще один распространенный вопрос, который может возникнуть при работе с корнями числа, например 324, заключается в том, является ли данное число рациональным или иррациональным. Рациональные числа можно записать в виде дроби, а иррациональные — нет.
Самый быстрый способ проверить, является ли число рациональным или иррациональным, — определить, является ли оно полным квадратом. Если да, то это рациональное число, а если не полный квадрат, то это иррациональное число.
Мы уже знаем, что 324 — рациональное число, потому что мы знаем, что это полный квадрат.
Вычисление квадратного корня из 324
Чтобы вычислить квадратный корень из 324 с помощью калькулятора, введите число 324 в калькулятор и нажмите клавишу √x:
√324 = 18,0000
Чтобы вычислить квадратный корень из 324 в Excel, Numbers of Google Sheets, вы можете использовать функцию SQRT() :
SQRT(324) = 18
Округление квадратного корня из 324
Иногда, когда вы работаете с квадратным корнем из 324, вам может понадобиться округлить ответ до определенного числа знаков после запятой:
10-й: √324 = 18,0
100-й: √324 = 18,00
1000-й: √324 = 18,000
Нахождение квадратного корня из 324 с помощью длинного деления
Если у вас нет калькулятора или компьютерной программы, вам придется использовать старое доброе деление в длину, чтобы извлечь квадратный корень из 324. Именно так математики вычисляли его задолго до того, как были изобретены калькуляторы и компьютеры.
Шаг 1
Установите 324 в парах из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный знак:
Шаг 2
Начиная с первого набора: самый большой совершенный квадрат, меньший или равный 3, равен 1, а квадратный корень из 1 равен 1. Поэтому ставим 1 сверху и 1 снизу вот так:
| 1 | |
3 | 24 |
1 |
Шаг 3
Вычислите 3 минус 1 и поместите разницу ниже. Затем переместитесь вниз к следующему набору чисел.
| 1 | |
3 | 24 |
1 | |
2 | 24 |
Шаг 4
Удвойте число, выделенное зеленым сверху: 1 × 2 = 2. Затем используйте 2 и нижнее число, чтобы решить эту задачу:
2? × ? ≤ 224
Знаки вопроса «пробел» и такие же «пробел». Путем проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 8.
Путем проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 8.
Теперь введите 8 сверху:
| 1 | 8 |
3 | 24 |
1 | |
2 | 24 |
Надеюсь, это дало вам представление о том, как извлечь квадратный корень с помощью деления в большую сторону, чтобы вы могли самостоятельно решать будущие задачи.
Практика извлечения квадратных корней на примерах
Если вы хотите продолжить изучение квадратных корней, взгляните на случайные вычисления на боковой панели справа от этой записи в блоге.
Мы перечислили несколько совершенно случайных чисел, которые вы можете щелкнуть и следовать информации о вычислении квадратного корня из этого числа, чтобы помочь вам понять числовые корни.
Вычислить другую задачу на квадратный корень
Введите число в поле А ниже и нажмите «Рассчитать», чтобы вычислить квадратный корень из заданного числа.


 7807435157923
7807435157923 Объявление темы урока и целей урока.
Объявление темы урока и целей урока. Найдите значение корня -√81
Найдите значение корня -√81 Решите уравнение
Решите уравнение