Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Производная косинуса Производная синуса Производная логарифма по основанию a Производная экспоненциальной функции
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
| Дата: 20.11.2014 Таблица производных.Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует. Приступим к знакомству?) Термины и обозначения. В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного. Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных.В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию:Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования. |
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Составить отношение и вычислить предел .
Откуда появилась таблица производных и правила дифференцирования ? Благодаря единственному пределу . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных , оттачивая алгоритм и технические приёмы решения:
На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных , оттачивая алгоритм и технические приёмы решения:
Пример 1
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку , принадлежащую области определения функции , в которой существует производная. Зададим в данной точке приращение (разумеется, не выходящее за рамки о/о -я) и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение :
Домножим числитель и знаменатель на сопряженное выражение :
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций .
Поскольку в качестве можно выбрать ЛЮБУЮ точку интервала , то, осуществив замену , получаем:
Ответ
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции , пользуясь определением производной
Решение : рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы использовать букву .
Рассмотрим произвольную точку , принадлежащую области определения функции (интервалу ), и зададим в ней приращение . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только).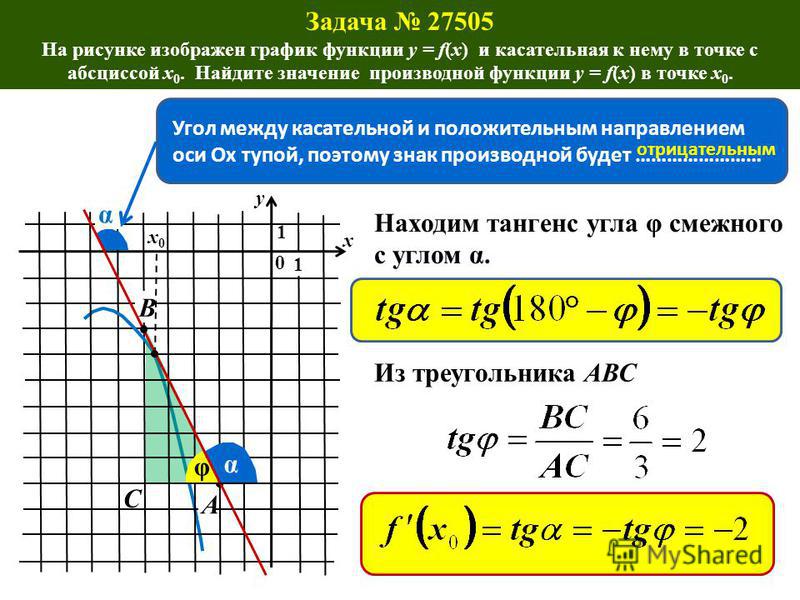 Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости закомментирую пошагово:
(1) Используем свойство логарифма .
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом , при этом в качестве бесконечно малой величины выступает .
Ответ : по определению производной:
Или сокращённо:
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 3: Решение : рассмотрим некоторую точку , принадлежащую области определения функции .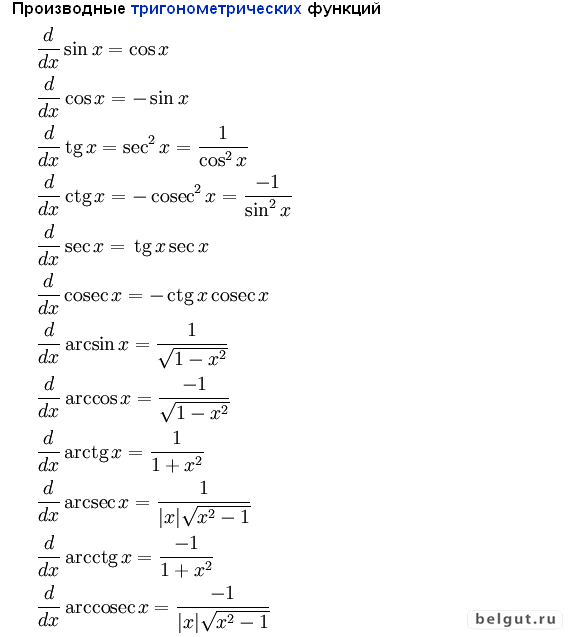 Зададим в данной точке приращение и составим соответствующее приращение функции:
Зададим в данной точке приращение и составим соответствующее приращение функции:
Найдём производную в точке :
Так как в качестве можно выбрать любую точку области определения функции , то и
Ответ : по определению производной
Пример 4
Найти производную по определению
А тут всё необходимо свести к замечательному пределу . Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных . Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой .
Пример 4: Решение , принадлежащую , и зададим в ней приращение
Найдём производную:
Используем замечательный предел
Ответ : по определению
Пример 5
Найти производную функции , используя определение производной
Решение : используем первый стиль оформления. Рассмотрим некоторую точку , принадлежащую , изададим в ней приращение аргумента . Тогда соответствующее приращение функции:
Рассмотрим некоторую точку , принадлежащую , изададим в ней приращение аргумента . Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку (число) и находим в ней значение функции: , то есть в функцию вместо «икса» следует подставить . Теперь берём тоже вполне конкретное число и так же подставляем его в функцию вместо «икса»: . Записываем разность , при этом необходимо полностью взять в скобки .
Составленное приращение функции бывает выгодно сразу же упростить . Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
Поскольку в качестве можно выбрать любое действительное число, то проведём замену и получим .
Ответ : по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы :
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Пример 6: Решение : рассмотрим некоторую точку , принадлежащую , и зададим в ней приращение аргумента . Тогда соответствующее приращение функции:
Вычислим производную:
Таким образом:
Поскольку в качестве можно выбрать любое действительное число, то и
Ответ : по определению.
Вернёмся к стилю №2:
Пример 7
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции :
Решение : рассмотрим произвольную точку , принадлежащую , зададим в ней приращение аргумента и составим приращение функции:
Найдём производную:
(1) Используем тригонометрическую формулу .
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое .
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел . Таким образом, неопределённость устранена, причёсываем результат.
Ответ : по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Пример 8: Решение : рассмотрим произвольную точку , принадлежащую , зададим в ней приращение и составим приращение функции:
Найдём производную:
Используем тригонометрическую формулу и первый замечательный предел:
Ответ : по определению
Разберём более редкую версию задачи:
Пример 9
Найти производную функции в точке , пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Вычислим ответ стандартным способом:
Решение : с точки зрения наглядности это задание значительно проще, так как в формуле вместо рассматривается конкретное значение.
Зададим в точке приращение и составим соответствующее приращение функции:
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов и в который раз сведём решение к первому замечательному пределу :
Ответ : по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить на или просто в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10
Используя определение, найти производную функции в точке (одно из которых может оказаться и бесконечным) , о котором я в общих чертах уже рассказал на теоретическом уроке о производной .
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс обладает общей производной и общей касательной (ось абсцисс) в точке . Кривой, да дифференцируемый на ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
Кривой, да дифференцируемый на ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-11
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Производная от корня из x. Производная степенной функции (степени и корни)
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
На котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией , а функцию – внутренней (или вложенной) функцией .
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.
Первый шаг , который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней .
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .
Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением , в данном случае:
Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением , в данном случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем .
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Постоянный множитель обычно выносят в начало выражения:
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения . Таким образом, результат применения правила дифференцирования сложной функции следующий:
Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения . Таким образом, результат применения правила дифференцирования сложной функции следующий:
Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени .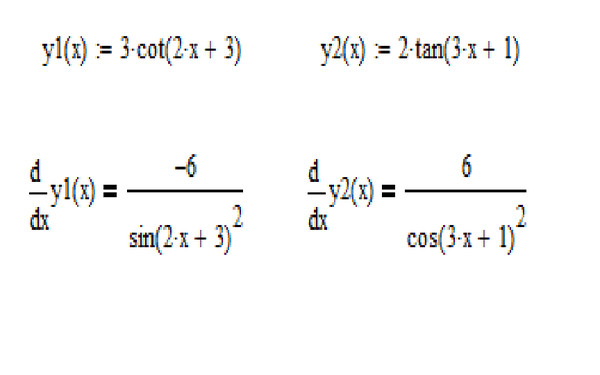 Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение необычно. Вот характерный пример:
Вот характерный пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
14. Производная натурального логарифма Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т. е.
е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант . Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение ) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
определение, как найти, примеры решений
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x — любое фиксированная точка интервала (a, b) , а Δx — произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) — f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 . Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 . Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:
Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x — некоторое фиксированное значение аргумента из этого интервала, Δx — любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A — некоторое число, не зависящее от Δx , а α — функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема . Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| — непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx — дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Теорема . Если каждая из функций u(x) и v(x) дифференцируема в данной точке x , то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0 ) также дифференцируемы в этой точке, причем имеют место формулы:
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x — независимой переменной .
Теорема . Если y=f(u) и u=φ(x) — дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.
Если y=f(u) и u=φ(x) — дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) — дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) — дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
Если y=f(x) , x=φ(t) — дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t .
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x .
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
10.3. Производная и ее геометрический смысл.
Автор Татьяна Андрющенко На чтение 4 мин. Просмотров 9.9k. Опубликовано
В координатной плоскости хОу рассмотрим график функции y=f (x). Зафиксируем точку М(х0; f (x0)). Придадим абсциссе х0 приращение Δх. Мы получим новую абсциссу х0+Δх. Это абсцисса точки N, а ордината будет равна f (х0+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.
Зафиксируем точку М(х0; f (x0)). Придадим абсциссе х0 приращение Δх. Мы получим новую абсциссу х0+Δх. Это абсцисса точки N, а ордината будет равна f (х0+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.
Δy=f (х0+Δх) — f (x0). Через точки M и N проведем секущую MN, которая образует угол φ с положительным направлением оси Ох. Определим тангенс угла φ из прямоугольного треугольника MPN.
Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ, а угол φ станет углом α. Значит, тангенс угла α есть предельное значение тангенса угла φ:
Значит, тангенс угла α есть предельное значение тангенса угла φ:
Определение производной. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:
Смотрите видео 10.3. Определение производной. Геометрический смысл производной.
Примеры.
1. Найти приращение аргумента и приращение функции y=x2, если начальное значение аргумента было равно 4, а новое —4,01.
Решение.
Новое значение аргумента х=х0+Δx. Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х0+Δх) — f (x0). Так как у нас функция y=x2, то Δу=(х0+Δx)2— (х0)2=(х0)2+2x0 · Δx+(Δx)2— (х0)2=2x0 · Δx+(Δx)2=
Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х0+Δх) — f (x0). Так как у нас функция y=x2, то Δу=(х0+Δx)2— (х0)2=(х0)2+2x0 · Δx+(Δx)2— (х0)2=2x0 · Δx+(Δx)2=
=2 · 4 · 0,01+(0,01)2=0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх=0,01; приращение функции Δу=0,0801.
Можно было приращение функции найти по-другому: Δy=y (х0+Δx) -y (х0)=у(4,01) -у(4)=4,012-42=16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х0, если f ‘(х0) = 1.
Решение.
Значение производной в точке касания х0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f ‘(х0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45°.
3. Вывести формулу производной функции y=xn.
Смотрите видео: «10.3.0. Вывод формулы производной степени».
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (xn)’ = nxn-1.
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования.
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Производная тангенса х — формула, доказательство, примеры
Производная тангенса х есть квадрат сек х. Прежде чем доказывать это, напомним некоторые факты о tan x. Тангенс х в прямоугольном треугольнике представляет собой отношение стороны, противоположной х, к стороне, примыкающей к х, и поэтому его можно записать как (sin x)/(cos x). Мы используем это при дифференцировании тангенса х.
Давайте изучим дифференцирование тангенса х вместе с его доказательством различными методами, а также решим несколько примеров, используя производную тангенса х.
| 1. | Что такое производное Tan x? |
| 2. | Производная Tan x Доказательство по первому принципу |
| 3. | Производная Tan x Доказательство по цепному правилу |
| 4. | Производная Tan x Доказательство по частному правилу |
| 5. | Часто задаваемые вопросы о производном Tan x |
Что такое производное Tan x?
Производная тангенса х по х обозначается d/dx (тангенс х) (или) (тангенс х)’ и ее значение равно сек 2 х. Tan x дифференцируем в своей области определения. Чтобы доказать, что дифференцирование tan x равно sec 2 x, мы используем существующие тригонометрические тождества и существующие правила дифференцирования. Мы можем доказать это следующими способами:
- Доказательство по первому принципу
- Доказательство по цепному правилу
- Доказательство по правилу частных
Производная формулы Tan x
Формула дифференцирования тангенса x is,
- d/dx (tan x) = sec 2 x (или)
- (tan x)’ = сек 2 x
Теперь мы докажем это различными методами в следующих разделах.
Производная Tan x Доказательство по первому принципу
Чтобы найти производную от тангенса х, предположим, что f(x) = тангенс х. Тогда по первому принципу его производная дается следующим пределом.
f'(x) = limₕ→₀ [f(x + h) — f(x)] / h … (1)
Так как f(x) = tan x, то f(x + h ) = тангенс (х + ч).
Подставляя их в (1),
f'(x) = limₕ→₀ [tan(x + h) — tan x] / h
= limₕ→₀ [ [sin (x + h) / cos ( x + h)] — [sin x / cos x] ] / h
= limₕ→₀ [ [sin (x + h ) cos x — cos (x + h) sin x] / [cos x · cos(x + ч)] ]/ ч
По формулам суммы и разности sin A cos B — cos A sin B = sin (A — B).
f'(x) = limₕ→₀ [sin (x + h — x)] / [h cos x · cos(x + h)]
= limₕ→₀ [sin h] / [h cos x · cos(x + h)]
= limₕ→₀ (sin h)/ h · limₕ→₀ 1 / [cos x · cos(x + h)]
По предельным формулам limₕ→₀ (sin h)/ h = 1.
f'(x) = 1 [ 1 / (cos x · cos(x + 0))] = 1/cos 2 x
Мы знаем, что обратное значение cos равно сек. Итак,
Итак,
f'(x) = сек 2 х.
Отсюда доказано.
Производная Tan x Доказательство по цепному правилу
Докажем дифференцирование формулы tan x по цепному правилу. Для этого заметим, что мы можем записать y = tan x как y = 1 / (cot x) = (cot x) -1 . Теперь, по степенному правилу и цепному правилу,
y’ = (-1) (cot x) -2 · d/dx (cot x)
Мы имеем d/dx (cot x) = -csc 2 х. Кроме того, по свойству показателей а -т = 1/а м .
y’ = -1/cot 2 x · (-csc 2 x)
y’ = tan 2 x · csc 2 x
Теперь, tan x/ (cos x) и csc x = 1/(sin x). Таким образом,
y’ = (sin 2 x)/(cos 2 x) · (1/sin 2 x)
= 1/cos 2 x
. сек х. Итак,
у’ = сек 2 х
Отсюда доказано.
Производная Tan x Доказательство по частному правилу
Мы можем применить правило частных, чтобы вывести формулу производной от tan x. Для этого нам нужно записать тангенс х в виде дроби. Мы знаем, что tan x = (sin x)/(cos x). Итак, мы предполагаем, что y = (sin x)/(cos x). Тогда по правилу частных
Для этого нам нужно записать тангенс х в виде дроби. Мы знаем, что tan x = (sin x)/(cos x). Итак, мы предполагаем, что y = (sin x)/(cos x). Тогда по правилу частных
y’ = [cos x · d/dx (sin x) — sin x · d/dx (cos x)] / (cos 2 x)
= [cos x · cos x — sin x (-sin x)] / (cos 2 x)
= [cos 2 x + sin 2 x] / (cos 2 x)
По одному из тождеств Пифагора, cos 2 x + sin 2 x = 1. Итак,
y’ = 1 / (cos 2 x) = sec 2 x
Отсюда доказано. Это доказательство является самым простым среди всех других доказательств производных от tan x.
Распространенные заблуждения, связанные с производной Tan x:
Вот некоторая ясность в отношении некоторых распространенных заблуждений относительно дифференциации Tan x.
- d/dx (tan x) НЕ равно d/dx (sin x) / d/dx (cos x). Вместо этого мы должны использовать правило частных, чтобы найти производную от tan x (записав ее как (sin x)/(cos x)).

- d/dx (tan x) НЕ является кроваткой x. кроватка х есть просто величина, обратная тангенсу х.
- Производные tan x и tan -1 x НЕ совпадают.
d/dx(тангенс х) = сек 2 х
d/dx(тангенс -1 х) = 1/(1 + х 2 )
Темы, относящиеся к дифференциации Tan x:
Вот некоторые темы, которые могут вас заинтересовать при изучении производной Tan x.
- Расчетные формулы
- Расчетный калькулятор
- Производные формулы
- Калькулятор производных
Часто задаваемые вопросы о производном Tan x
Какая производная от Tan x относительно x?
Производная tan x по x равна квадрату sec x. т. е. d/dx(tan x) = sec 2 x. Его также можно записать как (tan x)’ = sec 2 x.
Как найти производную формулы Tan x?
Пусть y = tan x. У нас есть tan x = sin x/cos x. По правилу частных y’ = [cos x · d/dx (sin x) — sin x · d/dx (cos x)] / (cos 2 x) = [cos 2 x + sin 2 x] / (cos 2 x) = 1/(cos 2 x) = сек 2 x.
Какая производная от Tan x
2 ?Мы знаем, что d/dx(tan x) = sec 2 x. Итак, d/dx(tan x 2 ) = sec 2 x 2 d/dx(x 2 ) = 2xsec 2 x 2 (по цепочке).
В чем отличие Tan x от Cos x?
Мы знаем, что производная от tan x равна sec 2 x. Кроме того, sec x = 1/(cos x). Итак, d/d(tan x) = 1/cos 2 x.
Что такое производная tan x
-1 ?Используя производную от tan x и цепное правило, d/dx(tan x -1 ) = sec 2 x -1 d/dx(x -1 ) = sec 2 x -1 (-1 х -2 ) = (-сек 2 х -1 )/(х 2 ).
Равна ли производная Tan x производной Tan
-1 x? Нет, производные tan x и tan -1 x различны. Производная tan x равна sec 2 x, тогда как производная tan⁻¹x равна 1/(1 + x 2 ).
В чем разница между производной Tan x и первообразной Tan x?
Производная тангенса x сек 2 х. Первообразная tan x есть не что иное, как интеграл от tan x и ∫ tan x dx = ln |sec x| + К.
| 1 | Найти производную — d/dx | натуральное бревно х | |||||||||||||||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | 92) | ||||||||||||||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |||||||||||||||
| 22 | Найти производную — d/dx | грех(2x) | |||||||||||||||
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||||||||||||||||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |||||||||||||||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |||||||||||||||
| 43 | Оценка интеграла 9бесконечность | ||||||||||||||||
| 45 | Найти производную — d/dx | х/2 | |||||||||||||||
| 46 | Найти производную — d/dx | -cos(x) | |||||||||||||||
| 47 | Найти производную — d/dx | грех(3x) | 92+1|||||||||||||||
| 68 | Оценить интеграл | интеграл от sin(x) по x | |||||||||||||||
| 69 | Найти производную — d/dx | угловой синус(х) | |||||||||||||||
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |||||||||||||||
| 85 | Найти производную — d/dx | лог х | |||||||||||||||
| 86 | Найти производную — d/dx | арктан(х) | |||||||||||||||
| 87 | Найти производную — d/dx | бревно натуральное 5х92 х$. Кто-нибудь может объяснить это наглядным геометрическим способом, используя единичный круг?
$\endgroup$ 8 $\begingroup$ Следующее, возможно, немного сумбурно, но идея, надеюсь, ясна. Если $\theta$ — это угол $EAH$ на рисунке, то $\tan \theta$ — это длина отрезка $BC$. Если мы немного увеличим этот угол (или «бесконечно малый»), то отрезок $EF$ будет приблизительно равен $d\theta$, и мы хотели бы знать длину $CD$, так как это изменение $\tan \theta $. 92 \ тета} . $$ $\endgroup$ $\begingroup$ Во-первых, посмотрите на график $\tan(x)$. Он имеет вертикальные асимптоты при целых кратных $\dfrac{\pi}{2}$ и не определен при $-\dfrac{\pi}{2}$ и $\dfrac{\pi}{2} $. Правило произведения для дифференцирования утверждает, что производная от f(x).g(x) равна f'(x)g(x) + f(x).g'(x) Правило произведения: Сначала пусть F(x) = tan 2 (x) Тогда помните, что tan 2 (x) равен tan(x).tan(x) Итак, F(x) = tan(x)tan(x) Установив f( x) и g(x), поскольку tan(x) означает, что F(x) = f(x).g(x), и мы можем применить правило произведения, чтобы найти F'(x)
Шаг 1: Проанализируйте, является ли тангенс угла функцией того же самого угла. Например, если правая часть уравнения равна $latex \tan{(x)}$, проверьте, является ли она функцией того же угла x или f(x) . Примечание: Если $latex \tan{(x)}$ является функцией другого угла или переменной, такой как 9{2}{(u)} \cdot \frac{d}{dx} (u)$ Шаг 1: Выразите функцию в виде $latex F(x) = \tan{ (u)}$, где $latex u$ представляет собой любую функцию, кроме x . Шаг 2: Рассмотрим $latex \tan{(u)}$ как внешнюю функцию $latex f(u)$ и $latex u$ как внутреннюю функцию $latex g(x)$ составная функция $latex F(x)$. Отсюда имеем $latex f(u) = \tan{(u)}$ 9{2}{(u)}$ Шаг 4: Получите производную внутренней функции $latex g(x) = u$. Используйте соответствующее производное правило, применимое к $latex u$. Шаг 5: Примените базовую формулу цепного правила, алгебраически умножив производную внешней функции $latex f(u)$ на производную внутренней функции $latex g(x)$ $latex \ frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$ 9{2}{(u)} \cdot \frac{d}{dx} (u)$ Шаг 6: Замените $latex u$ на $latex f'(u)$ Шаг 7: Упростите и примените любой закон функции, когда это применимо, чтобы получить окончательный ответ. График касательнойx VS. Производная тангенса xУчитывая функцию $latex f(x) = \tan{(x)}$ , график изображается как 9{2}{(x)}$, что графически проиллюстрировано как . Проиллюстрировав оба графика в одном, мы имеем . Анализируя различия этих функций на этих графиках, вы можете заметить, что исходная функция $latex f(x ) = \tan{(x)}$ имеет область определения $latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left (-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\ справа)$ в пределах конечных интервалов 9{2}{(x)}$ имеет домен$latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left( -\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right )$ в конечных интервалах $latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$ и существует в диапазон $latex [1,\infty)$ или $latex y \geq 1$ Примеры Ниже приведены некоторые примеры использования первого или второго метода для получения функции тангенса. ПРИМЕР 1Вывод: $latex f(\beta) = \tan{(\beta)}$ Решение: Анализируя заданную функцию тангенса, мы видим, что это только тангенс одной угол $латекс\бета$. Следовательно, мы можем использовать первый метод для вывода этой задачи. Шаг 1: Проанализируйте, является ли тангенс $latex \beta$ функцией $latex \beta$. В этой задаче есть. Следовательно, перейдите к шагу 2. Шаг 1: 92+2))}$ См. такжеХотите узнать больше о производных тригонометрических функций? Взгляните на эти страницы:
Узнайте о производной функции касательнойОпределение функции производной касательной Функции касания являются одними из наиболее важных функций в тригонометрии. tan=sincostan=\frac{sin}{cos}tan=cossin Обзор функции производной тангенсаисточник. – координата y, деленная на координату x, которые в данном случае равны и , соответственно. На приведенной выше диаграмме четыре квадранта. Верхний правый квадрант известен как первый квадрант, а остальные квадранты называются при движении против часовой стрелки следующим образом: Производные определяются как наклон функции в любой заданной точке. Они оцениваются по первому принципу производной или с использованием фундаментальных производных. Есть вопрос по этой теме?Что вы узнаете:
|

 п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания. Вот они эти три кита:
Вот они эти три кита:
 Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
 По формуле косинуса двойного угла:
По формуле косинуса двойного угла:


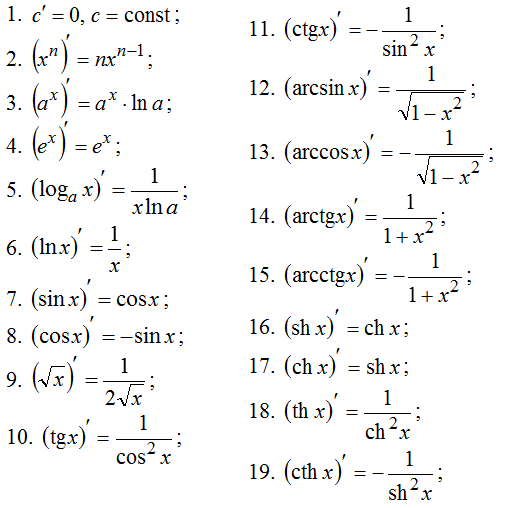
 Так как u=x 4
+1,то
(2
x 4
+2+ .
Так как u=x 4
+1,то
(2
x 4
+2+ . Что касается Матвея — у его дохода производная вообще отрицательна.
Что касается Матвея — у его дохода производная вообще отрицательна.

 Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.