Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Определение 1Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.
Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19, x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Определение 3Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3,7·x+0,6=1 является уравнением с одной переменной x, а x−z=5 – уравнением с двумя переменными x и z. Примером уравнения с тремя переменными может быть выражение x2+(y−6)2+(z+0,6)2=26.
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a+1=5 мы заменим букву числом 2, то равенство станет неверным, а если 4, то получится верное равенство 4+1=5.
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Определение 4Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Пример 2Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a+1=5. Согласно определению, корнем в данном случае будет 4, потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2+1=5.
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0·x=5. Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0.
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Пример 3Так, в уравнении x−2=4 есть только один корень – шесть, в x2=9 два корня – три и минус три, в x·(x−1)·(x−2)=0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅. Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня -2, 1 и 5, то пишем -2, 1, 5 или {-2, 1, 5}.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y, а корнями являются 2 и 7, то мы пишем y=2 и y=7. Иногда к буквам добавляются нижние индексы, например, x1=3, x2=5. Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N, целых – Z, действительных – R. Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x∈Z, а если любое действительное от единицы до девяти, то y∈1, 9.
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Определение 5Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Пример 4Допустим, у нас есть выражение x+y=7, которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4, то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3,4).
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
2+1=3
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
x+2-2=7-2
x+0=7-2
x=7-2
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
x=5
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
x-4+4=12+4
x=12+4
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
При переносе через равно знаки меняются на противоположные.
x=16
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x=2x-5
4+3x-2x=-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4+3x-2x=-5
3x-2x=-5-4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅(-9)=2⋅(-9)-5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
Обязательно делим правую и левую сторону одновременно.
5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
1x=21 или x=21
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
3x=45
Далее делим все уравнение на 3.
3x:3=45:3
(3:3)x=15
1x=15 или x=15
Сделаем проверку. Подставим в уравнение найденный корень.
5=5
Ответ: x=15
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Как найти корень уравнения. Что такое корень уравнения
Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения :
Определение.
Уравнение – это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p , t , u и т.п., но наиболее часто используются буквы x , y и z .
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т. п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18 и x+3·(x+2·(x−2))=3 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8 , 7−3=z+1 или 3·x−4=2·(x+12) .
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений , изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
Уравнением называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7 – уравнение с переменной x , а 3·z−1+z=0 – уравнение с переменной z .
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
Уравнения с одной, двумя, тремя и т.д. переменными – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1
– это уравнение с одной переменной x
, в свою очередь уравнение вида x−y=3
– это уравнение с двумя переменными x
и y
. И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
. Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a в уравнение a+1=5 подставить число 2 , то получится неверное числовое равенство 2+1=5 . Если же мы в это уравнение подставим вместо a число 4 , то получится верное равенство 4+1=5 .
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5 . Согласно озвученному определению корня уравнения, число 4 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5 , а число 2 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5 .
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
имеет корень 4
, а уравнение 0·x=5
не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
, мы получим неверное равенство 0=5
.
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4 имеет единственный корень 6 , корнями уравнения x 2 =9 являются два числа −3 и 3 , уравнение x·(x−1)·(x−2)=0 имеет три корня 0 , 1 и 2 , а решением уравнения x=x является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
Решением уравнения с двумя, тремя и т.д. переменными называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7 . Решение этого уравнения x=4 , y=3 кратко можно записать как (4, 3) .
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений .
Список литературы.
- Математика . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
Способы найти корень уравнения — правила вычисления.
Уравнение – математическое выражение, содержащее одну или несколько неизвестных. Решить уравнение – значит найти такие значения аргументов, при которых достигается равенство левой и правой частей выражения (заданных функций). Найденные значения называются корнями уравнения.
Найденные значения называются корнями уравнения.
В математике выделяют линейные, квадратные и кубические уравнения. Для того чтобы найти корень уравнения определенного типа используются различные методы.
Линейное уравнение
Выражение вида а*х=b называется линейным уравнением. В нем а – коэффициент при переменной, b – свободный член. При его решении может быть три случая, в которых:
- а 0. Корень в этом случае вычисляется по формуле: x=b/a. Например, дано уравнение x+3=9-2*x. Выражения с «Х» переносятся в одну сторону, а свободные члены – в другую: х+2*х=9-3, или 3*х=6. Тогда х=6/3, х=2.
- а=0, b=0. Уравнение примет вид 0*х=0. Это равенство будет верным при любом значении «Х». Значит, корнем уравнения будет любое действительное число.
- а=0, b 0. Получится выражение 0*х=b, для которого не существует корней.
Квадратное уравнение
Уравнение вида называется квадратным (а 0). «А» и «B» называются коэффициентами, а «С» – свободным членом. Количество корней зависит от значения дискриминанта, который вычисляется по формуле. В том случае, если:
Количество корней зависит от значения дискриминанта, который вычисляется по формуле. В том случае, если:
- D
- D=0 – есть один корень, который находится по формуле: x=-b/(2*a).
- D>0 – существует два корня, определяемые следующим образом: Например, дано уравнение 3*х2-2*х-5=0. Дискриминант D=4-4*3*(-5)=64. Будет два корня.
Кубическое уравнение
Выражение вида называется кубическим уравнением. Оно может обладать несколькими корнями, для вычисления которых нужно:
- Найти один из корней, который представляет собой делитель свободного члена «d» путем подстановки всех возможных делителей, пока левая часть выражения не станет равной нулю.
- Разделить исходное уравнение на найденный корень, в результате чего выражение будет приведено к виду квадратного.
- Найти корни полученного уравнения. Например, дано уравнение. Делители свободного члена 12 – ±2, ±3, ±4, ±6, ±12. Левая часть принимает значение, равное 0 при х=2. Значит 2 – первый корень.
 Затем нужно разделить исходное выражение на (х-2). Получится квадратное уравнение. Его корнями будут числа..
Затем нужно разделить исходное выражение на (х-2). Получится квадратное уравнение. Его корнями будут числа..
Другие способы
Помимо алгебраического вычисления необходимых значений можно воспользоваться:
- Бесплатным онлайн-калькулятором (allcalc.ru).
- Графическим способом, когда строится график функции, точки пересечения которого с осью «Х» будут корнями уравнения.
Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?
Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.
Например, 3x=9 — это уравнение, а 3 . 3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.
Вот этим мы и займемся — будем находить корень уравнения.
Задание 1 — найдите корень уравнения 2 1-4x =32
Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.
Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2 5
Таким образом, наше уравнение будет выглядеть так: 2 1-4х =2 5
Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:
Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:
Делаем проверку: 2 1-4(-1) =32
Мы нашли корень уравнение. Ответ: х=-1.
Самостоятельно найдите корень уравнения в следующих заданиях:
б) 2 1-3х =128
Задание 2 — найдите корень уравнения
Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.
В нашем случае — к основанию степени 2.
Используем следующее свойство степени:
По этому свойству мы получим для правой части нашего уравнения:
Если равны основания степени, значит, равны и показатели степени:
Ответ: х=9.
Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.
Мы нашли корень уравнения правильно.
Задание 3 — найдите корень уравнения
Заметим, что справа у нас стоит 1/8, а 1/8 — это
Тогда наше уравнение запишется в виде:
Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:
Ответ: х=5. Проверку сделайте самостоятельно.
Задание 4 — найдите корень уравнения log 3 (15-х)=log 3 2
Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
Ответ: х=13
Задание 5 — найдите корень уравнения log 3 (3-x)=3
Число 3 — это log 3 27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Смотрите на картинке:
Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:
log 3 (3-x)=log 3 27
Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:
Сделаем проверку:
log 3 (3-(-24))=log 3 27
log 3 (3+24)= log 3 27
log 3 27=log 3 27
Ответ: x=-24.
Найдите корень уравнения. Задание 6.
log 2 (x+3)=log 2 (3x-15)
Проверка: log 2 (9+3)=log 2 (27-15)
log 2 12=log 2 12
Ответ: x=9.
Найдите корень уравнения. Задание 7.
log 2 (14-2x)=2log 2 3
log 2 (14-2x)=log 2 3 2
Проверка: log 2 (14-5)=2log 2 3
log 2 9=2log 2 3
log 2 3 2 =2log 2 3
2log 2 3=2log 2 3
Ответ: x=2,5
Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы и .
Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.
Что это такое?
Уравнение — это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество — одна.
Решить его — это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.
Какие виды уравнений существуют?
Линейное. Оно содержит переменную, степень которой равна единице.
- Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени.
- Уравнение высшей степени.
- Дробно-рациональное.
 Когда переменная величина оказывается в знаменателе дроби.
Когда переменная величина оказывается в знаменателе дроби. - С модулем.
- Иррациональное. То есть такое, которое содержит алгебраический корень.
Как решается линейное уравнение?
Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.
- Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые.
- Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой.
- Привести подобные члены в каждой части решаемого уравнения.
- В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой — число.
- Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.
Как найти корни квадратного уравнения?
Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.
В правой части равенства должен остаться только ноль.
- Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение.
- Оцените значение дискриминанта. Он отрицательный — решение закончено, так как у него корней нет. Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Как решить кубическое уравнение?
Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х 3 — 3х 2 — 4х + 12 = 0.
Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 — это первый корень кубического уравнения.
Значит число 2 — это первый корень кубического уравнения.
Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х 2 — х — 6 = 0.
Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.
Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.
Как решаются системы линейных уравнений?
Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.
Если в них переменные обозначены буквами х 1 и х 2 , то можно из первого равенства вывести, к примеру, х 2 . Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.
Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.
Теперь возвратитесь к первому уравнению и найдите корень уравнения x 2 , используя получившееся равенство. Эти два числа являются ответом.
Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку. Ее не обязательно записывать.
Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось — решение верное.
При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.
В алгебре существует понятие двух видов равенств — тождества и уравнения. Тождества — это такие равенства, которые выполнимы при любых значениях букв, в них входящих. Уравнения — это тоже равенства, но выполнимы они лишь при некоторых значениях входящих в них букв.
Буквы по условию задачи обычно бывают неравноправными. Это значит, что одни из них могут принимать любые допустимые значения, называемые коэффициентами (или параметрами), другие же — их называют неизвестными — принимают значения, которые необходимо найти в процессе решения. Как правило, неизвестные величины обозначают в уравнениях буквами, последними в (x.y.z и т.д.), либо такими же буквами, но с индексом (х 1 ,х 2 , и т.д.), а известные коэффициенты — первыми буквами того же алфавита.
По количеству неизвестных выделяют уравнения с одним, двумя и несколькими неизвестными. Таким образом, все значения неизвестных, при которых решаемое уравнение превращается в тождество, называются решениями уравнений. Уравнение можно считать решенным в том случае, если найдены все его решения или доказано, что оно таковых не имеет. Задание «решить уравнение» на практике встречается часто и означает, что нужно отыскать корень уравнения.
Определение : корнями уравнения называются те значения неизвестных из области допустимых, при которых решаемое уравнение превращается в тождество.
Алгоритм решения абсолютно всех уравнений одинаков, и смысл его заключается в том, чтобы с помощью математических преобразований данное выражение привести к более простому виду.
Уравнения, которые имеют одинаковые корни, в алгебре называются равносильными.
Простейший пример: 7х-49=0, корень уравнения х=7;
х-7=0, аналогично, корень х=7, следовательно, уравнения равносильные. (В частных случаях равносильные уравнения могут совсем не иметь корней).
Если корень уравнения одновременно является корнем другого, более простого уравнения, полученного из исходного путем преобразований, то последнее называется следствием предыдущего уравнения.
Если их двух уравнений одно является следствием другого, то они считаются равносильными. Еще их называют эквивалентными. Приведенный выше пример это иллюстрирует.
Решение даже самых простых уравнений на практике нередко вызывает сложности. В результате решения можно получить один корень уравнения, два и более, даже бесконечное количество — зависит это от вида уравнений. Есть и такие, у которых нет корней, они называются неразрешимыми.
Есть и такие, у которых нет корней, они называются неразрешимыми.
Примеры:
1) 15х -20=10; х=2. Это единственный корень уравнения.
2) 7х — y=0. Уравнение имеет бесконечное множество корней, так как у каждой переменной может быть бесчисленное количество значений.
3) х 2 = — 16. Число, возведенное во вторую степень, всегда дает положительный результат, поэтому невозможно отыскать корень уравнения. Это и есть одно из неразрешимых уравнений, о которых говорилось выше.
Правильность решения проверяется подстановкой найденных корней вместо букв и решением получившегося примера. Если тождество соблюдается, решение верное.
Как определить корни уравнения. Как находить корень уравнения
Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения :
Определение.
Уравнение – это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p , t , u и т.п., но наиболее часто используются буквы x , y и z .
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т.п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18 и x+3·(x+2·(x−2))=3 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8 , 7−3=z+1 или 3·x−4=2·(x+12) .
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений , изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
Уравнением называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7 – уравнение с переменной x , а 3·z−1+z=0 – уравнение с переменной z .
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
Уравнения с одной, двумя, тремя и т.д. переменными – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1 – это уравнение с одной переменной x , в свою очередь уравнение вида x−y=3 – это уравнение с двумя переменными x и y . И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27 . Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x , y и z .
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a в уравнение a+1=5 подставить число 2 , то получится неверное числовое равенство 2+1=5 . Если же мы в это уравнение подставим вместо a число 4 , то получится верное равенство 4+1=5 .
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5 . Согласно озвученному определению корня уравнения, число 4 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5 , а число 2 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5 .
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5 имеет корень 4 , а уравнение 0·x=5 не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x , мы получим неверное равенство 0=5 .
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4
имеет единственный корень 6
, корнями уравнения x 2 =9
являются два числа −3
и 3
, уравнение x·(x−1)·(x−2)=0
имеет три корня 0
, 1
и 2
, а решением уравнения x=x
является любое число, то есть, оно имеет бесконечное множество корней.
Например, уравнение x−2=4
имеет единственный корень 6
, корнями уравнения x 2 =9
являются два числа −3
и 3
, уравнение x·(x−1)·(x−2)=0
имеет три корня 0
, 1
и 2
, а решением уравнения x=x
является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
Решением уравнения с двумя, тремя и т.д. переменными называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7 . Решение этого уравнения x=4 , y=3 кратко можно записать как (4, 3) .
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений .
Список литературы.
- Математика . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России).
 — ISBN 978-5-09-028297-0.
— ISBN 978-5-09-028297-0. - Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
Алгоритм преобразований:
- перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
- разделить обе части получившегося равенства на коэффициент «а».
Общий вид решения такой:
х = -в/а .
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0 . Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с . После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
х 1,2 = (-в ± √Д) / (2 * а) .
Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
х 1 + х 2 = -в
и
х 1 * х 2 = с.
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х 1,2 = ± 1, х 3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.
Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Если есть две величины, а между ними стоит знак равенства, то это пример, который называют уравнением. Высчитав неизвестное, мы узнаем корень. Чтобы рассекретить это неизвестное, придется потрудиться над вычислением.
Понятнее будет, если возьмем в работу конкретное уравнение: x+10=16-2х. Оно относится к линейным, составляют его свободные члены и неизвестное х. Разносим эти составляющие в разные стороны от знака равенства. Теперь уравнение приобрело такой вид: 2х + х = 16 – 10 или 3х = 6; х = 2. Результат: Х = 2.
Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате. Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0. Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90. Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0. Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3. В итоге получим 6 – значит, доведя до конца расчет, обнаружим, что у этого уравнения корней 2. Если бы дискриминант выражался числом отрицательным, то изощряться в вычислении корней было бы нерационально – их просто нет. В случае если D=0, корень только 1. Теперь все-таки выполним расчет, чтобы определить эти 2 корня. Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2.
Результат: Х = 2.
Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате. Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0. Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90. Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0. Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3. В итоге получим 6 – значит, доведя до конца расчет, обнаружим, что у этого уравнения корней 2. Если бы дискриминант выражался числом отрицательным, то изощряться в вычислении корней было бы нерационально – их просто нет. В случае если D=0, корень только 1. Теперь все-таки выполним расчет, чтобы определить эти 2 корня. Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2. Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2.
Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2.
Сложнее квадратного уравнение кубическое. Вид у него такой: х3-3х2-4х+20=0. Подбираем число, на которое можно поделить свободный член, чтобы слева появился 0. Делители для 20 – это ±1, ±2, ±4, ±5, ± 10, ± 20. Получается, что это делитель 5, он же и один из искомых корней. Остается решить квадратное уравнение и все корни известны.
Вот и все премудрости. Нет ничего сложного, но чтобы было совсем просто, можно воспользоваться онлайн-калькулятором.
Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.
Что это такое?
Уравнение — это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество — одна.
Причем количество неизвестных величин может быть произвольным. Минимальное количество — одна.
Решить его — это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.
Какие виды уравнений существуют?
Линейное. Оно содержит переменную, степень которой равна единице.
- Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени.
- Уравнение высшей степени.
- Дробно-рациональное. Когда переменная величина оказывается в знаменателе дроби.
- С модулем.
- Иррациональное. То есть такое, которое содержит алгебраический корень.
Как решается линейное уравнение?
Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.
- Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые.

- Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой.
- Привести подобные члены в каждой части решаемого уравнения.
- В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой — число.
- Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.
Как найти корни квадратного уравнения?
Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.
- Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение.
- Оцените значение дискриминанта. Он отрицательный — решение закончено, так как у него корней нет.
 Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Как решить кубическое уравнение?
Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х 3 — 3х 2 — 4х + 12 = 0.
Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 — это первый корень кубического уравнения.
Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х 2 — х — 6 = 0.
Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.
Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.
Как решаются системы линейных уравнений?
Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.
Если в них переменные обозначены буквами х 1 и х 2 , то можно из первого равенства вывести, к примеру, х 2 . Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.
Теперь возвратитесь к первому уравнению и найдите корень уравнения x 2 , используя получившееся равенство. Эти два числа являются ответом.
Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку. Ее не обязательно записывать.
Ее не обязательно записывать.
Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось — решение верное.
При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Внеклассный урок — Уравнение с одной переменной. Корень уравнения. Уравнения n-й степени. Уравнение с одной переменной.
Уравнение с одной переменной. Корень уравнения. Уравнения n-й степени
Уравнение – это равенство, содержащее переменную, обозначенную буквой.
Корень уравнения (или решение уравнения) – это такое значение переменной, при котором уравнение превращается в верное равенство.
Пример: решим уравнение (то есть найдем корень уравнения): 4x – 15 = x + 15
Итак:
4х – х = 15 + 15
3х = 30
х = 30 : 3
х = 10
Результат: уравнение имеет один корень – число 10.
Уравнение может иметь и два, три, четыре и более корней. Например, уравнение (х-4)(х-5)(х-6) = 0 имеет три корня: 4, 5 и 6.
Уравнение может вовсе не иметь корней. Например, уравнение х+2=х не имеет корней, т.к. при любом значении х равенство невозможно.
Равносильность уравнений.
Два уравнения являются равносильными, если они имеют одинаковые корни либо если оба уравнения не имеют корней.
Пример1:
Уравнения х + 3 = 5 и 3х – 1 = 5 равносильны, так как в обоих уравнениях х=2.
Пример 2:
Уравнения х4 + 2 = 1 и х2 + 5 = 0 равносильны, так как оба уравнения не имеют корней.
Целое уравнение с одной переменной
Целое уравнение с одной переменной – это уравнение, левая и правая части которого являются целыми выражениями (о целых выражениях см. раздел «Рациональные выражения»).
раздел «Рациональные выражения»).
Уравнение с одной переменной может быть записано в виде P(x) = 0, где P(x) – многочлен стандартного вида.
Например:
y2 + 3y – 6 = 0
(здесь P(x) представлен в виде многочлена y2 + 3y – 6).
В таком уравнении степень многочлена называют степенью уравнения.
В нашем примере представлено уравнение второй степени (так как в нем многочлен второй степени).
Уравнение первой степени.
Уравнение первой степени можно привести к виду:
ax + b = 0,
где x – переменная, a и b – некоторые числа, причем a ≠ 0.
Отсюда легко вывести значение x:
b
x = – —
a
Это значение x является корнем уравнения.
Уравнения первой степени имеют один корень.
Уравнение второй степени.
Уравнение второй степени можно привести к виду:
ax2 + bx + c = 0,
где x – переменная, a, b, c – некоторые числа, причем a ≠ 0.
Число корней уравнения второй степени зависит от дискриминанта:
— если D > 0, то уравнение имеет два корня;
— если D = 0, то уравнение имеет один корень;
— если D < 0, то уравнение корней не имеет.
Уравнение второй степени может иметь не более двух корней.
(о том, что такое дискриминант и как находить корни уравнения, см.разделы «Формулы корней квадратного уравнения. Дискриминант» и «Другой способ решения квадратного уравнения»).
Уравнение третьей степени.
Уравнение третьей степени можно привести к виду:
ax3 + bx2 + cx + d = 0,
где x – переменная, a, b, c, d – некоторые числа, причем a ≠ 0.
Уравнение третьей степени может иметь не более трех корней.
Уравнение четвертой степени.
Уравнение четвертой степени можно привести к виду:
ax4 + bx3 + cx2 + dx + e = 0,
где x – переменная, a, b, c, d, e – некоторые числа, причем a ≠ 0.
Уравнение третьей степени может иметь не более четырех корней.
Обобщение:
1) уравнение пятой, шестой и т.д. степеней можно легко вывести самостоятельно, следуя приведенной выше схеме;
2) уравнение n-й степени может иметь не более n корней.
Пример 1: Решим уравнение
x3 – 8x2 – x + 8 = 0.
Мы видим, что это уравнение третьей степени. Значит, у него может быть от нуля до трех корней.
Найдем их и тем самым решим уравнение.
Разложим левую часть уравнения на множители:
x2(x – 8) – (x – 8) = 0.
Применим правило разложения многочлена способом группировки его членов. Для этого поставим перед вторыми скобками число 1:
x2(x – 8) – 1(x – 8) = 0.
Теперь сгруппируем многочлены x2 и –1, являющиеся множителями многочлена x–8.
Получим две группы многочленов: (x2 –1) и (x – 8). Следовательно, наше уравнение примет новый вид:
(x – 8)(x2 – 1) = 0.
Здесь выражение x2 – 1 можно представить в виде x2 – 12.
А значит, можем применить формулу сокращенного умножения: x2 – 12 = (x – 1)(x + 1).
Подставим в наше уравнение это выражение и получим:
(x – 8)(x – 1)(x + 1) = 0.
Дальше все просто. При x – 8 = 0 всё уравнение тоже равно нулю.
При x – 8 = 0 всё уравнение тоже равно нулю.
И так – в случае и с двумя остальными выражениями x – 1 и x + 1. Таким образом:
x – 8 = 0
x – 1 = 0
x + 1 = 0
Осталось найти корни нашего уравнения:
x1 = 0 + 8 = 8
x2 = 0 + 1 = 1
x3 = 0 – 1 = –1.
Уравнение решено. Оно имеет три корня: 8, 1 и –1.
Пример 2: Решим уравнение
(x2 – 5x + 4)(x2 – 5x +6) = 120.
Это уравнение сложнее. Но его можно упростить оригинальным образом – методом введения новой переменной.
В нашем уравнении дважды встречается выражение x2 – 5x.
Мы можем обозначить его переменной y. То есть представим, что x2 – 5x = y.
Тогда наше уравнение обретает более простой вид:
(y + 4)(y + 6) = 120.
Раскроем скобки:
y2 + 4y + 6y + 24 = 120
y2 + 10y + 24 = 120
Приравняем уравнение к нулю:
y2 + 10y + 24 – 120 = 0
y2 + 10y – 96 = 0
Мы получили обычное квадратное уравнение. Найдем его корни. Нет необходимости производить расчеты: о том, как решать подобные уравнения, подробно написано в разделах «Квадратные уравнения» и «Формулы корней квадратного уравнения. Дискриминант». Здесь же мы сразу выведем результат. Квадратное уравнение y2 + 10y – 96 = 0 имеет два корня:
y1 = -16
y2 = 6
Буквой y мы заменили выражение x2 – 5x. А значит, мы уже можем подставить значения y и найти корни заданного уравнения, тем самым решив задачу:
1) Сначала применяем значение y1 = –16:
x2 – 5x = –16
Чтобы решить это уравнение, превращаем его в квадратное уравнение:
x2 – 5x + 16 = 0
Решив его, мы обнаружим, что оно не имеет корней.
2) Теперь применяем значение y2 = 6:
x2 – 5x = 6
x2 – 5x – 6 = 0
Решив это квадратное уравнение, мы увидим, что у него два корня:
x1 = –1
x2 = 6.
Уравнение решено. Оно имеет два корня: –1 и 6.
Метод введения новой переменной позволяет легко решать уравнения четвертой степени, которые являются квадратными относительно x2 (такие уравнения называют биквадратными).
Что такое корень уравнения. Уравнение Объяснение темы уравнение и его корни
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Yandex.RTB R-A-339285-1
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Тогда оно определяется так:
Определение 1
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6: x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · (x − 1) = 19 , x + 6 · (x + 6 · (x − 8)) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · (8 + 1) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · (x + 17) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Определение 2
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Определение 3
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + (y − 6) 2 + (z + 0 , 6) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Пример 1
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Определение 4
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Пример 2
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Пример 3
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · (x − 1) · (x − 2) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или { — 2 , 1 , 5 } .
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Определение 5
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Пример 4
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3 , 4) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В предложенном видео речь идет о понятии уравнения и его корнях. Для начала рассмотрена задача о гусях. В задаче стая гусей отвечает гусю, что если бы их было столько, сколько сейчас, да еще столько, да еще полстолька, да еще четверть столько, да еще он, то их было бы сто гусей. Вопрос: Сколько гусей в стае?
Неизвестное число гусей в стае обозначили через Х.
В результате получили: Х + Х +1/2Х+ 1/4Х + 1 = 100.
В этом равенстве присутствует неизвестная нам величина Х, значение которой мы ищем. Это значение мы можем найти из составленного нами равенства. Подобные равенства называют уравнениями с одной переменной, или уравнениями с одним неизвестным.
Искомую неизвестную величину принято обозначать буквой Х, хотя можно обозначать любой буквой. Впервые неизвестную величину обозначил буквой и составил уравнение в явном виде с неизвестным древнегреческий математик Диофант в своем труде «Арифметика».
Впервые неизвестную величину обозначил буквой и составил уравнение в явном виде с неизвестным древнегреческий математик Диофант в своем труде «Арифметика».
В составленном уравнении необходимо найти такое значение переменной, которое превращает уравнение в правильное числовое равенство. Такое значение неизвестной называют корнем уравнения.
Делаем вывод, что корнем уравнения называется значение переменной, превращающее уравнение в верное числовое равенство. Решить уравнение означает найти множество его корней, число которых может быть различным. Корень может быть один, их может быть несколько, а может и не быть ни одного. В конечном итоге, чтобы решить уравнение, необходимо определить все его корни или убедиться, что у уравнения нет корней.
Количество корней уравнения может быть разным в зависимости от вида уравнения. В некоторых случаях и число может быть бесконечным, а может быть равно нулю. Для убедительности автор предлагает рассмотреть примеры уравнений, которые имеют разное количество корней. Это уравнения Х + 1 = 6, (Х — 1)(Х — 5)(Х — 8) = 0, Х = Х + 4, 3(Х + 5) = 3Х + 15. В первом случае корень один, так как только в случае, когда Х = 5, уравнение становится верным числовым равенством 6 = 6. Второе уравнение имеет три корня. Это числа 1, 5, 8. Именно при этих значениях переменной выражения в скобках по очереди принимают значение 0. При умножении на 0 все выражение становиться равным 0. Получаем равенство 0 = 0. Третье уравнение не имеет корней, потому что при любом значении Х правая часть принимает значение больше, чем левая. Четвертое уравнение в свою очередь имеет бесконечное число корней в силу применения сочетательного свойства умножения. После раскрытия скобок и левая, и правая части уравнения имеют одинаковый вид: 3Х + 15 = 3Х = 15.
Это уравнения Х + 1 = 6, (Х — 1)(Х — 5)(Х — 8) = 0, Х = Х + 4, 3(Х + 5) = 3Х + 15. В первом случае корень один, так как только в случае, когда Х = 5, уравнение становится верным числовым равенством 6 = 6. Второе уравнение имеет три корня. Это числа 1, 5, 8. Именно при этих значениях переменной выражения в скобках по очереди принимают значение 0. При умножении на 0 все выражение становиться равным 0. Получаем равенство 0 = 0. Третье уравнение не имеет корней, потому что при любом значении Х правая часть принимает значение больше, чем левая. Четвертое уравнение в свою очередь имеет бесконечное число корней в силу применения сочетательного свойства умножения. После раскрытия скобок и левая, и правая части уравнения имеют одинаковый вид: 3Х + 15 = 3Х = 15.
Далее автор вводит понятие допустимых значений неизвестного. Для этого рассматриваются уравнения 17 — 3Х = 2Х — 2 и (25 — Х)/(Х — 2) = Х + 9. Если в первом случае неизвестное Х может принимать любые значения, то во втором при Х = 2 получаем деление на 0. Следовательно, значения переменной, которые можно подставлять в уравнение в первом случае все числа, а во втором — все числа, кроме 2.
Следовательно, значения переменной, которые можно подставлять в уравнение в первом случае все числа, а во втором — все числа, кроме 2.
Область определения уравнения — это множество значений переменно, при которых обе части уравнения имеют смысл.
После этого вводится понятие равносильности уравнений. Рассматриваются уравнения Х 2 = 36 и (Х — 6)(Х + 6) = 0. У этих уравнений одинаковые корни; такие уравнения принято называть равносильными.
При решении уравнений их заменяют равносильными уравнениями, но более простыми по форме. Необходимо помнить некоторые правила замены уравнения на равносильное уравнение. Во время переноса слагаемого через знак равенства знак слагаемого меняем на противоположный. При умножении или делении обеих частей уравнения на одно и то же число, неравное 0, уравнение останется равносильным. Можно выполнять тождественные преобразования, если они не влияют на область определения уравнения.
Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения :
Определение.
Уравнение – это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p , t , u и т.п., но наиболее часто используются буквы x , y и z .
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т. п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18 и x+3·(x+2·(x−2))=3 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8 , 7−3=z+1 или 3·x−4=2·(x+12) .
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений , изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
Уравнением называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7 – уравнение с переменной x , а 3·z−1+z=0 – уравнение с переменной z .
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
Уравнения с одной, двумя, тремя и т.д. переменными – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1
– это уравнение с одной переменной x
, в свою очередь уравнение вида x−y=3
– это уравнение с двумя переменными x
и y
. И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
. Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a в уравнение a+1=5 подставить число 2 , то получится неверное числовое равенство 2+1=5 . Если же мы в это уравнение подставим вместо a число 4 , то получится верное равенство 4+1=5 .
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5 . Согласно озвученному определению корня уравнения, число 4 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5 , а число 2 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5 .
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
имеет корень 4
, а уравнение 0·x=5
не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
, мы получим неверное равенство 0=5
.
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4 имеет единственный корень 6 , корнями уравнения x 2 =9 являются два числа −3 и 3 , уравнение x·(x−1)·(x−2)=0 имеет три корня 0 , 1 и 2 , а решением уравнения x=x является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
Решением уравнения с двумя, тремя и т.д. переменными называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7 . Решение этого уравнения x=4 , y=3 кратко можно записать как (4, 3) .
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений .
Список литературы.
- Математика . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- обобщить и систематизировать знания по теме “Уравнения”;
- способствовать развитию логического мышления и речи учащихся.
Технические средства обучения: мультимедийный проектор.
Ход урока
1. Домашнее задание: п. 6, № 113, 117, 120.
2. Математический диктант (под копирку).
Дети сдают диктанты, обмениваются тетрадями, проверяют друг у друга работы. Ответы проецируются на доску.
3. Сообщение темы урока.
Каким было последнее задание в диктанте? (Решить уравнение).
Учиться решать уравнения вы начали ещё в начальных классах. С этой темой мы встречались в 5 и 6 классах, узнавая каждый раз что – то новое об уравнениях. Задачей нашего сегодняшнего урока является обобщение и систематизация знаний об уравнениях.
4. Изучение нового материала (с
применением компьютерной презентации).
1) – Запишите тему нашего урока “Уравнение и его корни”. (Слайд 1)
2) – Давайте постараемся дать определение уравнению. Что же это такое? (Слайд 2)
Равенство, содержащее переменную, называется уравнением с одной переменной или уравнением с одним неизвестным.
3) Помня определение уравнения, определите, является ли данная запись уравнением:
а) х + 2 = 1,3;
г) 16 * 5 – 8 = 72;
д) 1.5 х + 2.8 = 5,8. (Слайд 3)
Дети объясняют свои ответы, подчёркивая, является ли данная запись равенством и содержит ли она переменную.
4) — Вспомните, пожалуйста, что называют корнем уравнения.
Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.
Проверим ваши ответы. (Слайд 4)
5) – Как узнать, является ли данное число корнем
уравнения или нет? (Надо подставить число в
уравнение вместо переменной, посмотреть,
обратится ли при этом уравнение в верное
равенство или нет. )
)
Выясните, является ли число 2 корнем уравнения:
а) 4 + 3х = 10;
б) (х – 5)(х + 1) = 11;
в) 6(3х – 1) = 12х + 6. (Слайд 5)
Учащиеся подставляют число 2 в каждое уравнение, проверяя, обращает ли оно данное уравнение в верное равенство. Делают соответствующий вывод.
6) – Следующее задание выполним письменно.
Определите, какие из чисел – 2, — 1, 0, 2, 3 являются корнем уравнения х 2 + 3х = 10. (Слайд 6)
Задание выполняется учащимися в тетради. Некоторые ученики по очереди делают соответствующие записи на доске.
Образец выполнения задания:
Корнем уравнения х 2 + 3х = 10 число
а) -2 не является, так как (-2) 2 + 3 * (-2) = 4 – 6 = — 2, а -2 10;
б) – 1 не является, так как (- 1) 2 + 3 * (- 1) = 1 – 3 = -2, а – 2 10;
в) 0 не является, так как 0 2 + 3 * 0 = 0, а 0 10;
г) 2 является, так как 2 2 + 3 * 2 = 4 + 6 = 10, а 10 = 10;
д) 3 не является, так как 3 2 + 3 * 3 = 9 + 9 = 18, а 18 10.
7) Физ. пауза.
пауза.
А теперь немного отдохнём. Сядьте удобно.
1. Делаем вертикальные движения глазами вверх – вниз.
2. Горизонтальные движения глазами вправо – влево.
3. “Нарисуем глазами линию” (на плакате изображено несколько линий, дети “ведут” по ним глазами от точки до точки).
Следующие упражнения выполняем стоя.
4. – Поднимаем сначала правое плечо вверх, потом левое, опускаем сначала правое плечо, потом левое. Так продолжаем поочерёдно.
5. “Роняем руки”.
6. “Стряхиваем воду с кистей рук”.
Постарайтесь сами составить уравнение, корнем которого было бы число 3. (Слайд 7)
После самостоятельного выполнения задания некоторые учащиеся зачитывают получившиеся у них уравнения, класс определяет, правильно ли выполнено задание.
9) – Как вы думаете, что значит решить уравнение?
Решить уравнение – значит найти его корни или доказать, что корней нет. (Слайд 8)
10) – Какие из данных уравнений не имеют корней:
б) 4(х + 1) = 4х +7;
в) 3х + 12 = 3(х + 4). (Слайд 9)
(Слайд 9)
Дети дают ответы, обосновывая их.
11) – Что называется модулем числа?
Чему равен модуль положительного числа?
Модуль нуля? Отрицательного числа?
Может ли модуль числа равняться отрицательному числу?
Как вы думаете, имеют ли данные уравнения корни и, если имеют, то сколько:
в) l х l = — 1;
г) l х l = 2,5. (Слайд 10)
12) – Сегодня мы знакомимся с новым для вас понятием – это равносильные уравнение. Попробуйте догадаться, какие же уравнения называются равносильными.
Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. (Слайд 11)
13) – Какое уравнение равносильно уравнению 3х – 10 = 50? (Слайд 12)
Учащиеся составляют уравнения, равносильные данному, записывают их в тетрадь, некоторые из составленных уравнений зачитываются и обсуждаются классом.
14) – При решении уравнений используются свойства, которые мы с вами учили в 6 классе. Давайте их вспомним. (Слайд 13)
1) Если в уравнении перенести слагаемое из одной
части в другую, изменив его знак на
противоположный, то получится уравнение,
равносильное данному.
2) Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
15) – Замените уравнения равносильными уравнениями с целыми коэффициентами:
а) 0,1х = — 5;
б) – 0,19 у = 3;
в) — 0,7х = — 4,9. (Слайд 14)
Замените уравнения равносильными уравнениями вида ах = b:
а) 8х + 15 = 39;
б) 16 – 2х = 10. (Слайд 15)
5. Подведение итогов урока . (Слайд 16)
Дайте определение уравнения с одной переменной.
Что называют корнем уравнения?
Все ли уравнения имеют корни?
Что значит решить уравнение?
Какие уравнения называются равносильными?
Назовите свойства, которые используются при решении уравнений.
Использованная литература.
Учебник “Алгебра. 7 класс” под редакцией С. А. Теляковского, Москва “Просвещение”, 2009 год.
Как решить уравнение квадратного корня
Квадратный корень числа — это значение, которое при умножении само на себя дает исходное число. Например, квадратный корень из 0 равен 0, квадратный корень из 100 равен 10, а квадратный корень из 50 равен 7,071. Иногда вы можете вычислить или просто вспомнить квадратный корень из числа, которое само по себе является «полным квадратом», представляющим собой произведение целого числа, умноженного само на себя; по мере того, как вы продвигаетесь в учебе, вы, вероятно, разработаете в уме список этих чисел (1, 4, 9, 25, 36 . . .).
Например, квадратный корень из 0 равен 0, квадратный корень из 100 равен 10, а квадратный корень из 50 равен 7,071. Иногда вы можете вычислить или просто вспомнить квадратный корень из числа, которое само по себе является «полным квадратом», представляющим собой произведение целого числа, умноженного само на себя; по мере того, как вы продвигаетесь в учебе, вы, вероятно, разработаете в уме список этих чисел (1, 4, 9, 25, 36 . . .).
Задачи на квадратные корни незаменимы в инженерии, вычислениях и практически во всех областях современного мира. Хотя вы можете легко найти онлайн-калькуляторы уравнений с квадратным корнем (пример см. в разделе Ресурсы), решение уравнений с квадратным корнем — важный навык в алгебре, поскольку он позволяет вам ознакомиться с использованием радикалов и работать с рядом типов задач за пределами области. квадратных корней как таковых.
Квадраты и квадратные корни: основные свойства
Тот факт, что умножение двух отрицательных чисел вместе дает положительное число, важен в мире квадратных корней, поскольку подразумевает, что положительные числа на самом деле имеют два квадратных корня (например, квадратные корни из 16 равны 4 и −4, даже если только первый интуитивно понятен). Точно так же отрицательные числа не имеют действительных квадратных корней, потому что не существует действительного числа, которое принимает отрицательное значение при умножении само на себя. В этой презентации отрицательный квадратный корень из положительного числа будет игнорироваться, так что «квадратный корень из 361» можно принять за «19».» вместо » -19 и 19″.
Точно так же отрицательные числа не имеют действительных квадратных корней, потому что не существует действительного числа, которое принимает отрицательное значение при умножении само на себя. В этой презентации отрицательный квадратный корень из положительного числа будет игнорироваться, так что «квадратный корень из 361» можно принять за «19».» вместо » -19 и 19″.
Кроме того, при попытке оценить значение квадратного корня, когда нет под рукой калькулятора, важно понимать, что функции, включающие квадраты и квадратные корни, не являются линейными. Вы увидите подробнее об этом в разделе о графиках позже, но в качестве грубого примера вы уже заметили, что квадратный корень из 100 равен 10, а квадратный корень из 0 равен 0. На первый взгляд это может привести вас к предположению, что квадратный корень для 50 (что находится на полпути между 0 и 100) должно быть 5 (что находится на полпути между 0 и 10).Но вы также уже узнали, что квадратный корень из 50 равен 7,071.
Наконец, вы, возможно, усвоили идею о том, что умножение двух чисел дает число, большее, чем оно само, а это означает, что квадратные корни чисел всегда меньше исходного числа. Это не тот случай! У чисел от 0 до 1 тоже есть квадратные корни, и в каждом случае квадратный корень больше, чем исходное число. Это легче всего показать с помощью дробей. Например, 16/25, или 0,64, имеет полный квадрат как в числителе, так и в знаменателе. Это означает, что квадратный корень дроби — это квадратный корень из ее верхней и нижней частей, то есть 4/5. Это равно 0,80, что больше, чем 0,64.
Это не тот случай! У чисел от 0 до 1 тоже есть квадратные корни, и в каждом случае квадратный корень больше, чем исходное число. Это легче всего показать с помощью дробей. Например, 16/25, или 0,64, имеет полный квадрат как в числителе, так и в знаменателе. Это означает, что квадратный корень дроби — это квадратный корень из ее верхней и нижней частей, то есть 4/5. Это равно 0,80, что больше, чем 0,64.
Терминология квадратного корня
«Квадратный корень из x » обычно записывается с использованием так называемого знака корня или просто корня (√). Таким образом, для любого x :
\sqrt{x}
представляет собой его квадратный корень. Переворачивая это, квадрат числа x записывается с использованием показателя степени 2 ( x 2 ). Показатели принимают надстрочные индексы в текстовых процессорах и связанных с ними приложениях и также называются степенями. Поскольку радикальные знаки не всегда легко изготовить по запросу, другой способ записи «квадратный корень из 9{(y/z)}
означает «возвести x в степень y , затем взять из него корень z ». Таким образом, x 1/2 означает «возвести x в первую степень, что равно просто x , а затем извлечь из него корень 2 или квадратный корень». Расширяя это, x (5/3) означает «возвести x в степень 5, затем найти третий корень (или кубический корень) результата».
Таким образом, x 1/2 означает «возвести x в первую степень, что равно просто x , а затем извлечь из него корень 2 или квадратный корень». Расширяя это, x (5/3) означает «возвести x в степень 5, затем найти третий корень (или кубический корень) результата».
Радикалы могут использоваться для представления корней, отличных от 2, квадратного корня. Это делается простым добавлением надстрочного индекса в верхнем левом углу радикала. 95}
представляет то же число, что и x (5/3) из предыдущего абзаца.
Большинство квадратных корней являются иррациональными числами. Это означает, что они не только не являются красивыми, аккуратными целыми числами (например, 1, 2, 3, 4…), но и не могут быть выражены в виде аккуратного десятичного числа, которое заканчивается без округления. Рациональное число можно представить в виде дроби. Таким образом, хотя 2,75 не является целым числом, это рациональное число, потому что это то же самое, что и дробь 11/4. Ранее вам сказали, что квадратный корень из 50 равен 7,071, но на самом деле это округление от бесконечного числа знаков после запятой. Точное значение √50 равно 5√2, и вы скоро увидите, как оно определяется.
Ранее вам сказали, что квадратный корень из 50 равен 7,071, но на самом деле это округление от бесконечного числа знаков после запятой. Точное значение √50 равно 5√2, и вы скоро увидите, как оно определяется.
Графики функций квадратного корня
Вы уже видели, что уравнения, включающие квадраты и квадратные корни, нелинейны. Один простой способ запомнить это состоит в том, что графики решений этих уравнений не являются линиями. Это имеет смысл, потому что, если, как уже отмечалось, квадрат 0 равен 0, а квадрат 10 равен 100, но квадрат 5 не равен 50, график, полученный в результате простого возведения числа в квадрат, должен изогнуться до правильных значений.
Это случай с графиком 92
в чем вы сами можете убедиться, посетив калькулятор в Ресурсах и изменив параметры. Линия проходит через точку (0,0), а y не опускается ниже 0, чего и следовало ожидать, поскольку вы знаете, что x 2 никогда не бывает отрицательным. Вы также можете видеть, что график симметричен относительно оси y , что также имеет смысл, поскольку каждый положительный квадратный корень данного числа сопровождается отрицательным квадратным корнем равной величины. Следовательно, за исключением 0, каждые y значение на графике y = x 2 связано с двумя x -значениями.
Вы также можете видеть, что график симметричен относительно оси y , что также имеет смысл, поскольку каждый положительный квадратный корень данного числа сопровождается отрицательным квадратным корнем равной величины. Следовательно, за исключением 0, каждые y значение на графике y = x 2 связано с двумя x -значениями.
Задачи на квадратный корень
Один из способов решения основных задач на квадратный корень вручную — это поиск идеальных квадратов, «спрятанных» внутри задачи. Во-первых, важно знать о некоторых жизненно важных свойствах квадратов и квадратных корней. Один из них заключается в том, что √ x 2 просто равно x (поскольку радикал и показатель степени сокращают друг друга): 92y} = x\sqrt{y}
То есть, если у вас есть полный квадрат под радикалом, умножающим другое число, вы можете его «вытащить» и использовать как коэффициент того, что осталось. Например, возвращаясь к квадратному корню из 50
Например, возвращаясь к квадратному корню из 50
\sqrt{50} = \sqrt{(25)(2)} = 5\sqrt{2}
Иногда вы можете получить число, включающее квадратные корни, которое равно выражается в виде дроби, но все же является иррациональным числом, потому что знаменатель, числитель или оба содержат радикал. В таких случаях вас могут попросить рационализировать знаменатель. Например, число
\frac{6\sqrt{5}}{\sqrt{45}}
имеет радикал как в числителе, так и в знаменателе. Но после тщательного изучения числа 45 вы можете распознать его как произведение 9 и 5, что означает, что
\sqrt{45} = \sqrt{(9)(5)} = 3\sqrt{5}
Следовательно , дробь может быть записана как
\frac{6\sqrt{5}}{3\sqrt{5}}
Радикалы компенсируют друг друга, и у вас остается 6/3 = 2.
Дифференциальные уравнения — Реальные и различные корни
Онлайн-заметки Пола
Главная
/
Дифференциальные уравнения
/
DE второго порядка
/ Вещественные и различные корни
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-2: Действительные и различные корни 9{{г_{\,2}}\,т}}\]
Как и в предыдущем разделе, мы просим вас верить нам, когда мы говорим, что они «достаточно хороши». Вы сможете достаточно легко доказать это, как только мы дойдем до следующего раздела.
С реальными, отчетливыми корнями действительно нечего делать, кроме работы с парой примеров, так что давайте сделаем это.
Пример 1. Решите следующую IVP. \[y» + 11y’ + 24y = 0\hspace{0,25 дюйма}y\влево (0 \right) = 0\hspace{0,25in}y’\left(0 \right) = — 7\] 9{- 3t}}\end{выравнивание*}\]
Теперь подставьте начальные условия, чтобы получить следующую систему уравнений.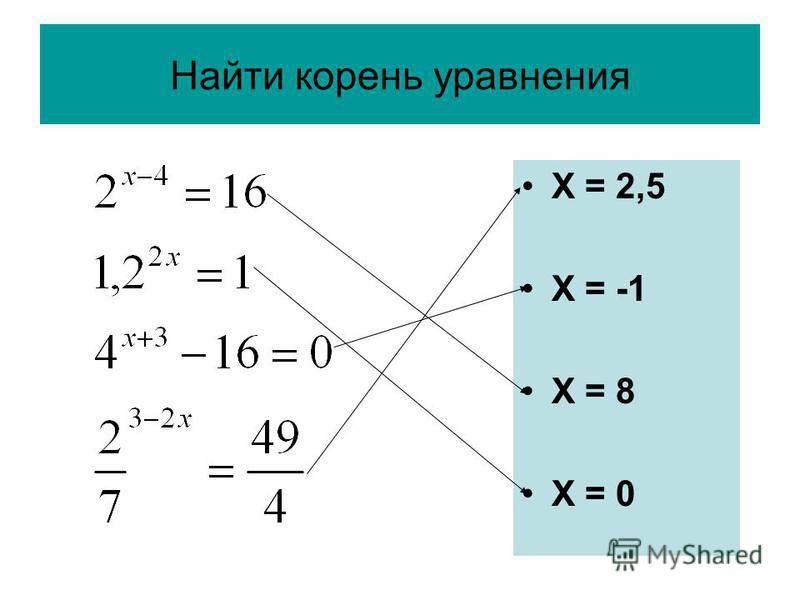
\[\begin{align*}0 & = y\left( 0 \right) = {c_1} + {c_2}\\ — 7 & = y’\left( 0 \right) = — 8{c_1} — 3 {c_2}\end{выравнивание*}\]
Решение этой системы дает \({c_1} = \frac{7}{5}\) и \({c_2} = — \frac{7}{5}\). Фактическое решение дифференциального уравнения тогда 9{2t}}\end{выравнивание*}\]
Теперь подставьте начальные условия, чтобы получить следующую систему уравнений.
\[\begin{align*}4 & = y\left( 0 \right) = {c_1} + {c_2}\\ — 2 & = y’\left( 0 \right) = — 5{c_1} + 2 {c_2}\end{выравнивание*}\]
Решение этой системы дает \({c_1} = \frac{{10}}{7}\) и \({c_2} = \frac{{18}}{7}\). Фактическое решение дифференциального уравнения тогда 9{ — 2t}}\end{выравнивание*}\]
Теперь подставьте начальные условия, чтобы получить следующую систему уравнений. { — \frac{5}{2}} }\конец{выравнивание*}\]
9{\ гидроразрыва {{5t}} {4} + \ гидроразрыва {5} {2}}} \]
{ — \frac{5}{2}} }\конец{выравнивание*}\]
9{\ гидроразрыва {{5t}} {4} + \ гидроразрыва {5} {2}}} \]
В классе дифференциальных уравнений большинство преподавателей (включая меня….) обычно используют начальные условия при \(t = 0\), потому что это немного облегчает работу студентов, когда они пытаются изучить предмет. Однако нет причин всегда ожидать, что это будет так, поэтому не начинайте всегда ожидать начальных условий при \(t = 0\)!
Давайте рассмотрим последний пример, чтобы подчеркнуть еще один момент, о котором вам нужно знать. 92} — 6г — 2 = 0\]
Корни этого уравнения.
\[{r_{1,2}} = 3 \pm \sqrt {11} \]
Теперь НЕ волнуйтесь об этих корнях, это всего лишь два действительных числа.
\[{r_1} = 3 + \sqrt {11} \hspace{0,25 дюйма}\hspace{0,25 дюйма}{\mbox{и }}\hspace{0,25 дюйма}\hspace{0,25 дюйма}{r_2} = 3 — \ кврт {11} \] 9{\ влево ( {3 — \ sqrt {11} } \ вправо) \, т}} \]
Если бы у нас были начальные условия, мы могли бы действовать так же, как в предыдущих двух примерах, хотя работа была бы несколько запутанной, поэтому мы не собираемся делать это для этого примера.
Смысл последнего примера в том, чтобы убедиться, что вы не привыкнете к «хорошим», простым корням. На практике корни характеристического уравнения, как правило, не будут хорошими, простые целые числа или дроби, так что не слишком привыкайте к ним!
Нахождение корней квадратного уравнения (уравнение, примеры и графики) – Новичок в математике уравнение p ( x ) = 0. Обычно нахождение корней многочлена более высокой степени затруднено. К счастью, для квадратичного уравнения у нас есть простая формула.
Формула квадратных корней (или решений)
Корни (или решения) квадратного многочлена (или уравнения): Ax 2 + Bx + C = 0 определяются по формуле:
x 1 = ( − B + √D)/(2A)
x 2 = ( − B − √D)/(2A)
х 1 и х 2 — два корня квадратного числа. Они также решают уравнение.
A, B и C действительные числа, а A ≠ 0.
Типы и числа корней
Квадратное число может иметь ноль, один или два действительных корня. Зависит от значения дискриминанта D = B 2 − 4AC:
Зависит от значения дискриминанта D = B 2 − 4AC:
| Discriminant | Root Type | Number of Roots |
|---|---|---|
| D < 0 | No Real Root | 0 |
| D = 0 | Real | 1 |
| D > 0 | Вещественное число | 2 |
Если мы факторизуем квадратное число с единственным корнем x 1 , множители имеют вид A(x − x 1 )(x − x 1 ). Поэтому x 1 также называют повторяющимся корнем.
В квадратичной формуле есть член √D. Поскольку квадратный корень из отрицательного числа не может быть действительным, при D < 0 никакого реального корня не существует. Однако у нас есть два комплексных корня.
Этапы поиска корней
Шаг 1: вычислить дискриминант
Учитывая уравнение Ax 2 + Bx + C = 0, вычислить дискриминант D = B 2 − 4AC
Шаг 2: найти корень = 0, √D часть формулы обращается в нуль.
 Итак, есть только один (повторяющийся) корень:
Итак, есть только один (повторяющийся) корень:x 1 = x 1 = ( − B)/(2A)
x 2 = ( − B − √D)/(2A)
Рассмотрим пример.
Пример 1
Найти корни x 2 − x − 12 = 0
Шаг 1: вычислить дискриминант = В
2 — 4AC:= ( — 1) 2 − (4)(1)( − 12) = 1 + 48 = 49
Шаг 2: поиск корней
Поскольку D > 0, мы получаем два действительных корня. Найдем их.
x 1 = ( − B + √D)/(2A)
=(1+49)/2
= 8/2 = 4
Другой корень:
x 2 = 1 2 1 ( − B − √D)/(2A) = (1−49)/2 = − 6/2 = − 3 Два корня равны 4 и −3. Давайте посмотрим примеры трех случаев и соответствующие графики. Следующие примеры вычисляют три типа корней. Они связывают их с графиком квадратичной функции. Найдите корни уравнения: x 2 + 6x + 9 = 0 Коэффициенты: A = 1, B = 9, C = 0 D = B 2 − 4AC = 6 2 − (4 × 1 × 9) = 36 − (36) = 0 При D = 0 у нас есть только один корень (решение). x 1 = x 2 = ( − B + √D)/(2A) = ( − B)/(2A) = − 6/2 = − 3. Вы можете убедиться, что x = − 3 действительно удовлетворяет уравнению. Если построить график квадратичной функции f(x) = x 2 + 6x + 9, то можно увидеть, что она достигает нулевого значения только в одной точке, x = − 3. Решите уравнение: x 2 − 3x + 2 = 0 Коэффициенты: A = 1, B = − 3, C = 2. Дискриминант D = B 2 − 4AC = ( − 3) 2 − 4(1)( 2) = 9 − (8) = 1 Поскольку D > 0, у нас есть два корня. x 1 = ( − B + √D)/(2A) = (3 + √1)/2 = 4/2 = 2 x 2 = ( − B − √D )/(2A) = (3 − √1)/2 = 2/2 = 1 Посмотрите на график x 2 − 3x + 2. Решить −3x 2 + 2x − 1 = 0 1. Вычислим дискриминант D: D = B 2 − 4AC = (2) 2 − 4( − 3)( − 1) = 4 − (12) = − 9 Поскольку D < 0, D=−9 не является действительным числом. В этом случае действительного решения уравнения нет. График −3x 2 + 2x − 1 не касается оси x. Ожидалось ли это? Если вы изучали комплексные числа, вы можете вычислить мнимые корни приведенного выше уравнения. x 1 = ( − B + √D)/(2A) =(−2+−9)/(−6)=(−2+3i)/(−6) = 1 /3 − i/2 x 2 = ( − B − √D)/(2A) = (−2−−9)/(−6)=(−2−3i)/(− 6) = 1/3 + i/2 Для любой функции f(x) ее корнями являются такие значения x, что f(x) = 0 Другими словами, корень является решением уравнения f(x) = 0. На следующем графике f(x) имеет три корня: График квадратичной функции (иллюстрации) ➤ Факторизация квадратичного уравнения за 4 шага (вопросы ⤵ 9+)0592 Разложение кубических полиномов на множители (+ вопросы) ➤ 12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Learn by Concept Precalculus Помощь »
Графические функции »
Решение квадратных уравнений »
Найдите корни квадратного уравнения с помощью дискриминанта Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b 2 — 4ac = 0, существует ровно один действительный корень. Возможные ответы: Верно Неверно Правильный ответ: Верно Объяснение: Это правда. Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оценить, могут произойти три случая: b 2 — 4ac > 0 b 2 — 4ac = 0 b 2 2 90 00 первый случай наличие положительного числа под функцией квадратного корня даст результат, который является ответом положительного числа. Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата. В среднем случае (в нашем примере) . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень. В последнем случае, если b 2 — 4ac < 0, это означает, что перед квадратным корнем находится отрицательное число. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения. Сообщить об ошибке Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b 2 — 4ac > 0, существует ровно 2 различных действительных корня уравнения . Возможные ответы: Неверно Верно Правильный ответ: Верно Объяснение: Это правда. Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оцениваете, могут произойти три случая: b 2 — 4ac > 0 b 2 — 4ac = 0 b 2 — 4ac < 0 В первом случае (случай нашего примера) наличие положительного числа под функцией квадратного корня даст результат, который является положительным числовым ответом. В среднем корпусе . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень. В последнем случае, если b 2 — 4ac < 0, это означает, что перед квадратным корнем находится отрицательное число. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения. Сообщить об ошибке Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b 2 — 4ac < 0, существует ровно два различных действительных корня. Возможных ответов: Верно Ложно Правильный ответ: Ложно Объяснение: Это неверно. b 2 — 4ac > 0 b 2 — 4ac = 0 b 2 — 4ac < 0 В первом случае наличие положительного числа под функцией извлечения квадратного корня приведет к положительному числовому ответу. Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата. В среднем корпусе . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень. Для последнего случая (случай нашего примера), если b 2 — 4ac < 0, это означает, что у вас есть отрицательное число под квадратным корнем. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения. Сообщить об ошибке Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: 4x 2 + 19x — 5 = 0. реальный или воображаемый. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения. Возможные ответы: Дискриминант: 0 Один из реальных корней: Дискриминант: 441 Два реальных корня: или Дискриминант: 441 мнимые корни: Дискриминант: 281 Два мнимых корня: Правильный ответ: Дискриминант: 441 Два действительных корня: или Объяснение: В приведенном выше уравнении a = 4, b = 19 и c = -5. Следовательно: b 2 — 4ac = (19) 2 — 4(4)(-5) = 361 + 80 = 441. Когда дискриминант больше 0, существует два различных действительных корня. Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция: Подключение наших значений A, B и C. значения x — два различных действительных корня данного уравнения. Сообщить об ошибке Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: 4x 2 + 12x + 10 = 0, Затем укажите, сколько у него корней, действительные они или мнимые. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения. Возможные ответы: Дискриминант: 304 Типы корней: два различных реальных корня Точные корни: Дискриминанты: 304 Типы корней: два различных реальных корня Точные корты: Дискриминирующие дискриминирующие : -16 Типы корней: Нет настоящих корней; 2 различных мнимых корня Точные корни: Дискриминант: 16 Типы корней: два различных действительных корня Точные корни: -1, -2 2 различных мнимых корня Точные корни: Правильный ответ: Дискриминант: -16 Типы корней: действительных корней нет; 2 различных мнимых корня Точные корни: Объяснение: В приведенном выше уравнении a = 4, b = 12 и c = 10. б 2 — 4ас = (12) 2 — 4(4)(10) = 144 — 160 = -16. Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два различных мнимых корня. Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция: Подставив наши значения a, b и c, мы получим: Это упрощает до: Другими словами, наши два различных воображаемых корня 30 90 0 Ошибка Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: -3x 2 + 6x — 3 = 0. Затем укажите, сколько корней оно имеет и являются ли они действительными или мнимыми. . Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения. Возможные ответы: Дискриминант: 72 Два разных реальных корня: Дискриминант: -72 Два различных воображаемых корней: Дискриминант: 0 Один из них: X = -1 Дискриминанту : 0 Один действительный корень: x = 1 Дискриминант: 72 Два различных действительных корня: Правильный ответ: Дискриминант: 0 Примеры корневого типа
Пример 2. Один действительный корень
Шаг 1: вычисление дискриминанта

Шаг 2: поиск корней
Пример 3 – Два действительных корня
Шаг 1: Вычисление дискриминанта
Шаг 2: Найдите корни
 Он пересекает ось x в обоих корнях.
Он пересекает ось x в обоих корнях. Пример 4 – нет действительных корней / комплексных корней
Шаг 2 : Найти корни
Вычисление мнимых/комплексных корней
Каковы корни любой функции?
 Это значение x, где график f(x) пересекает ось x.
Это значение x, где график f(x) пересекает ось x. Связанные
Поиск корней квадратного уравнения с использованием дискриминанта
Все ресурсы по предварительному исчислению


 Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.
Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата. Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оцениваете, могут произойти три случая:
Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оцениваете, могут произойти три случая:
 Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.
Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня. Следовательно:
Следовательно:
В приведенном выше уравнении a = -3, b = 6 и c = -3. Следовательно:
b 2 — 4ac = (6) 2 — 4(-3)(-3) = 36 — 36 = 0.
Когда дискриминант больше 0, существуют два различных действительных корня. . Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае существует ровно один действительный корень.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная формула:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
что упрощает до
90 xчто дает нам ответ значение x — это единственный действительный корень данного уравнения.
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 5x + 4 = 0.
Затем укажите, сколько корней оно имеет и являются ли они реальный или воображаемый. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 41
Два воображаемых корня:
Дискриминант: 9
Два реальных корня: x = 1 или x = 4
Дискриминант: 0
Один из реальных корней:
Дискриминанту : 9
Два действительных корня: x = -1 или x = -4
Дискриминант: 41
Два мнимых корня:
Правильный ответ:
Дискриминант: 9
Два действительных корня = -x1 или х = -4
Объяснение:
В приведенном выше уравнении a = 1, b = 5 и c = 4. Следовательно:
Следовательно:
b 2 — 4ac = (5) 2 — 4(1)(4) = 25 — 16 = 9.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
, что упрощает до
03 90, что дает нам два ответа
x = -1 или x = -4
Эти значения x являются двумя различными действительными корнями данного уравнения.
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: -x 2 + 3x — 3 = 0.
Затем укажите, сколько корней оно имеет и являются ли они действительными или мнимыми. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 0
Один действительный корень:
Дискриминант: -8
Два мнимых корня: .
Дискриминант: -21
Два мнимых корня:
Дискриминант: -21
Два мнимых корня:
Дискриминант: -8
Два мнимых корня:
Правильный ответ:
Два мнимых корня: -8
Два мнимых корня: -8
Объяснение:
В приведенном выше уравнении a = -1, b = 3 и c = -3. Следовательно:
b 2 — 4ac = (3) 2 — 4(-1)(-3) = 9 — 12 = -3.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два различных мнимых корня.
В этом случае у нас есть два различных мнимых корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставив наши значения a, b и c, мы получим:
Это упрощает до:
Потому что это упрощает до . Другими словами, наши два различных мнимых корня равны и
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 2x + 10 = 0,
Затем укажите, сколько у него корней и являются ли они реальными или мнимыми. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 36
Два действительных корня: x = -5 или x = 7
Дискриминант: 36
Два действительных корня: x = 5 или x = -7
2 Дискриминант: 36
Два мнимых корня:
Дискриминант: -36
Два мнимых корня:
Дискриминант: 0
Один действительный корень: x = -1
Правильный ответ:
Дискриминант: -36
Два мнимых корня:
Объяснение:
В приведенном выше уравнении a = 1, b = 2 и c = 10. Следовательно:
Следовательно:
b 2 — 4ac = (2) 2 — 4(1)(10) = 4 — 40 = -36.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два различных мнимых корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставив наши значения a, b и c, мы получим:
Это упрощает до:
Потому что , это упрощает до . Мы можем упростить это до . Другими словами, наши два различных воображаемых корня — это и .
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 8x + 16 = 0.
Затем укажите, сколько у него корней и являются ли они действительными или мнимыми. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 0
Один из реальных корней: x = -4
Дискриминант: 0
Один из реальных корней: x = 0
Дискриминант: 72
Два различных реальных корня:
Дискриминант: 0
Один действительный корень: x = 4
Дискриминант: 128
Два различных действительных корня:
Правильный ответ:
Дискриминант: 0
Один действительный корень: x = -4
Объяснение:
В приведенном выше уравнении a = 1, b = 8 и c = 16. Следовательно:
b 2 — 4ac = (8) 2 — 4(1)(16) = 64 — 64 = 0.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае существует ровно один действительный корень.
Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае существует ровно один действительный корень.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная формула:
Подставив значения a, b и c, мы получим:
различные действительные корни данного уравнения.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы Precalculus
12 Диагностические тесты
380 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
9.1: Функция извлечения квадратного корня
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19734
- Дэвид Арнольд
- Колледж Редвудс
В этом разделе мы обратим наше внимание на функцию квадратного корня, функцию, определяемую уравнением
\[\begin{array}{c} {f(x)= \sqrt{x}}\\ \end{array}\]
Мы начинаем раздел с рисования графика функции, затем обращаемся к домену и диапазону. После этого мы исследуем ряд различных преобразований функции.
После этого мы исследуем ряд различных преобразований функции.
График функции квадратного корня
Давайте создадим таблицу точек, удовлетворяющих уравнению функции, а затем отобразим точки из таблицы в декартовой системе координат на миллиметровой бумаге. Мы продолжим создавать и наносить точки, пока не убедимся в окончательной форме графика.
Мы знаем, что не можем извлечь квадратный корень из отрицательного числа. Поэтому мы не хотим помещать в нашу таблицу какие-либо отрицательные значения x . Чтобы еще больше упростить наши вычисления, давайте использовать числа, квадратный корень которых легко вычисляется. Это напоминает совершенные квадраты, такие как 0, 1, 4, 9 и так далее. Мы поместили эти числа как значения x в таблицу Рисунок 1 (b), а затем вычислили квадратный корень каждого. Рисунок 1 (a) вы видите, что каждая точка из таблицы представлена сплошной точкой. Если мы продолжим добавлять точки в таблицу, наносить их на график, то график в конечном итоге заполнится и примет форму сплошной кривой, показанной на рис. 2\), \(x \ge 0\), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c).
2\), \(x \ge 0\), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c).
Последовательность графиков в Рисунок 2 также помогает нам определить область и диапазон функции квадратного корня.
- В Рис. 2 (а) парабола бесконечно раскрывается наружу, как влево, так и вправо. Следовательно, областью определения является \(D_{f} = (−\infty, \infty)\), или все действительные числа. Кроме того, граф имеет вершину в начале координат и бесконечно открыт вверх, поэтому диапазон равен \(R_{f} = [0, \infty)\).
9{−1}} = [0,\infty)\).
Конечно, мы также можем определить область определения и диапазон функции квадратного корня, спроецировав все точки графика на оси x — и y , как показано на рисунках 3 (a) и ( б) соответственно.
Рисунок 3.} \text{Проекция на оси, чтобы найти домен и диапазон}}\\ \nonumber \end{массив}\] Некоторые могут возразить против диапазона, спросив: «Откуда мы знаем, что график изображение функции квадратного корня в 92\), \(x \ge 0\), бесконечно открывается вправо по мере того, как график поднимается до бесконечности. Следовательно, после отражения этого графика через линию y = x результирующий график должен бесконечно подниматься вверх по мере его движения вправо. Таким образом, диапазон функции квадратного корня равен \([0, \infty)\).
Следовательно, после отражения этого графика через линию y = x результирующий график должен бесконечно подниматься вверх по мере его движения вправо. Таким образом, диапазон функции квадратного корня равен \([0, \infty)\).
Переводы
Если мы сдвинем график \(y = \sqrt{x}\) вправо и влево или вверх и вниз, это повлияет на домен и/или диапазон.
Пример \(\PageIndex{4}\)
Нарисуйте график \(f(x) = \sqrt{x−2}\). Используйте свой график, чтобы определить домен и диапазон.
Мы знаем, что основное уравнение \(y=\sqrt{x}\) имеет график, показанный на рис. 1 (c). Если мы заменим x на x − 2, основное уравнение \(y=\sqrt{x}\) станет \(f(x) = \sqrt{x−2}\). Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сдвинет график на две единицы вправо, как показано на рисунках 4 (а) и (б).
Рисунок 4. Чтобы нарисовать график \(f(x) = \sqrt{x−2}\), сдвиньте график \(y=\sqrt{x}\) на две единицы вправо.
Чтобы найти область, мы проецируем каждую точку на графике f на ось x, как показано на Рис. 4 (a). Обратите внимание, что все точки справа от 2 или в том числе заштрихованы на оси X. Следовательно, область определения f равна
. Область определения = \([2, \infty)\) = {x: \(x \ge 0\)}
. одинаковый. Чтобы найти диапазон, мы проецируем каждую точку на графике на ось Y, как показано на рисунке 9.0591 Рисунок 4 (б). Обратите внимание, что все точки на уровне нуля и выше заштрихованы на оси Y. Таким образом, диапазон f равен
Range = \([0,\infty)\)= {y: \(y \ge 0\)}.
Мы можем найти область определения этой функции алгебраически, исследуя ее определяющее уравнение \(f(x) = \sqrt{x−2}\). Мы понимаем, что мы не можем извлечь квадратный корень из отрицательного числа. Следовательно, выражение под радикалом должно быть неотрицательным (положительным или нулевым). То есть
\(x − 2 \ge 0\).
Решение этого неравенства для x ,
\(x \ge 2\).
Таким образом, область определения f равна Domain = \([2, \infty)\), что соответствует приведенному выше графическому решению.
Давайте посмотрим на другой пример.
Пример \(\PageIndex{5}\)
Нарисуйте график \(f (x) = \sqrt{x + 4} + 2\). Используйте свой график, чтобы определить домен и диапазон f.
Опять же, мы знаем, что основное уравнение \(y=\sqrt{x}\) имеет график, показанный на Рис. 1 (в). Если мы заменим x на x +4, основное уравнение \(y=\sqrt{x}\) станет \(y=\sqrt{x+4}\). Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сдвинет график на \(y=\sqrt{x}\) на четыре единицы влево, как показано на рис. 5 (a).
Если мы знаем, что нужно добавить 2 к уравнению \(y=\sqrt{x+4}\), чтобы получить уравнение \(y=\sqrt{x+4} + 2\), это сдвинет график \ (y=\sqrt{x+4}\) на две единицы вверх, как показано на Рисунок 5 (б).
Рисунок 5. Преобразование исходного уравнения \(y = \sqrt{x}\) для получения графика \(y = \sqrt{x+4} + 2\) Чтобы определить th домен \(f ( x) = \sqrt{x + 4} + 2\), мы проецируем все точки графика f на ось x, как показано на рис. 6 (a). Обратите внимание, что все точки справа от − 4 или включая их заштрихованы на оси x . Таким образом, область определения \(f (x) = \sqrt{x + 4} + 2\) равна
6 (a). Обратите внимание, что все точки справа от − 4 или включая их заштрихованы на оси x . Таким образом, область определения \(f (x) = \sqrt{x + 4} + 2\) равна
Область определения = \([−4, \infty)\) = {x: \(x \ge −4 \)}
Рисунок 6. Проецирование точек f на оси для определения домена и диапазона Аналогичным образом, чтобы найти диапазон f , спроецируйте все точки графика f на ось y , как показано на Рис. 6 (b). Обратите внимание, что все точки на оси y больше или включая 2 заштрихованы. Следовательно, диапазон f равен
. Диапазон = \([2, \infty)\) = {y: \(y \ge 2\)}
. исследуя уравнение \(f (x) = \sqrt{x + 4} + 2\). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулем или положительным). Следовательно,
\(x + 4 \ge 0\).
Решение этого неравенства для x ,
\(x \ge −4\).
Таким образом, область определения f равна Domain = \([−4,\infty)\), что соответствует представленному выше графическому решению.
Размышления
Если мы начнем с основного уравнения \(y = \sqrt{x}\), затем заменим x на −x, то график полученного уравнения \(y = \sqrt{−x}\) захватывается путем отражения графика \(y = \sqrt{x}\) (см. Рисунок 1 (c)) по горизонтали по оси y. График \(y = \sqrt{−x}\) показан на Рисунок 7 (а).
Точно так же график \(y = −\sqrt{x}\) будет вертикальным отражением графика \(y = \sqrt{x}\) по оси x, как показано на рисунке . 7 (б).
Рисунок 7. Отражение графика \(y = \sqrt{x}\) по осям x и y. Чаще всего вам будет предложено выполнить отражение и перевод.
Пример \(\PageIndex{6}\)
Нарисуйте график \(f(x) = \sqrt{4− x}\). Используйте полученный график, чтобы определить домен и диапазон f.
Сначала перепишем уравнение \(f(x) = \sqrt{4− x}\) следующим образом:
\(f(x) = \sqrt{−(x−4)}\)
Определение
Первые размышления . Обычно более интуитивно понятно выполнять рефлексию перед переводом.
Обычно более интуитивно понятно выполнять рефлексию перед переводом.
Помня об этом, мы сначала нарисуем график \(f(x) = \sqrt{−x}\), который является отражением графика \(f(x) = \sqrt{x} \) по оси y . Это показано на рис. 8 (a).
Теперь в \(f(x) = \sqrt{−x}\) замените x на x − 4, чтобы получить \(f(x) = \sqrt{−(x−4)} \). Это сдвигает график \(f(x) = \sqrt{−x}\) на четыре единицы вправо, как показано на рис. 8 (b).
Рис. 8. Отражение с последующей трансляцией. Чтобы найти область определения функции \(f(x) = \sqrt{−(x−4)}\) или, что то же самое, \(f(x) = \sqrt{4−x}\), спроецируйте каждую точку на графике f на оси x , как показано на Рисунок 9 (а). Обратите внимание, что все действительные числа, меньшие или равные 4, заштрихованы по оси x . Следовательно, домен f равен
Domain = \((−\infty, 4]\) = {x: \(x \le 4\)}.
Аналогично, чтобы получить диапазон f, проект каждую точку на графике f на оси они, как показано на Рисунок 9 (b) Обратите внимание, что все действительные числа, большие или равные нулю, заштрихованы на оси Y. Следовательно, диапазон f равен
Следовательно, диапазон f равен
Диапазон = \([0,\infty)\) = {x: \(x \ge 0\)}.
Мы также можем найти область определения функции f , исследуя уравнение \(f(x) = \sqrt{4−x}\). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулем или положительным). Следовательно,
\(4 − x \ge 0\).
Рисунок 9. Определение домена и диапазона \(f(x) = \sqrt{4−x}\) Решите это последнее неравенство для x . Сначала вычтите 4 из обеих частей неравенства, затем умножьте обе части полученного неравенства на − 1. Конечно, умножение на отрицательное число меняет знак неравенства на противоположный.
\(−x \ge −4\)
\(x \le 4\)
Таким образом, область определения f равна {x: \(x \le 4\)}. В интервальной нотации домен = \((−\infty, 4]\). Это хорошо согласуется с графическим результатом, найденным выше. определить область определения функции извлечения квадратного корня
Пример \(\PageIndex{7}\)
Нарисуйте график \(f(x) = \sqrt{5−2x}\) Используйте график и алгебраический метод для определения области определения функции.
Загрузите функцию в Y1 в меню Y= вашего калькулятора, как показано на Рисунок 10 (a). Выберите 6:ZStandard в меню ZOOM, чтобы построить график, показанный на Рисунок 10 (b).
Рисунок 10. График f(x) = \sqrt{5−2x} на графическом калькуляторе. Внимательно посмотрите на график в Рисунок 10 (b) и обратите внимание, что трудно сказать, идет ли график полностью вниз, чтобы «касаться» оси x около \(x \примерно 2,5\). Однако наш предыдущий опыт работы с функцией квадратного корня заставляет нас полагать, что это всего лишь артефакт недостаточного разрешения калькулятора, который не позволяет графику «касаться» оси x в точке \(x \приблизительно 2,5\).
Алгебраический подход решит проблему. Мы можем определить область определения f, исследуя уравнение \(f(x) = \sqrt{5 − 2x}\). Следовательно, Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулевым или положительным).
\(5 − 2x \ge 0\).
Решите это последнее неравенство для x . Сначала вычтите 5 из обеих частей неравенства.
\(−2x \ge −5\).
Затем разделите обе части последнего неравенства на −2. Помните, что мы должны обратить неравенство в тот момент, когда мы разделим на отрицательное число.
\(\frac{−2x}{−2} \le \frac{−5}{−2}\).
\(x \le \frac{5}{2}\).
Таким образом, область определения f равна {x: \(x \le \frac{5}{2}\)}. В интервальных обозначениях домен = \((−\infty, \frac{5}{2}]\). Это хорошо согласуется с графическим результатом, найденным выше.
Дальнейшее самоанализ показывает, что этот аргумент также разрешает вопрос о том, график не «касается» оси x в точке \(x= \frac{5}{2}\). Если вы не уверены, то подставьте \(x=\frac{5}{2}\) в \(f(x) = \sqrt{5−2x}\) , чтобы увидеть
\(f(\frac{5}{2})= \sqrt{5−2(\frac{5}{2})} =\sqrt{0} = 0\).
Таким образом, график f «касается» оси x в точке \((\frac{5}{2}, 0)\).
В Упражнении 1-10 выполните каждое из следующих заданий:
- Установите систему координат на листе миллиметровой бумаги. Пометьте и масштабируйте каждую ось.
- Заполните таблицу баллов для данной функции. Постройте каждую из точек в вашей системе координат, а затем используйте их, чтобы нарисовать график данной функции.
- Используйте разноцветные карандаши, чтобы спроецировать все точки на оси x и y , чтобы определить домен и диапазон. Используйте обозначение интервала для описания области определения данной функции.
Упражнение \(\PageIndex{1}\)
\(f(x) = −\sqrt{x}\)
х
0
1
4
9
ф (х)
- Ответить
х
0
1
4
9
ф (х)
0
− 1
− 2
− 3
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 0]\).
Упражнение \(\PageIndex{2}\)
\(f(x) = \sqrt{−x}\)
х
0
− 1
− 4
− 9
ф (х)
Упражнение \(\PageIndex{3}\)
\(f(x)= \sqrt{x+2}\)
х
− 2
− 1
2
7
ф (х)
- Ответить
х
− 2
− 1
2
7
ф ( х )
0
1
2
3
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки на графике на ось X, чтобы определить домен: домен = \([ − 2, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
Упражнение \(\PageIndex{4}\)
\(f(x)= \sqrt{5−x}\)
х
− 4
1
4
5
ф (х)
Упражнение \(\PageIndex{5}\)
\(f(x)= \sqrt{x}+2\)
х
0
1
4
9
ф (х)
- Ответить
х
0
1
4
9
ф (х)
2
3
4
5
Отметьте точки в таблице и используйте их для построения графика f .
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([2, \infty)\).
Упражнение \(\PageIndex{6}\)
\(f(x)=\sqrt{x}−1\)
х
0
1
4
9
ф (х)
Упражнение \(\PageIndex{7}\)
\(f(x)= \sqrt{x+3}+2\)
х
− 3
− 2
1
6
ф (х)
- Ответить
х
− 3
− 2
1
6
ф (х)
2
3
4
5
Отметьте точки в таблице и используйте их для построения графика f .
- Спроецируйте все точки графика на ось X, чтобы определить домен: домен = \([ − 3, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([2, \infty)\).
Упражнение \(\PageIndex{8}\)
\(f(x)= \sqrt{x−1}+3\)
х
1
2
5
10
ф ( х )
Упражнение \(\PageIndex{9}\)
\(f(x)= \sqrt{3−x}\)
х
− 6
− 1
2
3
ф ( х )
- Ответить
х
− 6
− 1
2
3
ф ( х )
3
2
1
0
Отметьте точки в таблице и используйте их для построения графика f .
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \(( − \infty, 3]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
Упражнение \(\PageIndex{10}\)
\(f(x)=-\sqrt{x+3}\)
х
− 3
− 2
1
6
ф ( х )
В упражнениях 11 — 20 выполните каждое из следующих заданий.
- Установите систему координат на листе миллиметровой бумаги. Пометьте и масштабируйте каждую ось. Не забудьте провести все линии линейкой.
- Используйте геометрические преобразования для построения графика заданной функции в вашей системе координат без использования графического калькулятора. Примечание: вы можете проверьте свое решение с помощью калькулятора, но вы сможете построить график без использования калькулятора.
- Используйте разноцветные карандаши, чтобы спроецировать точки на графике функции на оси x и y . Используйте нотацию интервала, чтобы описать домен и диапазон функции.
Упражнение \(\PageIndex{11}\)
\(f(x)= \sqrt{x}+3\)
- Ответ
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем добавьте 3, чтобы получить уравнение \(y = \sqrt{x} + 3\). Это сдвинет график \(y = \sqrt{x}\) вверх на 3 единицы, как показано на (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Диапазон = \([3, \infty)\).
Упражнение \(\PageIndex{12}\)
\(f(x)=\sqrt{x+3}\)
Упражнение \(\PageIndex{13}\)
\(f(x)=\sqrt{x−2}\)
- Ответить
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на x − 2, чтобы получить уравнение \(y = \sqrt{x−2}\). Это сдвинет график \(y = \sqrt{x}\) вправо на 2 единицы, как показано в (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([2, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
Упражнение \(\PageIndex{14}\)
\(f(x)=\sqrt{x}−2\)
Упражнение \(\PageIndex{15}\)
\(f(x) = \sqrt{x+5}+1\)
- Ответ
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на x + 5, чтобы получить уравнение \(y = \sqrt{x+5}\). Затем добавьте 1, чтобы получить уравнение \(f(x)= \sqrt{x+5}+1\). Это сдвинет график \(y = \sqrt{x}\) влево на 5 единиц, а затем вверх на 1 единицу, как показано на (b).
Затем замените x на x + 5, чтобы получить уравнение \(y = \sqrt{x+5}\). Затем добавьте 1, чтобы получить уравнение \(f(x)= \sqrt{x+5}+1\). Это сдвинет график \(y = \sqrt{x}\) влево на 5 единиц, а затем вверх на 1 единицу, как показано на (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([−5, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([1, \infty)\).
Упражнение \(\PageIndex{16}\)
\(f(x)=\sqrt{x−2}−1\)
Упражнение \(\PageIndex{17}\)
\(y = −\sqrt{x + 4}\)
- Ответ
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем инвертируйте, чтобы получить \(y = −\sqrt{x}\). Это отразит график \(y = \sqrt{x}\) по оси x, как показано в (b). Наконец, замените x на x + 4, чтобы получить уравнение \(y = −\sqrt{x + 4}\). Это сдвинет график \(y = −\sqrt{x}\) на четыре единицы влево, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: домен = \([−4, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 0]\).
Упражнение \(\PageIndex{18}\)
\(f(x)=−\sqrt{x}+4\)
Упражнение \(\PageIndex{19}\)
\(f(x )=−\sqrt{x}+3\)
- Ответ
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем инвертируйте, чтобы получить \(y = −\sqrt{x}\). Это отразит график \(y = \sqrt{x}\) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \(y=−\sqrt{x}+3\). Это сдвинет график \(y = −\sqrt{x}\) на три единицы вверх, как показано на (c).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 3]\).
Упражнение \(\PageIndex{20}\)
\(f(x)=−\sqrt{x+3}\)
Упражнение \(\PageIndex{21}\)
Чтобы нарисовать график функции \(f(x) = \sqrt{3−x}\), выполните каждый из следующих шагов последовательно без помощи калькулятора.
- Установите систему координат и нарисуйте график \(y = \sqrt{x}\). Обозначьте график его уравнением.
- Установите вторую систему координат и нарисуйте график \(y = \sqrt{−x}\). Обозначьте график его уравнением.
- Установите третью систему координат и нарисуйте график \(y =\sqrt{−(x − 3)}\). Обозначьте график его уравнением. Это график \(y =\sqrt{3−x}\). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответить
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на − x , чтобы получить уравнение \(y = \sqrt{−x}\). Это будет отражать график \(y = \sqrt{x}\) по оси y , как показано на (b). Наконец, замените x на x − 3, чтобы получить уравнение0022 3)}\). Это сместит график \(y = \sqrt{−x}\) на три единицы вправо, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \((−\infty, 3]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \ ([0, \infty)\).
Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \ ([0, \infty)\).
Упражнение \(\PageIndex{22}\)
Чтобы нарисовать график функции \(f(x) = \sqrt{−x−3}\), последовательно выполните каждый из следующих шагов.
- Установите систему координат и нарисуйте график \(y = \sqrt{x}\). Обозначьте график его уравнением.
- Установите вторую систему координат и нарисуйте график \(y = \sqrt{−x}\). Обозначьте график его уравнением.
- Установите третью систему координат и нарисуйте график \(y =\sqrt{−(x + 3)}\). Обозначьте график его уравнением. Это график \(y =\sqrt{−x−3}\). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
Упражнение \(\PageIndex{23}\)
Чтобы нарисовать график функции \(f(x) = \sqrt{−x−3}\), выполните каждый из следующих шагов последовательно без помощи калькулятора.
- Установите систему координат и нарисуйте график \(y = \sqrt{x}\).
 Обозначьте график его уравнением.
Обозначьте график его уравнением. - Установите вторую систему координат и нарисуйте график \(y = \sqrt{−x}\). Обозначьте график его уравнением.
- Установите третью систему координат и нарисуйте график \(y =\sqrt{−(x + 1)}\). Обозначьте график его уравнением. Это график \(y =\sqrt{−x−1}\). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответить
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на −x, чтобы получить уравнение \(y = \sqrt{−x}\). Это отразит график \(y = \sqrt{x}\) по оси y, как показано в (b). Наконец, замените x на x + 1, чтобы получить уравнение \(y = \sqrt{−(x + 1)}\). Это сдвинет график \(y = \sqrt{−x}\) на одну единицу влево, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \((−\infty, −1]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
Упражнение \(\PageIndex{24}\)
Чтобы нарисовать график функции \(f(x) = \sqrt{1−x}\), последовательно выполните каждый из следующих шагов.
- Установите систему координат и нарисуйте график \(y = \sqrt{x}\). Обозначьте график его уравнением.
- Установите вторую систему координат и нарисуйте график \(y = \sqrt{−x}\). Обозначьте график его уравнением.
- Установите третью систему координат и нарисуйте график \(y =\sqrt{−(x−1)}\). Обозначьте график его уравнением. Это график \(y =\sqrt{1−x}\). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
В упражнениях 25 — 28 выполните каждое из следующих заданий.
- Нарисуйте график заданной функции с помощью графического калькулятора. Скопируйте изображение в окне просмотра на свой домашний лист. Пометьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Подпишите свой график его уравнением.
 Используйте график, чтобы определить область определения функции и описать область с помощью обозначения интервала.
Используйте график, чтобы определить область определения функции и описать область с помощью обозначения интервала. - Используйте чисто алгебраический подход для определения области определения заданной функции. Используйте интервальную нотацию для описания вашего результата. Согласуется ли это с графическим результатом из части 1?
Упражнение \(\PageIndex{25}\)
\(f(x)= \sqrt{2x+7}\)
- Ответ
Мы используем графический калькулятор для построения следующего графика \(f(x)= \sqrt{2x+7}\)
По нашим оценкам, домен будет состоять из всех действительных чисел справа примерно от − 3 . 5. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под радикалом в \(f(x)=\sqrt{2x+7}\) должно быть больше или равно нулю.
\(2x + 7 \ge 0\)
\(2x \ge −7\)
\(х \ge −\frac{7}{2}\)
Следовательно, домен равен \([−\frac{7}{2}, \infty)\).
Упражнение \(\PageIndex{26}\)
\(f(x)= \sqrt{7−2x}\)
Упражнение \(\PageIndex{27}\)
\(f(x) = \sqrt{12−4x}\)
- Ответ
Мы используем графический калькулятор для построения следующего графика \(f(x)= \sqrt{12−4x}\).
По нашим оценкам, домен будет состоять из всех действительных чисел примерно справа от 3. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под радикалом в \(f(x)=\sqrt{12−4x}\) должно быть больше или равно нулю.
\(12−4x \ge 0\)
\(−4x \ge −12\)
\(х \ле 3\)
Следовательно, домен равен \((−\infty, 3]\).
Упражнение \(\PageIndex{28}\)
\(f(x)= \sqrt{12+2x}\)
В Упражнениях 29 — 40 алгебраически найдите область определения заданной функции .
Упражнение \(\PageIndex{29}\)
\(f(x)= \sqrt{2x+9}\)
- Ответ
Четный корень отрицательного числа не определяется как действительное число. Таким образом, 2x + 9 должно быть больше или равно нулю. Поскольку из \(2x + 9 \ge 0\) следует, что \(x \ge −\frac{9{2}\), областью определения является интервал \([−\frac{9}{2},\infty)\).
Упражнение \(\PageIndex{30}\)
\(f(x)=\sqrt{−3x+3}\)
Упражнение \(\PageIndex{31}\)
\(f(x )=\sqrt{−8x−3}\)
- Ответ
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −8x−3 должно быть больше или равно нулю. Поскольку из \(−8x−3 \ge 0\) следует, что \(x \le −\frac{3}{8}\), областью определения является интервал \((−\infty, −\frac{3}{ 8}]\).
Упражнение \(\PageIndex{32}\)
\(f(x)=\sqrt{−3x+6}\)
Упражнение \(\PageIndex{33}\)
\(f(x) )=\sqrt{−6x−8}\)
- Ответ
Четный корень отрицательного числа не определяется как действительное число. Таким образом, -6x-8 должно быть больше или равно нулю. Поскольку из \(−6x−8 \ge 0\) следует, что \(x \le −\frac{4}{3}\), областью определения является интервал \((−\infty, \frac{4}{3} }]\).
Таким образом, -6x-8 должно быть больше или равно нулю. Поскольку из \(−6x−8 \ge 0\) следует, что \(x \le −\frac{4}{3}\), областью определения является интервал \((−\infty, \frac{4}{3} }]\).
Упражнение \(\PageIndex{34}\)
\(f(x)=\sqrt{8x−6}\)
Упражнение \(\PageIndex{35}\)
\(f(x)= \sqrt{−7x+2}\)
- Ответ
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −7x+2 должно быть больше или равно нулю. Поскольку из \(−7x+2 \ge 0\) следует, что \(x \le \frac{2}{7}\), областью определения является интервал \((−\infty, \frac{2}{7} ]\).
Упражнение \(\PageIndex{36}\)
\(f(x)=\sqrt{8x−3}\)
Упражнение \(\PageIndex{37}\)
\(f(x)=\sqrt{6x+3}\)
- Ответить
Четный корень отрицательного числа не определяется как действительное число. Таким образом, 6x+3 должно быть больше или равно нулю. Поскольку из \(6x+3 \ge 0\) следует, что \(x \ge −\frac{1}{2}\), областью определения является интервал \([−\frac{1}{2}, \infty )\).
Поскольку из \(6x+3 \ge 0\) следует, что \(x \ge −\frac{1}{2}\), областью определения является интервал \([−\frac{1}{2}, \infty )\).
Упражнение \(\PageIndex{38}\)
\(f(x)=\sqrt{x−5}\)
Упражнение \(\PageIndex{39}\)
\(f(x)=\sqrt{−7x−8}\)
- Ответ
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −7x−8 должно быть больше или равно нулю. Поскольку из \(−7x−8 \ge 0\) следует, что \(x \le −\frac{8}{7}\), областью определения является интервал \((−\infty, −\frac{8}{ 7}]\)
Упражнение \(\PageIndex{40}\)
\(f(x)=\sqrt{7x+8}\)
Эта страница под названием 9.1: Функция квадратного корня распространяется под лицензией CC BY-NC-SA 2.5, автором, ремиксом и/или куратором этой страницы является Дэвид Арнольд.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Арнольд
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 2,5
- Показать страницу TOC
- нет
- Теги
- отражение
- функция квадратного корня
2.
 6 Природа корней | Уравнения и неравенства
6 Природа корней | Уравнения и неравенства
 В этом случае у нас есть два различных мнимых корня.
В этом случае у нас есть два различных мнимых корня. Следовательно:
Следовательно: Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае существует ровно один действительный корень.
Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае существует ровно один действительный корень.- Последнее обновление
- Идентификатор страницы
- 19734
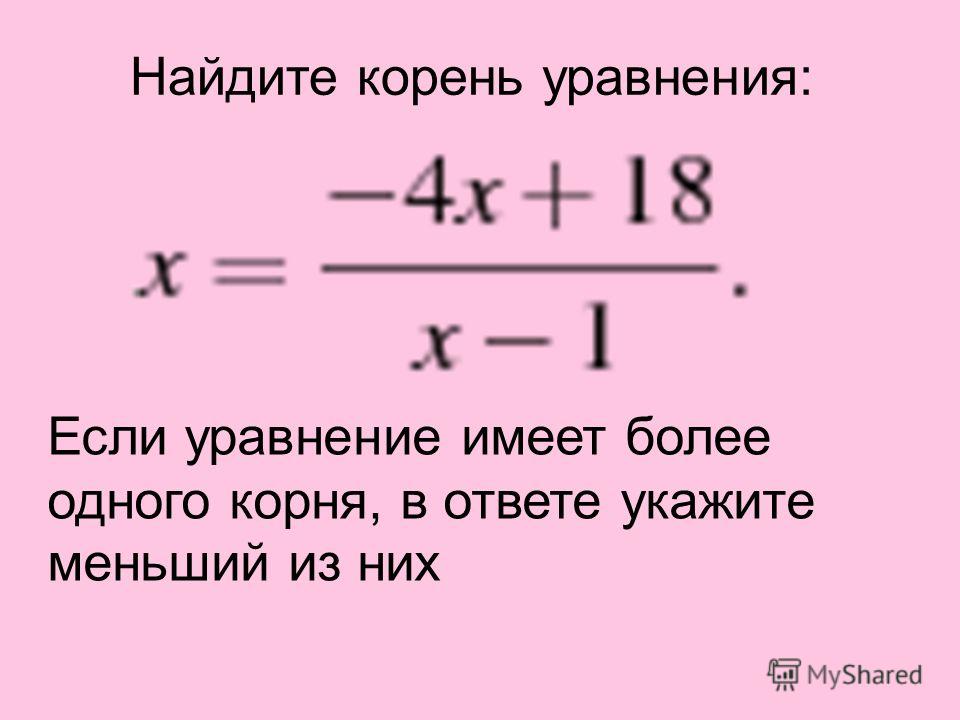 После этого мы исследуем ряд различных преобразований функции.
После этого мы исследуем ряд различных преобразований функции. 2\), \(x \ge 0\), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c).
2\), \(x \ge 0\), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c). Следовательно, после отражения этого графика через линию y = x результирующий график должен бесконечно подниматься вверх по мере его движения вправо. Таким образом, диапазон функции квадратного корня равен \([0, \infty)\).
Следовательно, после отражения этого графика через линию y = x результирующий график должен бесконечно подниматься вверх по мере его движения вправо. Таким образом, диапазон функции квадратного корня равен \([0, \infty)\).
 6 (a). Обратите внимание, что все точки справа от − 4 или включая их заштрихованы на оси x . Таким образом, область определения \(f (x) = \sqrt{x + 4} + 2\) равна
6 (a). Обратите внимание, что все точки справа от − 4 или включая их заштрихованы на оси x . Таким образом, область определения \(f (x) = \sqrt{x + 4} + 2\) равна
 Обычно более интуитивно понятно выполнять рефлексию перед переводом.
Обычно более интуитивно понятно выполнять рефлексию перед переводом. Следовательно, диапазон f равен
Следовательно, диапазон f равен


х
0
1
4
9
ф (х)
х | 0 | 1 | 4 | 9 |
ф (х) | 0 | − 1 | − 2 | − 3 |
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 0]\).
х
0
− 1
− 4
− 9
ф (х)
х
− 2
− 1
2
7
ф (х)
х | − 2 | − 1 | 2 | 7 |
ф ( х ) | 0 | 1 | 2 | 3 |
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки на графике на ось X, чтобы определить домен: домен = \([ − 2, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
х
− 4
1
4
5
ф (х)
х
0
1
4
9
ф (х)
х | 0 | 1 | 4 | 9 |
ф (х) | 2 | 3 | 4 | 5 |
Отметьте точки в таблице и используйте их для построения графика f .
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([2, \infty)\).
х
0
1
4
9
ф (х)
х
− 3
− 2
1
6
ф (х)
х | − 3 | − 2 | 1 | 6 |
ф (х) | 2 | 3 | 4 | 5 |
Отметьте точки в таблице и используйте их для построения графика f .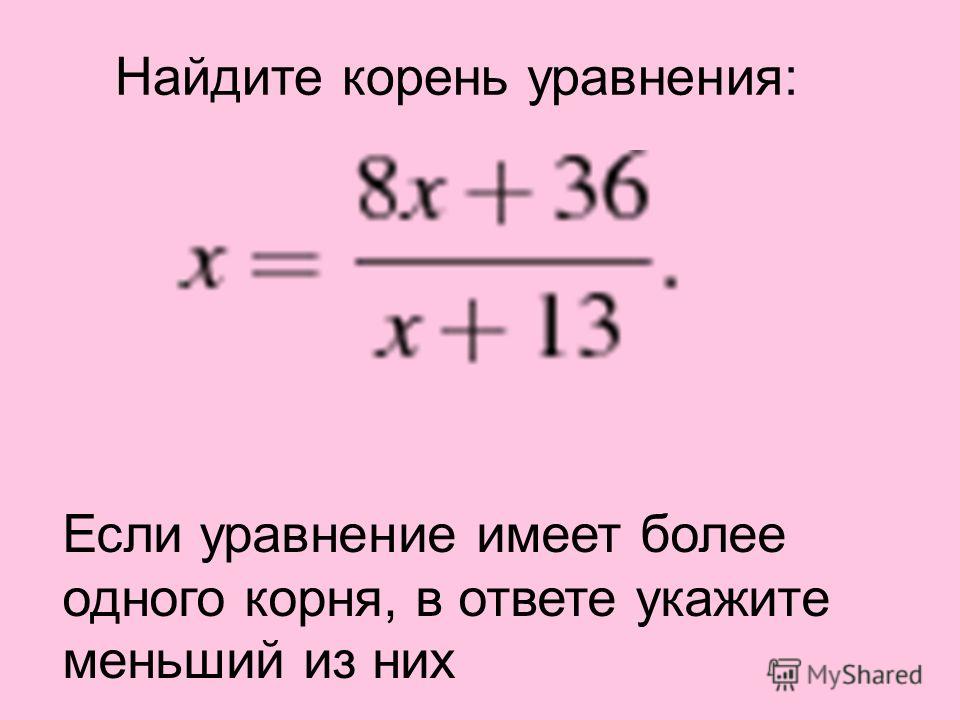
х
1
2
5
10
ф ( х )
х
− 6
− 1
2
3
ф ( х )
х | − 6 | − 1 | 2 | 3 |
ф ( х ) | 3 | 2 | 1 | 0 |
Отметьте точки в таблице и используйте их для построения графика f .
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \(( − \infty, 3]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
х
− 3
− 2
1
6
ф ( х )

Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем добавьте 3, чтобы получить уравнение \(y = \sqrt{x} + 3\). Это сдвинет график \(y = \sqrt{x}\) вверх на 3 единицы, как показано на (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Диапазон = \([3, \infty)\).
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на x − 2, чтобы получить уравнение \(y = \sqrt{x−2}\). Это сдвинет график \(y = \sqrt{x}\) вправо на 2 единицы, как показано в (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([2, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на x + 5, чтобы получить уравнение \(y = \sqrt{x+5}\). Затем добавьте 1, чтобы получить уравнение \(f(x)= \sqrt{x+5}+1\). Это сдвинет график \(y = \sqrt{x}\) влево на 5 единиц, а затем вверх на 1 единицу, как показано на (b).
Затем замените x на x + 5, чтобы получить уравнение \(y = \sqrt{x+5}\). Затем добавьте 1, чтобы получить уравнение \(f(x)= \sqrt{x+5}+1\). Это сдвинет график \(y = \sqrt{x}\) влево на 5 единиц, а затем вверх на 1 единицу, как показано на (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([−5, \infty)\). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \([1, \infty)\).
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем инвертируйте, чтобы получить \(y = −\sqrt{x}\). Это отразит график \(y = \sqrt{x}\) по оси x, как показано в (b). Наконец, замените x на x + 4, чтобы получить уравнение \(y = −\sqrt{x + 4}\). Это сдвинет график \(y = −\sqrt{x}\) на четыре единицы влево, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: домен = \([−4, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 0]\).
Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем инвертируйте, чтобы получить \(y = −\sqrt{x}\). Это отразит график \(y = \sqrt{x}\) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \(y=−\sqrt{x}+3\). Это сдвинет график \(y = −\sqrt{x}\) на три единицы вверх, как показано на (c).
Спроецируйте все точки графика на ось x, чтобы определить домен: домен = \([0, \infty)\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \((−\infty, 3]\).

Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на − x , чтобы получить уравнение \(y = \sqrt{−x}\). Это будет отражать график \(y = \sqrt{x}\) по оси y , как показано на (b). Наконец, замените x на x − 3, чтобы получить уравнение0022 3)}\). Это сместит график \(y = \sqrt{−x}\) на три единицы вправо, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \((−\infty, 3]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \ ([0, \infty)\).
Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \ ([0, \infty)\).
 Обозначьте график его уравнением.
Обозначьте график его уравнением.Сначала постройте график \(y = \sqrt{x}\), как показано в (a). Затем замените x на −x, чтобы получить уравнение \(y = \sqrt{−x}\). Это отразит график \(y = \sqrt{x}\) по оси y, как показано в (b). Наконец, замените x на x + 1, чтобы получить уравнение \(y = \sqrt{−(x + 1)}\). Это сдвинет график \(y = \sqrt{−x}\) на одну единицу влево, как показано на (c).
Спроецируйте все точки графика на ось X, чтобы определить домен: Domain = \((−\infty, −1]\). Спроецируйте все точки графика на ось Y, чтобы определить диапазон: Range = \([0, \infty)\).
 Используйте график, чтобы определить область определения функции и описать область с помощью обозначения интервала.
Используйте график, чтобы определить область определения функции и описать область с помощью обозначения интервала.Мы используем графический калькулятор для построения следующего графика \(f(x)= \sqrt{2x+7}\)
По нашим оценкам, домен будет состоять из всех действительных чисел справа примерно от − 3 . 5. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под радикалом в \(f(x)=\sqrt{2x+7}\) должно быть больше или равно нулю.
\(2x + 7 \ge 0\)
\(2x \ge −7\)
\(х \ge −\frac{7}{2}\)
Следовательно, домен равен \([−\frac{7}{2}, \infty)\).
Мы используем графический калькулятор для построения следующего графика \(f(x)= \sqrt{12−4x}\).
По нашим оценкам, домен будет состоять из всех действительных чисел примерно справа от 3. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под радикалом в \(f(x)=\sqrt{12−4x}\) должно быть больше или равно нулю.
\(12−4x \ge 0\)
\(−4x \ge −12\)
\(х \ле 3\)
Следовательно, домен равен \((−\infty, 3]\).

Четный корень отрицательного числа не определяется как действительное число. Таким образом, 2x + 9 должно быть больше или равно нулю. Поскольку из \(2x + 9 \ge 0\) следует, что \(x \ge −\frac{9{2}\), областью определения является интервал \([−\frac{9}{2},\infty)\).
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −8x−3 должно быть больше или равно нулю. Поскольку из \(−8x−3 \ge 0\) следует, что \(x \le −\frac{3}{8}\), областью определения является интервал \((−\infty, −\frac{3}{ 8}]\).
Четный корень отрицательного числа не определяется как действительное число. Таким образом, -6x-8 должно быть больше или равно нулю. Поскольку из \(−6x−8 \ge 0\) следует, что \(x \le −\frac{4}{3}\), областью определения является интервал \((−\infty, \frac{4}{3} }]\).
Таким образом, -6x-8 должно быть больше или равно нулю. Поскольку из \(−6x−8 \ge 0\) следует, что \(x \le −\frac{4}{3}\), областью определения является интервал \((−\infty, \frac{4}{3} }]\).
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −7x+2 должно быть больше или равно нулю. Поскольку из \(−7x+2 \ge 0\) следует, что \(x \le \frac{2}{7}\), областью определения является интервал \((−\infty, \frac{2}{7} ]\).
Четный корень отрицательного числа не определяется как действительное число. Таким образом, 6x+3 должно быть больше или равно нулю. Поскольку из \(6x+3 \ge 0\) следует, что \(x \ge −\frac{1}{2}\), областью определения является интервал \([−\frac{1}{2}, \infty )\).
Поскольку из \(6x+3 \ge 0\) следует, что \(x \ge −\frac{1}{2}\), областью определения является интервал \([−\frac{1}{2}, \infty )\).
Четный корень отрицательного числа не определяется как действительное число. Таким образом, −7x−8 должно быть больше или равно нулю. Поскольку из \(−7x−8 \ge 0\) следует, что \(x \le −\frac{8}{7}\), областью определения является интервал \((−\infty, −\frac{8}{ 7}]\)
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Арнольд
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 2,5
- Показать страницу TOC
- нет
- Теги
- отражение
- функция квадратного корня
Предыдущий 2.5 Нахождение уравнения | Следующий 2.7 Квадратные неравенства |
2.6 Природа корней (EMBFP)
Исследование природы корней
Используйте квадратную формулу для определения корней квадратных уравнений ниже, и обратите особое внимание на:
- выражение под знаком квадратного корня и 92 — 4х + 7 = 0\)

| рациональное | неравный | реальный | ||||||||||||||
| воображаемый | не идеальный квадрат | равно | ||||||||||||||
| идеальный квадрат | иррациональный | не определено 9{2}-4ас\). Это выражение под квадратным корнем в квадратной формуле. Дискриминант
определяет характер корней квадратного уравнения. Слово
«природа» относится к типам чисел, которыми могут быть корни, а именно
реальное, рациональное, иррациональное или воображаемое.
|

 Затем нужно разделить исходное выражение на (х-2). Получится квадратное уравнение. Его корнями будут числа..
Затем нужно разделить исходное выражение на (х-2). Получится квадратное уравнение. Его корнями будут числа.. Когда переменная величина оказывается в знаменателе дроби.
Когда переменная величина оказывается в знаменателе дроби. — ISBN 978-5-09-028297-0.
— ISBN 978-5-09-028297-0.
 Равен нулю — ответом будет одно число. Положительный — два значения у переменной.
Равен нулю — ответом будет одно число. Положительный — два значения у переменной.

