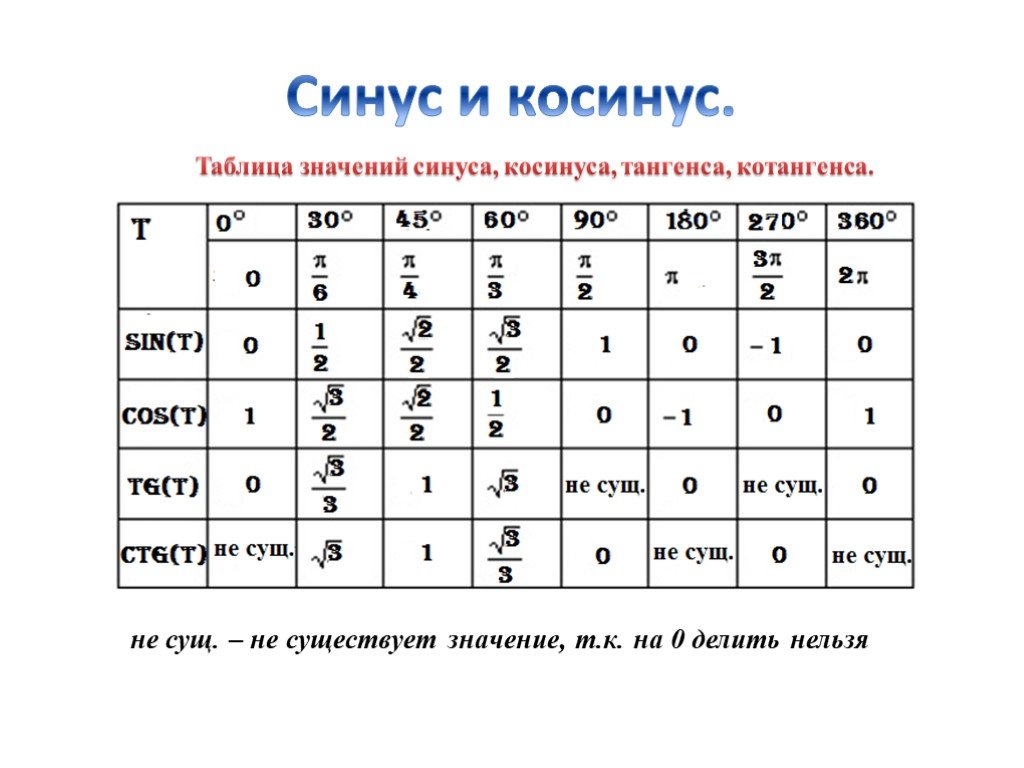
Электронный справочник по математике для школьников таблица значений тригонометрических функций синуса косинуса тангенса котангенса примеры вычисления значений
| Справочник по математике | Тригонометрия |
Содержание
| Таблица значений тригонометрических функций часто используемых углов |
| Вычисление значений тригонометрических функций |
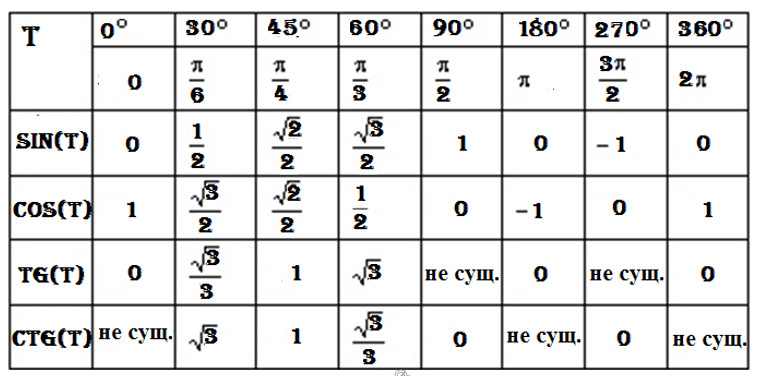
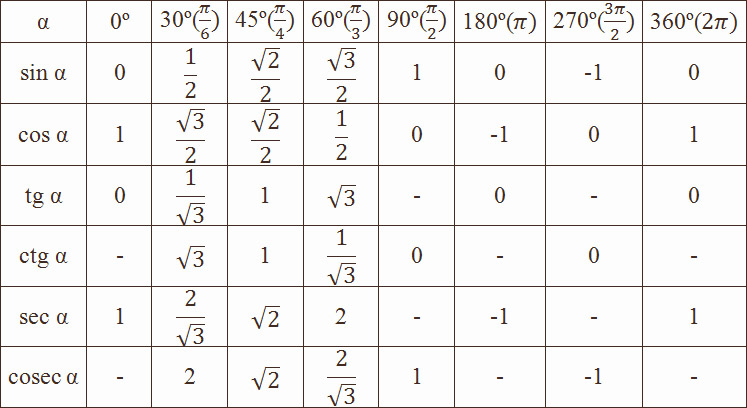
Таблица значений тригонометрических функций часто используемых углов
| I четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 0 | 0° | 0 | 1 | 0 | не существует |
| – 2π | – 360° | ||||
| 30° | – 330° | ||||
| 1 | 1 | ||||
| 45° | – 315° | ||||
| 60° | – 300° | ||||
| 1 | 0 | не существует | 0 | ||
| 90° | – 270° | ||||
| II четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 120° | – 240° | ||||
| – 1 | – 1 | ||||
| 135° | – 225° | ||||
| 150° | – 210° | ||||
| π | – π | 0 | – 1 | 0 | не существует |
| 180° | – 180° | ||||
| III четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 210° | – 150° | ||||
| 1 | 1 | ||||
| 225° | – 135° | ||||
| 240° | – 120° | ||||
| – 1 | 0 | не существует | 0 | ||
| 270° | – 90° | ||||
| IV четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 300° | – 60° | ||||
| – 1 | – 1 | ||||
| 315° | – 45° | ||||
| 330° | – 30° | ||||
| 2π | 0 | 0 | 1 | 0 | не существует |
| 360° | 0° | ||||
| I четверть | |
| α (рад): 0, – 2π α (град): 0°, – 360° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
| α (рад): , α (град): 30°, – 330° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 45°, – 315° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 60°, – 300° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 90°, – 270° | |
| sin α | 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| II четверть | |
| α (рад): , α (град): 120°, – 240° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 135°, – 225° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 150°, – 210° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): π, – π α (град): 180°, – 180° | |
| sin α | 0 |
| cos α | – 1 |
| tg α | 0 |
| ctg α | не существует |
| III четверть | |
| α (рад): , α (град): 210°, – 150° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 225°, – 135° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 240°, –120° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 270°, – 90° | |
| sin α | – 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| IV четверть | |
| α (рад): , α (град): 300°, – 60° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 315°, – 45° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 330°, –30° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): 2π, 0 α (град): 360°, 0° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
Примеры вычисления значений тригонометрических функций
ПРИМЕР 1. Найти sin 15°.
Найти sin 15°.
РЕШЕНИЕ. Воспользовавшись формулой «Синус разности», получаем:
ПРИМЕР 2. Найти cos 22,5°.
РЕШЕНИЕ. Воспользовавшись формулой «Косинус двойного угла», получаем:
ПРИМЕР 3. Найти sin 18°.
РЕШЕНИЕ. Поскольку
то, с помощью формул «Синус тройного угла» и «Косинус двойного угла», отсюда получаем:
Теперь, если ввести обозначение
sin 18° = t ,
то возникает кубическое уравнение
4t3 – 2t2 – 3t + 1 = 0 .
Решим это уравнение, раскладывая его левую часть на множители:
Поскольку
0 < sin 18° < 1 ,
то первый и второй корни должны быть отброшены. Следовательно,
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса
| |||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||
TehTab.ru Реклама на сайте | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||
|
Чтобы лучше понять некоторые проблемы, связанные с ракетами и движение необходимо использовать некоторые математические идеи из тригонометрия, изучение треугольников. Начнем с некоторых определений и терминологии. который мы будем использовать на этом слайде. А прямоугольный треугольник есть трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов это называется прямым углом , что дало название прямоугольному треугольнику. Мы выбираем один из двух оставшихся углов и обозначаем его c . а третий угол обозначим d .
Сумма углов любого треугольника равна 180 градусам.
Если мы знаем значение c ,
тогда мы знаем, что значение d : а третий угол обозначим d .
Сумма углов любого треугольника равна 180 градусам.
Если мы знаем значение c ,
тогда мы знаем, что значение d :90 + с + г = 180 д = 180 — 90 — в д = 90 — с Определим сторону треугольника, противоположную от прямого угла к быть гипотенуза . Это самая длинная сторона из трех сторон прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов что означает «растягиваться», так как это самая длинная сторона. Обозначим гипотенузу цифрой 9.0181 ч . Существует сторона, противоположная углу Нас интересуют отношения между сторонами и углами
правильный треугольник.
Начнем с некоторых определений. sin = о/ч Отношение прилежащей стороны прямоугольного треугольника к гипотенузе называется косинус и обозначен символ cos . cos = а/ч Наконец, отношение противолежащей стороны к прилежащей стороне называется касательная и обозначена символом tan . загар = о / а Мы утверждаем, что значение каждого отношения зависит только от значения
угол c образован прилежащим и гипотенузой.
Чтобы продемонстрировать этот факт,
давайте изучим три фигуры в середине страницы.
В этом примере мы имеем
8-футовая лестница, которую мы собираемся прислонить к стене. Стена
8 футов высотой, и мы нарисовали белые линии на стене
и синие линии вдоль земли с интервалом в один фут.
Длина лестницы фиксированная. о = 7,745 Отношение противоположности к гипотенузе равно 0,967 и определяется как
синус угла с = 75,5 градуса. Теперь предположим, что мы наклонили 8-футовую лестницу так, чтобы ее основание находилось на расстоянии 4 фута от стены.
Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем на
первый пример. Угол равен 60 градусов, а отношение прилежащего к
гипотенуза теперь 4/8 = 0,5. Уменьшение угла с увеличивает косинус угла, потому что гипотенуза фиксирована
а соседний увеличивается по мере уменьшения угла. Если мы наклоним 8 футов
лестнице так, чтобы ее основание было на расстоянии 6 футов от стены, угол уменьшается до
около 41,4 градуса, и соотношение увеличивается до 6/8, что составляет 0,75.
Как видите, для каждого угла
на земле есть уникальная точка, которой касается 8-футовая лестница,
и это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом.
Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы есть функция угла c , поэтому мы можем написать
символ как cos(c) = значение . Заметьте также, что по мере увеличения cos(c) sin(c) уменьшается. Если мы наклоним лестницу так, чтобы основание было на расстоянии 6,938 фута от стены, угол c становится равным 30 градусам и отношение прилежащего к гипотенуза равна 0,866. Сравнивая этот результат со вторым примером, мы находим, что: cos(c = 60 градусов) = sin (c = 30 градусов) sin(c = 60 градусов) = cos (c = 30 градусов) Мы можем обобщить это соотношение: грех (с) = потому что (90 — с) 90 — c есть величина угла d . Вот почему мы отношение прилежащего к гипотенузе называют косинусом угла. грех (с) = потому что (г) Поскольку синус, косинус и тангенс являются функциями угла c , мы можем
определить (измерить) коэффициенты один раз и составить таблицы значений
синус, косинус и тангенс для различных значений c . |

 …) + Таблицы Брадиса
…) + Таблицы Брадиса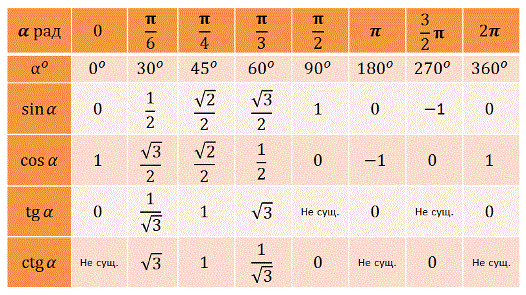
 Углы с шагом в 1°. Таблица значений синусов.
Углы с шагом в 1°. Таблица значений синусов.

 Мы позвоним
соотношение
стороны прямоугольного треугольника, противоположной гипотенузе
синуса и присвойте ему символ грех .
Мы позвоним
соотношение
стороны прямоугольного треугольника, противоположной гипотенузе
синуса и присвойте ему символ грех .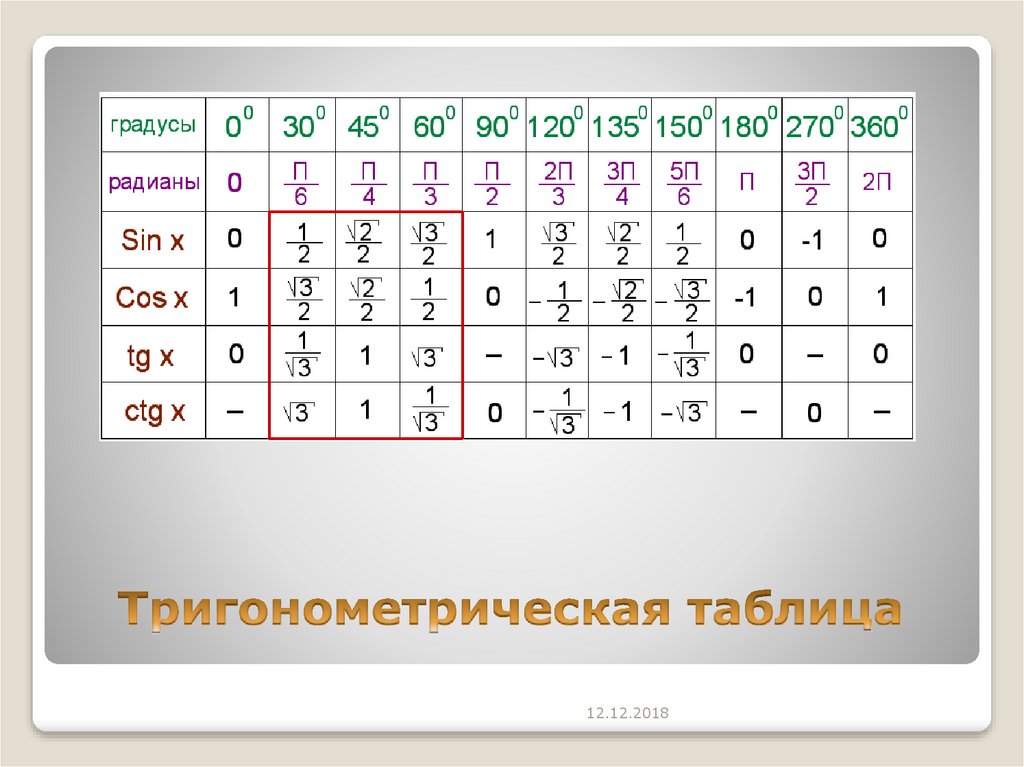 Если мы наклоним лестницу так, чтобы ее основание было в 2 футах от стены,
лестница образует с землей угол почти 75,5 градусов.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — примыкающая), к длине лестницы (h — гипотенуза), составляет 2/8 = 0,25.
Это определяется как косинус с = 75,5 градуса. (На
другая страница
мы покажем, что если бы лестница была в два раза длиннее (16 футов),
и наклонен под тем же углом (75,5 градусов), что он будет сидеть в два раза больше, чем
далеко (4 фута) от стены. Отношение
Если мы наклоним лестницу так, чтобы ее основание было в 2 футах от стены,
лестница образует с землей угол почти 75,5 градусов.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — примыкающая), к длине лестницы (h — гипотенуза), составляет 2/8 = 0,25.
Это определяется как косинус с = 75,5 градуса. (На
другая страница
мы покажем, что если бы лестница была в два раза длиннее (16 футов),
и наклонен под тем же углом (75,5 градусов), что он будет сидеть в два раза больше, чем
далеко (4 фута) от стены. Отношение