Сообщение на тему правильные многогранники: Правильные многогранники — урок. Геометрия, 10 класс.

Проект по теме: «Правильные многогранники вокруг нас»

 

 

 

 

 

 

 

Проект по теме

«Правильные многогранники вокруг нас»

 

 

 

 

 

 

 

 

Оглавление

I.Введение…………………………………………………………………………….3

II.Основная часть

2.1. История и понятие многогранников…………………………………………5

2.2.Виды правильных многогранников и их характеристики…………………….9

2.3. Связь геометрии и природы…………………………………………………..13

2.4.Многогранники в живописи………………………………………………….15

2.5. Многогранники в архитектуре………………………………………………..17

III.Практическая часть………………………………………………………………19

IV.Заключение……………………………………………………………………….23

V.Литература………………………………………………………………………..24

 

I. Введение

«Правильных многогранников вызывающе мало,

— но этот весьма скромный по  численности  отряд

 сумел пробраться в самые глубины различных наук».

Л. Кэролл

Есть в шкoльной геoмeтрии такиe тeмы,  кoтoрые  ждeшь  с  нeтeрпением, прeдвкушaя встрeчу с невероятно красивым материалом.  К  таким  темам  можно отнести «Правильные   многогранники».   Здесь   не   только    открывается удивительный мир геометрических тел,  обладающих  неповторимыми  свойствами, но и интересные научные факты. Но к сожалению в школьной программе мы не углубляемся в изучение правильных многогранников,  поэтому сведений об этих геометрических телах для меня недостаточно. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Они имеют красивые формы, обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед.

С древнейших времен представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.

Мы можем наблюдать, что многогранники встречаются и окружают нас повсюду.

Теория многогранников является современным разделом математики.

Безусловно, недостаточно узнавать и видеть многогранники в окружающем мире. Интересно уточнить их классификацию, разновидность, связь с миром людей. Этим и обусловлен выбор темы «Правильные многогранники  вокруг  нас».

Актуальность данного проекта состоит в том, что правильные многогранники – «вечные» тела. Интерес к ним тонкой нитью проходит через спираль всех времен.

Цель проекта: Изучить правильные многогранники.

Задачи проекта:

— ознакомиться с историей изучения многогранников;

— рассмотреть классификации многогранников;

— научиться моделировать многогранники;

— показать значение многогранников в повседневной жизни.

Гипотеза:  Если мы узнаем историю изучения многогранников, их классификацию, то сможем моделировать их на практике, находить в окружающем мире.

Объект исследования: раздел математики – геометрия.

Предмет исследования: многогранники.

Практическая значимость: изготовление объёмных фигур, развитие логического мышления  и применение  его на  практике  в решении задач  на нахождение  объёмов  и  построение  сечений  в  многогранниках.

 

 

II.Основная часть.

2. 1. История и понятие многогранников

Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.

              Рис.1

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них — пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

                          Рис.2

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти нарезных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

Начиная с 7 века до нашей эры в Древней Греции, создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.

Отличительным знаком пифагорейцев была пентаграмма, на языке математики – это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов. Пифагорейцев поражала красота, совершенство, гармония этих фигур. Они считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях. Первоосновам бытия – огню, воде земле, воздуху, придавалась форма соответственно тетраэдра, икосаэдра, куба, октаэдра, а вся Вселенная имела форму додекаэдра. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ – идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.

Платон также считал, что мир строится из четырёх «стихий» — огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; гексаэдр – самая устойчивая из фигур – землю, а октаэдр – воздух.

                      Рис.3

В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и плазменным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Это была одна из первых попыток ввести в науку идею систематизации.

Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого «тетра» — четыре, «эдрон» — грань.гексаэдр (куб) имеет 6 граней, «гекса» — шесть; октаэдр — восьмигранник, «окто» — восемь; додекаэдр — двенадцатигранник, «додека» — двенадцать; икосаэдр имеет 20 граней, «икоси» — двадцать.

Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.

Следующий серьезный шаг в науке о многогранниках был сделан в XVI11 веке Леонардом Эйлером (1707-1783), который без преувеличения «поверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.

Многогранник	Вершины Грани		Рёбра
Тетраэдр	4	4	6
Куб	8	6	12
Октаэдр	6	8	12
Додекаэдр	20	12	30
Икосаэдр	12	20	30

 

В соответствии с традицией, идущей от древних математиков, среди всех многогранников лучшие те, которые имеют своими гранями правильные многоугольники.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.2.Виды правильных многогранников и их характеристики.

Гексаэдр (более привычное название — куб).

 

 

            Рис.4

 

Древние греки дали многограннику имя по числу граней. «Гексо» означает шесть, «хедра» — означает грань (Гексаэдр – шестигранник). Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Гранью многогранника является квадрат. Каждый из четырех углов равен 90 градусов.

Тетраэдр.

 

 

             Рис.5

 «Тетра» означает четыре, «хедра» — означает грань (тетраэдр – четырехгранник).  Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Тетраэдр имеет следующие характеристики:

Тип грани – правильный треугольник;

Число сторон у грани – 3;

Общее число граней – 4;

Число рёбер примыкающих к вершине – 3;

Общее число вершин – 4;

Общее число рёбер – 6.

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Октаэдр.

 

 

         Рис.6

 

 «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).  Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Октаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;

Число сторон у грани – 3;

Общее число граней – 8;

Число рёбер примыкающих к вершине – 4;

Общее число вершин – 6;

Общее число рёбер – 12;

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.
Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Додекаэдр.

 

          Рис.7

 

 «Додека» означает двенадцать, «хедра» — означает грань (додекаэдр – двенадцатигранник).  Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Додекаэдр имеет следующие характеристики:

Тип грани – правильный пятиугольник;

Число сторон у грани – 5;

Общее число граней – 12;

Число рёбер примыкающих к вершине – 3;

Общее число вершин – 20;

Общее число рёбер – 30;

Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Додекаэдр имеет центр симметрии — центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

Икосаэдр.

«Икоси» означает двадцать, «хедра» — означает грань (Икосаэдр – двадцатигранник).   Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.

 

        Рис.8

 

Икосаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;

Число сторон у грани – 3;

Общее число граней – 20;

Число рёбер примыкающих к вершине – 5;

Общее число вершин – 12;

Общее число рёбер – 30;

Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 270°.
Икосаэдр имеет центр симметрии — центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

 

 

 

 

 

 

 

 2.3. Связь геометрии и природы.

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра.

Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии(Circjgjniaicosahtdra) по форме напоминает икосаэдр.

Большинство феодарий живут на морской глубине и часто служат добычей коралловых рыбок. Но это простейшее животное защищает себя двенадцатью иглами, которые выходят из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник.

Пчёлы – удивительные создания.

             Рис.9

Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов. Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».

 

              Рис.10

Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как это считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр.

Впрочем, многогранники – отнюдь не только объект научных исследований. Их формы – завершенные и причудливые, широко используются в искусстве.

 

2.4. Многогранники в живописи.

Титан Возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи (1452-1519) — символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосимметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности.

Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр

Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии МаурицаКорнилисаЭшера (1898-1972), голландского художника, родившегося в Леувардене. МаурицЭшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.

Правильные геометрические тела — многогранники — имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Изящный пример звездчатого додекаэдра можно найти в его работе «Порядок и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.

Наиболее интересная работа Эшера — гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров.

           Рис.11

Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра.

             Рис.12

Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ, т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.

Геометрия появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров. Поэтому архитектурные сооружения яркий тому пример.

 

 

2.5. Многогранники в архитектуре.

С точки зрения формы архитектура всегда была преимущественно кубической. Изредка встречались и другие Платоновы тела, то есть призмы, конусы, пирамиды, сферы, но все же куб имел подавляющее преимущество. По сути дела куб лежал в основе любой архитектурной формы нескольких последних тысячелетий.

Примером применения в архитектуре других Платоновых тел может служить Великая пирамида в Гизе. Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Она имеет форму правильного тетраэдра и является древнейшим из Семи чудес древности.

Также примером архитектурных сооружений с использованием многогранников является Фаросский маяк.

             Рис.13

Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. Он состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров.

Ещё один маяк, конструкция которого состоит из Платоновых тел — это Александрийский маяк. Он был построен в III веке до н.э., чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Это был первый в мире маяк, и простоял он 1500 лет.

Использование многогранников в архитектурных сооружениях можно наблюдать и в нашем городе. В первую очередь это конечно церкви, но наряду с историческими памятниками существуют и современные здания с яркими многогранниками.

 

 

 

IV.Практическая часть.

             Моделирование – построение моделей, процесс познания действительных объектов, метод изучения технических сооружений, мыслительный и практический вид деятельности, непосредственно создание моделей. Моделирование появилось тогда, когда человечество осознало свое место в окружающем мире и стало стремиться к пониманию и изменению его. Одной из разновидностей моделей являются геометрические модели. Они передают внешние признаки объекта: размеры, форму, цвет. Геометрические модели представляют собой некоторые объекты, геометрически подобные своему прототипу (оригиналу). Они служат для учебных и демонстрационных целей, используются при проектировании сооружений, конструировании различных изделий. Развитие творческих способностей заключается именно в том, чтобы раскрыть суть моделирования, его принципы и закономерности. На первых порах обучения дети работают по готовым эскизам и чертежам с использованием преимущественно репродуктивных, воспроизводящих методов. Частично применяются методы, способствующие умственному развитию учащихся, т.е. проблемные, исследовательские и др. Конструирование – один из способов моделирования. Оно представляет разработку совместимых типовых элементарных объектов (деталей) и создание более сложных объектов из этих деталей.

Практическая часть нашей работы заключалась в том, чтобы построить модели правильных многогранников. Для этого мы использовали такие развертки, в которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер.

 

 

 

 

 

 

 

 

 

IV.Заключение

Проделанная  работа помогла узнать и убедиться в том, что многогранники на протяжении всей истории человечества не перестали восхищать пытливые умы симметрией, мудростью и совершенством своих форм.

Мы рассмотрели правильные многогранники и убедились, что не человек, а природа придумала эти удивительные формы. Мы всего лишь позаимствовали, то что создано до человечества. Создания природы красивы и симметричны. В ходе работы, мы выяснили, что многогранники играют немало важную роль в окружающей среде. Дальнейшее изучение многогранников позволит человечеству улучшить качество жизни, решить многие проблемы. Этой работой мы хотим заинтересовать всех, и дать возможность открыть тайны неизвестного.

Таким образом, многогранные формы окружают нас в повседневной жизни повсюду: спичечный коробок, книга, комната, молочные пакеты в форме тетраэдра или параллелепипеда. Почти все сооружения, возведённые человеком, от древнеегипетских пирамид до современных небоскрёбов, имеют форму многогранников.

 

V.Литература.

1. Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.

2. Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.

3. Ворошилов А.В. Математика и искусство. – М. просвещение, 1992. – 352

4. Рыбников К.А. История математики: Учебник. – М.: Изд-во МГУ, 1994. – 495 с

5. Интернет Ресурсы: http://www.nips.riss-telecom.ru/polv/

6. Мир многогранников: http://www.sch57.msk.ru:8101/collect/smogl.htm

7. История математики:http://mschool.kubsu.ru/

8. Библиотека электронных учебных пособий:http://www.ega-math.narod.ru/

9. Статьи по математике:http://dondublon. chat.ru/math.htm

10. Популярная математика:http://www.uic.ssu.samara.ru/~nauka/index.htm

 

Правильные многогранники — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Реферат на тему: Правильные многогранники

Пермский техникум промышленных и информационных технологий им. Б. Г. Изгагина
Реферат на тему: Правильные
многогранники
Выполнила:
Фроленкова О. А. 19СПИ1
Пермь, 2020

2. Содержание

Теория
Историческая справка
Эйлер и правильные многогранники
Применение в различных науках и
аспектах человеческой жизни

3. Теория

Выпуклый многогранник называется правильным, если все его
грани — равные правильные многоугольники, и в каждой его
вершине сходится одно и то же число ребер.
Все ребра правильного многогранника равны, все двугранные
углы правильного многогранника равны, все многогранные
углы правильного многогранника равны. Существует ровно пять
выпуклых правильных многогранников:
Выпуклый многогранник называется правильным, если его грани
являются правильными многоугольниками с одним и тем же
числом сторон, и в каждой вершине многогранника сходится
одно и то же число ребер.
Все ребра правильного многогранника равны друг другу. Равны
также все его двугранные углы, содержащие две грани с общим
ребром.
Правильный тетраэдр (четырехгранник) — многогранник, составленный из
четырех правильных треугольников (рис. 1а).
Правильный гексаэдр (шестигранник) или куб — многогранник, составленный
из шести правильных четырехугольников (квадратов) (рис. 1б).
Правильный октаэдр (восьмигранник) — многогранник, составленный из
восьми правильных треугольников (рис. 1в).
Правильный додекаэдр (двенадцатигранник) — многогранник, составленный
из двенадцати правильных пятиугольников (рис. 1г).
Правильный икосаэдр (двадцатигранник) — многогранник, составленный из
двадцати правильных треугольников (рис. 1д).

5. Историческая справка

Правильные многогранники известны с древнейших времён. Их орнаментные
модели можно найти на резных каменных шарах, созданных в период
позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях,
которыми люди играли на заре цивилизации, уже угадываются формы
правильных многогранников.
В значительной мере правильные многогранники были изучены древними
греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их
открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр,
куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету
Афинскому, современнику Платона. В любом случае, Теэтет дал математическое
описание всем пяти правильным многогранникам и первое известное
доказательство того, что их ровно пять.

6. Эйлер и правильные многогранники

Теорема Эйлера для правильных
многогранников
Теорема Эйлера для многогранников —
теорема, устанавливающая связь между
числом вершин, рёбер и граней
для многогранников, топологически
эквивалентных сфере.

7. Многогранники в аспектах жизни

Правильные многогранники — самые выгодные
фигуры. И природа этим широко пользуется.
Кристаллы некоторых знакомых нам веществ имеют
форму правильных многогранников:
— куб передает форму кристаллов поваренной соли
NaCl;
— монокристалл алюминиево-калиевых квасцов имеет
форму октаэдра;
— кристалл сернистого колчедана FeS имеет форму
додекаэдра;
— сернокислый натрий – тетраэдр;
— бор — икосаэдр.

English     Русский Правила

9 правильных многогранников – TOM ROCKS MATHS

Gavin Jared Bala

Классическое понятие правильного многогранника:

• Конечная объемная фигура,
• ограничено одинаковыми правильными многоугольными гранями,
• со всеми одинаковыми вершинами (т.е. окруженными одинаковым количеством граней).

Знакомый пример — куб, ограниченный квадратными гранями, сходящимися по три к углу.

Это естественное обобщение определения правильного многоугольника на 3D:

• Конечная плоская фигура,
• ограничен одинаковыми отрезками,
• со всеми вершинами одинаковыми (что можно измерить их углами).

Например, у квадрата четыре равные стороны и четыре равных прямых угла.

Одна из самых известных теорем стереометрии состоит в том, что правильных многогранников всего пять.

Стандартное доказательство древнее! Он является частью книги XIII, предложения 18 великого произведения Евклида, Элементы (написано около 300 г. до н.э.).

Итак, давайте теперь рассмотрим, как можно использовать каждый правильный многоугольник для создания правильных многогранников.

Полный круг равен 360°, а угол должен быть меньше, если его нужно сложить в третье измерение.

Равносторонние треугольники имеют углы 60°, поэтому они могут вмещать три, четыре или пять углов; но не шесть, так как тогда не осталось бы места. Квадраты имеют углы 90°, а пятиугольники 108°; так что они могут поместиться только три в вершине. Три шестиугольника с углами 120° полностью заполняют вершину; более высокие полигоны имеют еще большие углы, поэтому попытки их использования бесполезны.

Достаточно просто взять кучу полигонов и попытаться соединить их, чтобы убедиться, что все эти случаи возможны. Они соответствуют соответственно тетраэдру, октаэдру, икосаэдру, кубу и додекаэдру.

Такова была история на протяжении тысячелетий. Однако, не замеченный всеми, у него был недостаток!

При анализе кейсов недостаточно проверить возможность выполнения каждого кейса. Мы также должны проверить , сколькими способами мы можем выполнить этот случай.

Итак, мы допустили ошибку, когда предположили, что покрыли каждого правильного многоугольника. Конечно, мы рассмотрели один вид правильного пятиугольника: выпуклый с углами 108°.

Но пятиконечная звезда, или пентаграмма , имеет пять равных углов по 36° и пять равных сторон. Это второй вид правильного пятиугольника!

Обратите внимание, что в центре правильной пентаграммы находится правильный пятиугольник. Это показывает, как эти правильные звезды естественным образом возникают в процессе звездчатая форма или расширение сторон правильных многоугольников.

Пронумеруем стороны правильного пятиугольника как 12345 последовательно. Сторона 3 уже встречается со сторонами 2 и 4. Если мы симметрично продолжим все стороны, то сторона 3 соединится с расширенными сторонами 1 и 5, образуя правильную пентаграмму.

Многоугольники более высокого уровня могут иметь несколько звездчатых форм. Если мы применим это к семиугольнику, то получим две звёздчатые формы. Пронумеровав стороны 1234567 последовательно, сторона 4 уже встречается со сторонами 3 и 5. Если мы продлим ее дальше, она встретится с расширенными сторонами 2 и 6; и если мы продлим его еще дальше, он встретится с расширенными сторонами 1 и 7. На этом процесс останавливается, потому что больше не с чем встречаться. Последовательные этапы видны ниже.

Не все звёздчатые формы создают единый полигон. Несмежные стороны шестиугольника находятся под углами 60 °, которые являются углами между двумя сторонами равностороннего треугольника. Поэтому, если мы будем настаивать на звездообразном расположении шестиугольника, мы не получим новый многоугольник. Получаем Звезду Давида: она распадается на два треугольных контура.

Но мы получаем все правильные многоугольники как звёздчатые формы выпуклых. Правильный звездчатый многоугольник с n вершинами имеет n ребер, поэтому его ядро ​​должно иметь не более n ребра. Но регулярность подразумевает, что все углы выглядят одинаково и, в частности, звезда имеет n -кратную симметрию вращения. Симметрия звезды — это симметрия ядра, поэтому ядро ​​имеет не более n сторон, но имеет n -кратную симметрию вращения. Таким образом, это должен быть обычный n -гон.

Важно подчеркнуть, что посторонние пересечения несмежных ребер составляют , а не вершин. Вершина — это просто место, где два соседних сторон пересекаются. Если стороны не смежные, то их пересечение не является вершиной! Это просто «случайный» перекресток.

Это мышление оправдывается топологией (красочно «геометрия резинового листа»). Здесь мы заботимся не столько о точном расположении вещей, сколько о вещах, которые сохраняются, когда мы непрерывно деформируем форму.

С этой точки зрения самое важное в многоугольнике — это то, как каждая его сторона соединяется со следующей, образуя в итоге петлю. Если рассматривать только ребра, пентаграмма и пятиугольник — это разные реализации одного и того же. Они оба имеют пять вершин и пять ребер в цикле.

Тот факт, что сторона может пересечься с другой где-то еще, не имеет значения, потому что мы можем просто оттолкнуть их друг от друга. Действительно, если мы достаточно деформируем пятиугольник, мы можем превратить его в пентаграмму!

Немецкий математик и астроном Иоганн Кеплер (1571–1630) понял, что мы можем использовать правильные звездчатые многоугольники в качестве граней правильных звездчатых многогранников! Вытекающие из этого возможности были впервые полностью исследованы французским математиком Луи Пуансо (1777–1859 гг.).). Вместе это привело к открытию четырех новых правильных многогранников, которые в честь них названы телами Кеплера-Пуансо .

Но как их получить и, что еще важнее, доказать, что они единственные? Мы пойдем по пути великого французского математика Огюстена-Луи Коши (1789–1857).

Очевидный способ, исходя из размерной аналогии, состоит в том, чтобы попробовать звездчатые правильные многогранники.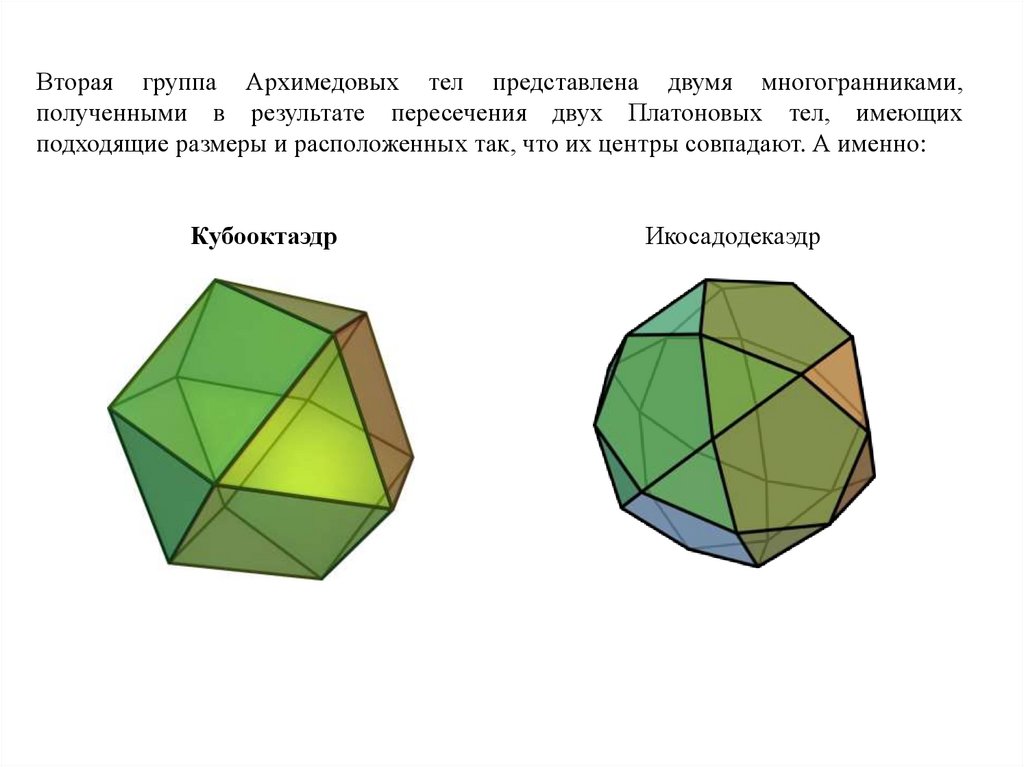 Мы можем сделать это либо путем расширения граней, либо путем расширения ребер. Последнее относится только к додекаэдру, так как есть только один вид правильного треугольника и квадрата, но есть два вида правильного пятиугольника.

Прежде, чем мы начнем звёздчатую форму, n -угольная грань встречается с n другими гранями вдоль каждой из её сторон, лежащих под общим углом к ​​ней по симметрии. Поскольку звёздчатая форма должна сохранять симметрию, после грань удлиняется, она должна снова встретить n новых граней вдоль своих сторон, которые всё ещё лежат под другим общим углом к ​​ней. Поэтому нам нужно исследовать структуры Платоновых тел так же, как мы делали это для структур пятиугольника и семиугольника.

Тетраэдр не может быть звездчатым, так как все его грани уже смежны, и у них нет возможности снова встретиться.

Куб сталкивается с той же проблемой, так как несмежные грани параллельны.

Октаэдр имеет более интересную структуру. Предположим, мы выделяем одну грань, чтобы она была наверху. Затем мы разбили октаэдр на четыре «слоя»:

• верхняя грань;
• пояс трехгранный, уже примыкающий;
• другой пояс из трех граней, примыкающий к параллельной грани снизу;
• параллельная грань внизу.

Итак, октаэдр может быть звездчатым. Расширьте каждую грань, пока она не встретится с тремя гранями, смежными с противоположной: они лежат под одним и тем же углом к ​​оригиналу, и, таким образом, симметричное расширение равностороннего треугольника коснется их всех. К сожалению, углы, под которыми они сходятся, — это углы между соседними гранями тетраэдра. Так что это дает только трехмерную версию Звезды Давида: два взаимопроникающих тетраэдра.

Додекаэдр имеет схожую структуру с октаэдром. Взяв одну грань сверху, мы имеем:

• верхняя грань;
• пояс из пяти граней, уже смежных;
• другой пояс из пяти граней, примыкающий к параллельной грани снизу;
• параллельная грань на самом дне.

Но теперь у нас есть две возможности для каждого из допустимых (непараллельных) случаев, потому что есть два вида пятиугольников, тогда как был только один вид треугольника.

Если каждый из его пятиугольников звёздообразно изобразить в виде пентаграммы, то все они пересекутся в новых вершинах. Это дает правильный маленький звездчатый додекаэдр . Грани правильные, и все вершины окружены одинаково, и, следовательно, это шестой правильный многогранник, составленный из двенадцати пентаграмм, сходящихся в углу с пятью. Каждое лицо по-прежнему встречается с пятью, которые изначально были рядом с ним.

Мы можем видеть первоначальный додекаэдр, спрятанный внутри, точно так же, как мы можем видеть первоначальный пятиугольник, спрятанный внутри пентаграммы. Это присутствует и в других звёздчатых формах додекаэдра, но менее очевидно.

Если мы заменим каждую из пентаграмм малого звёздчатого додекаэдра пятиугольником с такими же вершинами, то мы получим ещё одну звёздчатую форму, которая возникает в результате расширения граней , а не рёбер исходного додекаэдра, пока не встретится с пятью соседями его противоположной стороны, которые лежат под одним и тем же углом к ​​нему. Этот седьмой правильный многогранник называется великим додекаэдром .

Состоит из двенадцати пятиугольников, по пять в углу. Но пятиугольники соединены так, что они охватывают дважды вокруг вершины, точно так же, как края пентаграммы соединяются так, что они обертывают дважды вокруг центра.

Мы можем еще раз звездчато, так как пятиугольники большого додекаэдра сами поддаются звездообразной формы. Если мы расширим их до пентаграмм, мы сформируем восьмой правильный многогранник: большой звездчатый додекаэдр , с двенадцатью пентаграммами, сходящимися по три в углу.

Поскольку пятиугольники и пентаграммы комбинаторно идентичны, большой звездчатый додекаэдр комбинаторно идентичен исходному додекаэдру с двенадцатью пятиугольниками, встречающимися с тремя в углах! Мы могли бы считать их разными аватарами одного и того же абстракция правильный многогранник.

Это конец пути звездчатого додекаэдра. Вместо этого последнее тело Кеплера-Пуансо представляет собой звездчатую форму икосаэдра.

Итак, давайте установим икосаэдр гранью наверху и изучим его структуру. Имеем:

• оригинал лица;
• три грани, примыкающие к ней, с общей стороной;
• шесть смежных с ним граней, но только с общей вершиной;
• шесть граней, смежных с антиподом грань по общей вершине;
• три грани, смежные с противоположной гранью общей стороной;
• само антиподное лицо.

Однако оказывается, что третий слой наклонен к верхней грани под углами октаэдра, а четвертый слой под углами тетраэдра, и поэтому новых тел они не дают.

Единственный оставшийся вариант — расширить грани, чтобы они соответствовали граням пятого слоя, примыкающего к противоположной грани. Это дает окончательное тело Кеплера-Пуансо: великий икосаэдр . Здесь двадцать треугольников встречаются с пятью углами, что делает его комбинаторно таким же, как обычный икосаэдр; но они окружают каждую вершину дважды. Первоначальный икосаэдр спрятан глубоко внутри, и его нелегко обнаружить.

Теперь мы должны задать последний вопрос: как мы можем быть уверены, что это все возможные правильные многогранники?

По той же самой идее: мы докажем, что каждый правильный звездчатый многогранник является звёздчатой ​​формой обычного правильного многогранника .

Если мы построим два одинаковых правильных многогранника-звезды, то их ядрами должен быть какой-нибудь выпуклый многогранник. Если мы совместим две звезды-многогранника по некоторой симметрии, то мы совместим и их ядра по той же симметрии, и поэтому ядра будут иметь все те же симметрии, что и целые многогранники. Следовательно, грани жил должны быть равны, углы между ними должны быть равны, и они должны встречаться в одинаковом количестве в каждой вершине!

Это почти все определение правильного многогранника; нам просто нужно доказать, что грани действительно правильные.

Если правильная грань исходного звездчатого многогранника имела n -кратную симметрию, то такой же была бы и грань его ядра.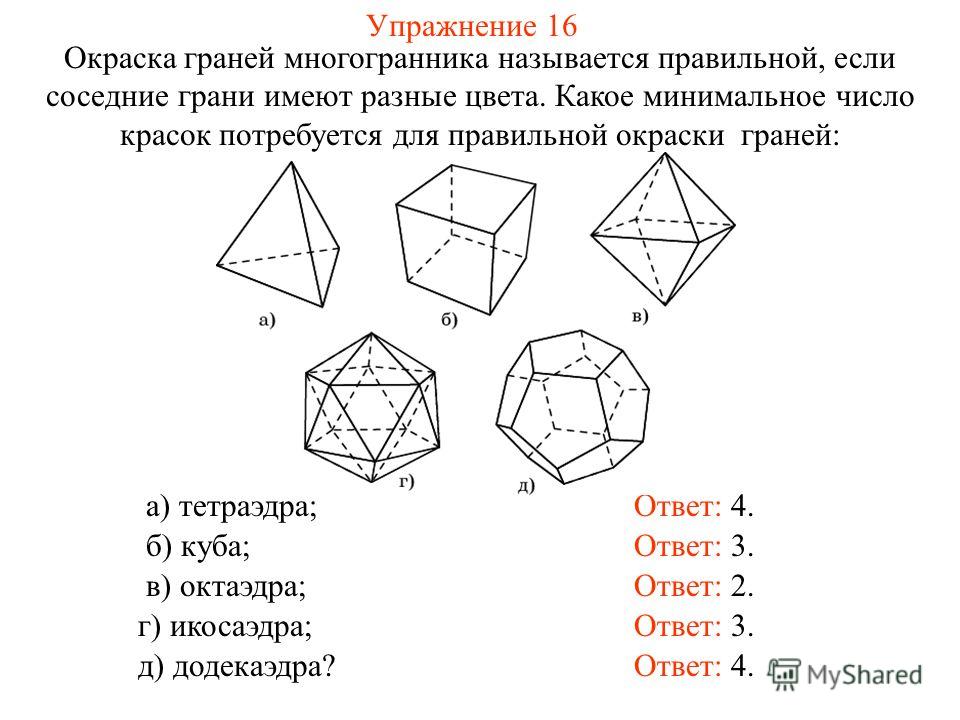 Следовательно, грани выпуклого ядра должны быть либо выпуклыми правильными n -угольниками, либо иметь не менее 2 n сторон. Но поскольку n не меньше 3, последний случай означает, что ядро ​​представляет собой выпуклый многогранник, все грани которого имеют не менее шести сторон.

Нам нужно вызвать формулу многогранника Эйлера . Пусть число вершин выпуклого многогранника равно V, количество ребер равно E, а количество граней равно F. Тогда формула многогранника Эйлера говорит нам, что V – E + F = 2,

Рассмотрим грани, которые затем встречаются в вершине ядра; их как минимум три. Каждая грань имеет не менее шести сторон, поэтому каждая грань дает не менее шести вершин. Но поскольку в каждой вершине встречаются не менее трех граней, это приводит к пересчету вершин как минимум в три раза. Следовательно, 3V ≤ 6F или V ≤ 2F.

Однако каждая грань имеет не менее шести ребер, и на каждом ребре сходятся ровно две грани. Таким образом, 6F ≤ 2E или 3F ≤ E.

Складываем их вместе, V – E + F ≤ 2F – 3F + F = 0. Но ядро ​​выпуклое, поэтому должно быть 2,9.0007

Это невозможно!

Следовательно, грани ядра выпуклые правильные n -угольников, а значит, ядро ​​правильное.

Таким образом, завершение списка правильных многогранников в основном сводится к составлению звездообразной формы каждого Платонового тела.

Но мы это уже сделали!

Основные статистические данные для девяти правильных многогранников представлены ниже:

	Вершины (V)	Ребра (E)	Faces (F)	V – E + F
Tetrahedron	4	6	4	2
Cube	8	12	6	2
Octahedron	6	12	8	2
Dodecahedron	20	30	12	2
Icosahedron	12	30	20	2
Small stellated dodecahedron	12	30	12	−6
Great dodecahedron	12	30	12	−6
Great stellated dodecahedron	20	30	12	2
Great icosahedron	12	30	20	2

As we can see, Euler’s polyhedron formula holds for the convex polyhedra. Но почему это работает только для двух звездных?

Формула многогранника Эйлера на самом деле относится к глубокому топологическому факту: классификации различных поверхностей. Значение V – E + F равно 2 , а именно , когда многогранник, рассматриваемый как поверхность, может непрерывно деформироваться в сферу. Это дает комбинаторный критерий для классификации поверхностей.

Платоновы тела явно являются топологическими сферами: представьте, что вы надуваете их, как надувные мячи.

Большой звездчатый додекаэдр и большой икосаэдр являются топологическими сферами, даже если они значительно искривлены, потому что они комбинаторно такие же, как нормальный додекаэдр и икосаэдр.

Но для малого звездчатого додекаэдра и большого додекаэдра V – E + F равно −6. Это , а не топологических сфер. Они составляют две аватары нового правильного многогранника, поверхность которого равна , а не непрерывно деформируется в сферу.

Существует много таких «обобщенных» правильных многогранников, которые обычно называют правильными картами . Их родиной является не сфера, как для Платоновых тел, а какая-то другая более экзотическая поверхность, которую они выступают в качестве регулярной мозаики. Для малого звездчатого додекаэдра и большого додекаэдра это четырехдырчатый тор: бублик с четырьмя отверстиями или сфера с четырьмя ручками.

Малый звездчатый додекаэдр и большой додекаэдр необычны тем, что могут быть вытеснены в обычное пространство и при этом сохранять геометрическую правильность – хотя и ценой болезненных самопересечений. Бесконечно многие другие не могут!

Также есть много тонкостей, связанных с использованием пентаграмм.

В случае обычного пятиугольника одно путешествие на 360° по краям проходит один раз вокруг центра и возвращает нас туда, откуда мы начали. Но с пентаграммой нам нужно совершить путешествие на 720°, обернув дважды по вокруг центра, прежде чем это произойдет.

Это напоминает острие конуса, только там для полного оборота требуется меньше 360°, а здесь больше 360°. И действительно, здесь проблемную область можно локализовать в центре, создав одну «особую точку» в середине пентаграммы, для полного поворота которой требуется поворот на 720°, в то время как везде требуется только 360°.

А еще это напоминает переход между уровнями автостоянки с пандусами: если мы совершаем круг на 360°, но при этом ограничены автостоянкой, мы будем подниматься или опускаться на уровень, а не возвращаться на то же место!

Такие структуры распространены в комплексном анализе. Существует много функций, таких как функции извлечения квадратного корня и логарифма, которые нельзя определить непрерывно на всей комплексной плоскости. Естественным доменом для них является набора сложных плоскостей, склеенных вместе, так что обход определенных точки ветвления перемещают нас из одной плоскости в другую. Такие конструкции называются римановыми поверхностями . Тела Кеплера-Пуансо также являются римановыми поверхностями, склеивающими сферы, а не плоскости!

Дальнейшие тонкости возникают при рассмотрении площади правильной пентаграммы! Что такое «интерьер»?

Если мы просто попытаемся разделить пентаграмму на треугольники для определения площади, то кажется, что центральный пятиугольник каким-то образом должен считаться «дважды». Это согласуется с идеей, что эта область обведена дважды.

И все же границы многоугольника обычно отделяют внутреннюю часть от внешней. Стороны пентаграммы отделены снаружи одной границей, но другая граница отделяет их от центра. Является ли эта область также «внешней»?

Получается, оба варианта законны! Отличаются они тем, на какой поверхности мы рисуем нашу пентаграмму — так что опять топология! Пентаграмма на плоской плоскости, естественно, имеет сердечник с двойной обмоткой; но пентаграмма на ленте Мёбиуса, естественно, полая.

Аналогичные и даже более хитрые тонкости возникают с объемами и внутренностями многогранников, так как они могут иметь в качестве граней звезды-многоугольники!

И из девяти правильных многогранников мы могли бы аналогичным образом распространить это обсуждение на четыре измерения, дав не менее шестнадцати правильных фигур – шесть выпуклых и десять звездчатых! Хотя обычных звезд не существует в измерениях выше четырех, в любом измерении нет недостатка в менее правильных звездах.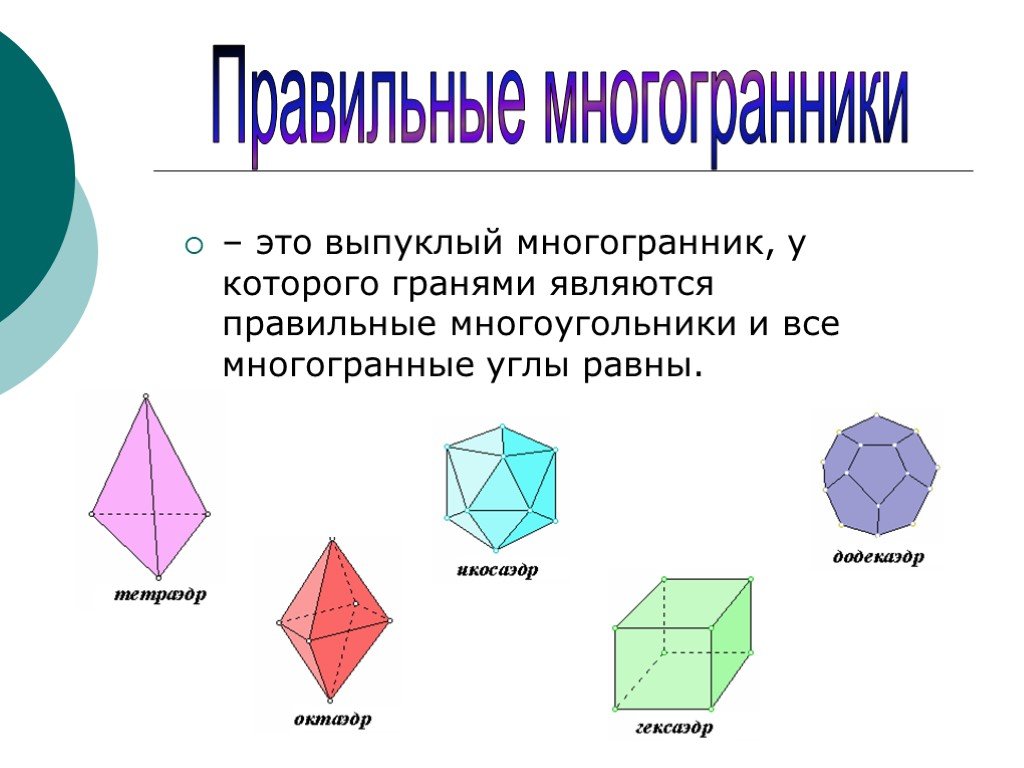

Завершение набора из девяти правильных многогранников, безусловно, является прекрасным упражнением в чистой геометрии. Но, как мы видели, он также включает в себя множество тонкостей и связывает многие разделы высшей математики.

---

А.-Л. Коши, «Recherches sur les polyèdres. Première party», Journal de l’École Polytechnique, Cahier 16, t. 9 (1813), стр. 68-74.

Английский перевод Гая Инчбальда можно найти по адресу http://www.steelpillow.com/polyhedra/StelFacet/Cauchy1813EngTrans.pdf

Inchbald, G. (2021, 3 июля). Морфические многогранники. Стальная подушка. http://www.steelpillow.com/polyhedra/morphic/morphic.html

Изображения правильных многоугольников были взяты из Википедии и находятся в открытом доступе.

Изображения правильных многогранников были сделаны пользователем Cyp в Википедии с использованием POV-Ray и под лицензией Creative Commons Attribution-Share Alike 3.0 Unported.

Нравится:

Нравится Загрузка. ..

Проект правильных многогранников

Проект правильных многогранников

Содержание I. Геометрические свойства II. Двойные многогранники Ссылки

Дополнения и ссылки Правильные многогранники Блокнот Mathematica Советы по этому проекту Решения для этого проекта Проект правильных многоугольников Проект регулярных многогранников

Цели: Развивать пространственное мышление, в частности, применяя методы планарной геометрии к трехмерным телам.	Необходимый фон: Опыт работы с плоской геометрией обязателен, но тригонометрия не требуется. Раздел II предполагает знание формулы Эйлера.
Резюме: В Разделе I учащиеся вычисляют объемы и площади поверхности пяти Платоновых тел через длины сторон.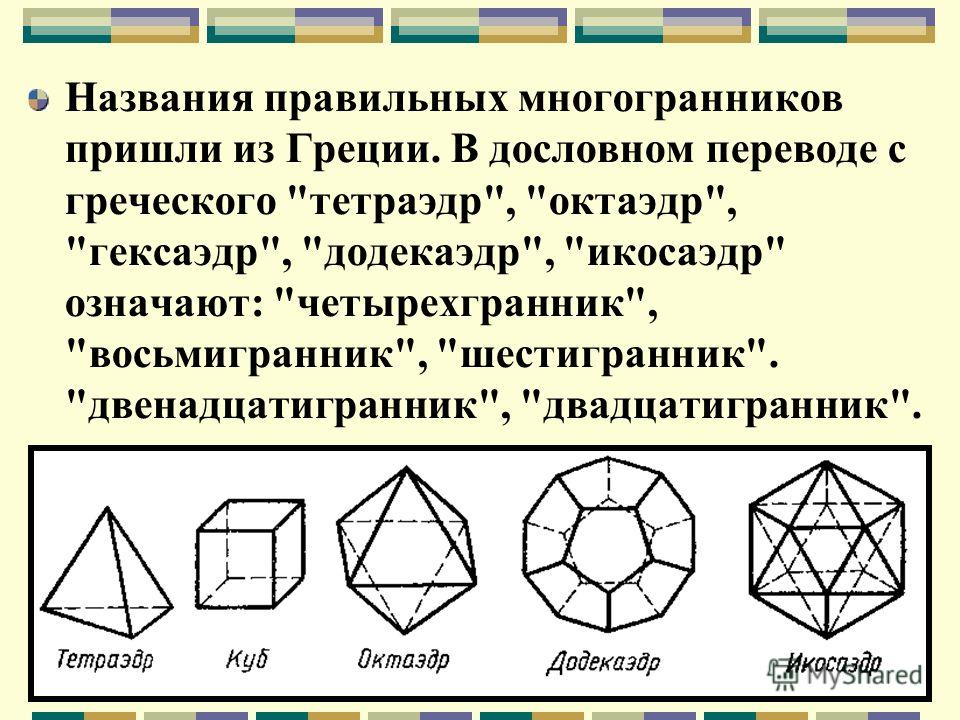 В разделе II учащиеся применяют формулу Эйлера к многогранникам, подсчитывают количество диагоналей в каждом из Платоновых тел и находят двойственные многогранники Платоновых тел.

I. Геометрические свойства

Как мы можем рассматривать многоугольники на плоскости, мы можем рассматривать многогранников в пространстве. Многогранник — это замкнутая трехмерная фигура, грани которой — многоугольники. Например, любой замкнутый ящик — это многогранник, потому что его грани — прямоугольники. Многогранник называется выпуклым , если отрезок, соединяющий любые две точки внутри фигуры, полностью лежит внутри фигуры. (Подобные звездчатые («звездчатые») многогранники не являются выпуклыми.) Многогранник называется обычный , если все его грани конгруэнтны и все его вершины идентичны (т. е. имеют одинаковое количество граней и углы между гранями одинаковы). Вам может показаться удивительным, что хотя правильных многоугольников бесконечно много, выпуклых правильных многогранников всего пять , известных как платоновы тела в честь Платона, который приравнял их к элементам природы. Посмотрите, сможете ли вы найти три из них, прежде чем двигаться дальше. (Есть четыре невыпуклых правильных многогранника, известных как тела Кеплера-Пуансо.)

Докажите, что куб является правильным многогранником. Чему равен объем куба со стороной х ? Какова площадь поверхности такого куба?

Чему равен радиус a сферы, вписанной в куб? Мы будем называть апофемой . Каков радиус r сферы, описанной вокруг куба?

Тетраэдр представляет собой многогранник с четырьмя гранями. Нарисуйте правильный тетраэдр и докажите, что это правильный многогранник. Какова площадь его поверхности?

Какова высота h правильного тетраэдра с длиной стороны s ? Каков его объем?

Пять Платоновых тел изображены ниже. Вращающиеся визуализации Платоновых тел представлены на веб-сайте Wolfram Research. Слева вверху это правильный тетраэдр (четыре грани), куб (шесть), правильный октаэдр (восемь), правильный додекаэдр (двенадцать) и правильный икосаэдр (двадцать).

Какова площадь поверхности правильного октаэдра со стороной s ? Каков его объем?

Каковы площади поверхности правильного додекаэдра и правильного икосаэдра?

Каков объем правильного икосаэдра? (Подсказка: как найти площади правильных многоугольников?)

Каков объем правильного додекаэдра? (Подсказка: разбейте додекаэдр на более мелкие компоненты.)

II. Сдвоенные многогранники

Мы можем «сжать» любой многогранник в двумерную плоскость, не заставляя ни одно из ребер пересекаться. Процесс проиллюстрирован для куба ниже и работает аналогично для любого многогранника. В случае куба результатом преобразования является кубический граф , показанный справа.

После этого преобразования вершины многогранника соответствуют точкам пересечения на плоскости, ребра — отрезкам, грани — областям (включая экстерьер «область», которая также начиналась как одна из граней многогранника). Мы получили планарный граф , т. е. граф, в котором никакие два ребра не пересекаются. Следовательно, мы можем применить к многограннику формулу Эйлера для плоских графов. Для многогранника с V вершин, E ребер и F граней формула Эйлера утверждает, что V , E и F связаны уравнением 1 E0512 + Ф = 2.

Убедитесь, что формула Эйлера верна для куба и тетраэдра.

Убедитесь, что формула Эйлера верна для октаэдров, додекаэдров и икосаэдров.

Для любого многогранника мы можем найти его -двойственный -многогранник с помощью следующего процесса: Из центра каждой грани многогранника провести отрезок прямой к центру каждой другой грани, смежной с этой гранью. Эти отрезки являются ребрами двойственного многогранника. Например, двойственным многогранником куба является правильный октаэдр:

Что двойственно правильному октаэдру?

Что такое двойник тетраэдра?

Какие двойники додекаэдра и икосаэдра?

Диагональ — это отрезок, проведенный между двумя вершинами многогранника, не смежными с общей гранью.

No related posts.