Косинус в квадрате производная: Производная косинуса: формулы и примеры

3 x}\)

Найти производную функции y 4x 1 cosx. Производная косинуса: (cos x)′

Представлено доказательство и вывод формулы для производной косинуса — cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка.

Производная по переменной x от косинуса x равна минус синусу x:
(cos x)′ = — sin x .

Доказательство

Чтобы вывести формулу производной косинуса, воспользуемся определением производной:
.

Преобразуем это выражение, чтобы свести его к известным математическим законам и правилам. Для этого нам нужно знать четыре свойства.
1) Тригонометрические формулы . Нам понадобится следующая формула:
(1) ;
2) Свойство непрерывности функции синус:
(2) ;
3) Значение первого замечательного предела:
(3) ;
4) Свойство предела от произведения двух функций:
Если и , то
(4) .

Применяем эти законы к нашему пределу. Сначала преобразуем алгебраическое выражение

.
Для этого применим формулу
(1) ;
В нашем случае
; . Тогда
;
;
;
.

Сделаем подстановку . При , . Используем свойство непрерывности (2):
.

Сделаем такую же подстановку и применим первый замечательный предел (3):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Тем самым мы получили формулу производной косинуса.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих косинус. Найдем производные от следующих функций:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2 x ; y = cos 3 x и y = cos n x .

Пример 1

Найти производные от cos 2x, cos 3x и cos nx .

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = cos nx . Затем, в производную от cos nx

, подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от cos 2x и cos 3x .

Итак, находим производную от функции
y = cos nx .
Представим эту функцию от переменной x как сложную функцию, состоящую из двух функций:
1)
2)
Тогда исходная функция является сложной (составной) функцией, составленной из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем .
.
Подставим :
(П1) .

Теперь, в формулу (П1) подставим и :
;
.

Ответ

;
;
.

Пример 2

Найти производные от косинуса в квадрате, косинуса в кубе и косинуса в степени n:
y = cos 2 x ; y = cos 3 x ; y = cos n x .

Решение

В этом примере также функции имеют похожий вид. Поэтому мы найдем производную от самой общей функции — косинуса в степени n:

y = cos n x .
Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от косинуса в квадрате и косинуса в кубе.

Итак, нам нужно найти производную от функции
.
Перепишем ее в более понятном виде:
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция является сложной функцией, составленной из двух функций и :
.

Находим производную от функции по переменной x:
.
Находим производную от функции по переменной :
.
Применяем правило дифференцирования сложной функции .
.
Подставим :
(П2) .

Теперь подставим и :

;
.

Ответ

;
;
.

Производные высших порядков

Заметим, что производную от cos x первого порядка можно выразить через косинус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Заметим, что дифференцирование cos x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Более строго эту формулу можно доказать с помощью метода математической индукции. Доказательство для n-й производной синуса изложено на странице “Производная синуса ”. Для n-й производной косинуса доказательство точно такое. Нужно только во всех формулах заменить sin на cos.

Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.

Производная по переменной x от синуса x равна косинусу x:
(sin x)′ = cos x .

Доказательство

Для вывода формулы производной синуса, мы воспользуемся определением производной:
.

Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и , то
(4) .

Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.

Для этого применим формулу
(3) .
В нашем случае
; . Тогда
;
;
;
.

Теперь сделаем подстановку . При , . Применим первый замечательный предел (1):
.

Сделаем такую же подстановку и используем свойство непрерывности (2):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Формула производной синуса доказана.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2 x и y = sin 3 x .

Пример 1

Найти производную от sin 2x .

Решение

Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.
Применяем .
.
Здесь .

Ответ

(sin 2x)′ = 2 cos 2x.

Пример 2

Найти производную от синуса в квадрате:
y = sin 2 x .

Решение

Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.

.
Здесь .

Можно применить одну из формул тригонометрии. Тогда
.

Ответ

Пример 3

Найти производную от синуса в кубе:
y = sin 3 x .

Производные высших порядков

Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Докажем это, применяя метод математической индукции.

Мы уже проверили, что при , формула (5) справедлива.

Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .

Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:

.
Здесь .
Итак, мы нашли:
.
Если подставить , то эта формула примет вид (5).

Формула доказана.

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале

(a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Дата: 10.05.2015

Правила дифференцирования.

Чтобы найти производную от любой функции, надо освоить всего три понятия:

2. Правила дифференцирования.

3. Производная сложной функции.

Именно в таком порядке. Это намёк.)

Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.

Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.

Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).

Рассмотрим несколько примеров. Сначала — самые простые.

Найти производную функции y=sinx — x 2

Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U , а x 2 — функция V. Имеем полное право написать:

y» = (sinx — x 2)» = (sinx)»- (x 2)»

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:

y» = (sinx)» — (x 2)» = cosx — 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.

А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:

Найти производную функции y=sinx — x 2 +cosx — x +3

Смело пишем:

y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3 )»

В конце урока дам советы по облегчению жизни при дифференцировании.)

Практические советы:

1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.

2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.

3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.

Поиск производной математической функции называется дифференцированием. Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе сайт у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, — сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе.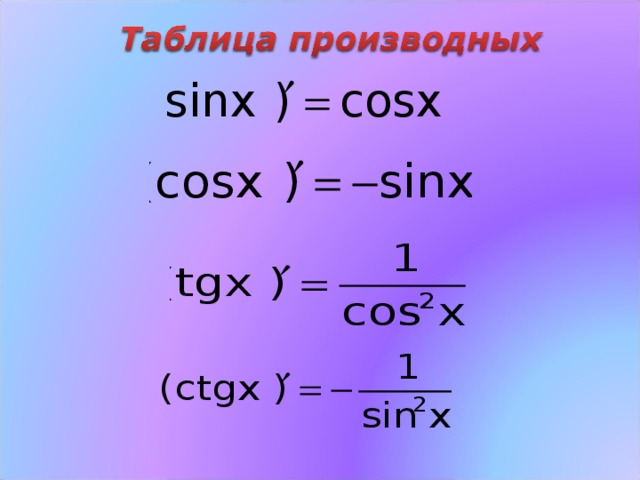 Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн.