| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.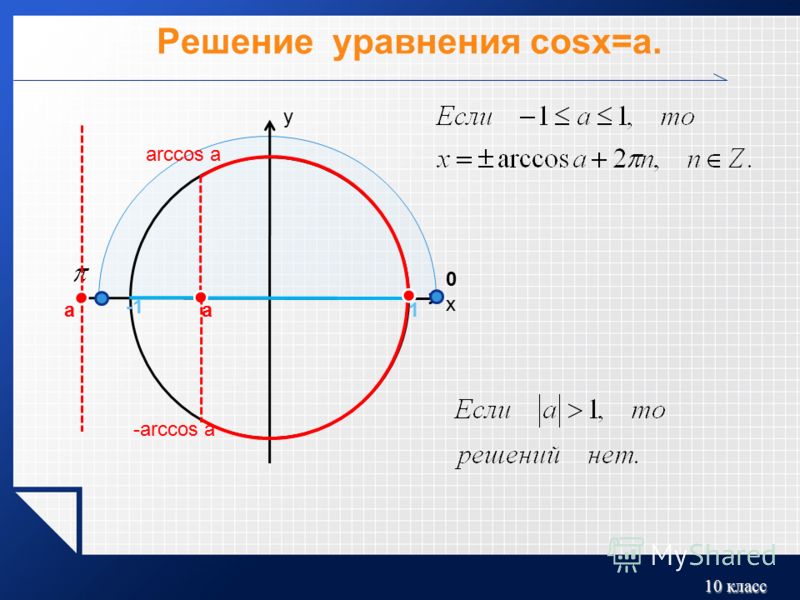 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град.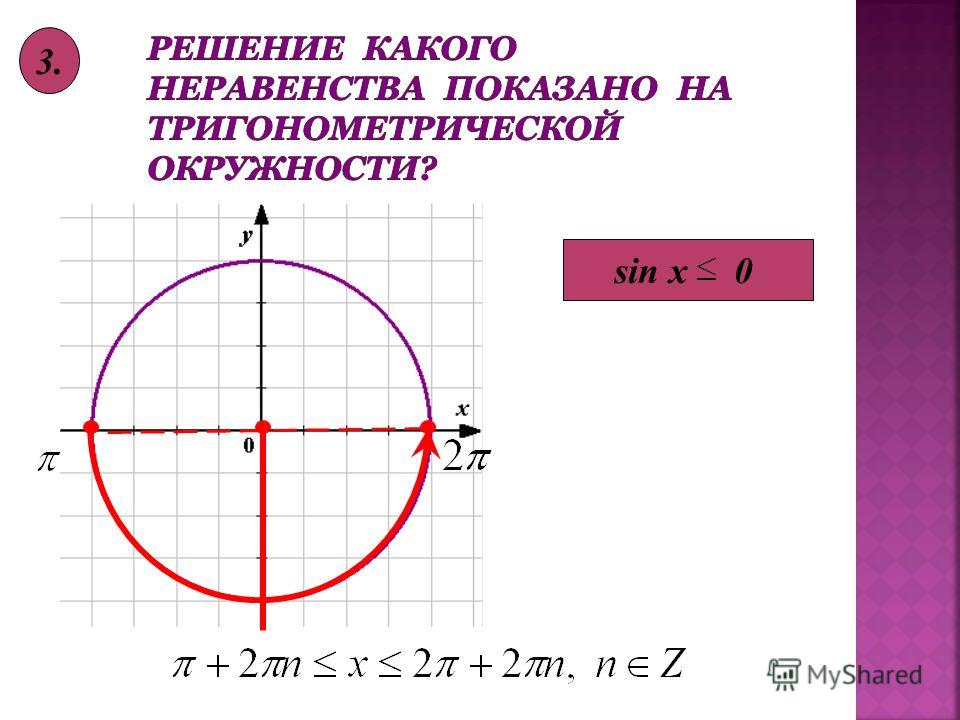 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
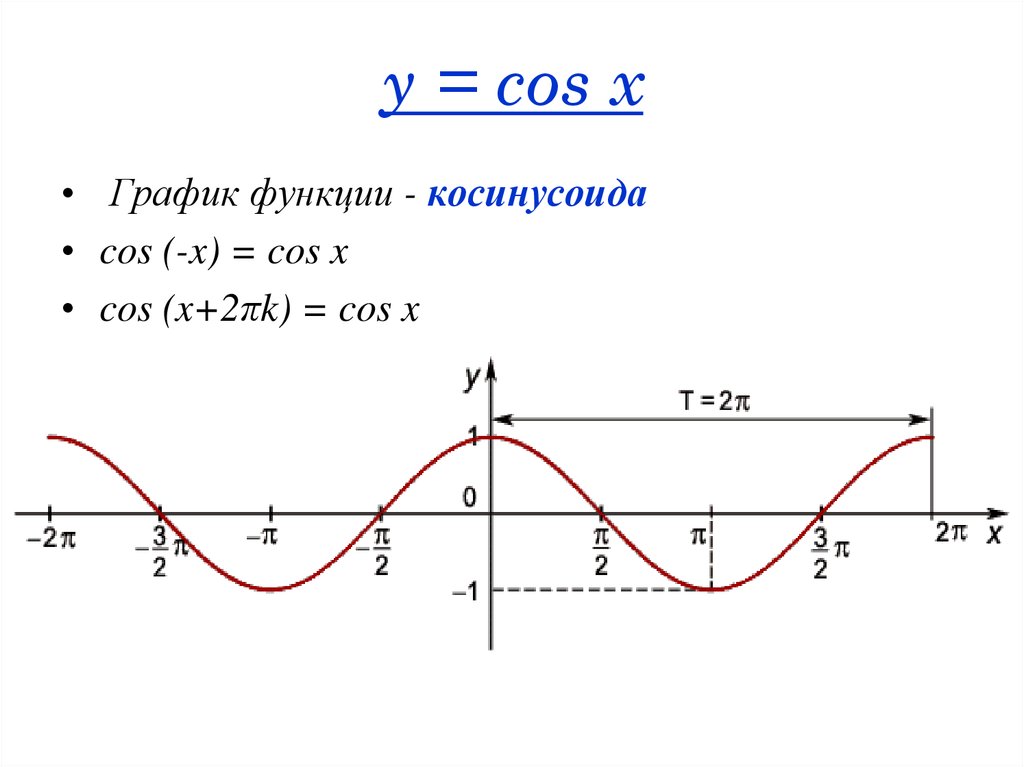
Решение уравнения Cos x=a — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема урока:
Решение уравненияCos x=a
2. Цели урока:
• сформировать у учащихся понятиеарккосинуса; вывести общую формулу
решения уравнения cos х=а; выработать
алгоритм решения данного уравнения;
• Рассмотреть частные случаи решения
уравнения
cos х= 0; cos х= 1; cos х= -1.
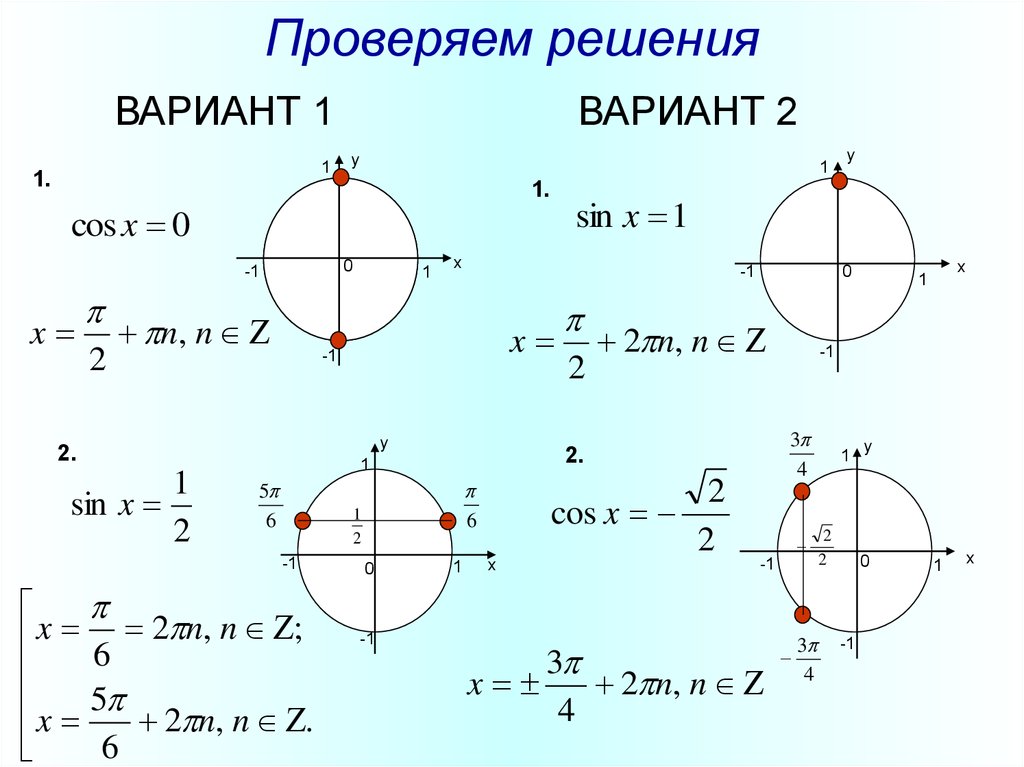
Решить уравнения:
1
cos x
2
1
cos x
2
1
cos x
2
y
x
1
2
M1
3
х1
х1
0
х2
3
1
2
x
х2
x
3
M2
2 n, n z
3
3
y
1
cos x
2
2
x1
3 3
2
3
2
M1
2
x2
3
x1
x1
1
2
2
3
2
x
2 n, n z
3
0
x2
M2
3
2
0
2
x
6.
 ВЫВОД1
ВЫВОД1cos x
2
cos x
1
2
Каждое из уравнений
и
Имеет бесконечное
множество корней. На отрезке 0 x имеет только
один корень: x — корень уравнения cos x 1
1
3
2
2
x2
3
cos x
1
2
и
— корень уравнения
Число называют арккосинусом числа
3
arccos
1
2 3
Число 2 называют арккосинусом числа
3
1 2
arccos
2 3
1
2
и записывают
1
и
2
записывают
Определение
Арккосинусом числа a 1;1 называют
такое число x 0; , косинус которого
равен а:
arccos x ,
если Cosx a
и
0 x
1
arccos ; т.к.
2
Пример 1
1
1
cos ; arccos
3 2
2 3
Пример 2
2
3
arccos(
)
2
4
4
Пример 3
arccos 0;
Пример 4
т.к. cos
2
arccos 1 0, т.к. cos 0 1;
0;
arccos 0
2
Пример 5
arccos( 1) , т.к. cos 1
№ 569 3,4
3) 12 arccos
3
2
1
3 arccos 12 3 2 3
0
6
3
2
2
3
2
3
4) 4 arccos
6 arccos
2
2
4
6
4
6
5 4
Определение
Все корни уравнения Cosx a , где a 1;1
Можно находить по формуле:
x arccos a 2 n, где n Z (1)
x arccos a 2 n, где n Z (1)
Пример 1
3
х1, 2 arccos
2 n, n z
2
3
;
Вычислим arccos
2
3
cos x
;
2
3
3
;
arccos
т.
 к. cos
к. cos 6
2
2
6
Ответ : х1, 2 2 n, n z
6
Пример 2
3
cos x
;
2
3
х1, 2 arccos( ) 2 n, n z
2
3
3
5
arccos( ) arccos
;
2
2
6 6
5
Ответ : х1, 2
2 n, n z
6
Решить уравнение:
2
Cosx
5
2
Ответ : х12 arccos 2 n, n Z ;
5
2
Cosx
5
2
Ответ : х12 arccos 2 n, n Z ;
5
14. Частные случаи решения уравнения
Cosx acos x 1
y
Х=1
0
x 2 n, n z
0
х
x
cos x 0
y
2
Х=0
0
x
Х=0
x
2
n, n z
Х= -1
y
cos x 1
1
0
x 2 n, n z
0
x
18. Частные случаи уравнения cosх = a
1. cos x 1, то2. cos x 0,
3. cos x 1,
x 2 n; n z
x
2
n; n z
x 2 n; n z
Пример 3
2
cos x
7
2
х1, 2 arccos 2 n, n z
7
Пример 4
cos x 1,2
1,2 1
Ответ: уравнение решения не имеет.
x 2 n, n z
a 1
a 0
x
2
a 1
Cosx a
x 2 n, n z
n, n z
a 1
Решений нет
Cos
6
4
2
2
3
3
1
2
a 1
x arccos a 2 n, где n Z (1)
аrcсos (-а) = π — аrcсos а
21.
 Закрепление № 573 (1,4,5)
Закрепление № 573 (1,4,5)1. cos 4 x 1; 4 x 2 k ; k Z ; x
4. 2 cos
k
2
; k Z
x
x
3
3; cos
;
3
3
2
x
2 k ; k Z ; x 6 k ; k Z
3
2
5. cos x 0; x k ; k Z ; x k ; k Z
3
3
3
№ 574
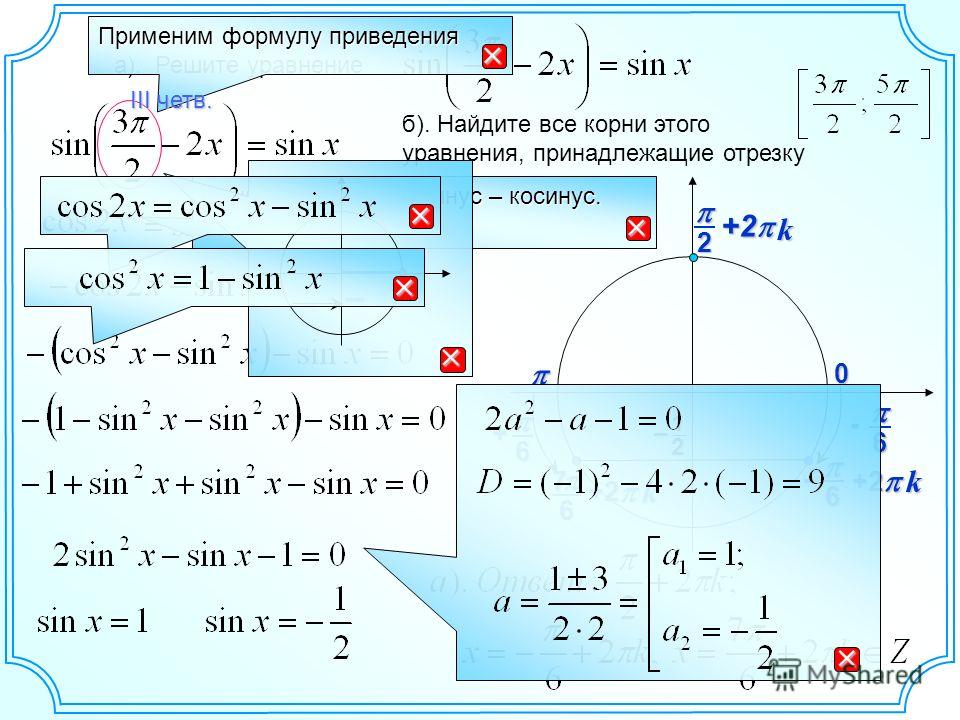
1. cos x cos 3x sin x sin 3x;
cos x cos 3x sin x sin 3x 0; применим формулу косинус суммы двух углов
cos 4 x 0;
4 x k ; k Z ;
x
k
4
; k Z
№ 576
1. cos 2 2 x 1 sin 2 2 x;
cos 2 2 x 1 sin 2 2 x 0;
Применив формулу косинуса двойного угла, получим :
cos 4 x 1;
4 x 2 k ; k Z ;
x
k
2
; k Z
5. 1 cos x 3 2 cos x 0;
1 cos x 0;
3 2 cos x 0;
cos x 1;
3
cos x ; решений нет, т.к. а 1
2
x 2 k ; k Z
Домашнее задание:
№ 571
№ 572
№ 573 (1, 2,3)
Спасибо за урок!
English Русский Правила
УРОК ОДНОГО УРАВНЕНИЯ SIN X + COS X = 1 презентация, доклад
МОУ Ненинская имени Героя Российской Федерации Лайса Александра Викторовича СОШ
алгебра и начала анализа 10 класс
УРОК ОДНОГО УРАВНЕНИЯ
SIN X + COS X = 1
Цели урока:
образовательные: повторить и систематизировать тему «Решение тригонометрических уравнений» на примере решения одного уравнения разными способами, создать условия контроля (самоконтроля) усвоения знаний и умений;
развивающие: способствовать формированию умений применять приемы переноса знаний в новую ситуацию, развивать логическое мышление, умение обобщать и делать выводы;
воспитательные: воспитание интереса к предмету, уважительное отношение к одноклассникам, воспитание активности, прилежания, внимания, прививать аккуратность.
Девиз урока
«Часто полезнее решить одну и ту же задачу тремя способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и наиболее эффективнее».
У.Сойер
«Разминка»
1.(1 балл) Верно ли, что cos²х — sin²х = 1?
А. Да Б. Нет
2.(2 балла) Период функции у=sin x равен …
А. π/2 Б. π В.2π Г. 4π
3. (3 балла) Сколько корней уравнения sin х=0 принадлежит отрезку
А. 3 Б. 0 В. 2 Г.1
4. (2 балла) Решите уравнение 2cos х = 0.
А. +πn, n∈Z; Б.2πn, n∈Z; В. πn, n∈Z; Г.± +2πn, n∈Z.
5. (1 балл) Найдите область значений функции y = 1 — sin x
А. Б. В. Г.
Проверь ответ
Работа в группах.
Группа 1.
1) Упростите выражение
а)
б)
2)Доказать тождество
а)
б)
Группа 2. 1) Упростите выражение а) б) 2)Доказать тождество а) б)
Леонард Эйлер.(1707 – 1783)
«Деятельность Эйлера многогранна и
разностороння. Он занимался
почти всем, что интересовало
в то время математиков».
С.И. Вавилов.
(Кратко об Эйлере)
Задача. Решите уравнение
различными способами:sin x +cos x = 1 .
Карточки-подсказки:
№1 №1 №2 №1 №2 №3 №1 №2 №3 №4 №1 №2 №3 №4 №5 №1 №2 №3 №4 №5 №6
Домашнее задание
Решите уравнения разными способами:
а)cos2x +3sin x=3;
б)2sin23x – 5sin3xcos3x + 3 cos23x=0;
в) sin x+cos3x = 0.
Карточка№1.
С помощью универсальной подстановки tg =t
1) Вспомните и сделайте подстановку.
2) Проверьте обязательно отдельно корень
, чтобы не потерять корни исходного уравнения.
Вернуться
Карточка№2.
Способом разложения на множители.
1)Представьте данное уравнение в виде уравнения с половинным аргументом, используя формулы
и .
2) разложите на множители.
Вернуться
Карточка№3.
Введение вспомогательного угла.
Вспомните, что , введите
вспомогательный угол .
Используя формулу,
или представьте данное уравнение с одной функцией
Вернуться
Карточка№4.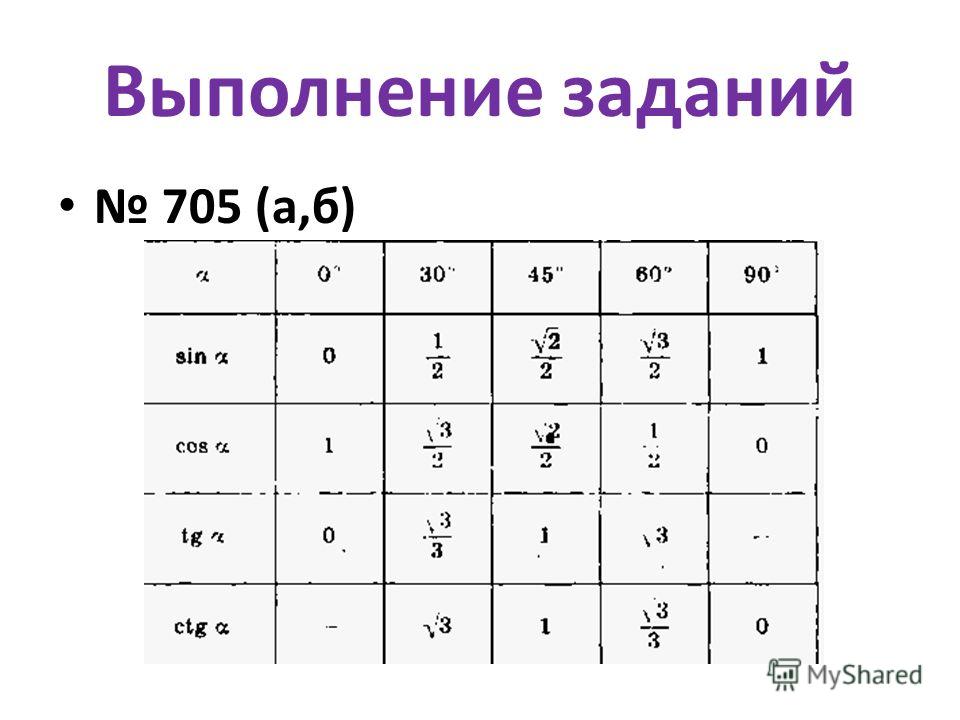
Метод вспомогательных неизвестных.
1) Пусть sin x=a,cos x=b. Помни! Две переменных, введенных в одно уравнение, связаны друг с другом системой уравнений.
Вернуться
Карточка№5.
Метод оценки обеих частей уравнения.
Помни! Если в уравнении правая часть положительна, то и левая часть уравнения должна быть положительной.
Возведи обе части уравнения в квадрат.
Вернуться
Карточка №6
Графический способ
Разбейте данное уравнение, так, чтобы тригонометрические функции находились в разных частях уравнения.
Постройте графики функций, записанные в левой и правой частях на одной координатной плоскости, учитывая период.
Найдите точки пересечения двух графиков, учитывая период.
Вернуться
Леонард Эйлер. (1707 – 1783)
(1707 – 1783)
В восемнадцатом столетии среди великих математиков, жил и работал в России и внес неоценимый вклад в развитие математической культуры и науки Леонард Эйлер, швейцарец по происхождению, которого, по праву, можно назвать самым знаменитым членом Академии наук России за время ее существования.
В 13 лет Эйлер поступил на факультет искусств Базельского университета. Среди других предметов на этом факультете изучались элементарная математика и астрономия, которые преподавал Иоганн Бернулли.
В 1724 г. по указу Петра I в Петербурге была организована Академия наук, куда был приглашен Эйлер на вакантную должность. Открытия Эйлера делают его имя широко известным. Улучшается его положение в Академии наук: в 1727 г. он начал работу в звании адъютанта, то есть младшего по рангу академика; в 1731 г. становится профессором физики, то есть действительным членом Академии наук, а в 1733 г. получает кафедру высшей математики. За первые четырнадцать лет пребывания в Петербурге Эйлер написал 80 крупных работ.
В конце 1740 г. власть в России перешла в руки регентши Анны Леопольдовны и ее окружения. В это время король Фридрих II решает возродить Общество наук и приглашает Эйлера в Берлин. Эйлер напряженно проработал в Берлине 25 лет. 28 июня 1766 г. он возвращается в Петербургскую Академию наук, где был встречен с величайшим почетом и устроен так хорошо, как только было можно.
Эйлер умер в 1783 г. и был похоронен в Петербурге. Посмертные почести, оказанные Эйлеру, не остались не замеченными в странах Европы и подняли авторитет России. Математик Кондорсе в речи, произнесенной во Французской Академии наук, сказал: «Народ, который мы вначале этого века принимали за варваров, в настоящем случае подает пример цивилизованной Европе – как чествовать великих людей при жизни и уважать память после смерти…»
Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера. В учебниках по высшей математике их еще больше. Даже в средней школе тригонометрию и логарифмы изучают до сих пор «по Эйлеру». Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее, проще. (Вернуться)
д., носящих имя Эйлера. В учебниках по высшей математике их еще больше. Даже в средней школе тригонометрию и логарифмы изучают до сих пор «по Эйлеру». Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее, проще. (Вернуться)
ответы
1.Б. 2.Г 3.В. 4.А. 5. В
Вернуться
Скачать презентацию
Решение тригонометрических уравнений. Как решить тригонометрическое уравнение.
Решение тригонометрических уравнений требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью «Основные тригонометрические формулы».
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения, для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а
cos x = a
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
- cos(x + /6) = 1
x + /6 = 2 k
x1 = — /6 + 2 k
- cos(x + /6) = ?
x + /6 = ±arccos 1/2 + 2 k
x2 = ± /3 — /6+ 2 k
Решение тригонометрических уравнений через разложение на множители
- 2sin(x/2) = 0
Это простейшее тригонометрическое уравнение, решение которого
х/2 = k
x1 = 2 k
- cos(x/2) — sin(x/2) = 0
Это уравнение является однородным и решается третьим методом, который мы рассмотрим ниже.

Делим уравнение на cos(x/2) и получаем опять же простейшее тригонометрическое уравнение:
1 — tg(x/2) = 0
tg(x/2) = 1
x/2 = arctg 1 + k
x/2 = /4+ k
x2 = /2+ 2 k
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Преобразование произведения в сумму
Универсальная подстановка
- x (2k + 1) ,
тогда, воспользовавшись тригонометрическими формулами, получим:3[(2tg(x/2))/(1 + tg2 (x/2)] — 4[(1 – tg2 (x/2))/(1 + tg2 (x/2)] = 3
6tg(x/2) – 4 + 4tg2 (x/2) = 3 + 3tg2 (x/2)
tg2 (x/2) + 6tg(x/2) – 7 = 0
Делаем замену tg(x/2) на y и получаем квадратное уравнение:
y2 + 6y -7 = 0
корни которого y1 = -7, y2 = 1
Идем обратно и получаем два простейших уравнения:
1) tg(x/2) = -7
х1 = -2arctg 7 + 2 k
2) tg(x/2) = 1
x2 = /2 + 2k
- x = (2k + 1) ,
тогда 3sin[(2k +1) ] – 4cos[(2k + 1) ] = 4 3
Получаем – решение имеет только первое условие.

Пример.
Решить уравнение 2cos2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y2 – 3y + 1 + 0
Корни которого y1 = 1, y2 = 1/2
Теперь идем в обратном порядке
cos(x + /6) = y
Подставляем найденные значения y и получаем два варианта ответа:
Пример.
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin2 (x/2) = 0
2sin(x/2) * [cos(x/2) — sin(x/2)] = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Пример.
Решить уравнение 3sin2x + 4 sin x • cos x + 5 cos2x = 2
Воспользуемся формулой sin2 x + cos2 x = 1 и избавимся от открытой двойки справа:
3sin2x + 4 sin x • cos x + 5 cos x = 2sin2x + 2cos2x
sin2x + 4 sin x • cos x + 3 cos2x = 0
Делим на cos x:
tg2x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y2 + 4y +3 = 0, корни которого y1=1, y2 = 3
Отсюда находим два решения исходного уравнения:
1) tg x = –1
x1 = /4+ k
2) tg x = –3
x2 = arctg 3 + k
Пример.
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos2 (x/2) + 5sin2 (x/2) = 7sin2 (x/2) + 7cos2 (x/2)
Пререносим все влево:
2sin2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos2 (x/2) = 0
Делим на cos(x/2):
tg2 (x/2) – 3tg(x/2) + 6 = 0
Ну а дальше уже по отработанной схеме …
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Пример.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
(/2) * sin 3x – (1/2)cos 3x = 1/2
cos( /6) * sin 3x – sin( /6) * cos 3x =1/2
sin(3x – /6) = 1/2
Получаем ответ
x = (-1) k * /18 + /18 + k/3
Здесь мы будем просто использовать тригонометрические формулы
Пример.
Решить уравнение 2 sin x * sin 3x = cos 4x
Левую часть преобразуем в сумму:
cos 4x – cos 8x = cos 4x
Получаем простейшее уравнение:
cos 8x = 0
8x = /2 + k
x = /16 + k/8
Пример.
Решить тригонометрическое уравнение 3sin x – 4cos x = 3
Здесь возможны 2 случая:
Основные методы решения тригонометрических уравнений, мы рассмотрели. Если у вас остались какие либо вопросы о том, как решать тригонометрические уравнения, задавайте их в комментариях ниже.
Будем рады любым ваших вопросам.
Заметка: собираетесь выступать http://prezentacii.com портал готовых презентаций.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
тригонометрия — Решение $\cos x+\sin x-1=0$
спросил
Изменено 2 года, 4 месяца назад
Просмотрено 3к раз
$\begingroup$
Как решить это уравнение? 92(х)=1$$ Обратите внимание на важное тождество: $$1+2\cos(x)\sin(x)=1$$ Затем упростите и обратите внимание на другое тождество: $$\sin(2x)=0$$
Можно взять отсюда?
$\endgroup$
3
$\begingroup$
Дано $$\color{blue}{\cos x+\sin x-1=0} $$$$\cos x+\sin x=1 $$ Разделите обе стороны на $\color{blue}{\sqrt{ 2}}$ получаем $$\frac{1}{\sqrt{2}}\cos x+ \frac{1}{\sqrt{2}}\sin x=\frac{1}{\sqrt{2} }$$ $$\cos x\cos\frac{\pi}{4}+\sin x\sin\frac{\pi}{4}=\cos\frac{\pi}{4}$$ Используя формулу $\color{purple}{\cos A\cos B+\sin A\sin B=\cos(AB)}$, получаем $$\color{green}{\cos\left(x-\frac{\pi }{4}\right)=\cos\frac{\pi}{4}}$$ Поскольку нет информации о неизвестном значении $x$, общие решения записываются следующим образом $$x-\frac{\pi {4}=2n\pi\pm \frac{\pi}{4}$$$$x=2n\pi\pm \frac{\pi}{4}+\frac{\pi}{4}$ $$$ \color{}{x=2n\pi} \quad \text{Or}\quad \color{}{x=2n\pi+\frac{\pi}{2}} $$
$$\color{blue}{x\in\{2n\pi\}\cup\{2n\pi+\frac{\pi}{2}\}}$$ Где, $\color{}{n \space \text{любое целое}}$ т. е. $\ n=0, \pm1, \pm2,\pm3, \ldots$
е. $\ n=0, \pm1, \pm2,\pm3, \ldots$
$\endgroup$
0
$\begingroup$
Как $\sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\left(\cos x+\sin x\right)$ по Формула сложения углов находим, что: \begin{уравнение} \begin{выровнено} \cos х+\sin х-1&=0\\ \ подразумевает \ sqrt {2} \ sin \ left (x + \ frac {\ pi} {4} \ right) & = 1 \\ \ подразумевает \ грех \ влево (х + \ гидроразрыва {\ пи} {4} \ вправо) & = \ гидроразрыва {\ sqrt {2}} {2} \\ \ подразумевает x + \ frac {\ pi} {4} & = \ frac {\ pi} {4} +2 \ pi n, \ frac {3 \ pi} {4} +2 \ pi n \\ \подразумевает x&=2\pi n,\frac{\pi}{2}+2\pi n \end{выровнено} \end{уравнение} для $n\in\mathbb{Z}$.
$\endgroup$
0
$\begingroup$
$\cos x+\sin x=\sqrt2\cos\Bigl(x-\dfrac\pi4\Bigr)$, поэтому уравнение эквивалентно:
$$\cos\Bigl(x-\frac\pi4\Bigr)=\frac1{\sqrt2}\iff x-\frac\pi4\equiv\pm\frac\pi4\mod 2\pi\iff x\equiv 0 ,\,\frac\pi2\mod2\pi. 2 \theta = 1$). Решения данного уравнения находятся на пересечении синей линии $x+y = 1$ с этим красным кругом, что дает $(\cos\theta, \sin\theta) = (1, 0)$ и $(0 , 1)$. 92 x+2\sin \cos x=1$$ $$1+\sin 2x=1$$$$\sin 2x=0$$
$$2x=к\пи$$
$$x=\frac{k\pi}{2}$$, где $k=0, \pm 1, \pm2, \ldots$
2 \theta = 1$). Решения данного уравнения находятся на пересечении синей линии $x+y = 1$ с этим красным кругом, что дает $(\cos\theta, \sin\theta) = (1, 0)$ и $(0 , 1)$. 92 x+2\sin \cos x=1$$ $$1+\sin 2x=1$$$$\sin 2x=0$$
$$2x=к\пи$$
$$x=\frac{k\pi}{2}$$, где $k=0, \pm 1, \pm2, \ldots$
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
г. Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Документация JDK 19 — Главная
- Домашняя
- Ява
- Java SE
- 19
Обзор
- Прочтите меня
- Примечания к выпуску
- Что нового
- Руководство по миграции
- Загрузить JDK
- Руководство по установке
- Формат строки версии
- Технические характеристики инструментов JDK
- Руководство пользователя JShell
- Руководство по JavaDoc
- Руководство пользователя средства упаковки
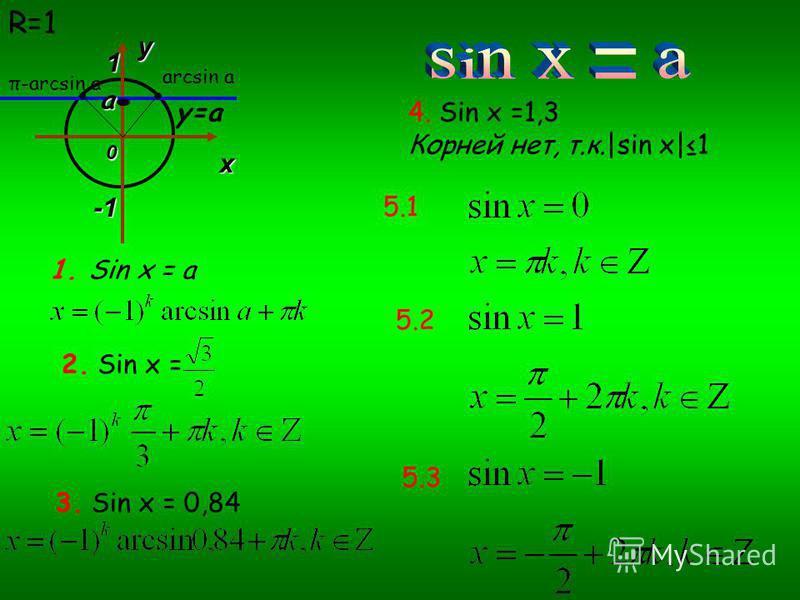
Язык и библиотеки
- Обновления языка
- Основные библиотеки
- HTTP-клиент JDK г.
- Учебники по Java
- Модульный JDK
- Руководство программиста API бортового регистратора
- Руководство по интернационализации г.

Технические характеристики
- Документация API
- Язык и ВМ
- Названия стандартных алгоритмов безопасности Java
- банка
- Собственный интерфейс Java (JNI)
- Инструментальный интерфейс JVM (JVM TI)
- Сериализация
- Проводной протокол отладки Java (JDWP)
- Спецификация комментариев к документации для стандартного доклета
- Другие характеристики г.

Безопасность
- Руководство по безопасному кодированию
- Руководство по безопасности
Виртуальная машина HotSpot
- Руководство по виртуальной машине Java
- Настройка сборки мусора
Управление и устранение неполадок
- Руководство по устранению неполадок
- Руководство по мониторингу и управлению
- Руководство по JMX
Client Technologies
- Руководство по специальным возможностям Java
Как сделать sin 2 cos 2? – Книга Vea
от jai
Содержание
Как сделать sin 2 cos 2?
Чтобы найти значение sin2x xd7 Cos 2x, используются тригонометрические формулы двойного угла. Для вывода используются значения sin 2x и cos 2x. Итак, Sin 2x Cos 2x 2 Cos x (2 Sin x Cos 2 x u2212 Sin x)
Чему равно sin 2x cos 2x?
список пифагорейских тождеств. Давайте рассмотрим пифагорейские тождества. Первое из этих трех утверждений гласит, что синус в квадрате плюс косинус в квадрате равно единице. Второй утверждает, что тангенс в квадрате плюс один равен секансу в квадрате. Для последнего в нем говорится, что один плюс квадрат котангенса равен косекансу в квадрате.
Что такое sin Square Cos Square? 9192 х U2039 OpenCurriculum.
Что такое интегрирование sin 2x cos 2x?
Решенные примеры Следовательно, интеграл от sin 2x cos 2x равен u222b (Sin 2x Cos 2x) (Sin 2x) 2 / 4 + C.
Почему sin 2x cos 2x равен 1?
Так же, как расстояние между началом координат и любой точкой (x,y) на окружности должно быть радиусом окружности, сумма квадратов значений sinu03b8 и cosu03b8 должна быть равна 1 для любого угла u03b8 .
Каково максимальное значение sin 2x * cos 2x?
Итак, x u03c0/8 – точка максимума. Следовательно, правильный вариант 1.
Какова формула квадрата косина квадрата синуса?
Тригонометрическое тождество квадрата синуса используется в качестве формулы в двух случаях. Квадрат функции sin расширяется как вычитание функции cos в квадрате из единицы. Вычитание функции квадрата косинуса из единицы упрощается как функция квадрата греха.
Что такое квадрат греха?
Квадрат синуса x означает грех х целое в квадрате. Есть две формулы квадрата греха х. Одно из них выводится из одного из тождеств Пифагора, а другое выводится из формулы двойного угла функции косинуса.
Почему квадрат греха плюс квадрат Cos равен единице?
Эта формула является замаскированной теоремой Пифагора. в треугольнике с единичной гипотенузой — это просто длины двух меньших сторон. Таким образом, возведение их в квадрат и сложение дает квадрат гипотенузы, который равен единице в квадрате, то есть единице.
Что такое кос в квадрате?
Квадрат функции косинуса равен вычитанию квадрата функции синуса из единицы и называется формулой квадрата косинуса. Его также называют квадратом тождества функции cos.
Что такое тождество cos 2x sin 2x?
Решенные примеры Следовательно, интеграл от sin 2x cos 2x равен u222b (Sin 2x Cos 2x) (Sin 2x) 2 / 4 + C.
Чему также равен sin 2x?
Так же, как расстояние между началом координат и любой точкой (x,y) на окружности должно быть радиусом окружности, сумма квадратов значений sinu03b8 и cosu03b8 должна быть равна 1 для любого угла u03b8 .
Чему равен квадрат греха?
Эта формула является замаскированной теоремой Пифагора. в треугольнике с единичной гипотенузой — это просто длины двух меньших сторон. Таким образом, возведение их в квадрат и сложение дает квадрат гипотенузы, который равен единице в квадрате, то есть единице.
Что такое квадрат синуса тета плюс квадрат косинуса тета?
Квадрат функции синуса равен вычитанию квадрата функции косина из единицы, называется формулой квадрата синуса. Его также называют квадратом идентичности функции греха. 92(x) 1/2*(1 – cos(2x)) и подставить в интеграл так, чтобы он стал в 1/2 раза больше интеграла от (1 – cos(2x)) dx.
Его также называют квадратом идентичности функции греха. 92(x) 1/2*(1 – cos(2x)) и подставить в интеграл так, чтобы он стал в 1/2 раза больше интеграла от (1 – cos(2x)) dx.
Синус равен 1 косинусу?
Sin 2x Cos 2x 2 Cos x (2 Sin x Cos 2 x u2212 Sin x)
Как вы доказываете, что Sin в квадрате, cos в квадрате 1?
Формула Sin2x — это формула двойного угла функции синуса, а sin 2x 2 sin x cos x — наиболее часто используемая формула. Но sin2x с точки зрения тангенса равен sin 2x 2tan(x)/(1 + tan 2(x)).
Каково значение sin 2x cos 2x?
Чтобы найти значение sin2x xd7 Cos 2x, используются тригонометрические формулы двойного угла. Для вывода используются значения sin 2x и cos 2x. Итак, Sin 2x Cos 2x 2 Cos x (2 Sin x Cos2 x u2212 Sin x)
Каково максимальное значение sin 2x?
Таким образом, максимум sin 2x равен 1. Ответ равен 1. Таким образом, мы ясно видим, что максимальное значение sin2x 1.
Что такое Cos Square sin Square?
1
Какова формула для cos Квадрат?
Квадрат функции косинуса равен вычитанию квадрата функции синуса из единицы и называется формулой квадрата косинуса. Его также называют квадратом тождества функции cos.
Что такое cos 2theta sin theta?
cos(2theta)sin(theta) Одним из тождеств для cos 2x является cos 2x 1 – 2 sin2(x). Это означает, что эквивалентный способ записи нашей задачи: 1 – 2sin 2x sin(x). Если мы допустим y sin(x), то уравнение становится квадратным: 1 – 2y2 y или более в более знакомой форме, 1 – 2y2 – y 0 или -2y2 – y + 1 0.
г. | Возвращает новый тензор с данными |
| Возвращает тензор размера |
| Возвращает тензор размера |
| Возвращает тензор размера |
| Возвращает тензор размера |
| Является |
| Является |
| Is |
| Является ли |
| Этот атрибут имеет значение |
| Псевдоним для |
| Возвращает новый тензор, содержащий действительные значения собственного |
| Возвращает новый тензор, содержащий мнимые значения собственного |
| См. |
| Местная версия |
| Псевдоним для |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Добавить скаляр или тензор к |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Псевдоним для |
| См. |
| См. |
| См. |
| См. |
| См. |
| Применяет функцию |
| См. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| atan2_(другое) -> Тензор |
| См. |
| См. |
| Вычисляет градиент тензора тока относительно |
| См. |
| Местная версия |
| Возвращает тензор результата, где каждый результат[i]\texttt{result[i]}result[i] независимо выбран из Бернулли(self[i])\text{Бернулли}(\texttt{self[i]}) Бернулли(я[i]). |
| Заполняет каждую ячейку |
| |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| |
| |
| См. |
| Заполняет тензор числами из распределения Коши: |
| См. |
| Местная версия |
| |
| См. |
| См. |
| См. |
| См. |
| См. |
| Устанавливаемая на месте версия зажима |
| Псевдоним для |
| Псевдоним для |
| См. |
| Возвращает непрерывный тензор в памяти, содержащий те же данные, что и |
| Копирует элементы из |
| См. |
| См. |
| Местная версия |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| акош() -> Тензор |
| acosh_() -> Тензор |
| Возвращает копию этого объекта в память ЦП. |
| См. |
| Возвращает копию этого объекта в память CUDA. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| |
| |
| |
| Возвращает адрес первого элемента |
| См. |
| Получив квантованный тензор, деквантуйте его и верните деквантованный плавающий тензор. |
| См. |
| Вернуть количество плотных измерений в разреженном тензоре |
| Возвращает новый тензор, отсоединенный от текущего графа. |
| Отсоединяет тензор от создавшего его графа, превращая его в лист. |
| См. |
| См. |
| См. |
| См. |
| диагональ (источник, смещение = 0, dim1 = 0, dim2 = 1) -> Тензор |
| Заполните главную диагональ тензора, имеющего по крайней мере 2 измерения. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| Возвращает число измерений собственного |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| |
| См. |
| См. |
| Возвращает размер отдельного элемента в байтах. |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Возвращает новый вид тензора |
| Расширить этот тензор до размера |
| Заполняет |
| См. |
| Местная версия |
| Заполняет |
| См. |
| См. |
| См. |
| См. |
| |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Пластовая версия |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Заполняет |
| См. |
| См. |
| Для тензоров CUDA эта функция возвращает порядковый номер устройства GPU, на котором находится тензор. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Накопить элементы |
| Неуместная версия |
| Копирует элементы тензора |
| Неуместная версия |
| Заполняет элементы тензора |
| Неуместная версия |
| Помещает значения из тензора |
| Внешняя версия |
| Накопить элементы источника |
| |
| См. |
| Возвращает тензор индексов разреженного тензора COO. |
| См. |
| |
| Учитывая квантованный тензор, |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| Возвращает True, если |
| Возвращает True, если тип данных |
| Возвращает True, если сопряженный бит |
| Возвращает True, если тип данных |
| См. |
| Все тензоры с |
| Возвращает true, если этот тензор находится в закрепленной памяти. |
| Возвращает True, если оба тензора указывают на одну и ту же память (одинаковое хранилище, смещение, размер и шаг). |
| Проверяет, находится ли тензор в общей памяти. |
| Возвращает True, если тип данных |
| Является |
| См. |
| См. |
| Возвращает значение этого тензора в виде стандартного числа Python. |
| См. |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| Версия на месте |
| Заполняет |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| Версия на месте |
| См. |
| Местная версия |
| |
| См. |
| См. |
| Местная версия |
| л (другое) -> тензор |
| Местная версия |
| См. |
| См. |
| Создает экземпляр |
| Применяет |
| Копирует элементы из |
| Неуместная версия |
| Заполняет элементы собственного тензора |
| Неуместная версия |
| См. |
| См. |
| Примечание |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| См. |
| То же, что и |
| Псевдоним для |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| См. |
| Местная версия |
| Псевдоним для |
| См. |
| Версия на месте |
| См. |
| См. |
| Заполняет |
| См. |
| Возвращает |
| См. |
| См. |
| См. |
| См. |
| Копирует тензор в закрепленную память, если она еще не закреплена. |
| См. |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Копирует элементы из |
| См. |
| Возвращает схему квантования данного QTensor. |
| См. |
| См. |
| При заданном тензоре, квантованном линейным (аффинным) квантованием, возвращает масштаб базового квантователя(). |
| При наличии тензора, квантованного линейным (аффинным) квантованием, возвращает нулевую точку базового квантователя(). |
| При заданном тензоре, квантованном линейным (аффинным) поканальным квантованием, возвращает тензор масштабов базового квантователя. |
| При заданном тензоре, квантованном линейным (аффинным) поканальным квантованием, возвращает тензор нулевых точек базового квантователя. |
| Для заданного тензора, квантованного линейным (аффинным) поканальным квантованием, возвращает индекс измерения, к которому применяется поканальное квантование. |
| См. |
| Заполняет |
| см. |
| См. |
| Местная версия |
| Гарантирует, что память тензора не будет повторно использоваться для другого тензора, пока не будут завершены все текущие задачи, поставленные в очередь в потоке . |
| Регистрирует обратный хук. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Повторяет этот тензор по указанным измерениям. |
| См. |
| Является |
| Изменить, должен ли autograd записывать операции с этим тензором: устанавливает атрибут |
| Возвращает тензор с теми же данными и количеством элементов, что и |
| Возвращает этот тензор той же формы, что и |
| Изменяет размеры |
| Изменяет размер тензора |
| Позволяет этому тензору заполнять свои |
| Является |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Версия на месте |
| Неуместная версия |
| Записывает все значения из тензора |
| Складывает все значения из тензора |
| Неуместная версия |
| Сводит все значения из тензора «24 prod» |
| Неуместная версия |
| См. |
| См. |
| Устанавливает основное хранилище, размер и шаги. |
| Перемещает основное хранилище в общую память. |
| |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Возвращает размер собственного |
| См. |
| См. |
| См. |
| См. |
| Возвращает новый разреженный тензор со значениями из шагового тензора |
| Возвращает количество разреженных измерений в разреженном тензоре |
| См. |
| Местная версия |
| См. |
| Устанавливаемая на месте версия |
| См. |
| Местная версия |
| См. |
| См. |
| Возвращает основное хранилище. |
| Возвращает |
| Возвращает тип базового хранилища. |
| Возвращает шаг |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Сумма |
| См. |
| См. |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| См. |
| Выполняет преобразование Tensor dtype и/или устройства. |
| Возвращает копию тензора в макете |
| См. |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Возвращает тензор в виде (вложенного) списка. |
| См. |
| Возвращает разреженную копию тензора. |
| См. |
| См. |
| Местная версия |
| См. |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| См. |
| Местная версия |
| Возвращает тип, если dtype не указан, в противном случае приводит этот объект к указанному типу. |
| Возвращает это приведение тензора к типу данного тензора. |
| См. |
| Возвращает вид исходного тензора, который содержит все срезы размера |
| Заполняет |
| Возвращает уникальные элементы входного тензора. |
| Удаляет все элементы, кроме первого, из каждой последующей группы эквивалентных элементов. |
| См. |
| Местная версия |
| Возвращает тензор значений разреженного тензора COO. |
| См. |
| См. |
| Возвращает новый тензор с теми же данными, что и собственный |
| Просмотр этого тензора того же размера, что и |




 abs()
abs() 
 sspaddmm
sspaddmm  аминмакс
аминмакс  asin_
asin_  atan2()
atan2() 
 bitwise_or
bitwise_or  bmm
bmm  to(torch.int8)
to(torch.int8) 
 resolve_neg
resolve_neg  count_nonzero()
count_nonzero() 
 cfloat()
cfloat()  detach
detach 
 деление
деление  equal
equal  expm1
expm1 
 пол_
пол_  gather()
gather() 
 hardshrink
hardshrink  игамма
игамма  2224 .
2224 .
 isclose
isclose 
 lcm
lcm 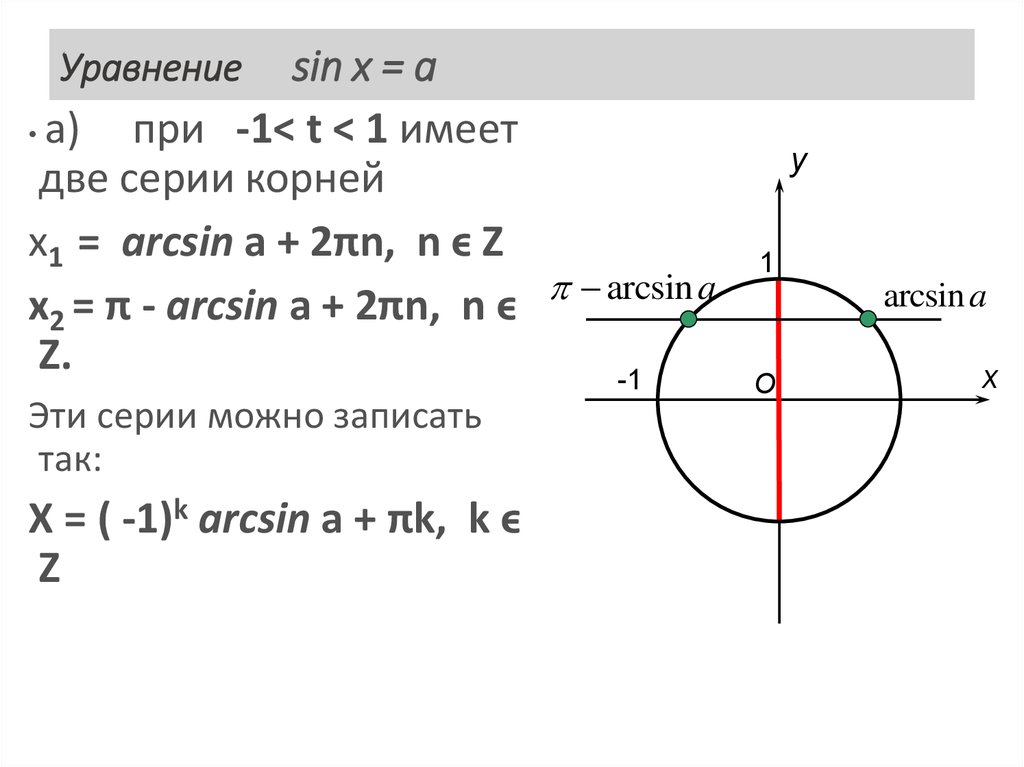 lerp_
lerp_  log1p_
log1p_ 
 lu_solve
lu_solve 
 среднее
среднее  movedim
movedim 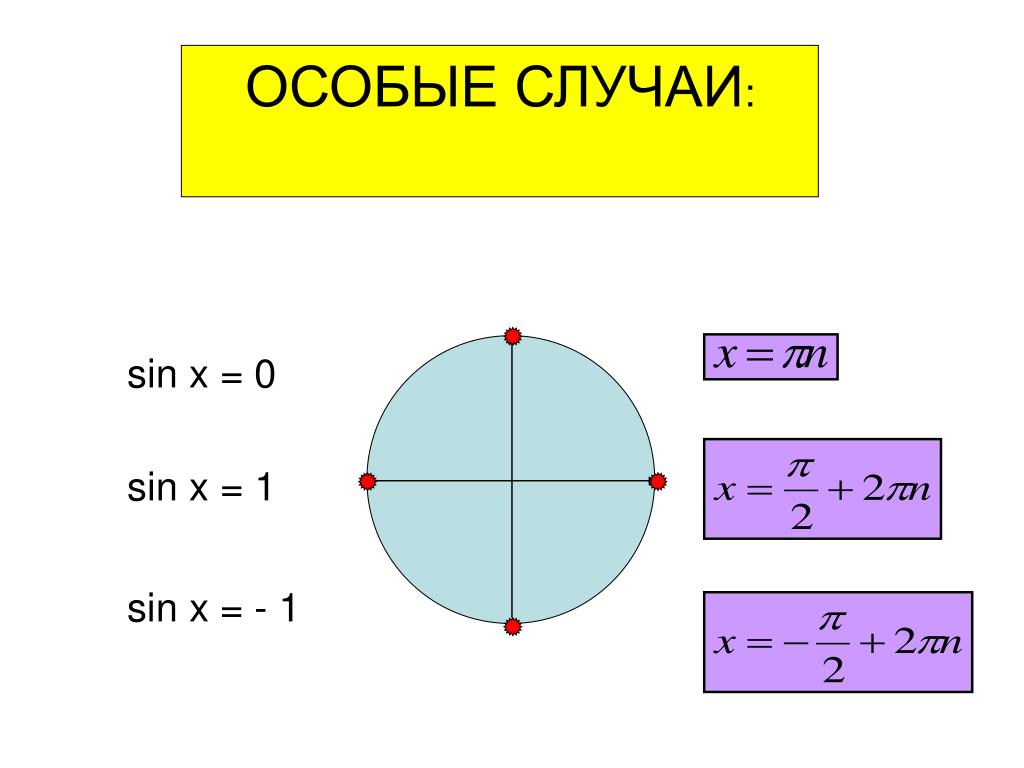 mv()
mv() 
 элемент
элемент 
 положительный
положительный