Косинусы и синусы формулы: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

Тригонометрия формулы приведения примеры решения. Изменение синуса, косинуса и тангенса при возрастании угла

С центром в точке A .
α — угол, выраженный в радианах.

Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус — нечетная. Функция косинус — четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	— ∞	— ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

Выражения через гиперболические функции

;
;

Производные

; . Вывод формул > > >

Производные n-го порядка:
{ -∞

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.

Задача. Найдите значение выражения:

В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.

Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:

То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:

1. Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
2. Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.

Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.

Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:

Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y ). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.

На основании этих размышлений мы можем записать окончательное выражение:

Задача B11 — 1 вариант

Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:

Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.

Теперь смотрим на знаменатель:

sin 131° = sin (90° + 41°) = cos 41°

Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).

Осталось разобраться с последним элементом:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.

Теперь подставляем полученные числа в исходную формулу и получаем:

Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений.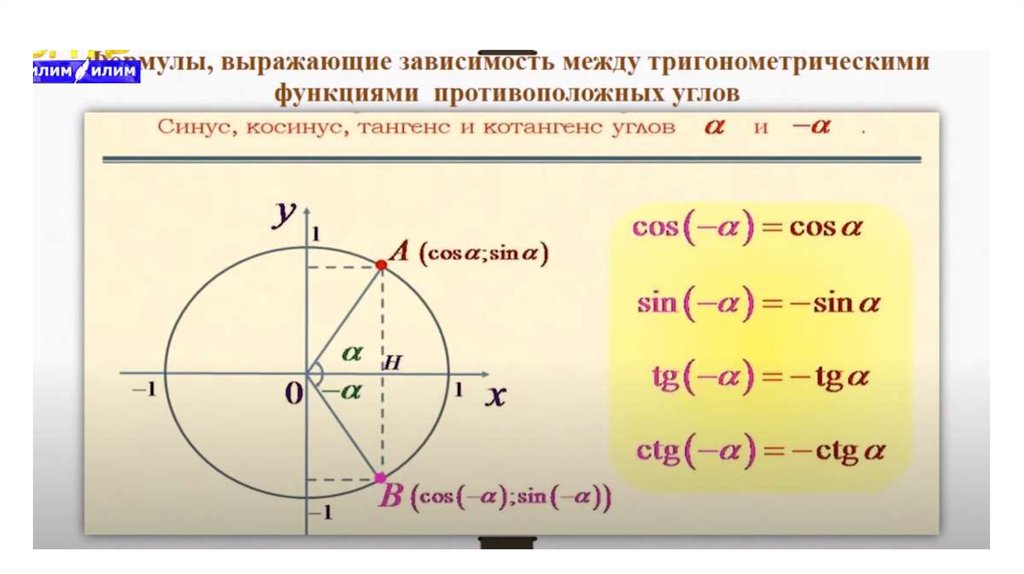 Ответ в любом случае получится −10. Все, задача B11 решена!

Задача B14 — 2 вариант

Переходим ко второй задаче. Перед нами снова дробь:

Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):

sin 117° = sin (90° + 27°) = cos 27°

Очевидно, перед нами снова формула приведения : 90° — это вертикальная ось, следовательно, синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.

Возвращаемся к исходному выражению, которое требуется вычислить:

Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.

Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.

Для использования формул приведения существует два правила.

1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.

Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.

2. Правило «каким ты был, таким ты и остался».

Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».

На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.

Вычислить Sin(150˚)

Воспользуемся формулами приведения:

Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.

Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.

При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.

Урок и презентация на тему: «Применение формул приведения при решении задач»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса

1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов

Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.

Повторение тригонометрических функций

Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?

Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.

Правило для формул приведения

Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.

Вспомним некоторые формулы:

• sin(t + 2π*k) = sin(t)
• cos(t + 2π*k) = cos(t)
• sin(t + π) = -sin(t)
• cos(t + π) = -cos(t)
• sin(t + π/2) = cos(t)
• cos(t + π/2) = -sin(t)
• tg(t + π*k) = tg(x)
• ctg(t + π*k) = ctg(x)

формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :

• Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
• Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
  3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом.
• Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0

Эти правила применимы и когда аргумент функции задан в градусах!

Так же мы можем составить таблицу преобразований тригонометрических функций:

Примеры применения формул приведения

1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2

2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)

3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0

4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t).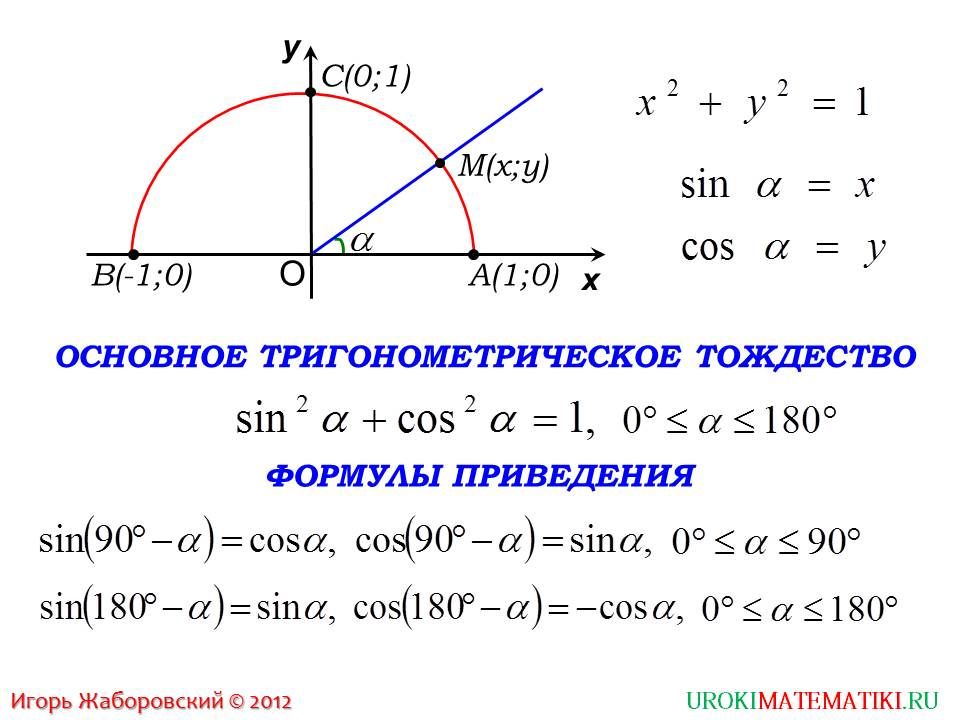 Далее предположим что 0

Задачи с формулами приведения для самостоятельного решения

Ребята, преобразуйте самостоятельно, используя наши правила:

1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).

Как запомнить формулы приведения тригонометрических функций? Это легко, если использовать ассоциацию.Данная ассоциация придумана не мной. Как уже говорилось, хорошая ассоциация должна «цеплять», то есть вызывать яркие эмоции. Не могу назвать эмоции, вызываемые этой ассоциацией, позитивными. Но она дает результат — позволяет запоминать формулы приведения, а значит, имеет право на существование. В конце концов, если она вам не понравится, вы же ее можете не использовать, правильно?

Формулы приведения имеют вид: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запоминаем, что +α дает движение против часовой стрелки, — α — движение по часовой стрелке.

Для работы с формулами приведения нужны два пункта:

1) ставим знак, который имеет начальная функция (в учебниках пишут: приводимая. Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.

2) Горизонтальный диаметр — π±α, 2π±α, 3π±α… — в общем, когда нет дроби — название функции не меняет. Вертикальный π/2±α, 3π/2±α, 5π/2±α…- когда дробь есть — название функции меняет: синус — на косинус, косинус — на синус, тангенс — на котангенс и котангенс — на тангенс.

Теперь, собственно, ассоциация:

вертикальный диаметр (есть дробь) —

пьяный стоит. Что с ним случится рано

или поздно? Правильно, упадет.

Название функции изменится.

Если же диаметр горизонтальный — пьяный уже лежит. Спит, наверное. С ним уже ничего не случится, он уже принял горизонтальное положение. Соответственно, название функции не меняется.

То есть sin(π/2±α), sin(3π/2±α), sin(5π/2±α) и т.д. дают ±cosα,

а sin(π±α), sin(2π±α), sin(3π±α), … — ±sinα.

Как , уже знаем.

Как это работает? Смотрим на примерах.

1) cos(π/2+α)=?

Становимся на π/2. Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,

cos(π/2+α)=-sin α.

Становимся на 2π. Так как -α — идем назад, то есть по часовой стрелке. Попадаем в IV четверть, где тангенс имеет знак «-«. Название функции не меняется (диаметр горизонтальный, «пьяный уже лежит»). Таким образом, tg(2π-α)=- tgα.

3) ctg²(3π/2-α)=?

Примеры, в которых функция возводится в четную степень, решаются еще проще. Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается. Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.

Тригонометрические формулы приведения

Тип урока: дифференцированный, проблемный.

>Цель урока: Совершенствование навыков взаимодействия на уроке в группах, решая проблемные задачи. Развитие способности самооценки учащихся. Организация совместной учебной деятельности, дающая возможность формулировать и решать проблемные задачи.

Задачи урока:

Образовательная:

• повторить числовые значения точек числовой окружности, которые получены делением каждой четверти на 2 и 3 равные части; закрепить умения нахождения значения синуса и косинуса числовых значений числовой окружности и определения их знака; познакомить учащихся с углами вида , где ; разработать алгоритм вывода формул приведения для функции синус и косинус; закрепить умение применения тригонометрических формул приведения в различных заданиях.

Развивающая: Научить выдвигать гипотезу и умело доказательно отстаивать свое мнение. Уметь распознавать и решать проблемные задачи. Проверить умение обобщать и систематизировать свои знания.

Воспитательная: Повысить интерес к предмету и подготовить к решению более сложных задач.

Этапы урока	Время	Методы и приемы
1. Организационное введение. Постановка учебной задачи.	2	Запись темы урока. Рассказ учителя
2. Повторение	3	Повторить числовые значения точек числовой окружности макета 1 и 2 . с использованием слайдов. Демонстрация на слайдах числовых значений.
	3	Повторить значения синуса и косинуса в точках макета 1и 2 числовой окружности и определить их знак. Демонстрация на слайдах значений синуса и косинуса.
3. Работа в группах	5	Самостоятельное выполнение в группах работы по выводу формул приведения для некоторых углов. Демонстрация на слайдах формул приведения.
4. Групповой зачет по проблемной теме	9	Составление схемы-конспекта по теме “Тригонометрические формулы приведения”
5. Формулы приведения	10	Вывод формул приведения.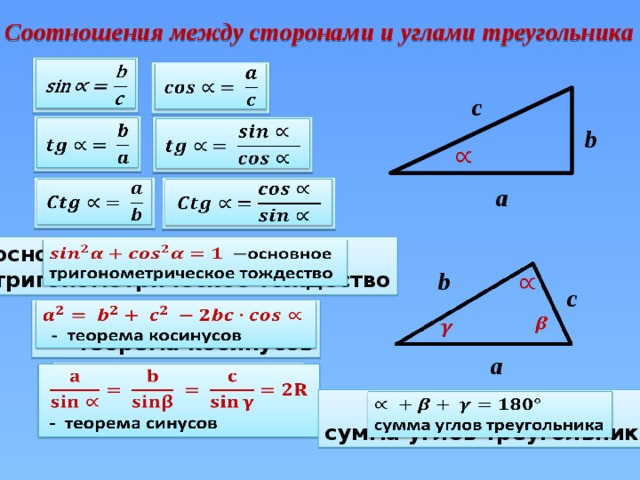 Демонстрация на слайдах схемы-конспекта.
6. Тренинг по применению формул приведения	10	Решение заданий на применение формул приведения.
7. Подведение итогов	2	Выделение учителем главного на уроке и определения достижения целей.
8. Домашнее задание	1	Творческое задание: вывести формулы проведения для функций тангенса и котангенса и привести примеры

1. Организационное введение. Постановка учебной задачи. (2 мин)

Учитель: Класс делятся на четыре группы, которые объединяют около лидера учащихся одного уровня знаний:

• I группа “А” Лидер учащийся А
• II группа “В” Лидер учащийся В
• III группа “С” Лидер учащийся С
• IV группа “D” Лидер учащийся D

Каждая группа учащихся получает форму схемы-конспекта (см. Приложение 2) и лист учета активности в группе (см. Приложение 1).

Учитель: Рассмотрите внимательно форму схемы-конспекта и лист учета активности в группе. Запишите фамилию и имя каждого ученика группы

Тема  урока “Тригонометрические формулы приведения”. Мы с вами сегодня:

• повторим числовые значения точек числовой окружности, которые получены делением каждой четверти на 2 и 3 равные части;
• закрепим умения нахождения значения синуса и косинуса числовых значений числовой окружности и определения их знака;
• познакомимся с углами вида , где ;
• разработаем алгоритм вывода формул приведения для функции синус и косинус;
• закрепим умение применения тригонометрических формул приведения в различных заданиях.

2. Повторение (3+3 мин)

Повторение значений чисел числовой окружности проводится с помощью слайдов (см. Презентация.ppt).

Учитель: “Назовите число, которое соответствует точке выделенной на окружности” (задание той группе, чей номер совпадает с номером четверти, в которой выделяется точка).

Затем, показываются симметричные точки относительно оси OX , оси OY и центра системы координат, для которых учитель просит назвать число тем группам, чьи номера совпадают с номером четверти.

На слайде появляются точки по следующим схемам:

I — (III, IV, II) III — (II, I, IV) II — (I, III, IV)

(раскрывается 3 лист слайда постепенно шаг за шагом):

Учитель: (задание той группе, чей номер совпадает с номером четверти, в которой находится угол синуса или косинуса) “Назовите значение синуса (косинуса) числа”.

На слайде появляются точки по следующей схеме:

II — ; IV — ; III — ; I — ;

III — ; I -; IV -; II — .

(раскрывается 4 лист слайда постепенно шаг за шагом):

Учитель: В “Лист учета активности в группе” лидер каждой группы выставляет баллы.

2. Работа в группах (5 мин)

Учитель: На слайде изображены две схемы, используя эти схемы, запишите тригонометрические тождества, продолжив равенство одной из функций или .

(раскрывается 5 лист слайда постепенно шаг за шагом):

Учитель: Ответьте на вопросы:

Зависит ли от аргумента название функции в двух частях равенства?

Как проявляется эта зависимость?

Объясните появление или отсутствие знака перед функцией в тождествах.

Можно ли ваши рассуждения применить на выражениях вида , где и , где ?

Учитель: Каждая группа у доски приводит доводы своим рассуждениям, отвечая на вопросы учителя.

Учитель: В “Лист учета активности в группе” лидер каждой группы выставляет баллы.

4. Групповой зачет по проблемной теме (3+3+3 мин)

Учитель: Заполните схему-конспект по теме “Тригонометрические формулы приведения”

Формулы приведения
Выражения под знаком тригонометрической функции
Гипотеза: Существуют выражения под знаком тригонометрической функции, которые могут менять или не менять наименование функции.
	; ; ;							; ; ;
Вывод:						Вывод:
На конкретных примерах поясните изменение наименования функции, рассмотрев выражения:
и						и
Вывод:						Вывод:
Определите, на каком рисунке показаны знаки синуса, косинуса, тангенса и котангенса.

Учитель: Каждая группа у доски приводит доводы своим рассуждениям, дополняя ответы учащихся из других групп.

Формулы приведения (10 мин)

Учитель: У доски выходят решать задание, учащиеся

той группы, чей номер совпадает с номером четверти аргумента тригонометрической функции. Каждое решение будет проверяться демонстрацией слайдов.

Задания учитель выписывает на доске в следующем порядке: , , , , , , , , , , , .

(раскрываются 6-17 листы слайдов постепенно шаг за шагом):

Учитель: В “Лист учета активности в группе” лидер каждой группы выставляет баллы.

6. Тренинг по применению формул приведения (10 мин)

Учитель: Решите два задания на применение формул приведения, обсуждая решение внутри каждой группы:

; .

Учитель: Задание получает каждый учащийся группы, решение будет проверено лидерами групп. Не выводя формулы приведения для тангенса и котангенса, решите задания, предложенные в тренинге:

1	Упростите: A) 0 B) cosx C) sin2x D) 2 E) 1
2	Упростите A) B) C) sin D) cos E) 1
3	Найдите значение выражения , если a — b = A) B) C) D) 1 E) 2
4	Упростите выражение: A) B) C) D) E)
5	Упростите . A) tg2a B) ctg2a C) —tg2a D) E)
6	Упростите выражение A) cosctg B) —cos ctg C) —cos tg D) sin tg E) —sin ctg
7	Упростите выражение: A) B) - C) — D) E) —
8	Упростите выражение: A) —sin tg B) cos tg C) sin tg D) —cos tg E) sin
9	Упростите: A) B) C) D) E) 1

Учитель: В “Лист учета активности в группе” лидер каждой группы выставляет баллы.

7. Подведение итогов (2 мин)

Учитель: Мы с вами сегодня

• повторили числовые значения точек числовой окружности, которые получены делением каждой четверти на 2 и 3 равные части;
• повторили нахождения значения синуса и косинуса числовых значений числовой окружности и определения их знака;
• познакомились с выражением вида , где ;
• разработали алгоритм вывода формул приведения для функции синус и косинус;
• вывели формулы приведения для синуса и косинуса;
• упрощали выражения, применения тригонометрические формулы приведения.

8. Домашняя работа (1 мин): Выведите формулы приведения для тангенса и котангенса, содержащих выражения под знаком тригонометрической функции.

Приложения:

Приложение 1. Лист учета активности в группе

Приложение 2. Форма схемы-конспекта по теме “Тригонометрические формулы приведения”

Нахождение косинуса сумм и разностей углов

Авторы: Ян Куанг и Эллейн Кейс и

Обновлено: 22 сентября 2022

Книга по тригонометрии. формулы суммы и разности для косинуса для вычисления косинуса суммы и разности углов аналогично тому, как вы можете использовать формулы суммы и разности для синуса, потому что формулы внешне очень похожи друг на друга. При работе с синусом и косинусом суммы и разности углов вы просто подставляете заданные значения переменных (углов).

Просто убедитесь, что вы используете правильную формулу, основанную на информации, которую вы дали в вопросе.

Вот формулы суммы и разности для косинусов:

Формулы суммы и разности для косинуса (и синуса) могут сделать больше, чем вычислить триггерное значение для угла, не отмеченного на единичной окружности (по крайней мере, для углов, кратных 15 градусов). Их также можно использовать для нахождения косинуса (и синуса) суммы или разности двух углов на основе информации о двух углах. Для таких задач вам будут даны два угла (назовем их А и В), синус или косинус А и В и квадрант(ы), в котором расположены два угла.

Используйте следующие шаги, чтобы найти точное значение cos(A + B), учитывая, что cos A = –3/5, с A в квадранте II координатной плоскости, и sin B = –7/25, с B в квадранте III:

1. Выберите подходящую формулу и замените известной вам информацией, чтобы определить недостающую информацию.

   , то подстановки приводят к этому уравнению:

   Чтобы продолжить, вам нужно найти cos B и sin A.

2. Нарисуйте изображения, изображающие прямоугольные треугольники в квадранте(ах).

   Рисование картинок поможет визуализировать недостающую информацию.

   Вам нужно нарисовать один треугольник для угла A в квадранте II и один треугольник для угла B в квадранте III. Используя определение синуса как opp / hyp и косинуса как adj / hyp, на этом рисунке показаны эти треугольники. Обратите внимание, что значение катета отсутствует в каждом треугольнике.

3. Чтобы найти пропущенные значения, используйте теорему Пифагора.

   Длина отсутствующего участка на рис. а равна 4, а длина отсутствующего участка на рис. б равна –24.

4. Определите отсутствующие коэффициенты триггера для использования в формуле суммы или разности.

   Вы используете определение косинуса, чтобы найти, что cos B = –24/25, и определение синуса, чтобы найти, что sin A = 4/5.

5. Замените отсутствующие тригонометрические соотношения в формулу суммы или разности и упростите.

   Теперь у вас есть это уравнение:

   Следуйте порядку операций, чтобы получить этот ответ:

   Это уравнение упрощается до cos(A + B) = 4/5.

Эту статью можно найти в категории:

• Предварительное исчисление,

Закон синусов и косинусов — формулы и примеры

Законы синусов и косинусов — это отношения, которые позволяют нам найти длину одной стороны треугольника или мера одного из его углов. В зависимости от имеющейся у нас информации, мы можем использовать закон синусов или закон косинусов. Закон синусов связывает длину одной стороны с синусом ее угла, а закон косинусов связывает длину двух сторон треугольника с их промежуточным углом.

Здесь мы узнаем о формулах закона синусов и закона косинусов. Мы научимся отличать ситуации, в которых мы можем использовать закон синусов, от ситуаций, в которых мы можем использовать закон косинусов. Кроме того, мы увидим некоторые проблемы с практикой.

ТРИГОНОМЕТРИЯ

Актуально для …

Изучение закона синусов и косинусов на примерах.

См. примеры

Содержимое

ТРИГОНОМЕТРИЯ

Актуально для …

Изучение закона синусов и косинусов на примерах.

См. примеры

Какова формула закона синусов?

Формула закона синусов — это уравнение, связывающее стороны треугольника с синусами соответствующих углов. Ниже приводится формула закона синусов:

$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{ \sin(C)}$

, где a, b, c представляют собой длины сторон треугольника, а A, B, C представляют собой углы треугольника. Углы обозначают их противоположные стороны. Это означает, что a — это сторона, противоположная углу A, b — сторона, противоположная углу B, а c — сторона, противоположная углу C, как мы можем видеть в следующем треугольнике.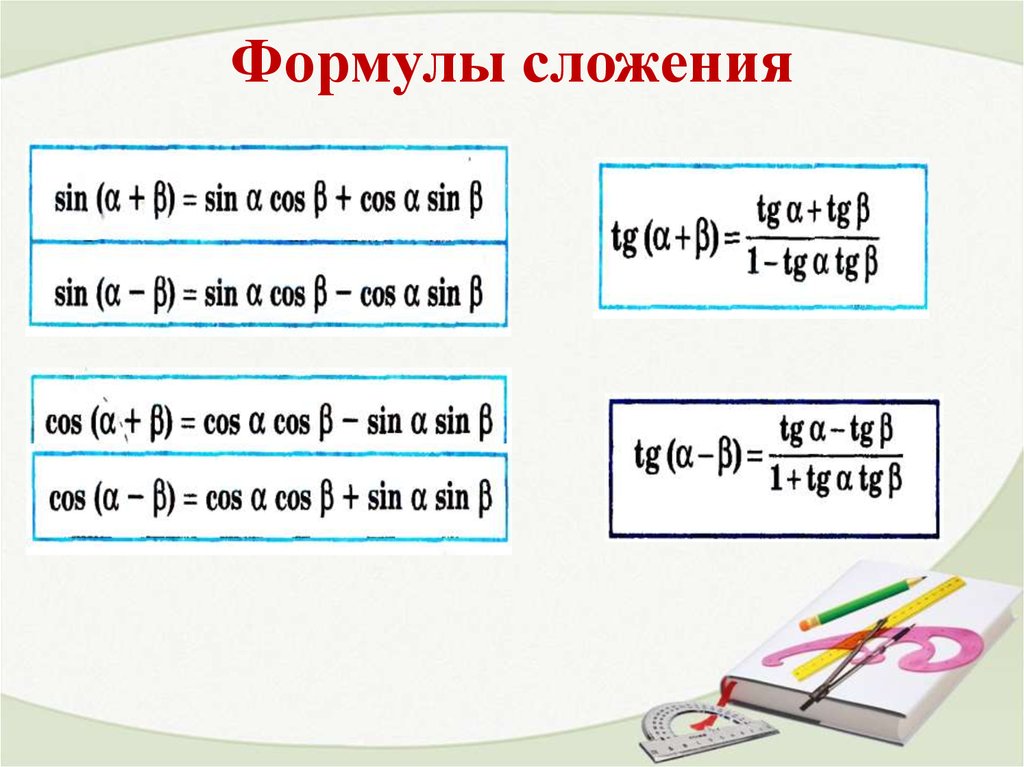

---

Какова формула закона косинусов?

Формула закона косинусов — это уравнение, связывающее длины двух сторон треугольника с углом между двумя сторонами. Формула закона косинусов: 92}-2ab\cos(\gamma)$

где a, b, c представляют длины сторон треугольника, а α, β, γ представляют углы треугольника как показано на следующем изображении.

---

Когда использовать закон синусов и когда использовать закон косинусов?

Закон синусов можно использовать в следующих ситуациях:

•  Мы хотим найти длину одной стороны и знаем величину двух углов и длину одной стороны.

•  Мы хотим вычислить угол и знаем размеры двух сторон и угла.

Чтобы использовать закон синусов, мы должны связать углы с их противоположными сторонами. Например, мы можем применить закон синусов к следующему треугольнику, если мы хотим найти длину стороны 90 121 b 90 122 и нам известны меры углов A, B и длина стороны 90 121 a 90 122 .

Кроме того, мы можем также применить закон синусов, если мы хотим найти меру угла A и узнать длины сторон a, b,  и мера угла B.

Закон косинусов можно использовать, когда у нас есть следующие ситуации:

•  Мы хотим найти длину одной стороны, и мы знаем длины двух стороны и их промежуточный угол.

•  Нам нужно найти величину любого угла, и мы знаем длины трех сторон треугольника.

Чтобы использовать закон косинусов, мы всегда используем угол между двумя известными сторонами. Например, мы можем применить закон косинусов, если мы хотим найти длину стороны c  в треугольнике ниже, и мы знаем длины a и b и меру угла γ.

---

Закон синусов и косинусов – Примеры с ответами

Следующие примеры решаются с использованием законов синусов и косинусов. Каждое упражнение имеет свой ответ, но рекомендуется попробовать решить задачи самостоятельно, прежде чем искать решение.

ПРИМЕР 1

У нас есть треугольник с углами A=40° и B=50° со стороной и =12. Какова длина стороны b ?

Решение

У нас есть следующая информация:

• A=40°
• B=50°
• a=12

В этом случае мы можем использовать закон синусов. Таким образом, мы имеем:

$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$

$latex \frac{12}{\sin(40) }=\frac{b}{\sin(50)}$

$latex \frac{12}{0,643}=\frac{b}{0,766}$

$latex 15,55=\frac{b}{0,766 }$

$латекс b=15,55(0,766)$

$латекс b=11,9$

Длина b равна 11,9.

ПРИМЕР 2

Чему равен угол А в треугольнике, если a = 10, B = 30° и b = 8?

Решение

У нас есть следующие значения:

• a=10
• B=30°
• b=8

Снова используем закон синусов. Таким образом, мы имеем:

$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$

$latex \frac{10}{\sin(A) }=\frac{8}{\sin(30)}$ 9{-1}}(\frac{10}{16})$

$латекс A=38,7$°

Угол A равен 38,7°.

ПРИМЕР 3

В треугольнике длины b = 12 и c = 10 и угол A = 45°, какова длина стороны a ?

Решение

Извлекаем следующие значения:

• b=12
• c=10
• A=45°

В этом случае мы можем использовать закон косинусов, чтобы найти длину 912}=74,3$

$латекс c=8,62$

Длина a равна 8,62.

ПРИМЕР 4

В треугольнике стороны a = 7, b = 8 и c = 9. Чему равен угол С?

Решение

У нас есть следующая информация:

• a=7
• b=8
• c=9

Снова воспользуемся законом косинусов. Следовательно, при решении угла C имеем:

9{-1}}(\frac{32}{112})$

$латекс C=73,4$°

Угол C равен 73,4°.

---

Закон синусов и косинусов. Практические задачи

Используйте закон синусов и закон косинусов для решения следующих практических задач.