Кусочный график функции: Кусочные функции. Как построить график кусочной функции

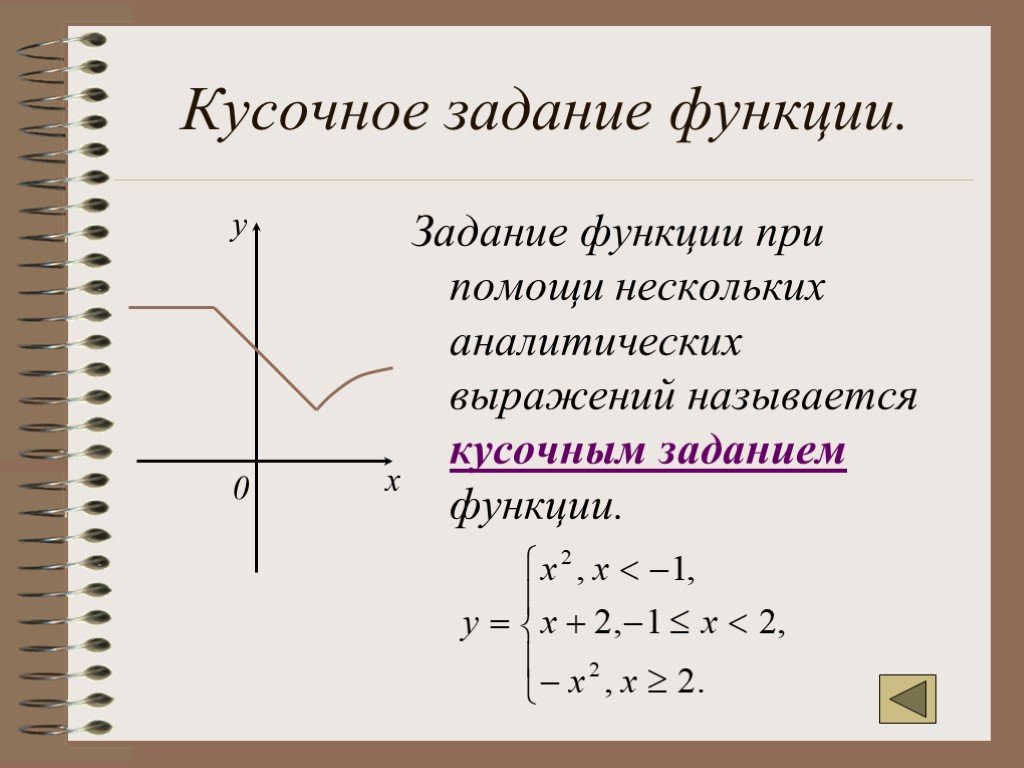
Кусочная функция — что это, определение и ответ

Кусочная функция – это функция, части которой заданы на определенном промежутке.

Например, рассмотрим две функции: \(y = 3x\ –\ 5\ \)и\(\ y = \frac{x}{2}\)

Данные функции не являются кусочными. Это две линейные функции. Построим их на одной координатной плоскости:

Можем сделать из двух функций одну, для этого зададим для каждой функции промежуток.

Пример №1:

\(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x \geq 2 \\ \frac{x}{2},\ если\ x < 2 \\ \end{matrix} \right.\ \)

Получим новую функцию, которая задается кусочками двух линейных. Она и будет являться кусочной. Чтобы её построить, рассмотрим таблицу точек для этих функции по отдельности.

1. y = 3x – 5, если x ≥ 2.

Из условия мы видим, что минимальный x равен 2. Точка x = 2 будет закрашенной, так как знак нестрогий. Меньше это точки мы брать не будем:

2. y = 0,5x, если x < 2.

Для данной функции x = 2 – будет максимальным значением, при этом x ≠ 2, так как знак неравенства строгий. Возьмем эту точку. На графике для этой функции она будет выколотой.

Видим, что закрашенная точка x = 2 у первого графика перекрывает пустую точку второго графика, значит у этой кусочной функции нет разрывов и она называется неразрывна.

Пример №2:

Если задать другие промежутки для кусочной функции, она поменяет свой вид:

\(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x \leq 2 \\ \frac{x}{2},\ если\ x > 2 \\ \end{matrix} \right.\ \)

1. y = 3x – 5, если x ≤ 2.

Теперь у этой функции x = 2 – максимально возможная абсцисса:

2. y = 0,5x, если x > 2.

А для этой функции, наоборот, x = 2 – минимальная абсцисса. Аналогично первому примеру эта точка будет выколота, но перекроется точкой первого графика:

Кусочные функции, представленные выше, называются непрерывными, так как одна линейная функция заканчивается там, где начинается вторая, т. е. между кусочками функции нет разрыва.

Пример №3:

Примером кусочной разрывной функции может служить следующая функция:

\(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x > 2 \\ \frac{x}{2},\ если\ x < 2 \\ \end{matrix} \right.\ \)

Этот график будет выглядеть так же, как график в примере №1, но с одним отличием. Точка x = 2 не принадлежит ни одной из функций, поэтому в этой точке как раз находится разрыв.

1. y = 3x – 5, если x > 2.

2. y = 0,5x, если x < 2.

Пример №4:

Или, например, такая функция тоже является разрывной и кусочной:

\(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x > 3 \\ \frac{x}{2},\ если\ x < \ –2 \\ \end{matrix} \right.\ \)

1. y = 3x – 5, если x > 3.

Здесь будем брать все значения x больше 3. Сама точка x = 3 будет выколотой:

2. y = 0,5x, при x < –2.

Значение x = –2 – максимальное. А сама эта точка тоже выколотая:

Урок. 8 класс. Построение графиков «кусочных» функций.

Построение графиков «кусочных функций».

Цель урока: повторить, закрепить и обобщить умения обучающихся строить и читать графики кусочных функций, решать задания из ГИА.

Тип урока: урок обобщения и систематизации знаний.

Задачи:

Образовательные — обеспечить повторение, обобщение и систематизацию материала темы. Создать условия контроля (самоконтроля) усвоения знаний и умений.

Развивающие — способствовать формированию умения применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Воспитательные — содействовать воспитанию интереса к математике и информатике, активности, умения общаться, общей культуры.

Методы обучения: использование ИКТ, частично — поисковый. Работа по обобщающей схеме, создание презентаций, работа по решению экзаменационных заданий, системные обобщения, самопроверка, взаимопроверка.

Формы организации урока: фронтальная, индивидуальная, групповая.

Оборудование и материалы: интерактивная доска, мультимедийный проектор, компьютер, магнитная доска, указка.

ХОД УРОКА.

1. Организационный момент.

Построение графиков кусочных функций мы изучали еще в 7 классе, а в экзаменационных материалах содержатся задачи по данной теме. Поэтому сегодня на уроке мы будем повторять, обобщать, приводить в систему изученный материал, решать задания из ГИА.

Итак, проверим домашнее задание.

2. Проверка домашнего задания.

а)У доски: задание из ГИА: Для каждого графика укажи соответствующую ему формулу.

А					Б			1
								2
В					Г			3
								4
	А	Б	В	Г

б) заполни таблицу

№	Формула	Название графика	Схематические рисунки
1
2
3
4
5
6
7

Учитель: Вспомним, какие основные алгебраические функции мы изучали и что представляют графики этих функций?

/ Идет опрос класса по обобщающей схеме на интерактивной доске (слайд 2)/

Учитель: А теперь посмотрим, как справились с домашнем заданием.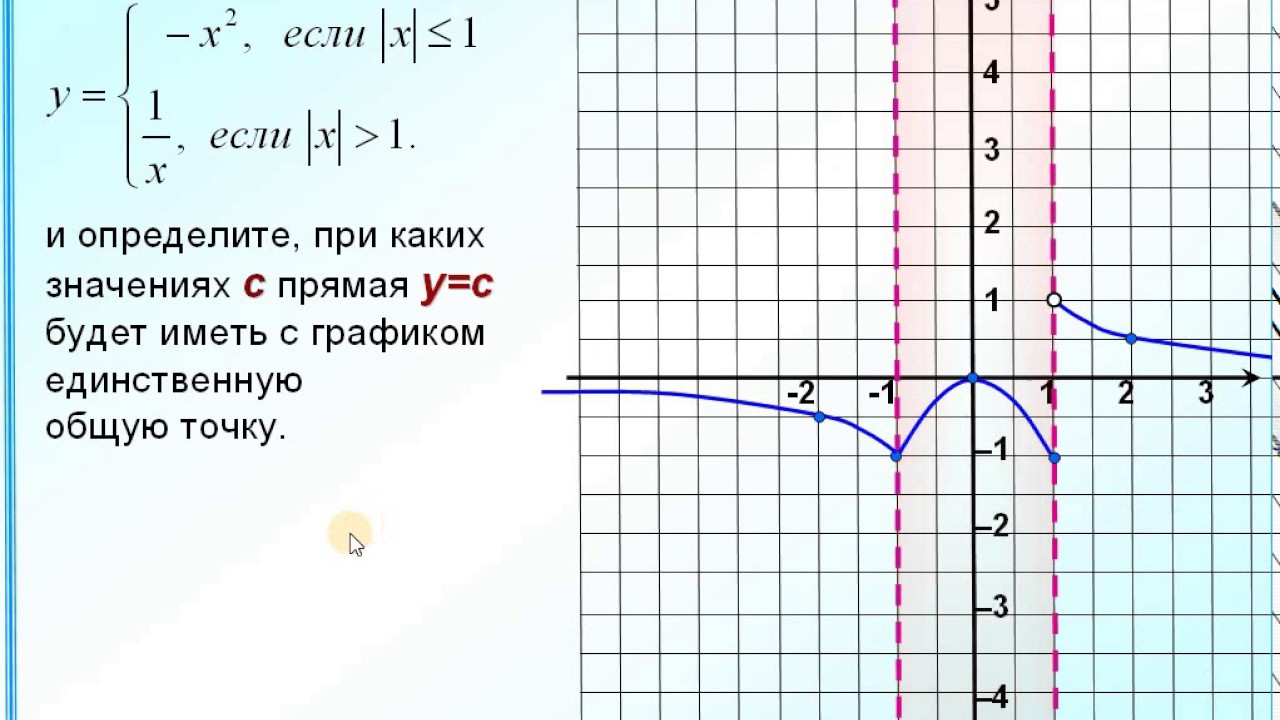

/ Проверка таблицы и устного задания/

3.Построение графиков.

Учитель: В чем особенность графиков кусочных функций? Повторим как строить графики кусочных функций.

/ Идет работа по слайдам./

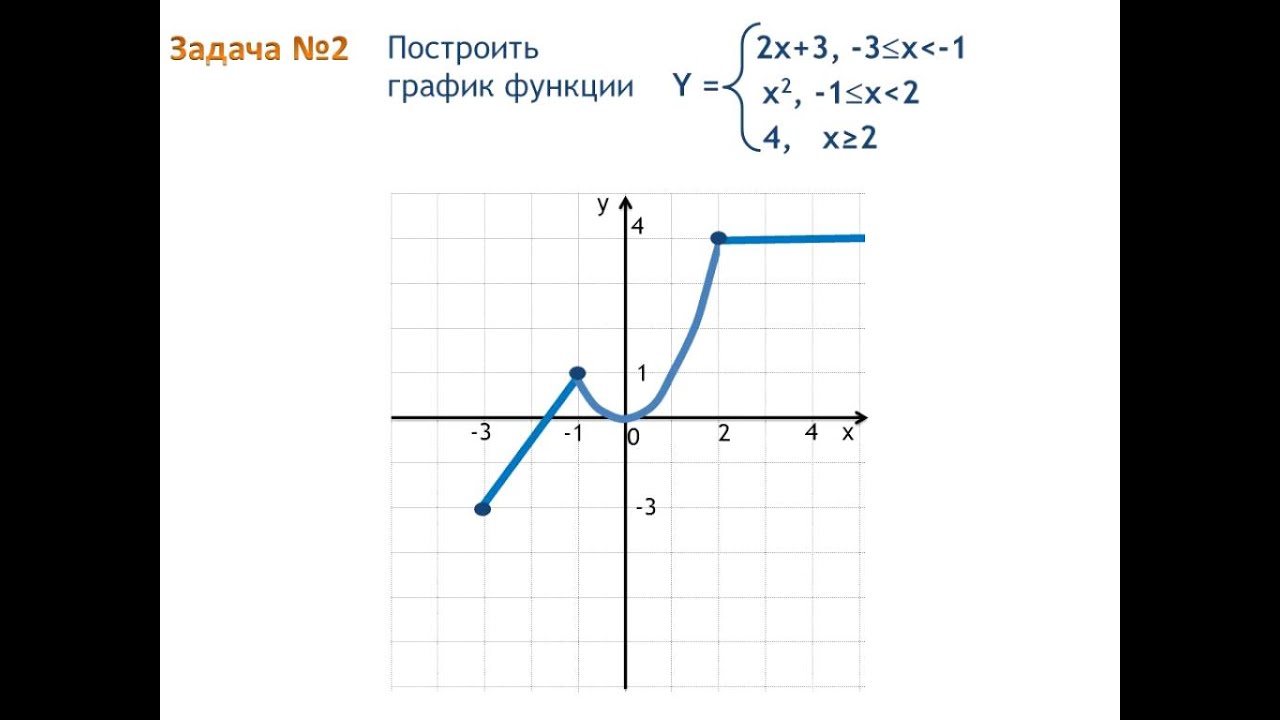
Задание 1: построить график функции (слайд 3,4)

Задание 2: построить график функции. Задать пошаговые команды компьютеру. (слайд 5,6)

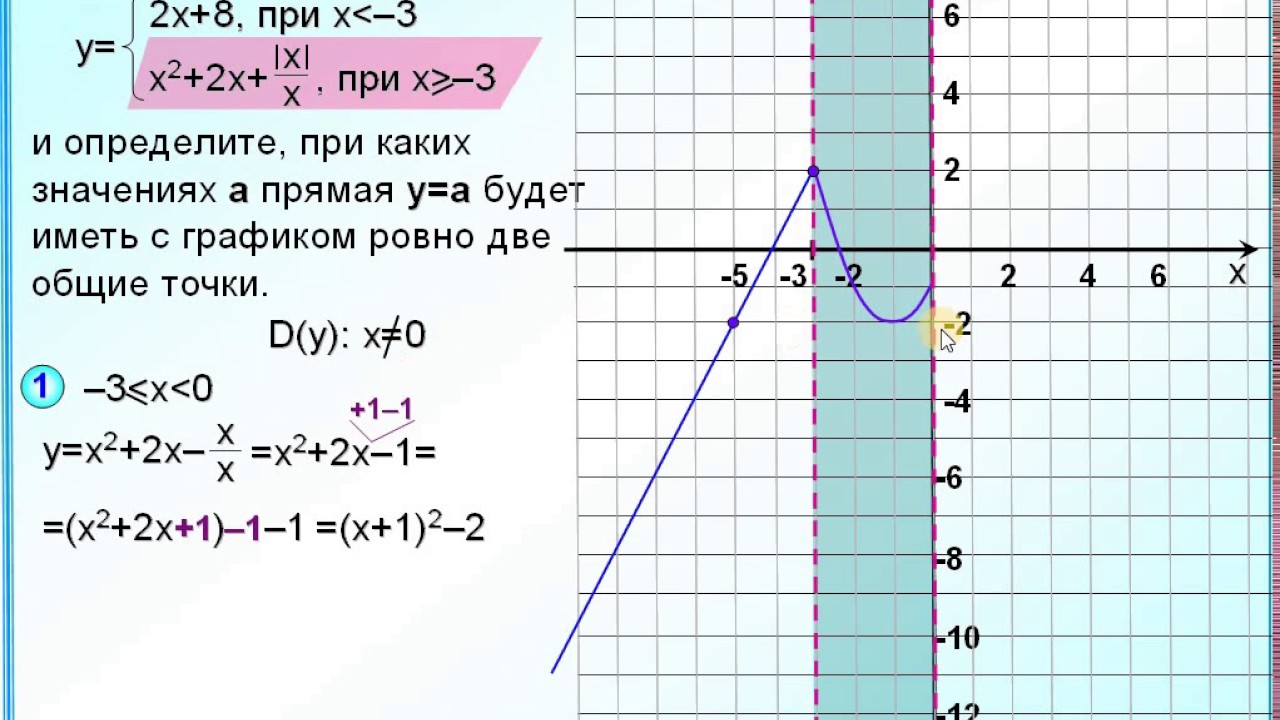
Обычно на экзамене дают и какое- либо дополнительное задание. Например, определите при каких значениях К прямая у = К имеет с графиком функции только одну общую точку. (слайд 7)

Учитель: А теперь решим задание из ГИА.И.В. Ященко, вариант 9, №22.

Мы видим, что выполнение таких заданий достаточно трудоемко и требует много времени. Поэтому, следующее задание из сборника Е.А. Бунимович, вариант 6, № 21подготовили заранее в виде презентации под руководством учителя информатики Костюрина В. и Гончарова А. (слайд 8-19)

Учитель информатики: Почему при решении задачи по математике вы в своей работе ставите цель моделирования?

А на следующей презентации рассмотрим построение еще одной кусочной функции.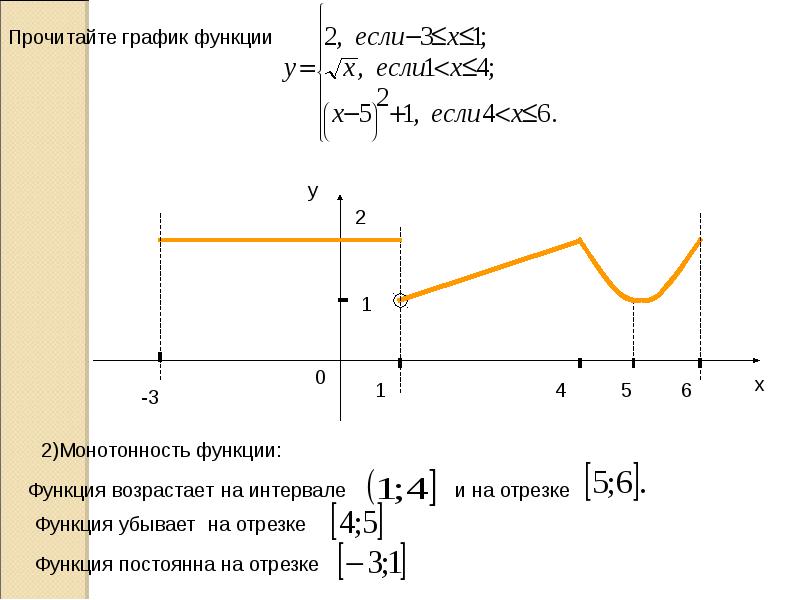 (слайд 20 — 24)

1. Построить график функции

2.Укажите промежуток, на котором функция возрастает.

Учитель информатики: Какую модель получили в результате решения задачи?

4. Обучающая работа в группах.

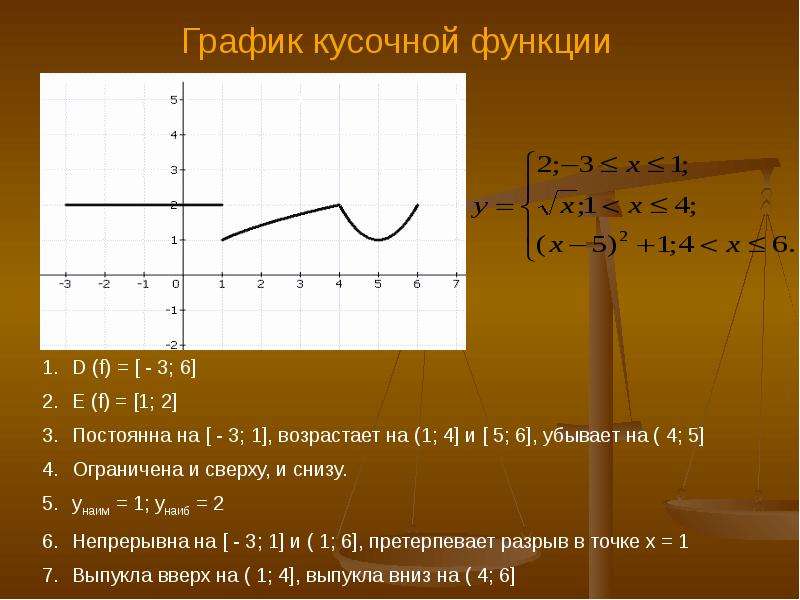
Учитель Сегодня на уроке мы повторили как по формуле построить график, а бывает обратная задача: по графику определить формулу задающею функцию.

Задание: График функции состоит из двух лучей, исходящих из точек А и В и части параболы. Задайте эту функцию формулой.

П рограмму данного задания из ГИА приготовил заранее Фадеев А. (слайд 31 — 37)

Рассмотрим луч, исходящий из т. А.

— Каким уравнением можно задать этот луч?

у=кх + в

Значит, нам надо определить к и в. Для этого по графику выберем по две точки с координатами выраженными целыми числами.

Решить систему методом сложения.

Значит, уравнение первой части графика у = 5х + 7, при х -1.

Для определения остальных частей графика разобьемся на группы:

1 вариант определяют часть АВ,

2 вариант- луч исходящий из т. В.

Проверим правильность выбранных ответов.

6. Итог урока.

Итак, сегодня мы с вами повторили, как строить графики кусочных функций.

Какой алгоритм мы будем при этом применять?

7. Домашнее задание.

Ященко, вариант 10. №22, вариант3, № 22, вариант 2, №22.

Кусочная функция — Как построить график? Примеры, вычисление

Кусочная функция — это функция, график которой состоит из нескольких частей кривых. Это означает, что он имеет разные определения в зависимости от значения ввода. т. е. кусочная функция ведет себя по-разному для разных входных данных.

Давайте узнаем больше о кусочной функции, а также о том, как построить ее график, как ее оценить и как найти ее область определения и диапазон.

1.	Что такое кусочная функция?
2.	Кусочно-функциональный график
3.	Домен и диапазон кусочной функции
4.	Оценка кусочной функции
5.	Кусочно-непрерывная функция
6.	Часто задаваемые вопросы о кусочной функции

Что такое кусочная функция?

Кусочная функция — это функция f(x), которая имеет разные определения в разных интервалах x. График кусочной функции имеет разные части, соответствующие каждому из ее определений. Функция абсолютного значения — очень хороший пример кусочной функции. Давайте разберемся, почему он так называется. Мы знаем, что функция абсолютного значения есть f(x) = |x| и определяется как: \(f(x)=\left\{\begin{array}{ll}
х, & \текст { если } х \geq 0 \\
-x, & \text { если } x < 0
\end{массив}\right.\). Мы должны читать эту кусочную функцию как

• f(x) равно x, когда x больше или равно 0 и
• f(x) равно -x, когда x меньше 0

Тогда график функции абсолютного значения f(x) состоит из двух частей: одна соответствует x (когда x находится в интервале [0, ∞) ), а другая часть соответствует -x (когда x находится в интервале ( -∞, 0)).

Его график выглядит следующим образом:

Кусочно-функциональный график

Мы уже знаем, что график кусочной функции состоит из нескольких частей, каждая из которых соответствует своему определению на интервале. Вот шаги для построения графика кусочной функции.

• Во-первых, поймите, что представляет собой каждое определение функции. Например, f(x) = ax + b представляет собой линейную функцию (которая дает прямую), f(x) = ax ² + bx + c представляет квадратичную функцию (которая дает параболу) и т. д., так что мы будем иметь представление о том, к какой форме приведет часть функции.
• Запишите интервалы, показанные в определении функции, вместе с их определениями.
• Создайте таблицу с двумя столбцами, помеченными x и y, соответствующими каждому интервалу. Обязательно включать конечные точки интервала. Если конечная точка исключена из интервала, обратите внимание, что мы получаем открытую точку, соответствующую этой точке на графике.
• В каждой таблице возьмите больше чисел (случайных чисел) в столбце x, которые лежат в соответствующем интервале, чтобы получить идеальную форму графика. Если кусок представляет собой прямую линию, то достаточно двух значений x. Возьмите 3 или более чисел для x, если кусок НЕ является прямой линией. 9{2} и х>0
  \end{массив}\right.\).

  Решение:

  f(x) имеет 3 определения:

  • -2 ^x , когда x меньше -2, и это экспоненциальная функция.
  • -|х| когда -2 меньше или равно x меньше или равно 0, и это функция абсолютного значения.
  • 2-x ² , когда x больше 0 и это квадратичная функция.

  Запишем интервалы и соответствующие им определения. Кроме того, давайте создадим таблицы, которые включают конечные точки интервалов, а также несколько других случайных чисел из каждого интервала. Мы будем вычислять значение y в каждом случае, используя соответствующее определение.

  Теперь давайте нанесем все эти точки на график, имея в виду общие формы соответствующих функций. Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо.

  Обратите внимание, что самая левая (светло-оранжевая) кривая расширена влево, поскольку она соответствует интервалу x < -2. Кроме того, крайняя правая (синяя) кривая расширена в интервале x > 0. Средняя (темно-оранжевая) кривая НЕ расширена ни в одну из сторон, так как принадлежит интервалу -2 ≤ x ≤ 0,9.0003

  Домен и диапазон кусочной функции

  Чтобы найти область определения кусочной функции, мы можем просто посмотреть на определение данной функции. Возьмите объединение всех интервалов с x, и это даст нам домен. В приведенном выше примере область определения f(x) равна {x | х < -2} U {х | -2 ≤ х ≤ 0} U {х | х > 0}. Объединение всех этих множеств есть просто множество всех действительных чисел. Таким образом, область определения f(x) (в приведенном выше примере) равна R.

  Чтобы найти диапазон кусочной функции, проще всего построить ее график и посмотреть на ось y. Посмотрите, какие значения y охватываются графиком. В приведенном выше примере все значения y меньше 2 (исключая 2, так как в точках (0, 2) есть открытая точка) покрываются графиком. Таким образом, его диапазон равен {y | y < 2} (или) (-∞, 2).

  Точно так же мы можем найти область определения и область значений любой кусочной функции, просто построив ее график.

  Оценка кусочной функции

  Чтобы вычислить кусочную функцию на любом заданном входе,

  • сначала посмотрите, какому из заданных интервалов (или неравенств) принадлежит данный вход.
  • Затем просто подставьте данный ввод в определение функции, соответствующее этому конкретному интервалу.

  Вот пример для понимания шагов. 92, \text { если } x<0 \\-2 \sqrt{x}, \text { если } x>0 \\ 5, \text { если } x=0\end{массив}\right. \) .

  Решение:

  Нам нужно найти f(4). Здесь x = 4, и оно удовлетворяет условию x > 0. Таким образом, соответствующая функция равна f(x) = -2√x.

  Замените x = 4 в этом определении:

  f(4) = -2 √4 = -2 (2) = -4.

  Следовательно, f(4) = -4.

  Кусочно-непрерывная функция

  Кусочно-непрерывная функция, как следует из ее названия, является кусочно-непрерывной функцией. Это означает, что ее график состоит из разных частей, но тем не менее мы сможем нарисовать график, не отрывая карандаша. Вот пример кусочно-непрерывной функции.

  \(f(x)=\left\{\begin{array}{l} x-1, \text {if } x<-2 \\-3, \text {if } x\geq -2\ конец {массив}\справа.\).

  Его график показан ниже.

  Важные замечания по кусочным функциям

  • Чтобы оценить кусочную функцию на входе, посмотрите, какому интервалу она принадлежит, и подставьте его в соответствующее определение функции.
  • При построении графика кусочной функции используйте незакрашенные точки в точках, координаты x которых не принадлежат соответствующим интервалам. Открытая точка в точке означает, что конкретная точка НЕ ​​является частью функции.
  • Чтобы найти область определения кусочной функции, просто возьмите объединение всех интервалов, заданных в определении функции.
  • Чтобы найти диапазон кусочной функции, просто постройте ее график и найдите значения y, которые охватываются графиком.

  ☛ Похожие темы:

  • Калькулятор графических функций
  • Калькулятор квадратичных функций
  • Графический калькулятор
  • Калькулятор линейной функции 92-2 & \text { если } x \geq 3
    \end{массив}\right.\).

    Как строить графики кусочных функций?

    Чтобы нарисовать кусочный график функции:

    • Составьте таблицу (с двумя столбцами x и y) для каждого определения функции в соответствующих интервалах.
    • Включить конечные точки (в столбце x) каждого интервала в соответствующую таблицу вместе с несколькими другими случайными числами из интервала.
    • Подставьте каждое значение x в соответствующее выражение f(x), которое дает значение в столбце y.
    • Нанесите на график все точки (поставьте открытые точки для исключенных значений x) и соедините их кривыми.
    • Если левая/правая конечная точка равна ∞ или -∞, то соответственно удлините кривую с этой стороны.

    Как решать кусочные функции?

    Чтобы решить значение кусочной функции на определенном входе:

    • Просто посмотрите, в каком из заданных интервалов находится этот вход.
    • Возьмите соответствующую функцию.
    • Заменить данный ввод в функции из последнего шага.

    Приведите пример кусочно-линейной функции.

    Кусочно-линейная функция — это кусочно-линейная функция, в которой все части соответствуют прямым линиям. Например, функция абсолютного значения, ступенчатая функция (функция минимального значения или функция наибольшего целого числа), функция потолка и т. д. являются примерами кусочно-линейных функций.

    Что такое кусочно-непрерывная функция?

    Кусочно-непрерывная функция — это кусочно-непрерывная функция. Его график состоит более чем из одной части, и все же его можно изобразить, не отрывая карандаша.

    Как найти область определения и область значений кусочной функции?

    Область определения кусочной функции — это объединение всех интервалов, указанных в ее определении. Диапазон — это набор всех значений y, которые покрывает его график. Итак, чтобы найти диапазон кусочной функции, сначала нарисуйте ее график.

    Кусочные функции

    Кусочные функции

    Дополнительно

    Показать рекламу

    Скрыть рекламу
    О рекламе

    Функция может состоять из частей

    Мы можем создавать функции, которые ведут себя по-разному в зависимости от входного значения (x).

    Функция, состоящая из 3 штук

    Пример:

    • Когда x меньше 2, он дает x ² ,
    • , когда x ровно 2, дает 6
    • , когда x больше 2 и меньше или равно 6, это дает строку 10-x

    Выглядит так:

    (сплошная точка означает «включая»,
    открытая точка означает «не включая»)

     

    Вот как мы это запишем:

    Домен (все значения, которые могут войти в функцию) — это все действительные числа до 6 включительно, которые мы можем записать так:

    Дом( f) = (-∞, 6] (с использованием интервальной нотации)

    Dom(f) = {x | x ≤ 6} (с использованием нотации Set Builder)

    Вот несколько примеров значений:

    X	Д
    −4	16
    −2	4
    0	0
    1	1
    2	6
    3	7

     

    Пример: Вот еще одна кусочная функция:

    , которая выглядит так:

    Что такое h(−1)?

    x ≤ 1, поэтому мы используем h(x) = 2, поэтому h(−1) = 2

    Что такое h(1)?

    x ≤ 1, поэтому мы используем h(x) = 2, поэтому h(1) = 2

    Что такое h(4)?

    x > 1, поэтому мы используем h(x) = x, поэтому h(4) = 4

    Кусочные функции позволяют нам создавать функции, которые делают все, что мы хотим!

    Пример: Плата за услуги врача зависит от продолжительности лечения.

    

    No related posts.