Извлечение корня квадратного
Репетиторы ❯ Математика ❯ Извлечение корня квадратного
Автор: Валентина Галиневская
●
04.08.2015
●
Раздел: Математика
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного

√81= 9 92 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
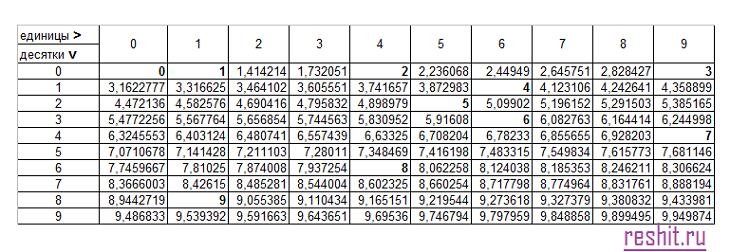
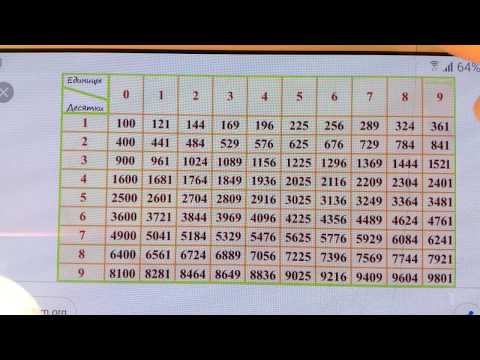
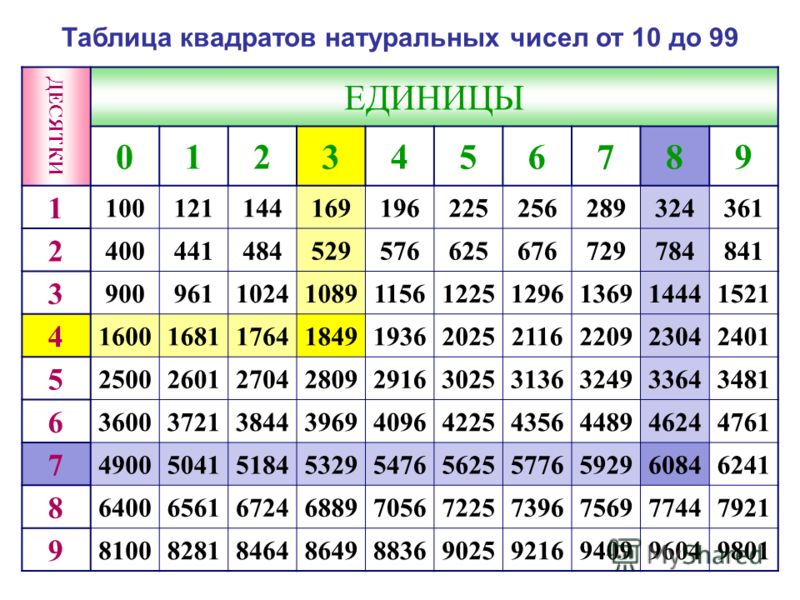
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676.
Замечаем, что 202 = 400, а 302 = 900, значит 20 < √676 < 900.
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 42 и 62.
Осталось проверить: 242 = 576, 262 = 676.
Ответ: √676 = 26.
Еще пример: √6889.
Так как 802 = 6400, а 902 = 8100, то 80 < √6889 < 90.
Цифру 9 дают 32 и 72, то √6889 равен либо 83, либо 87.
Проверяем: 832 = 6889.
Ответ: √6889 = 83.
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025.
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √36 ∙52 ∙72 = 33 ∙5 ∙7 = 945.
Еще пример: √20736
Получаем √20736 = √28 ∙34 = 24 ∙32 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных. Давайте познакомимся с этим правилом на примерах.
Давайте познакомимся с этим правилом на примерах.
Вычислите √279841.
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.

Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей. Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример. Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается.
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
361 — триста шестьдесят один.
 натуральное нечетное число. в ряду натуральных чисел находится между числами 360 и 362. Все о числе триста шестьдесят один.
натуральное нечетное число. в ряду натуральных чисел находится между числами 360 и 362. Все о числе триста шестьдесят один.- Главная
- О числе 361
361 — триста шестьдесят один. Натуральное нечетное число. В ряду натуральных чисел находится между числами 360 и 362.
Like если 361 твое любимое число!
Изображения числа 361
Склонение числа «361» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 361 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | триста шестьдесят один |
| Родительный | Нет | Кого? Чего? | трёхсот шестидесяти одного |
| Дательный | Дать | Кому? Чему? | трёмстам шестидесяти одному |
| Винительный | Видеть | Кого? Что? | триста шестьдесят один |
| Творительный | Доволен | Кем? Чем? | тремястами шестьюдесятью одним |
| Предложный | Думать | О ком? О чём? | трёхстах шестидесяти одном |
Перевод «триста шестьдесят один» на другие языки
- Азербайджанский
- üç yüz altmış bir
- Албанский
- 361
- Английский
- three hundred sixty-one
- Арабский
- 361
- Армянский
- երեք հարյուր վաթսուն — մեկ
- Белорусский
- 361
- Болгарский
- триста шестдесет и един
- Вьетнамский
- 361
- Голландский
- 361
- Греческий
- τριακόσια εξήντα ένα
- Грузинский
- სამას სამოცდაერთი
- Иврит
- 361
- Идиш
- 361
- Ирландский
- 361
- Исландский
- 361
- Испанский
- trescientos sesenta y un
- Итальянский
- Китайский
- 361
- Корейский
- 삼백예순하나
- Латынь
- trecenti sexaginta
- Латышский
- 361
- Литовский
- 361
- Монгольский
- гурван зуун жаран нэг нь
- Немецкий
- 361
- Норвежский
- 361
- Персидский
- 361
- Польский
- trzysta sześćdziesiąt jeden
- Португальский
- 361
- Румынский
- 361
- Сербский
- триста шездесет један
- Словацкий
- 361
- Словенский
- 361
- Тайский
- 361
- Турецкий
- 361
- Украинский
- триста шістдесят одна
- Финский
- kolmesataakuusikymmentäyksi
- Французский
- 361
- Хорватский
- 361
- Чешский
- 361
- Шведский
- 361
- Эсперанто
- tricent sesdek — unu
- Эстонский
- 361
- Японский
- 三六〇から一
Перевод «361» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- CCCLXI
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ٣٦١
- Восточно-арабскими цифрами
- ۳۶۱
- Деванагари
- ३६१
- Бенгальскими цифрами
- ৩৬১
- Гурмукхи
- ੩੬੧
- Гуджарати
- ૩૬૧
- Ория
- ୩୬୧
- Тамильскими цифрами
- ௩௬௧
- Телугу
- ౩౬౧
- Каннада
- ೩೬೧
- Малаялам
- ൩൬൧
- Тайскими цифрами
- ๓๖๑
- Лаосскими цифрами
- ໓໖໑
- Тибетскими цифрами
- ༣༦༡
- Бирманскими цифрами
- ၃၆၁
- Кхемерскими цифрами
- ៣៦១
- Монгольскими цифрами
- ᠓᠖᠑
В других системах счисления
- 361 в двоичной системе
- 101101001
- 361 в троичной системе
- 111101
- 361 в восьмеричной системе
- 551
- 361 в десятичной системе
- 361
- 361 в двенадцатеричной системе
- 261
- 361 в тринадцатеричной системе
- 21A
- 361 в шестнадцатеричной системе
- 169
QR-код, MD5, SHA-1 числа 361
Адрес для вставки QR-кода числа 361, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/361/8a7af2e597146fa56019d51d6d447eb3.png
- MD2 от 361
- a9e83970f56d9acfddfec73b4a8b5664
- MD4 от 361
- 797ca5a03511afe9c47ac1b5a8a13d71
- MD5 от 361
- 52720e003547c70561bf5e03b95aa99f
- SHA1 от 361
- b6e7a22c25e9e7146913841b0995288c688f9bf8
- SHA256 от 361
- 73daa9289ddd08a53ba86f065ddb07bf915aba208bec652e999613d2a8444228
- SHA384 от 361
- 92a4d1c7e5561f29ca8a82e368199db089720742e27288614d34e633cca9aebe89805f69026c7e2daee095661c5b95bf
- SHA512 от 361
- e1840ffcd569c7f4b8baed965fb76f21f043b8abe1fbdebc2943a37bf4f51749f56767c2b733aae12348aa56e6460adc2bf9d9dfd8c9054532c81ccad391676b
- GOST от 361
- 7b2833ec8106f3d923fa687fa9b711d1cf08d77b3cf1979b311cfd65341cdfb7
- Base64 от 361
- MzYx
361й день в году
361й день в не високосном году — 27 декабря
День спасателя
День спасателя
Математические свойства числа 361
- Простые множители
- 19 * 19
- Делители
- 1, 19, 361
- Количество делителей
- 3
- Сумма делителей
- 381
- Простое число
- Нет
- Предыдущее простое
- 359
- Следующее простое
- 367
- 361е простое число
- 2437
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Нет
- Регулярное число (Число Хемминга)
- Нет
- Совершенное число
- Нет
- Полигональное число
- квадрат(19)
- Квадрат
- 130321
- Квадратный корень
- 19
- Натуральный логарифм (ln)
- 5.
 8888779583329
8888779583329 - Десятичный логарифм (lg)
- 2.5575072019057
- Синус (sin)
- 0.27938655435957
- Косинус (cos)
- -0.96017870901363
- Тангенс (tg)
- 0.29097349455559
Комментарии о числе 361
← 360
362 →
- Изображения числа 361
- Склонение числа «361» по падежам
- Перевод «триста шестьдесят один» на другие языки
- Перевод «361» на другие языки и системы
- QR-код, MD5, SHA-1 числа 361
- 361й день в году
- Математические свойства числа 361
- Комментарии о числе 361
Квадратный корень из 0 09. Квадратный корень
Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению. На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным.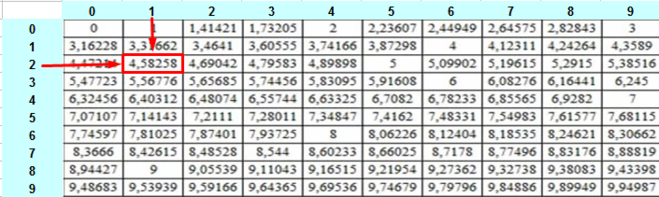 Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю. Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Следующее нечетное число — это 11, остаток у нас следующий: 1
Для таких случаев существует разложение в ряд Тейлора:
√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
Возведение в степень предполагает, что данное число необходимо умножить само на себя определенное количество раз. Например, возведение числа 2 в пятую степень будет выглядеть следующим образом:
Число, которое нужно умножать само на себя, называется основанием степени, а количество умножений – ее показателем. Возведению в степень соответствуют два противоположных действия: нахождение показателя и нахождение основания.
Извлечение корня
Нахождение основание степени называется извлечением корня. Это означает, что необходимо найти число, которое нужно возвести в степень n, чтобы получить данное.
Например, необходимо извлечь корень 4-й степени из числа 16, т.е. определить, нужно умножить само на себя 4 раза, чтобы в итоге получить 16. Это число – 2.
Такое арифметическое действие записывается с помощью особого знака – радикала: √, над которым слева указывается показатель степени.
Арифметический корень
Если показатель степени является четный числом, то корнем могут оказаться два числа с одинаковым модулем, но с – положительное и отрицательное. Так, в приведенном примере это могут быть числа 2 и -2.
Выражение должно быть однозначным, т.е. иметь один результат. Для этого и было введено понятие арифметического корня, который может представлять собой только положительное число. Быть меньше нуля арифметический корень не может.
Таким образом, в рассмотренном выше примере арифметическим корнем будет только число 2, а второй вариант ответа – -2 – исключается по определению.
Квадратный корень
Для некоторых степеней, которые используются чаще других, в существуют специальные названия, которые изначально связаны с геометрией. Речь идет о возведении во вторую и третью степени.
Во вторую степень длину стороны квадрата, когда нужно вычислить его площадь. Если же нужно найти объем куба, длину его ребра возводят в третью степень. Поэтому называется квадратом числа, а третья – кубом.
Соответственно, корень второй степени называется квадратным, а корень третьей степени – кубическим. Квадратный корень – единственный из корней, при записи которого над радикалом не ставится показатель степени:
Итак, арифметический квадратный корень из данного числа – это положительное число, которое необходимо возвести во вторую степень, чтобы получить данное число.
Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам.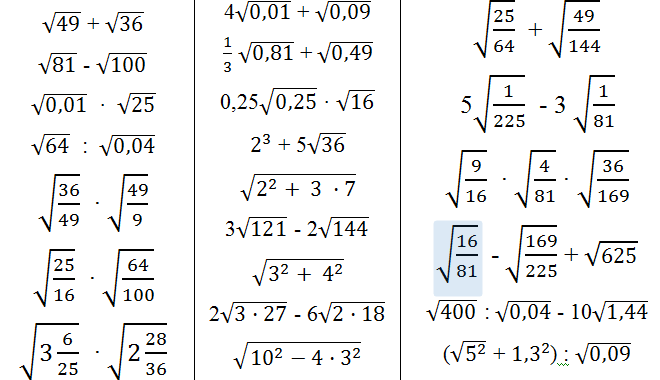 Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а .
Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.
Арифметический квадратный корень из числа а обозначается так: √а.
Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.
Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х , мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.
Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Квадратный корень из дроби
Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .
Так как и , то равенство верно. Итак, .
Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .
Так как √а ≥0 и √b > 0, то .
По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.
Вычислить , по доказанной теореме .
Второй пример: Доказать, что , если а ≤ 0, b .
Еще примерчик: Вычислить .
.
Преобразование квадратных корней
Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;
Вычислить при х = 2. Непосредственная подстановка х = 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.
Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Число 361, 0x000169, триста шестьдесят один
Энциклопедия чисел
Свойства натурального числа 361, 0x000169, 0x169:
Системы счисления Основные свойства Степени, корни
Тригонометрия Хэши, криптография Языки программирования
Дата и время Цвет по числу Интернет
Другие свойства
Рейтинг 10 из 10,
оценок: 1.
Системы счисления, перевод в систему счисления
Десятичное число 361
- 361 в шестнадцатеричной системе счисления
- 169
- 361 в двоичной системе счисления
- 101101001
- 361 в восьмеричной системе счисления
- 551
Шестнадцатеричное число 169
- 169 в десятичной системе
- 361
- 169 в двоичной системе
- 101101001
- 169 в восьмеричной системе
- 551
Двоичное число 101101001
- 101101001 в десятичной системе
- 361
- 101101001 в шестнадцатеричной системе
- 169
- 101101001 в восьмеричной системе
- 551
Восьмеричное число 551
- 551 в десятичной системе
- 361
- 551 в шестнадцатеричной системе
- 169
- 551 в двоичной системе
- 101101001
Основные арифметические и алгебраические свойства
- Число 361 на русском языке, number in Russian, число 361 прописью:
- триста шестьдесят один
- Четность
- Нечетное число 361
- Разложение на множители, делители числа 361
- 19, 19, 1
- Простое или составное число
- Составное число 361
- Числа делящиеся на целое число 361
- 722, 1083, 1444, 1805, 2166, 2527, 2888, 3249
- Число 361 умноженное на число два
- 722
- 361 деленное на число 2
- 180.
 5
5
- Список 8-ми простых чисел перед числом
- 359, 353, 349, 347, 337, 331, 317, 313
- Сумма десятичных цифр
- 10
- Количество цифр
- 3
- Десятичный логарифм 361
- 2.5575072019057
- Натуральный логарифм 361
- 5.8888779583329
- Это число Фибоначчи?
- Нет
- Число на 1 больше числа 361,
следующее число - число 362
- Число на 1 больше числа 361,
- Число на 1 меньше числа 361,
предыдущее число - 360
- Число на 1 меньше числа 361,
Степени числа, корни
- 361 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 130321
- 361 во второй степени (в квадрате)
- В третьей степени (в кубе, 361 в степени 3, x³) равно
- 47045881
- Корень квадратный из 361
- 19
- Корень кубический из числа 361 =
- 7.120367358902
Тригонометрические функции, тригонометрия
- Синус, sin 361 градуса, sin 361°
- 0.
 0174524064
0174524064
- Косинус, cos 361 градуса, cos 361°
- 0.9998476952
- Тангенс, tg 361 градуса, tg 361°
- 0.0174550649
- Синус, sin 361 радиан
- 0.27938655435957
- Косинус, cos 361 радиан
- -0.96017870901363
- Тангенс, tg 361 радиан равно
- -0.29097349455559
- 361 градус, 361° =
- 6.3006385996995 радиан
- 361 радиан =
- 20683.776404223 градуса, 20683.776404223°
Контрольные суммы, хэши, криптография
- MD-5 хэш(361)
- 52720e003547c70561bf5e03b95aa99f
- CRC-32, CRC32(361)
- 28185492
- SHA-256 hash, SHA256(361)
- 73daa9289ddd08a53ba86f065ddb07bf915aba208bec652e999613d2a8444228
- SHA1, SHA-1(361)
- b6e7a22c25e9e7146913841b0995288c688f9bf8
- ГОСТ Р 34.
 11, GOST R 34.11-94, GOST(361)
11, GOST R 34.11-94, GOST(361) - 7b2833ec8106f3d923fa687fa9b711d1cf08d77b3cf1979b311cfd65341cdfb7
- ГОСТ Р 34.
- Base64
- MzYx
Языки программирования
- C++, CPP, C значение 361
- 0x000169, 0x169
- Delphi, Pascal значение числа 361
- $000169
Дата и время
- 361-й день года
- 27 декабря
- 361-й день високосного года
- 26 декабря
- Конвертация UNIX timestamp 361 в дату и время
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
- Конвертация в IPv4 адрес Интернет
- 0.0.1.105
- 361 в Википедии:
- 361
Другие свойства числа
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/361
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x169
- Номер телефона
- 3-61
- Телефонный код страны
- +361
Цвет по числу 361, цветовая гамма
- html RGB цвет 361, 16-ричное значение
- #000169 — (0, 1, 105)
- HTML CSS код цвета #000169
- .color-mn { color: #000169; }
.color-bg { background-color: #000169; }
Цвет для данного числа 361
Здесь вы можете изменить составляющую цвета для данного числа 361 или цвета 000169:
Какова площадь 361? – Celebrity.
 fm
fmКод города Северной Америки 361 — это телефонный код штата Техас для номера в районе Корпус-Кристи. Он был создан до 13 февраля 1999 года в отличие от кода города 512.
Здесь, какой код города 361?
CORPUS CHRISTI, Техас — Код города Корпус-Кристи, 361, представляет собой один из семи кодов города Техаса, который вскоре должен будет перейти на 10-значный местный набор вместо обычного семизначного набора.
Соответственно, каков главный корень числа 361?
Интерактивные вопросы
| Правда | |
|---|---|
| √361 рационально. | TrueTrue – √, 361 рационально. |
| Квадратный корень из 361 равен 19 . | TrueTrue — квадратный корень из 361 равен 19. |
| Квадратный корень из 361 — это целое число, так как это не полный квадрат. | TrueTrue — Квадратный корень из 361 — это целое число, поскольку оно не является полным квадратом. |
Какой код города 361 в Канаде?
Код города 361 — это код города для Корпус-Кристи, Техас и прилегающие районы.
Следовательно, когда Корпус-Кристи изменил свой код города?
On 13 февраля 1999, код города 512 был уменьшен до его нынешнего размера, когда южная часть (включая Корпус-Кристи) стала 361. Чтобы предотвратить истощение к концу 2013 года, в июле 737 года был введен код города 512 в качестве наложения 2013.
Содержание
К какому региону принадлежит 347?Код города Нью-Йорка 347 является одним из трех основных кодов города, которые охватывают пять районов Нью-Йорка который включает Бронкс, Бруклин, Квинс, Статен-Айленд и несколько частей Манхэттена.
Какой код города 405 в США?Код города 405 обслуживает все или части 19 округов в центральной части штата, включая Оклахома-Сити, столица штата и самый густонаселенный город штата. Новый код города 572 будет обслуживать ту же географическую зону, которая в настоящее время обслуживается существующим кодом города 405.
361 — идеальный куб?361 — идеальный куб? Число 361 при разложении на простые множители дает 19 × 19. … Следовательно, кубический корень из 361 иррационален, поэтому 361 — не идеальный куб.
… Следовательно, кубический корень из 361 иррационален, поэтому 361 — не идеальный куб.
1128 — не идеальный квадрат.
Какими могут быть возможные квадраты 361?→ √361 = 19 = Единичная цифра 9 (Ответ.) Следовательно, возможная цифра единицы в квадратном корне из 361 равна 9 .
В каком округе находится Корпус-Кристи?Округ Нуэсес, Техас
| Округ Нуэсес | |
|---|---|
| Область | Техас |
| Основанный | 1847 |
| Назван для | Река Нуэсес |
| Seat | Корпус-Кристи |
Код города Северной Америки 956 — это телефонный код штата Техас для номеров в Браунсвилл, Макаллен, Ларедо и остров Саут-Падре области. Он был создан 25 мая 1997 года в отделении от кода города 210. Округа, обслуживаемые этим кодом города: Кэмерон, Идальго, Джим Хогг, Ла Саль, Старр, Уэбб, Уилласи и Сапата.
Округа, обслуживаемые этим кодом города: Кэмерон, Идальго, Джим Хогг, Ла Саль, Старр, Уэбб, Уилласи и Сапата.
Код города 281 охватывает юго-восточную часть. Техаса. Сюда входят Хьюстон и многие его пригороды и города.
Сколько почтовых индексов в Корпус-Кристи?Корпус-Кристи, штат Техас, охватывает 30 почтовых индексов
| Почтовый индекс | Тип | Район |
|---|---|---|
| 78418 | Стандарт | Орешки |
| 78419 | Стандарт | Орешки |
| 78426 | Почтовый ящик | Орешки |
| 78427 | Почтовый ящик | Орешки |
Коды зон 718, 347 и 929 — это телефонные коды в Североамериканском плане нумерации (NANP) для районы Нью-Йорка Город Бронкс, Бруклин, Квинс и Стейтен-Айленд, а также район Марбл-Хилл на Манхэттене.
В результате 917, 718, 646, 347 и даже 212 теперь могут подключаться к стационарному или сотовому телефону. … 917 стационарных телефонов являются общими, а 646 — в обе стороны, хотя 347 по-прежнему предназначены в основном для сотовых телефонов за пределами Манхэттена.
Когда начался код города 773?К середине 1990-х продолжающийся рост Чикаго и распространение сотовых телефонов и пейджеров сделали очевидным, что городу нужен новый код города. Было решено выделить весь город за пределами центра города под номером 773. Новый код города вступил в силу 12 октября 1996.
Что означает 405?Ошибка HTTP 405 указывает, что веб-браузер запросил доступ к одной из ваших страниц, и ваш веб-сервер распознал запрос. Однако сервер отклонил конкретный метод HTTP, который он использует. В результате ваш веб-браузер не может получить доступ к запрошенной веб-странице.
Какой код города 425 в Соединенных Штатах?Код города 425 — это код города штата Вашингтон, который включает северные и восточные пригороды Сиэтла. Восточный регион, расположенный к востоку от Сиэтла, известный под общим названием Истсайд, охватывает основные районы, такие как Белвью, Дюваль, Иссакуа, Киркленд, Мейпл-Вэлли, Редмонд и Рентон.
Восточный регион, расположенный к востоку от Сиэтла, известный под общим названием Истсайд, охватывает основные районы, такие как Белвью, Дюваль, Иссакуа, Киркленд, Мейпл-Вэлли, Редмонд и Рентон.
Код 408 в настоящее время включает Округ Санта-Клара к югу от Саннивейла и Купертино, а также небольшие части графств Аламеда, Санта-Крус и Станислав. Большая часть кода города 408 содержится в статистической зоне Сан-Хосе (MSA).
Является ли 325 идеальным квадратом?С 325 — не идеальный квадрат, квадратный корень из 325 — это десятичное число, а не целое число.
Почему 81 — идеальный квадрат?81 — идеальный квадрат. Потому что 9 * 9 = 81.
Какой куб равен 400?Разложение 400 на простые множители равно 2 × 2 × 2 × 2 × 5 × 5, следовательно, кубический корень 400 в его низшей радикальной форме выражается как 2 ∛50 .
…
Кубический корень 400.
| 1. | Что такое кубический корень из 400? |
|---|---|
| 3. | Является ли кубический корень из 400 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 400 |
1156 имеет корни 34, что является целым числом. Таким образом 1156 идеальный квадрат.
Сколько идеальных квадратов между 1 и 50?Ответ: Есть 7 идеальных квадратов от 1 до 50. Квадраты 1, 4, 9, 16, 25, 36 и 49.
1681 — это идеальный квадрат?1681 — это число, которое идеальный квадрат, потому что он имеет натуральное число в качестве квадратного корня. … Квадратный корень из 1681 равен либо +41, либо -41. 41 и -41 можно выразить как 41/1 и -41/1.
Последнее обновление: 15 дней назад — Авторов: 7 — Авторов: 5 — Ссылки: 47 интервью и постов; 9 Видео.
Узнайте все о своем любимом. знаменитости в Интервью со знаменитостями и не забудьте поделиться этим постом!
знаменитости в Интервью со знаменитостями и не забудьте поделиться этим постом!
Квадратный корень из 361 — Как найти квадратный корень из 361?
LearnPracticeDownload
Календарь бахаи состоит из 19 месяцев по 19 дней в каждом. Следовательно, количество дней в году в этом солнечном календаре составляет 19 × 19 = 361. Нахождение квадратного корня — это операция, обратная возведению числа в квадрат. В этом мини-уроке давайте научимся вычислять квадратный корень из 361 и выражать квадратный корень из 361 в простейшей подкоренной форме.
- Квадратный корень из 361 : √ 361 = 19
- Квадрат 361: 361 2 = 130 321
| 1. | Что такое квадратный корень из 361? |
| 2. | Является ли квадратный корень из 361 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 361? |
4. | Нестандартное мышление! |
| 5. | Важные примечания о квадратном корне из 361 |
| 6. | Часто задаваемые вопросы о квадратном корне из 361 |
Что такое квадратный корень из 361?
- Квадратный корень из 361 равен 361, возведенному в степень ½. 361 ½ = (число × число) ½ = (19 × 19) ½ = (19 2 ) ½ = 19
- + 19 × +19 = √ 361 и — 19 × — 19 = √ 361
- √ 361 = ± 19
Является ли квадратный корень из 361 рациональным или иррациональным?
Квадратный корень из 361 является совершенным квадратным числом. Таким образом, это целое число, которое можно выразить как рациональное число формы p/q. Квадратный корень из 361 — это рациональное число .
Как найти квадратный корень из 361?
Квадратный корень из любого числа можно вычислить разными способами. Вот некоторые из них: метод простой факторизации, метод повторного вычитания и метод длинного деления.
Вот некоторые из них: метод простой факторизации, метод повторного вычитания и метод длинного деления.
Квадратный корень из 361 методом многократного вычитания
Любое совершенное квадратное число представляет собой сумму последовательных нечетных чисел. Поскольку 361 — это идеальный квадрат, это сумма последовательных нечетных чисел. Таким образом, повторным вычитанием мы можем убедиться, что квадратный корень из 361 равен 19.
- 361 — 1 = 360
- 360 — 3 = 357
- 357 — 5 = 352
- 352 — 7 = 345
- 345 — 9 = 336
- 336 — 11 = 325
- 325 — 13 = 312
- 312 — 15 = 297
- 297- 17 = 280
- 280 — 19 = 261
- 261 — 21 = 240
- 240 — 23 = 217
- 217 — 25 = 202
- 202 — 27 = 175
- 175 — 29 = 146
- 146 — 31 = 115
- 115 — 33 = 82
- 82 — 35 = 37
- 37- 37 = 0
Повторное вычитание мы сделали 19 раз. Таким образом √ 361 = 19.
Таким образом √ 361 = 19.
Квадратный корень из 361 методом деления в длину
Давайте посмотрим, как найти корень квадратный из 361 методом деления в длину. Вот желаемые шаги, которые необходимо выполнить.
- Запишите 361 как 3 61. Разделите 3 на 1 и получите остаток как 2. Сократите пару 61. У нас есть 2 61, которые нужно разделить сейчас.
- Умножьте частное на 2 и получите 2 x в качестве нового делителя.
- Найдите число вместо x такое, что 2 x × x дает 61 или меньше. Находим 2 9 × 9 равно 261. Остаток получаем как 0, .
- Таким образом, √ 361 = 19,
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 169
- Квадратный корень из 289
- Квадратный корень из 324
- Квадратный корень из 81
- Квадратный корень из 225
Think Tank
- Знаете ли вы, что сумма первых 19 нечетных чисел (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 +19 + 21 + 23 + 25 + 27 + 29 + 31 + 33 + 35 + 37) = 361? Вы можете найти эту сумму без фактического сложения.
 Можете ли вы попробовать это с любым другим идеальным квадратом и убедиться в этом сами?
Можете ли вы попробовать это с любым другим идеальным квадратом и убедиться в этом сами?
Важные примечания
- Квадратный корень из 361 равен 19.
- 361 — идеальный квадрат.
- √361 — рациональное число.
Пример 1 : Риа купила 361 саженец цветов, чтобы посадить их на квадратную грядку. Сколько рядов и столбцов рассады будет на квадратной грядке?
Решение:
Площадь квадратной кровати = строки × столбцы
Площадь квадратной кровати = ряды × ряды
Строки 2 = площадь = 361
Извлекая квадратный корень из обеих сторон, мы получаем
. (строки 2 ) ½ = (361) ½
Ряды = √361 = 19
Таким образом, рассада высаживается в 19 рядов и 19 столбцов.Пример 2: Марк выпекает столько тортов, сколько дней в месяце.
 Если он испек всего 361 пирог, то сколько пирогов он испек и за сколько дней?
Если он испек всего 361 пирог, то сколько пирогов он испек и за сколько дней?Решение:
тортов в день × дни = общее количество тортов
Количество тортов в день = количество использованных дней = n
п × п = 361
п 2 = 361
n = √361 = 19
Таким образом, Марку потребовалось 19 дней, чтобы испечь по 19 тортов каждый день, и всего он испек 361 торт.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 361
Что такое квадратный корень из 361?
Квадратный корень из 361 равен ± 19.
Чему равен отрицательный квадратный корень из 361?
Квадратный корень из 361 равен отрицательному числу 19.
361 — это квадратный корень из какого числа?
361 — это квадратный корень из 130 321.
Является ли квадратный корень из 361 рациональным числом?
Квадратный корень из 361 является рациональным числом, поскольку значение √361 равно 19. 19 выражается как p/q = 19/1.
Как найти квадратный корень из √361?
Если число представляет собой точный квадрат, из него легко извлечь квадратный корень, используя операцию, обратную операции возведения в квадрат. √361 – точный квадрат. √361 можно вычислить, используя метод деления на простые множители или метод повторного вычитания.
Рабочие листы по математике и визуальный учебный план
Квадратный корень из 361 (√361)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 361. Мы начнем с определения, а затем ответим на некоторые общие вопросы.
вопросы о квадратном корне из 361. Затем мы покажем вам различные способы вычисления квадратного корня из 361 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Мы начнем с определения, а затем ответим на некоторые общие вопросы.
вопросы о квадратном корне из 361. Затем мы покажем вам различные способы вычисления квадратного корня из 361 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Квадратный корень из 361 определение
Квадратный корень из 361 в математической форме записывается с таким знаком радикала, как √361. Мы называем это квадратным корнем из 361 в радикальной форме.
Квадратный корень из 361 — это величина (q), которая при умножении сама на себя будет равна 361.
√361 = q × q = q 2
Является ли число 361 полным квадратом?
361 является полным квадратом, если квадратный корень из 361 равен целому числу. Как мы рассчитали дальше
внизу на этой странице квадратный корень из 361 — это целое число.
361 — правильный квадрат.
Является ли квадратный корень из 361 рациональным или иррациональным?
Квадратный корень из 361 является рациональным числом, если 361 является полным квадратом. Это иррациональное число, если оно не является полным квадратом.
Поскольку 361 — совершенный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 361?» не будет иметь десятичных знаков.
√361 является рациональным числом
Можно ли упростить квадратный корень из 361?
Квадратный корень из полного квадрата можно упростить, потому что квадратный корень из полного квадрата будет равен целому числу:
√361 = 19
Как вычислить квадратный корень из 361 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 361 — воспользоваться калькулятором!
Просто введите 361, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
√361 = 19
Как вычислить квадратный корень из 361 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT(361) в ячейку, чтобы получить квадратный корень из 361.
Ниже приведен результат, который мы получили:
SQRT(361) = 19
Чему равен квадратный корень из 361, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробным показателем степени. Квадратный корень из 361 не является исключением. Вот правило и ответ
на «квадратный корень из 361, преобразованный в основание с показателем степени?»:
√b = b ½
√361 = 361 ½
Как найти квадратный корень из 361 методом деления в длину метод длинного деления. это потерянный
искусство того, как они вычисляли квадратный корень из 361 вручную до того, как были изобретены современные технологии.
это потерянный
искусство того, как они вычисляли квадратный корень из 361 вручную до того, как были изобретены современные технологии.
Шаг 1)
Наберите 361 парами по две цифры справа налево:
Шаг 2)
Начиная с первого набора: самый большой совершенный квадрат, меньший или равный 3, равен 1, а квадратный корень из 1 равен 1. Поэтому поместите 1 сверху и 1 снизу следующим образом:
| 1 | ||||
| 03 | 61 | |||
| 1 | ||||
Step 3)
Calculate 3 minus 1 and put the difference below. Затем переместитесь вниз к следующему набору чисел.
| 1 | ||||
| 03 | 61 | |||
| 1 | ||||
| 2 | 61 | |||
Шаг 4)
Удвойте число, выделенное зеленым сверху: 1 × 2 = 2. Затем используйте 2 и нижнее число, чтобы решить эту задачу:
Затем используйте 2 и нижнее число, чтобы решить эту задачу:
2? × ? ≤ 261
Знаки вопроса «пробел» и такие же «пробел». Методом проб и ошибок мы нашли, что наибольшее число, которое может быть пустым, равно 9.. Замените вопросительные знаки в задаче на 9, чтобы получить:
29 × 9 = 261.
Теперь введите 9 сверху и 261 снизу:
| 1 | 9 302 9304 9 9 9||||
| 03 | 61 | |||
| 1 | ||||
| 2 | 61 | |||
| 2 | 61 | |||
Разница между двумя нижними числами равна нулю, поэтому все готово! Ответ — зеленые цифры сверху. Еще раз, квадратный корень из
361 равно 19.
Еще раз, квадратный корень из
361 равно 19.
Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 361 на этой странице.
Примечания
Помните, что отрицательное значение, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 361 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 362
Вот следующее число в нашем списке, о котором у нас есть такая же подробная информация о квадратном корне.
Авторское право | Политика конфиденциальности | Отказ от ответственности | Контакт
Квадратный корень из 361
Sqrt(361).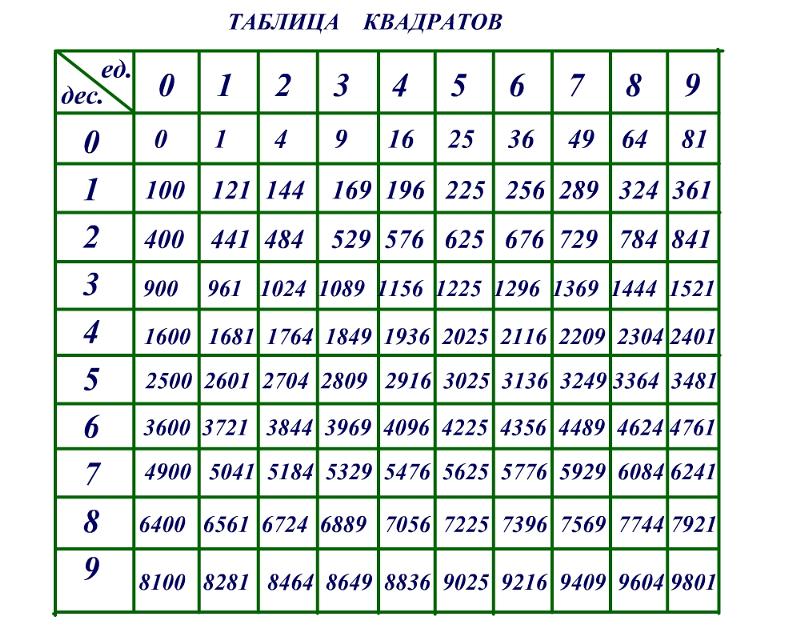 Найдите квадратный корень из 361 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 361 или что такое квадратный корень из 361?
Найдите квадратный корень из 361 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 361 или что такое квадратный корень из 361?
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа ‘x’ – это число y такое, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 19 — это квадратный корень из 361, потому что 19 2 = 19•19 = 361, —19 — это квадратный корень из 361, потому что (—19) 2 = (—19)•(—19) = 361. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как радикальный знак или основание.
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 округляются до тысячных.
| номер | квадрат | квадрат корень |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1.414 |
| 1.732 | ||
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.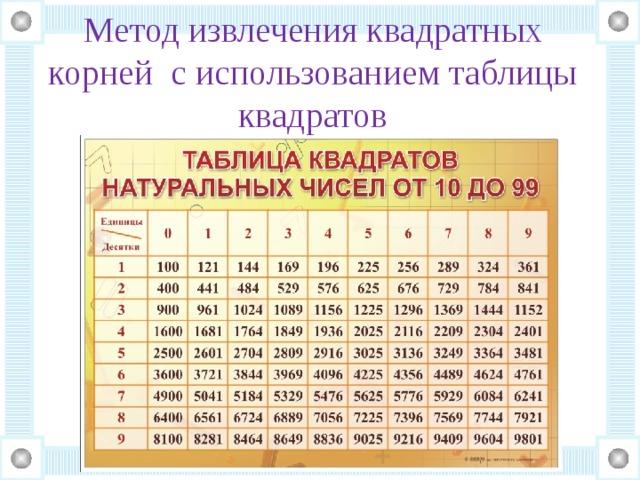 000 000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| номер | квадрат | квадрат корень |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.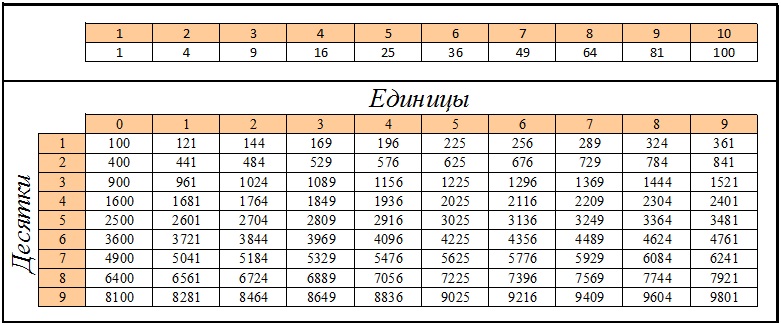 568 568 |
| 32 | 1024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6. 856 856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7.000 |
| 50 | 2,500 | 7.071 |
| number | квадрат | квадрат корень |
|---|---|---|
| 51 | 2 601 | 7.141 |
| 52 | 2 704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7. 874 874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5625 | 8.660 |
| число | квадрат | квадрат корень |
|---|---|---|
| 76 | 5,776 | 8. 718 718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8,944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9. 592 592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10 000 | 10.000 |
Квадратный корень значений около 361
| Номер | SQRT |
|---|---|
| 357 | 990|
| 357 | 9 990|
| 357 | 9 990|
| 357 | 9 9|
| 358 | 18.921 |
| 359 | 18.947 |
| 360 | 18.974 |
| 362 | 19.026 |
| 363 | 19. 053 053 |
| 364 | 19.079 |
| 365 | 19.105 |
| 366 | 19.131 |
Реклама
Как найти квадратный корень из 361Квадрат 361 :
- В математике найти квадрат любого числа в основном легко, потому что, когда мы умножаем одно и то же число на себя, мы получаем квадрат этого числа.
Например:
- Предположим, нам нужно найти квадрат любого числа, скажем, X , затем мы умножаем X 9.0009 сам по себе, то есть X , и мы получим его квадрат как Y . Это можно записать как (X) 2 = X*X= Y
- Аналогичным образом находим квадрат числа 19 .
- Чтобы найти квадрат 19, мы умножаем 19 на само число, то есть на 19, и запишем это следующим образом.

- (361) 2 = 19*19= 361
Квадратный корень из 361:
- Теперь в обратном порядке, если нам нужно найти квадратный корень из Д . Квадратный корень из Y — это единственное значение, которое при умножении само на себя дает значение Y .
- Это означает, что √ Y = √(X*X) = X
Где √ — символ, названный радикалом.
Например:
- Квадратный корень из 19 можно записать как
√361 = √ (19*19) = 19
Где √ – это символ, который называется подкоренным знаком.
- Короче говоря, мы помним квадрат 19и квадратный корень из 361 как
Примечание:
- Каждое положительное действительное число имеет два корня.
- Квадрат любого отрицательного числа всегда является положительным числом.

Например:
- 361 — положительный совершенный квадрат, который также имеет два корня +19 и -19.
- Но в основном берется положительное значение квадратного корня, которое называется главным квадратным корнем или неотрицательным квадратным корнем.
- Следовательно, √361 = √(-19)*(-19) = -19 и √361 = √(19)*(19) = 19
Аналогично,
- (-19)*(-19) = (-19) 2 = +361 и (+19)*(+19) = (+19)7 2 =361
Методы нахождения квадратного корня из полного квадрата, например 361:
Существует множество методов нахождения квадратного корня из полного квадрата, из которых мы подробно рассмотрим следующий метод.
- Метод повторного вычитания
- Метод простой факторизации
- В методе многократного вычитания мы должны вычесть последовательные нечетные числа, начиная с 1, из совершенного квадратного числа, квадратный корень которого мы должны найти.

- эл. чтобы найти квадратный корень из 361, сначала мы вычитаем из него 1. 361 – 1 = 360
- Тогда следующее нечетное число равно 3, поэтому мы должны вычесть его из 360. 360–3 = 357
- Таким образом, мы вычитаем последовательные нечетные числа из соответствующих значений, полученных после непрерывного вычитания, пока не получим окончательное значение 0.
- И значение количества нечетных чисел, необходимых для получения 0, является искомым квадратным корнем.
Например:
- Квадратный корень из 361 находим методом многократного вычитания следующим образом:
361– 1 = 360
360– 3 = 357
357– 5 = 352
352– 7 = 345
345– 9 = 336
336– 11 = 325
325 – 13 = 312
312– 15 = 297
297 — 17 = 280
280 — 19 = 261
261 — 21 = 240
240 — 23 = 217
217 — 25 = 192
192 — 27 = 165
165 — 29 . = 136
= 136
136 – 31 = 105
105 – 33 = 72
72 – 35 = 37
37 37 = 0
- Таким образом, здесь используются нечетные числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35 и 37, которые в цифрах равны 19.
- Следовательно, квадратный корень из 361 методом многократного вычитания равен 19.
- В методе простой факторизации мы должны разделить идеальное квадратное число, квадратный корень которого мы должны найти, на простое число, начиная с 2, 3, 5… и так далее, пока мы не получим остаток как 1.
- Сначала мы должны разделить на простое число 2, если это число не делится на 2, тогда мы должны взять следующее простое число, то есть 3, и процесс будет продолжаться до тех пор, пока мы не получим остаток как 1.
- Наконец, мы должны составить пары простых чисел, взятых в форме умножения, а затем мы должны извлечь из них квадратный корень.

Например:
- Ниже описан процесс нахождения квадратного корня из 81 методом простой факторизации. 92
И 361= (19*19)
- Извлекая квадратный корень с обеих сторон, мы получаем
√361 = √(19*19)= √(19*19)
√361 = 19
- Таким образом, мы нашли квадратный корень из 361 как 19.
Вопросы с несколькими вариантами ответов:1) 361 ———тип числа
а) простое
3 0составное0002 в)четноег)все эти
Ответ: б) составное
2) 361 делится на ———— число.
а) 4
б) 18
в) 19
г) 20
а) Составное число
б) Простое число
в) Четное число
г) Ни одно из этих
Ответ: б) простое число
Обновлено: 12 марта 2022 г.
 — 15:53
— 15:53 Квадратный корень из 361 пошаговое решение
ЦитатыПожалуйста, введите реальное число: Результат квадратного корня: Вот ответ на такие вопросы, как: Квадратный корень из 361 пошаговое решение | √361 или чему равен квадратный корень из 361?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа. См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя.
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число x, такое что x 2 = a, другими словами, число x, квадрат которого равен a. Например, 19 — это квадратный корень из 361, потому что 19 2 = 19.•19 = 361, -19 — это квадратный корень из 361, потому что (-19) 2 = (-19)•(-19) = 361.

Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до ближайшей тысячной.
3нет нет 2 √ 1 1 1.000 2 4 1.414 3 9 1.732 4 16 2.000 5 25 2.236 6 36 2.449 7 49 2.646 8 64 2.828 9 81 3.000 10 100 3.162 11 121 3.317 12 144 3.464 13 169 3.  606
60614 196 3.742 15 225 3.873 16 256 4.000 17 289 4.123 18 324 4.243 19 361 4.359 20 400 4.472 21 441 4.583 22 484 4.690 23 529 4.796 24 576 4,899 25 625 5,000 нет нет 2 √ 26 676 5.099 27 729 5.196 28 784 5.  292
29229 841 5.385 30 900 5.477 31 961 5.568 32 1,024 5.657 33 1,089 5.745 34 1,156 5.831 35 1,225 5.916 36 1,296 6.000 37 1,369 6.083 38 1,444 6.164 39 1,521 6.245 40 1,600 6.325 41 1,681 6.403 42 1,764 6.481 43 1,849 6.557 44 1,936 6.  633
63345 2,025 6.708 46 2,116 6.782 47 2,209 6.856 48 2,304 6.928 49 2,401 7.000 50 2,500 7.071 нет нет 2 √ 51 2,601 7.141 52 2,704 7.211 53 2,809 7.280 54 2,916 7.348 55 3,025 7.416 56 3,136 7.483 57 3,249 7.550 58 3,364 7,616 59 3,481 7,681 60 3600 7,746624 4
4
4
4
4
 0024
00243,721 7.810 62 3,844 7.874 63 3,969 7.937 64 4,096 8.000 65 4,225 8.062 66 4,356 8.124 67 4,489 8.185 68 4,624 8.246 69 4,761 8.307 70 4,900 8.367 71 5,041 8.426 72 5,184 8.485 73 5,329 8.544 74 5,476 8.602 75 5,625 8.660 нет нет 2 √ 76 5,776 8.  718
71877 5,929 8.775 78 6,084 8.832 79 6,241 8.888 80 6,400 8,944 81 6,561 9,000 82 6,724 9.055 83 6,889 9.110 84 7,056 9.165 85 7,225 9.220 86 7,396 9.274 87 7,569 9.327 88 7,744 9.381 89 7,921 9.434 90 8,100 9.487 91 8,281 9.539 92 8,464 9. 

 ru/data/moduleImages/QRCodes/361/8a7af2e597146fa56019d51d6d447eb3.png
ru/data/moduleImages/QRCodes/361/8a7af2e597146fa56019d51d6d447eb3.png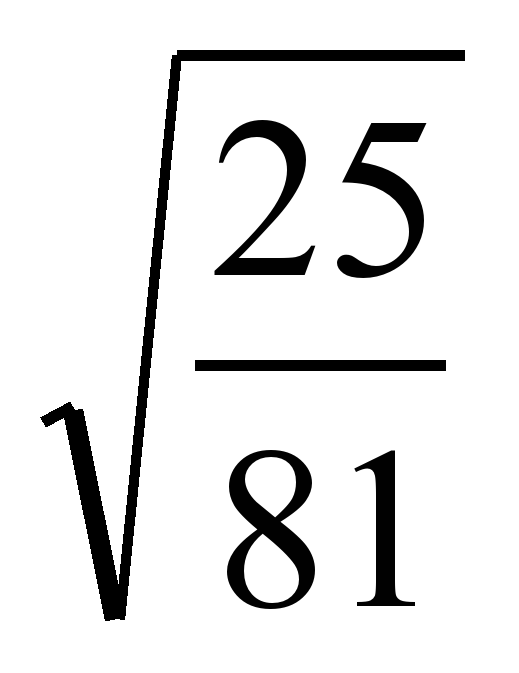 8888779583329
8888779583329
 5
5 0174524064
0174524064 11, GOST R 34.11-94, GOST(361)
11, GOST R 34.11-94, GOST(361) Можете ли вы попробовать это с любым другим идеальным квадратом и убедиться в этом сами?
Можете ли вы попробовать это с любым другим идеальным квадратом и убедиться в этом сами?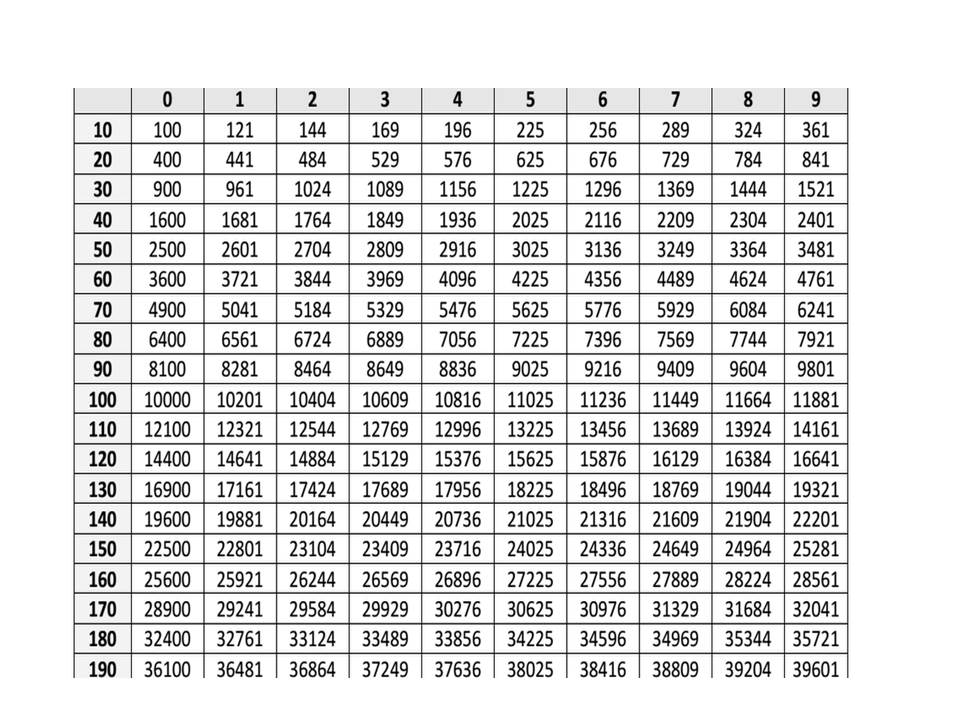 Если он испек всего 361 пирог, то сколько пирогов он испек и за сколько дней?
Если он испек всего 361 пирог, то сколько пирогов он испек и за сколько дней?