Деление дробей (п.6).
Правило | Примеры | ||
1.Представить в виде произведения первой дроби и перевернутой второй дроби. | |||
2. Выполнить умножение получившихся дробей. | |||
3. Записать ответ. | |||
Задания: Выполните деление: | |||
1) 2) 3) 4) 5) | |||
1) 2) 3) 4) 5) | |||
1) 2) 3) 4) 5) | |||
Коррекционная карточка 8 класс:
Квадратный корень из произведения и частого.
 Произведение и частное корней (п.15).
Произведение и частное корней (п.15).Правило | Примеры |
Задания: Найдите значение выражения: | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
Квадратный корень из степени(п.
 16).
16).Правило | Примеры |
частный случай | – не имеет смысла, т.к.–2<0 (–2)9<0 ,т.к с2 всегда положительно если x>0, то если x<0, то |
Задания: Упростите выражение: | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | |
Коррекционная карточка 8 класс:
Возведение
квадратного корня в четную степень
(п.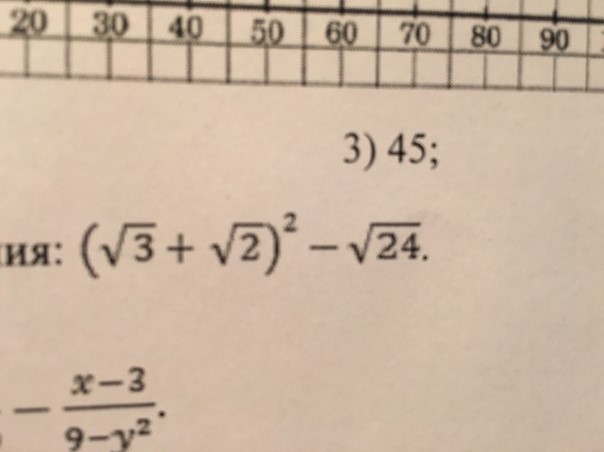 11).
11).
Правило | Примеры |
частный случай | |
Задания: Упростите выражение: | |
1) 2) 3) 4) 5) 6) 7) 8) 9) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) | |
1) 2) 3) 4) 5) 6) 7) 8) 9) | |
Коррекционная карточка 8 класс:
Решение уравнения х2=а (п.12).
| Правило | Примеры | ||
х2=−9 | х2=16 | х2−27=0 | |
Если а>0, то х= Если а=0, то х=0 Если а<0, то решений нет | −9<0 нет решений | х= х = 4 | х2=27 х= |
Коррекционная карточка 8 класс:
 17).
17).Правило | Примеры | ||
1. Разложить на множители подкоренное выражение так, чтобы были множители, из которых можно извлечь корень. | |||
2. К получившемуся выражению применить свойство | |||
3. Вычислить значения корней или воспользоваться свойством частный случай | Так как p стоит под знаком корня p0 | ||
Запись решения: | |||
Коррекционная карточка 8 класс:
Арифметический корень из числа.
 Корень n-ой степени: определения, обозначение, примеры
Корень n-ой степени: определения, обозначение, примерыПришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0
до 99
включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5
, а квадратный корень из знаменателя равен 13
. Тогда . На этом извлечение корня из обыкновенной дроби 25/169
завершено.
Тогда . На этом извлечение корня из обыкновенной дроби 25/169
завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо .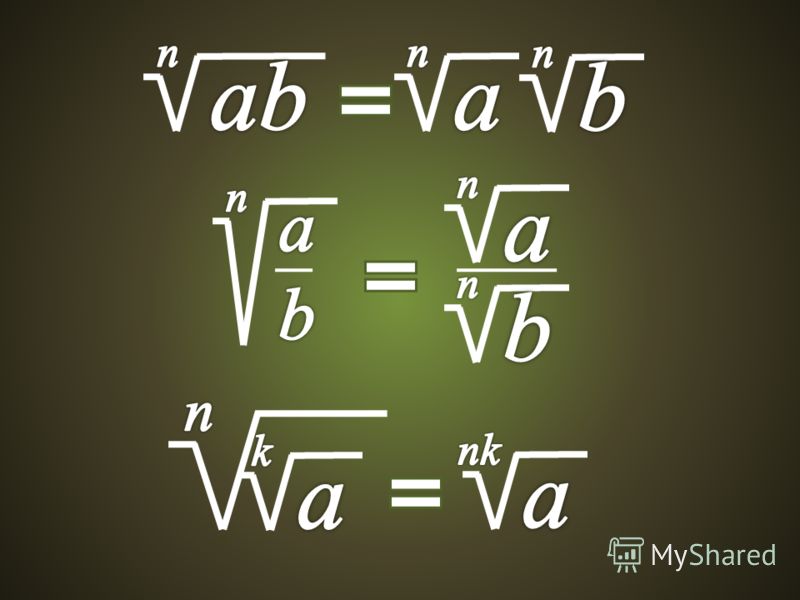 Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n
-ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Среди множества знаний, которые являются признаком грамотности, на первом месте стоит азбука. Следующим, таким же «знаковым» элементом, являются навыки сложения-умножения и, примыкающие к ним, но обратные по смыслу, арифметические операции вычитания-деления. Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Сначала уточним, что же это такое — квадратный корень числа. Вообще говоря, «извлечь корень из числа» означает выполнить арифметическое действие противоположное возведению в степень — вот вам и единство противоположностей в жизненном приложении. допустим, квадрат, это умножение числа на самое себя, т.е., как учили в школе, Х * Х = А или в другой записи Х2 = А, а словами — «Х в квадрате равняется А». Тогда обратная задача звучит так: квадратный корень числа А, представляет собой число Х, которое будучи возведено в квадрат равно А.
Извлекаем квадратный корень
Из школьного курса арифметики известны способы вычислений «в столбик», которые помогают выполнить любые подсчеты с применением первых четырех арифметических действий. Увы… Для квадратных, и не только квадратных, корней таких алгоритмов не существует. А в таком случае, как извлечь квадратный корень без калькулятора? Исходя из определения квадратного корня вывод один — необходимо подбирать значение результата последовательным перебором чисел, квадрат которых приближается к значению подкоренного выражения. Только и всего! Не успеет пройти час-другой, как можно посчитать, используя хорошо известный прием умножения в «столбик», любой квадратный корень. При наличии навыков для этого достаточно пары минут. Даже не совсем продвинутый пользователь калькулятора или ПК делает это одним махом — прогресс.
Увы… Для квадратных, и не только квадратных, корней таких алгоритмов не существует. А в таком случае, как извлечь квадратный корень без калькулятора? Исходя из определения квадратного корня вывод один — необходимо подбирать значение результата последовательным перебором чисел, квадрат которых приближается к значению подкоренного выражения. Только и всего! Не успеет пройти час-другой, как можно посчитать, используя хорошо известный прием умножения в «столбик», любой квадратный корень. При наличии навыков для этого достаточно пары минут. Даже не совсем продвинутый пользователь калькулятора или ПК делает это одним махом — прогресс.
А если серьезно, то вычисление квадратного корня часто выполняют, используя прием «артиллерийской вилки»: сначала берут число, квадрат которого, примерно, соответствует подкоренному выражению. Лучше, если «наш квадрат» чуть меньше этого выражения. Затем корректируют число по собственному умению-разумению, например, умножают на два, и… вновь возводят в квадрат. Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Да, чуть не забыл, чтобы подтвердить свою возросшую грамотность, вычислим квадратный корень ранее указанного числа 12345. Делаем пошагово:
1. Возьмем, чисто интуитивно, Х=100. Подсчитаем: Х * Х = 10000. Интуиция на высоте — результат меньше 12345.
2. Попробуем, тоже чисто интуитивно, Х = 120. Тогда: Х * Х = 14400.И опять с интуицией порядок — результат больше 12345.
3. Выше получена «вилка» 100 и 120. Выберем новые числа — 110 и 115. Получаем, соответственно, 12100 и 13225 — вилка сужается.
4. Пробуем на «авось» Х=111. Получаем Х * Х = 12321. Это число уже достаточно близко к 12345. В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
Совсем немного истории…
Додумались до использования квадратных корней еще пифагорейцы, ученики школы и последователи Пифагора, за 800 лет до н.э. и тут же, «нарвались» на новые открытия в области чисел. И откуда что взялось?
1. Решение задачи с извлечением корня, дает результат в виде чисел нового класса. Их назвали иррациональными, иначе говоря, «неразумными», т.к. они не записываются законченным числом. Самый классический пример такого рода — квадратный корень из 2. Этот случай соответствует вычислению диагонали квадрата со стороной равной 1 — вот оно, влияние школы Пифагора. Оказалось, что у треугольника с вполне конкретным единичным размером сторон, гипотенуза имеет размер, который выражается числом, у которого «нет конца». Так в математике появились
2. Известно, что Оказалось, что эта математическая операция содержит еще один подвох — извлекая корень, мы не знаем, квадратом какого числа, положительного или отрицательного, является подкоренное выражение. Эта неопределенность, двойной результат от одной операции, так и записывается.
Эта неопределенность, двойной результат от одной операции, так и записывается.
Изучение связанных с этим явлением проблем стало направлением в математике под названием теория комплексной переменной, имеющим большое практическое значение в математической физике.
Любопытно, что обозначение корня — радикал — применил в своей «Универсальной арифметике» все тот же вездесущий И. Ньютон, а в точности современный вид записи корня известен с 1690 года из книги француза Ролля «Руководство алгебры».
Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а .
Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.
Арифметический квадратный корень из числа а обозначается так: √а.
Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.
Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х , мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.
Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Квадратный корень из дроби
Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .
Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .
Так как и , то равенство верно. Итак, .
Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .
Так как √а ≥0 и √b > 0, то .
По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.
Вычислить , по доказанной теореме .
Второй пример: Доказать, что , если а ≤ 0, b .
Еще примерчик: Вычислить .
.
Преобразование квадратных корней
Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;
Вычислить при х = 2. Непосредственная подстановка х = 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.
Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.
Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.

Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.

Корень степени N
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)
У вас тоже так? Читайте дальше — и всё поймётеМногие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt[4]{a}$ и даже $\sqrt[116]{a}$ ) и нечётной степени (всякие $\sqrt[3]{a}$, $\sqrt[7]{a}$ и т.
{2}}=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
\[\begin{align} & \sqrt[3]{27}=3; \\ & \sqrt[3]{-64}=-4; \\ & \sqrt[3]{343}=7. \\ \end{align}\]
Ну, и парочка «экзотических примеров»:
\[\begin{align} & \sqrt[4]{81}=3; \\ & \sqrt[5]{-32}=-2. \\ \end{align}\]
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. {n}}=a\]
{n}}=a\]
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
\[\sqrt{2}=1,414213562…\]
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
Пример.
\[\begin{align} & \sqrt{2+\sqrt[3]{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt[3]{\sqrt[5]{-32}}=\sqrt[3]{-2}\approx -1,2599… \\ \end{align}\]
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}=4\]
{2}}=4\]
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
\[\sqrt{4}=2\]
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
- Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
- Из отрицательных чисел корень с чётным $n$ вообще не извлекается.
 {3}}$:Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
{3}}$:Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числаИз этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке.
 Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок.
 {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
\[\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}\]
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
\[\begin{align} & \sqrt[3]{-8}=-\sqrt[3]{8}=-2; \\ & \sqrt[3]{-27}\cdot \sqrt[5]{-32}=-\sqrt[3]{27}\cdot \left( -\sqrt[5]{32} \right)= \\ & =\sqrt[3]{27}\cdot \sqrt[5]{32}= \\ & =3\cdot 2=6.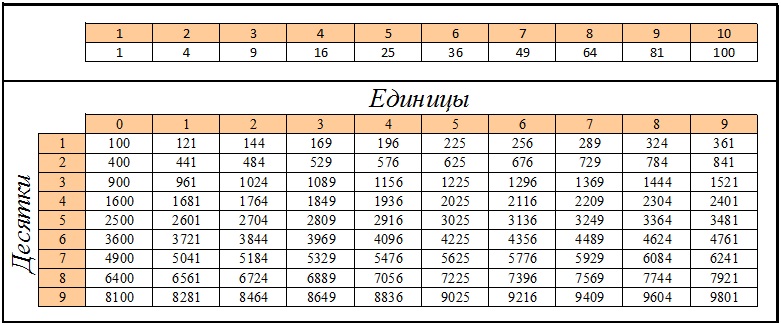 \end{align}\]
\end{align}\]
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.
{n}}=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
Область поиска арифметического корня — неотрицательные числаКак видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
{2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]
{n}}=a \right. \right\}\]
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt[3]{-27}};\quad \overline{\sqrt[4]{-16}}.
\]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt[3]{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt[4]{-16}}=\varnothing \]
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt[4]{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются.
Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)
Смотрите также:
- Умножение корней n-й степени
- Свойства арифметического квадратного корня
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Тест по методу интервалов для строгих неравенств
- Вебинар по задачам 18: модуль и окружности
- Решение задач на движение по воде
Извлечение квадратного корня в столбик на бумаге
Сегодня калькуляторы доступны повсеместно, и операцию извлечения корня так и подмывает выполнить на каком-нибудь устройстве. Но вычисляя корень на бумаге ученики используют и повторяют весь устный и письменный счёт, квадраты чисел, таблицу умножения. Рекомендуем учителю или родителю возводить в квадрат трёхзначные числа, и ученику раз в неделю или месяц вычислять корни.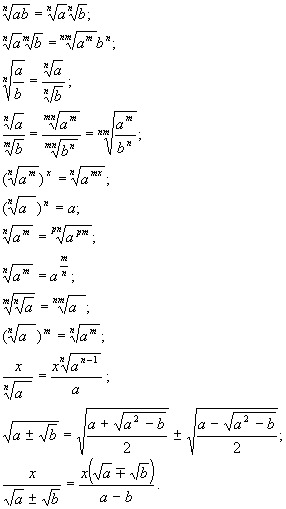 В конце каждого примера ученика ждёт автоматическая подсказка: если выше допущена хоть одна ошибка, то корень не будет извлекаться нацело. А если в остатке получился ноль, значит строгая дисциплина при вычислении корня была соблюдена полностью. Чтобы вы могли запомнить не только пример, а сам метод, который иллюстрируется примерами — мы разобрали целых три примера.
В конце каждого примера ученика ждёт автоматическая подсказка: если выше допущена хоть одна ошибка, то корень не будет извлекаться нацело. А если в остатке получился ноль, значит строгая дисциплина при вычислении корня была соблюдена полностью. Чтобы вы могли запомнить не только пример, а сам метод, который иллюстрируется примерами — мы разобрали целых три примера.
Извлечение квадратного корня из целых чисел. Пример 1.
Чтобы извлечь квадратный корень из целого числа мы будем циклично предпринимать одну и ту же последовательность действий: Подбери, Занеси, Вычти, Снеси, Удвой, Припиши. Сокращённо ПЗВ СУП — для запоминания: ПоЗоВи {гостей есть} СУП.
Пример 1: 763876.
Число разделяем на грани (по два разряда) от запятой: 763876. В числе три грани — значит в корне будет три разряда. Сначала старшая грань 76.
Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был меньше, чем 76. Это число 8 (т.к. 8 × 8 = 64, а 9 × 9 = уже 81, то есть > 76). Заносим 8 в ответ — это старший разряд ответа (сотни).
Вычитаем 64 из 76 — остаётся 12.
Сносим к 12-ти следующую грань — 38. Получается 1238.
Удваиваем то что в ответе — восьмёрку. Получается 16 — запишем 16 слева от 1238.
Приписываем к 16 справа коробочку для ещё одного разряда.
Заносим 8 в ответ — это старший разряд ответа (сотни).
Вычитаем 64 из 76 — остаётся 12.
Сносим к 12-ти следующую грань — 38. Получается 1238.
Удваиваем то что в ответе — восьмёрку. Получается 16 — запишем 16 слева от 1238.
Приписываем к 16 справа коробочку для ещё одного разряда.
Снова
Подбираем наибольшее число от 1 до 9 такое, чтоб 16# × # было не больше, чем 1238. Это число 7 (т.к. 166 × 6 = 996 < 1238, 167 × 7 = 1169 < 1238, а 168 × 8 = 1344, то есть уже > 1238). Заносим 7 в ответ — это следующий разряд ответа (десятки). Вычитаем 167 × 7 из 1238 — остаётся 69. Сносим к 69-ти следующую грань — 76. Получается 6976. Удваиваем то, что в ответе — 87. Получается 174 — запишем 174 слева от 6976. Приписываем к 174 справа коробочку для ещё одного разряда.
Снова
Подбираем наибольшее число от 1 до 9 такое, чтоб 174# × # было не больше, чем 6976. Это число 4 (т.к. 1743 × 3 = 5229, 1744 × 4 = 6976, а 1745 × 5 = 8725, то есть уже > 6976).
Заносим четвёрку в ответ — это будет разряд единиц. Вычитаем 1744 × 4 из 6976 — остаётся ноль.
Вычитаем 1744 × 4 из 6976 — остаётся ноль.
Значит, квадратный корень из данного числа 763876 — число 874.
Пример 2: 79524.
Число разделяем на грани (по два разряда) от запятой: 079524. В числе три грани — значит, в корне будет три разряда. Старшую грань дополнили ноликом (и стало 07). Вот сначала направляем внимание на старшую грань 07.
Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был меньше, чем 7. Это число 2 (т.к. 1 × 1 = 1 < 7, 2 × 2 = 4 < 7, а 3 × 3 = 9, а это уже > 7). Заносим 2 в ответ — это старший разряд ответа (сотни). Вычитаем 4 из 07 — остаётся 3. Сносим к 3 следующую грань — 95. Получается 395. Удваиваем то, что в ответе — двойку. Получается 4. Запишем 4 слева от 395. Припишем к 4 справа коробочку для ещё одного разряда.
Подбираем наибольшее число от 1 до 9 такое, чтоб 4# × # было не больше, чем 395. Это число 8 (т.к. 47 × 7 = 329 < 395, 48 × 8 = 384 < 395, а 49 × 9 = 441, то есть уже > 395)
Заносим 8 в ответ — это будет разряд десятков. Вычитаем (48 × 8 = ) 384 из 395 — остаётся 11.
Сносим к 11 следующую грань — 24. Получается 1124.
Удваиваем то, что в ответе — 28. Получается 56. Запишем 56 слева от 1124.
Приписываем к 56 справа коробочку для ещё одного разряда.
Вычитаем (48 × 8 = ) 384 из 395 — остаётся 11.
Сносим к 11 следующую грань — 24. Получается 1124.
Удваиваем то, что в ответе — 28. Получается 56. Запишем 56 слева от 1124.
Приписываем к 56 справа коробочку для ещё одного разряда.
Подбираем наибольшее число от 1 до 9 такое, чтоб 56# × # было не больше, чем 1124. Это число 2 (т.к. 561 × 1 = 561 < 1124, 562 × 2 = 1124, 563 × 3 = 1689 > 1124). Заносим 2 в ответ — это будут единицы ответа. Вычитаем 562 × 2 из 1124 — остаётся 0. Значит квадратный корень из данного числа 79524 — это число 282.
Пример 3: 487204.
Число разделяем на грани (по два разряда) от запятой: 48’72’04. В числе три грани, значит в корне будет три разряда. Сначала старшая грань 48.
Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был не больше 48. Это число 6 (т.к. 6 × 6 = 36, а 7 × 7 = 49).
Заносим 6 в ответ. Это разряд сотен.
Вычитаем 36 из 48 — остаётся 12.
Сносим к 12 следующую грань — 72. Получается 1272.
Удваиваем то, что в ответе — 6. Получается 12. Припишем 12 слева от 1272.
Приписываем к 12 коробочку для ещё одного разряда.
Получается 12. Припишем 12 слева от 1272.
Приписываем к 12 коробочку для ещё одного разряда.
Подбираем наибольшее число от 1 до 9 такое, чтоб 12# × # было не больше, чем 1272. Это число 9, т.к. 129 × 9 = 1161 < 1272. Заносим 9 в ответ — это разряд десятков. Вычитаем (129 × 9 = )1161 из 1272 — остаётся 111. Сносим к 111 следующую грань — 04. Получается 11104. Удваиваем то, что в ответе — 69. Получается 138. Приписываем 138 слева от 11104. Приписываем к 111 справа коробочку для следующего разряда.
Подбираем наибольшее число от 1 до 9 такое, чтоб 138# × # было не больше, чем 11104. Это число 8 (т.к. 1388 × 8=11104, а 1389 × 9 = 12501 > 11104) Заносим 8 в ответ — это разряд единиц. Вычитаем 1388 × 8 = 11104 из 11104 — остаётся 0. Значит квадратный корень из данного числа 487204 — это число 698.
← Предыдущий урок
Оглавление
Чему равен квадратный корень из минус 6? – Обзоры Вики
Аналогично, что такое квадратный корень из отрицательного числа? Любое число в квадрате даст положительное число, поэтому нет истинного квадратного корня из отрицательного числа. Квадратные корни отрицательных чисел можно определить только с помощью мнимого числа, называемого йотой, или i.
Квадратные корни отрицательных чисел можно определить только с помощью мнимого числа, называемого йотой, или i.
Из чего 6 является квадратным корнем? Квадратный корень числа — это число, которое при умножении само на себя дает желаемое значение. Так, например, квадратный корень из 49 равен 7 (7×7=49). Процесс умножения числа на само себя называется возведением в квадрат.
…
Список идеальных квадратов.
| НОМЕР | ПЛОЩАДЬ | КВАДРАТНЫЙ КОРЕНЬ |
|---|---|---|
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
• 17 ноября 2021 г.
Является ли квадратный корень из отрицательных 6 действительным числом? Отрицательные числа не имеют действительных квадратных корней, поэтому я предполагаю, что вы работаете с мнимыми числами.
Во-вторых, как найти отрицательные корни? Отрицательные вещественные корни.
Для числа отрицательных действительных корней найти f (–x) и снова посчитать. Поскольку отрицательные числа, возведенные в четные степени, являются положительными, а отрицательные числа, возведенные в нечетные степени, отрицательными, это изменение влияет только на члены с нечетными степенями.
Что такое упрощенный квадратный корень 6?
Следовательно, квадратный корень из 6 в простейшей форме равен 2.449.
то Является ли отрицательный квадратный корень действительным числом? Квадратный корень из любого отрицательное число не является действительным числом.
Сколько корней, если дискриминант отрицательный?
Если дискриминант: Положительный, у вас есть 2 действительных корня. Ноль, у вас есть 1 реальный корень. минус, у тебя 0 настоящих корней(нет решения).
минус, у тебя 0 настоящих корней(нет решения).
Что такое куб числа 6? Кубический корень из 6 выражается как ∛6 в радикальной форме и как (6) ⅓ или (6) 0 . 33 в экспоненциальной форме.
…
Кубический корень из 6 в радикальной форме: ∛6.
| 1. | Что такое кубический корень из 6? |
|---|---|
| 3. | Является ли кубический корень из 6 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 6 |
6 — идеальный квадрат?
Например, произведение числа 2 само по себе равно 4. В этом случае 4 называется полным квадратом. Квадрат числа обозначается как n × n. Точно так же экспоненциальное представление квадрата числа равно n 2 , обычно произносится как «n» в квадрате.
…
Пример 1.
| Целое | Идеальный квадрат |
|---|---|
| 4 х 4 | 16 |
| 5 х 5 | 25 |
| 6 х 6 | 36 |
| 7 х 7 | 49 |
Чему равен квадрат шести? Квадраты от 02 до 62
| 0 в квадрате | = | 0 |
|---|---|---|
| 3 в квадрате | = | 9 |
| 4 в квадрате | = | 16 |
| 5 в квадрате | = | 25 |
| 6 в квадрате | = | 36 |
Что такое отрицательный квадратный корень из 81?
com/embed/ka0cQVd1aWM» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Что такое отрицательный квадратный корень из 100?
6 действительное число? Все натуральные числа являются целыми числами, но не все целые числа являются натуральными числами. Это набор всех счетных чисел, таких как 1, 2, 3, 4, 5, 6, 7, 8, 9, ……. ∞. Действительные числа — это числа, которые включают в себя как рациональные, так и иррациональные числа..
Могут ли корни уравнений быть отрицательными? Корни квадратного уравнения
Мы говорим это потому, что корень отрицательного числа не может быть никаким действительным числом. Скажи х2 = -1 является квадратным уравнением. Не существует действительного числа, квадрат которого отрицателен. … Следовательно, выражение (b2 – 4ac) называется дискриминантом квадратного уравнения ax2 + Ьх + с = 0.
Ноль — это действительное число?
На самом деле настоящие числа — это практически любые числа, которые вы можете придумать. … Действительные числа могут быть положительными или отрицательными, и включить число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел.
Каковы положительные и отрицательные квадратные корни из 16? Квадратный корень из 16 выражается как √16 в радикальной форме и как 161/2 в экспоненциальной форме. Квадратный корень числа является как отрицательным, так и положительным для одного и того же числового значения, т. е. квадратный корень из 16 будет 4.
Сколько корней у числа √ 16?
Квадратный корень из 16 равен 4 . Это положительное решение уравнения x 2 = 16. Число 16 представляет собой полный квадрат.
…
Корень квадратный из 16 в радикальной форме: √16.
| 1. | Что такое квадратный корень из 16? |
|---|---|
4 . | Часто задаваемые вопросы о квадратном корне из 16 |
Что такое отрицательный дискриминант? Что такое дискриминант? … Положительный дискриминант указывает на то, что квадратичный имеет два различных решения действительных чисел. Дискриминант, равный нулю, указывает на то, что квадратичная функция имеет повторяющееся действительное числовое решение. Отрицательный дискриминант указывает что ни одно из решений не является действительным числом.
Если дискриминант отрицателен, то квадрат корней равен?
Если дискриминант квадратного уравнения отрицателен, то квадратный корень из дискриминанта будет неопределенным.
Что такое куб отрицательного числа? Кубический корень отрицательного числа всегда будет отрицательным
Поскольку возведение числа в куб означает возведение его в третью степень (что является нечетным), кубические корни отрицательных чисел также должны быть отрицательными.
Что такое куб корня 6?
Кубы и список корней кубов от 1 до 15
| Число | Куб (а 3 ) | Кубический корень ∛a |
|---|---|---|
| 6 | 216 | 1. 817 817 |
| 7 | 343 | 1.913 |
| 8 | 512 | 2.000 |
| 9 | 729 | 2.080 |
Как написать 6 в кубе? Куб числа 6, или 6 в кубе, это 216. Чтобы найти куб числа x, мы возводим число x в третью степень или в степень 3.
Является ли 6 несовершенным квадратом?
6 — не идеальный квадрат.
Является ли квадратный корень из 6 рациональным или иррациональным числом?
Таким образом, значение, полученное для корня из 6, удовлетворяет условию быть неконечным и неповторяющимся десятичным числом, которое продолжается дальше после десятичной точки, что составляет √6 иррациональное число. Следовательно, √6 — иррациональное число.
Чему равны первые 6 квадратных чисел? Квадратные числа
Оно называется квадратным числом, потому что дает площадь квадрата, длина стороны которого является целым числом. Первое квадратное число равно 1, потому что. Первые пятнадцать квадратных чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 и 225.
Первые пятнадцать квадратных чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 и 225.
Квадратный корень из 6 — Как найти квадратный корень из 6?
LearnPracticeDownload
Квадратный корень из 6 выражается как √6 в радикальной форме и как (6) ½ или (6) 0,5 в экспоненциальной форме. Квадратный корень из 6, округленный до 7 знаков после запятой, равен 2,4494897. Это положительное решение уравнения x 2 = 6.
Квадратный корень из 6, округленный до 7 знаков после запятой, равен 2,4494897. Это положительное решение уравнения x 2 = 6.
- Корень квадратный из 6: 2,449489742783178
- Квадратный корень из 6 в экспоненциальной форме: (6) ½ или (6) 0,5
- Квадратный корень из 6 в подкоренной форме: √6
| 1. | Что такое квадратный корень из 6? |
| 2. | Является ли квадратный корень из 6 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 6? |
| 4. | Важные примечания |
| 5. | Часто задаваемые вопросы о квадратном корне из 6 |
Что такое квадратный корень из 6?
Квадратный корень из числа n записывается как √n. Квадратный корень из 6 можно записать по-разному.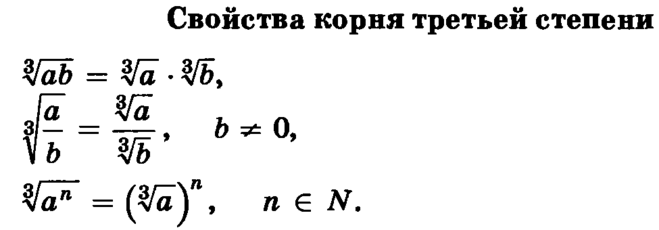
- Радикальная форма: √6
- Десятичная форма: 2,449
- Форма экспоненты: (6) 1/2
Является ли квадратный корень из 6 рациональным или иррациональным?
- Квадратный корень из 6 — это иррациональное число с неконечными цифрами.
- Квадратный корень из 6 нельзя записать в виде p/q. Следовательно, это иррациональное число.
Как найти квадратный корень из 6?
Есть 2 основных метода, которые мы используем, чтобы найти квадратный корень из 6.
- Факторизация простых чисел
- Длинное деление
Разложение на простые множители
- Чтобы найти квадратный корень из 6, мы сначала выразим его через простые множители.
6 = 2 × 3 - Теперь найдем квадратный корень.
√6 = √(2 × 3)
√6 = √2 × √3
= 1,414 × 1,732
= 2,449
Следовательно, квадратный корень из 6 равен 2,449
Длинное деление
- Шаг 1: Составьте пару цифр (поместив над ними черту) с места, как показано на рисунке.
 г.
г. - Шаг 2: Найдите такое число, чтобы при умножении его на себя произведение было меньше или равно 6. Мы знаем, что 2 × 2 = 4, что меньше 6. Поместите 2 в частное и разделите на 6 на 2, чтобы получить остаток как 2.
- Шаг 3: Поместите десятичную дробь после частного, так как мы сейчас делим, используя 0 из десятичной части 6. Не забудьте перетащить пару нулей вниз, получив делимое 200. Кроме того, добавление 2 само по себе дает нам 4 который становится начальной цифрой нашего следующего делителя. г.
- Шаг 4: Теперь у нас есть новый делитель 4X. Нам нужно найти такое значение X, чтобы 4X × X дало нам значение меньше 200. Число 4 заполняет позицию X, поэтому делимое равно 44, а частное теперь равно 2,4.
- Шаг 5: Следующим делителем будет 44 + 4, а делимое будет 2400. Мы будем продолжать делать те же шаги, пока не получим необходимое количество десятичных знаков.
Итак, наше длинное деление теперь выглядит так:
Следовательно, квадратный корень из 6 равен 2,449
Исследуйте квадратный корень с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 5
- Квадратный корень из 8
- Квадратный корень из 9
- Квадратный корень из 4
- Квадратный корень из 3
Важные примечания
- Квадратный корень из 6 = 2,449
- √6 иррационально и не завершается.
 г.
г. - Квадратный корень из 6 имеет 2 действительных корня: +2,449 и -2,449
Решенные примеры
Пример 1: У Кати есть кубик. Площадь всех 6 сторон куба равна 36 см 2 . Помогите ей рассчитать длину ребра куба.
Решение:
Общая площадь поверхности 36 см 2
Площадь поверхности каждой стороны = 36/6 = 6 см 2
Длина ребра = квадратный корень (6) = 2,45 см
г. Следовательно, длина ребра куба равна 2,45 см.Пример 2: Какое расстояние преодолевает человек, бегущий со скоростью 6√6 миль в час за 1 час?
Решение:
Пройденное расстояние = скорость × время
Следовательно, человек преодолевает общее расстояние 6√6 × 1 = 14,697 × 1 = 14,697 милиПример: Если площадь поверхности сферы составляет 24π в 2 .
 Найдите радиус сферы.
Найдите радиус сферы.Решение:
Пусть ‘r’ будет радиусом сферы.
⇒ Площадь сферы = 4πr 2 = 24π в 2
⇒ r = ±√6 в 91 912 Поскольку радиус не может быть отрицательным,
⇒ г = √6
Квадратный корень из 6 равен 2,449.
⇒ г = 2,449 в
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 6
Каково значение квадратного корня из 6?
Квадратный корень из 6 равен 2,44948.
Почему квадратный корень из 6 является иррациональным числом?
При простой факторизации 6, т.е. 2 1 × 3 1 , 2 находится в нечетной степени. Следовательно, квадратный корень из 6 иррационален.
Следовательно, квадратный корень из 6 иррационален.
Чему равен квадратный корень из -6?
Квадратный корень из -6 является мнимым числом. Это можно записать как √-6 = √-1 × √6 = i √6 = 2,449i
где i = √-1 и называется мнимой единицей.
Является ли число 6 идеальным квадратом?
Разложение числа 6 на простые множители = 2 1 × 3 1 . Здесь простого множителя 2 нет в паре. Следовательно, 6 не является идеальным квадратом.
Каково значение 1 квадратного корня из 6?
Квадратный корень из 6 равен 2,449. Следовательно, 1 √6 = 1 × 2,449 = 2,449.
Чему равен квадрат квадратного корня из 6?
Квадрат квадратного корня из 6 равен самому числу 6, т. е. (√6) 2 = (6) 2/2 = 6. √6)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 6. Мы начнем с определения, а затем ответим на некоторые общие вопросы.
вопросы о квадратном корне из 6.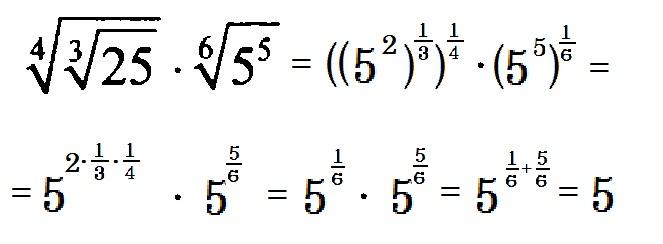 Затем мы покажем вам различные способы вычисления квадратного корня из 6 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Затем мы покажем вам различные способы вычисления квадратного корня из 6 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Квадратный корень из 6 определение
Квадратный корень из 6 в математической форме записывается с радикальным знаком, таким как √6. Мы называем это квадратным корнем из 6 в радикальной форме.
Квадратный корень из 6 — это величина (q), которая при умножении сама на себя будет равна 6.
√6 = q × q = q 2
Является ли число 6 полным квадратом?
6 является полным квадратом, если квадратный корень из 6 равен целому числу. Как мы рассчитали дальше
внизу на этой странице квадратный корень из 6 не является целым числом.
6 не является полным квадратом.
Является ли квадратный корень из 6 рациональным или иррациональным?
Квадратный корень из 6 является рациональным числом, если 6 является полным квадратом. Это иррациональное число, если оно не является полным квадратом.
Поскольку 6 не является полным квадратом, это иррациональное число. Это означает, что ответ на вопрос «квадратный корень из 6?» будет бесконечное количество
десятичных знаков. Десятичные дроби не прекратятся, и вы не сможете превратить их в точную дробь.
Это иррациональное число, если оно не является полным квадратом.
Поскольку 6 не является полным квадратом, это иррациональное число. Это означает, что ответ на вопрос «квадратный корень из 6?» будет бесконечное количество
десятичных знаков. Десятичные дроби не прекратятся, и вы не сможете превратить их в точную дробь.
√6 — иррациональное число
Можно ли упростить квадратный корень из 6?
Вы можете упростить число 6, если сможете уменьшить число 6 внутри корня. Мы называем этот процесс «упрощать сурд».
Квадратный корень из 6 нельзя упростить.
√6 уже находится в простейшей радикальной форме.
Как вычислить квадратный корень из 6 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 6 — воспользоваться калькулятором!
Просто введите 6, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ
с 9десятичные числа:
√6 ≈ 2,449489743
Как вычислить квадратный корень из 6 на компьютере
получить квадратный корень из 6. Ниже приведен результат, который мы получили с 13 десятичными знаками. Мы называем это квадратным корнем из 6 в десятичной форме.
Ниже приведен результат, который мы получили с 13 десятичными знаками. Мы называем это квадратным корнем из 6 в десятичной форме.
SQRT(6) ≈ 2,4494897427832
Чему равен квадратный корень из 6 с округлением?
Квадратный корень из 6, округленный до ближайшей десятой, означает, что вам нужна одна цифра после запятой. Квадратный корень из 6, округленный до сотых, означает, что вы
нужны две цифры после запятой. Квадратный корень из 6, округленный до ближайшей тысячной, означает, что вам нужны три цифры после запятой.
10-й: √6 ≈ 2,4
100-й: √6 ≈ 2,45
1000-й: √6 ≈ 2,449
Чему равен квадратный корень из 6?
Как мы сказали выше, поскольку квадратный корень из 6 является иррациональным числом, мы не можем превратить его в точную дробь.
Однако мы можем превратить его в приблизительную дробь, используя квадратный корень из 6, округленный до сотых.
√6
≈ 2,45/1
≈ 245/100
≈ 2 9/20
Чему равен квадратный корень из 6, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (по основанию) с дробной степенью. Квадратный корень из 6 не является исключением. Вот правило и ответ
к «квадратному корню из 6, преобразованному в основание с показателем степени?»:
√b = b ½
√6 = 6 ½
Как найти квадратный корень из 6 путем деления в большую сторону method
Здесь мы покажем вам, как вычислить квадратный корень из 6, используя метод деления в длину с точностью до одного десятичного знака. это потерянный
искусство того, как они вычисляли квадратный корень из 6 вручную до того, как были изобретены современные технологии.
Шаг 1)
Разместите 6 в парах из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный знак:
Шаг 2)
Начиная с первого набора: самый большой полный квадрат, меньший или равный 6, равен 4, а квадратный корень из 4 равен 2. Следовательно, положите 2 сверху и 4 снизу следующим образом:
Следовательно, положите 2 сверху и 4 снизу следующим образом:
Шаг 3)
Вычислите 6 минус 4 и положите разница ниже. Затем переместитесь вниз к следующему набору чисел.
| 2 | ||||
| 6 | 00 | |||
| 4 | ||||
| 2 | 00 | |||
Шаг 4)
Удвойте число, выделенное зеленым сверху: 2 × 2 = 4. Затем используйте 4 и нижнее число, чтобы решить эту задачу:
4? × ? ≤ 200
Знаки вопроса «пробел» и такие же «пробел». Путем проб и ошибок мы нашли, что наибольшее число «пустых» может быть равно 4.
Теперь введите 4 сверху:
Путем проб и ошибок мы нашли, что наибольшее число «пустых» может быть равно 4.
Теперь введите 4 сверху:
| 2 | 4 | |||
| 6 | 00 | |||
| 4 | ||||
| 2 | 00 | |||
Вот и все! Ответ сверху. Квадратный корень из 6 с точностью до одной цифры после запятой равен 2,4.
Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 6 на этой странице.
Примечания
Помните, что отрицательное число, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 6 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
Таким образом, квадратный корень из 6 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 7
Вот следующее число в нашем списке, о котором у нас есть такая же подробная информация о квадратном корне.
Авторское право | Политика конфиденциальности | Отказ от ответственности | Контакт
Квадратный корень из 6 — значение, вычисление, упрощение, пример решения и часто задаваемые вопросы
Квадратный корень — это тема, которую многим учащимся трудно понять. Однако, как только вы хорошо поймете концепцию, нахождение квадратных корней больше не будет для вас проблемой. Итак, простыми словами, квадратный корень в математике — это множитель числа, который при умножении на себя дает исходное число. Например, и 3, и -3 являются квадратными корнями из 9..
Например, и 3, и -3 являются квадратными корнями из 9..
Квадратный корень из числа a — это число b, такое что b² = a. Квадратный корень любого числа представлен символом и также часто известен как радикал. Число или выражение, данное под символом квадратного корня, известно как подкоренное число. Квадратный корень — часто используемая функция в математике. Он широко используется в таких предметах, как математика и физика. Иногда бывает утомительно находить квадратный корень числа, особенно числа, которое не является полным квадратом числа. В этой статье мы обсудим квадратный корень из 6 и как вычислить значение корня 6 с помощью упрощающего метода квадратного корня.
Какое значение корня 6?
Значение корня 6 равно 2,449
Квадратный корень из 6 Определение
Квадратный корень из числа 6 — это число y, такое что y² = 6. Квадратный корень из 6 в радикальной форме записывается как √6. Квадратный корень из 6 в радикальной форме выражается как √6
Как рассчитать значение нижнего корня 6?
Мы можем вычислить значение нижнего корня 6, используя различные методы извлечения квадратных корней. Этими методами могут быть методы деления в длину, метод простой факторизации или упрощающий метод квадратного корня. Давайте обсудим, как рассчитать значение 6 под корнем, используя упрощающий метод квадратного корня.
Этими методами могут быть методы деления в длину, метод простой факторизации или упрощающий метод квадратного корня. Давайте обсудим, как рассчитать значение 6 под корнем, используя упрощающий метод квадратного корня.
Чтобы упростить вычисление квадратного корня, сделайте число под ним как можно меньше, но при этом сохраните его как целое число. Математически это можно выразить так: √x.y=√x×√y
Чтобы выразить квадратный корень из 6 в простейшей форме, мы сделаем число 6 как можно меньше, сохранив его как целое число. Следовательно, квадратный корень из 6 в простейшей форме представлен как √6=√2×√3. Это можно упростить, подставив значения √2 и √3
\[\sqrt{6}=\sqrt{2}\times \sqrt{3}\]
\[\sqrt{6}=1,414\times 1,732\]
\[\sqrt{6}=2,449\]
Следовательно, квадратный корень из 6 в простейшей форме равен 2,449. Точно так же мы можем вычислить квадратный корень из любых других целых чисел и их множителей. Следовательно, упрощение метода квадратного корня является самым простым методом вычисления квадратного корня. Мы также можем рассчитать значение под корнем 6 с помощью калькулятора, так как это даст нам точное значение. Точное значение квадратного корня всегда будет даваться в виде десятичного числа, поскольку невозможно определить положительное целое число как корень для нерациональных чисел.
Следовательно, упрощение метода квадратного корня является самым простым методом вычисления квадратного корня. Мы также можем рассчитать значение под корнем 6 с помощью калькулятора, так как это даст нам точное значение. Точное значение квадратного корня всегда будет даваться в виде десятичного числа, поскольку невозможно определить положительное целое число как корень для нерациональных чисел.
Упрощение извлечения квадратного корня с помощью метода полного квадрата
Ниже приведены шаги по упрощению извлечения квадратного корня с помощью метода полного квадрата:
Найдите правильный квадрат, на который делится подкоренное число.
Выразите числа как множители полного квадрата.
Упростите радикалы.
Решенный пример
1. Упростить $\mathbf{\sqrt{300}}$
Упростить $\mathbf{\sqrt{300}}$
Решение:
\[\sqrt{300}=\sqrt{100\times 3}\]
\[\sqrt{300}=\sqrt{10\times 10\times 3}\]
\[\sqrt{ 300}=10\sqrt{3}\]
Следовательно, \[\sqrt{300}\] можно упростить как \[10\sqrt{3}\]
2. Упростите следующие радикальные выражения:
\[\sqrt{48}\]
\[\sqrt{75}\]
Решения:
i.$\mathbf{\sqrt{48}}0 1: Полный квадрат 16 будет делить число 48.
Шаг 2: умножьте 48 на 16
48=16×3
Шаг 3: уменьшите квадратный корень из 16, как показано ниже:
\[\sqrt{48}=\sqrt{16\times 3}\]
\[\sqrt{48}=\sqrt{4\times 4\times 3}\]
\[\sqrt{48}=4\sqrt{3}\]
Следовательно,\ [\sqrt{48}\] можно упростить как \[4\sqrt{3}\]
ii. $\mathbf{\sqrt{75}}$
$\mathbf{\sqrt{75}}$
Шаг 1: Совершенный квадрат 25 будет делиться число 75.
Шаг 2: умножьте 75 на 25.
75=25×3
Шаг 3. Упростите радикалы, как показано ниже: sqrt{5\times 5\times 3}\]
\[\sqrt{75}=5\sqrt{3}\]
Следовательно, \[\sqrt{75}\] можно упростить как\[5 \sqrt{3}\]
Калькулятор корня шестой онлайн — Впечатляющий Калькулятор корня шестой
Категории
Калькуляторы корня Математические калькуляторы
Содержание
- Калькулятор корня шестой онлайн:
- Корень шестой Формула расчета:
- Корень шестой Определение:
- Как вычислить корень шестой степени
- Что такое корень шестой степени из 64?
- Чему равен корень 6-й степени из 729?
- Чему равен 6-й корень из 4096?
- Perfect 6th Roots
- Таблица шестого корня от 1 до 50:
- Таблица шестого корня от 51 до 100:
- больше корневого калькулятора
Шестой калькулятор корня.
 .
.Объявления
- Корень шестой из 2 равен ± 1,122.
- Корень 6 из 64 равен ± 2.
- Корень 6 из 85 равен ± 2,096.
- Корень шестой из 125 равен ± 2,236.
- Корень шестой из 216 равен ± 2,449.
- Корень шестой из 256 равен ± 2,519.
- Корень шестой из 729 равен ± 3.
- Корень шестой из 4096 равен ± 3,999.
Формула вычисления корня шестого:
a 6 = x., 6 √x =a
Формула 9 корня шестого2521
Sixth Root Definition:
Definition of Sixth Root :
In mathematics, an sixth root of a number x , is a number r which, when raised to the power 6 дает x :
r 6 =x.
Как вычислить корень шестой степени
Что такое корень шестой степени из 64?
Корень шестой степени из 64 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.
Шестой корень из 64 — это число, которое умножается само на себя 6 раз, что дает нам 64.
Разделив 64 на 2, мы получим 32, что равно:
64 = 2 X 32
= 2 X (16 X 2 )
= 2 X 2 X (8 X 2)
= 2 X 2 X 2 X (4 X 2)
= 2 X 2 X 2 X 2 X 2 X 2.
Шестой корень из 64 равен 2.
Чему равен 6-й корень из 729?
Корень шестой степени из 729 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.
Корень шестой степени из 729это число, которое умножается само на себя 6 раз, чтобы дать нам 729. Складывая цифры 729, мы получаем 7 + 2 + 9 = 18, это среднее значение кратно 9, это говорит нам, что 729 кратно 9.
Деление 729 на 9 дает нам 81, что равно:
729 = 9 х 81 = 9 х 9 х 9, что дает нам:
729 = 3 х 3 х 3 х 3 х 3 х 3.
Корень шестой степени из 729 равен 3.
Чему равен корень шестой степени из 4096?
Корень шестой степени из 4096 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.
Шестой корень из 4096 — это число, которое умножается на себя 6 раз, что дает нам 4096.
Разделив 4096 на 4, мы получим 1024, что равно:
4096 = 4 X 1024
= 4 X (4 X 256).
= 4 х 4 х (4 х 64).
= 4 х 4 х 4 х (4 х 16).
= 4 х 4 х 4 х 4 х 4 х 4.
Корень шестой степени из 4096 равен 4, что является полным корнем шестой степени.
Совершенные корни шестой степени
| X | 6 √x |
| Sixth root of 1 | 1 |
| Sixth root of 64 | 2 |
| Sixth root of 729 | 3 |
| Sixth root of 4 096 | 4 |
| Шестой корень 15 625 | 5 |
| Шестой корень 46 656 | 6 |
| Шестой корень из 117 649 | 7 |
| 6 Шестой корень из 26249499999 | |
6. 0011 0011 | |
| Sixth root of 531 441 | 9 |
| Sixth root of 1 000 000 | 10 |
| Sixth root of 1 771 561 | 11 |
| Sixth root of 2 985 984 | 12 |
Table of Sixth Root from 1 to 50:
| x | 6 √x | x | 6 √x | ||
| Шестой корень 1 | 1 0000 | Шестой корень 26 | 1 7212 | ||
| Шестой корень 2 | 1,1225 | Sixth root из 270005 | 1,1225 | Sщико. | 1 7321 |
| Шестой корень 3 | 1 2009 | Шестой корень 28 | 1 7426 | ||
| Шестой корень 4 | 1,2599 | 4. ,7528 ,7528 | |||
| Корень шестой степени из 5 | 1 3077 | Шестой корень из 30 | 1 7627 | ||
| Шестой корень 6 | 1 3480 | Шестой корень 31 | 1 7724 | ||
| 40005 | 444724 | ||||
| 4000 40004 | 994444724 | ||||
| 40005 | 9000 4000449724 | ||||
| . 1 3831 | Шестой корень 32 | 1 7818 | |||
| Шестой корень 8 | 1,4142 | Шестой корень 33 | 1 7910 | ||
| Шестой корень | 1,7910 | ||||
| . 4422 | Корень шестой из 34 | 1,7999 | |||
| Sixth root of 10 | 1,4678 | Sixth root of 35 | 1,8086 | ||
| Sixth root of 11 | 1,4913 | Sixth root of 36 | 1 8171 | ||
| Шестой корень из 12 | 1 5131 | Шестой корень 37 | 1 8254 | ||
| Шестой корень 13 | 1 5334 | Шестой корень 38 | 10004 1 5334 | 4.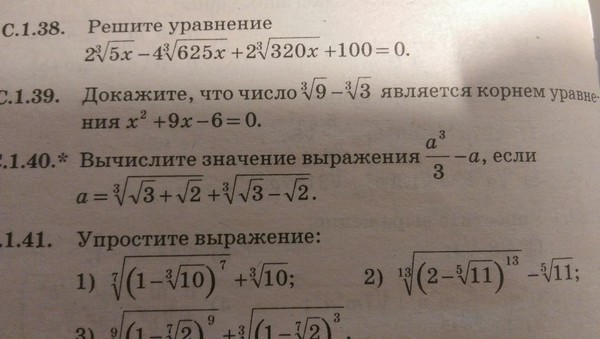 8336 8336 | |
| Корень шестой из 14 | 1 5525 | Шестой корень 39 | 1 8415 | ||
| Шестой корень из 15 | 1 5704 | Шестой корень 40 | 1 8493 | 493 | 9000 90004000 40004493 | 9000 9000 4000 4000 40004493 9000 9000 4000 4000 40004493 9000 9000 4000 4000 4000493 | 9000 9000 400093 | 9000 9000 400093 | . 1 5874 | Шестой корень из 41 | 1 8569 |
| Шестой корень 17 | 1,6035 | Шестой корень 42 | 1 8644 | ||
| Шестой корень из 18 | 4 1,8644 | ||||
| 4000 | 4 1,8644 | ||||
| 40005 | 9 1,8644 | ||||
| 4000 | 9 1,8644 | Корень шестой из 43 | 1 8717 | ||
| Шестой корень из 19 | 1 6335 | Шестой корень 44 | 1 8789 | ||
| Шестой корень 20 0005 | 1,6475 | Sixth root 45 9000 9000 | 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 90001,6475 9005 | ||
| 1 8860 | |||||
| Шестой корень из 21 | 1 6610 | Шестой корень 46 | 1 8929 | ||
| Шестой корень 22 | 1,6739 | Шестой корень 47 9000 40004 10004 1,6739 | 4 8997 | ||
| Корень шестой из 23 | 1 6864 | Шестой корень 48 | 1 9064 | ||
| Шестой корень из 24 | 1,6984 | Шестой корень 49 | 1,9129 | ||
| 4 | 129 | 9129 | 9000 39129 | 9000 9000 4 1,7100Sixth root of 50 | 1,9194 |
Table of Sixth Root from 51 to 100:
| x | 6 √x | x | 6 √x | ||||
| Sixth root of 51 | 1,8 | Sixth root of 76 | 2,058112 | ||||
| Sixth root of 52 | 1, | 1Sixth root of 77 | 2,062601 | ||||
| Sixth root of 53 | 1,938114 | Sixth root of 78 | 2,067041 | ||||
| Sixth root of 54 | 1,944161 | Шестой корень из 79 | 2,071434 | ||||
| Sixth root of 55 | 1,950116 | Sixth root of 80 | 2,075782 | ||||
| Sixth root of 56 | 1,955981 | Sixth root of 81 | 2,080084 | ||||
| Sixth root of 57 | 1,96176 | Sixth root of 82 | 2,084342 | ||||
| Sixth root of 58 | 1,967454 | Sixth root of 83 | 2, 088557 | ||||
| Шестой корень из 59 | 1 973068 | Шестой корень из 84 | 2 09273 | ||||
| Шестой корень из 60 | 1 978602 | 4. | Sixth root of 61 | 1,984061 | Sixth root of 86 | 2,100953 | |
| Sixth root of 62 | 1,989445 | Sixth root of 87 | 2,105005 | ||||
| Sixth корень из 63 | 1,994757 | Sixth root of 88 | 2,109019 | ||||
| Sixth root of 64 | 2 | Sixth root of 89 | 2,112994 | ||||
| Sixth root of 65 | 2, 005175 | Sixth root of 90 | 2,116933 | ||||
| Sixth root of 66 | 2,010284 | Sixth root of 91 | 2,120835 | ||||
| Sixth root of 67 | 2,015328 | Шестой корень из 92 | 2,124702 | ||||
| Шестой корень 68 | 2 020311 | Шестой корень 93 | 2,128534 | ||||
| Sixth root из 69 | 2,02523232 | 29 | 2 1323331 | ||||
| Шестой корень 70 | 2 030095 | Шестой корень 95 | 2 136095 | ||||
| Шестой корень 71 | 2000,0349 9005 | Sixth root 9000 | 2,0349 | Sixty Root | 2,0349 | Sixth root 9000 9000 40004 2,0349 9005 | Six. |




 {2}}=1$.
{2}}=1$. {3}}$:Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
{3}}$:Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение. \]
\]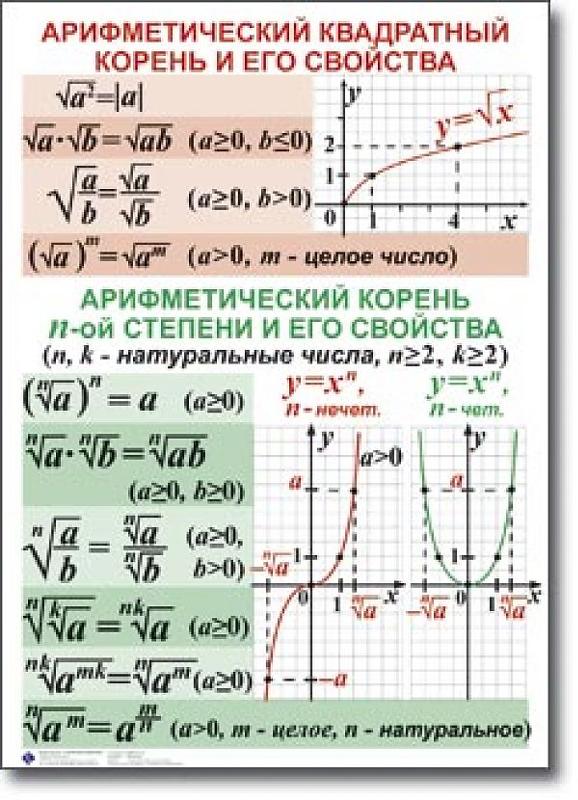 Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».

 Найдите радиус сферы.
Найдите радиус сферы.