Алгебра, 20.11.2020 13:40, katelove8
2) lim x стремится к 0 arcsin 2x/4x
Всего ответов: 3
Посмотреть ответы
Другие вопросы по Алгебре
Алгебра, 27.02.2019 12:50, karina36517
Решить систему уравнений: 5sinx=siny 3cosx+cosy=2
Ответов: 2
Посмотреть
Алгебра, 27.02.2019 16:50, ikol2912
Разложить многочлен на множители 5y в квадрате — 10y — yz — 2z
Ответов: 3
Посмотреть
Алгебра, 28.02.2019 00:40, glebyurchenko
(6 в шестой степени)во 2 степени умноженое на 6 в 8 это деленое на 6 в 18 степени
Ответов: 2
Посмотреть
Алгебра, 28.02.2019 03:00, Манипуляция
.(Паша купил 6 апельсинов. все они без первого весили 1660г без второго 1685г бе третьего 1680г без четвёртого 1670г без пятого 1665г без шестого 1640г. какова масса всех шести апельсинов?).
Ответов: 4
Посмотреть
Алгебра, 28.
2-4+3a) x 0 внизу =2б)…
Вопросы по предметам
Математика, 22.12.2020 15:49
Упростите выражение: 9 *14 *11*19 2114 9 19 11*23*
23*2721 28…
Литература, 22.12.2020 15:49
Ситуация: В Новогоднюю ночь осуществилось ваше самое заветное желание. Опишите такую Новогоднюю ночь, уделив особое внимание описанию собственных ощущений и впечатлений. …
Литература, 22.12.2020 15:49
Как по другому можно было Вишнёвый сад? (Чехов, Пьеса «Вишнёвый сад») ваш вариант сада. …
Английский язык, 22.12.2020 15:49
Последние не могу решить
As people around the world, the Japanese celebrate New Year on December 31st. But the
important part of the holiday for them is not New Year’s E…
Українська мова, 22.12.2020 15:49
З наведеного переліку оберіть особливості пам’яток готичного мистецтва …
История, 22.12.2020 15:49
Задание 1. Вставьте в текст пропущенные слова В середине XIX века главным вопросом для внешней политики России стал ___(1) вопрос.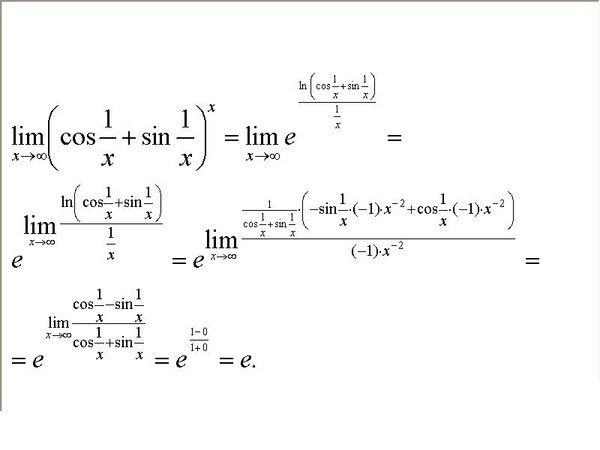
В октябре 1853 года началась (2)война.
Главн…
Химия, 22.12.2020 15:49
1 Напишите уравнения реакций горения магния, угля, железа, метана СН4. Подпишите названия продуктов реакции. 2. Осуществите цепочку превращений. Укажите, где необходимо, условия пр…
Биология, 22.12.2020 15:49
Найдите ошибки в приведенном тексте, укажите номера предложений, в которых они сделаны, перепишите эти предложения без ошибок. 1) Соперничество между особями за самку представляет…
История, 22.12.2020 15:49
Почему открытие и изучение кургана «Иссык» является очень важным для изучения истории Казахст ана? Приведите не менее 3-х доказательств.
Информатика, 22.12.2020 15:49
Томендеги кестедеде деректер типын аныктаныз ,…
Больше вопросов по предмету: Алгебра Случайные вопросы
Как считать пределы
В учебниках по математическому анализу значительное внимание уделяется приемам вычисления пределов функций и последовательностей.
2 стремится к нулю.
Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, авеличина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией описывается замедление хода поезда, можно говорить о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.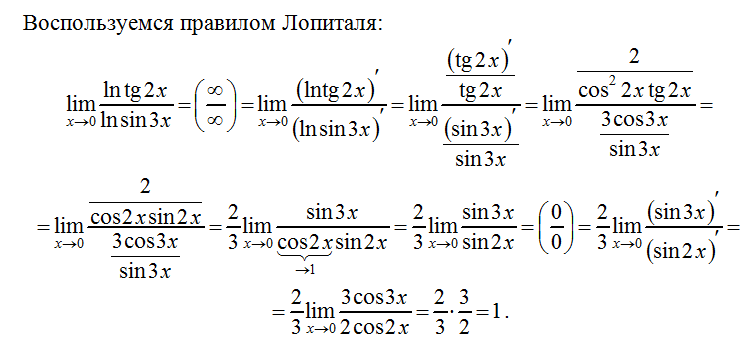
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1
x→0
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность — ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f'(x)/l'(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности.
(n-1)
Что такое каравелла | Как найти площадь сечения шара | Как перевести миллиметры ртутного столба в паскали |
Социальная структура как признак общества | Как найти периметр равнобедренной трапеции | Как найти неизвестный делитель |
предел sin(x)/x при приближении x к бесконечности
Пределы и производные
Уоррен Д.
спросил 13.10.16Думаю, это равно 1, но как? Я попробовал правило Лопиталя и до сих пор не могу получить просто Cos(x), когда x приближается к бесконечности
Подписаться І 4
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Артуро О.
ответил 13.10.16
Репетитор
5,0 (66)
Опытный преподаватель физики для репетиторства по физике
Смотрите таких репетиторов
Смотрите таких репетиторов
Если форма неопределенная, то применить правило Лопиталя. Однако в этой задаче форма не является неопределенной, поскольку знаменатель стремится к бесконечности, а числитель остается конечным, поэтому форма стремится к нулю.
Правило Лопиталя отлично работает для таких задач, как:
Предел как x → 0 sin(x)/x.
В этом случае форма неопределенна, и правило Лопиталя дает 1 для предела. Но в вашей заявленной задаче x → ∞. Как объяснили воспитатели, в поставленной задаче можно рассуждать, что предел равен нулю.
Голосовать за 1 голос против
Еще
Отчет
Майкл А.
ответил 13.10.16
Репетитор
5,0 (1878)
AFOQT, TEAS, алгебра, ASVAB, HESI, предварительный исчисление, подготовка к математике/вербальному тесту
Об этом репетиторе ›
Об этом репетиторе ›
Функция синуса колеблется между -1 и 1 для всех x. Поскольку x приближается к бесконечности, это означает, что знаменатель также будет стремиться к бесконечности. Предел этой функции будет равен нулю при приближении x к бесконечности.
Голосовать за 1 голос против
Подробнее
Отчет
Питер Г. ответил 13.10.16
Репетитор
4.9 (43)
Успехи в математике и английском языке; Магистр математики/логики; 99-й процентиль
Смотрите таких репетиторов
Посмотреть таких репетиторов
Чтобы показать это, можно использовать правило сжатия, сжимая функцию по абсолютному значению между 0 и 1/x.
Поскольку 1/x приближается к 0, то и sin x/x приближается.
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Пределы и производная
Пределы и производная
I.
Викторина
II. Домашнее задание
III. Ограничивает бесконечности и нули.
При работе с ограничениями полезно иметь следующие символьные дроби.
A) (бесконечность)/(конечность) = бесконечность
B) 0/(конечный ненулевой) = бесконечность
C) (конечное)/(бесконечность) = 0
D) (конечный ненулевой)/0 = бесконечность
E) (бесконечность)/(бесконечность) = Заниматься алгеброй
F) 0/0 = заниматься алгеброй
Пример:
1) lim x -> 0 (3x + 5)/(2x 2 + x) = 5/0 = ДНЭ
2) lim х -> 1 из (х 2 — 1)/(х + 3) = 0/4 = 0
3) lim x -> 2 из (x 2 — 4)/(x — 2) = 0/0
Мы факторим, чтобы получить: ((x — 2)(x + 2))/(x — 2) = x + 2 = 4
4) Попробуйте lim x -> -1 из (x 2 — 2x — 3)/(х 2 + 8х + 7)
5) Попробуйте lim x -> 3/2 от (6x 2 + x — 15)/(8x 2 — 6x — 9)
6) lim x -> 2 of (sqrt(x — 1) — 1)/(x 2 — 4) = 0/0
мы рационализируем знаменатель, умножив его на сопряженный корень: sqrt(x — 1) + 1 для получения
7) Найти lim x -> 0 из (sqrt(3 + x) — sqrt(3))/x
IV.
Пределы и тригонометрия
Используйте свой калькулятор, чтобы построить график (sinx)/x и обнаружить, что
lim x -> 0 of (sinx)/x = 1
Следствие:
lim x -> 0 из (1 — cosx)/x = 0
доказательство: (1 — cosx)/x = (1 — sqrt(1 — sin 2 x))/x =
((1 + sqrt(1 — sin 2 x)) (1 – кв.(1 – sin 2 x)))/((x)(1 + sqrt(1 — sin 2 x)))
= (1 — (1 — sin 2
= sin 2 x/((x)(1 + sqrt(1 — sin 2 x)))
= ((sinx)/x) (sinx)/((1 + sqrt(1 — sin 2 x))
= (1) (0/2) = 0
приложений:
1) lim x -> 0 из (tanx)/x = ((sinx)/(cosx))/x = ((sinx)/x)(1/cosx) = (1)(1) = 1
2) lim x -> 0 из (1 — cos(2x))/x
Мы устанавливаем u = 2x, тогда, когда x стремится к нулю, то же самое и u.