Линейная регрессия примеры решения задач: Парная линейная регрессия и метод наименьших квадратов (МНК). Решение задач и контрольных работ по статистике и эконометрике онлайн

Парная линейная регрессия. Задачи регрессионного анализа

• Понятие линейной регрессии. Парная линейная регрессия
• Уравнение парной линейной регрессии и метод наименьших квадратов
• Анализ качества модели линейной регрессии
• Интерпретация коэффициентов уравнения парной линейной регрессии
• Задачи регрессионного анализа
• Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины

y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

y = ax + b,

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную

y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

где

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

или

где

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа  , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X  и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

• прямая парной линейной регрессии проходит через точку ;
• среднее значение отклонений равна нулю: ;
• значения  и  не связаны: .

Пройти тест по теме Теория вероятностей и математическая статистика

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

---

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2.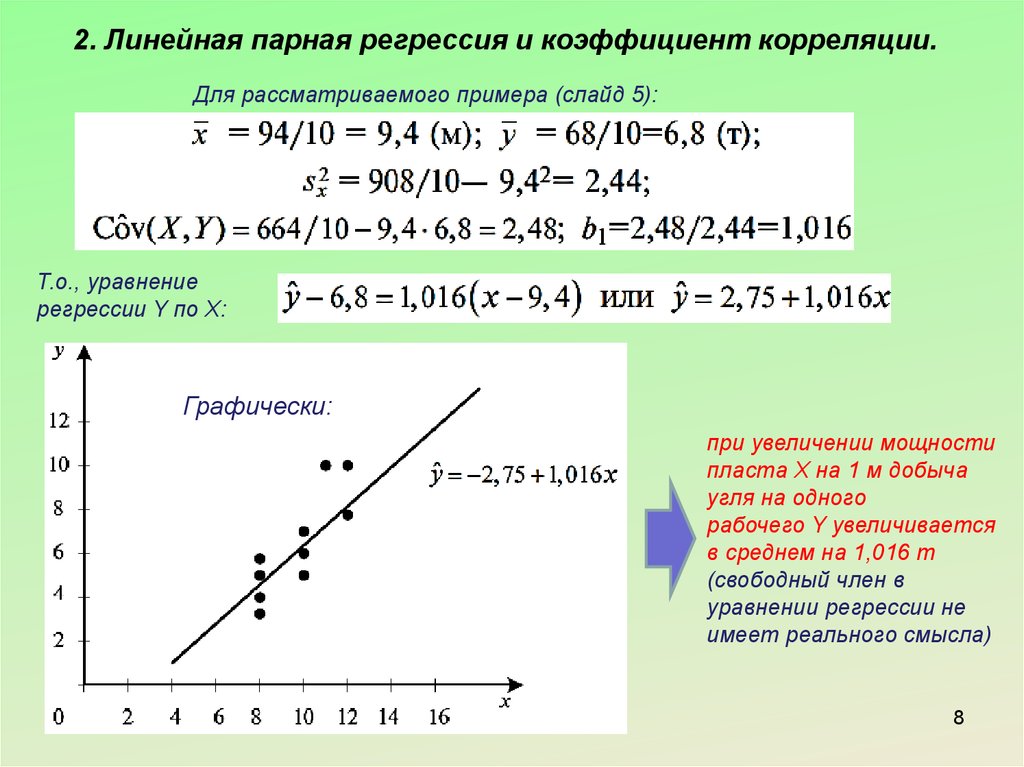 Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Правильное решение и ответ.

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

где

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

Правильное решение и ответ.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

где

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593, SSE = 10 459,587, SSR = 53 311,007.

Можем убедиться, что выполняется закономерность SSR = SST — SSE:

63770,593-10459,587=53311,007.

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии xi = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. yi = 17036,4662.

Подставляем в уравнение парной линейной регрессии xi = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. yi = 4161,9662.

Если доход не меняется, то xi = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

• установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
• выявление причинных связей между переменными величинами;
• прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.

Нулевую гипотезу

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2,

где — стандартная погрешность коэффициента направления прямой линейной регресии b1.

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b1:

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пройти тест по теме Теория вероятностей и математическая статистика

К началу страницы

Назад

Листать

Вперёд>>>

Всё по теме «Математическая статистика»

Характеристики выборки и генеральной совокупности: среднее значение, дисперсия, погрешности выборки

Доверительный интервал для математического ожидания

Распределение Стьюдента и малые выборки

Проверка статистических гипотез

Корреляционная зависимость, коэффициент корреляции

Множественная корреляция, её коэффициент. Частная корреляция

Множественная линейная регрессия. Улучшение модели регрессии

Дисперсионный анализ: соединение теории и практики

примеры и вычисление функции потерь

Линейная регрессия (Linear regression) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.

Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала простым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.

Применение линейной регрессии

Предположим, нам задан набор из 7 точек (таблица ниже).

Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:

Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.

Функция потерь — метод наименьших квадратов

Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y(х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями  красными пунктирными линиями.

Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.

Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.

Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.

Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.

Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0. 5, 1.0). Если мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.

Больше размерностей

Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:

f(x) = b+w_1*x_1 + … + w_n*x_n

Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:

f(x) = b*1+w_1*x_1 + … + w_n*x_n

Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.

Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.

Проклятие нелинейности

Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.

Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).

Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.

Минимум функции

Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.

Линейная регрессия — примеры, уравнение, формула и свойства

Линейная регрессия используется для прогнозирования взаимосвязи между двумя переменными путем применения линейного уравнения к наблюдаемым данным. Существует два типа переменных: одна переменная называется независимой, а другая — зависимой. Линейная регрессия обычно используется для прогнозного анализа. Основная идея регрессии состоит в том, чтобы исследовать две вещи. Во-первых, хорошо ли набор переменных-предикторов предсказывает результирующую (зависимую) переменную? Во-вторых, какие переменные являются значимыми предикторами переменной результата? В этой статье мы обсудим концепцию уравнения линейной регрессии, формулу и свойства линейной регрессии.

 

Примеры линейной регрессии

Вес человека линейно связан с его ростом. Таким образом, это показывает линейную зависимость между ростом и весом человека. Соответственно, по мере увеличения роста будет увеличиваться и вес человека. Не обязательно, чтобы одна переменная зависела от других или одна вызывала другую, но между двумя переменными существует некоторая критическая связь. В таких случаях мы используем точечную диаграмму, чтобы упростить связь между переменными. Если между переменными нет связи или связи, то точечная диаграмма не указывает ни на увеличение, ни на уменьшение. В таких случаях план линейной регрессии не подходит для данных.

 

Уравнение линейной регрессии

Мера связи между двумя переменными представлена ​​коэффициентом корреляции. Диапазон коэффициента лежит в пределах от -1 до +1. Этот коэффициент показывает силу связи наблюдаемых данных между двумя переменными.

 

Уравнение линейной регрессии приведено ниже:

 

Y=a+bX

 

где X — независимая переменная, отложенная по оси x

 

Y — зависимая переменная, отложенная по оси Y.

 

Здесь наклон линии равен b, а a — точка пересечения (значение y при x = 0).

 

Формула линейной регрессии

Как мы знаем, линейная регрессия показывает линейную зависимость между двумя переменными. Уравнение линейной регрессии аналогично формуле наклона. Мы уже изучали эту формулу на более ранних занятиях, таких как линейное уравнение с двумя переменными. Формула линейной регрессии задается уравнением 9{2}}\]

Простая линейная регрессия

Простая линейная регрессия — это самый простой случай, когда используется одна скалярная предикторная переменная x и одна скалярная переменная отклика y. Уравнение для этой регрессии имеет вид y=a+bx

 

Расширение до множественных и векторнозначных переменных-предикторов известно как множественная линейная регрессия. Он также известен как многомерная линейная регрессия. Уравнение для этой регрессии имеет вид Y = a+bX. Почти все реальные модели регрессии включают несколько предикторов. Основные объяснения линейной регрессии часто объясняются в терминах множественной регрессии. Обратите внимание, что в этих случаях зависимая переменная y все же является скаляром.

 

Линия наименьших квадратов регрессии или линия линейной регрессии

Самый популярный метод подгонки линии регрессии к графику XY — это использование метода наименьших квадратов. Этот процесс используется для определения наиболее подходящей линии для заданных данных путем уменьшения суммы квадратов вертикальных отклонений от каждой точки данных до линии. Если точка точно лежит на аппроксимируемой линии, то значение ее перпендикулярного отклонения равно 0. Это 0, потому что вариации сначала возводятся в квадрат, а затем складываются, поэтому их положительные и отрицательные значения не будут аннулированы. Линейная регрессия определяет прямую линию, известную как линия регрессии наименьших квадратов или LSRL. Предположим, что Y — зависимая переменная, а X — независимая переменная, тогда линия регрессии населения задается уравнением;

Y= B ₀ +B ₁ X

Где

B ₀ — константа

B ₁ — коэффициент регрессии 9 0003

Когда дана случайная выборка наблюдений, регрессия строка выражается как;

ŷ = b ₀ +b ₁ x

где b ₀ — константа

b ₁ — коэффициент регрессии,

90 002 x — независимая переменная,

ŷ известна как прогнозируемое значение зависимой переменной.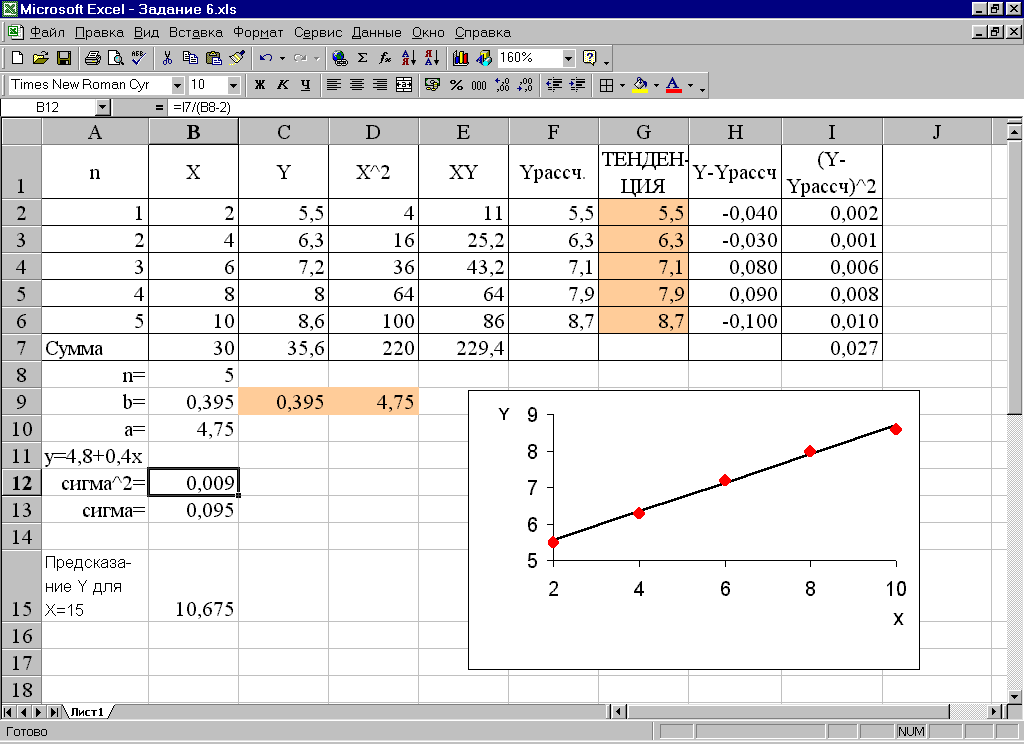

 

Свойства линейной регрессии

Для линии регрессии, где определены параметры регрессии b ₀ и b ₁ , применимы следующие свойства:

• Линия регрессии сокращает сумма квадратов разностей между наблюдаемые значения и прогнозируемые значения.

• Линия регрессии проходит через среднее значение переменных X и Y.

• Константа регрессии b ₀ равно y-пересечению линейной регрессии.

• Коэффициент регрессии b ₁ — наклон линии регрессии. Его значение равно среднему изменению зависимой переменной (Y) на единицу изменения независимой переменной (X)

Коэффициент регрессии

Коэффициент регрессии определяется уравнением:

Y= B ₀ +B ₁ X

Где

B ₀ — константа

B ₁ — коэффициент регрессии

Ниже приведена формула для определения значения коэффициента регрессии.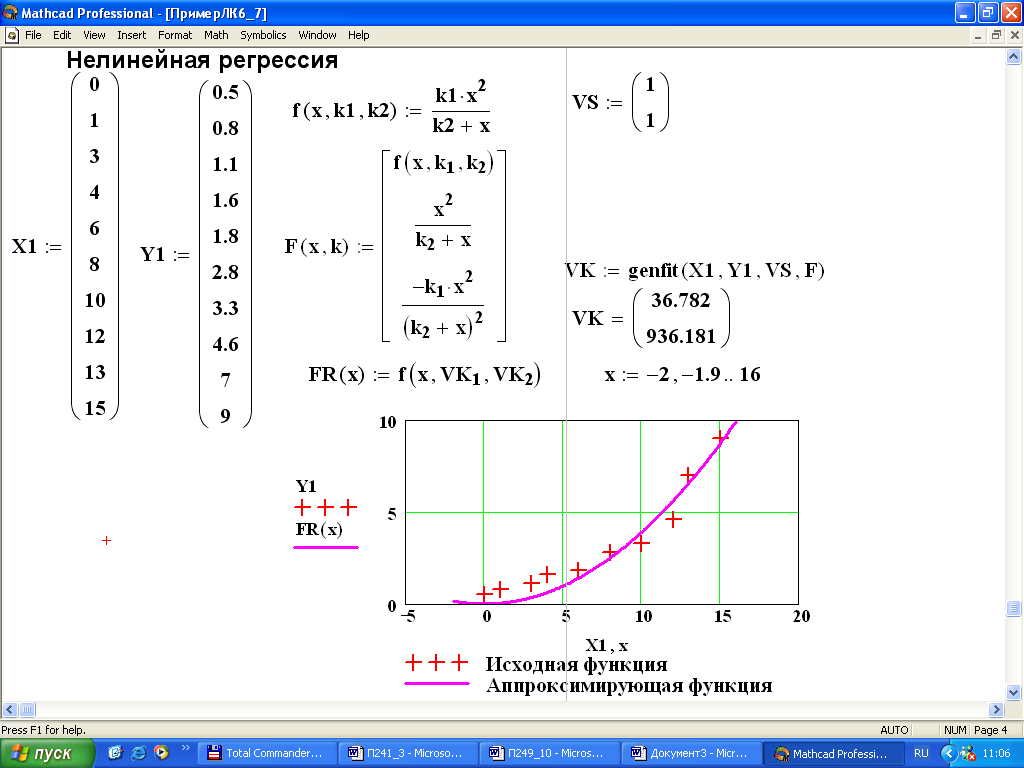

B ₁ =b ₁ = ∑[(x _i -x)(y _i -y)]/∑[(x _i -x) ^{2 9016 9 ]}

Где х _i и y _i — наблюдаемые наборы данных.

А x и y — среднее значение.

Важность линии регрессии 

Линия регрессии используется для описания поведения набора данных. Логический подход помогает нам изучать и анализировать взаимосвязь между двумя различными непрерывными переменными. Затем это применяется в моделях машинного обучения, математическом анализе, области статистики, секторах прогнозирования и других подобных количественных приложениях. Глядя на финансовый сектор, где финансовые аналитики используют линейную регрессию для прогнозирования цен на акции и цены на товары и выполняют различные оценки акций для различных ценных бумаг. Несколько известных компаний используют линейную регрессию для прогнозирования продаж, запасов и т. д. 

Ключевые идеи линейной регрессии 

• Корреляция объясняет взаимосвязь между переменными в данных.

• Дисперсия — это степень разброса данных.

• Стандартное отклонение — это дисперсия среднего из набора данных путем изучения квадратного корня дисперсии.

• Остаток (термин ошибки) — это фактическое значение, найденное в наборе данных, за вычетом ожидаемого значения, предсказанного в линейной регрессии.

Важные свойства линии регрессии 

• Значения коэффициентов регрессии остаются прежними, поскольку смещение начала координат происходит из-за изменения масштаба. Свойство говорит, что если переменные x и y заменить на u и v соответственно, u= (x-a)/p v=(y-c)/q, Здесь p и q — константы. Byz =q/p*bvu Bxy=p/ к*був.

• Если есть две линии регрессии и обе линии пересекаются в выбранной точке (x’, y’). Переменные x и y рассматриваются. В соответствии со свойством пересечение двух линий регрессии равно (x`, y`), что является решением уравнений для обеих переменных x и y.

• Как вы понимаете, коэффициент корреляции между двумя переменными x и y представляет собой среднее геометрическое обоих коэффициентов. При этом знак над значениями коэффициентов корреляции будет общим знаком обоих коэффициентов. Так, если по свойству коэффициенты регрессии равны byx= (b) и bxy= (b’), то коэффициент корреляции равен r=+-sqrt (byx + bxy), поэтому в некоторых случаях оба значения коэффициентов равны отрицательное значение, и r также отрицательно. Если оба значения коэффициентов положительны, то r будет положительным.

• Константа регрессии (a ₀ ) равна точке пересечения линии регрессии по оси y, а также ₀ и ₁ являются параметрами регрессии.

 

Формула линии регрессии:

Уравнение линии линейной регрессии записывается следующим образом:
Y = a + bX

, где X откладывается по оси X, а Y откладывается по оси Y. X — независимая переменная, Y — зависимая переменная. Здесь b — наклон линии, а a — точка пересечения, то есть значение y при x=0.

Формула линии множественной регрессии: y= a +b ₁ x ₁ +b ₂ x ₂ + b ₃ x ₃ +…+ b 900 68 т х _т + у

Допущения, сделанные в линейной регрессии

• Зависимая/целевая переменная является непрерывной.

• Между независимыми переменными нет никакой связи.

• Должна существовать линейная зависимость между зависимой и объясняющей переменными.

• Остатки должны подчиняться нормальному распределению.

• Остатки должны иметь постоянную дисперсию.

• Остатки должны быть независимо распределены/без автокорреляции.

Решенные примеры

1. Найдите уравнение линейной регрессии для следующих двух наборов данных: 7

x

2

4

6

8

y

3

7

5

10

Sol: To find уравнение линейной регрессии нам нужно найти значение Σx, Σy, Σx

2

2

и Σxy 

Построить таблицу и найти значение

9029 0 90 318

x	y	x²	xy 9 0301
2	3	4	6
4	7	16	28
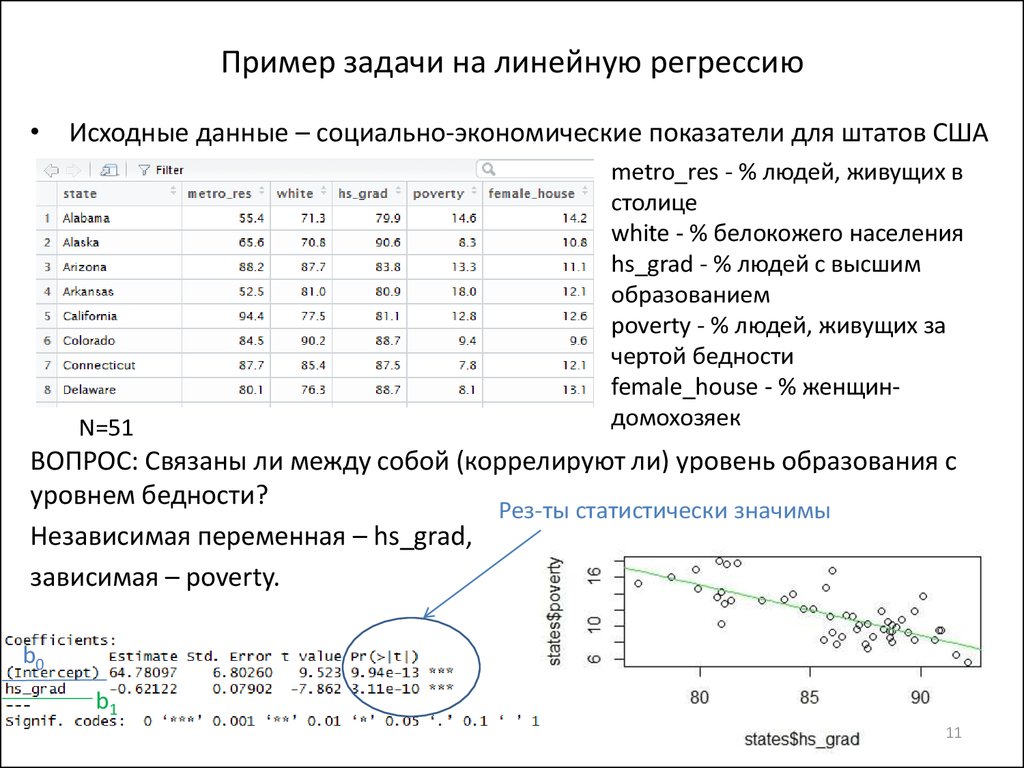
6 9 0003	5	36 9{2}}\] Подставьте значения в уравнение \[b=\frac{4\times 144-20\times 25}{4\times 120-400}\] b=\[ \frac{76}{80}\] b=0,95 Следовательно, мы получили значение a = 1,5 и b = 0,95 Линейное уравнение имеет вид Y = a + bx Теперь положим значения a и b в уравнении Следовательно, уравнение линейной регрессии имеет вид y = 1,5 + 0,95x 2,9 — Примеры простой линейной регрессии Пример 1: данные о рождаемости подростков и уровне бедности Этот набор данных размером n = 51 относится к 50 штатам и округу Колумбия в США (poverty. txt). Переменные: y = коэффициент рождаемости в 2002 году на 1000 женщин в возрасте от 15 до 17 лет и x = уровень бедности, который представляет собой процент населения штата, проживающего в домохозяйствах с доходами ниже установленного на федеральном уровне уровня бедности. (Источник данных: Mind On Statistics , 3-е издание, Уттс и Хекард). График данных ниже (коэффициент рождаемости по вертикали) показывает в целом линейную зависимость, в среднем с положительным наклоном. По мере увеличения уровня бедности рождаемость девочек в возрасте от 15 до 17 лет также имеет тенденцию к увеличению. На следующем графике показана линия регрессии, наложенная на данные. Уравнение подобранной линии регрессии приведено в верхней части графика. В уравнении действительно должно быть указано, что оно предназначено для «средней» рождаемости (или «прогнозируемая» рождаемость тоже подойдет), потому что уравнение регрессии описывает среднее значение 90 510 y 90 511 как функцию одной или нескольких переменных x. В статистической записи уравнение можно было бы записать \ (\ шляпа {у} = 4,267 + 1,373x \). Интерпретация наклона (значение = 1,373) заключается в том, что коэффициент рождаемости в возрасте от 15 до 17 лет увеличивается в среднем на 1,373 единицы на каждую единицу (один процент) увеличения уровня бедности. Интерпретация отрезка (значение = 4,267) заключается в том, что если бы были штаты с уровнем бедности = 0, прогнозируемое среднее значение коэффициента рождаемости в возрасте от 15 до 17 лет было бы 4,267 для этих штатов. Поскольку нет государств с уровнем бедности = 0, такая интерпретация отрезка не имеет практического смысла для этого примера. На графике с линией регрессии мы также видим информацию о том, что s = 5,55057 и r 2 = 53,3%. Значение s говорит нам примерно о стандартном отклонении различий между значениями y отдельных наблюдений и предсказаниями y на основе линии регрессии. Значение r 2 можно интерпретировать как означающее, что уровень бедности «объясняет» 53,3% наблюдаемой вариации среднего уровня рождаемости в возрасте от 15 до 17 лет в штатах. Значение R 2 (прил.) (52,4%) является корректировкой R 2 на основе количества переменных x в модели (здесь только одна) и размера выборки. Только с одной переменной x скорректированное значение R 2 не имеет значения. Пример 2: Функция легких у детей в возрасте от 6 до 10 лет Данные взяты из n = 345 детей в возрасте от 6 до 10 лет. Переменные: y = объем форсированного выдоха (ОФВ), мера того, сколько воздуха человек может принудительно выдохнуть из легких, и x = возраст в годах. (Источник данных: приведенные здесь данные являются частью набора данных, приведенного в Kahn, Michael (2005). «Выдающаяся проблема для обучения статистике», 9.0510 Журнал статистического образования , 13(2). Ниже приведен график данных с наложенной простой линией линейной регрессии. Расчетное уравнение регрессии таково, что средний ОФВ = 0,01165 + 0,26721 × возраст. Например, для 8-летнего ребенка мы можем использовать уравнение, чтобы оценить, что средний ОФВ = 0,01165 + 0,26721 × (8) = 2,15. Интерпретация наклона заключается в том, что средний ОФВ увеличивается на 0,26721 на каждый год увеличения возраста (в наблюдаемом возрастном диапазоне). Интересной и, возможно, важной особенностью этих данных является то, что отклонение отдельных значений y от линии регрессии увеличивается с возрастом. Эта особенность данных называется непостоянной дисперсией . Например, значения ОФВ у 10-летних детей более изменчивы, чем значения ОФВ у 6-летних. Это видно, если посмотреть на вертикальные диапазоны данных на графике. Это может привести к проблемам при использовании простой модели линейной регрессии для этих данных, что мы рассмотрим более подробно в уроке 49. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт