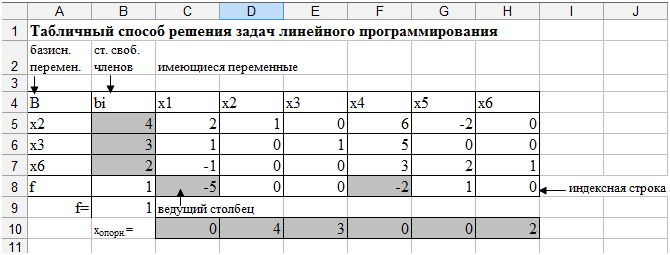
Анализ задач линейного программирования в Excel
Похожие презентации:
Решение задач линейного программирования в MS Excel
Двойственные задачи линейного программирования
Линейное программирование
Задачи линейного программирования. (Тема 3)
Симплекс-метод для решения задач линейного программирования
Задача линейного программирования
Линейное программирование
Введение в линейное программирование
Дополнительные возможности анализа данных в MS Excel. Аппроксимация экспериментальных данных. Линии тренда
Симплекс-метод решения задач линейного программирования
Далее
Кротова Наталья
Майорова Татьяна
Студентки группы 411-П.
Анализ задач
линейного
программирования в
Excel
Выход
Содержание
Введение
Задача
Отчет по результатам
Отчет по устойчивости
Отчет по пределам
Тест
Выход
Анализ оптимального
решения
• Анализ оптимального решения выполняется на
основании применения положений симплекс-метода и
экране появится диалоговое окно Результат поиска
решения.
 Решение найдено. С помощью этого
Решение найдено. С помощью этогодиалогового окна можно вызвать отчеты трех типов:
• Результаты;
• Устойчивость;
• Пределы.
Рассмотрим на конкретном примере.
Задача
Цех по выпуску двух видов обуви применяет сырье 3-х видов, запасы
которого составляют соответственно 100, 60, 40 единиц.
Нормы затрат сырья на каждый вид обуви, а также прибыль от одной пары обуви
приведены в таблице.
Вид
сырья
Нормы затрат
1
2
3
Прибыль от одной
пары обуви (руб)
3
2
1
1
6
4
Вид продукции (обуви)
1
2
2
0
Определить план выпуска продукции, обеспечивающий максимальную прибыль.
Решаем задачу в Excel 7.0.
1.Сервис, Поиск решения…
На экране диалоговое окно Поиск решения.
2. Назначить целевую функцию.
3. Ввести адреса искомых переменных.
4. Ввести ограничения.
5. Нажать на кнопку Выполнить.
После успешного решения задачи на экране появляется диалоговое окно
С помощью этого диалогового окна можно вызвать отчеты трех типов:
— результаты;
— устойчивость;
— пределы.

• Для этого устанавливаем курсор на тип вызываемого отчета и ОК.
• На экране: вызванный отчет на новом листе, на ярлычке которого
указано название отчета.
• Курсор на ярлычок с названием отчета.
• На экране: вызванный отчет.
Содержание
Отчет по результатам
Отчет состоит из трех таблиц:
• Таблица 1 приводит сведения о целевой функции.
В столбце Исходно приведены значения целевой
функции до начала вычислений.
• Таблица 2 приводит значения искомых переменИзменяемые ячейки
ных, полученные в результате решения задачи.
Имя
Исходно Результат
• Таблица 3 показывает результаты оптимального ре$F$13
Объем
30
30
шения для ограничений и для граничных условий.
$F$14
Объем
5
5
Для Ограничений в графе Формула приведены зависимости, которые были введены в диалоговое окно ПоОграничения
иск решения ; графе Значение приведены величины
Ячейка
Имя
Значение формула Статус Разница использованного ресурса; в графе Разница показано
$B$16 Нормы затрат
100 $B$16<=$B$15связанное
0
количество неиспользованного ресурса.
 Если ресурс
Если ресурс$C$16
60 $C$16<=$C$15связанное
0
используется полностью, то в графе Состояние ука$D$16
35 $D$16<=$D$15не связан.
5
зывается связанное; при неполном использовании ре$F$13
Объем
30
$F$13>=0 не связан. 30
сурса в этой графе указывается не связан.
$F$14
Объем
5
$F$14>=0 не связан.
5
Для Граничных условий приводятся аналогичные
величины с той лишь разницей, что вместо величины
неиспользованного ресурса показана разность между
значением переменной в найденном оптимальном реСодержание
шении и заданным для нее граничным условием.
Целевая ячейка (Максимум)
Ячейка
Имя
Исходно Результат
$B$17 Прибыль
200
200
Отчет по устойчивости
Отчет по устойчивости состоит из двух таблиц.
В таблице 1 приводятся значения для переменных:
Результ. Нормир. Целевой Допустимое Допустимое • результат решения задачи;
Ячейка Имя значение стоимость Коэффициент Увеличение Уменьшение • редуцированная стоимость, т.
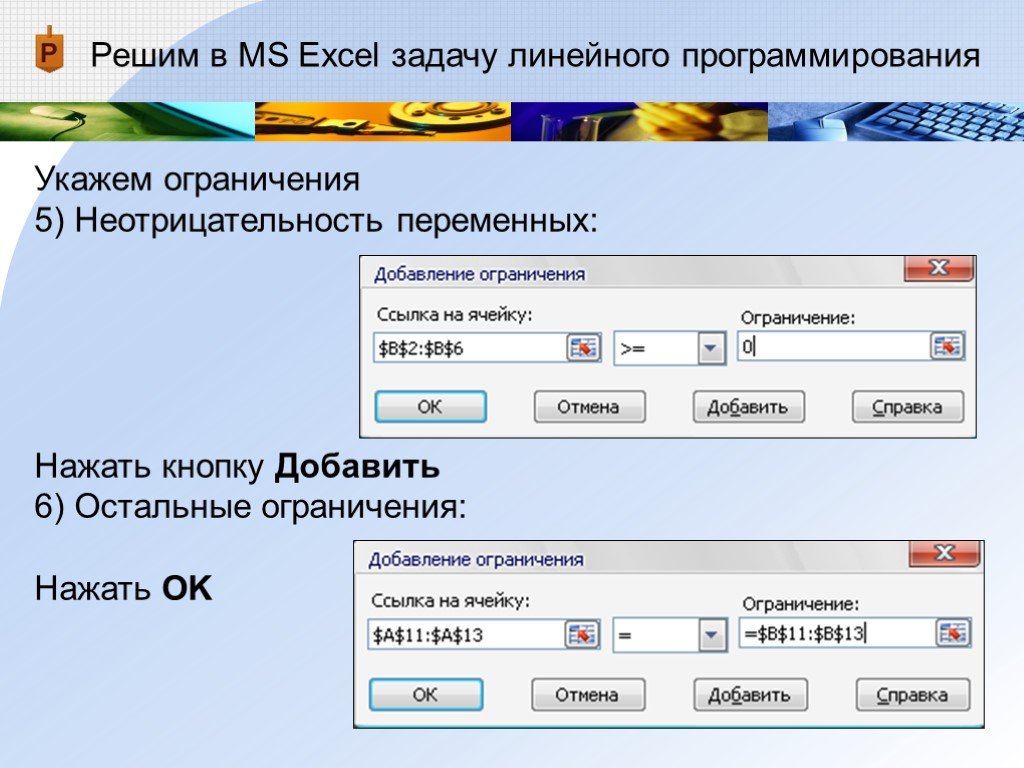 е. дополнительные
е. дополнительныедвойственные переменные vј, которые показывают,
$F$13 Объем
30
0
6
1E + 30
0
насколько изменяется целевая функция при
5
0
4
0
4
принудительном включении единицы этой продукции
в оптимальное решение;
• коэффициенты целевой функции;
Ограничения
Результ. Теневая Ограничение Допустимое Допустимое • предельные значения приращения коэффициентов Δcј
целевой функции, при которых сохраняется набор
Ячейка Имя значение Цена Правая часть Увеличение Уменьшение
переменных, входящих в оптимальное решение.
$B$16 Нормы затрат 100
2
100
10
10
В таблице 2 приводятся аналогичные значения для огра$C$16
60
0
60
7
20
ничений:
$D$16
35
0
40
1E + 30
5
• величина использованных ресурсов;
• теневая цена, т.е. двойственные оценки zi, которые
показывают, как изменится целевая функция при измении ресурсов на единицу;
• значения приращения ресурсов Δbi, при которых сохраняется оптимальный набор переменных, входящих
в оптимальное решение.

Содержание
Изменяемые ячейки
Отчет по пределам
Целевое
Ячейка Имя значение
$B$17 Прибыль 200
Изменяемое
Нижний Целевое Верхний Целевое
Ячейка Имя значение предел результат предел результат
$F$13 Объем 30
0
20
30 200
$F$14 Объем 5
0
180
5
200
В отчете показано, в каких пределах может изменяться выпуск продукции, вошедший в оптимальное решение, при сохранении структуры оптимального решения:
приводятся значения xј в оптимальном
решении;
приводятся нижние пределы изменения значений xј, т.е. допустимое уменьшение.
указаны значения целевой при выпуске данной
продукции на нижнем пределе;
приводятся верхние пределы изменения xј , т.е.
допустимое увеличение.
приводятся значения целевой функции при выпуске продукции, вошедшей в оптимальное
Содержание
выход
English Русский Правила
1.2 Анализ задач линейного программирования в Excel
При
рассмотрении симплексного метода было
показано, как решение задачи линейного
программирования выполнить с помощью
надстройки Excel Поиск решения.
На рис. 1.4 приведено найденное таким образом решение задачи о выпуске продукции.
Кроме этого решения, как было указано, Excel позволяет представить результаты поиска решений в форме отчета трех типов:
Результаты. В отчет включаются исходные и конечные значения целевой и изменяемой ячеек, дополнительные сведения об ограничениях.
Устойчивость. Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы. Помимо исходных и конечных значений изменяемых и целевой ячеек, в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
Содержание указанных отчетов – в таблицах 1.1 – 1.3.
отчет
по результатам (табл.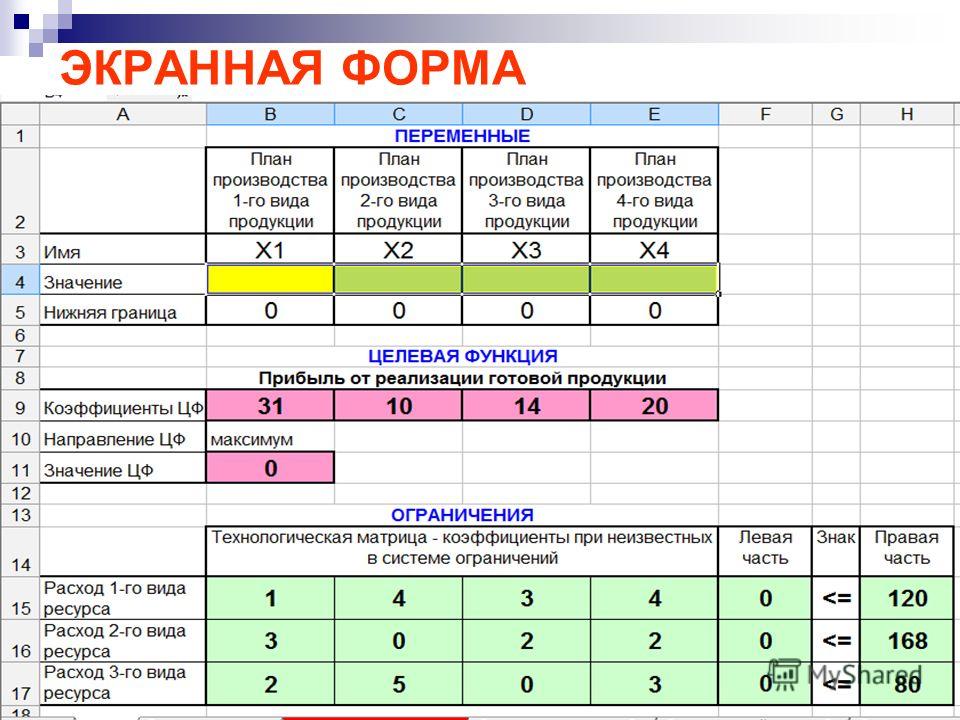 1.1) состоит из трех таблиц:
1.1) состоит из трех таблиц:
таблица 1 приводит сведения о целевой функции. В столбце Исходное значение приведены значения целевой функции до начала вычислений;
таблица 2 приводит значения искомых переменных, полученные в результате решения задачи;
таблица 3 показывает результаты оптимального решения для ограничений и граничных условий.
Таблица 1.1 – Содержание отчета по результатам.
Microsoft Excel 10.0 Отчет по результатам | ||||||
Рабочий лист: [Книга1]Лист1 | ||||||
Отчет
создан: 15. | ||||||
Целевая ячейка (Максимум) | ||||||
Ячейка | Имя | Исходное значение | Результат | |||
$F$4 | коэф.в ЦФ ЦФ | 0 | 1320 | |||
Изменяемые ячейки | ||||||
Ячейка | Имя | Исходное значение | Результат | |||
$B$3 | значение Х1 | 0 | 10 | |||
$C$3 | значение Х2 | 0 | 0 | |||
$D$3 | значение Х3 | 0 | 6 | |||
$E$3 | значение Х4 | 0 | 0 | |||
Ограничения | ||||||
Ячейка | Имя | Значение | Формула | Статус | Разница | |
$F$7 | труд левая часть | 16 | $F$7<=$H$7 | связанное | 0 | |
$F$8 | оборудование левая часть | 100 | $F$8<=$H$8 | связанное | 0 | |
$F$9 | полуфабрикаты левая часть | 84 | $F$9<=$H$9 | не
связан. | 26 | |
Для ограничений в графе формула приведены зависимости, которые были введены в диалоговой окно Поиск решения; в графе Значение приведены величины использованного ресурса; в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается связанное; при неполном использовании ресурса в этой графе указывается не связан.
Для граничных условий приводятся величины с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Итак,
в табл. 1.1 (в отчете по результатам)
содержатся оптимальные значения
переменных х1,
х2,
х3,
х4,
которые соответственно равны 10; 0; 6; 0;
значение целевой функции – 1320, а также
величина левых частей ограничений
соответственно полученному оптимальному
плану.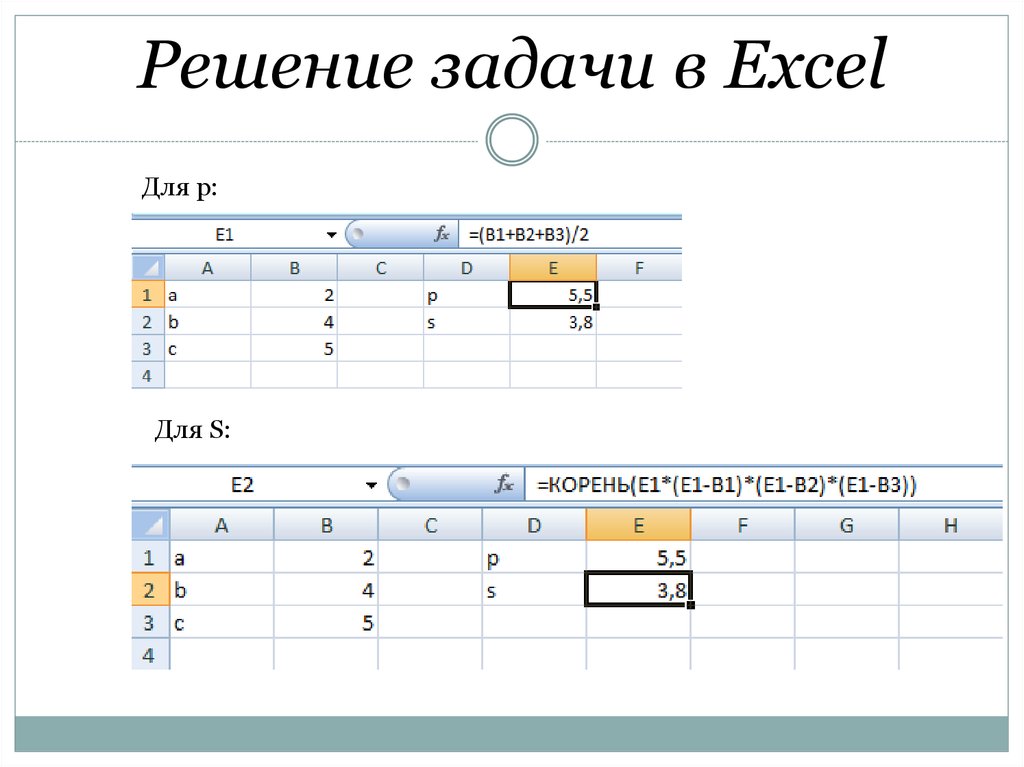 Так, в рассматриваемой задаче
первое и второе ограничения выполнились
как равенства, а в третьем левая часть
(потребленное количество полуфабрикатов)
меньше правой части на 26 (столбец
Разница).
Так, в рассматриваемой задаче
первое и второе ограничения выполнились
как равенства, а в третьем левая часть
(потребленное количество полуфабрикатов)
меньше правой части на 26 (столбец
Разница).
Решение двойственной задачи можно найти, выбрав команду Поиск решений => Отчет по устойчивости. Этот отчет для условий рассматриваемой задачи приводится в табл. 1.2.
Отчет по устойчивости состоит из двух таблиц.
В таблице 1 приводятся следующие значения для переменных:
результат решения задачи;
нормированная стоимость, т.е. дополнительные двойственные переменные, которые показывают, как изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;
коэффициенты целевой функции;
предельные значения приращения коэффициентов cj целевой функции, при которых сохраняется оптимальное решение.

В таблице 2 приводятся аналогичные значения для ограничений:
величина использованных ресурсов;
теневая цена, т.е. двойственные оценки yi, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
значение приращения ресурсов bi, при которых сохраняется структура базиса оптимального плана, а следовательно, и величина оптимальных оценок.
Таблица 1.2 – Содержание отчета по устойчивости.
Microsoft Excel 10.0 Отчет по устойчивости | |||||||
Рабочий лист: [Книга1]Лист1 | |||||||
Отчет
создан: 15. | |||||||
Изменяемые ячейки | |||||||
|
| Результ. | Нормир. | Целевой | Допустимое | Допустимое | |
Ячейка | Имя | значение | стоимость | Коэффициент | Увеличение | Уменьшение | |
$B$3 | значение Х1 | 10 | 0 | 60 | 40 | 12 | |
$C$3 | значение Х2 | 0 | -10 | 70 | 10 | 1E+30 | |
$D$3 | значение Х3 | 6 | 0 | 120 | 30 | 13,33333333 | |
$E$3 | значение Х4 | 0 | -20 | 130 | 20 | 1E+30 | |
Ограничения | |||||||
|
| Результ. | Теневая | Ограничение | Допустимое | Допустимое | |
Ячейка | Имя | значение | Цена | Правая часть | Увеличение | Уменьшение | |
$F$7 | труд левая часть | 16 | 20 | 16 | 3,545454545 | 6 | |
$F$8 | оборуд. | 100 | 10 | 100 | 60 | 36 | |
$F$9 | полуф. левая часть | 84 | 0 | 110 | 1E+30 | 26 | |
Так,
в первой таблице отчета
по устойчивости для рассматриваемой
задачи (табл.
1.2) нормированная стоимость для продукции
второго вида равна -10 ден.ед./шт. Это
означает, что если
мы, несмотря на
оптимальное решение (10; 0; 6; 0),
попробуем
включить
в план выпуска одно изделие второго
вида, то новый
план
выпуска принесет нам доход 1310 ден.ед.,
что на 10 ден.ед.
меньше,
чем прежнее оптимальное решение.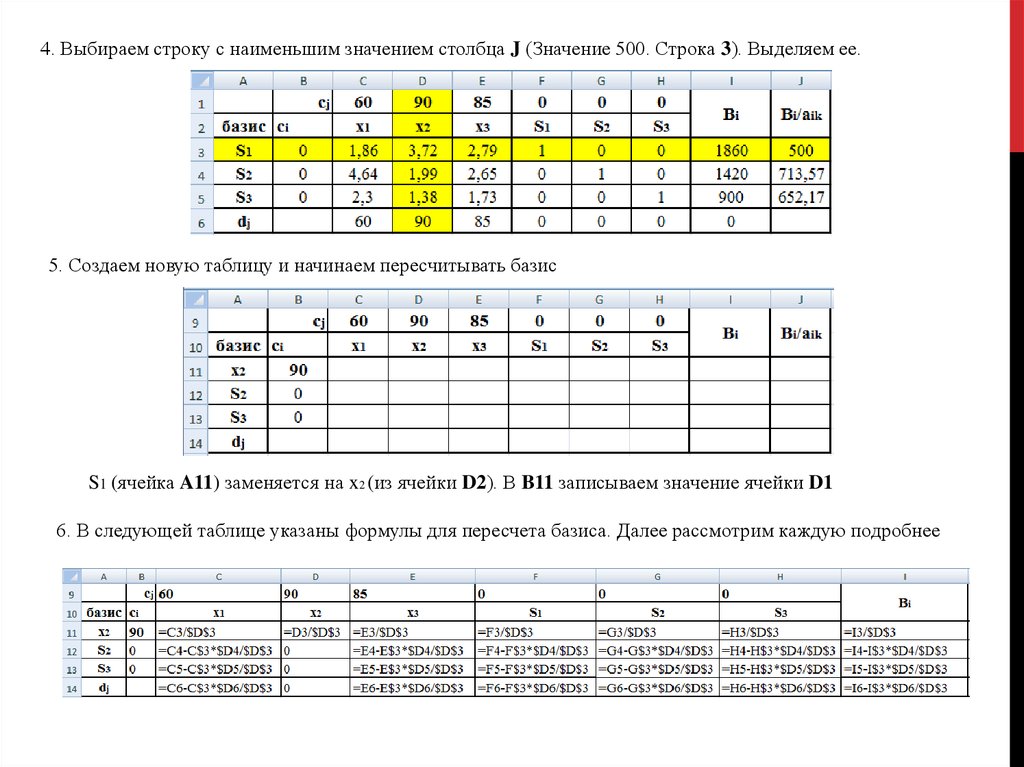
Предельные значения приращения целевых коэффициентов сj, при которых сохраняется первоначальное оптимальное решение, показывают, что, например, допустимое увеличение прибыльности продукции первого вида равно 40 ден. ед./шт., а допустимое уменьшение составляет 12 ден. ед. По изделию второго вида допустимое увеличение прибыльности составляет 10 ден. ед, а допустимое уменьшение — практически не ограничено. Это означает, что если прибыль на одно изделие второго вида возрастет более чем на 10 ден.ед./шт., то оптимальное решение изменится: станет целесообразным выпускать изделия второго вида. А если прибыльность второго изделия будет снижаться вплоть до нуля, то оптимальное решение (10; 0; 6; 0) останется прежним.
вторая
часть табл. 1.2 содержит информацию,
относящуюся
к ограничениям. Так, в графе Допустимое
уменьшение показано, на сколько можно уменьшить
(устранить
излишек) или увеличить (повысить
минимально необходимое
требование) ресурс, сохранив при этом
допустимое
решение и, что очень важно, оставив
неизменной величину оптимальной оценки
(«теневой цены»).
Рассмотрим дефицитные ресурсы. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие предприятию выпускать больше П2, чем в оптимальном решении, и получать более высокий доход. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы «труд» и «оборудование». Поскольку знак ограничений этих запасов имеет вид « », то возникает вопрос, на сколько максимально должен возрасти запас этих ресурсов, чтобы обеспечить увеличение выпуска продукции. Ответ на этот вопрос показан в графе Допустимое увеличение. Ресурс «труд» имеет смысл увеличивать не более, чем на 3,5 чел.-часа, а ресурс «оборудование» – не более, чем на 60 станко-час.
Ценность дополнительной единицы i-го ресурса («теневая цена») рассчитывается только для дефицитных ресурсов и характеризует прирост результата в расчете на одну дополнительную единицу соответствующего ресурса.
Ценность
различных видов ресурсов нельзя
отождествлять с действительными ценами,
по которым осуществляется его закупка. В данном случае речь идет о некоторой
мере, имеющей экономическую природу,
которая характеризует ценность ресурса
только относительно полученного
оптимального решения.
В данном случае речь идет о некоторой
мере, имеющей экономическую природу,
которая характеризует ценность ресурса
только относительно полученного
оптимального решения.
Таблица 1.3 – Содержание отчета по пределам
Microsoft Excel 10.0 Отчет по пределам | |||||||||
Рабочий лист: [Книга1]Отчет по пределам 1 | |||||||||
Отчет создан: 15.04.2006 1:22:43 | |||||||||
| Целевое |
| |||||||
Ячейка | Имя | Значение | |||||||
$F$4 | коэф. | 1320 | |||||||
| Изменяемое |
| Нижний | Целевой | Верхний | Целевой | |||
Ячейка | Имя | Значение | предел | результат | предел | результат | |||
$B$3 | значение Х1 | 10 | 0 | 720 | 10 | 1320 | |||
$C$3 | значение Х2 | 0 | 0 | 1320 | 0 | 1320 | |||
$D$3 | значение Х3 | 6 | 0 | 600 | 6 | 1320 | |||
$E$3 | значение Х4 | 0 | 0 | 1320 | 0 | 1320 | |||
В
отчете по пределам (табл.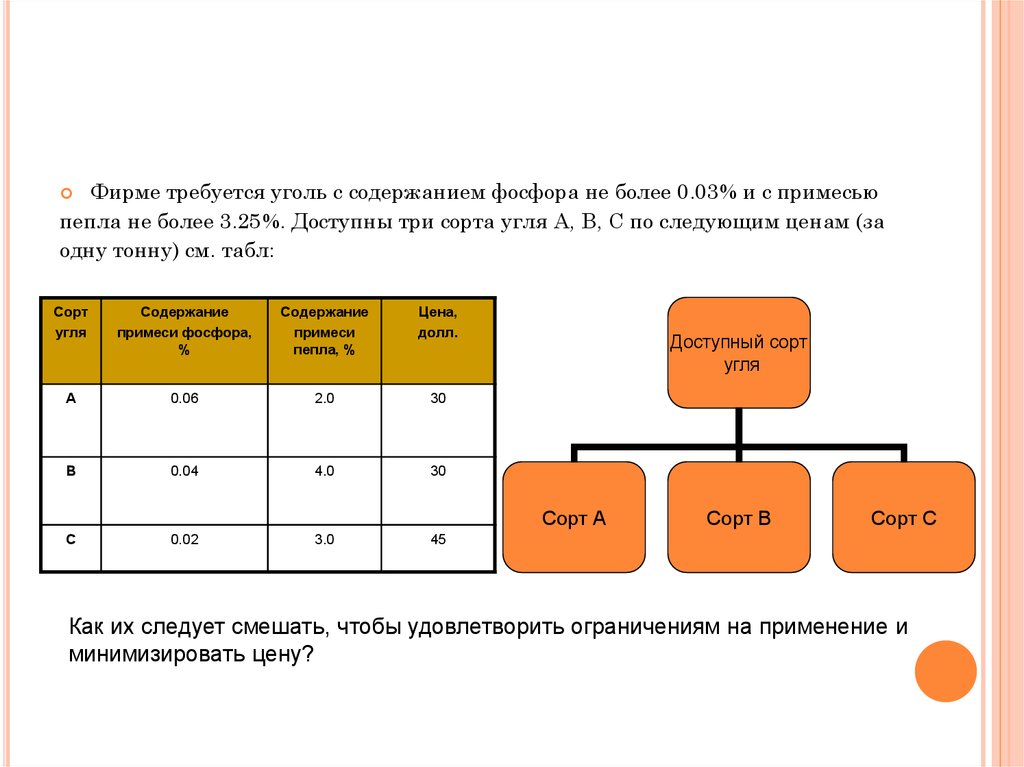 1.3) показано, в каких пределах
может изменяться выпуск продукции,
вошедшей в оптимальный план, при
сохранении структуры оптимального
решения:
1.3) показано, в каких пределах
может изменяться выпуск продукции,
вошедшей в оптимальный план, при
сохранении структуры оптимального
решения:
Кроме этого, в отчете указаны значения целевой функции при выпуске данного продукта на нижнем пределе. Так, значение 720 соответствует следующей ситуации:
F = c1x1 + c3x3 = 60 0 + 120 6 = 720.
Далее приводятся верхние пределы изменения xj и значения целевой функции при выпуске продукции, вошедшей в оптимальный план на верхнем пределе. Поэтому везде F = 60 10 + 120 6 = 1320.
Линейное программирование в Excel | Как использовать линейное программирование в Excel?
Линейное программирование в Excel (оглавление)
- Введение в линейное программирование в Excel
- Методы решения задач линейного программирования с помощью Excel Solver
Линейное программирование является наиболее важным, а также увлекательным аспектом прикладной математики, который помогает в оптимизации ресурсов (минимизации потерь или максимизации прибыли с заданными ресурсами). Если у нас есть ограничения и целевая функция хорошо определена, мы можем использовать систему для прогнозирования оптимального решения для данной проблемы. В Excel у нас есть Excel Solver, который помогает нам решать задачи линейного программирования, также известные как LPP. В этой статье мы увидим, как использовать Excel Solver для оптимизации ресурсов, связанных с бизнес-задачами, с помощью линейного программирования.
Если у нас есть ограничения и целевая функция хорошо определена, мы можем использовать систему для прогнозирования оптимального решения для данной проблемы. В Excel у нас есть Excel Solver, который помогает нам решать задачи линейного программирования, также известные как LPP. В этой статье мы увидим, как использовать Excel Solver для оптимизации ресурсов, связанных с бизнес-задачами, с помощью линейного программирования.
Первым делом. Давайте посмотрим, как мы можем включить Excel Solver (ключевой компонент LPP в Excel).
Методы решения линейного программирования с помощью решателя Excel
Давайте разберемся, как использовать линейное программирование с помощью решателя Excel с некоторыми методами.
Вы можете скачать этот шаблон Excel для линейного программирования здесь — Шаблон Excel для линейного программирования
Метод №1 — Включение решателя в Microsoft Excel
В Microsoft Excel мы можем найти решатель на вкладке «Данные», которую можно найти на ленте Excel, расположенной в верхней части, как показано ниже:
Если вы не видите эту утилиту там, вам нужно включить ее через параметры Excel. Выполните следующие действия, чтобы включить Solver в Excel.
Выполните следующие действия, чтобы включить Solver в Excel.
Шаг 1: Перейдите к меню «Файл» и нажмите «Параметры», которое является последним в этом списке.
Шаг 2: Появится новое окно с названием «Параметры Excel». Нажмите «Надстройки» в списке параметров, представленных в левой части окна.
Шаг 3: В разделе «Управление» в нижней части окна выберите «Надстройки Excel» из раскрывающегося списка и нажмите кнопку «Перейти…», расположенную рядом.
Шаг 4: Как только вы нажмете кнопку «Перейти…», вы сможете увидеть список всех надстроек, доступных в Excel, в новом окне. Установите флажок, чтобы выбрать надстройку Solver, чтобы ее можно было использовать на вкладке «Данные» для решения уравнений. Нажмите кнопку OK после выбора надстройки Solver.
Таким образом, вы можете включить Excel Solver в Microsoft Excel.
Метод № 2. Решение задачи линейного программирования с помощью Excel Solver
Теперь мы попытаемся решить задачу линейного программирования с помощью инструмента Excel Solver.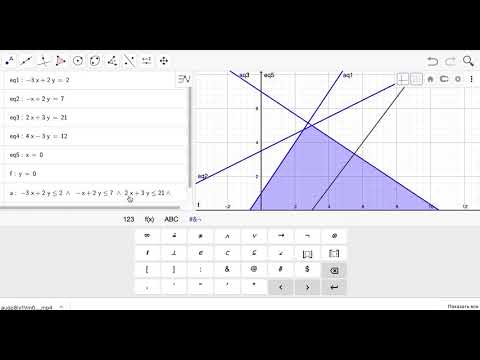
Пример: Химический завод производит два продукта: A. Для этих двух продуктов требуется сырье, как показано ниже: Для продукта A требуется три типа сырья – Материал_1 20 кг, Материал_2 30 кг, Материал_3 5 кг. Аналогично, для продукта B требуется 10 кг материала_1, 30 кг материала_2 и 10 кг материала_3. Производителю требуется минимум 460 кг или Материал_1, 960 кг материала_2 и 220 кг материала_3. Если стоимость единицы продукта А составляет 30 долларов, а стоимость продукта В — 35 долларов, сколько продуктов должен смешать производитель, чтобы удовлетворить минимальные потребности в материалах при минимально возможных затратах? Давайте используем информацию, представленную в этом примере, для моделирования уравнений.
Шаг 1: Мы можем увидеть все ограничения уравнения, которые мы можем сформировать, используя информацию, представленную в приведенном выше примере.
Шаг 2: Используйте эти уравнения, чтобы добавить ограничения по ячейкам в Excel на A2: C8 данного листа.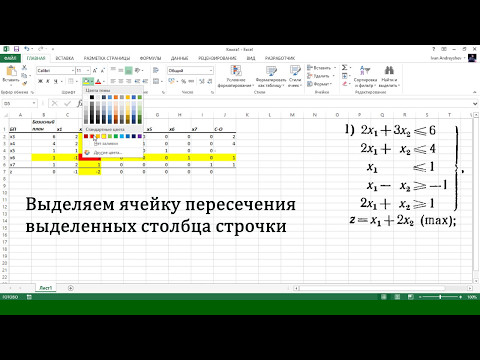 См. снимок экрана, как показано ниже:
См. снимок экрана, как показано ниже:
Шаг 3: Теперь нам нужно использовать формулу Количество * Стоимость единицы и просуммировать ее для обоих продуктов, чтобы получить фактические потребности в материалах. Вы можете увидеть это в столбце D для всех ячеек, содержащих ограничения B3, B4, C3). См. прикрепленный снимок экрана ниже:
Если вы внимательно посмотрите на эту формулу, мы использовали B3 и C3 в качестве фиксированных членов для каждой формулы в разных ячейках в столбце D. Это связано с тем, что B3 и C3 являются ячейки, обозначающие количество Продукта А и Продукта Б соответственно. Эти величины появятся после того, как система уравнений будет решена с помощью Excel Solver.
Шаг 4: Нажмите на вкладку «Данные», а затем на «Решатель», который находится в разделе «Анализ» на вкладке.
Шаг 5: После того, как вы нажмете Solver, откроется новая вкладка под названием «Solver Parameter», в которой вам нужно установить параметры для этого набора уравнений, которые необходимо решить.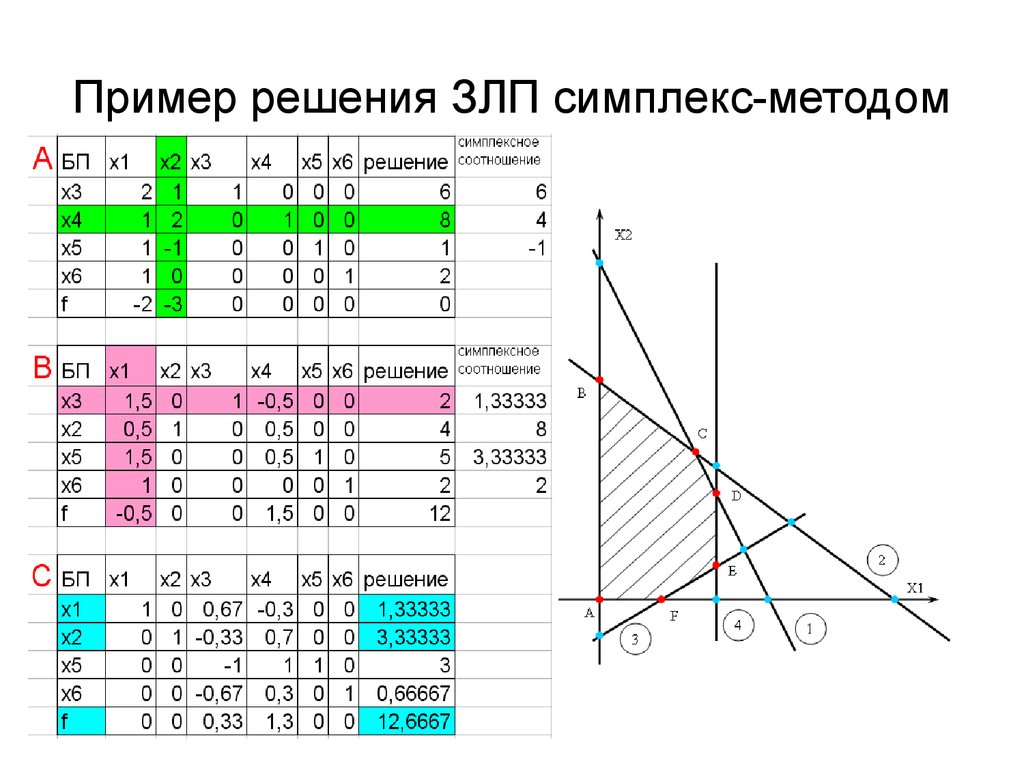
Шаг 6: Первое, что нам нужно определить, это Se t Цель: Поскольку наша цель состоит в том, чтобы вычислить общие затраты, чтобы их можно было минимизировать, установите для этого параметра значение D4.
Шаг 7: Поскольку нам нужно минимизировать стоимость при максимально возможном производстве, установите следующий параметр как Mi n . Вы можете сделать это, нажав на кнопку-переключатель Min.
Шаг 8: в разделе «Изменение ячеек переменных»: нам нужно упомянуть B3 и C3, поскольку эти ячейки будут содержать количества для продукта A и продукта B, соответственно, после того, как проблема будет решена.
Шаг 9: Теперь добавьте ограничения. Нажмите кнопку A dd под объектом S u в разделе Constraints:, и откроется новое окно для добавления ограничений. Под этим окном – B3:C3 в качестве ссылки на ячейку, >= и 0 в качестве ограничений.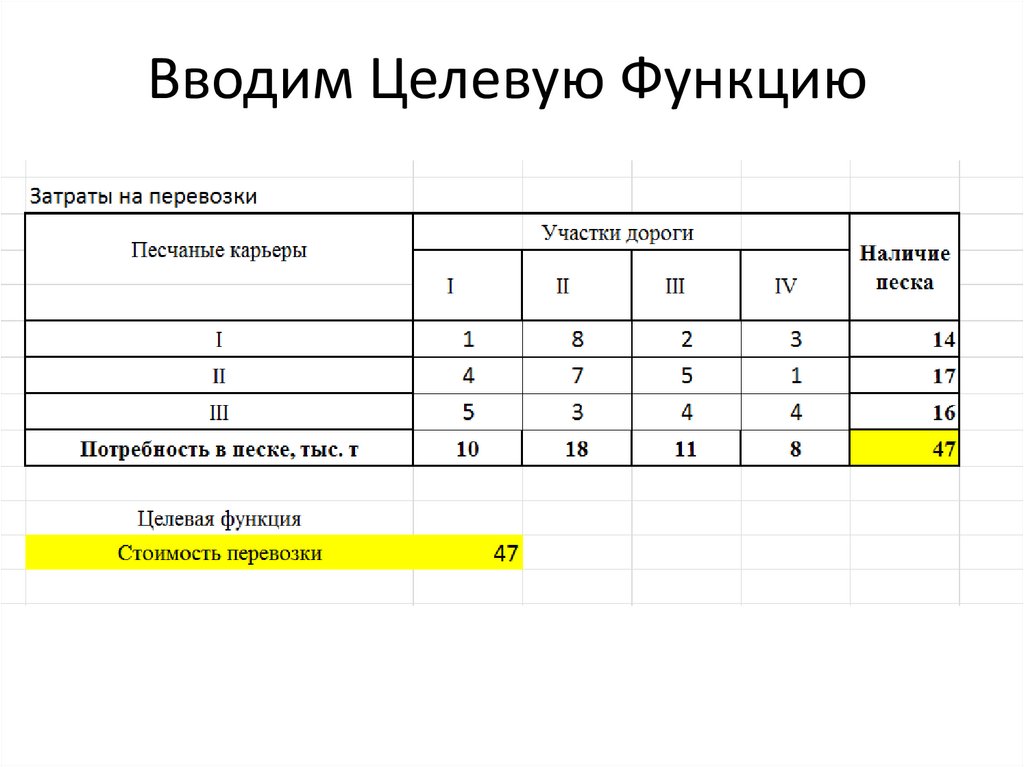 Это мы делаем, поскольку основным ограничением в любом LPP является то, что X и Y должны быть больше нуля.
Это мы делаем, поскольку основным ограничением в любом LPP является то, что X и Y должны быть больше нуля.
Шаг 10: Нажмите еще раз на кнопку «Добавить» и на этот раз используйте B3:C3 в качестве ссылки на ячейку и F6:F8 в качестве ограничений с неравенством >=. Нажмите кнопку OK, чтобы добавить это ограничение под решатель.
Решатель теперь имеет все параметры, необходимые для решения этой системы линейных уравнений, и выглядит следующим образом: уравнения и найти оптимальное решение.
Как только мы нажимаем кнопку решения, система начинает поиск оптимального решения поставленной нами задачи, и мы получаем значения для B3, C3, используя которые мы также получаем значения в столбце F для F4 , F6:F8, которые являются оптимальными затратами и стоимостью материалов, которые можно использовать для продукта A и продукта B.
Это решение сообщает нам, что если нам нужно минимизировать стоимость производства продукта A и продукта B при оптимальном использовании Material_1, Material_2 и Material_3, мы должны произвести 14 количеств продукта A и 18 количеств продукта B.
Это из этой статьи. Давайте подытожим некоторые моменты, которые следует помнить:
Что нужно помнить о линейном программировании в Excel
- Обязательно решать задачи линейного программирования с помощью Excel Solver. Другого метода, с помощью которого мы могли бы это сделать, нет.
- Мы всегда должны иметь готовые ограничения и объектную переменную.
- Если Решатель не включен, вы можете включить его в параметрах надстройки Excel.
Рекомендуемые статьи
Это руководство по линейному программированию в Excel. Здесь мы обсуждаем, как использовать линейное программирование в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть другие наши рекомендуемые статьи —
- Интерполяция в Excel
- Программирование в Excel
- Линейная интерполяция в Excel
- Линейная регрессия в Excel
Обучение линейному программированию с помощью Excel Solver (CHEER v9 n3)
Зигги Макдональд
Университет Лестера
Линейное программирование (ЛП) является одним из наиболее широко применяемых О. Р.
техники и обязана своей популярностью, главным образом, Джорджу Данцигу.
симплекс-метод (Данциг, 1963) и революция в вычислительной технике. Это
очень мощная техника для решения проблем распределения и
стал стандартным инструментом для многих предприятий и организаций.
Хотя симплекс-метод Данцига позволяет генерировать решения
вручную, итеративный характер создания решений настолько
утомительно, что если бы компьютер никогда не был изобретен, то линейный
программирование оставалось бы интересной академической идеей,
переведены в кабинет математики. К счастью, компьютеры
были изобретены, и так как они стали такими мощными за так мало
стоимость, линейное программирование стало, возможно, одним из самых
Широкое использование персонального компьютера.
Р.
техники и обязана своей популярностью, главным образом, Джорджу Данцигу.
симплекс-метод (Данциг, 1963) и революция в вычислительной технике. Это
очень мощная техника для решения проблем распределения и
стал стандартным инструментом для многих предприятий и организаций.
Хотя симплекс-метод Данцига позволяет генерировать решения
вручную, итеративный характер создания решений настолько
утомительно, что если бы компьютер никогда не был изобретен, то линейный
программирование оставалось бы интересной академической идеей,
переведены в кабинет математики. К счастью, компьютеры
были изобретены, и так как они стали такими мощными за так мало
стоимость, линейное программирование стало, возможно, одним из самых
Широкое использование персонального компьютера.
Конечно, существует множество программных пакетов, которые
предназначенный для решения линейных программ (и других типов
математическая программа), из которых, возможно, LINDO, GAMS и
XPRESS-MP являются наиболее популярными. Все эти пакеты имеют тенденцию быть DOS
основаны и предназначены для специализированного рынка, который требует
инструменты, предназначенные для решения LP. Однако в последние годы несколько
стандартные бизнес-пакеты, такие как электронные таблицы, запущены
включить вариант решения LP, и Microsoft Excel не
исключение. Включение возможности решения LP в
такие приложения, как Excel, привлекательны как минимум для двух
причины. Во-первых, Excel, пожалуй, самая популярная электронная таблица.
используется как в бизнесе, так и в университетах и поэтому очень
доступный. Во-вторых, электронная таблица предлагает очень
удобные функции ввода и редактирования данных, которые позволяют
учащиеся лучше понимают, как строить
линейные программы.
Однако в последние годы несколько
стандартные бизнес-пакеты, такие как электронные таблицы, запущены
включить вариант решения LP, и Microsoft Excel не
исключение. Включение возможности решения LP в
такие приложения, как Excel, привлекательны как минимум для двух
причины. Во-первых, Excel, пожалуй, самая популярная электронная таблица.
используется как в бизнесе, так и в университетах и поэтому очень
доступный. Во-вторых, электронная таблица предлагает очень
удобные функции ввода и редактирования данных, которые позволяют
учащиеся лучше понимают, как строить
линейные программы.
Чтобы использовать Excel для решения задач LP, надстройка Solver должна быть включены. Обычно эта функция не устанавливается по умолчанию, когда Excel сначала устанавливается на ваш жесткий диск. Чтобы добавить это средство в в меню «Инструменты» вам необходимо выполнить следующие шаги (только один раз):
- Выберите пункт меню Инструменты | Add_Ins (это займет несколько минут, чтобы загрузить необходимый файл).

- В представленном диалоговом окне установите флажок для надстройки Solver.
- После нажатия кнопки «ОК» вы сможете получить доступ к параметру «Решатель» из нового пункта меню «Инструменты | Решатель (отображается в меню Инструменты | Сценарии…)
Чтобы проиллюстрировать Excel Solver, я рассмотрю метод Хиллиера и Либермана.
достаточно известный пример, проблема Wyndor Glass Co.
(Хиллиер и Либерман, 1995). Проблема касается стакана
производитель, который использует три производственных предприятия для сборки своих
продукты, в основном стеклянные двери (x1) и окна с деревянными рамами (x2).
Каждому продукту требуется разное время на трех заводах и
существуют определенные ограничения на доступное время производства в
каждое растение. Обладая этой информацией и знанием
взносы в прибыль двух продуктов управление
компания хочет определить, какое количество каждого продукта они
должны производить, чтобы максимизировать прибыль. Другими словами,
задача Wyndor Glass Co. — классическая, хотя и очень простая,
проблема ассортимента товаров.
— классическая, хотя и очень простая,
проблема ассортимента товаров.
Задача формулируется в виде следующей линейной программы:
max z = 3x1 + 2x2 (цель)
при условии x1 <= 4 (Первый завод)
2x2 <= 12 (второй завод)
3x1 + 2x2 <= 18 (Третий завод)
x1, x2 >= 0 (требования неотрицательности)
где z = общая прибыль за неделю
x1 = количество партий дверей, производимых в неделю
x2 = количество партий окон, произведенных за неделю.
Сформулировав проблему, и ваша может существенно
больше переменных решения и ограничений, вы можете перейти к
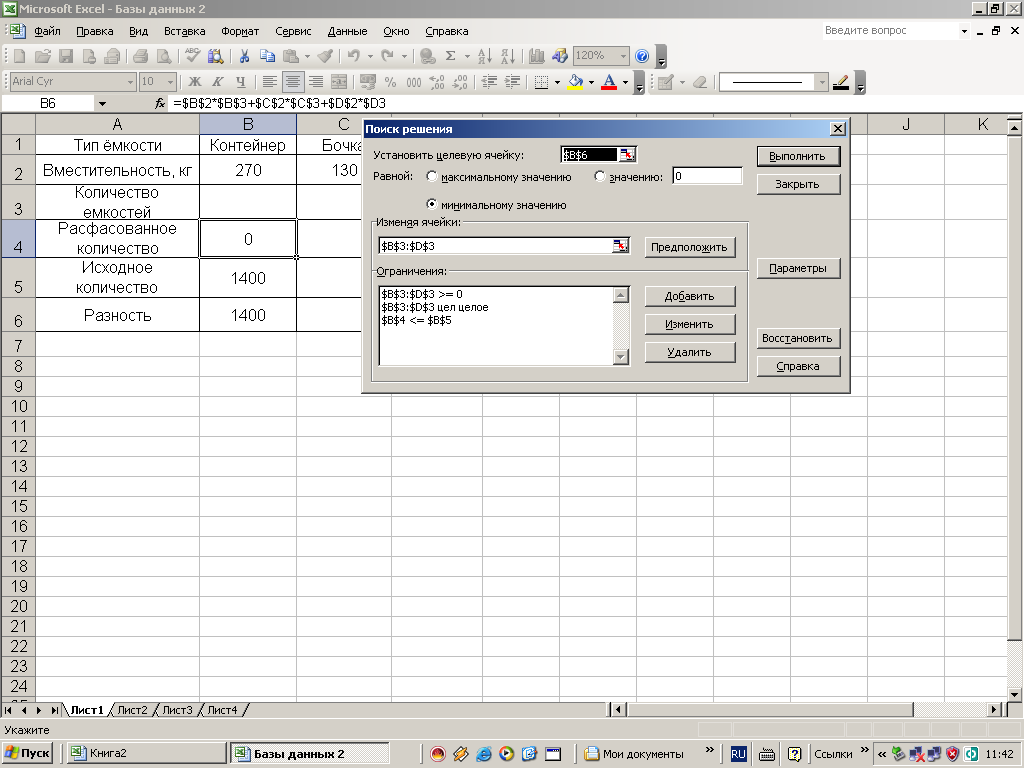
ввод его в Excel. Лучший подход к проблеме
в Excel сначала перечислить в столбце имена
целевая функция, переменные решения и ограничения. Ты можешь
затем введите произвольные начальные значения в ячейки для
переменные решения, обычно равные нулю, показаны на рисунке 1. Excel будет
варьировать значения ячеек, так как это определяет оптимальные
решения.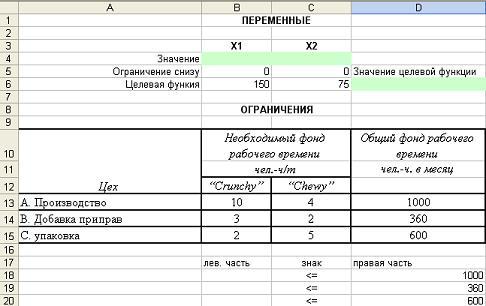 Присвоив переменным решения некоторые
произвольные начальные значения, вы можете использовать эти ссылки на ячейки
явным образом при записи формул для целевой функции и
ограничений, не забывая начинать каждую формулу с ‘=’ .
Присвоив переменным решения некоторые
произвольные начальные значения, вы можете использовать эти ссылки на ячейки
явным образом при записи формул для целевой функции и
ограничений, не забывая начинать каждую формулу с ‘=’ .
Рисунок 1. Настройка задачи в Excel
Введя формулы для цели и ограничений, целевая функция в B5 будет иметь вид:
=3*В9+2*В10
Ограничения будут заданы (положив правую часть Значения {RHS} в соседних ячейках):
Завод Один (B14) =B9 Второй завод (B15) = 2*B10 Завод №3 (B16) =3*B9+2*B10 Неотрицательный 1 (B17) =B9 Неотрицательный 2 (B19) =B10
Теперь вы готовы использовать Солвер.
При выборе пункта меню Инструменты | Решите диалоговое окно показано на рисунке 2, и если вы выберете цель ячейке перед вызовом Solver, правильная целевая ячейка будет идентифицировано. Это значение Solver попытается либо максимизировать или минимизировать.
Рисунок 2. Диалоговое окно «Решатель»
Выберите, хотите ли вы минимизировать это или максимизировать проблему,
в этом случае вы хотели бы установить целевую ячейку (
объектив) до макс. Обратите внимание, что вы можете использовать Solver, чтобы найти
результат, который достигнет указанного значения для целевой ячейки
нажав «Значение:». При этом вы можете использовать Solver в качестве
прославленный искатель цели. Далее вы вводите диапазон ячеек, которые вы хотите
Решатель варьироваться, переменные решения. Нажмите на белое поле
и выберите ячейки B9& B10 или введите их. Примечание.
что вы можете попытаться заставить Solver угадать, какие ячейки вы хотите
изменить, нажав кнопку «Угадай». Если вы определили свой
проблема логическим образом, Solver обычно должен решить их правильно.
Обратите внимание, что вы можете использовать Solver, чтобы найти
результат, который достигнет указанного значения для целевой ячейки
нажав «Значение:». При этом вы можете использовать Solver в качестве
прославленный искатель цели. Далее вы вводите диапазон ячеек, которые вы хотите
Решатель варьироваться, переменные решения. Нажмите на белое поле
и выберите ячейки B9& B10 или введите их. Примечание.
что вы можете попытаться заставить Solver угадать, какие ячейки вы хотите
изменить, нажав кнопку «Угадай». Если вы определили свой
проблема логическим образом, Solver обычно должен решить их правильно.
Теперь вы можете ввести ограничения, сначала нажав кнопку «Добавить ..». кнопка. Откроется диалоговое окно, показанное на рисунке 3.
Рисунок 3. Ввод ограничений
Ссылка на ячейку относится к ячейке, содержащей ваше ограничение
формуле, поэтому для ограничения Plant One вы вводите B14. К
по умолчанию <= выбрано, но вы можете изменить это, щелкнув значок
Стрелка раскрывающегося списка, чтобы открыть список других типов ограничений.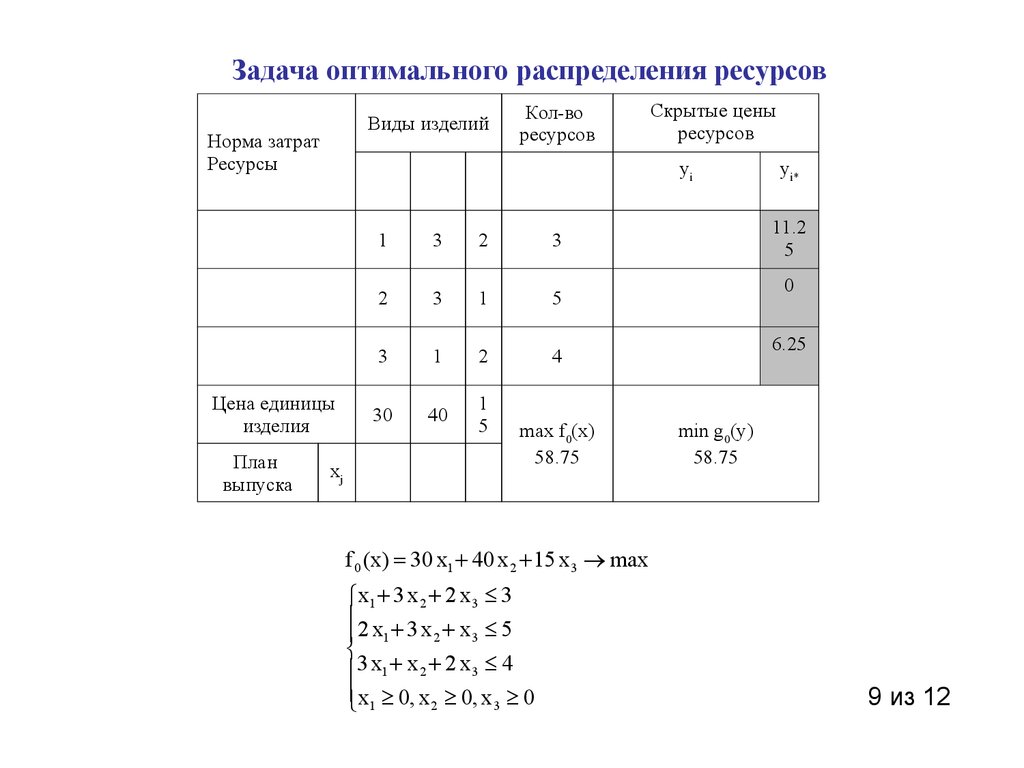 В
в правом белом поле вы вводите ссылку на ячейку на ячейку
содержащее значение RHS, которое для ограничения Plant One равно
ячейка С14. Затем вы нажимаете «Добавить», чтобы добавить остальные
ограничения, не забывая включить неотрицательность
ограничения.
В
в правом белом поле вы вводите ссылку на ячейку на ячейку
содержащее значение RHS, которое для ограничения Plant One равно
ячейка С14. Затем вы нажимаете «Добавить», чтобы добавить остальные
ограничения, не забывая включить неотрицательность
ограничения.
Добавив все ограничения, нажмите «ОК», и Решатель диалоговое окно должно выглядеть так, как показано на рисунке 4.
Рисунок 4. Диалоговое окно «Завершенный решатель»
Прежде чем нажимать «Решить», рекомендуется при выполнении LP идти
в «Параметры» и установите флажок «Предполагать линейную модель», если только
конечно, ваша модель не является линейной (решатель может справиться с большинством
математические типы программ, в том числе нелинейные и целочисленные
проблемы). Это может ускорить время, затрачиваемое на
Решатель, чтобы найти решение проблемы и на самом деле, это будет
также обеспечить правильный результат и, что очень важно, обеспечить
соответствующий отчет о конфиденциальности. Выбрав этот вариант, вы
Теперь все готово.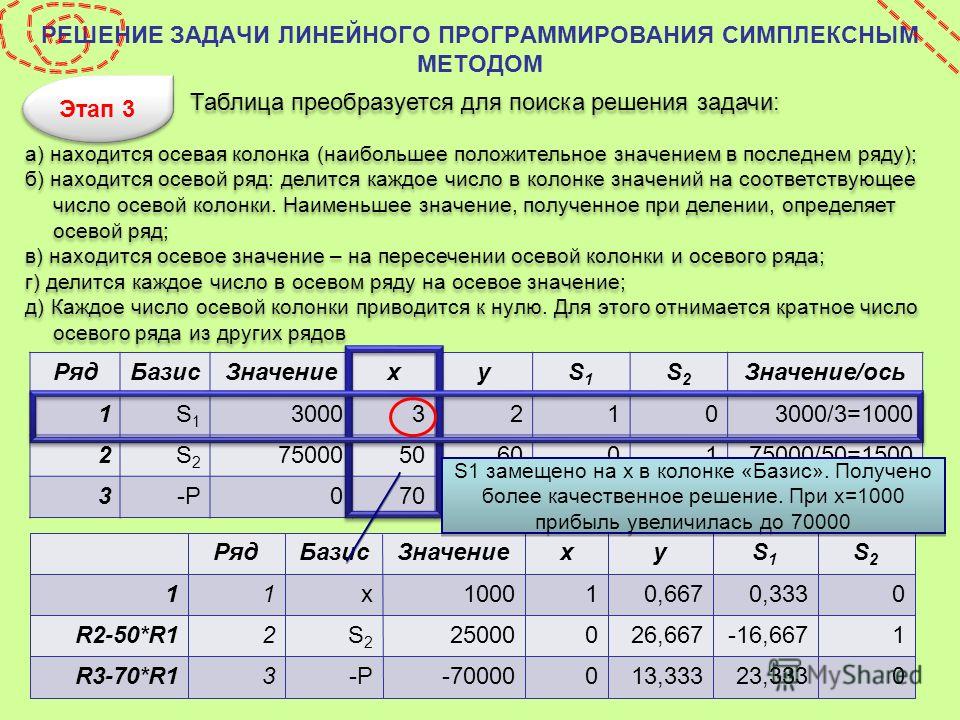 Нажмите «Решить» и посмотрите, как «Решатель» находит оптимальные значения.
для дверей и окон. При этом в нижней части
экран Excel сообщит вам о прогрессе Solver, затем на
поиск оптимального решения диалоговое окно, показанное на рисунке 5
будет появляться. Вы также заметите, что Solver изменил все
значения в вашей электронной таблице, заменив их оптимальными
Результаты.
Нажмите «Решить» и посмотрите, как «Решатель» находит оптимальные значения.
для дверей и окон. При этом в нижней части
экран Excel сообщит вам о прогрессе Solver, затем на
поиск оптимального решения диалоговое окно, показанное на рисунке 5
будет появляться. Вы также заметите, что Solver изменил все
значения в вашей электронной таблице, заменив их оптимальными
Результаты.
Вы можете использовать диалоговое окно Solver Results, чтобы сгенерировать три отчеты. Чтобы выбрать все три сразу, либо удерживайте нажатой клавишу CTRL, либо нажмите каждый по очереди или перетащите мышь на все три.
Рисунок 5: Результаты решателя
В то же время часто бывает полезно заставить Solver восстанавливать ваши исходные значения в электронной таблице, чтобы вы могли вернуться к первоначальной формулировке задачи и внести коррективы в модели, такие как изменение доступности ресурсов. Три отчеты создаются на новых листах в текущей рабочей книге Эксель.
Отчет об ответах содержит подробные сведения о решениях (в данном случае
максимальная прибыль составляет 36, когда производится 2 двери в неделю и
6 окон в неделю — не особо загруженная фирма!) и
информация о статусе каждого ограничения с
предоставляются сопутствующие резервы / избыточные значения.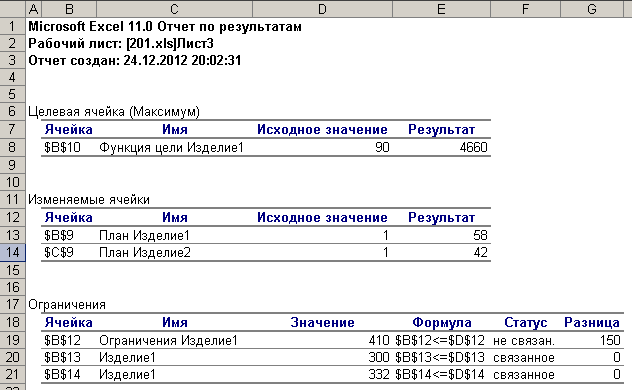 Чувствительность
Отчет о проблеме Wyndor, в котором содержится информация о
насколько чувствительно ваше решение к изменениям в ограничениях,
показано на рисунке шесть.
Чувствительность
Отчет о проблеме Wyndor, в котором содержится информация о
насколько чувствительно ваше решение к изменениям в ограничениях,
показано на рисунке шесть.
Рисунок 6. Отчет о чувствительности для Wyndor
Как видно из рисунка 6, отчет довольно стандартный, предоставление информации о теневых значениях, уменьшенной стоимости и верхний и нижний пределы для переменных решения и ограничения. Отчет о лимитах также обеспечивает чувствительность информация о значениях RHS. Все отчеты можно просто скопировано и вставлено в Word, и это, пожалуй, один из самых больших Преимущества использования Excel по сравнению с решателем LP на базе DOS. Хотя отчеты вставляются в Word в виде таблиц, легко конвертируются в текст, а затем им можно манипулировать, если кто-то производит письменный отчет о вашей находке.
Наконец, есть несколько опций Solver, которые могут позволить вам
изменить/вмешаться в процесс генерации решения.
Кнопка «Параметры» в диалоговом окне «Решатель» открывает диалог
поле, показанное на рисунке 7.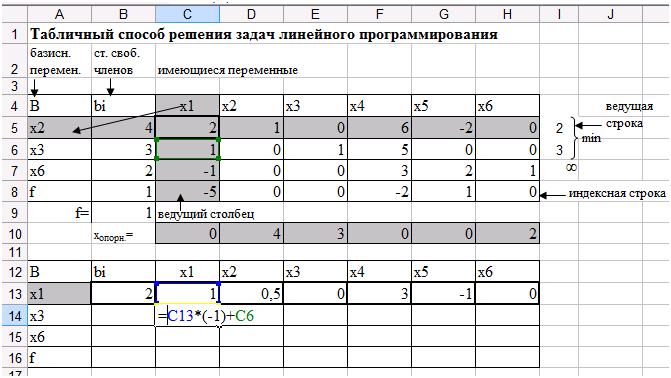 Вы можете использовать это, чтобы повлиять на то, как
точное ваше решение, сколько «усилий» Solver вкладывает в
найти решение и хотите ли вы увидеть результаты
каждую итерацию.
Вы можете использовать это, чтобы повлиять на то, как
точное ваше решение, сколько «усилий» Solver вкладывает в
найти решение и хотите ли вы увидеть результаты
каждую итерацию.
Рисунок 7: Опции решателя
Параметр «Допуск» требуется только для целочисленных программ (IP), и позволяет Солверу использовать «почти целые» значения в пределах допуск, который вы указываете, и это помогает ускорить IP расчеты. Установка флажка «Показать результаты итерации» позволяет чтобы увидеть каждый шаг расчета, но имейте в виду, если ваша модель является сложным, это может занять неоправданно много времени. Использовать Автоматическое масштабирование полезно, если есть огромная разница в величина между вашими переменными решения и целью ценить.
Нижние три варианта: оценки, производные и поиск.
влияют на то, как Solver подходит к поиску базового возможного
решение, как Solver находит частные дифференциалы цели
и ограничения, а также то, как Solver решает, в каком направлении искать
следующая итерация.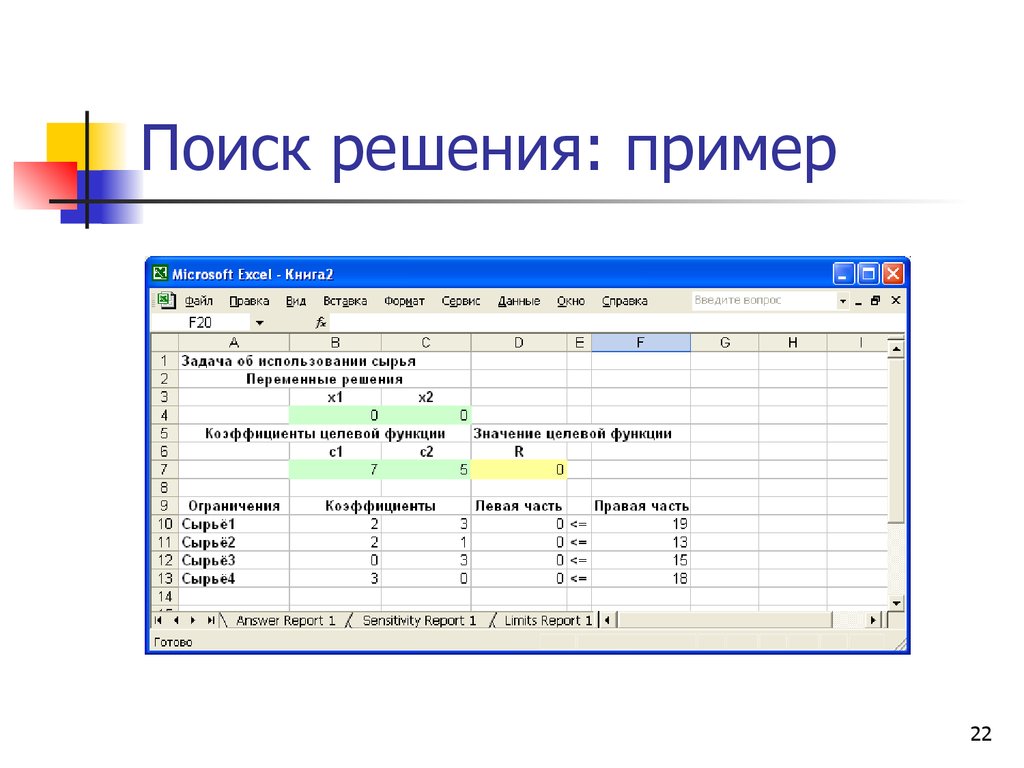 По существу параметры влияют на то, как решатель
использует память и количество вычислений, которые он делает. Для большинства
проблемы с LP, их лучше оставить со значениями по умолчанию.
По существу параметры влияют на то, как решатель
использует память и количество вычислений, которые он делает. Для большинства
проблемы с LP, их лучше оставить со значениями по умолчанию.
Кнопка «Сохранить модель» очень полезна, особенно если вы сохраняете ваша модель как именованный сценарий. Щелчок по этой кнопке позволяет вам чтобы присвоить имя текущим значениям ваших переменных ячеек. Затем эта опция позволяет вам выполнить дальнейший анализ «что, если» на множестве возможных альтернативных результатов — очень полезно для изучить вашу модель более подробно.
В заключение, Excel Solver предоставляет простой, но эффективный,
среда, позволяющая пользователям исследовать линейные программы. Может быть
используется для больших задач, содержащих сотни переменных и
ограничений, и делает это относительно быстро, но в качестве обучения
инструмент с использованием небольших иллюстративных задач, он очень мощный,
тем более, что учащийся должен понимать структуру
LP при вводе его в электронную таблицу.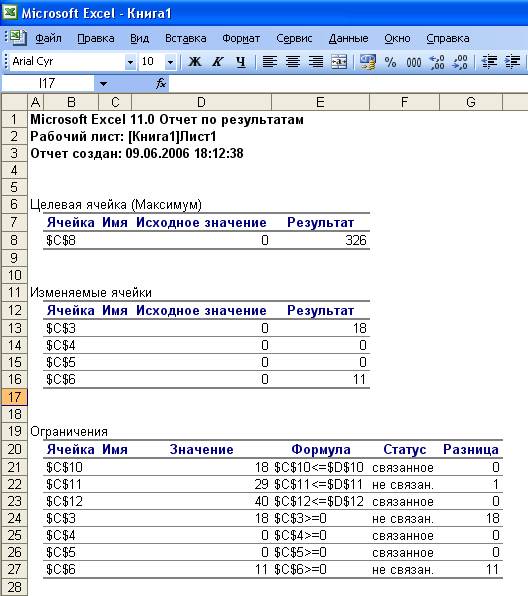
С другой стороны, вы не может просматривать Таблицу, так как она создается на каждой итерации и поэтому те учителя, которые хотели бы, чтобы их ученики были опытными в ручных методах LP нашел бы Solver менее превосходным, скажем, Линдо, что позволяет это. Однако он производит превосходный набор результатов и отчетов о чувствительности по сравнению с Линдо и, благодаря характеру электронной таблицы, позволяет учащемуся очень быстро наблюдать за последствиями любых изменений, внесенных в ограничения или целевая функция.
Это особенно заметно, поскольку формулировка модели легко доступна на в то же время, что и результаты модели, они просто помещаются в соседние рабочие листы, доступные простым щелчком мыши. В целом, использование Excel, знакомого большому количеству студентов, обеспечивает богатую среду для обучения линейным программирование, и это позволяет учащимся исследовать свои модели в структурированный, но гибкий способ.
Ссылки
- Джордж Б.


 04.2006 1:22:43
04.2006 1:22:43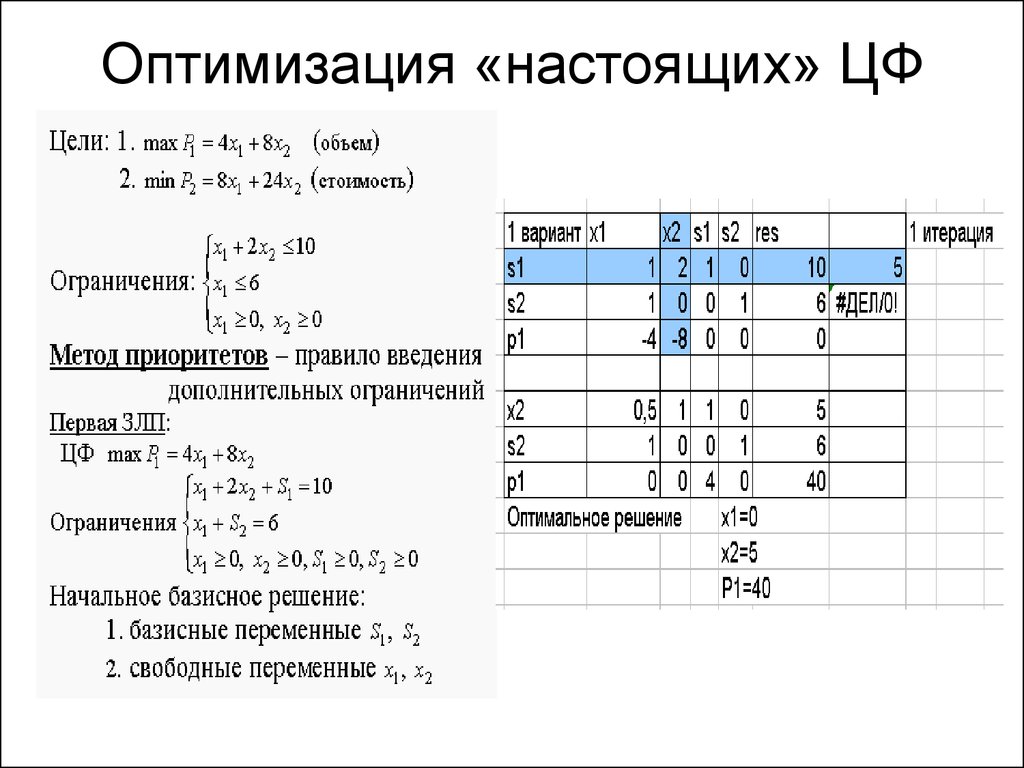

 04.2006 1:22:43
04.2006 1:22:43
 левая часть
левая часть в
ЦФ
в
ЦФ