Умножение и деление на 5 примеры: Умножение и деление числа на 5, таблица умножения и деления на 5, карточки, задачи и примеры с ответами, скачать

3. Стадия вызова

Направлена на вызов у воспитанников уже имеющихся знаний по изучаемому вопросу, активизации их деятельности, мотивацию к дальнейшей работе.

Игра “Верю, не верю” (прием верные и неверные утверждения). Повторение теоретического материала.

У воспитанников в руках цветные сигнальные карточки (зеленый цвет – да, красный – нет). Преподаватель задает вопросы, воспитанники отвечают, используя карточки. Вопросы, вызывающие затруднения обсуждаются тут же.

“Верю, не верю”.

1. Числа, которые перемножают, называют множителями. +
2. Выражение называют суммой. —
3. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. +
4. При умножении числа на единицу получиться то же самое число. +
5. Числа, которые делят, называют множителями. –
6. Результат деления называют частным. +
7. Чтобы найти неизвестный делитель, нужно частное разделить на делимое. –
8. Чтобы найти неизвестное делимое, нужно частное умножить на делитель. +
9. При делении числа на нуль в результате получиться нуль. –
10. Если один множитель увеличить в 2 раза, а другой в 5 раз, по произведение увеличиться в 7 раз. –
11. Если среди множителей есть нуль, по произведение равно нулю. +
12. Чтобы найти во сколько раз одно число больше другого, нужно выполнить вычитание.

4. Смысловая стадия

Непосредственная работа с новой информацией, постепенное продвижение от знания старого к новому. Используемые приемы для поддержания активности: интересные факты и комментарии; проблемные вопросы.

Эпиграф: “Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно.

Где есть желание, найдется путь!”

Д. Пойа.

1) Историческая справка.

ДьёрдьПомйа, ДжорджПомлиа — венгерский, швейцарский и американский математик.

Окончил Будапештский университет (1912), в 1914—1940 работал в Высшей технической школе в Цюрихе (с 1928 — профессор). В 1940 переехал с женой в США, где после двух лет в университетах поступил на работу в Станфорд, в котором и прошла вся его дальнейшая научная карьера. Основные труды по теории чисел, функциональному анализу, математической статистике (распределение Пойа) и комбинаторике (теорема Пойа).

Живя в США, Пойа много работал со школьными учителями математики и внёс большой вклад в популяризацию науки. Он написал несколько книг о том, как люди решают задачи и как надо учить решать задачи.

2) Решение упражнений.

Воспитанники решают задачи и уравнения. Слабоуспевающие воспитанники работают по индивидуальным карточкам. Приложение 1. (Элемент Технологии индивидуализированного обучения).

Фронтальная работа с дальнейшей проверкой проверка решения у доски.

Задача № 1.

Для нормального протекания физиологических функций человеку в среднем требуется 3 л воды в сутки (с учетом поступления воды с пищевыми продуктами). Человек выпивает примерно 1л 500 мл воды, а остальное получает с пищевыми продуктами.

Сколько литров воды потребуется человеку в месяц? за год?

Решение.

1. 1500 * 30 = 45 000 мл = 45 л – требуется выпить человеку за месяц.
2. 1500 * 365 = 547500 мл = 547 л 500 мл – требуется выпить человеку за год.

Задача № 2. Решите разными способами.

В Санкт-Петербурге часты наводнения. Одно из крупнейших произошло 7 ноября 1824 года. Русский художник Ф.Я. Алексеев отобразил это событие на картине “На площади у Большого театра”.

Историческая справка:

Большой театр(Каменный театр) — петербургский театр, существовавший в 1784—1886 гг.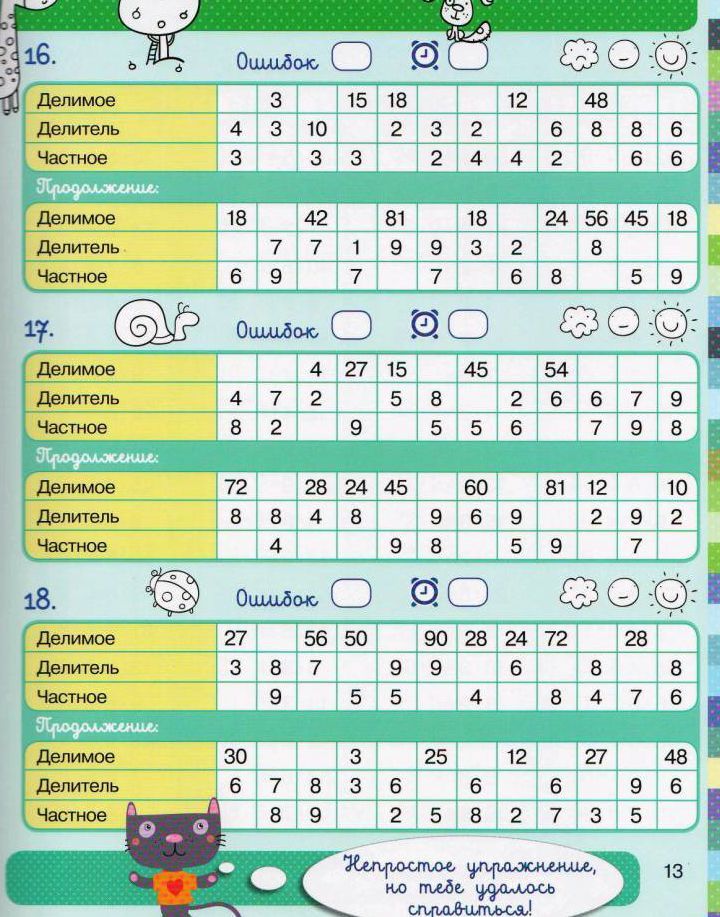 Первое постоянное в Санкт-Петербурге и одно из крупнейших в России XVIII века театральных зданий. Находился на Театральной площади. В 1886 году здание Каменного театра разобрано и перестроено в современное здание Петербургской консерватории.

Задача. Однажды во время наводнения затопило подвал дома на набережной. Из подвала нужно было выкачать воду. Спасатели установили 5 больших и 3 малых насоса. Большой насос выкачивает за 1 час 4537 литров воды, а малый – 2120 литров. Через 6 часов вся вода была выкачана. Сколько литров воды скопилось в подвале во время наводнения? (Решите задачу 2 способами: по действиям; выражением).

Решение: 1 способ.

1. 5 * 4537 = 22685 л – 5 б. насосов за 1 час.
2. 3 * 2120 6360 л – 3 м. насосов за 1 час.
3. 22685 + 6360 = 29 045 л всего за час.
4. 29045 * 6 = 174270 л скопилось в подвале во время наводнения.

2 способ: (5 * 4537 + 3 * 2120 6360) * 6 = 174270 л

Ответ: 174270 л.

Слабоуспевающие воспитанники сдают работы на проверку.

Задание № 3. Найдите ошибки, допущенные при решении уравнений. Решите уравнения самостоятельно.

а) 2х – 35 = 101
2х = 101 – 35
2х = 66
х = 66*2
х = 132

Ответ: х = 132. (Ответ: х = 68)

б) (у + 15) : 3 = 25
у + 15 = 25*3
у + 15 = 75
у = 75 + 15
у = 100

Ответ: у = 100. (Ответ: х = 60).

5. Контроль знаний.

Воспитанники выполняют тест. Приложение 2.

Дополнительные задания для тех, кто досрочно справился с тестом. (Элемент Технологии индивидуализированного обучения).

Карточка.

№ 1.Сердце человека перекачивает за сутки 8т. крови. Сколько тонн крови сердце перекачивает за 1 год? За 75 лет?

Решение.
1)365*8=2920(т) – сердце перекачивает за год.
2)2920*75=219000(т) – сердце перекачивает за 75 лет.

№ 2. По обеим сторонам аллеи посадили 30 лип и кусты камелии. С каждой стороны посадили одинаковое число лип, а камелию посадили так: между каждыми 2 липами – 2 куста. Сколько кустов камелии посадили?

Решение.

1. 30 : 2 = 15 лип с каждой стороны аллеи.
2. Между липами 14 промежутков. 14*2 = 28 кустов с одной стороны аллеи.
3. 28*2 = 56 кустов камелии посадили всего.

Ответ: 56 кустов.

6.

Рефлексия.

Воспитанники соотносят “новую” информацию со старой, используя знания, полученные на стадии осмысления.

– Какие способы решения задач вы использовали сегодня на уроке?

– Знание каких свойств умножения и деления помогли нам при вычислениях?

– Какие задания для вас были трудными?

– Какие задания вы решали с удовольствием, с радостью? Почему?

– Что нам нужно еще повторить, чтобы на уроке было у вас хорошее настроение?

7. Домашнее задание.

Карточка.

№ 1. Решите уравнения:

1. 51 * у = 1530
2. 40 + 5m = 90
3. 400 : х + 20 = 100

№2. Что это за число: если к нему прибавить 7, сумму разделить на 7, а из частного вычесть 7 и остаток помножить на 7, то в результате получится 7.
Ответ:49.

Недаром Платон приписывал числу божественную сущность. Например, числу 7 – 7дней недели, 7 цветов радуги. Числа встречаются в пословицах и поговорках.

№3. Найти пословицы и поговорки, в которых встречаются числа.

Приложение 3 – презентация.

Используемая литература:

1. Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбург.
Математика: Учеб.для 5-го кл. общеобразоват. учреждений/ М34. – 16-е изд., перераб. – М.: Мнемозина 2009.
2. С.И. Заир – Бек, И.В. Муштавинская.
Развитие критического мышления на уроке. Пособие для учителей общеобразовательных учреждений. 2 изд., доработанное – М.: Просвещение 2011.
3. А.С. Чесноков, К.И. Нешков,
Дидактические материалы по математике 5 класс. М.: Просвещение 2003.
4. Энциклопедия “Вокруг света”. Электронный адрес: http://www.vokrugsveta.ru/encyclopedia/

Умножение и деление целых чисел

В математике мы изучаем различные типы чисел и операции сложения, вычитания, умножения и деления между ними. Мы знаем о счетных числах, которые называются натуральными числами, а d Целые числа представляют собой набор натуральных чисел вместе с числом 0. Мы также знаем, что если мы вычитаем целое число из другого целого числа, разница не всегда может быть целым числом. На самом деле, когда меньшее целое число вычитается из большего целого числа, мы получаем целое число. Например, 14 – 8 = 6, 20 = 13 = 7 – это целые числа. Но у нас нет целых чисел для представления 3 – 7, 14 = 18, 20 – 35 и так далее. Итак, нам нужен другой набор чисел, отличный от натуральных чисел и целых чисел, для представления таких различий. Здесь мы вводим множество целых чисел. Итак, что такое целые числа и как их умножать и делить? Давайте узнаем.

В соответствии с натуральными числами, 1, 2, 3, 4, 5 …… и т. д., мы создаем новые числа, -1, -2, -3, -4, -5 и так далее. Эти числа называются минус один, минус два, минус три и т. д. такие, что –

1 + ( – 1 ) = 0

2 + ( – 2 ) = 0

3 + ( – 3 ) = 0

Итак , – 1 называется отрицательным числом 1, -2 называется отрицательным числом 2, а каждое отрицательное число противоположно своему положительному аналогу. Если мы объединим эти отрицательные числа с положительными, вместе мы получим набор чисел, которые мы называем целыми числами.

Итак, целое число — это целое число, которое может быть положительным, отрицательным или нулевым. Следовательно, мы можем сказать, что целые числа представляют собой совокупность целых чисел и отрицательных чисел. Набор целых чисел представлен Z и может быть записан как – 

Z = { ……. . – 3, – 2 , – 1, 0, 1, 2, 3 …….. }

Здесь числа, 1, 2, 3, 4 ….. являются натуральными числами и называются целыми положительными числами, а числа – 1, – 2 , – 3 и т. д. называются отрицательными целыми числами. Давайте теперь узнаем о делении и умножении целых чисел.

Мы знаем, что процесс нахождения произведения двух или более чисел называется умножением, а полученный таким образом результат называется произведением . Умножение целых чисел похоже на умножение натуральных чисел и целых чисел, за исключением того факта, что мы также должны позаботиться об умножении отрицательных чисел. Итак, что представляет собой процесс умножения целых чисел? Давайте узнаем.

Следующие правила соблюдаются для умножения целых чисел –

Случай 1 – Когда у вас есть два целых числа противоположных знаков – Произведение двух целых чисел противоположных знаков равно аддитивной обратной величине произведения их абсолютных значений . Это означает, что для того, чтобы найти произведение положительного и отрицательного целых чисел, нам нужно найти произведение абсолютных значений и присвоить произведению знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение 7 и -4 будет равно 

7 x (– 4) = – (7 x 4) = – 28

Аналогично, (– 6) x 9 = – (6 x 9) =  = – 54

Случай 2. Произведение двух целых чисел с одинаковыми знаками равно произведению их абсолютных значений. Это означает, что для того, чтобы найти произведение двух целых чисел, где либо оба числа положительные, либо оба отрицательные, нам нужно будет найти произведение их абсолютных значений. Давайте разберемся в этом на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение – 7 и -4 будет равно

( – 7 ) x ( – 4 ) = ( 7 x 4 ) = 28

Аналогично, ( 6 ) x 9 = ( 6 x 9 ) =  =  54

Мы знаем, что Деление — это процесс повторяющегося вычитания. То же самое относится и к делению целых чисел. В делении есть четыре важных члена, а именно делитель, делимое, частное и остаток. Формула для делителя составляет все эти четыре термина. На самом деле именно соотношение этих четырех членов между собой определяет формулу деления. Если мы умножим делитель на частное и прибавим результат к остатку, то получим делимое. Это значит,

Делимое = Делитель x Частное + Остаток

Напомним, что деление целых чисел — это процесс, обратный умножению. Распространим ту же идею на деление целых чисел. При делении целых чисел соблюдаются следующие правила: 

Случай 1 – Частное двух целых чисел, как положительных, так и отрицательных, является положительным целым числом, равным частному соответствующих абсолютных значений целых чисел. Это означает, что при делении двух целых чисел с одинаковыми знаками мы делим значения независимо от знака и ставим положительный знак в частном. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и -4, и вы хотите разделить первое целое число на другое. У нас будет

-20 ÷ -4 = $\frac{20}{4}$ = 5

Случай 2 – Частное положительного и отрицательного целых чисел является отрицательным целым числом, и его абсолютное значение равно частное соответствующих модулей целых чисел. Это означает, что при делении целых чисел с разными знаками мы делим значение независимо от знака и присваиваем частному знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и 4, и вы хотите разделить первое целое число на другое. Мы будем иметь,

-20 ÷ 4 = –  $\frac{20}{4}$ = – 5

операция выполняется над двумя числами, порядок расположения чисел не имеет значения.

Переместительное свойство для умножения целых чисел — Если одно целое число умножается на другое, не имеет значения, какое целое число помечено как множитель, а какое число помечено как множимое. Верно ли это для умножения целых чисел? Давайте узнаем.

Возьмем два целых числа 8 и 5.

Сначала отметим 8 как множитель и 5 как множимое.

Получаем, 8 х 5 = 40.

Теперь обратим порядок, т.е. 5 станет множителем, а 8 станет множимым.

Теперь получаем 5 х 8 = 40.

Оба процесса дают нам один и тот же ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет коммуникативному свойству. Получаем

a x b = b x a

Следовательно, умножение целых чисел является коммуникативным.

Коммутативное свойство для деления целых чисел – Если одно число делится на другое, то не имеет значения, какое число отмечено делителем, а какое делимым. Верно ли это для деления целых чисел?

Давайте выясним.

Предположим, у нас есть два числа 10 и 4.

Мы хотим разделить 10 на 4. Частное будет 2,5, а остаток равен 0.

Теперь, если мы поменяем местами делитель и делимое, получим ли мы тот же ответ? №

Это означает, что если у нас есть два числа, a и b, то

a ÷ b ≠ b ÷ a

Следовательно, деление не является коммутативным для целых чисел.

Свойство замыкания указывает, что когда операция выполняется над двумя числами, результат также будет того же типа, что и числа, над которыми была выполнена операция.

Свойство замыкания для умножения целых чисел — Если вы умножаете одно целое число на другое, произведение также будет целым числом. Проверим, выполняется ли свойство замыкания при умножении целых чисел?

Рассмотрим два числа, 15 и 3.

Умножьте 15 на 3. Мы получим произведение 45 как 15 x 3 = 45. В этом случае произведение также является целым числом.

Это означает, что свойство замыкания верно для умножения целых чисел. .

Следовательно, мы можем сказать, что умножение целых чисел удовлетворяет свойству замыкания.

Свойство замыкания для деления целых чисел — Если вы разделите одно целое число на другое, то частное также будет целым числом. Проверим, выполняется ли свойство замыкания при делении целых чисел?

Рассмотрим два числа, 15 и 3.

Разделим 15 на 3. Мы получим частное как 5, а остаток как 0, так как 3 x 5 = 15. В этом случае частное является целым числом.

Теперь разделим 26 на 4. Получим частное как 6,5 и 0 как остаток. Но 6,5 — это не целое число.

Это означает, что свойство замыкания может быть верным или неверным для деления.

Следовательно, мы можем сказать, что деление целых чисел на не удовлетворяет свойству замыкания.

Ассоциативное свойство утверждает, что когда операция выполняется более чем с двумя числами, порядок, в котором расположены числа, не имеет значения.

Ассоциативное свойство для умножения целых чисел — Если мы хотим умножить 3 целых числа, сначала можно выбрать два из них, одно как множитель, а второе как множимое. Результат умножения будет служить множителем, а третье число — множителем для получения окончательного ответа. Является ли умножение целых чисел ассоциативным? Давайте узнаем.

Возьмем 3 числа, 8, 5 и 2.

Возьмем сначала 8 и 5.

Сначала мы помечаем 8 как множитель и 5 как множимое.

Получаем 8 х 5 = 40.

Теперь умножаем 40 на 2, получаем 40 х 2 = 80

Теперь давайте обратим порядок и сначала выберем 5 и 2.

Получаем, 5 x 2 = 10

Теперь умножаем этот результат на 8, получаем 10 x 8 = 80

Оба процесса дают нам одинаковый ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет ассоциативному свойству. Получаем

(a x b) x c = a x (b x c)

Следовательно, умножение целых чисел ассоциативно.

Ассоциативное свойство для деления целых чисел — Поскольку деление не является коммутативным, оно также является ассоциативным.

Произведение целого числа на 0 всегда равно 0. Например,

45 x 0 = 0 x 45 = 0 быть тождеством для умножения, если число, умноженное на это тождественное число, дает само число. Здесь, 1 является элементом идентичности для умножения целых чисел . Давайте посмотрим, почему?

4 x 1 = 4

-15 x 1 = -15

-20 x 1 = -20

Следовательно, любое число при умножении на 1 дает само число. Это тождественное свойство умножения.

Число называется обратным мультипликативным, если число умножается на обратное мультипликативное, полученный результат является тождеством операции, в этом случае 1 ( 1 является мультипликативным тождеством всех целых чисел ).

Это означает, что для всех ненулевых целых чисел, числа, умноженные на их обратные числа, дадут ответ как 1, то есть

4 x 1/4 = 1

Отсюда $\frac{1}{a} $ , которое также записывается как ^-1 , является мультипликативной инверсией a.

Когда два числа складывают или вычитают, а результат умножают на другое число, их можно умножать отдельно.

Следовательно, для любых трех целых чисел a, b и c дистрибутивное свойство умножения над сложением утверждает, что

a x ( b + c) = (a x b) + (a x c)

Аналогично, для любых трех чисел a, b и c, распределительное свойство умножения над вычитанием утверждает, что

a x (b – c) = (a x b) – (a x c)

Например, давайте сначала рассмотрим 10 x (18 + 12)

Есть два способа решить эту проблему.

Первый способ

Сначала прибавляем 18 и 12, получаем 30. Теперь умножаем 30 на 10, получаем 10 х 30 = 300

  Второй способ

Теперь используем свойство распределения умножения над сложением.

Имеем 10 х (18 + 12)

 = (10 х 18) + (10 х 12)

 = 180 + 120

 = 300

Оба метода дают одинаковый ответ. Следовательно,

10 х (18 + 12) = (10 х 18) + (10 х 12)

Теперь рассмотрим 10 x (18 – 12)

Снова решим это обоими методами.

Первый способ

Находим разницу между 18 и 12. Имеем 18 – 12 = 6

Теперь умножаем 10 на 6. Получаем 10 х 6 = 60.

Второй способ

Теперь мы используем распределительное свойство умножения вместо вычитания.

У нас есть 10 х (18 – 12)

 = (10 х 18) – (10 х 12)

 = 180 – 120

 = 60

Оба метода дают один и тот же ответ. Следовательно,

10 x (18 – 12) = (10 x 18) – (10 x 12)

1. Если a и b целые числа, то a ÷ b не обязательно целое число.
2. Если a — целое число, отличное от 0, то a ÷ a  = 1
3. Для каждого целого числа a, которое у нас есть, a ÷ 1 = a
4. Если a — ненулевое целое число, то a ÷ 0 не существует .

1. Целое число — это целое число, которое может быть положительным, отрицательным или равным нулю.
2. Процесс нахождения произведения двух или более чисел называется умножением, а полученный результат называется произведением.
3. Произведение двух целых чисел противоположных знаков равно аддитивной обратной величине произведения их модулей.
4. Умножение целых чисел является коммутативным и ассоциативным, в то время как деление целых чисел не является ни коммутативным, ни ассоциативным.
5. Умножение целых чисел удовлетворяет свойству замыкания, тогда как деление целых чисел не удовлетворяет свойству замыкания.
6. Если a и b — целые числа, то a ÷ b не обязательно является целым числом.
7. Если a — целое число, отличное от 0, то a ÷ a  = 1
8. Для каждого целого числа a, которое у нас есть, a ÷ 1 = a
9. Если a — ненулевое целое число, то a ÷ 0 не существует .
10. Эти операции над целыми числами удовлетворяют всем свойствам операций над всеми целыми числами.
11. Чтобы найти произведение двух целых чисел, мы умножаем абсолютные значения и присваиваем результату знак плюс, если оба числа имеют один и тот же знак, или знак минус в противном случае.
12. Чтобы найти частное от деления одного целого числа на другое, отличное от нуля целое число, мы делим абсолютные значения и присваиваем результату знак плюс, если оба числа имеют один и тот же знак, или знак минус в противном случае.

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

1.5 Раздел | СНКГ

Просмотр навигации

ДЕЛЕНИЕ: ДЕЛЕНИЕ НА МЕЛКИЕ ЧАСТИ

Разделение используется для разделения группы на более мелкие секции. Предположим, в шкафчике для хранения есть 24 пары перчаток, и вы хотите равномерно распределить их между 8 членами экипажа. Сколько пар перчаток получит каждый член экипажа. Разделив 24 на 8, мы получим 3; каждый член экипажа получит 3 пары перчаток. Некоторые слова и символы, часто встречающиеся в разделении,  разделить на , на , символ «÷» и символ «/». Точно так же, как умножение рассматривается как многократное сложение, деление можно рассматривать как многократное вычитание.

Некоторые термины, используемые при делении, включают:
Делитель — число, на которое делится большее число.
Дивиденд — сумма, подлежащая разделу и распределению.
Частное — число, полученное в результате деления одного числа на другое.
Остаток — число, оставшееся после деления меньше делителя.

В уравнении b/a = c, b — делимое, a — делитель, c — частное.

Пример 1- 20 форсунок на 5 двигателей. Если бы форсунки были разделены поровну для двигателей, сколько форсунок было бы на каждом двигателе?

20 — 5 = 15  — 5 = 10  — 5 = 5  — 5 = 0 . В данном случае из 20 вычитали 5 всего 4 раза. Ответ на 20, разделенный на 5, записывается как 20 ÷ 5 = 4
 

Пример 2. Разделите 15 на 4, 9.0423 15 — 4 = 11  — 4 = 7  — 4 = 3
Поскольку 4 нельзя вычесть из 3, 3 называется остатком и обозначается символом «R».

Остаток никогда не больше делителя. Делитель в данном примере равен 4. Значит, 15/4 = 3 R 3

Если бы на вашем участке было пятнадцать форсунок на четыре двигателя, то на три двигателя пошло бы четыре форсунки и на последний двигатель пошли бы только три форсунки.
 

ДЛИННОЕ ДЕЛЕНИЕ ДЛЯ БОЛЬШИХ ЧИСЕЛ

Длинное деление можно использовать при работе с большими числами. Здесь повторное вычитание делается по-другому. Чтобы разделить, начните с цифры старшего разряда и закончите цифрой младшего разряда. На каждом этапе спрашивайте, кратно ли число в ответе.

Пример 3. Разделите 3654 на 5.

Шаг 1.  Начните с разряда тысяч в делимом числе. 5 больше, чем 3, поэтому переходите к следующему шагу.

Шаг 2.  Посмотрите на разряд сотен. Может ли 5 ​​перейти в 36? Да: 7 × 5 = 35. Заполните разряды единиц и десятков «0» и вычтите.

Шаг 4 . Перейдите к разряду десятков остатка (число 154), которое было вычтено на предыдущем шаге. Может ли 5 ​​перейти в 15? Да: 5 × 3 = 15. Вставьте «0» в разряде единиц и вычтите

Шаг 5.  Перейдите в разряд единиц. Может ли 5 ​​перейти в 4? № 4 меньше, чем 5. Поставьте «0» в разряде единиц ответа. Остаток 4.

Ответ на 3654 ÷ 5 записывается 730 R 4
Чтобы проверить ответ на эту задачу на деление в длинную, умножьте 730 × 5, чтобы получить 3650.