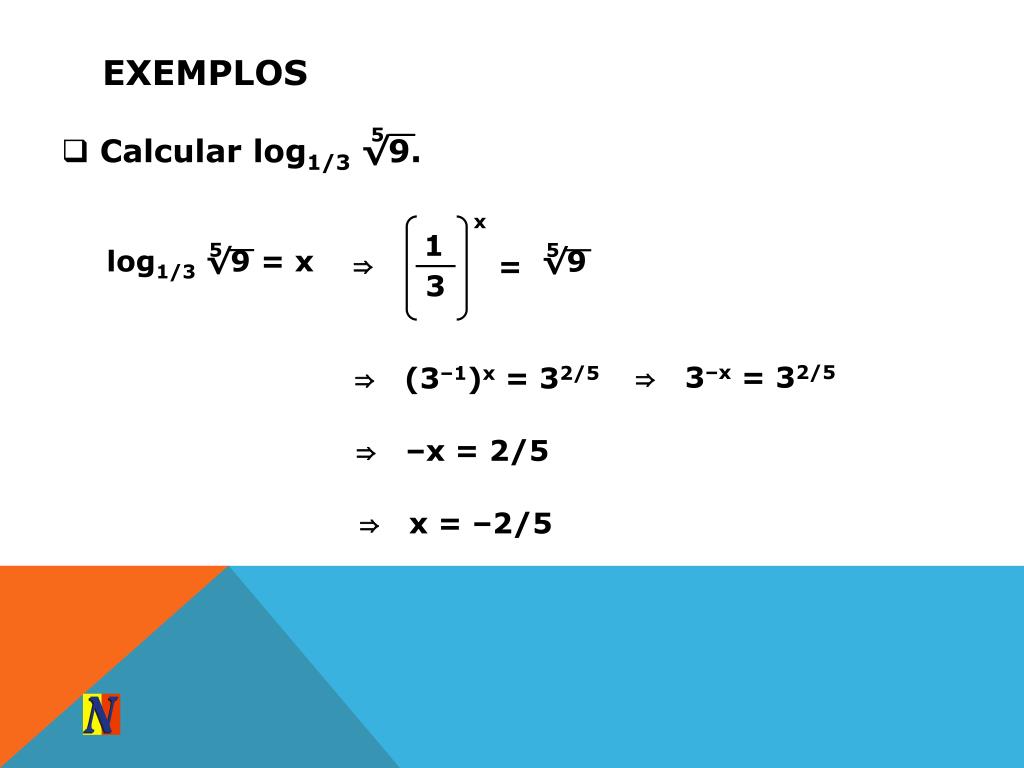Логарифмы. Решение заданий №10 по материалам открытого банка задач ЕГЭ по математике
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение заданий №10 ЛОГАРИФМЫ по материалам открытого банка задач ЕГЭ по математике 2015 года http://mathege.ru/or/ege/Main.html
МБОУ СОШ №5 – «Школа здоровья и развития»г. Радужный
Решение заданий
№10
ЛОГАРИФМЫ
по материалам открытого банка
задач ЕГЭ по математике 2015 года
http://mathege.
 ru/or/ege/Main.html
ru/or/ege/Main.htmlучитель математики Е.Ю. Семёнова
Задания открытого банка задач
1. Найдите значение выражения
Решение.
log2 16 log 6 36 log2 24 log 6 62 4 2 8
Использована формула:
loga a n n .
log5 4
7 5
.
2. Найдите значение выражения
Решение.
7 5log5 4 7 4 28
Использована формула:
a loga b b.
Задания открытого банка задач
36log6 5.
3. Найдите значение выражения
Решение.
log6 5
36
6
2 log6 5
log6 5 2
6
Использованы формулы:
52 25.
a
n m
a
m n
;
a loga b b.
4. Найдите значение выражения log 0 ,25 2.
Решение.
1
log 0 ,25 2 log 2 2 2 0,5.
2
1
Использована формула: logаk a .
k
Задания открытого банка задач
log 4 8.
5. Найдите значение выражения
Решение.
3
log 4 8 log 22 2 1,5.
2
3
n
Использована формула: logаk a .

k
n
log5 60 log 5 12.
6. Найдите значение выражения
Решение.
log 5 60 log5 12 log5
60
log 5 5 1.
12
b
Использованы формулы: logа b logа c logа ;
c
logа a 1.
Задания открытого банка задач
7. Найдите значение выражения log5 0,2 log 0 ,5 4.
Решение.
2
log 5 0,2 log 0 ,5 4 log 5 5 1 log 2 1 22 1 3.
1
n
n
Использована формула: logаk a .
k
log 3 25
.
8. Найдите значение выражения
log 3 5
Решение.
log 3 25
log5 25 log 5 52 2.
log 3 5
logс b
loga b ;
Использованы формулы:
logс a
loga a n n .
9. Найдите значение выражения
log5 9 log 3 25.
Решение.
log5 9 log 3 25 log 3 9 log 5 25 log 3 32 log 5 52 2 2 4.
Использованы формулы: logа b logd c logd b loga c ;
1
logаk a .
log 7 13
.
10. Найдите значение выражения
log 49 13
Решение.

log 7 13
log 7 13
log 7 13
2.
log 49 13 log 72 13 1 log 13
7
2
1
Использована формула: logаk a .
k
Задания открытого банка задач
11. Найдите значение выражения
1 log 2 12 1 log 6 12 .
Решение.
1 log 2 12 1 log 6 12
2
6
log 2 2 log 2 12 log 6 6 log 6 12 log 2
log 6
12
12
1
1
log 2 log 6 log 6 6 1 log 2 2 1 1 1 1.
6
2
Использованы формулы:
logа a 1;
b
logа b logа c logа ;
c
logа a 1 1.
Задания открытого банка задач
log 5 50
9
12. Найдите значение выражения
.
log 2
9
Решение.
5
log 50
50
log 5
9 5
log 5 50 log 52
log 525
2
2
9
9
9
9
81.
log 52
9
an
n m
Использованы формулы:
a
;
m
a
logа a n n .
b
logа b logа c logа .
c
Задания открытого банка задач
6 log 7 3 7.
13. Найдите значение выражения
Решение.

6 log 7
3
1
3
1
7 6 log 7 7 6 2.
3
Использованы формулы:
n
a
m
m
n
a ;
logа a n n .
log 13 13.
14. Найдите значение выражения
Решение.
6
log 6 13 13 log
1 13
13 6
1
log 13 13 6.
1
6
Использованы формулы:
n
a
m
m
n
a ;
1
logаk a .
k
Задания открытого банка задач
log 3 18
.
15. Найдите значение выражения
2 log 3 2
Решение.
log 3 18
2 log 3 2
2 log 3 2
2 log 3 2
2 log 3 2
log 3 9 log 3 2
2 log 3 2
log 3 32 log 3 2
2 log 3 2
1.
Использованы формулы: logа bc logа b logа c ;
logа a n n.
Задания открытого банка задач
log 3 5
log 7 0,2.
16. Найдите значение выражения
log 3 7
Решение.
log 3 5
log 3 7
log 7 0,2 log 7 5 log 7 0,2 log 7 5 0,2 log 7 1 0.

Использованы формулы: logс b
logс a
loga b ;
logа b logа c logа bc ;
logа 1 0.
Задания открытого банка задач
log 0 ,8 3 log 3 1,25.
17. Найдите значение выражения
Решение.
5
log 0 ,8 3 log 3 1,25 log 3 3 log 0 ,8 1,25 1 log 4 1.
5 4
Использованы формулы: logа b logd c logd b loga c ;
logа a 1;
1
logа 1.
a
Задания открытого банка задач
log
49
5 25 .
18. Найдите значение выражения
Решение.
log 25 49
5
log
5
52
72
5
2
log 5 7
2
log 5 7
5
7.
n
Использованы формулы: logak b loga b ;
k
n
a loga b b.
log 27 49.
19. Найдите значение выражения
Решение.
log
2
49 log
7
2
7
7
4
log
Использована формула:
7
7
4 2
42 16.
loga a n n .
Задания открытого банка задач
3 log 2
5
5
.

20. Найдите значение выражения
Решение.
5
3 log 5 2
log 5 2
5 5
3
125 2 250.
Использованы формулы:
a m n a m a n ;
a loga b b.
2 log8 3
8
.
21. Найдите значение выражения
Решение.
8
2 log8 3
log8 32
8
32 9.
n
Использованы формулы: n loga b loga b ;
a loga b b.
Задания открытого банка задач
log 8 3
64
.
22. Найдите значение выражения
Решение.
log 8 3
64
8
2 log 8 3
log 8 3
8
Использованы формулы:
3
2
a
m n
2
a
3.
n m
;
a loga b b.
log 4 log 5 25.
23. Найдите значение выражения
Решение.
1
2
log 4 log5 25 log 4 log5 5 log 4 2 log 2 2 0,5.
2
1
n
Использованы формулы: loga a n ; loga k a .
k
2
Задания открытого банка задач
24
.
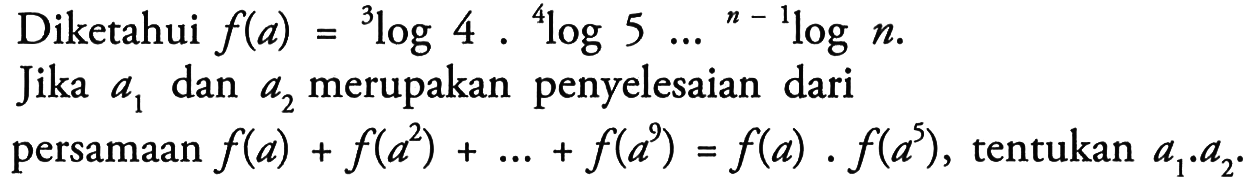
24. Найдите значение выражения
log 2
3
Решение.
3
24
24
12.
log 3 2
2
3
Использована формула: a
loga b
b.
log 1 13.
25. Найдите значение выражения
13
Решение.
1
1
1
2
2
log 1 13 log13 13
0,5.
1
2
13
1
Использована формула:
logak a n
n
.
k
Задания открытого банка задач
log 3 8,1 log 3 10.
26. Найдите значение выражения
Решение.
log 3 8,1 log 3 10 log 3 8,1 10 log 3 81 log 3 34 4.
Использованы формулы: logа b logа c logа bc ;
logа a n n .
log 6 13
.
27. Найдите значение выражения
log 6 13
Решение.
1
log 6 13
1
log13 13 log13 13 2 0,5.
log 6 13
2
logc b
Использованы формулы:
loga b ;
logc a
loga a n n .
Задания открытого банка задач
log ab
28.

log b a
Решение.
1
.
7
3
a
log a ab 3 log a a log a b 3 1 3 log a b 1
3
log b a
3
1 1 21 22.
1
7
Использованы формулы:
logа bc logа b logа c ;
n
logа b n logа b ;
1
loga b
.
logb a
Задания открытого банка задач
a
log
29. Найдите значение выражения , если
a
b3
log b a 5.
Решение.
a
3
3
log a 3 log a a log a b 1 3 log a b 1
b
logb a
3 2
1 0,4.
5 5
Использованы формулы: logа
b
logа b logа c ;
c
n
logа b n logа b ;
logа a 1;
1
loga b
.
logb a
Задания открытого банка задач
log a b
30. Найдите значение выражения , если
log a 2.
b
a
2
3
Решение.
log a a 2b 3 log a a 2 log a b 3 2 3 log a b 2
3
log b a
3
2
2 1,5 0,5.

2
Использованы формулы: logа bc logа b logа c ;
n
logа b n logа b ;
1
loga b
.
logb a
Задания открытого банка задач
log 2 3 log 3 2
3
.
31. Найдите значение выражения
Решение (1 способ).
3
log 2 3 log 3 2
log 3 2 log 2 3
3
log 2 3
2
Использованы формулы:
3.
a
m n
a
n m
;
a loga b b.
Решение (2 способ).
3
log 2 3 log 3 2
log 3 2 log 2 3
3
log 2 2 log 3 3
3
Использованы формулы: a m
n
31 3.
loga b logd c logd b loga c .
Используемые материалы
http://mathege.ru/or/ege/Main.html − Материалы открытого банка
заданий по математике 2013 года
English Русский Правила
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
Решено
Помогите пожалуйста
Дан куб ABCDA1B1C1D1
Задание 1. Назовите:
а)пару параллельных прямых;
б) пару пересекающихся прямых;
в) пару скрещивающихся прямых;
г) пару
Назовите:
а)пару параллельных прямых;
б) пару пересекающихся прямых;
в) пару скрещивающихся прямых;
г) пару
Решено
Определи скалярное произведение данных векторов, если длина ребра куба равна 2 ед. изм 1. A1D1⋅BC 2. D1B1⋅BD 3. AD⋅AC 4.DA⋅B1D1
По шоссе в одном направлении с постоянной скоростью через равные интервалы времени идут без остановок автобусы. Один человек прошел по шоссе 4 км,
Боря купил 4 книги. Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Пользуйтесь нашим приложением
Найдите значение числового логарифмического выражения – как решать
Формулировка задачи: Найдите значение числового логарифмического выражения.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).
Рассмотрим, как решаются подобные задачи на логарифмы на примерах.
Пример задачи 1:
Найдите значение выражения log0,310 – log0,33
Решение:
Разность логарифмов с одинаковым основанием равна логарифму частного:
log0,310 – log0,33 = log0,3(10/3)
Возведем 10/3 в степень -1, вынесем степень из под логарифма (логарифм степени):
log0,3(10/3) = -log0,3(3/10) = -1
Ответ: -1
Пример задачи 2:
Найдите значение выражения log713 / log4913
Решение:
Преобразуем знаменатель: для этого вынесем степень основания из под логарифма:
log4913 = log(7)213 = 1/2 ⋅ log713
Тогда значение выражения равно:
log713 / log4913 = 2 ⋅ log713 / log713 = 2
Ответ: 2
Пример задачи 3:
Найдите значение выражения 9log550 / 9log52
Решение:
Преобразуем выражение:
9log550 / 9log52 = 9log550 – log52
Разность логарифмов с одинаковыми основаниями равна логарифму частного:
log550 – log52 = log5(50/2) = log525 = 2
Тогда значение выражения равно:
92 = 81
Ответ: 81
Пример задачи 4:
Найдите значение выражения 6log7∛7
Решение:
Вынесем корень за пределы логарифма:
6log7∛7 = 6 ⋅ 1/3 ⋅ log77 = 2
Ответ: 2
Пример задачи 5:
Найдите значение выражения log35 / log37 + log70,2
Решение:
Преобразуем частное с помощью формулы перехода от логарифма в одном основании к логарифму при другом основании:
log35 / log37 = log75
Сумма логарифмов с одним основанием равна логарифму произведения:
log75 + log70,2 = log71 = 0
Ответ: 0
Пример задачи 6:
Найдите значение выражения log0,83 ⋅ log31,25
Решение:
Преобразуем второй множитель и приведем его к тому же основанию:
log31,25 = log3(5/4) = -log3(4/5) = -log30,8 = -1 / log0,83
И найдем значение выражения:
log0,83 ⋅ log31,25 = -log0,83 / log0,83 = -1
Ответ: -1
Пример задачи 7:
Найдите значение выражения 5log2549
Решение:
Вынесем степень основания логарифма за его пределы:
log2549 = 1/2 ⋅ log549
Внесем ее обратно как логарифм корня:
1/2 ⋅ log549 = log5(49)1/2 = log57
И воспользуемся основным логарифмическим тождеством:
5log2549 = 5log57 = 7
Ответ: 7
Пример задачи 8:
Найдите значение выражения log4(log216)
Решение:
Вычислим значение выражения в скобках:
log216 = 4
Тогда значение выражения равно:
log4(log216) = log44 = 1
Ответ: 1
Пример задачи 9:
Найдите значение выражения log42 + log0,258
Решение:
Найдем значения каждой части выражения и получим результат:
log42 =1/2 ⋅ log22 = 1/2 ⋅ 1 = 0,5
log0,258 = log1/48 = 1/2 ⋅ log1/28 = 1/2 ⋅ log1/223 = 1/2 ⋅ (-3) = -1,5
Тогда значение выражения равно:
log42 + log0,258 = 0,5 – 1,5 = -1
Ответ: -1
Пример задачи 10:
Найдите значение выражения 2log26 – 3
Решение:
Разложим число на множители:
2log26 – 3 = 2log26 ⋅ 2–3
Применим основное логарифмическое тождество к первому множителю и выполним оставшиеся вычисления:
2log26 ⋅ 2-3 = 6 ⋅ 1/8 = 0,75
Ответ: 0,75
Пример задачи 11:
Найдите значение выражения 7–2log72
Решение:
Вынесем множитель перед логарифмом в степень, чтобы избавиться от него:
–2log72 = log72–2 = log70,25
И применим основное логарифмическое тождество:
7–2log72 = 7log70,25 = 0,25
Ответ: 0,25
Пример задачи 12:
Найдите значение выражения (3log23)log32
Решение:
Если мы возведем число сначала в степень log32, а потом уже в степень log23, то сможем применить основное логарифмическое тождество:
(3log23)log32 = (3log32)log23 = 2log23 = 3
Ответ: 3
Пример задачи 13:
Найдите значение выражения (1 – log212) ⋅ (1 – log612)
Решение:
Преобразуем логарифмы:
log212 = log2(2 ⋅ 6) = log22 + log26 = 1 + log26
log612 = log6(2 ⋅ 6) = log62 + log66 = log62 + 1
Подставим полученные значения в выражение:
(1 – (1 + log26)) ⋅ (1 – (log62 + 1)) = (1 – 1 – log26) ⋅ (1 – log62 – 1) = – log26 ⋅ (– log62) = log26 ⋅ log62
Преобразуем второй множитель, чтобы логарифмы имели одинаковые основания, и выполним остальные действия:
log26 ⋅ log62 = log26 ⋅ 1/log26 = 1
Ответ: 1
Пример задачи 14:
Найдите значение выражения log318 / (2 + log32)
Решение:
Преобразуем 2 в знаменателе в логарифм с основанием 3 (возведем 3 в степень 2 и получим число под логарифмом):
2 = log39
Сумма логарифмов с одним основанием в знаменателе равна логарифму произведения:
2 + log32 = log39 + log32 = log3(9 ⋅ 2) = log318
Осталось сократить числитель и знаменатель:
log318 / log318 = 1
Ответ: 1
3-8
ПЛАТОН | Базовая математика | Логарифмы
Пусть a и N — положительные действительные числа, и пусть N = a n . Тогда n называется логарифмом N по основанию a . Мы пишем это как:
Тогда n называется логарифмом N по основанию a . Мы пишем это как:
| n = лог a N |
Пример 1:
(а)Поскольку 16 = 2 4 , тогда 4 = log 2 16
(b) Так как 81 = 3 4 , тогда 4 = log 3 81
(c) Поскольку 3 = √9, тогда 1 ⁄ 2 = log 9 3
(d) Поскольку 3 −1 = 1 ⁄ 3, то −1 = log 3 (1 ⁄ 3)
Упражнение 1: Используйте приведенное выше определение логарифмов, чтобы определить значение x в каждом из следующих случаев:
(а) x = логарифм 3 27
г. Решение:
По определению логарифма имеем:
3 х = 27
Но 27 = 3 3 , поэтому имеем:
3 x = 27 = 3 3
Так:
x = 3
(б) x = log 5 125
Решение: г.
По определению логарифма имеем:
25 х = 5
В настоящее время:
5 = √25 = 25 ½
Так:
25 x = 5 = 25 ½
Отсюда мы видим, что х = ½
(в) x = логарифм 2 (1 ⁄ 4)
Решение: По определению логарифма имеем:
2 x = 1 ⁄ 4 = 1 ⁄ (2 2 ) = 2 −2
Таким образом, х = −2
(г)2 = журнал x (16)
Решение: По определению логарифма имеем:
x 2 = 16 = 4 2
Таким образом, х = 4
(e)3 = логарифм 2 x
Решение: По определению логарифма имеем:
2 3 = х
Таким образом, х = 8
Нажмите на вопросы, чтобы открыть решения
Пусть a , M , N — положительные действительные числа, а k — любое число. Тогда к логарифмам применяются следующие важные правила:
Тогда к логарифмам применяются следующие важные правила:
| Правило 1 | журнал a (MN) | = | бревно a M + бревно a N |
|---|---|---|---|
| Правило 2 | журнал a ( M / N ) | = | журнал а М − лог а С |
| Правило 3 | бревно а ( м к ) | = | к бревно а М |
| Правило 4 | бревно а а | = | 1 |
| Правило 5 | журнал a 1 | = | 0 |
Proof that log a MN = log a M + log a N :
Пусть м = log a M and n = log a N , so, by definition, M = a m and N = a n . Затем:
Затем:
MN = a m × a n = a m + n
— где мы использовали соответствующее правило для показателей степени. Отсюда, используя определение логарифма, имеем:
м + н = лог а ( МН )
Но м + n = log a M + log a N , и приведенное выше уравнение может быть записано:
log A M + log A N = log A (
— что мы и хотели доказать.
Пример 2:
(a) log 6 4 + log 6 9 = log 6 (4 × 9) = log 6 36
Если x = log 6 36, то 6 x = 36 = 6 2 . Таким образом, log 6 4
+ log 6 9 = 2.
Таким образом, log 6 4
+ log 6 9 = 2.
(б) журнал 5 20 + логарифм 4 1 ⁄ 4 = логарифм 5 (20 × 1 ⁄ 4)
Теперь 20 × 1 ⁄ 4 = 5, поэтому log 5 20 + log 4 (1 ⁄ 4) = log 5 5 = 1
Тест 1: До какого из следующих чисел упрощается выражение log 3 15 + log 3 0,6?
(a)4Неверно — попробуйте еще раз!
(b)3Неверно. Повторите попытку!
(с)2Правильно — молодец!
(d)1Неверно. Повторите попытку!
Решение:
Используя правило 1, мы имеем: log 3 15 + log 3 0,6 = log 3 (15 × 0,6) = log 3 9
Но 9 = 3 2 , поэтому log 3 15 + log 3 0,6
= журнал 3 3 2 = 2.
Доказательство того, что журнал a M/N = log a M − log a N :
Как и раньше, пусть м = log a M и n = log a N . Тогда M = a m и N = a n . Теперь у нас есть:
М/Н = а м / а н = а м — н
— где мы использовали соответствующее правило для индексов. По определению логарифма имеем:
м − n = лог a ( M / N )
Из этого мы можем сделать вывод, что:
бревно а М − бревно a N = м − n = лог a ( M /
(a) log 2 40 − log 2 5 = log 2 (40 ⁄ 5) = log 2 8
Если х = log 2 8, то 2 х = 8 = 2 3 , поэтому х = 3.
(б) Если log 3 5 = 1,465, то мы можем найти log 3 0,6.
Поскольку 3 ⁄ 5 = 0,6, то log 3 0,6 = log 3 (3/5) = log 3 3 − log 3 5.
Теперь log 3 3 = 1, так что log 3 0,6 = 1 — 1,465 = -0,465
Тест 2: К какому из следующих чисел относится выражение log 2 12 − log 2 (3 ⁄ 4) упростить?
(a)0Неверно. Повторите попытку!
(b)1Неверно. Повторите попытку!
(c)2Неверно — попробуйте еще раз!
(d)4Правильно — молодец!
Решение:
Используя Правило 2, мы имеем: log 2 12 − log 2 (3 ⁄ 4) = log 2 (12 ÷ 3)
Теперь у нас есть 12 ÷ (3 ⁄ 4) = 12 × (4 ⁄ 3) = 12 × 4/3 = 16.
Таким образом, log 2 12 − log 2 (3 ⁄ 4) = log 2 16 = журнал 2 2 4 .
Если x = log 2 2 4 , то 2 x = 2 4 , поэтому x = 4.
Доказательство того, что log a ( M k ) = k log а М :
Пусть м = log a M , поэтому M = a m . Затем:
M K = ( A M ) K = A MK = A KM
 Отсюда имеем по определению логарифма:
Отсюда имеем по определению логарифма:км = log a ( M k )
Но м = log a M , поэтому последнее уравнение можно записать:
k log a M = km = log a ( M k )
— это тот результат, который мы хотели.
Пример 4:
(a) Найдите журнал 10 (1 ⁄ 10000).
У нас есть 10000 = 10 4 , поэтому 1 ⁄ 10000 = 1 ⁄ 10 4 = 10 −4 .
Таким образом, log 10 (1 ⁄ 10000) = log 10 (10 −4 )
= −4 log 10 10 = −4, где мы использовали Правило 4, чтобы записать log 10 10 = 1.
(b) Найдите журнал 36 6.
У нас есть 6 = √36 = 36 1 ⁄ 2 .
Таким образом, log 36 6 = log 36 (36 1 ⁄ 2 ) = 1/2 log 36 36 = 1/2.
Тест 3: Если log 3 5 = 1,465, какое из следующих чисел будет log 3 0,04?
(а)−2,930Правильно — молодец!
(b)−1,465Неверно — попробуйте еще раз!
(c)−3,465Неверно — попробуйте еще раз!
(d)2.930Неверно — попробуйте еще раз!
Решение:
Обратите внимание, что: 0,04 = 4 ⁄ 100 = 1 ⁄ 25 = 1 ⁄ 52 = 5 −2 .
Таким образом, log 3 0,04 = log 3 (5 −2 ) = −2 log 3 5.
Так как log 3 5 = 1,465, мы имеем log 3 0,05 = -2 × 1,465 = -2,930
В этом разделе мы рассмотрим некоторые приложения правил логарифмирования.
Пример 5:
(а) log 4 1 = 0,
(б)log 10 10 = 1,
(в) лог 10 125 + логарифм 10 8 = логарифм 10 (125 × 8) = логарифм 10 1000
= log 10 (10 3 ) = 3 log 10 10 = 3.
(г) 2 log 10 5 + log 10 4 = log 10 (5 2 ) + log 10 4 = log 10 (25 × 4)
= логарифм 10 100 = логарифм 10 (10 2 ) = 2 log 10 10 = 2.
(e) 3 log a 4 + log a (1 ⁄ 4) − 4 лог a 2 = log a (4 3 ) + log a (1 ⁄ 4) − log a (1 2
= log a (4 3 × 1/4) − log a (2 4 ) = log a (4 2 ) − log a (2 4 )
= журнал a 16 − log a 16 = 0.
Упражнение 2: Используйте правила логарифмирования, чтобы упростить каждое из следующих действий:
(а)3 log 3 2 − log 3 4 + журнал 3 (1/2)
Решение:
Прежде всего, по правилу 3 имеем 3 log 3 2 = журнал 3 (2 3 ) = журнал 3 8. Таким образом, выражение принимает вид:
log 3 8 — log 3 4 + log 3 (1/2) = [log 3 8 + log 3 (1/2)] — log 3 4. (1/2)] — log 3 4.
log 3 (8 × 1/2) = log 3 4
Тогда выражение упрощается до:
логарифм 3 4 − логарифм 3 4 = 0
(б)3 log 10 5 + 5 log 10 2 − журнал 10 4
Решение:
Сначала мы используем Правило 3, чтобы переписать первые два термина:
3 log 10 5 = log 10 (5 3 )
а также:
5 log 10 2 = log 10 (2 5 )
Таким образом:
3 логарифм 10 5 + 5 log 10 2 = log 10 (5 3 ) + log 10 (2 5 ) = log 10 (5 3 × 2 5 )
— где мы воспользовались Правилом 1 для получения правой части. Таким образом:
Таким образом:
3 log 10 5 + 5 log 10 2 − log 10 4 = log 10 (5 3 × 2 5 ) − log 10 4
и, используя Правило 2, это упрощается до:
log 10 (5 3 × 2 5 /4) = log 10 (10 3 ) = 3 log 10 10 = 3
(C) 2 10 10 = 3
(C) 2 log 9181 10 . 6 — (log a 4 + 2 log a 3)
Решение:
Имея дело сначала с выражением в скобках, мы имеем:
логарифм а 4 + 2 логарифм a 3 = log a 4 + log a (3 2 ) = log a (4 × 3 2 )
— где мы последовательно использовали Правила 3 и 2. Теперь:
Теперь:
2 log a 6 = log a (6 2 )
так что, наконец, мы имеем:
| 2 лог a 6 − (log a 4 + 2 log a 3) | = | log a (6 2 ) − log a (4 × 3 2 ) |
| = | журнал a (6 2 /4 × 3 2 ) | |
| = | журнал a 1 | |
| = | 0 |
(г)5 log 3 6 − (2 log 3 4 + log 3 18)
Решение:
Имея дело сначала с выражением в скобках, мы имеем:
2 log 3 4 + log 3 18 = log 3 (4 2 ) + логарифм 3 18 = логарифм 3 (4 2 × 18)
— где мы сначала использовали Правило 3, а затем Правило 1. Теперь, используя Правило 3 на первом члене, а затем Правило 2, мы получаем:
Теперь, используя Правило 3 на первом члене, а затем Правило 2, мы получаем:
| 5 log 3 6 − (2 log 3 4 + log 3 18) | = | логарифм 3 (6 5 ) − логарифм 3 (4 2 × 18) |
| = | бревно 3 (6 5 /4 2 × 18) | |
| = | бревно 3 (2 5 × 3 5 /4 2 × 2 × 9) | |
| = | журнал 3 (3 3 ) | |
| = | 3 log 3 3 = 3 |
— так как лог 3 3 = 1
(e)3 log 4 ( √3) − 1/2 лог 4 2 + 3 log 4 2 − журнал 4 6
Решение:
Прежде всего отметим, что √3 можно записать как 3 ½ 9. 1812 .
Сначала упростим некоторые термины. Они есть:
1812 .
Сначала упростим некоторые термины. Они есть:
3 log 4 (√3) = 3 log 4 (3 ½ ) = 3/2 log 4 3
а также
log 4 6 = log 4 (2 × 3) = log 4 2 + log 4 3
Соединяем все это вместе:
| 3 log 4 ( √3) − 1/2 лог. 4 2 + 3 log 4 2 − журнал 4 6 | = | 3/2 бревно 4 3 − 1/2 лог. 4 3 + 3 log 4 2 − (log 4 2 + log 4 3) |
| = | (3/2 − 1/2 − 1) log 4 3 + (3 − 1) log 4 2 | |
| = | 2 log 3 2 = log 4 (2 2 ) = log 4 4 = 1 |
Нажмите на вопросы, чтобы открыть решения
В каждом из следующих найдите x
1. log x 1024 = 2
log x 1024 = 2
(a)2 3
(b)2 4
(c)2 2
(d)2 5
2. x = (log A √27 — log A √8 — log a √8 — log A √8 — log A √8 — log A √8 — log A √8 — log a √8 — log a √8) a 20)
(a)1
(b)3
(c)3 ⁄ 2
(d)−2 ⁄ 3
3.log c (10 + х ) − log c x = log c 5
(а)2,5
(б)4,5
(в)5,5
(г)7,5
Есть еще одно правило для логарифмов, чрезвычайно полезное на практике. Это связывает логарифмы по одному основанию с логарифмами по другому основанию.
другая база. Большинство калькуляторов в стандартной комплектации имеют возможность нахождения логарифмов по основанию 10, а также логарифмов. по основанию e (натуральные логарифмы). Что произойдет, если потребуется логарифмирование по другому основанию, например 2? Следующее правило
что нужно:
по основанию e (натуральные логарифмы). Что произойдет, если потребуется логарифмирование по другому основанию, например 2? Следующее правило
что нужно:
| бревно а в = бревно а б × бревно 5 в |
Доказательство приведенного выше правила:
Пусть x = log a b и y = log b c . Тогда по определению логарифмов:
а х = б и б у = в
5
5 Это означает, что:c = b y = ( a x ) y = a xy
— с последним равенством, вытекающим из законов индексов. С года с = a xy , по определению логарифмов это означает, что:
С года с = a xy , по определению логарифмов это означает, что:
log a c = xy = log a b × log b c
Properties of Logarithms
Properties of Logarithms
Раздел 9.0B
Найдите x для
журнал 3 3 2 = х
переписать
3 х = 3 2
поэтому
х = 2
Журнал 5 25 = х
5 х = 25
х = 2
Ln e 3 = х
г.е х = е 3
х = 3
Журнал 10 = х
10 х = 10
х = 1
Обратные свойства:
log10 х = х
x = x
г.
Не путайте лог с пер.
журнал e x х
и
10 x х ,
Больше инверсий (функции отменяют друг друга).
Для пример
( ) 2 = х
е лн х = х
10 logx = x
Пример 1: Решение показательных уравнений.
а) 10 х = 3 Возьмите общее бревно обеих сторон
Log10 x = журнал 3 Обратная собственность
X = логарифм 3 = 0,47712155 Воспользуйтесь калькулятором
г.б) 2e 3x = 5 основание равно e, но перед тем, как взять ln с обеих сторон, изолируйте e 3x
е 3x = 5/2 возьми с обеих сторон
ln e 3x = ln (5/2) Обратная собственность
3x = пер (5/2) Решите для х
х = ln(5/2) = 0,305430244
3
Свойство: Экспонента становится множителем
журнал А р = г лог А
пер А г = г пер А
Доказательство:
Лет
журнал А = у
г.
переписать
10 г = А
поднять обе стороны на n
(10 y ) н = А н
взять бревно с обеих сторон
журнал 10 ny = журнал A n
Инверсное свойство
ny = журнал A п
, но
у = журнал А (дано)
Поэтому
n(y) = n(log A)
Пример 3:
Решить
3 2x = 5
Основание не равно ни 10, ни е, но мы все еще можем взять общее бревно обеих сторон и используйте правило множителя.
г.Журнал 3 2x = журнал 5
2xlog 3 = log 5
Икс = log5/2log3 = 0,73248676
Подразделение становится свойство вычитания .
журнал A/B = журнал A журнал B
ln A/B = ln A ln B
Примечание: лог А/лог Б журнал А журнал Б
г.
Доказательство:
Пусть а = журнал А б = журнал B
Переписать 10 а = А 10 б = Б
Разделить А/В = 10 а / 10 б
Свойство показателей А/В = 10 а б
г. Взять журнал обоих журнал А/В = журнал 10 а б
Инверсное свойство журнал А/В = а б
Дано журнал A/B = журнал A журнал B
ПРИМЕР 5:
Переписать
а) журнал 5x/3
без дроби
журнал 5x журнал 3
г.
б) журнал 3 журнал 2x
в виде единого журнала
журнал 3/2x
Умножение становится дополнительным свойством.
журнал (AB) = журнал A + журнал B пер (АВ) = пер А + пер В
Дополнительный кредит: Докажите это свойство.
г.Упражнение 6:
Переписать
а) журнал 4x
в виде отдельных журналов
Журнал 4 + лог х
б) журнал 5 + журнал 3x
в виде единого журнала
журнал 15x
Упражнение 7:
Используя все три свойства (множитель, деление,
дополнение) решить следующее.
Лог х + лог 5 = 3 Дополнение свойство
Лог 5x = 3 Перепишем в экспоненциальной форме
10 3 = 5x Упростить
1000 = 5х Решите для х
1000/5 = х = 200
Вернуться к экспоненциалам и логарифмам Главная страница
г.Вернуться на главную страницу обзора математических идей
Назад на главную страницу математического факультета
электронная почта Вопросы и предложения
Решение логарифмических уравнений – объяснение и примеры
Как вы хорошо знаете, логарифм – это математическая операция, обратная возведению в степень. Логарифм числа обозначается аббревиатурой « log ».
Прежде чем мы приступим к решению логарифмических уравнений, давайте сначала ознакомимся со следующими правилами логарифмирования:
- Правило произведения:
Правило произведения гласит, что сумма двух логарифмов равна произведению логарифмов. Первый закон представлен как;
Первый закон представлен как;
⟹ log b (x) + log b (y) = log b (xy)
- отношение логарифмов.
⟹ бревно б (х) – бревно b (y) = log (x/y)
- The power rule:
⟹ log b (x) n = n log b (x)
- Change базового правила.
⟹ log B x = (log A x)/ (log a b)
- Правило идентификации 93
- Логарифм числа 1 по любому ненулевому основанию всегда равен нулю.
b 0 =1 ⟹ log b 1 = 0. - Уравнения, содержащие логарифмы на одной стороне уравнения.
- Уравнения с логарифмами по разные стороны от знака равенства.
- Упростите логарифмические уравнения, применив соответствующие законы логарифмирования.
- Перепишите логарифмическое уравнение в экспоненциальной форме.
- Теперь упростите показатель степени и найдите переменную.
- Проверьте свой ответ, подставив его обратно в логарифмическое уравнение.
 Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент. - Если логарифмы имеют общее основание, упростите задачу и перепишите ее без логарифмов.
- Упростите, собрав одинаковые члены, и найдите переменную в уравнении.
- Проверьте свой ответ, подставив его обратно в исходное уравнение. Помните, что приемлемый ответ приведет к положительному аргументу. Пример 71824 (40)
Решение
Сначала упростим логарифмы.

логарифм 6 (2x – 4) + логарифм 6 (4) = логарифм 6 (40) ⇒ логарифм 6 [4(2x – 4)] = логарифм 6 (40)
Now drop the logarithms
⇒ [4(2x – 4)] = (40)
⇒ 8x – 16 = 40
⇒ 8x = 40 + 16
8x= 56
x = 7
Example 8
Решите логарифмическое уравнение: log 7 (x – 2) + log 7 (x + 3) = log 7 14
Решение
Упростите уравнение, применив правило произведения.
Log 7 [(x – 2) (x + 3)] = log 7 14
Отбросить логарифмы.
⇒ [(x – 2) (x + 3)] = 14
Распределите ФОЛЬГА, чтобы получить;
⇒ х 2 – х – 6 = 14
⇒ х 2 – х – 20 = 0
⇒ (х + 4) (х – 5) = 0
x = -4 или x = 5
, когда x = -5 и x = 5 подставляются в исходное уравнение, дают отрицательный и положительный аргумент соответственно.
 Следовательно, x = 5 является единственным приемлемым решением.
Следовательно, x = 5 является единственным приемлемым решением.Example 9
Solve log 3 x + log 3 (x + 3) = log 3 (2x + 6)
Solution
Given the equation; log 3 (x 2 + 3x) = log 3 (2x + 6), отбросьте логарифмы, чтобы получить;
⇒ x 2 + 3x = 2x + 6
⇒ x 2 + 3x – 2x – 6 = 0
x 2 + x – 6 = 0……………… (Квадратное уравнение)
получить квадратное уравнение;(x – 2) (x + 3) = 0
x = 2 и x = -3Проверив оба значения x, мы получаем, что x = 2 является правильным ответом. Пример 101810 log 5 (30x – 10) – 2 = log 5 (x + 6)
Это уравнение можно переписать как;
⇒ log 5 (30x – 10) – log 5 (x + 6) = 2
Упростим логарифмы
log 5 + 2 [(30)/x – 0]
Переписать логарифм в экспоненциальной форме.

⇒ 5 2 = [(30x – 10)/ (x + 6)]
⇒ 25 = [(30x – 10)/ (x + 6)]
При перекрестном умножении получаем;
⇒ 30х – 10 = 25 (х + 6)
⇒ 30x — 10 = 25x + 150
⇒ 30x — 25x = 150 + 10
⇒ 5x = 160
x = 32
его закон тоже законы логаритов
его закон.Copyright 20022022 Стэн Браун, BrownMath.com
Сводка: У вас есть проблемы с запоминанием законов логарифмов? Делать вы знаете, почему вы можете преобразовать log(x)+log(y) в другую форму, но не лог(х+у)? Эта страница поможет вам разобраться в законах логарифмы.
г.См. также: Все законы логарифмов текут непосредственно из законов показателей . Если вы чувствуете себя немного неустойчиво с законами экспонент, пожалуйста, просмотрите их перед продолжением.
Содержимое:
- Логарифм? Что такое логарифм?
- Откуда взялись журналы?
- Зачем нам это?
- Базовые факты
- логарифм 1, логарифм, равный 1
- Журнал как обратный
- Что такое In?
- Объединение журналов с одной и той же базой
- Умножение чисел, сложение их логарифмов
- Экспонента, умножить логарифм
- Возведение чисел в любую степень
- Разделить числа, вычесть их логарифмы
- Замена базы
- Резюме
- Заключение
- Что нового?
Логарифм? Что такое логарифм?
Логарифм — это просто показатель степени.

Если быть точным, логарифм числа x по основанию b это просто показатель степени, который вы прибавляете к b , чтобы получить результат равно х . Например, поскольку 5 = 25, мы знаем, что 2 (значение мощность) является логарифмом 25 по основанию 5. Символически, log 5 (25) = 2,
В более общем смысле, если x = b y , то мы скажем, что y является логарифмом x по основанию b или основание- b логарифм x . В символах y = log b ( x ), часто пишут без скобок, y = log b x . Каждое показательное уравнение можно переписать как логарифмическое уравнение, и наоборот, просто поменяв местами x и y этим способом.
Вы не часто видите это слово, но могли бы также говорят, что x — это антилогарифм от г до база б .
 Логарифм — это показатель степени, а антилогарифм — это
результат возведения основания в этот показатель.
Логарифм — это показатель степени, а антилогарифм — это
результат возведения основания в этот показатель.Другой способ взглянуть на это состоит в том, что журнал б x функция определяется как обратная b x функция. Эти два утверждения выражают эта обратная связь, показывающая, как экспоненциальное уравнение эквивалентно логарифмическому уравнению:
х = б у такой же как у = логарифм б х
В любом уравнении x является антилогарифмом и y — это логарифм по основанию b .
Пример 1: 1000 = 10 3 – это то же самое, что 3 = логарифм 10 1000. Логарифм равен 3, а антилогарифм равен 1000.
Пример 2: журнал 3 81 = ? то же самое как 3 ? = 81. Неизвестный ? это логарифм, а 81 это антилогарифм.
Нельзя слишком часто говорить: логарифм — не что иное, как показатель степени.
 Вы можете написать приведенное выше определение
компактно и показать журнал в виде экспоненты,
подставив второе уравнение в первое, чтобы исключить г :
Вы можете написать приведенное выше определение
компактно и показать журнал в виде экспоненты,
подставив второе уравнение в первое, чтобы исключить г :Прочтите, что логарифм x по основанию b является показатель, который вы поставили на b , чтобы в результате получить x .
Откуда взялись журналы?
Раньше карманный калькулятортолько несколько десятков лет назад, но в студенческие годы это эпоха динозавровответ было просто. Вам нужны были журналы, чтобы вычислить большинство степеней и корней с честным точность; даже умножение и деление большинства чисел было с логами проще. В каждой приличной книге по алгебре были страницы и страницы журнальных таблиц на спина.
Изобретение бревен в начале 1600-х годов подстегнуло научный революция. В то время ученые, особенно астрономы, тратили огромные суммы времени хруст числа на бумаге. Сократив время, которое они тратили на выполнение арифметика, логарифмы фактически дали им более продолжительное время продуктивной работы.
 жизнь. Логарифмическая линейка,
когда-то почти мультяшный товарный знак ученого,
был не чем иным, как устройством, созданным для выполнения различных вычислений
быстро, используя логарифмы.
См. Эли Маорс e: История числа , чтобы узнать больше
это.
жизнь. Логарифмическая линейка,
когда-то почти мультяшный товарный знак ученого,
был не чем иным, как устройством, созданным для выполнения различных вычислений
быстро, используя логарифмы.
См. Эли Маорс e: История числа , чтобы узнать больше
это.Сегодня журналы больше не используются для рутинной обработки чисел. Но все же есть веские причины для их изучения.
Зачем нам это?
Почему мы вообще пользуемся логарифмами? Я мог бы написать целую статью о них, может быть, однажды. Но сейчас. …
- Чтобы найти количество платежей на кредит или время, чтобы достичь инвестиционная цель.
- Для моделирования многих природных процессов, особенно в живых системах. Мы воспринимаем громкость звука как логарифм фактического звука. интенсивность, а дБ (децибелы) — логарифмическая шкала. Звездные величины измеряется в логарифмическом масштабе.
- Для измерения pH или кислотности химического раствора.
рН представляет собой отрицательный логарифм концентрации свободного
ионы водорода.

- Для измерения интенсивности землетрясений по шкале Рихтера.
- Для анализа экспоненциальных процессов. Поскольку логарифмическая функция является обратной экспоненциальной функцию, мы часто анализируем экспоненциальную кривую с помощью логарифмы. Нанесение набора измеренных точек на логарифмическую или полулогарифмическую бумагу может легко выявить такие отношения. Применения включают охлаждение мертвого тела, рост бактерий, и распад радиоактивных изотопов. Распространение эпидемии в популяции часто следует модифицированному логарифмическая кривая называется логистической.
- Для решения некоторых задач с площадями в исчислении. (Площадь под кривой 1/ x , между x = 1 и x = A , равна № А .)
- Также в исчислении дифференцирование сложного произведения становится намного проще, если вы сначала возьмете логарифм.
(Исторически основная причина обучения журналы в начальной школе было упростить вычисления, потому что логарифм умножения понижает его до дополнения, а журнал мощности выражение понижает его до умножения.
г. Конечно,
с широкой доступностью персональных вычислительных устройств,
сложность вычислений больше не вызывает беспокойства, но журналы по-прежнему имеют
множество самостоятельных приложений.)
Конечно,
с широкой доступностью персональных вычислительных устройств,
сложность вычислений больше не вызывает беспокойства, но журналы по-прежнему имеют
множество самостоятельных приложений.)Основные факты
Из определения бревна как обратного экспоненциальный, вы можете сразу получить некоторые основные факты. Например, если построить график y = 10 x (или экспонента с любым другим положительным основанием), вы увидеть, что его диапазон является положительным реалом; поэтому область y = log x (по любому основанию) — положительные действительные числа. В других словами, вы не можете взять логарифм 0 или логарифм отрицательного числа.
(На самом деле, если вы хотите выйти за пределы реальности, вы можете взять журнал отрицательного числа. Эта техника преподается на многих курсах по тригонометрии.)
г.Журнал 1, логарифм, равный 1
Вы знаете, что все в нулевой степени равно 1: b 0 = 1.  Измените это в логарифмическую форму с определением журналов, и вы получите
Измените это в логарифмическую форму с определением журналов, и вы получитеlog b 1 = 0 для любого основания b Точно так же вы знаете, что первая степень любого числа равна именно этому числу: Опять же, превратите это в логарифмическую форму, и у вас будет log b b = 1 для любого основания b Пример 3: пер 1 = 0
Пример 4: журнал 5 5 = 1
Журнал как обратный
Журнал — это показатель степени, поскольку функция журнала — это обратная экспоненциальная функция. Обратная функция отменяет действие исходной функции. (Я не большой поклонник большинства случаев использования термина «отмена» в математике, но это подходит в этой ситуации.)
г.Это означает, что если вы возьмете логарифм экспоненты (разумеется, с тем же основанием), вы вернетесь к тому, с чего начали: log b b x = x для любого основания b 9477 вычисление фактов Пример 5: журнал 5 125 = журнал 5 (5) = 3
Пример 6: log 10 10 3,16 = 3,16
Пример 7: ln e − k t /2 = − k t /2
Что такое In?
В качестве основания логарифмов подходит любое положительное число, но две базы используются больше, чем любые другие:
основание
логарифмовсимвол имя 10 журнал
(если база не показана)десятичный логарифм e пер. 
натуральный логарифм,
произносится как элл-энн или ланНатуральные логарифмы являются логарифмами и подчиняются всем тем же правилам, что и любой другой логарифм. Просто запомните: ln x означает log e x Почему база e? Что особенного в е? Большинство объяснений нуждаются в некоторых вычислениях, например, что e x — единственная функция, которая одновременно является интегральной и свою собственную производную, или что e имеет это красивое определение в число факториалов:
е = 1/0! + 1/1! + 1/2! + 1/3! + …
Числовое значение e равно примерно 2,7182818284. Его иррациональное (десятичное расширение никогда не заканчивается и никогда не повторяется), и на самом деле, как и π, его трансцендентное (ни одно полиномиальное уравнение с целыми коэффициентами не имеет π или e в качестве корня.
 )
)e (как и π) встречается во всех видах маловероятные места, такие как расчет сложных процентов. Потребовалась бы книга, чтобы объяснить, и к счастью там есть книга, Эли Маорс е: История одного Номер . Он также углубляется в историю логарифмов, и книга стоит получить из вашей библиотеки.
Объединение журналов с одной и той же базой
Через минуту хорошо посмотрите на различные комбинации. Но сначала ты может захотеть узнать общий принцип: журнала сокращают количество операций по одному уровню. Логи превращают умножение в сложение, деление на вычитание, показатель степени на умножение и радикальное разделение. Теперь давайте разберемся, почему, и рассмотрим несколько примеров.
Умножение чисел, сложение их логарифмов
Умножение двух выражений соответствует сложению их логарифмов. Можем ли мы понять это?
Согласно компактному определению, x = b log b x and y = b log b y and therefore, substituting for x and г , x y = б бревно б x б 1 бревно 4 б 188194 91 9 гНо когда вы умножаете две степени одного и того же основания, вы складываете их степени.  Таким образом, правая часть становится
Таким образом, правая часть становитсяx y = b log b x +log b y Now apply the compact definition to the left=hand side: b log b ( x y ) = x y Combine that with the preceding equation to obtain b log b ( x y ) = b log b x +log b y Now у нас есть две силы одной базы. Если степени равны, то и показатели должны быть равны. Поэтому log b ( x y ) = log b x + log b y So whats the bottom line? Умножение двух чисел и взятие log — это то же самое, что взять их журналы и добавить.

Пример 8: log 8 ( x )+log 8 ( x ) совпадает с журнал 8 ( x x ) или просто журнал 8 ( x ). (Как вы увидите в следующем разделе, это может быть далее упрощено до 3log 8 x .)
Пример 9: логарифм 10 (20)+логарифм 10 (50) = log 10 (2050) = log 10 (1000) = 3,
Поскольку эта статья поможет вам,
, пожалуйста, нажмите, чтобы сделать пожертвование!Поскольку эта статья поможет вам,
, пожалуйста, сделайте пожертвование на
BrownMath.com/donate.Экспонента, умножить логарифм
Продолжая тему логарифмов, снижающих уровень операций, если у вас есть и -я степень числа и взять log, результат будет y раз больше логарифмического числа. Здесь почему, начиная с x y :
Начните с компактного определения логарифма: х = б бревно б х и поднимите обе стороны к y power: x y = ( b log b x ) y A power of a power is equivalent to just multiplying the exponents.  Упростите правую часть:
Упростите правую часть:х у = B ( Y Log B x ) Переписывает левую сторону, используя компактное определение лога b log b ( x y ) = x y (The font may be hard to read: это x в степени y слева и справа.) и объедините последние два уравнения: b log b ( x y ) = b ( y log b x ) If the powers are равны и основания равны, степени должны быть равны: log b ( x y ) = y log b x Пример 10: ln(2 6 ) = 6 ln 2 (где ln означает log e , натуральный логарифм).

Пример 11: log 5 (5 x ) равно , а не равно 2 log 5 (5 x ). Будьте внимательны с порядком действий! 5 x равно 5 ( x ), а не (5 x ). log 5 (5 x ) необходимо сначала разложить как журнал продукта: бревно 5 5 + журнал 5 ( x ). Тогда второй член может использовать правило мощности, журнал 5 ( x ) = 2 log 5 x . Первый член всего 1. Подводя итог, log 5 (5 x ) = 1 + 2 log 5 x .
Возведение чисел в любую степень
Хитрость при вычислении таких выражений, как 6.7 4.4 , заключается в следующем. использовать правило экспоненты и определение log-as-inverse:
х = 6,7 4,4
log x = 4,4 (log 6,7) = около 3,634729132
х = 10 3,63472… = около 4312,5
Здесь нет ничего особенного в журналах с основанием 10.
 расчет может быть равен
расчет может быть равенх = 6,7 4,4
ln x = 4,4 (ln 6,7) = около 8,3616
х = е 8,36927… = около 4312,5
Это будет работать для любого положительного основания и любого действительного показателя степени, поэтому например
х = п п
log x = π (log π) = около 1,561842388
х = 10 1,5618… = около 36,46215961
Вы можете комбинировать это с умножение чисел = добавление правила логарифмов к оценить степени, которые слишком велики для вашего калькулятора. Например, что такое 671 217 ?
х = 671 217
log x = 217 (log 671) = около 613,3987869
Теперь разделите целые и дробные части числа логарифм.
log х = около 0,3987869 + 613
х = 10 0,3987869 + 613
х = 10 0,3987869 10 613
х = около 2,505 10 613
Для подобных примеров вам действительно нужно использовать 10-ю систему счисления.
 журналы.
журналы.Если основание отрицательное или показатель степени сложный, см. Силы и корни комплексного числа.
Разделить числа, вычесть их логарифмы
Поскольку деление противоположно умножению, а вычитание является противоположностью сложения, поэтому неудивительно, что деление двух выражений соответствует вычитанию их журналов. Пока мы могли идти снова вернуться к компактному определению, его вероятно, проще использовать два предыдущих свойства.
г.Начнем с того, что 1/ y = y −1 (см. определение отрицательных показателей): x / y = x (1 / y ) = x y -1 и возьмите журнал из оба Стоя. логарифм б ( x / у ) = логарифм b ( x y −1 ) Правая часть представляет собой логарифм произведения, который становится суммой логов: 9 Log B ( x / y ) = log B x + log B ( + Log B ( + B ( + B ( + .  это логарифм степени, который становится (-1) умноженным на логарифм или просто минус логарифм:
это логарифм степени, который становится (-1) умноженным на логарифм или просто минус логарифм:log b ( x / y ) = log b x − log b y In words, if you divide and take the log , то же самое, что вычитание отдельных журналов.
Пример 12: 67515=45 и, следовательно, журнал 10 675 − журнал 10 15 = log 10 45. (Попробуйте на своем калькуляторе!)
г.Пример 13: журнал ( x y ) – журнал( x y ) = log( x y / x y ) = лог( x / y ) = log( x ) − log( y ).
Замена основания
Теперь у вас есть все необходимое для изменения логарифмов из единицы базу в другую. Посмотрите еще раз на компакт уравнение, определяющее журнал в базе b :
Чтобы изменить журнал с базы b на другую базу (назовем ее a ), вам нужно найти журнал a ( x ).  Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошим началом будет взять основание- и логарифм с обеих сторон:
Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошим началом будет взять основание- и логарифм с обеих сторон:журнал a ( b журнал b x ) = журнал a x Но левая часть этого уравнения — это просто логарифм степени. Вы помните, что log( x y ) это просто log( x ) умноженный на y . Таким образом, уравнение упрощается до (log a b ) (log b x ) = log a x Обратите внимание, что log a b является константой. Этот означает, что журналы всех чисел в данной базе a являются пропорционально логарифмам тех же чисел в другой базе b , а константа пропорциональности log a b равна лог одной базы в другой базе.
г. Если вы похожи на меня, у вас могут возникнуть проблемы с запоминанием
то ли умножать, то ли делить. Если да, то просто выведите
уравнение, как видите, занимает всего два шага.
Если вы похожи на меня, у вас могут возникнуть проблемы с запоминанием
то ли умножать, то ли делить. Если да, то просто выведите
уравнение, как видите, занимает всего два шага.В некоторых учебниках формула замены основания представлена в виде дроби. Чтобы получить дробь из приведенного выше уравнения, просто разделите на константу пропорциональности log a b : Log B x = (log A x )/ (Log A B) B) B) Пример 15: Большинство калькуляторов не умеет строить графики y = log 3 x напрямую. Но вы можете изменить базу на e и легко построить y = (ln x )(ln 3).
 (Ты мог
одинаково хорошо использовать основание 10.)
(Ты мог
одинаково хорошо использовать основание 10.)Интересная боковая дорога ведет от приведенной выше формулы. Замените везде x на a это допустимо, так как формула верна для всех положительных a , b и x . Вы получаете log b a = (log a a ) / (log a b ) But log a a = 1 (см. журнал 1 выше), поэтому формула принимает вид log b a = 1 / (log a b ) 3 Пример 96: журнал 10 е = 1/(лн 10). (Вы можете проверить это на своем калькуляторе.)
Пример 17: журнал 125 5 = 1/(лог 5 125). Это легко проверить: 5 3 = 125, а 5 – кубический корень из 125.
г. Следовательно, log 125 5 = 1/3 и
log 5 125 = 3, а 1/3 действительно равно
1/3.
Следовательно, log 125 5 = 1/3 и
log 5 125 = 3, а 1/3 действительно равно
1/3.Резюме
Законы логарифмов разбросаны по этому длинному странице, поэтому может быть полезно собрать их в одном месте. Делать этот еще более удивительно полезный <ухмылка>, связанный здесь также показаны законы показателей.
Ради бога, не пытайтесь запомнить эту таблицу! Просто используйте его, чтобы встряхните свою память по мере необходимости. Еще лучше, поскольку журнал является показателем степени, используйте законы показателей для повторного получения любого свойства логарифмов, которые вы, возможно, забыли. Таким образом, вы действительно получите мастерство владения этим материалом, и вы будете чувствовать себя уверенно в операции.
г.exponents logarithms (All laws apply for any positive a , b , x , and y .) x = б г такой же как y = log b x b 0 = 1 бревно б 1 = 0 б 1 = б Log B B = 1 B (log B X ) = x ) = X ) = X ) log b b x = x b x b y = б х + у log b ( x y ) = log b x + log b y b x / b у = б х − у журнал б ( x / у ) = журнал b x − log b y ( b x ) y = b x y Log B ( x Y ) = Y Log B X 1111820 X 
(журнал а б ) (log B x ) = log A x B 4 9 40004 B B . log a b ) log b a = 1 / (log a b ) Dont get creative! Большинство вариаций вышеперечисленного недействительны.
г.Пример 18: log (5+ x ) отличается от log 5 + log x . Как вы знаете, log 5 + log x = log(5 x ), не журнал (5+ x ). Посмотрите внимательно на приведенную выше таблицу, и вы увидите что вы ничего не можете сделать, чтобы разделить журнал ( x + y ) или журнал ( х — у ).
Пример 19: (логарифм x ) / (log y ) не совпадает с log( x / и ).
 В
на самом деле, когда вы делите два бревна на одно и то же основание, вы
работая по формуле замены основания в обратном порядке. Хотя это не часто
полезно, (log x ) / (log y ) =
журнал г x . Только не пишите лог( x / y )!
В
на самом деле, когда вы делите два бревна на одно и то же основание, вы
работая по формуле замены основания в обратном порядке. Хотя это не часто
полезно, (log x ) / (log y ) =
журнал г x . Только не пишите лог( x / y )!Пример 20: (log 5)(log x ) не является то же, что и журнал (5 x ). Вы знаете, что журнал (5 x ) log 5 + log x . Там действительно не так много, вы можете делать с произведением двух бревен, когда они имеют одинаковую основу. (Вы можете переписать произведение как журнал( x log 5 ), но это вряд ли проще.)
См. также: Объединение операций (распределительные законы)
Заключение
Ну вот и все: законы логарифмов демистифицировано! Общее правило заключается в том, что журналы просто удаляют операцию вниз на один уровень: показатели степени становятся множителями, деления становятся вычитания и так далее.
г. Если когда-либо вы не уверены в операции, например
как изменить базу, работа
это, используя определение журнала и
применяя законы показателей, и вы
не пойдет не так.
Если когда-либо вы не уверены в операции, например
как изменить базу, работа
это, используя определение журнала и
применяя законы показателей, и вы
не пойдет не так.Что нового?
- 15 ноября 2021 г. : обновлены внешние ссылки.
- 28 мая 2021 г. : Добавил ссылку на мой новый страницу звездных величин и удалил утверждение, что мы воспринимаем интенсивность света логарифмически, так как недавние исследования поставили под сомнение на что.
- 7 декабря 2020 г. :
- Добавлен термин антилогарифм, с дополнительным текстом здесь, здесь и здесь.
- Обратил внимание на обычай опускания круглые скобки с функцией журнала.
- Изменено три десятилетия на несколько десятилетия до появления карманных калькуляторов. (Студенты в моем классы впервые начали получать НР-35 в 1973 г.)
- Добавлена переписанная форма (журнал 5)(лог x ).
- 20/23 октября 2020 г.

- Логарифм? Что такое логарифм?
Правило 93 Правило 9966 . всегда 1.
b 1 =b ⟹ log б (б)=1.Пример:
Уравнение, в показателях которого стоят переменные, называется показательным уравнением.
 Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением.
Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением.Целью решения логарифмического уравнения является нахождение значения неизвестной переменной.
В этой статье мы узнаем, как решать два основных типа логарифмических уравнений, а именно:
Как решать уравнения с логарифмами на одной стороне?
Уравнения с логарифмами с одной стороны принимают log b M = n ⇒ M = b n .
Чтобы решить этот тип уравнений, выполните следующие шаги:
Пример 1
Журнал решения 2 (5x + 7) = 5
Решение
Перепишите уравнение в экспоненциальную форму
журналов 2 (5x + 7) = 5 ⇒ 2 5 = 5x + 7
18151815181518181818181818 гг. 5x + 7⇒ 5x = 32 -7
5x = 25
Разделение обеих сторон на 5, чтобы получить
x = 5
Пример 2
810 27x). = 2
Решение
Поскольку основание этого уравнения не задано, мы принимаем основание 10.
Теперь измените запись логарифма в экспоненциальной форме.
⇒ 10 2 = 5x – 11
⇒ 100 = 5x -11
111= 5x
111/5 = x
1 Следовательно, x = 11.
Пример 3
Решение log 10 (2x + 1) = 3
Раствор
Перезар.
9 Обращение в Экстрационном Форме
Обращение в Экстрационном Форме. Повторный уравнение
919 919 919 91 91 91 91 91 91 91 91 91 91 91 91 91 91 91 91 91 91 91 2 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 911 91 2 9189 2 911 91 2 9189 2 911 91 2 918 918 (2x + 1). + 1 = 10 3 ⇒ 2x + 1 = 1000
2x = 999
Разделив обе части на 2, мы получим;
x = 499,5
Проверьте свой ответ, подставив его в исходное логарифмическое уравнение;
⇒ log 10 (2 x 499,5 + 1) = log 10 (1000) = 3 с 10 3 = 1000
Пример 4 9
9188 .Решение
Перепишите уравнение в экспоненциальной форме как;
LN (4x -1) = 3 ⇒ 4x -3 = E 3
, но, как вы знаете, E = 2,718281828
4x -3 = (2,718281828) 3 = 20.0855377781828) 3 = 20.0853777781828) 3 = 20.08537777787828) 3 = 20.
 085377777781828) 3 = 20.085377777781828) 3 = 2008537777777828) 3 = 20×0853777777878) Пример 5
085377777781828) 3 = 20.085377777781828) 3 = 2008537777777828) 3 = 20×0853777777878) Пример 5 Решите уравнение логарифма показано ниже.
журнал 2 (x +1) – журнал 2 (x – 4) = 3 ⇒ log 2 [(x + 1)/ (x – 4)] = 3
Теперь перепишем уравнение в экспоненциальной форме
⇒ 2 3 = [( x + 1)/ (x – 4)]
⇒ 8 = [(x + 1)/ (x – 4)]
Перемножить уравнение
⇒ [(x + 1) = 8(x – 4) )]
⇒ x + 1 = 8x -32
7x = 33 …… (сбор подобных терминов)
x = 33/7
Пример 6
SELTE (х) + журнал 4 (x -12) = 3
Решение
Упростите логарифм, используя следующее правило произведения;
log 4 (x) + log 4 (x -12) = 3 ⇒ log 4 [(x) (x — 12)] = 3
⇒ log 4 (1 2
(1 2 ) – 12x) = 3 Преобразуйте уравнение в экспоненциальную форму.

⇒ 4 3 = x 2 – 12 x
⇒ 64 = x 2 – 12 x
x 2 -12x – 64 ⇒ (x + 4) (x – 16) = 0
x = -4 или 16
Если в исходное уравнение подставить x = -4, получим отрицательный ответ что воображаемое. Поэтому 16 — единственное приемлемое решение.
Как решать уравнения с логарифмами в обеих частях уравнения?
Уравнения с логарифмами по обе стороны от знака равенства принимают log M = log N, что совпадает с M = N.
Процедура решения уравнений с логарифмами по обе стороны от знака равенства.

 11.20
11.20 Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением.
Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением. Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент. Обращение в Экстрационном Форме
Обращение в Экстрационном Форме 085377777781828) 3 = 20.085377777781828) 3 = 2008537777777828) 3 = 20×0853777777878) Пример 5
085377777781828) 3 = 20.085377777781828) 3 = 2008537777777828) 3 = 20×0853777777878) Пример 5 

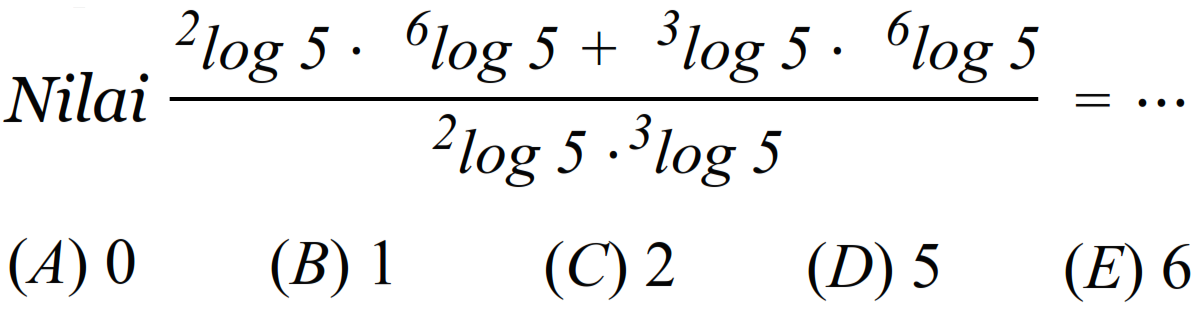 Следовательно, x = 5 является единственным приемлемым решением.
Следовательно, x = 5 является единственным приемлемым решением.
 Логарифм — это показатель степени, а антилогарифм — это
результат возведения основания в этот показатель.
Логарифм — это показатель степени, а антилогарифм — это
результат возведения основания в этот показатель. Вы можете написать приведенное выше определение
компактно и показать журнал в виде экспоненты,
подставив второе уравнение в первое, чтобы исключить г :
Вы можете написать приведенное выше определение
компактно и показать журнал в виде экспоненты,
подставив второе уравнение в первое, чтобы исключить г : жизнь. Логарифмическая линейка,
когда-то почти мультяшный товарный знак ученого,
был не чем иным, как устройством, созданным для выполнения различных вычислений
быстро, используя логарифмы.
См. Эли Маорс e: История числа , чтобы узнать больше
это.
жизнь. Логарифмическая линейка,
когда-то почти мультяшный товарный знак ученого,
был не чем иным, как устройством, созданным для выполнения различных вычислений
быстро, используя логарифмы.
См. Эли Маорс e: История числа , чтобы узнать больше
это.
 Конечно,
с широкой доступностью персональных вычислительных устройств,
сложность вычислений больше не вызывает беспокойства, но журналы по-прежнему имеют
множество самостоятельных приложений.)
Конечно,
с широкой доступностью персональных вычислительных устройств,
сложность вычислений больше не вызывает беспокойства, но журналы по-прежнему имеют
множество самостоятельных приложений.) Измените это в логарифмическую форму с определением журналов, и вы получите
Измените это в логарифмическую форму с определением журналов, и вы получите
 )
) Таким образом, правая часть становится
Таким образом, правая часть становится
 Упростите правую часть:
Упростите правую часть:
 расчет может быть равен
расчет может быть равен журналы.
журналы.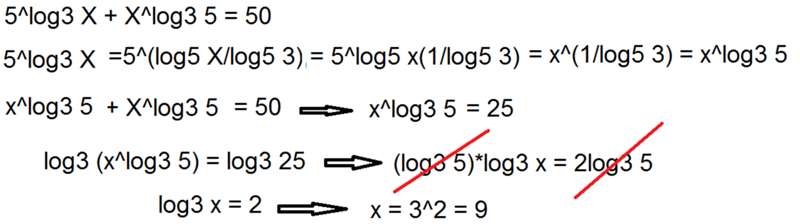 это логарифм степени, который становится (-1) умноженным на логарифм или просто минус логарифм:
это логарифм степени, который становится (-1) умноженным на логарифм или просто минус логарифм: Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошим началом будет взять основание- и логарифм с обеих сторон:
Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошим началом будет взять основание- и логарифм с обеих сторон: Если вы похожи на меня, у вас могут возникнуть проблемы с запоминанием
то ли умножать, то ли делить. Если да, то просто выведите
уравнение, как видите, занимает всего два шага.
Если вы похожи на меня, у вас могут возникнуть проблемы с запоминанием
то ли умножать, то ли делить. Если да, то просто выведите
уравнение, как видите, занимает всего два шага. (Ты мог
одинаково хорошо использовать основание 10.)
(Ты мог
одинаково хорошо использовать основание 10.) Следовательно, log 125 5 = 1/3 и
log 5 125 = 3, а 1/3 действительно равно
1/3.
Следовательно, log 125 5 = 1/3 и
log 5 125 = 3, а 1/3 действительно равно
1/3.
 В
на самом деле, когда вы делите два бревна на одно и то же основание, вы
работая по формуле замены основания в обратном порядке. Хотя это не часто
полезно, (log x ) / (log y ) =
журнал г x . Только не пишите лог( x / y )!
В
на самом деле, когда вы делите два бревна на одно и то же основание, вы
работая по формуле замены основания в обратном порядке. Хотя это не часто
полезно, (log x ) / (log y ) =
журнал г x . Только не пишите лог( x / y )! Если когда-либо вы не уверены в операции, например
как изменить базу, работа
это, используя определение журнала и
применяя законы показателей, и вы
не пойдет не так.
Если когда-либо вы не уверены в операции, например
как изменить базу, работа
это, используя определение журнала и
применяя законы показателей, и вы
не пойдет не так.