|
Логика очень древняя наука. Ещё в античные времена была известна формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения. Например, уже в древности был известен закон исключения третьего. Его содержательная трактовка была такова: «Во время своих странствований Платон  В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано. В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано.
Другой закон логики — закон непротиворечивости. Если сказать: «Во время своих странствий Платон был в Египте И не был Платон в Египте», то очевидно, любое высказывание, имеющее такую форму, всегда будет ложно. Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута. Ещё один закон, известный в древности — закон отрицания: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте». Формальная логика основана на “высказываниях”. “Высказывание” — это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит. 
Например: Листва на деревьях опадает осенью. Земля прямоугольная. Первое высказывание содержит истинную информацию, а второе — ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается. Пример предложений, не являющихся высказываниями: Не пейте сырую воду! Кто не хочет быть счастливым? Высказывания могут быть и такими: 2>1, Н2О+SO3=h3SO4. Здесь используются языки математических символов и химических формул. Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить  .. либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные. .. либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные.
Высказывания бывают общими, частными и единичными. Общее высказывание начинается со слов: всё, все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным. Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке. В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики. В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ. 1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения аргументов функции, т.е. входные величины, а в правой указывается соответствующее им значение логической функции. 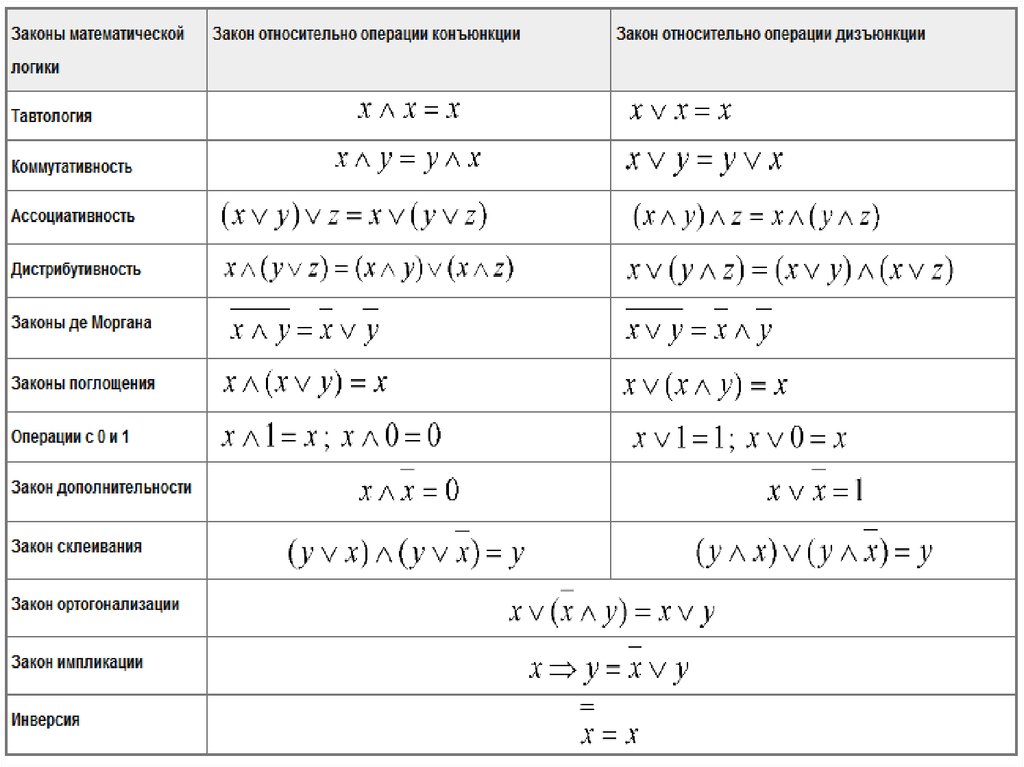 Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид: Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:
Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через А простое высказывание «Летом я поеду в деревню», а через В — простое высказывание «Летом я поеду в туристическую поездку». Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным. 2. Логическая операция И. Таблица истинности для этой функции имеет вид: Из таблицы истинности следует, что операция И — это логическое умножение, которое ничем не отличается от традиционно известного умножения в обычной алгебре. В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид: В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ — дизъюнкцией, операцию И — конъюнкцией. Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Логическая операция “строгая дизъюнкция”. Этой логической операции соответствует логическая связка “либо … либо”. Таблица истинности для этой функции имеет вид: Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул: и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
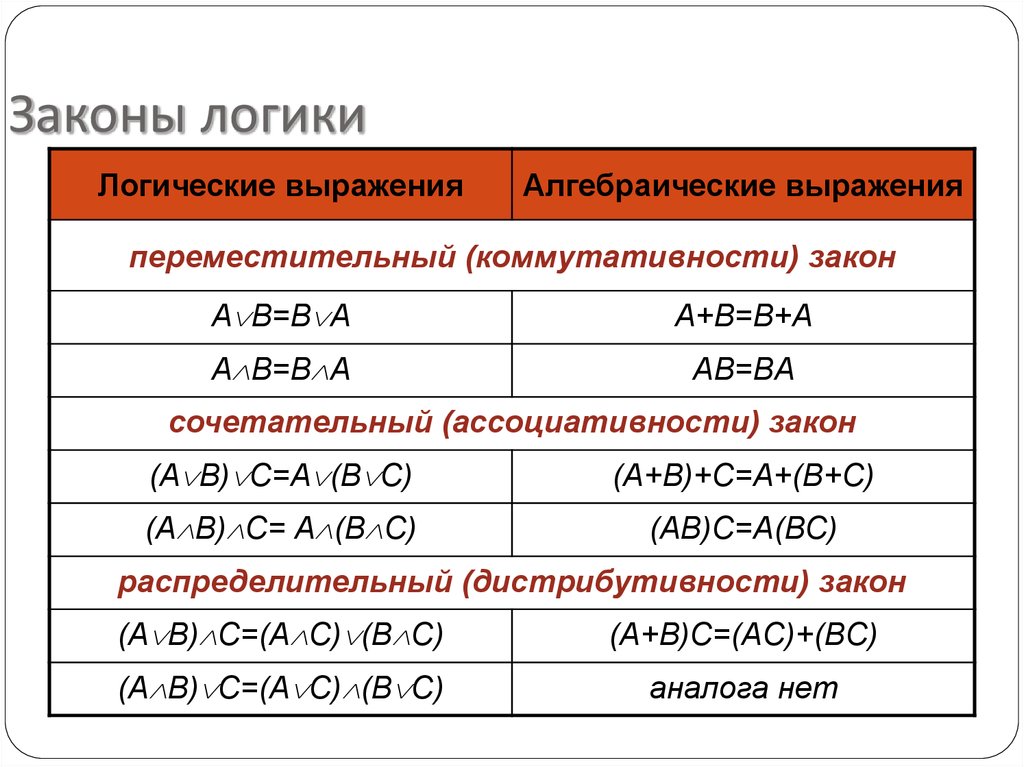
Операцию “импликация” можно обозначить по-разному: Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид: Операция “эквивалентность” обозначается по-разному. Выражения обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство. В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома |
|
||
Логические выражения | Кабинет информатики
В меню кабинета | Логические выражения
Понятие логического выражения или логической формулы вводится индуктивно.
Логической формулой является
1) любая логическая переменная (переменная, принимающая одно из двух значений: истина или ложь, обозначаемых далее 1 и 0 соответственно), а также каждая из двух логических констант (постоянных) — 0 и 1, является формулой;
2) если A и B — формулы, то, А*В и (А*В) — тоже формулы, где знак “*” означает любую из логических бинарных операций (см. “Логические операции. Кванторы”).
Формулой является, например, следующее выражение (x & y) z.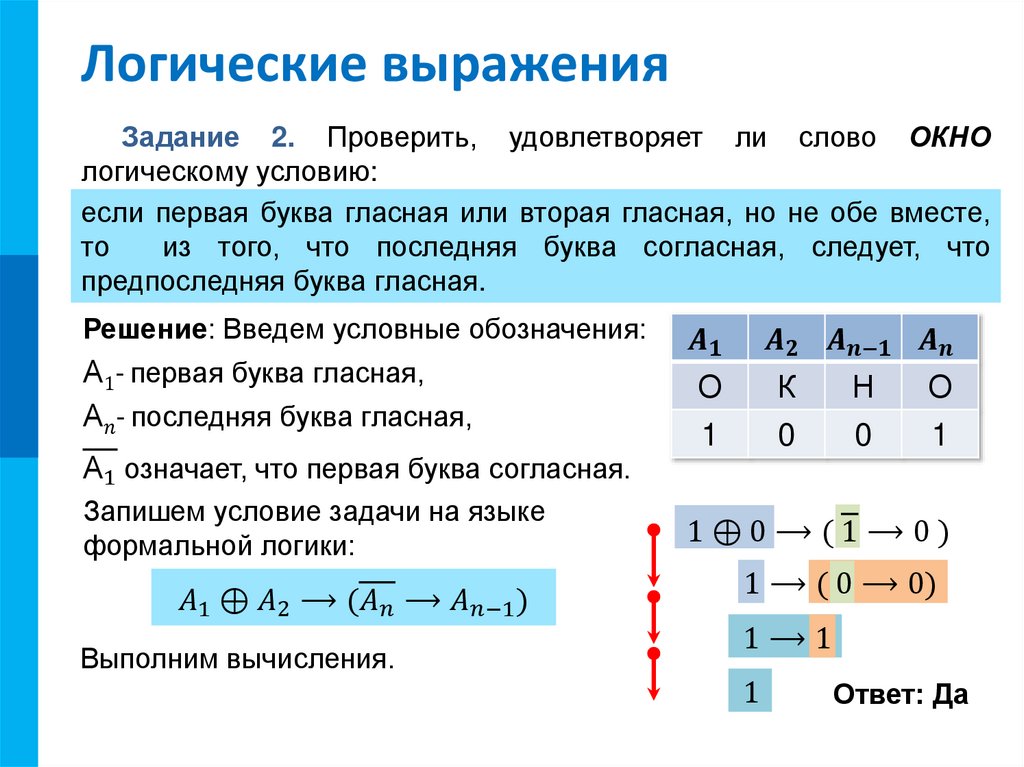 Каждой формуле при заданных значениях входящих в нее переменных можно приписать одно из двух значений — 0 или 1.
Каждой формуле при заданных значениях входящих в нее переменных можно приписать одно из двух значений — 0 или 1.
Формулы А и В, зависящие от одного и того же списка переменных x1, x2, x3, …, xn, называют равносильными, или эквивалентными, если на любом наборе значений переменных x1, x2, x3, …, xn они принимают одинаковые значения. Для обозначения равносильности формул используется знак равенства, например, А = В.
Любую формулу можно преобразовать к равносильной ей, в которой используются только операции &, и отрицание.
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, справедливые для любых переменных x, y, z. Эти свойства называют законами алгебры логики:
Любой из этих законов может быть легко доказан с помощью таблиц истинности, или путем логических рассуждений, или с помощью тождественных преобразований, использующих доказанные ранее законы.
Приоритет выполнения логических операций
Для логических операций в одном логическом выражении установлен следующий порядок вычислений:
· отрицание — первый, наивысший приоритет;
· конъюнкция — второй приоритет;
· дизъюнкция, разделительная дизъюнкция — третий приоритет;
· импликация, эквивалентность — низший приоритет.
Изменить порядок выполнения операций можно с помощью расстановки скобок.
В алгебре логики дизъюнкция (логическое сложение) играет роль, аналогичную сложению в алгебре действительных чисел, конъюнкция (логическое умножение) — умножению, а отрицание (инверсия значения логической формулы) — унарному минусу (инверсия знака обычной формулы). Операция эквивалентность аналогична операции отношения “=”, а операция импликация — операции отношения “”.
Канонические формы
Очевидно, что если имеется логическая формула, то, используя тождественные преобразования, можно изменить ее, построив сколь угодно сложную равносильную формулу.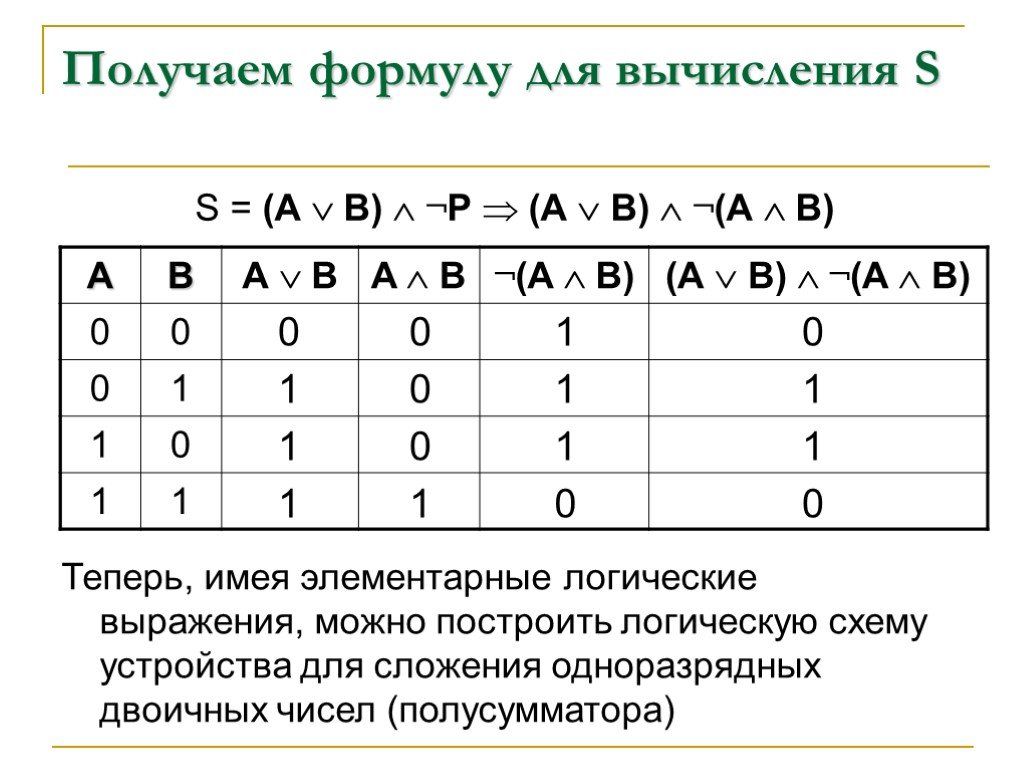 Одна из основных задач алгебры логики — нахождение канонических форм (т.е. формул, построенных по определенному правилу, канону), а также формул, имеющих наиболее простой вид.
Одна из основных задач алгебры логики — нахождение канонических форм (т.е. формул, построенных по определенному правилу, канону), а также формул, имеющих наиболее простой вид.
Если логическая формула выражена через дизъюнкцию, конъюнкцию и отрицание, то такая форма представления называется нормальной. Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Особую роль в алгебре логики играет класс совершенных дизъюнктивных нормальных форм. В их основе лежат понятия элементарной дизъюнкции и элементарной конъюнкции.
Формулу называют элементарной конъюнкцией, если она является конъюнкцией одной или нескольких переменных, взятых с отрицанием или без отрицания. Например, формулы x2, x2, x1 & x3, x1 & x3 & x1 & x3 являются элементарными конъюнкциями.
Формула называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией элементарных конъюнкций. ДНФ записываются в виде A1 A2 … An, где каждое Ai — элементарная конъюнкция. Например, x2x1 & x3, x2 & x2x1 & x2— дизъюнктивные нормальные формы.
Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если
1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных x1, x2, …, xk, причем на i-м месте этой конъюнкции стоит либо переменная xi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи.
Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи.
Логической функцией называется функция, аргументы которой и сама функция принимают значения 0 или 1. Логические функции могут быть заданы таблично (таблицей истинности) или в виде соответствующих формул. Тем самым каждая формула может рассматриваться как способ задания логической функции. При этом одна и та же функция может задаваться различными формулами.
Возникает вопрос: всякую ли логическую функцию можно представить в одном из канонических совершенных видов? Да, любую булеву функцию, не равную тождественно лжи, можно представить в виде СДНФ. Сформулируем это утверждение в виде следующей теоремы.
Теорема. Пусть — f (x1, x2, …, xn)булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию f, которую можно построить по следующему алгоритму:
1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно единице.
В таблице истинности отмечаем наборы переменных, на которых значение функции f равно единице.
2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.
Доказательство. Каждая элементарная конъюнкция, вошедшая в СДНФ, принимает значение 1 только на единственном наборе. Отсюда следует, что если функция на каком-то наборе равна 1, то и вся СДНФ равна 1 в силу того, что по построению соответствующая элементарная конъюнкция, вошедшая в СДНФ, равна 1. А если функция равна 0, то и СДНФ равна 0, т.к. на этом наборе равны 0 все вошедшие в СДНФ элементарные конъюнкции. Таким образом, СДНФ равносильна исходной функции.
Следствие. Любую логическую функцию можно представить формулой, в которой используются только логические операции дизъюнкции, конъюнкции и отрицания.
Доказательство. Для всех функций, отличных от 0, это можно сделать с помощью СДНФ, а ноль можно выразить, например, как x &`x.
Методические рекомендации
Умения строить логические выражения (логические формулы), вычислять их значение, выполнять над ними тождественные преобразования требуются при изучении разных тем информатики: при построении алгоритмов, в программировании, при решении логических задач, конструировании запроса при работе с БД, при работе с электронными таблицами и т.п. Для формирования этих умений важно обращать внимание на следующие моменты.
1) Любое логическое выражение (логическая формула) реализует логическую функцию на конечном наборе различных значений переменных, в него входящих. Часто (при построении запросов или условия ветвления) по словесному описанию логического выражения (логического условия) требуется построить его аналитическое выражение. Словесное выражение является высказыванием. Для правильного построения логического выражения вначале в сложном высказывании необходимо выделить элементарные высказывания, а затем, используя семантику языковых связок, построить формулу. Такое умение можно формировать уже в базовом курсе информатики.
Такое умение можно формировать уже в базовом курсе информатики.
2) Во многих языках программирования используется только несколько логических операций, как правило, операция логического сложения, логического умножения и отрицания, а также операция разделительной дизъюнкции. Поэтому, если полученная формула содержит не только операции &, и отрицание, то учащиеся должны уметь выполнять тождественные преобразования для построения ДНФ (дизъюнктивной нормальной формы). Умение выполнять тождественные преобразования основано на знании основных законов алгебры логики, но формируется это умение в результате выполнения большого числа заданий. На формирование этого умения времени практически не отводится, но практика показывает, что достаточно научить учащихся выражать операции импликации и эквивалентности через &, и отрицание. Большинство законов алгебры логики ученикам интуитивно понятны и не требуют запоминания. Исключение составляют законы поглощения и де Моргана. Последние особенно часто применяются в программировании. Знакомство с законами алгебры логики начинается в базовом курсе информатики и продолжается в старшей школе.
Знакомство с законами алгебры логики начинается в базовом курсе информатики и продолжается в старшей школе.
3) Для построения СДНФ учащиеся должны уметь без ошибок строить таблицу истинности для конкретной логической формулы. А для этого надо требовать, чтобы учащиеся строго соблюдали порядок перечисления набора значений переменных: если каждый набор значений переменных рассматривать как двоичное число, то все числа должны быть записаны в порядке возрастания. Например, для формулы от трех переменных перечисление набора значений в таблице истинности должно быть выполнено в следующем порядке:
4) Перед изложением формулировки теоремы о СДНФ надо пояснить, для чего используются нормальные формы (поиск аналитического вида булевой функции, заданной таблицей истинности; минимизация представления булевой функции с использованием только трех логических операций &, и отрицания: такая задача возникает при конструировании микросхем, в частности, для производства компьютеров, и т. д.). Учащимся на примерах надо показать, что проблема представления формул в виде СДНФ не надуманна, ее решение имеет важное практическое значение в информатике. Данная тема подлежит рассмотрению в старших профильных классах.
д.). Учащимся на примерах надо показать, что проблема представления формул в виде СДНФ не надуманна, ее решение имеет важное практическое значение в информатике. Данная тема подлежит рассмотрению в старших профильных классах.
5) Если вы задаете своим ученикам задания на построение отрицания к сложному высказыванию (а проще всего это делать через построение отрицания к соответствующему логическому выражению), то им следует пояснить, почему в этом случае квантор общности заменяется на квантор существования и наоборот (см. “Логические операции. Кванторы”).
Очевидно, что высказывание, содержащее квантор общности (например, “Все мужчины старше 70 лет имеют длинную седую бороду”), можно заменить на следующее: “И Иванов А.П., и Кравцов И.Г., и Петухов С.П., и … старше 70 лет и имеют длинную седую бороду”. Это высказывание можно записать следующей формулой: И & К & П & …, где буквой И обозначено высказывание “Иванов А.П. (который старше 70 лет) носит длинную седую бороду”, буквой К обозначено высказывание “Кравцов И. Г. носит длинную седую бороду” и т.д. При построении отрицания к первоначальному сложному высказыванию, содержащему квантор общности, воспользуемся законом де Моргана. Тогда получим:
Г. носит длинную седую бороду” и т.д. При построении отрицания к первоначальному сложному высказыванию, содержащему квантор общности, воспользуемся законом де Моргана. Тогда получим:
Этой формуле соответствует высказывание “Или Иванов А.П. не имеет длинной седой бороды, или Кравцов И.Г. не имеет длинной седой бороды, или Петухов С.П. … или … не имеет длинной седой бороды”, другими словами, “Существует мужчина старше 70 лет, который не имеет длинной седой бороды”.
6 От латинских слов idem — тот же самый и potens — сильный; дословно — равносильный.
3.2: Логика высказываний в компьютерных программах
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48306
- Эрик Леман, Ф.
 Томсон Лейтон и Альберти Р. Мейер
Томсон Лейтон и Альберти Р. Мейер - Google и Массачусетский технологический институт через MIT OpenCourseWare
Предложения и логические связки постоянно возникают в компьютерных программах. Например, рассмотрим следующий фрагмент, который может быть написан на C, C++ или Java:
.\[\begin{align} \text{if } &(x > 0) || (x <= 0 \text{ && } y > 100) \\ & \vdots \\ &\textit{(дальнейшие инструкции)} \end{aligned}\]
Java использует символ || для «\(\text{OR}\)» и символ && для «\(\text{AND}\)». дальнейшие инструкции выполняются только в том случае, если предложение, следующее за словом , если истинно. При ближайшем рассмотрении это большое выражение состоит из двух более простых утверждений.
Пусть \(A\) будет утверждением, что \(x > 0\), и пусть \(B\) будет утверждением, что \(y > 100\). Тогда мы можем переписать условие как
\[\label{3.2.1} A \text{ ИЛИ } (\text{НЕ}(A) \text{ И } B)\]
Расчет таблицы истинности
Расчет таблицы истинности показывает, что более сложное выражение 3. 2 всегда имеет то же значение истинности, что и
2 всегда имеет то же значение истинности, что и
\[\label{3.2.2} A \text{ ИЛИ } B.\]
Начнем с таблицы, содержащей только истинные значения \(A\) и \(B\):
\[ \nonumber \begin{array}{cc|ccccc|c}
A & B & A & \text { ИЛИ } & (\text{НЕ}(A) & \text { AND } & B) & A \text { ИЛИ } B \\
\hline \mathbf{T} & \mathbf{T} & & & & & & & \\
\mathbf{T} & \mathbf{F} & & & & & & & \\
\mathbf {F} & \mathbf{T} & & & & & & \\
\mathbf{F} & \mathbf{F} & & & & & & &
\end{array}\]
Этих значений достаточно, чтобы заполнить еще два столбца:
\[\nonumber \begin{array} {cc|ccccc|c}
A & B & A & \text {ИЛИ} & (\text{НЕ}(A) & \text {И} & B) & A \text {ИЛИ} B \\
\ hline \mathbf{T} & \mathbf{T} & & & \mathbf{F} & & & \mathbf{\large T} \\
\mathbf{T} & \mathbf{F} & & & \mathbf{ F} & & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{T} & & & \mathbf{T} & & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{F} & & & \mathbf{ T} & & & \mathbf{\large F}
\end{array}\]
Теперь у нас есть значения, необходимые для заполнения столбца \(\text{AND}\):
\[\nonumber \ begin{array}{cc|ccccc|c}
A & B & A & \text { ИЛИ } & (\text{НЕ}(A) & \text { И } & B) & A \text { ИЛИ } B \\
\hline \mathbf{T} & \mathbf{T} & & & \mathbf{F} & \mathbf{F} & & \mathbf{\large T} \\
\mathbf{T} & \mathbf{F} & & & \mathbf{F} & \mathbf{F} & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{T} & & & \mathbf{T} & \mathbf{T} & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{F} & & & & \mathbf{T} & \mathbf{F} & & \mathbf{\large F}
\end{array}\]
, и это обеспечивает значения, необходимые для заполнения оставшегося столбца для первого \(\text{OR}\):
\[\nonumber \begin{массив}{cc|ccccc|c}
A & B & A & \text { ИЛИ } & (\text{НЕ}(A) & \text { И } & B) & A \text { ИЛИ } B \\
\hline \mathbf{T} & \mathbf{T} & & \mathbf{\large T} & \mathbf{F} & \mathbf{F} & & \mathbf{\large T} \\
\mathbf{T} & \mathbf{F} & & \mathbf{\large T} & \mathbf{F} & \mathbf{F} & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{T} & &\mathbf{\large T} & \mathbf{T} & \mathbf{T} & & \mathbf{\large T} \\
\mathbf{F} & \mathbf{F} & & \mathbf{\large F} & \mathbf{T} & \mathbf{F} & & \mathbf{\large F}
\end{массив}\]
Выражения, истинностные значения которых всегда совпадают, называются эквивалентными . Поскольку два выделенных столбца значений истинности двух выражений одинаковы, они эквивалентны. Таким образом, мы можем упростить фрагмент кода без изменения поведения программы, заменив сложное выражение эквивалентным более простым:
Поскольку два выделенных столбца значений истинности двух выражений одинаковы, они эквивалентны. Таким образом, мы можем упростить фрагмент кода без изменения поведения программы, заменив сложное выражение эквивалентным более простым:
\[\begin{aligned} \text{if } &(x > 0 || y > 100) \\ & \vdots \\ &\textit{(дальнейшие инструкции)} \end{aligned}\]
Эквивалентность (\ref{3.2.1}) и (\ref{3.2.2}) можно также подтвердить, рассуждая по случаям:
\(A\) есть \(\textbf{T}\). Выражение вида (\(\textbf{T} \text{ ИЛИ}\) что угодно) эквивалентно \(\textbf{T}\). Поскольку \(A\) есть \(\textbf{T}\), то и (\ref{3.2.1}), и (\ref{3.2.2}) в данном случае имеют такую форму, поэтому они имеют одинаковую истину значение, а именно \(\textbf{T}\).
\(A\) равно \(\textbf{F}\). Выражение вида (\(\textbf{F} \text{ ИЛИ}\) что-нибудь ) будет иметь то же истинностное значение, что и что-нибудь . Поскольку A является \(\textbf{F}\), (\ref{3.2.2}) имеет то же значение истинности, что и \(B\).
Выражение вида (\(\textbf{T} \text{ AND}\) что угодно ) эквивалентно что угодно , как и любое выражение вида \(\textbf{F} \text{ ИЛИ}\) ничего . Таким образом, в этом случае \(A \text{ ИЛИ } (\text{НЕ}(A) \text{ И } B)\) эквивалентно \((\text{НЕ}(A) \text{ И } B )\), что, в свою очередь, эквивалентно \(B\).
Следовательно, и (\ref{3.2.1}), и (\ref{3.2.2}) будут иметь в этом случае одно и то же значение истинности, а именно значение \(B\).
Упрощение логических выражений имеет большое практическое значение в информатике. Упрощение выражений в программах, подобных приведенной выше, может облегчить чтение и понимание программы. Упрощенные программы также могут работать быстрее, поскольку требуют меньше операций. В аппаратном обеспечении упрощение выражений может уменьшить количество логических элементов на кристалле, поскольку цифровые схемы можно описать логическими формулами (см. задачи 3.5 и 3.6). Минимизация логических формул соответствует уменьшению числа вентилей в схеме. Выгода от минимизации вентилей потенциально огромна: микросхема с меньшим количеством вентилей меньше по размеру, потребляет меньше энергии, имеет более низкий уровень брака и дешевле в производстве.
Выгода от минимизации вентилей потенциально огромна: микросхема с меньшим количеством вентилей меньше по размеру, потребляет меньше энергии, имеет более низкий уровень брака и дешевле в производстве.
Cryptic Notation
Java использует такие символы, как «&&» и «||» вместо \(\text{И}\) и \(\текст{ИЛИ}\). Разработчики схем используют «\(\cdot\)» и «+,» и фактически ссылаются на \(\text{И}\) как на произведение, а на \(\text{ИЛИ}\) как на сумму. Математики используют и другие символы, приведенные в таблице ниже.
\[\nonumber \begin{array}{cc} \textbf{English} & \textbf{Символическая нотация} \\
\text{НЕ}(P) & \lnot P \quad \text{(альтернативно} \overline{P}) \\ P \text{ AND } Q & P \wedge Q \\ P \text{ OR } Q & P \lor Q \\ P \text{ ПРЕДПОЛАГАЕТ } Q & P \longrightarrow Q \\ \text{If } P \text{ then } Q & P \longrightarrow Q \\ P \text{ IFF } Q & P \longleftrightarrow Q \\ P \text{ XOR } Q & P \oplus Q \end{array} \]
Например, используя эту запись, «Если \(P \text{ AND NOT } (Q)\), то \(R\)» будет записано:
\[\nonumber P \wedge \overline{Q } \rightarrow R. \]
\]
Математическая запись краткая, но загадочная. Такие слова, как «\(\text{И}\)» и «\(\text{ИЛИ}\)», легче запомнить, и их не спутаешь с операциями над числами. Мы часто будем использовать \(\overline{P}\) в качестве сокращения для \(\text{NOT}(P)\), но помимо этого мы в основном придерживаемся слов, за исключением тех случаев, когда в противном случае формулы убегали бы от текста. страница.
Эта страница под названием 3.2: Пропозициональная логика в компьютерных программах распространяется в соответствии с лицензией CC BY-NC-SA, ее авторами, ремикшированием и/или кураторами являются Эрик Леман, Ф. Томсон Лейтон и Альберти Р. Мейер (MIT OpenCourseWare ).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Эрик Леман, Ф.
 Томсон Лейтон и Альберти Р. Мейер
Томсон Лейтон и Альберти Р. Мейер
- Лицензия
- CC BY-NC-SA
- Теги
- таблицы истинности
Математическая логика. Логика использовалась для тысяч… | Брэндон Скеррит | Заметки по информатике
Photo by Michał Grosicki on UnsplashЛогика использовалась на протяжении тысячелетий, от философии до математики, а теперь и до искусственного интеллекта. Логика связана с истинностью и ложностью утверждений. Логика, которую мы будем изучать, будет отвечать на вопрос: «когда утверждение следует из набора утверждений?»
Ранее я уже писал здесь о логике, и поэтому эта статья будет относительно короткой, если говорить о объяснении всего о логике. Если вы хотите понять логику, пожалуйста, прочитайте статью, которую я написал о логике. Это просто расширение того, что мы узнали.
Это просто расширение того, что мы узнали.
Предложения могут быть только истинными или ложными.
Интерпретация присваивает пропозициональному утверждению истинностное значение Истина или Ложь. True или False могут быть представлены как 0 и 1 соответственно.
Существует около 500 000 способов представления логических символов, вот наиболее распространенные способы
Символ в логике
¬или ! или ~
Символ в электронике
Что он делает
Инвертирует то, что когда-либо вводилось в него. 9или И или ,
Символ в электронике
Что он делает
Принимает >1 входных данных, и если оба входных значения истинны, выдает истинные значения.
Правда Таблица
Символ в логике
В, или, «Или»
Символ в Electronics
, что это делает
, что это делает
. чем вывод верен.
чем вывод верен.
Таблица истинности
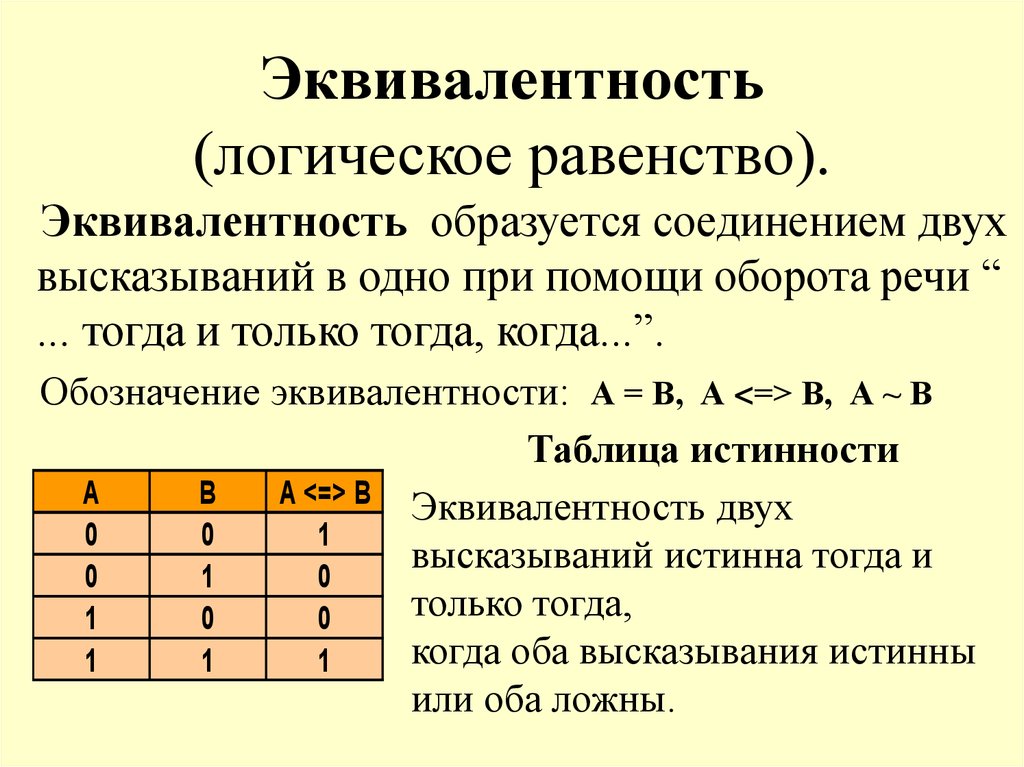
Символ в логике <=> или ≡
Символ в электронике Нет, это концепция, а не ворота.
Что он делает A и B должны принимать одно и то же значение истинности
Таблица истинности
A B A <=> B 1 1 = 1 0 1 = 0 1 0 = 0 0 0 = 1
Symbolin 9 Логика => или «если a, то b»
Символ в электронике Нет
Что делает Если A верно, то B
Таблица истинности
Имея интерпретацию I, мы можем вычислить истинностное значение любой формулы P при I. То есть, имея версию формулы, мы можем вычислить истинностное значение.
если I(P) = 1, то мы говорим, что P истинно при интерпретации I. если I(P) = 0, то мы говорим, что P ложно при интерпретации I.
Этот раздел может помочь читателю разобраться в логических головоломках. .
.
На острове есть два типа жителей: рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Вы отправляетесь на остров и встречаете А и Б. А говорит, что «Б — рыцарь» Б говорит, что «Мы двое противоположных типов»
Что такое А и Б?
Итак, у нас есть 2 варианта, р: «А — рыцарь»; и q: «B — рыцарь»
У нас есть 2 варианта, потому что один из них должен быть рыцарем. Либо и A, и B — лжецы, что делает B рыцарем, поскольку он сказал правду, значит, он солгал, либо A — рыцарь и говорит правду, что B — рыцарь.
Варианты для лица A p верно, то есть утверждение «A — рыцарь» верно. P => Q p ложно, то есть утверждение «A — рыцарь» ложно. ¬P => ¬Q
Варианты для человека B q верно, тогда q => ¬p q ложно, тогда ¬q => ¬p
Теперь нам просто нужно построить таблицу истинности для этих значений
p q ¬p ¬q p => q ¬p => ¬q q => ¬p ¬q => ¬p 0 0 1 1 1 1 1 1 = 1
Тогда мы остановимся здесь, потому что мы нашли удовлетворительную интерпретацию, согласно которой они оба являются лжецами.
Примечание. Слайды лекций для этого не помогли, и для этого нет звука. Пожалуйста, напишите мне, что это такое.
Современные компьютеры используют для работы логические вентили. Вы должны иметь представление о логических элементах из приведенного выше.
Никогда не объединяйте два входных провода
Если есть 2 отдельных входа, A и B, вы не можете объединить их в один провод.
Один входной провод можно разделить на части и использовать как вход для двух отдельных ворот
Если у вас есть один вход A, его можно разделить на 2 отдельных провода.
Выходной провод можно использовать как входной
Выход провода можно использовать как вход.
Ни один выход логического элемента не может в конечном итоге вернуться к этому логическому элементу.
Имея таблицу, подобную приведенной ниже, как бы мы построили для нее логическую схему?
Сначала вычисляем, где оно равно 1 (истинно), а затем уже оттуда формализуем его в математической логике, из математической логики мы можем вывести для него схему. Иногда проще сразу догадаться, какие логические вентили используются.
Иногда проще сразу догадаться, какие логические вентили используются.
Две схемы эквивалентны, если они производят одинаковый результат при одинаковых входных данных.
2 формулы эквивалентны, если они содержат одно и то же значение истинности при всех возможных интерпретациях.
Символ «≡» используется для обозначения отношения эквивалентности.
Факты
≡ рефлексивно ≡ транзитивно ≡ симметрично
Есть несколько правил, которые мы можем использовать для упрощения пропозициональных формул.
Коммуникативное право
AB = BA, A + B = B + A
Примеры: 6 * 2 = 12 и 2 * 6 = 12 3 + 4 = 7 и 4 + 3 = 7
Ассоциативный закон
2 + 4) + 5 = 6 + 5 = 11 2 + (4 + 5) = 2 + 9 = 11
Распределительный закон
a(b+c) = ab + ac
Пример: 3 × ( 2 + 4) = 3 * 6 = 18 3 × 2 + 3 × 4 = 6 + 12 = 18
Законы Деморгана
(A ∪ B)’ = (A)’ ∩ (B)’ Первый закон гласит, что дополнением объединения двух множеств является пересечение дополнений.
(A ∩ B)’ = (A)’ ∪ (B)’ Второй закон гласит, что дополнение пересечения двух множеств есть объединение дополнений.
Чтобы получить хороший пост в блоге о понимании этих законов, нажмите (здесь)[https://brilliant.org/wiki/de-morgans-laws/]
Прочие правила
Not Not A = A A или A и B = A A или не A и B = A и B (A или B) (A или C) = A или B и C
Что делать дальше С этого момента превратите схему в логическое выражение и упростите ее используя приведенные выше правила. 9, v или ¬.
В этом разделе мы еще немного познакомимся с логическими вентилями, рассмотрев семейство неисключающих вентилей.
Символ в логике
Нет
Символ в электронике
Что он делает
Логический элемент XOR принимает >1 вход и выполняет исключающую дизъюнктуру. Выход вентиля XOR истинен только в том случае, если один из его входов отличается от другого входа.
Таблица истинности
Символ в логике
Нет
Символ в электронике
Что он делает
Логический элемент И-НЕ принимает >1 вход, а выход противоположен вентилю И. Вывод истинен, когда один или несколько, но не все входные данные ложны.
Таблица истинности
Все логические функции могут быть созданы с использованием вентилей XOR или NAND.
Двоичная система счисления, состоящая из 0 и 1.
Преобразование десятичного числа в двоичное
В качестве альтернативы вы можете запомнить степени 2. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… А затем, чтобы преобразовать число в двоичное, давайте скажем, 6, вы строите это из разных сил. Итак, 6 — это 011, а затем переверните это, 110
Двоичное сложение
Кое-что, что вам нужно знать о двоичном коде 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10
Как только вы узнаете эти основные правила, вы можете складывать любые числа в двоичном формате так же, как вы можете складывать обычные числа. Попробуйте это упражнение
Попробуйте это упражнение
011
полусумматор
полусумматор — это тип двоичного сумматора в электронике, который складывает вместе два одиночных двоичных разряда и обеспечивает вывод плюс значение переноса.
Примечание. Полусумматор Бориса слишком сложен, вы можете добиться того же, заменив 3 его логических элемента одним элементом XOR.
Таблица истинности
Полный сумматор
Полный сумматор позволяет выполнять перенос и перенос.
Посмотрите это видео для лучшего понимания
Обозначение черного ящика
Мы можем представить полный сумматор в виде черного ящика, нам не нужно знать, что происходит внутри это, только входы и выходы.
4-битный сумматор
Используя нотацию черного ящика, мы можем создать 4-битный сумматор
http://www.electronics-tutorials.ws/combination/comb_7. html
html
Компьютерное представление отрицательных целых чисел Для представления целых чисел используется фиксированное количество битов: 8, 16, 32 или 64 бита. Беззнаковое целое может занимать все доступное пространство.
Вы можете «подписать» двоичное число, чтобы указать, отрицательное оно или нет. Например, число 10 может быть представлено в 8-битном виде как 00001010, а -10 может быть представлено в 8-битном виде как 10001010
. Но иногда это вызывает проблемы, например, 10000000 представляет -0. Чтооо?? Отрицательный 0? Да! Это верно, и это именно та проблема, которую это вызывает.
Здесь в игру вступает дополнение до 2.
Дополнение до двух
Преобразование десятичной дроби в дополнение до двух
1) Преобразовать число в двоичное, игнорируя пока знак. Таким образом, 5 — это 0101, а -5 — это 0101.
2) Если число положительное, то все готово, дальше ничего не нужно. В противном случае…
3) Если число отрицательное, то:
- Найдите дополнение (например, преобразуйте все 0 в 1 и все 1 в 0)
- Добавьте 1 к дополнению
Итак, инвертируйте все цифры и добавьте 1 .


 Операцию
Операцию 
 Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
 технологии
технологии Томсон Лейтон и Альберти Р. Мейер
Томсон Лейтон и Альберти Р. Мейер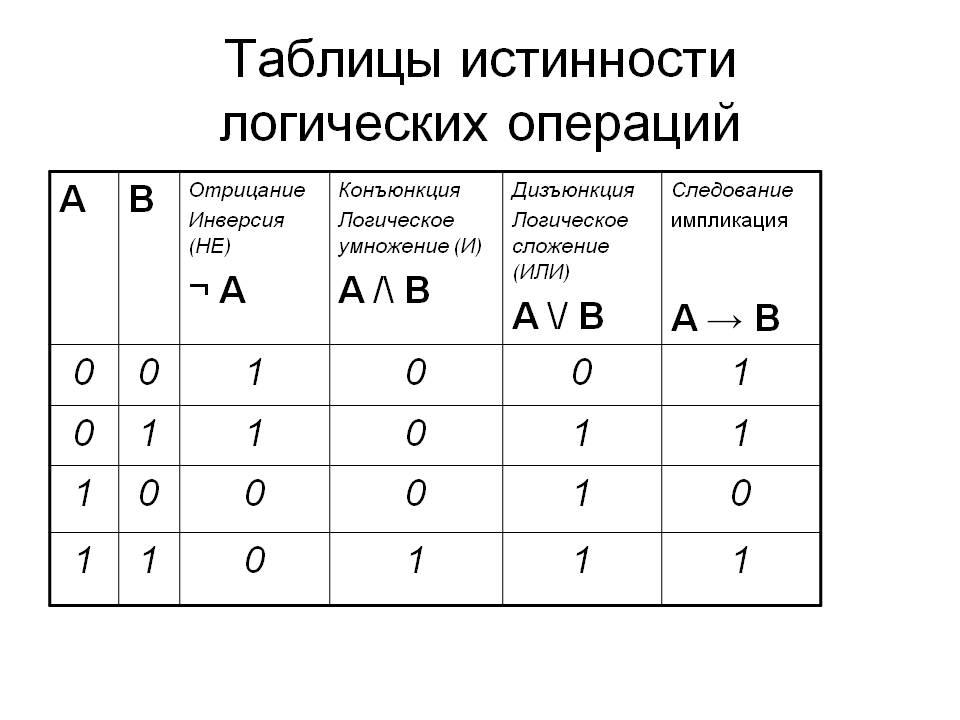 Томсон Лейтон и Альберти Р. Мейер
Томсон Лейтон и Альберти Р. Мейер