Математическая индукция как решать: Математическое Бюро. Страница 404

Содержание

Использование метода математической индукции при решении различных задач.

Муниципальное бюджетное общеобразовательное учреждение «Лицей №20»

Школьная научно-практическая конференция обучающихся 5-11 классов

Математика

Использование метода математической индукции

при решении различных задач

Автор: Бедарева Арина Алексеевна

Класс: 10

ОУ: МБОУ «Лицей №20»

Руководитель:

Фролова Елена Ивановна, учитель математики

Междуреченск — 2016

Оглавление.

I. Введение……………………………………………………………………………………………………………. 2

II. Основная часть……………………………………………………………………………………………. 4

1) Из истории метода математической индукции………………………………… 4

2) Принцип математической индукции…………………………………………………….. 5

3) Виды индукции……………………………………………………………………………………………….. 6

4) Решение различных задач…………………………………………………………………………… 8

III. Заключение…………………………………………………………………………………………………. 10

IV. Список литературы…………………………………………………………… ……………………… 11

V. Приложение…………………………………………………………………………………………………. 12

Индукция применяется при переходе от частных результатов к общим. Метод математической индукции можно наглядно представить в виде выстроенных друг за другом костей домино. Если мы толкнем первую из них, то упадут и все остальные.

Актуальность: в математических олимпиадах часто встречаются достаточно трудные задачи, и перед школьниками встает вопрос: «Есть ли универсальный математический метод, с помощью которого можно решать эти задачи?» Оказывается, с помощью метода математической индукции, можно решить множество олимпиадных задач. Также в современном мире возросла область применения метода математической индукции.

Гипотеза: я предполагаю, что метод математической индукции можно использовать при решении различных задач.

Цель работы: изучить метод математической индукции и показать его применение при решении различных задач.

Задачи:

1) Проанализировать литературу по данной теме.

2) Обобщить и систематизировать знания по данной теме.

3) Прорешать задачи различных видов, применяя данный метод.

4) Составить приложение;

5) Сделать выводы.

Объект исследования: метод математической индукции.

Предмет исследования: решение различных задач с использованием данного метода.

Методы исследования:

1) Познавательно — поисковая деятельность.

2) Анализ математической литературы и ресурсов Интернета по данной теме.

3) Постановка гипотезы и её проверка.

4) Решение задач различных видов.

5) Анализ полученных результатов.

Математической индукцией фактически пользовались еще некоторые древнегреческие ученые. Однако впервые он был явно выражен Герсонидом в 1321 году. Характеристика принципа математической индукции содержится у широко образованного итальянского математика ХVI века Ф. Мавролико, переводчик Архимеда. В « Трактате об арифметическом треугольнике» Б. Паскаль доказывает закон образования членов этого треугольника методом математической индукции. После этого метод начинает постепенно привлекать внимание некоторых ученых, в частности Бернулли. Лишь со второй половины ХIХ века, после трудов Больцано, Коши, Гаусса, Абеля чисто индуктивные методы доказательств теряют значение в математике. На первый план выдвигается дедукция и математическая индукция.

Рассмотрим задачу и сформулируем, что собой представляет метод математической индукции.

Задача. Показать, что любую сумму, начиная с 8 копеек, можно уплатить монетами в 3 и 5 копеек.

Решение. Рассмотрим, как уплатить 8, 9 и 10 копеек:

8 = 5 + 3;

9 = 3 + 3 + 3;

10 = 5 + 5:

Добавив ещё одну трёхкопеечную монету, получаем

11 = 8 + 3 = (5 + 3) + 3;

12 = 9 + 3 = (3 + 3 + 3) + 3;

13 = 10 + 3 = (5 + 5) + 3:

Ещё одна трёхкопеечная монета позволит уплатить

14 = 11 + 3;

15 = 12 + 3;

16 = 13 + 3

копеек, и так далее. Наша задача решена. Сформулируем принцип математической индукции.

Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены два условия:

А) утверждение верно для n=1;

Б)из справедливости утверждения для n=k, где k – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n=k+1.[1]

Иногда требуется доказать утверждение

не для всех натуральных n, а для n≥p. Тогда на первом шаге проверяют справедливость утверждения для n=p, а в остальном схема применения метода математической индукции та же.

[2]

Различают два вида индуктивных умозаключений – полную и неполную индукцию.

Полной индукцией называется такое умозаключение, в котором общее заключение обо всех элементах класса предметов делается на основании рассмотрения каждого элемента этого класса.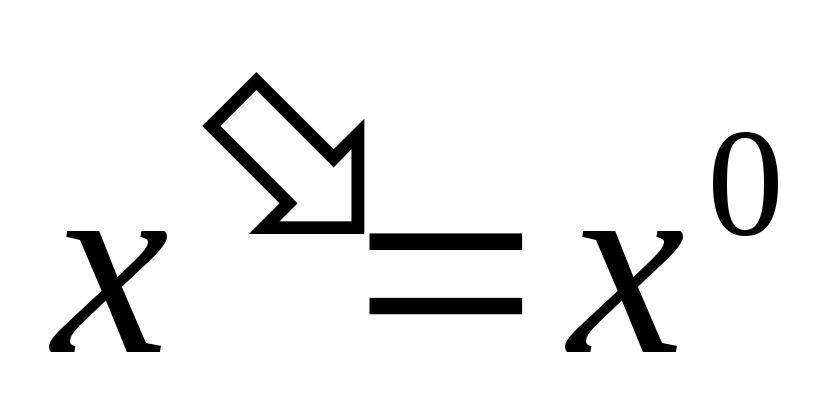 В полной индукции рассматриваются все предметы данного класса, а посылками служат единичные суждения. Вывод в полной индукции будет истинным, если посылки истинны. Например:

Иванов хорошо знает математику, Петров хорошо знает математику, Сидоров хорошо знает математику, Титова хорошо знает математику, Полякова хорошо знает математику. Иванов, Петров, Сидоров, Титова, Полякова учатся в 7 «Б» классе. Следовательно, все ученики 7 «Б» хорошо знают математику.

В данном умозаключении рассматриваются все ученики 7 «Б». Следовательно, вывод будет истинным.

Полная индукция дает достоверное заключение, поэтому она часто применяется в математических и в других самых строгих доказательствах. Чтобы использовать полную индукцию, надо выполнить следующие условия:

1. Точно знать число предметов или явлений, подлежащих рассмотрению.

2. Убедиться, что признак принадлежит каждому элементу этого класса.

3. Число элементов должно быть невелико.

Неполная индукция применяется в тех случаях, когда мы

-не можем рассмотреть все элементы, рассматриваемого класса явлений;

-если число объектов либо бесконечно, либо конечно, но достаточно велико.

В неполной индукции рассматриваются не все, а только некоторые элементы класса. Такой переход от некоторых ко всем не может давать истинный вывод. На этом основании неполную индукцию относят к правдоподобным умозаключениям. В таких выводах заключение следует из истинных посылок только с определенной степенью вероятности, которая может колебаться от маловероятной до весьма правдоподобной. О неполной индукции в одном из своих писем говорил французский ученый Пьер де Ферма: «…можно было бы предложить такой вопрос и взять такое правило для его решения, которое подходило бы для многих частных случаев, и все же было бы на самом деле ложным и не всеобщим…».[3]

Задача №1. Задача на делимость, взятая из школьного этапа 11 класса «Всероссийской олимпиады школьников» по математике 2015-2016 учебного года.

Доказать, что (7ⁿ⁺¹+8²ⁿ^-1):19.

1) n=1;

7²⁺8¹=57:19-верно;

2) n=k;

7^k⁺¹+8²^k^-1 – верно;

3) n=k+1;

Доказать (7^k⁺²+8²^k+1):19;

7^k+2+8

2k+1=7^k+1*7+8^2k-1*8²=7^k+1*7+8^2k-1*64=7^k+1*7+8^2k-1*57+8^2k-1*7= (7*(7^k+2+8^2k-1)+

+8²^k^-1*57), что кратно 19. Значит и исходное выражение (7ⁿ⁺¹+8²ⁿ^-1) кратно 19, что и требовалось доказать.

Задача №2. Задача на суммирование.

Найти сумму Sn=+++…+. Рассмотрим S₁, S₂, S₃.

S₁= = . S₂= = . S₃= = =.

Проанализировав полученные суммы, можно предположить, что S_n_{=. Проверим наше предположение методом математической индукции.}

1) При n=1. S₁= = – верно.

2) При n=k. S_k= – верно.

3) При n=k+1.

S_k+1

S_k+1= S_k+ = + = = = .

Значит, S_n_{= , что и
требовалось доказать.}

Задача №3. Задача на доказательство неравенства.

Доказать, что для n≥2 и (1) (его называют неравенство Бернулли в честь швейцарского математика Якоба Бернулли (1654 – 1705))[4].

получим верное неравенство:

2) Предположим, что неравенство Бернулли верно и для n=k (k≥2): .

3) Докажем что неравенство верно при n=k+1.

В самом деле, умножив обе части неравенства (1) на одно и то же положительное число , получим:

. Значит, мы доказали, что По принципу математической индукции делаем вывод, что неравенство Бернулли справедливо для любого n≥2.

В ходе проделанной работы я изучила и проанализировала множество материалов по данной теме. Я выполнила поставленные перед собой цели и задачи и, как мне кажется, подтвердила свою гипотезу: метод математической индукции, действительно, можно применить при решении различного рода задач, включая задачи на суммирование, доказательство неравенств, геометрические и логические задачи. Также я поняла, что одним из достоинств метода математической индукции является его универсальность и узнала, что метод математической индукции используется не только в математике, но и в физике, химии и других науках.

1) Википедия свободная энциклопедия [Электронный ресурс]. — Режим доступа: https://ru.wikipedia.org/wiki/, свободный – (05.03.2016).

2) Виленкин Н. Я., Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. Москва: Просвещение, 1996г.

3) Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень). -10-е изд., стер. — М: Мнемозина, 2013. – 424 с. : ил.

4) С.Н. Носуля, В.В. Шеломовский. Тематические комплекты, 2013.

5) Шарыгин И. Ф. Факультативный курс по математике. Решение задач учебное пособие для 10 класса средней школы – М.: Просвещение,1989г.

6) Шень А. Математическая индукция. 3-е изд., дополн. — М.: МЦНМО, 2007. — 32 с.: ил.

1) Задачи на суммирование и доказательство тождеств.

Задача №1. Доказать формулу

1) . Левая часть равна 1. Правая часть . Следовательно, при верно.

3) n=. Получим: +(k+1)².

Действительно, = = ,что и требовалось доказать.

Задача№2. Доказать, что 1³+2³+3³+4³+…+n³=(1+2+3+4+…+n)².

1) При n=1. 1³=1² – верно.

2) При n=k. 1³+2³+3³+4³+…+k³=(1+2+3+4+…+k)² – верно.

3) При n=k+1. Доказать, что 1³+2³+3³+4³+…+k³+(k+1)³=(1+2+3+4+…+k+(k+1))².

1³+2³+3³+4³+…+k³+(k+1)³=(1+2+3+4+…+k+(k+1))². Отсюда (1+2+3+4+…+k+(k+1))² — 1³+2³+3³+4³+…+k³=(k+1)³. Тогда:

(1+2+3+4+…+k+(k+1))² — (1+2+3+4+…+k)² = ((1+2+3+…+k+(k+1))-(1+2+3+…+k))*(( 1+2+3+…+k+(k+1))+(1+2+3+…+k)) = (k+1)(2*(1+2+3+…+k)+(k+1)) = (k+1)(2* *k+(k+1)) = (k+1)(k(k+1)+( k+1)) = (k+1)(k²+2k+1)=(k+1)(k+1)²=(k+1)³, что и требовалось доказать. [5]

Задачи на доказательство неравенств.

Задача №1. Доказать, что при n≥2 справедливо равенство

1) При n=2.

Это неравенство верно, так как правая часть явно больше 2, а левая меньше 2.

2) При n=k.

Верно.

3) При n=k+1. Доказать:

Прибавим к обеим частям неравенства и получим:

Теперь, если мы докажем, что ,то по свойству транзитивности числовых неравенств докажем полученное неравенство.

Рассмотрим разность правой и левой части неравенства .

Полученное выражение положительно, значит неравенство верно, а поэтому верно неравенство , что и требовалось доказать.

Задача №2. Доказать неравенство , при a и b≥0.

1) При n=1. a+b≤ 2(a+b) – верно.

2) При n=k. .

3) При n=l+1. = так как разность и, следовательно, .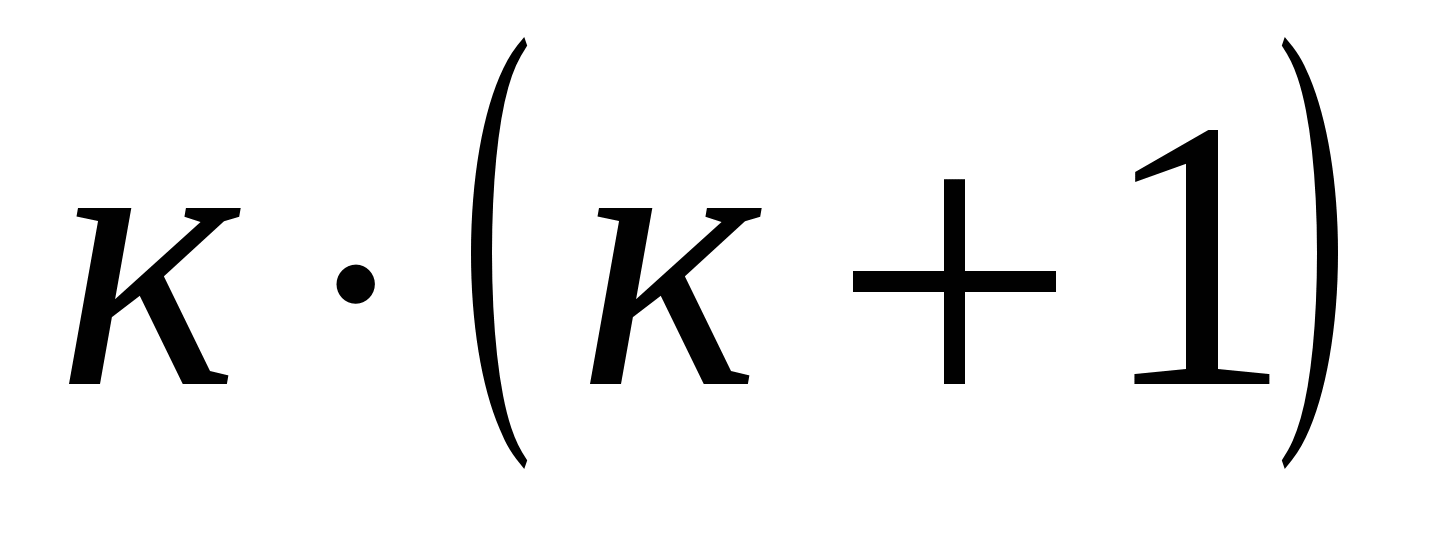 Что и требовалось доказать.

3) Задачи на делимость.

Задача №1. Доказать, что (11ⁿ⁺²+12²ⁿ⁺¹) кратно 133.

1) При n =1. 11³+12³=(11+12)(11³-132+12³)=23 133. Так как (23*133) кратно 133, то и (11³+12³) кратно 133.

2) При n=k. (11^k⁺²+12²^k⁺¹) кратно 133.

3) При n=k+1. Доказать, что (11^k⁺³+12²^k⁺³) кратно 133.

11^k⁺³+12²^k⁺³=11*11^k⁺²+12²*12²^k⁺¹=11(11^k⁺²+12²^k⁺¹)+133*12²^k⁺¹. В данном выражении второе слагаемое кратно 133, а первое слагаемое кратно 133 из второго пункта. Тогда по свойству делимости полученная сумма кратна 133, значит (11ⁿ⁺²+12²ⁿ⁺¹) кратно 133, что и требовалось доказать.

Задача №2. Доказать, что (n³+3n²+8n) кратно 3.

1) При n=1. 1+3+8=12, 12 кратно 3 – верно.

2) При n=k. (k³+3k²+8k) кратно 3 – верно.

3) При n=k+1. Доказать, что ((k+1)³+3(k+1)²+8(k+1)) кратно 3.

(k+1)³+3(k+1)²+8(k+1)=k³+3k²+3k+1+3k²+k+1+8k+8=(k³+3k²+8k)+3k²+9k+9. Полученное выражение кратно 3, так как каждое из слагаемых кратно 3. Значит (n³+3n²+8n) кратно 3, что и требовалось доказать.

Задача№3. Доказать, что (2²ⁿ⁺¹+1) кратно 3.

1) При n=1. 2³+1=8+1=9, кратно 3 – верно.

2) При n=k. (2²^k⁺¹+1) кратно 3 – верно.

3) При n=k+1. Доказать, что (2^2k+3+1) кратно 3.

2²^k⁺³+1=2²^k⁺¹*2²+1=2²^k⁺¹*2²+2²-3=2²(2²^k⁺¹+1)-3. Полученное выражение кратно 3, так как каждое из слагаемых кратно 3. Значит (2²ⁿ⁺¹+1) кратно 3, что и требовалось доказать.

4) Логические задачи.

Задача№1.

На доске написаны два числа 1; 1. Вписав между числами их сумму, мы получим числа 1; 2; 1. Повторив эту операцию ещё раз, получим числа 1; 3; 2; 3; 1. После трёх операций будут числа 1; 4; 3; 5; 2; 5; 3; 4; 1. Какова будет сумма всех чисел на доске после 100 операций?

Решение. Ясно, что для выполнения 100 операций нам не хватит ни места, ни времени. Значит, нужно пытаться найти какую-то общую формулу для суммы чисел после n операций (обозначим её Sn ). Посмотрим на таблицу и найдем закономерность.

n	Sn
0	2
1	4
2	10
3	28

На самом деле можно не выписывать числа, а сразу сказать, как изменится сумма после добавления новых чисел. Пусть сумма была равна S. Разобьём каждое новое число в сумму двух старых. Например, от

1; 3; 2; 3; 1

мы переходим к

1; 1 + 3; 3; 3 + 2; 2; 2 + 3; 3; 3 + 1; 1:

Каждое старое число (кроме двух крайних единиц) входит теперь в сумму три раза, поэтому новая сумма равна 3S − 2 (мы вычли 2, чтобы учесть недостающие единицы). Поэтому S5 = 3S4 − 2 = 244 и вообще Sn = 3Sn−1 − 2: Попробуем составить общую формулу. Если бы не вычитание двух единиц, то каждый раз сумма увеличивалась бы в три раза, как в степенях тройки (1; 3; 9; 27; 81; 243; : : : ). А наши числа, как теперь видно, на единицу больше. Таким образом, можно предположить, что Sn = 3n + 1. Докажем это по индукции.

1) N=1. Смотри таблицу (для n = 0; 1; 2; 3).

2) Если Sn−1 = 3n−1 + 1; то Sn = 3Sn−1 − 2 = 3(3n−1 + 1) − 2 = 3 · 3n−1 + 3 − 2 = 3n + 1, что и требовалось доказать. Из формулы видно, что после ста операций сумма всех чисел на доске будет равна 3100 + 1. Задача решена.

Задача №2. Несколько прямых делят плоскость на части. Доказать, что можно раскрасить эти части в белый и чёрный цвет так, чтобы соседние части (имеющие общий отрезок границы) были разного цвета.

Заметим, что не любую картинку можно так раскрасить. Например, если в одной точке сходятся несколько прямых, то одна из них может быть белой, а две другие, хоть и граничат между собой, будут черными. Но для плоскости, разделенной на части прямыми,

это произойти не может. Докажем это.

Пусть прямая только одна. Тогда всё просто: одна полуплоскость белая, другая – чёрная.

Если прямых две, получатся четыре части. Посмотрим, что произойдёт, если мы на рисунке с двумя прямыми и четырьмя частями проведём третью прямую. Она поделит три части из четырёх; при этом появятся новые участки границы, по обе стороны

которых цвет один и тот же. Что же делать? С одной стороны от новой прямой поменяем цвета (белый на черный и наоборот) и получим раскраску, соответствующую условию. Тогда, используя этот метод, мы можем добавить еще сколько угодно прямых. Что и требовалось доказать.

Задача №3. Игрушка («Ханойские башни») имеет три стержня. На одном находится пирамидка из нескольких колец уменьшающихся снизу вверх). Эту пирамидку нужно переложить на другой стержень, соблюдая правила игры: нельзя переносить сразу несколько колец и нельзя класть большее кольцо поверх меньшего. Например, пирамидку из двух колец можно переложить так: положить меньшее кольцо на второй стержень, затем большее на третий, а затем меньшее поверх большего (1 – 2, 1 – 3, 2 – 3 , если стержни нумеровать слева направо).

Наша задача доказать, что возможно переместить на другой стержень пирамидку из любого числа колец, соблюдая правила игры.

Пусть в пирамидке три кольца. Временно забудем про нижнее, самое большое (мысленно приклеим его к основанию). Тогда останется пирамидка из двух колец, которую мы уже умеем перекладывать. Переложим её с первого стержня на третий. После этого вспомним про большое кольцо и переложим его на второй стержень (который пока пуст).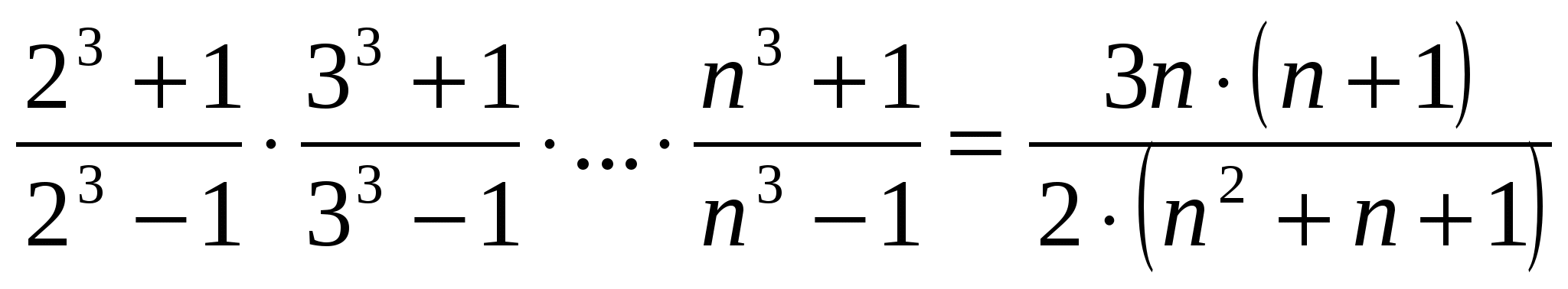 Теперь переложим пирамидку из двух верхних колец с третьего стержня на второй. Теперь, зная, как перекладывать пирамидку из трех колец, мы можем переложить четыре кольца (достаточно в наших предыдущих рассуждениях заменить пирамидку из двух колец на пирамидку из трёх). После этого можно переложить пять колец, зная, как перекладывать четыре кольца, и так далее. Что и требовалось доказать.

5) Геометрические задачи.

Задача №1.Найти, на сколько частей делит прямую n точек.

Рассмотрим 1 точку. Она делит прямую на 2 части. 2 точки делят прямую на 3 части, 3 точки на 4 части. Тогда мы можем предположить, что n точек делят прямую на N(n)=n+1 частей. Докажем это утверждение.

1) При n=1. Верно, так как мы рассмотрели это в рассуждениях.

2) Если добавленная точка расположена между какими то двумя, она разделит соединяющий эти точки отрезок на два. Если она расположена на луче, она добавит один отрезок. То есть добавление точки увеличивает число частей на 1. Значит: N(n+1)=N(n)+1=(n+1)+1. Следовательно, наше утверждение доказано.

Задача №2. Доказать, что сумма внутренних углов любого n-угольника равна π(n-2).

Так как минимальный n-угольник – это треугольник, то на нашу задачу накладывается условие: n≥3.

1) При n=3. π*1=π – верно.

2) При n=k. π(k-2) – верно.

3) При n=k+1. π(k-1). Разобьем (k+1)-угольник на треугольник и k-угольник, проведя диагональ. Тогда сумма углов треугольника и k-угольника равна π(n-2) (из 1 и 2 шага). Следовательно, сумма внутренних углов любого n-угольника равна π(n-2), что и требовалось доказать.

Метод математической индукции — презентация онлайн

Метод
математической
индукции
Содержание:
1.Введение.
2.Основная часть и примеры.
3.Заключение.
Знаменитый математик XVII в. П.Ферма
проверив, что числа
20
2 1 1 3
2
2 2 1 5
2
2
2
,
2
23
1 17
, 1 257
24
1 65537
простые, сделал по индукции
предположение, что для всех
n=1,2,3,… числа вида
2
простые.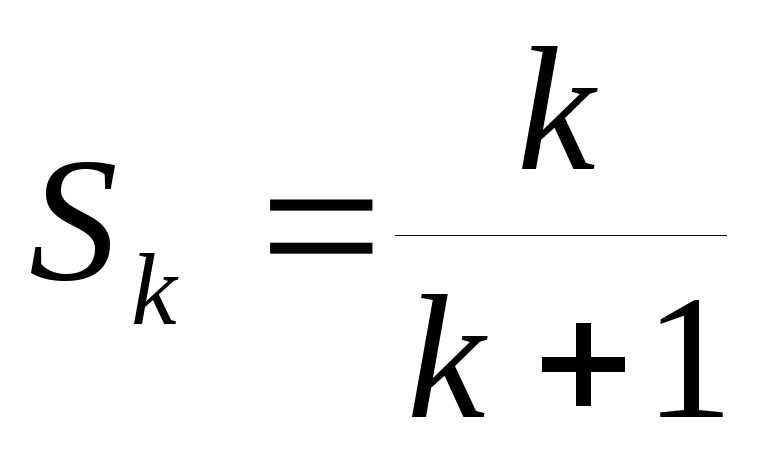
2
n
1
В XVIII веке Л.Эйлер нашел, что при n=5
2
25
1 4294967297 641 6700417
составное число
Введение
В основе всякого математического исследования
лежат дедуктивный и индуктивный методы.
Дедуктивный метод рассуждений — это
рассуждение от общего к частному, т.е.
рассуждение, исходным моментом которого
является общий результат, а заключительным
моментом – частный результат. Индукция
применяется при переходе от частных результатов
к общим, т.е. является методом, противоположным
дедуктивному.
Основная часть
По своему первоначальному смыслу слово
“индукция” применяется к рассуждениям,
при помощи которых получают общие
выводы, опираясь на ряд частных
утверждений. Простейшим методом
рассуждений такого рода является полная
индукция. Вот пример подобного
рассуждения.
Пусть требуется установить, что каждое
натуральное чётное число n в пределах
4< n < 20 представим в виде суммы двух
простых чисел. Для этого возьмём все такие
числа и выпишем соответствующие
разложения:
4=2+2; 6=3+3; 8=5+3;
10=7+3; 12=7+5; 14=7+7;
16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое
из интересующих нас чисел действительно
представляется в виде суммы двух простых
слагаемых.
Таким образом, полная индукция заключается
в том, что общее утверждение доказывается
по отдельности в каждом из конечного числа
возможных случаев.
Иногда общий результат удаётся предугадать
после рассмотрения не всех, а достаточно
большого числа частных случаев (так
называемая неполная индукция).
Полная индукция имеет в математике
лишь ограниченное применение. Многие
интересные математические утверждения
охватывают бесконечное число частных
случаев, а провести проверку для
бесконечного числа случаев мы не в
состоянии. Неполная же индукция часто
приводит к ошибочным результатам.
Во многих случаях выход из такого рода
затруднений заключается в обращении к
особому методу рассуждений,
называемому методом математической
индукции.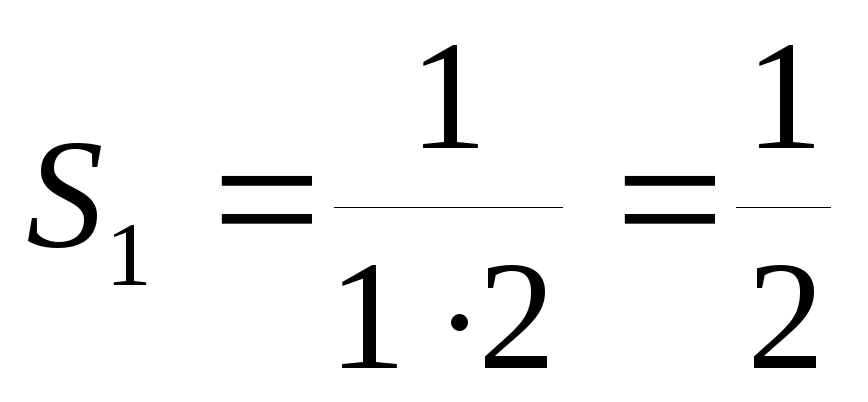
Принцип математической
индукции.
Если предложение А(n), зависящее от
натурального числа n, истинно для n=1 и из
того, что оно истинно для n=k (где k-любое
натуральное число), следует, что оно истинно и
для следующего числа n=k+1, то
предположение А(n) истинно для любого
натурального числа n.
Если предложение А(n) истинно при n=p и
если А(k) >А(k+1) для любого k>p, то
предложение А(n) истинно для любого n>p.
Док-во по методу математической индукции
проводиться следующим образом. Сначала
доказываемое утверждение проверяется для
n=1, т.е. устанавливается истинность
высказывания А(1). Эту часть
доказательства называют базисом
индукции. Затем следует часть док-ва,
называемая индукционным шагом. В этой
части доказывают справедливость
утверждения для n=k+1 в предположении
справедливости утверждения для n=k ,т.е.
доказывают, что А(k) >A(k+1).

12. Алгоритм доказательства методом математической индукции

Проверяют справедливость гипотезы для наименьшего
из натуральных чисел при котором гипотеза имеет смысл
(базис индукции).

1.
Сделав предположение, что гипотеза верна для
некоторого значения k, стремятся доказать
справедливость ее для k+1 (индукционный шаг).
2.
Если такое доказательство удалось довести до конца,
то, на основе принципа математической индукции можно
утверждать, что высказанная гипотеза справедлива для
любого натурального числа n.
3.
Метод математической индукции
в решении задач на делимость.
Пример 1
Доказать, что при любом n , 7 n-1 делится на
6 без остатка.
Решение:
1)Пусть n=1, тогда Х1 =71-1=6 делится на 6
без остатка. Значит при n=1 утверждение
верно.
2) Предположим, что при n=k ,7k-1 делится
на 6 без остатка.
3) Докажем, что утверждение справедливо
для n=k+1.
X k+1 =7 k+1 -1=7
7 k -7+6=7(7 k -1)+6.
Первое слагаемое делится на 6, поскольку
7 k-1 делится на 6 по предположению, а
вторым слагаемым является 6. Значит 7 n-1
кратно 6 при любом натуральном n. В силу
метода математической индукции
утверждение доказано.

Применение метода к
суммированию рядов.
Пример 2
Доказать, что
1+х+х
2
+х
3
+…+х
n
=(х
n+1
-1)/(х-1), где х (1)
Решение:
1) При n=1 получаем
2
1+х=(х -1)/(х-1)=(х-1)(х+1)/(х-1)=х+1
следовательно, при n=1 формула верна; А(1)
истинно.
2) Пусть k-любое натуральное число и пусть
формула верна при n=k, т.е.
1+х+х 2 +х 3 +…+х k =(х k+1 -1)/(х-1).
Докажем, что тогда выполняется равенство
2
3
k
k+1
k+2
1+х+х +х +…+х +x
=(x
-1)/(х-1).
В самом деле
2
3
k
k+1
2
3
1+х+х +x +…+х +x
=(1+x+x +x +…+x
k
)+x k+1 = (x k+1 -1)/(x-1)+x k+1 =
=(x k+2 -1)/(x-1).
Итак, А(k) > A(k+1).
На основании принципа математической
индукции заключаем, что формула верна для
любого натурального числа n.
Применения метода к
доказательству неравенств.
Пример 3
Доказать, что при n>2 справедливо неравенство
1+(1/2
2
)+(1/3
2
)+…+(1/n
2
)<1,7-(1/n).

Решение:
1) При n=3 неравенство верно
1+(1/2 2 )+(1/3 2 )=245/180<246/180=1,7-(1/3).
2)Предположим, что при n=k
1+(1/2
2
)+(1/3
2
)+…+(1/k 2 )=1,7-(1/k).
3) Докажем справедливость неравенства при n=k+1
(1+(1/2
2
)+…+(1/k
2
))+(1/(k+1)
2
)<
<1,7(1/k)+(1/(k+1) 2 ).
Докажем, что
1,7-(1/k)+(1/(k+1) 2 )<1,7-(1/k+1) U
(1/(k+1) 2 )+(1/k+1)<1/k U (k+2)/(k+1) 2 <1/k U
k(k+2)<(k+1) 2 U k 2 +2k < k 2 +2k+1.
Последнее очевидно, а поэтому
1+(1/2
2
)+(1/3
2
)+…+(1/(k+1) 2 )<1,7-(1/k+1).
В силу метода математической индукции неравенство
доказано.
Метод в применение к другим
задачам.
Пример 4
Доказать, что число диагоналей выпуклого nугольника равно n(n-3)/2.
Решение:
1) При n=3 утверждение справедливо, ибо в
треугольнике
А 3 =3(3-3)/2=0 диагоналей;
А 2 А(3) истинно.
2) Предположим, что во всяком
выпуклом k-угольнике имеет ся А k =k(k-3)/2
диагоналей.

3)Докажем, что тогда в выпуклом
А k+1 (k+1)-угольнике число
диагоналей А k+1 =(k+1)(k-2)/2.
Пусть А 1 А 2 А 3 …A k A k+1 -выпуклый (k+1)угольник. Проведём в нём диагональ A 1 A k . Чтобы
подсчитать общее число диагоналей этого (k+1)угольника нужно подсчитать число диагоналей в kугольнике A 1 A 2 …A k , прибавить к полученному
числу k-2, т.е. число диагоналей (k+1)-угольника,
исходящих из вершины А k+1 , и, кроме того, следует
учесть диагональ А 1 А k. Таким образом,
k+1=k+(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.
Итак, А(k) > A(k+1). Вследствие принципа математической
индукции утверждение верно для любого выпуклого
n-угольника.
Заключение
В частности изучив метод математической
индукции, я повысила свои знания в этой
области математики, а также научилась
решать задачи, которые раньше были мне
не под силу.
В основном это были логические и
занимательные задачи, т.е. как раз те,
которые повышают интерес к самой
математике как к науке.

Решение таких
задач становится занимательным занятием
и может привлечь в математические
лабиринты всё новых любознательных. Помоему, это является основой любой науки.
«Понимание и умение
правильно применять
принцип математической
индукции, является хорошим
критерием логической
зрелости, которая
совершенно необходима
математику»
А.Н. Колмогоров

23. Ханойские башни

Есть три стержня и колец
разного размера. Класть
можно
только
кольцо
меньшего
размера
на
кольцо большего размера.
Можно ли переместить
пирамидку
с
одного
стержня на другой?

24. Пересечение прямых

Докажите, что любые n
прямых, расположенных на
одной плоскости, никакие
две
из
которых
не
параллельны, и никакие
три не пересекаются в
одной точке, пересекаются
ровно в
точках.

25. Докажите тождество

1. [БАЗА]Проверим, работает ли эта формула при n=1:
2.

[ПРЕДПОЛОЖЕНИЕ] Предположим, что тождество верно при n=k, то есть
3.[ШАГ] Шаг индукции будет соответствовать проверке этого тождества
при n=k+1, то есть нужно доказать, что
4.[ВЫВОД] Тождество верно для любого .
Группа 1.
Задача 1. Докажите, что при каждом
натуральном , начиная с , существует
выпуклый -угольник, имеющий ровно
три острых угла.
Задача 2. Доказать, что 1+3+5+…+(2n1)=n 2 .
Задача 3.Доказать, что (11 n+2 +12 2n+1 )
делится на 133 без остатка.
Группа 3.
Задача 1. Докажите что сумма углов
выпуклого n-угольника равна
(или
радиан). В частности для
треугольника получаем
а для четырехугольника
Задача 2. Доказать, что при любом n
справедливо утверждение:
1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.
Задача 3.Доказать, что 3 3n-1 +2 4n-3 при
произвольном натуральном n делится на
11.
Группа 2.
Задача 1. Плоскость разделена на части n
прямыми. Докажите, что эти части
можно раскрасить в два цвета так, что
соседние куски будут раскрашены в
разные цвета.

Задача 2. Доказать, что
1+х+х 2 +х 3 +…+х n =(х n+1 -1)/(х-1).
Задача 3.Доказать, что при любом n 7 n -1
делится на 6 без остатка.
Группа 4.
Задача 1. Чему равно количество
кусочков, на которые n прямых (не
проходящих через одну точку) делят
плоскость на части? Одна прямая — на две
части, две — на четыре. А пятнадцать
прямых?
Задача 2. Доказать, что 1 3 -2 3 +3 3 4 3 +…+(2n-1) 3 -(2n) 3 =-n 2 (4n+3) для
любого натурального n.
Задача 3.Доказать, что 11 2n -1 при
произвольном натуральном n делится на 6
без остатка.

27. Рефлексия

Другой мой урок по математической индукции посвящен доказательству утверждений о делимости.

Поверьте, этапы доказательства с помощью математической индукции поначалу могут показаться сложными. Но когда вы действительно начнете это делать, вы поймете, что это очень интуитивно понятно и просто. Изучив приведенные ниже примеры, вы получите хорошее представление и уверенность в себе, чтобы решать гораздо более сложные задачи математической индукции, связанные с суммированием.

Этапы доказательства методом математической индукции

Показать, что базовый шаг верен. Это означает, что утверждение верно для n=1.
Предположим, что верно для n=k. Этот шаг называется гипотезой индукции .
Докажите, что утверждение верно для n=k+1. Этот шаг называется индукционным шагом .

Схема математической индукции с использованием домино

Примеры доказательства суммирования с помощью математической индукции

Пример 1: Используйте математику, чтобы доказать, что формула верна для всех натуральных чисел \mathbb{N}.

3 + 7 + 11 + … + \left( {4n — 1} \right) = n\left( {2n + 1} \right)

а) Проверить шаг базиса n=1, если он истинный.

3= n\влево( {2n + 1} \вправо)

3 = 1\влево[ {2\влево( 1 \вправо) + 1} \вправо]

3 = 1\влево( 3 \вправо )

3 = 3

Да, это правда!

b) Предположим, что утверждение верно для n=k.

\color{red}3 + 7 + 11 + … + \left( {4k — 1} \right) = k\left( {2k + 1} \right)

c) Теперь мы собираемся доказать, что это верно для n=k+1.

3 + 7 + 11 + … + \left( {4k — 1} \right) + \left[ {4\left( {k + 1} \right) — 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]

Обратите внимание, что мы можем значительно упростить уравнение, используя часть b) .

{\color{red}3 + 7 + 11 + … + \left( {4k — 1} \right)} + \left[ {4\left( {k + 1} \right) — 1} \right ] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]

{\color{red}k\left( {2k + 1} \right)} + \left[ {4\left( {k + 1} \right) — 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]

Следующий очевидный шаг — упростить обе части уравнения. Но вот в чем дело. Мы хотим максимально упростить левую часть (LHS), а правую часть (RHS) — с наименьшим количеством шагов при упрощении.

Нет ничего плохого в том, что мы сильно упрощаем обе стороны, пока можем показать, что обе стороны равны. Но более элегантно, если мы сохраняем наименьшее количество упрощений с правой стороны и наибольшее с левой. Вы поймете это лучше, чем больше будете практиковаться в математической индукции.

Не касаясь левой части уравнения, мы немного упростим правую часть. Распределите 2 в бином внутри скобок, затем добавьте числа.

{\color{red}k\left( {2k + 1} \right)} + \left[ {4\left( {k + 1} \right) — 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]

k\left( {2k + 1} \right) + \left[ {4\left ({k + 1} \right) — 1} \right] = \left( {k + 1} \right)\left( {2k + 2 + 1} \right)

k\left( {2k + 1 } \right) + \left[ {4\left( {k + 1} \right) — 1} \right] = \left( {k + 1} \right)\left( {2k + 3} \right) 92} + 5k + 3= \left( {k + 1} \right)\left( {2k + 3} \right)

\left( {k + 1} \ right)\left( {2k + 3} \right)= \left( {k + 1} \right)\left( {2k + 3} \right) ✔︎

Мы показали, что если утверждение верно для n=k, то оно верно и для n =к+1. Следовательно, утверждение верно для всех натуральных чисел.◾️

Пример 2: Используйте математическую индукцию, чтобы доказать, что формула верна для всех натуральных чисел \mathbb{N}.

— 1 + 2 + 5 + … + \left( {3n — 4} \right) = {\ Large {{n \over 2}}}\left( {3n — 5} \ right)

а) Проверка базового шага; п=1 верно.

— 1 = {\ Большой {{n \ более 2}}} \ влево ( {3n — 5} \ вправо)

— 1 = {\ Большой {{1 \ более 2}}} \ влево [ {3 \left( 1 \right) — 5} \right]

— 1 = {\Large{{1\более 2}}}\left[{3-5}\right]

— 1 = {\Large{ {1 \over 2}}}\left( { — 2} \right)

— 1 = — 1

Да, это правда!

b) Предположим, что утверждение верно для n=k.

\color{red} — 1 + 2 + 5 + … + \left( {3k — 4} \right) = {\Large{{k \over 2}}}\left( {3k — 5} \right )

c) Теперь мы покажем, что это верно для n=k+1.

— 1 + 2 + 5 + … + \left( {3k — 4} \right) + \left[ {3\left( {k + 1} \right) — 4} \right] = {\Large{ {{k + 1} \over 2}}}\left[ {3\left( {k + 1} \right) — 5} \right]

Мы будем использовать часть b) , чтобы подставить ее в уравнение .

{\color{red} — 1 + 2 + 5 + … + \left( {3k — 4} \right)} + \left[ {3\left( {k + 1} \right) — 4} \ вправо] = {\ Большой {{{k + 1} \ более 2}}} \ влево [ {3 \ влево ( {k + 1} \ вправо) — 5} \ вправо]

{\color{red}{\Large{k \более 2}}\left({3k — 5} \right)} + \left[ {3\left({k + 1} \right) — 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3\left( {k + 1} \right) — 5} \right]

Сосредоточимся на упрощении правой части сначала уравнение.

{\Large{k\более 2}}\left({3k — 5}\right) + \left[ {3\left({k + 1}\right) — 4}\right] = {\Large {{k + 1} \более 2}}\left[ {3\left( {k + 1} \right) — 5} \right]

{\ Large{k \over 2}}\left( {3k — 5} \right) + \left[ {3\left( {k + 1} \right) — 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3k + 3 — 5} \справа]

{\Large{k\более 2}}\left({3k — 5}\right) + \left[ {3\left({k + 1}\right) — 4}\right] = {\Large {{k + 1} \over 2}}\left( {3k — 2} \right)

Пришло время упростить и изменить левую часть, чтобы она выглядела так же, как правая часть уравнения.

Мы показали, что если утверждение верно для n=k, то оно верно и для n=k+1. Следовательно, утверждение верно для всех натуральных чисел.◾️

Пример 3: Докажите, используя математическую индукцию, что уравнение верно для всех натуральных чисел \mathbb{N}. 9+.

4 + 9 + 14 + 19 + … + \left( {5n — 1} \right) = {\Large{ {n \over 2}}}\left( {5n + 3} \right)

а) Показать базовый шаг; п=1 верно.

4 = {\ Большой {{n \ более 2}}} \ влево ( {5n + 3} \ вправо)

4 = { \ Большой {{1 \ более 2}}} \ влево [ {5 \ влево ( 1 \right) + 3} \right]

4 = {\Large{{1 \over 2}}}\left[ {5 + 3} \right]

4 ={ \Large{{1 \over 2}}}\left( 8 \right)

4 = 4

Да!

b) Предположим, что верно для n=k.

\color{red}4 + 9 + 14 + 19 + … + \left( {5k — 1} \right) = {\Large{{k \over 2}}}\left( {5k + 3} \ справа)

в) Если верно для n=k, то и n=k+1 должно быть верно.

4 + 9 + 14 + 19 + … + \left( {5k — 1} \right) + \left[ {5\left( {k + 1} \ right) — 1} \right] = {\Large {{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right]

Выполните замену, используя информацию в части b) . Казалось бы, сложное уравнение будет еще более упрощено.

{\color{red}4 + 9 + 14 + 19 + … + \left( {5k — 1} \right)} + \left[ {5\left( {k + 1} \right) — 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left({k + 1} \right) + 3} \right]

{\color{red} {\ Большой {{k \ более 2}}} \ влево ({5k + 3} \ вправо)} + \ влево [ {5 \ влево ( {k + 1} \ вправо) — 1} \ вправо] = {\ Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right]

Пока игнорируйте левую часть уравнения. Сначала мы очистим правую часть уравнения, упростив ее.

{\ Большой {{k \ более 2}}} \ влево ({5k + 3} \ вправо) + \ влево [ {5 \ влево ( {k + 1} \ вправо) — 1} \ вправо] = { \Large{{{k + 1} \более 2}}}\left[ {5\left( {k + 1} \right) + 3} \right]

{\Large{{k \over 2}} }\left( {5k + 3} \right) + \left[ {5\left( {k + 1} \right) — 1} \right] = {\Large{{{k + 1} \over 2} }}\left( {5k + 5 + 3} \right)

{\ Large{{k \over 2}}}\left( {5k + 3} \right) + \left[ {5\left( { k + 1} \right) — 1} \right] = {\ Large {{{k + 1} \более 2}}}\left( {5k + 8} \right)

9+.

\Large{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \over {n\left ( {n + 1} \right)}} = {n \over {n + 1}}

a) Показать, что базисный шаг верен для n=1.

\Large{1 \over {1 \cdot 2}} = {n \over {n + 1}}

\Large{1 \over 2} = {n \over {n + 1}}

\ Большой {1 \более 2} = {1 \более {1 + 1}}

\Большой{1 \более 2} = {1 \более 2}

Верно!

b) Предположим, что верно для n=k.

\color{red}\Large{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \ over {k\left( {k + 1} \right)}} = {k \over {k + 1}}

c) Теперь мы собираемся показать, что это верно для n=k+ 1.

\Large{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \over {k\left ( {к + 1} \ справа)}} + {1 \ над {\ влево ( {к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \ вправо]} } = {{к + 1} \ над {\ влево ( {к + 1} \ вправо) + 1}}

Используйте предположение, записанное в части b) , чтобы выполнить замену. Это значительно упростит уравнение, над которым мы работаем.

\Large{\color{red}{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \ над {к \ влево ( {к + 1} \ вправо)}}} + {1 \ над {\ влево ( {к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \right]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}

\Large{\color{red}{k \over {k + 1}}} + {1 \ над {\ влево ( {к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \ вправо]}} = {{к + 1 } \ над {\ влево ( {к + 1} \ вправо) + 1}}

Не обращая внимания на левую часть уравнения, упростим правую часть.

\ Большой {к \ над {к + 1}} + {1 \ над {\ влево ( {к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \ справа]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}

\Large{k \over {k + 1}} + {1 \over {\ влево ({к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \ вправо]}} = {{к + 1} \ над {к + 1 + 1}}

\ Большой {к \ над {к + 1}} + {1 \ над {\ влево ( {к + 1} \ вправо) \ влево [ {\ влево ( {к + 1} \ вправо) + 1} \ справа]}} = {{k + 1} \over {k + 2}} 9{k + 1}}}}

Правую часть оставим без изменений, поскольку она достаточно упрощена. Мы будем работать с левой стороной, чтобы она выглядела так же, как справа.

Мы показали, что если утверждение верно для n=k, то оно верно и для n=k+1. Следовательно, утверждение верно для всех положительных целых чисел.

Университет штата Иллинойс, математический факультет

MAT 305: Темы комбинаторики для K-8 Учителя

Доказательство по индукции

Здесь мы иллюстрируем и объясняем полезное обоснование техника под названием Доказательство по индукции . Процесс описывается с использованием четырех шагов, краткого предоставляется резюме, и немного практики представлены проблемы.

Мы проиллюстрируем процесс доказательства индукцией , чтобы показать что

(Я)

Процесс

Шаг 1: Убедитесь, что желаемый результат справедлив для n=1.

Здесь, когда 1 заменяется на n как в левой, так и в правой части выражения в (I) выше, результат равен 1. В частности,

. Этот завершает шаг 1.

Шаг 2: Предположим, что желаемый результат верен для n=k.

В нашем примере это означает, что мы предполагаем сумму первых k положительные целые числа. Будет полезно показать это как

(II)

Шаг 2 завершен.

Шаг 3: Используйте допущение из шага 2, чтобы показать, что результат верно для n=(k+1).

То есть мы хотим это показать. Другими словами, покажите, что если предположить, что результат для n=k подразумевает результат для n=(k+1).

Здесь мы основываемся на уравнении, представленном в (II):

Если , добавление (k+1) в каждую сторону гарантирует, что

(III)

Левая часть (III) — это просто расширение выражения , это сумма первых (k+1) натуральных чисел.

Осталось показать, что правая часть (III) эквивалентна , что наш формула говорит нам, что это правильная сумма.

Перепишите правую часть (III) с общим знаменателем:

(IV)

Теперь сложим числители и выразим над общим знаменателем:

(В)

В числителе (V) k+1 является общим для обоих членов, поэтому мы можем фактор числитель, в результате чего эквивалентная форма:

(VI)

Выражение (VI) — это как раз тот результат, который мы искали.

Шаг 4: Подведите итоги своей работы.

По индукции мы показали, что сумма первых n положительных целые числа могут быть представлены выражением .

Уравнение имеет практическое применение каждый раз, когда мы ищем суммы последовательных положительных целые числа. Например, теперь мы можем использовать результат, чтобы сделать вывод, что . Мы также можем используйте результат, чтобы показать, что, например,.

Сводка

Индукция процесс основан на эффекте домино. Если мы сможем показать, что результат верно от k-го до (k+1)-го случая, и мы действительно можем показать это верно для первого случая (k=1), мы можем связать цепочку из выводы: истина для k=1 подразумевает истину для k=2, истина для k=2 подразумевает истинность для k=3 и так далее. Нажатие на первую костяшку вызывает все из оставшихся костяшек домино выпадают подряд.

Практика

Вот практические задачи, которые вы должны выполнить, чтобы закрепить индукционный процесс.