Що таке метод математичної індукції?
Метод математичної iндукцiї — це метод доведення, застосовуючи який ми намагаємося вивести якесь загальне твердження з вужчого. Використовуючи метод математичної iндукцiї, починаємо з припущення, що щось справджується для певного значення. Потiм треба показати, що якщо це припущення справджується для певного значення, то воно має бути правильним й для наступного значення. Якщо це припущення справджується для довiльного значення, воно має правильним для всiх значень.
Ось три кроки, якi дуже корисно виконати, використовуючи метод математичної iндукцiї:
Правило
Доведення методом математичної iндукцiї
- 1.
- Перевiр, чи твердження справджується для першого значення n.

- 2.
- Припусти, що твердження справджується для n=k, так що …
- 3.
- Потiм потрiбно показати, що твердження справджується для n=k+1, так що …
Зверни увагу! Ключ до методу математичної iндукцiї полягає в тому, щоб пiдставити наше припущення з Пункт 2 в Пункт 3. Це є основним моментом у доведеннi методом математичної iндукцiї!
Приклад 1
Застосування iндукцiї до числового ряду
Доведи, що 1+3+5+⋯+ (2n−1)=n2
- 1.
- Перевiрмо, чи це твердження справджується для першого значення n, пiдставивши його у вираз 2n−1: 1=12✓
- 2.
- Припустiмо, що це твердження справджується для n=k, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k)
| 1+3+5+⋯+ (2k−1)=k2 | (1) |
- 3.

- Потрiбно показати, що це справджується для n=k+1, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k+1. Пам’ятай про круглi дужки!)
| 1+⋯+(2k−1)+(2(k+1)−1)=(k+1)2 | (2) |
| 1+3+⋯+ (2k−1)+ (2 (k+1)−1)= (k+1)2 | (3) |
- 4.
- Переходимо до розрахункової частини доведення. Почнемо з лiвої частини (3) й продовжимо з використанням припущення (1). Подивись уважно на те, що вiдбувається нижче! Нарештi ми отримаємо те, що знаходиться в правiй частинi рiвностi в (3).

Тепер треба використати припущення, щоб записати гарний вираз для перших членiв k:
=1+3+5+⋯+ (2k−1)︸Пiдставмо вираз iз (1)+ (2 (k+1)−1)=k2+ (2 (k+1)−1)=k2+2k+1= (k+1)2.
1+3+5+⋯+ (2k−1)︸Пiдставмо вираз iз (1)+ (2 (k+1)−1)=k2+ (2 (k+1)−1)=k2+2k+1= (k+1)2,що й треба було довести.
Q.E.D
Приклад 2
Застосування iндукцiї до подiльностi
Доведи, що n2−n n дiлиться на 2.
Якщо число дiлиться на 2, його можна розкласти на множник 2. Iнакше кажучи, таке число можна записати як n2−n=2t, де t – це цiле число.
- 1.
- Перевiрмо, чи це твердження справджується для першого значення n, пiдставивши у вираз n2−n: 12−1=0=2⋅0✓
- 2.
- Припустiмо, що це твердження справджується для n=k, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k)
| k2−k=2t | (4) |
- 3.

- Потрiбно показати, що це справджується для n=k+1, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k+1. Пам’ятай про круглi дужки!)
| (k+1)2− (k+1)=2u | (5) |
- 4.
- Переходимо до розрахункової частини доведення. Почнемо з лiвої частини (5) й продовжимо пiдставляючи припущення (4). Подивись уважно на те, що вiдбувається нижче! Нарештi ми отримаємо те, що знаходиться в правiй частинi рiвностi в (5).

Тепер, використавши припущення, n=k+1 дасть нам:
(k+1)2− (k+1)=k2+2k+1−k−1︸Перекладемо члени мiсцями, щоб використати (4)=k2−k︸Використовуючи (4), отримаємо+2k=2u+2k=2 (u+k)=2t, де t=u+k,що й треба було довести.
Q.E.D
Приклад 3
Застосування iндукцiї до похiдних
Нехай f (x)=e2x. Доведи, що f (n)=2ne2x.
Тут f (n) означає, що функцiя fдиференцiйована n разiв.
- 1.
- Перевiрмо, чи це твердження справджується для першого значення n, оцiнивши вираз f (n)=2ne2x: f (1) (x)=2e2x=21e2x✓
- 2.
- Припустiмо, що це твердження справджується для n=k, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k).
| f (k) (x)=2ke2x | (6) |
- 3.
- Потрiбно показати, що з цього витiкає, що твердження справджується для n=k+1, так що (використовуючи вираз, даний в умовi задачi, тiльки замiнюючи n на k+1.
 Пам’ятай про круглi дужки!)
Пам’ятай про круглi дужки!)
| f (k+1) (x)=2k+1e2x | (7) |
- 4.
- Переходимо до розрахункової частини доведення. Почнемо з лiвої частини (7) й продовжимо пiдставляючи припущення (6). Подивись уважно на те, що вiдбувається нижче! Нарештi ми отримаємо те, що знаходиться в правiй частинi рiвностi в (7).
Тепер потрiбно використати припущення, щоб записати f (k+1) (x) як (f (k) (x))′: f (k+1) (x)= (f (k) (x))′︸Пiдставимо (6)= (2ke2x)′=2⋅2ke2x=2k+1e2x,що й треба було довести.
Q.E.D
Математична індукція та геометрія.

Приклад 1. Довести, що кількість діагоналей dn випуклого n – кутника можна обчислити за формулою .
Зазначимо, що n≥3, причому n може набувати лише натуральних значень. При n = 3 рівність справедлива
dn = = = 0
Припустимо, що рівність справедлива для n = k
dk =
Доведемо справедливість рівності для n = k + 1, тобто
d
A3
k+1 =
Щ
A2
A5
A4
Ak
A 1
об знайти кількість діагоналей (k+1) – кутника, потрібно додати до кількості діагоналей k – кутника кількість діагоналей, що виходять з (k + 1)-ї вершини Ak + 1
A2
A1
в
Ak+1
Малюнок 1
ершини Akі
A1. З
ескізу довільного многокутника (малюнок
1) очевидно, що з однієї вершини n
– кутника виходить (n
– 3) діагоналі.
З
ескізу довільного многокутника (малюнок
1) очевидно, що з однієї вершини n
– кутника виходить (n
– 3) діагоналі.
Маємо: dk+1 = dk+ (k + 1 – 3) + 1 = dk + k – 2 + 1 = +1 = =
Отже, рівність доведено для усіх натуральних значень n.
Математична індукція і повсякденне життя.
Матіндукція, як не дивно, розповсюджена й в повсякденному житті.
Приклад. Є три стрижня та n кілець різного розміру (малюнок 2). На кільце можна класти тільки кільця, що менші за розмірами. Чи можливо перекласти вежуp з одного стрижня на інший?
Малюнок 2
Вежу, в якій одне кільце (n=1) перемістити можливо.
Припустимо, що можливо перемістити вежу з n = k
Спробуємо
навчитись перекладати пірамідку з
n
= k
+
1 . Пірамідку
з K кілець,
що
лежать на найбільшому
k+
1-м
кільці,
ми
можемо згідно припущенню
перемістити
на будь-який стрижень.
Зробимо
це,
перекладемо
її на третій стрижень.
Нерухоме
k +
1-е
кільце
не буде нам заважати провести алгоритм
переміщення,
так
як воно найбільше.
Після
переміщення K кілець
перемістимо k +
1-е
кільце,
яке залишилось,
на
другий стрижень.
Ми
можемо це зробити, так як другий стрижень
вільний.
Тепер
звернемо увагу,
той
факт,
що
другий стрижень не пустий,
не
заважає перекладати на нього будь-які
кільця, так як кільце на ньому найбільше
(,
будь-яке
кільце можна покласти на більше за
умовою задачі)і потім знов застосуємо
відомий нам по припущенню алгоритм
переміщення k кілець
і перемістимо їх
на
другий стрижень,
стрижень,
на якому внизу лежить
k +
1-е
кільце.
Таким
чином,
якщо
ми вміємо переміщувати пірамідки
з k кільцями,
то
вміємо переміщувати пірамідки і з k +
1кільцем.
Пірамідку
з K кілець,
що
лежать на найбільшому
k+
1-м
кільці,
ми
можемо згідно припущенню
перемістити
на будь-який стрижень.
Зробимо
це,
перекладемо
її на третій стрижень.
Нерухоме
k +
1-е
кільце
не буде нам заважати провести алгоритм
переміщення,
так
як воно найбільше.
Після
переміщення K кілець
перемістимо k +
1-е
кільце,
яке залишилось,
на
другий стрижень.
Ми
можемо це зробити, так як другий стрижень
вільний.
Тепер
звернемо увагу,
той
факт,
що
другий стрижень не пустий,
не
заважає перекладати на нього будь-які
кільця, так як кільце на ньому найбільше
(,
будь-яке
кільце можна покласти на більше за
умовою задачі)і потім знов застосуємо
відомий нам по припущенню алгоритм
переміщення k кілець
і перемістимо їх
на
другий стрижень,
стрижень,
на якому внизу лежить
k +
1-е
кільце.
Таким
чином,
якщо
ми вміємо переміщувати пірамідки
з k кільцями,
то
вміємо переміщувати пірамідки і з k +
1кільцем.
Подвійна та потрійна математична індукція.
а) подвійна математична індукція
Подвійна
матіндукція — це метод застосування
математичної індукції, що заключає в
собі використання методу матіндукції
один раз, після чого доведення отриманого
висновку за допомогою ще одного
застосування методу математичної
індукції з іншим індуктивним припущенням.
Приклад. Довести, що для будь – яких значень n справедливе твердження:
32n + 3 + 40n – 27 /./ 64
Для n = 1 рівність справедлива:
243 + 40 – 27 /./ 64
256 /./ 64
Припустимо, що для n = k твердження справедливе:
32k + 3 + 40k – 27 /./ 64
Доведемо справедливість твердження для n = k + 1:
32k + 5 + 40k + 60 /./ 64
32k + 5 + 40k + 60 = 9*32k + 3 + 40k – 27 + 40 =
= (32k + 3 + 40k – 27) + (8*32k + 3 + 40)
Перший доданок ділиться на 64 за припущенням. Доведемо, що й другий доданок ділиться на 64:
8*32k + 3 + 40 /./ 64
8(32k + 3 + 5) /./ 64
32k + 3 + 5
/.
При k = 1 твердження справедливе:
243 + 5 /./ 8
248 /./ 8
Припустимо, що твердження справедливе для k = t:
32t + 3 + 5 /./ 8
Доведемо справедливість твердження для k = t + 1:
32t + 3 + 5 /./ 8
32t + 5 + 5 = 9*32t + 3 + 5 =( 32t + 3 + 5) + 8*32t + 3
Перший доданок ділиться на 8 за припущенням, а другий складається з множників, один з яких – 8. Отже, 32k + 3 + 5 ділиться націло на 8, а, отже, і перше твердження справедливе для усіх натуральних значень n.
б) потрійна математична індукція.
Потрійна матіндукція аналогічна подвійній, але якесь твердження, яке ми отримали в результаті подвійної математичної індукції ми маємо довести ще раз за допомогою матіндукції.
Приклад. Довести,
що для будь – яких значень n
справедливе твердження:
Довести,
що для будь – яких значень n
справедливе твердження:
22n — 1 – 9n2 + 21n – 14 /./ 27
Для n = 1 твердження правильне:
2 – 9 + 21 – 14 /./ 27
0 /./ 27
Припустимо, що для n = k твердження справедливе:
22k — 1 – 9k2 + 21k – 14 /./ 27
Доведемо справедливість твердження для n = k + 1:
22k + 1 – 9(k + 1)2 + 21(k + 1) – 14 /./ 27
22k + 1 – 9(k + 1)2 + 21(k + 1) – 14 = 4*22k — 1 – 9k2 – 18k – 9 +21k + 21 — — 14 = (22k — 1 – 9k2 + 21k – 14) + (3*22k – 1 – 18k + 12)
Перший доданок ділиться націло на 27 за припущенням. Доведемо, що і другий доданок ділиться націло на 27:
3*22k – 1 – 18k + 12 /.
 / 27
/ 27
3(22k – 1 – 6k + 4) /./ 27
22k – 1 – 6k + 4 /./ 9
При k = 1 твердження правильне:
2 – 6 + 4 /./ 9
0 /./ 9
Припустимо, що для k = t твердження справедливе:
22t – 1 – 6t + 4 /./ 9
Доведемо справедливість твердження для k = t + 1:
22t + 1 – 6t – 2 /./ 9
22t + 1 – 6t – 2 = 4*22t – 1 – 6t + 4 – 6 = (22t – 1 – 6t + 4) + (3*22t – 1 – 6)
Перший доданок ділиться націло на 9 за припущенням. Доведемо, що другий доданок теж ділиться націло на 9:
3*22t – 1 – 6 /./ 9
3(22t – 1 – 6) /./ 9
22t – 1 – 2 /. / 3
/ 3
При t = 1 твердження справедливе:
2 – 2 /./ 3
0 /./ 3
Припустимо, твердження справедливе для t = m:
22m – 1 – 2 /./ 3
Доведемо справедливість твердження для t = m + 1:
22m + 1 – 2 /./ 3
22m + 1 – 2 = 4*22m – 1 – 2 = (22m – 1 – 2) + (3*22m – 1)
Перший доданок ділиться націло на 3 за припущенням, а другий складається з множників, один з яких – 3. Отже, твердження 2 і 3 справедливі для усіх натуральних значень t та m відповідно, з чого випливає справедливість твердження 1 для усіх натуральних значень n.
Математическая индукция
Математическая индукция — это особый способ доказательства вещей. У него всего 2 шага:
- Шаг 1. Покажите, что верно для первый
- Шаг 2. Покажите, что если любой из верен, то следующий верен
Тогда все верны
Вы слышали об «эффекте домино»?
- Шаг 1.
 Первые 9 0007 домино падает
Первые 9 0007 домино падает - Шаг 2. Когда выпадает любая костяшка костяшки, следующая костяшка костяшки выпадает
Итак… все костяшки упадут!
Так работает математическая индукция.
В мире чисел мы говорим:
- Шаг 1. Покажите, что это верно для первого случая, обычно n=1
- Шаг 2. Покажите, что если n=k верно, то n=k+1 также верно
Как это сделать
Шаг 1 обычно прост, нам просто нужно доказать, что он верен для n=1
Шаг 2 лучше всего сделать так:
- Предположим, что верно для n=k
- Докажите , что это верно для n=k+1 (мы можем использовать случай n=k как факт .)
Это все равно, что сказать «ЕСЛИ мы можем заставить костяшку домино упасть, Упадет ли следующая?»
Шаг 2 часто может быть сложным , нам, возможно, придется использовать творческие трюки, чтобы заставить его работать!
Как в этом примере:
Пример: кратно ли 3
n −1 2? Это правда? Давайте узнаем.
1. Покажите, что это верно для n = 1
3 1 −1 = 3–1 = 2
Да 2 ранее 2. Это было легко.
3 1 −1 верно
2. Предположим, что верно для n=k
3 k −1 верно
(Подождите!
Мы не знаем!
Это предположение … что мы рассматриваем
как факт для остальной части этого примера)
Теперь докажите, что 3 k+1 −1 кратно 2
3 k+1 тоже 3×3 k
А затем разделить 3× на 2× и 1×
Каждое из них кратно 2
:3 03
- 2×3 k кратно 2 (мы умножаем на 2)
- 3 k −1 верно (это мы сказали в предположении выше)
Итак:
3 k+1 −1 верно
ГОТОВО!
Вы видели, как мы использовали случай 3 k −1 как истинное , хотя и не доказали этого? Это нормально, потому что мы полагаемся на эффект домино . ..
..
… мы спрашиваем если выпадет любая костяшка домино, выпадет ли следующая ?
Итак, мы принимаем как факт (временно), что костяшка домино « n=k » падает (т.е. 3 k −1 верно), и смотрим, означает ли это, что » n=k+1 «домино тоже упадет.
Трюки
Я уже говорил, что нам часто приходится использовать воображение.
Обычный трюк состоит в том, чтобы переписать случай n=k+1 на 2 части:
- одна часть представляет собой случай n=k (который считается верным)
- затем можно проверить другую часть, чтобы убедиться, что она также верна
Мы сделали это в примере выше, а вот еще один:
Пример: сложение нечетных чисел
1 + 3 + 5 + … + (2n−1) = n 2
1. Показать, что верно для n=1
1 = 1 2 верно
7
верно 006 н=к
1 + 3 + 5 + . .. + (2k−1) = k 2 верно
.. + (2k−1) = k 2 верно
(предположение!)
Теперь докажите, что это верно для «k+1»
1 + 3 + 5 + . .. + (2k−1) + (2(k+1)−1) = (k+1) 2 ?
Мы знаем, что 1 + 3 + 5 + … + (2k−1) = k 2 (предположение выше), поэтому мы можем сделать замену для всех членов, кроме последнего:
Теперь разверните все термины:
k 2 + 2k + 2 − 1 = k 2 + 2k+1
И упростите:
k + 1 2 9 901 + 2 k 102 + 2k+1
Они одинаковые! Так что это правда.
Итак:
1 + 3 + 5 + … + (2(k+1)−1) = (k+1) 2 верно
ГОТОВО!
Ваша очередь
Теперь, вот еще два примера для практики .
Сначала попробуйте сами, а затем посмотрите на наше решение ниже.
Пример: треугольные числа
Треугольные числа — это числа, которые могут образовывать треугольный узор из точек.
Докажите, что n-е треугольное число равно:
T n = n(n+1)/2
Пример: сложение кубических чисел
Кубические числа — это кубы натуральных чисел
Докажите, что: 102 = ¼n 2 (n + 1) 2
. . . . . . . . . . . . . . . . . .
Пожалуйста, не читайте решения, пока вы сами не попробуете ответы на вопросы, это единственные вопросы на этой странице, над которыми вы можете попрактиковаться!
Пример: треугольные числа
Докажите, что n-е треугольное число равно:
T n = n(n+1)/2
7
0 1. Покажите, что это
2. верно для n=1T 1 = 1 × (1+1) / 2 = 1
2. Предположим, что верно для n=k 3 3 = к (k+1)/2 является истинным (предположение!) Теперь докажите, что это верно для «k+1» T k+1 = (k+1)(k+2)/2 ? Мы знаем, что T k = k(k+1)/2 (предположение выше) T k+1 имеет дополнительный ряд из (k + 1) точек Итак, T k+1 = T k + (k + 1) (k+1)(k+2)/2 = k(k+1) / 2 + (k+1) Умножить все члены на 2: (к + 1) (к + 2) = к (к + 1) + 2 (к + 1) (к + 1) (к + 2) = (к + 2) (к + 1) ) Они одинаковые! Так что это правда . Итак: T k+1 = (k+1)(k+2)/2 верно ГОТОВО! Докажите, что: 1 3 + 2 3 + 3 3 + … + n 3 = 1 0 n 3 = 1 0 n 90 102 0 п + 1) 2 1. Покажите, что верно для n=1 1 3 = ¼ × 1 2 1 × 102 90 102 90 03 2. Предположим, что верно для n=k 1 3 + 2 3 + 3 3 + … + 3 + … + k 2 9090¼0 101 2 (к + 1) 2 верно (предположение!) Теперь докажите, что это верно для «k+1» 1 3 + 2 3 + 3 3 + … + (k + 1) 3 = ¼(k + 1) 2 (k + 2) 2 ? Мы знаем, что 1 3 + 2 3 + 3 3 + … + k 3 = ¼k 2 (k + 1) 2 (предположение выше), поэтому мы можем сделать замену для всех членов, кроме последнего: ¼k 2 (k + 1) 2 + (k + 1) 3 = ¼(k + 1) 2 (k + 2) 2 Умножить все члены на 4:
Пример: сложение кубических чисел
1
3 k 2 (k + 1) 2 + 4(k + 1) 3 = (k + 1) 2 (k + 2) 2
Все члены имеют общий делитель (k + 1) 2 , поэтому его можно сократить:
k 2 + 4(k + 1) = (k + 2) 2
И упростить:
k 2 0 4 + 4k 2 + 4k + 4
Они одинаковые! Так что это правда.
Итак:
1 3 + 2 3 + 3 3 + … + (k + 1) 3 = ¼(k + 1) 2 2 (0 01) 1 9 верно
ГОТОВО!
Математическая индукция | Определение, принцип и доказательство
Peano, Giuseppe
Смотреть все медиа
- Похожие темы:
- индукция доказательство
Просмотреть все связанные материалы →
математическая индукция , один из различных методов доказательства математических утверждений, основанный на принципе математической индукции.
Принцип математической индукции
Класс целых чисел называется наследственным, если всякий раз, когда любое целое число x принадлежит классу, преемник x (то есть целое число x + 1) также принадлежит классу. Тогда принцип математической индукции таков: если целое число 0 принадлежит классу F и F является наследственным, то каждое неотрицательное целое число принадлежит классу F . В качестве альтернативы, если целое число 1 принадлежит классу F и F является наследственным, то каждое положительное целое число принадлежит F . Принцип формулируется иногда в одной форме, иногда в другой. Поскольку любая форма принципа легко доказывается как следствие другой, нет необходимости проводить различие между ними.
В качестве альтернативы, если целое число 1 принадлежит классу F и F является наследственным, то каждое положительное целое число принадлежит F . Принцип формулируется иногда в одной форме, иногда в другой. Поскольку любая форма принципа легко доказывается как следствие другой, нет необходимости проводить различие между ними.
Этот принцип также часто формулируется в интенсиональной форме: свойство целых чисел называется наследственным, если всякий раз, когда любое целое число x обладает этим свойством, его преемник также обладает этим свойством. Если целое число 1 имеет определенное свойство, и это свойство является наследственным, то этим свойством обладает каждое натуральное число.
Доказательство методом математической индукции
Примером применения математической индукции в простейшем случае является доказательство того, что сумма первых n нечетных положительных целых чисел равно n 2 — то есть, что (1. ) 1 + 3 + 5 +⋯+ (2 n − 1) = n 2 для каждого положительного целого числа n . Пусть F будет классом целых чисел, для которых выполняется уравнение (1.) ; тогда целое число 1 принадлежит F , так как 1 = 1 2 . Если любое целое число x принадлежит F , то (2.) 1 + 3 + 5 +⋯+ (2 х — 1) = х 2 .
Следующее нечетное целое число после 2 x — 1 равно 2 x + 1, и, если прибавить его к обеим частям уравнения (2.) , получится (3.) 1 + 3 + 5 +⋯+ (2 x + 1) = x 2 + 2 x + 1 = ( x + 1) 2 Уравнение (2.) называется гипотезой индукции и утверждает, что уравнение (1.) выполняется, когда n равно x , а уравнение (3.
) 1 + 3 + 5 +⋯+ (2 n − 1) = n 2 для каждого положительного целого числа n . Пусть F будет классом целых чисел, для которых выполняется уравнение (1.) ; тогда целое число 1 принадлежит F , так как 1 = 1 2 . Если любое целое число x принадлежит F , то (2.) 1 + 3 + 5 +⋯+ (2 х — 1) = х 2 .
Следующее нечетное целое число после 2 x — 1 равно 2 x + 1, и, если прибавить его к обеим частям уравнения (2.) , получится (3.) 1 + 3 + 5 +⋯+ (2 x + 1) = x 2 + 2 x + 1 = ( x + 1) 2 Уравнение (2.) называется гипотезой индукции и утверждает, что уравнение (1.) выполняется, когда n равно x , а уравнение (3. ) утверждает, что уравнение (1.) выполняется, когда n + равно 9064 уравнение 44 ( 3.) было доказано как следствие уравнения (2.) , было доказано, что каждый раз, когда x принадлежит F , преемник x принадлежит F . Следовательно, по принципу математической индукции все натуральные числа принадлежат Ф .
) утверждает, что уравнение (1.) выполняется, когда n + равно 9064 уравнение 44 ( 3.) было доказано как следствие уравнения (2.) , было доказано, что каждый раз, когда x принадлежит F , преемник x принадлежит F . Следовательно, по принципу математической индукции все натуральные числа принадлежат Ф .
Вышеизложенное является примером простой индукции; иллюстрацией многих более сложных видов математической индукции является следующий метод доказательства с помощью двойной индукции. Чтобы доказать, что конкретное бинарное отношение F выполняется среди всех положительных целых чисел, достаточно сначала показать, что отношение F выполняется между 1 и 1; во-вторых, всякий раз, когда F находится между x и y , оно удерживается между x и и + 1; и в-третьих, всякий раз, когда F находится между x и некоторым положительным целым числом z (которое может быть фиксированным или может зависеть от x ), оно находится между x + 1 и 1.
Логический статус метода доказательства с помощью математической индукции до сих пор вызывает разногласия среди математиков. Джузеппе Пеано включил принцип математической индукции в число своих пяти аксиом арифметики. Многие математики соглашаются с Пеано в том, что этот принцип рассматривается лишь как один из постулатов, характеризующих определенную математическую дисциплину (арифметику) и ничем принципиально не отличающийся от других постулатов арифметики или других разделов математики.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Анри Пуанкаре утверждал, что математическая индукция является синтетической и априорной, то есть она не сводится к принципу логики или не доказуема только на логических основаниях и тем не менее познается независимо от опыта или наблюдения. Таким образом, математическая индукция занимает особое место как составляющая математического рассуждения par excellence и позволяет математике перейти от своих предпосылок к действительно новым результатам, что якобы невозможно с помощью одной лишь логики.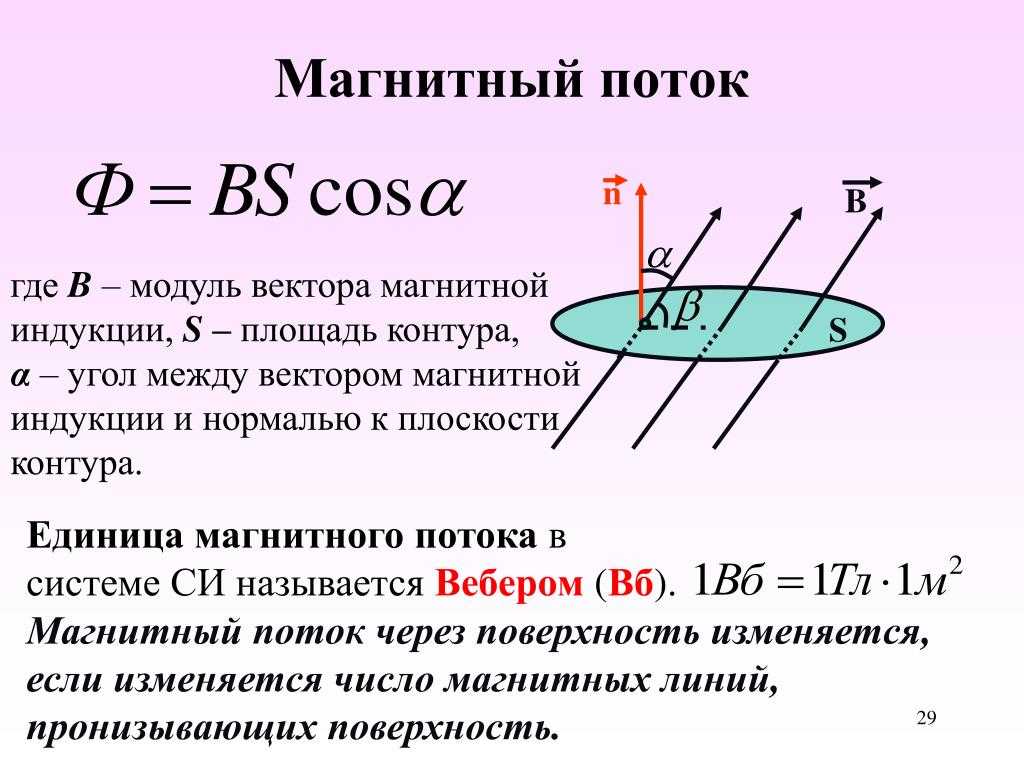 В этой доктрине за Пуанкаре последовала школа математического интуитивизма, которая рассматривает математическую индукцию как высшую основу математического мышления, несводимую ни к чему предшествующему и априорно синтетическую в смысле Иммануила Канта.
В этой доктрине за Пуанкаре последовала школа математического интуитивизма, которая рассматривает математическую индукцию как высшую основу математического мышления, несводимую ни к чему предшествующему и априорно синтетическую в смысле Иммануила Канта.
Прямо противоположно этому намерение Готтлоба Фреге, за которым позже последовали Альфред Норт Уайтхед и Бертран Рассел в Principia Mathematica , показать, что принцип математической индукции является аналитическим в том смысле, что он сводится к принципу чистой логики. подходящим определением используемых терминов.
Трансфинитная индукция
Обобщение математической индукции, применимое к любому хорошо упорядоченному классу или области D вместо области положительных целых чисел, является методом доказательства трансфинитной индукцией. Домен D считается хорошо упорядоченным, если принадлежащие ему элементы (числа или объекты любого другого вида) расположены или были расположены в таком порядке, что: 1. ни один элемент не предшествует себя в порядке; 2. если x предшествует y по порядку, и y предшествует z , то x предшествует z ; 3. в каждом непустом подклассе D есть первый элемент (тот, который предшествует всем остальным элементам в подклассе). От 3. следует, в частности, что сам домен D , если он не пустой, имеет первый элемент.
ни один элемент не предшествует себя в порядке; 2. если x предшествует y по порядку, и y предшествует z , то x предшествует z ; 3. в каждом непустом подклассе D есть первый элемент (тот, который предшествует всем остальным элементам в подклассе). От 3. следует, в частности, что сам домен D , если он не пустой, имеет первый элемент.
Когда элемент x предшествует элементу y в только что описанном порядке, можно также сказать, что y следует за x . Преемник элемента x упорядоченного домена D определяется как первый элемент, следующий за x (поскольку по 3. , если есть какие-либо элементы, следующие за x , среди них должен быть первый). Точно так же преемник класса E элементов D является первым элементом, который следует за всеми элементами E . Класс F элементов D называется наследственным, если всякий раз, когда все члены класса E элементов D принадлежат F , преемник E , если таковой имеется, также принадлежит до F (и, следовательно, в частности, всякий раз, когда элемент x из D принадлежит F , преемник x , если таковой имеется, также принадлежит F ). Доказательство с помощью трансфинитной индукции тогда зависит от принципа, что если первый элемент хорошо упорядоченной области D принадлежит наследственному классу F , то все элементы D принадлежат F .
Класс F элементов D называется наследственным, если всякий раз, когда все члены класса E элементов D принадлежат F , преемник E , если таковой имеется, также принадлежит до F (и, следовательно, в частности, всякий раз, когда элемент x из D принадлежит F , преемник x , если таковой имеется, также принадлежит F ). Доказательство с помощью трансфинитной индукции тогда зависит от принципа, что если первый элемент хорошо упорядоченной области D принадлежит наследственному классу F , то все элементы D принадлежат F .
Один из способов рассмотрения математической индукции состоит в том, чтобы рассматривать ее как частный случай трансфинитной индукции. Например, есть смысл, в котором простая индукция может рассматриваться как трансфинитная индукция, примененная к области D натуральных чисел. Фактическое сведение простой индукции к этому частному случаю трансфинитной индукции требует использования принципов, которые сами по себе обычно доказываются математической индукцией, особенно упорядочения положительных целых чисел и принципа, согласно которому преемник класса положительных целых чисел, если существует равно единице, должно быть преемником определенного целого числа (последнего или наибольшего целого числа) в классе.






 Пам’ятай про круглi дужки!)
Пам’ятай про круглi дужки!)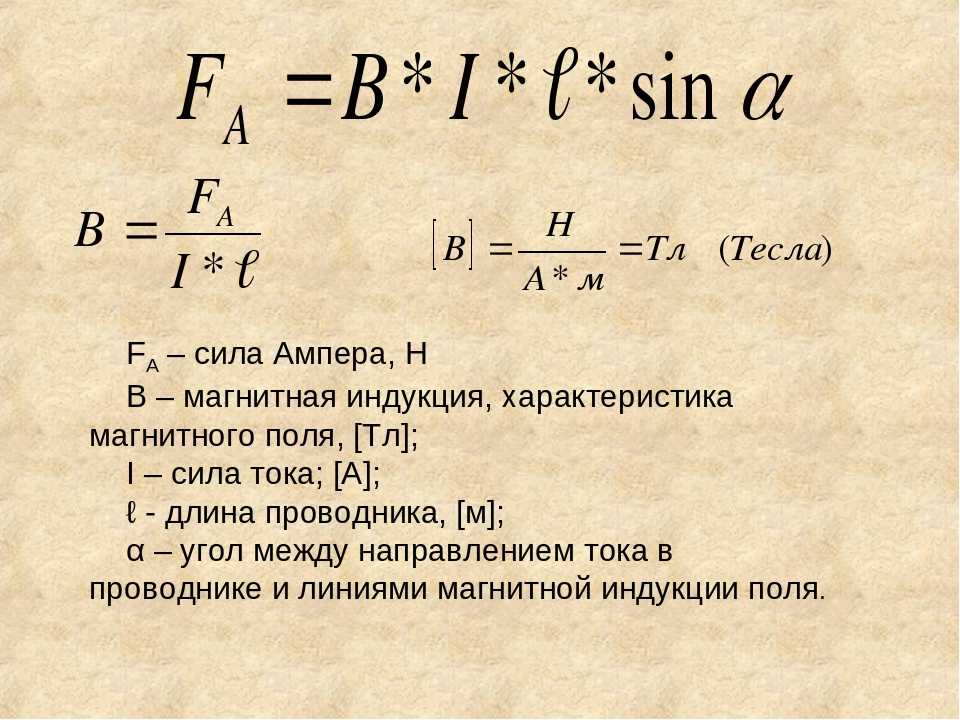 / 27
/ 27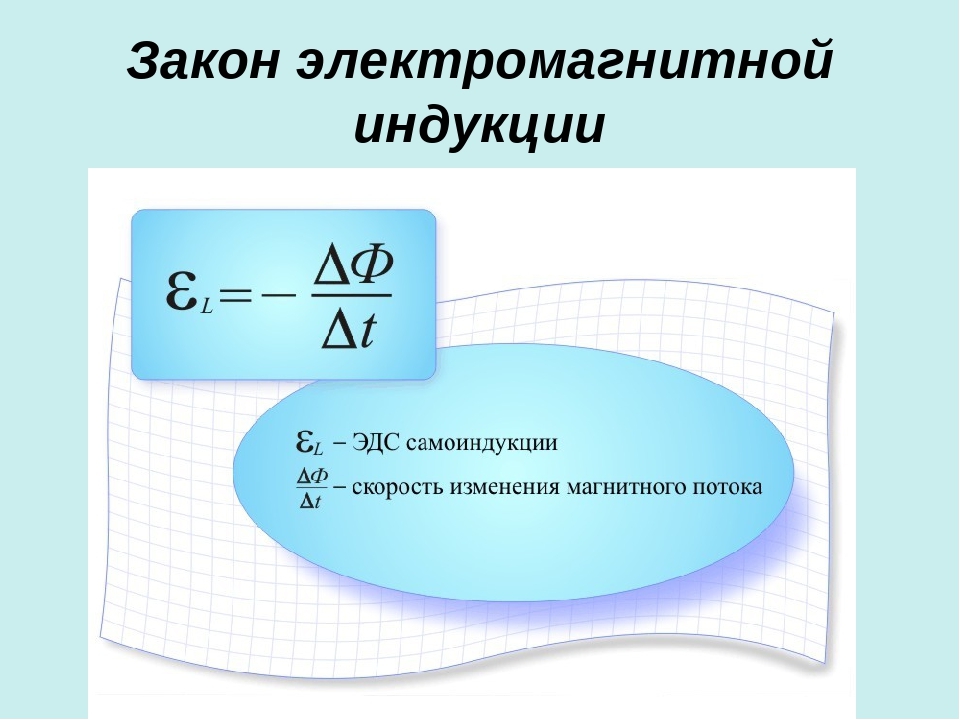 Первые 9 0007 домино падает
Первые 9 0007 домино падает