примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Пример 2Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102 Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Пример 2Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102 Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Пример 2Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
#11. Произведение матриц и векторов, элементы линейной алгебры
Смотреть материал на видео
Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую:
a = np.arange(1, 10).reshape(3, 3) b = np.arange(10, 19).reshape(3, 3) a*b
В консоли увидим результат:
array([[
10, 22, 36],
[ 52, 70, 90],
[112, 136,
162]])
Матричное умножение
Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:
то для этого
следует использовать специальные функции и операторы. Начнем с функций. Итак,
чтобы перемножить две матрицы a иbпо всем правилам
математики, запишем следующую команду:
Начнем с функций. Итак,
чтобы перемножить две матрицы a иbпо всем правилам
математики, запишем следующую команду:
np.dot(a, b)
Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:
array([[ 84, 90, 96],
[201,
216, 231],
[318, 342,
366]])
Тот же результат можно получить и с помощью функции:
np.matmul(a, b)
Считается, что этот вариант предпочтительнее использовать при умножении матриц.
Векторное умножение
Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:
то их умножение можно реализовать в двух видах:
и
Первое умножение реализуется либо через функцию:
a = np.arange(1, 10) b = np.ones(9) np.dot(a, b) # значение 45
Либо, более предпочтительной функцией для внутреннего умножения векторов:
np.inner(a, b) # 45
Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:
np.outer(a, b)
получим результат в виде следующей матрицы:
array([[1.,
1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[7., 7., 7., 7., 7., 7., 7., 7., 7.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])
Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:
a @ b # значение 45
или, с использованием матриц:
a.resize(3, 3) b.resize(3, 3) a @ b # аналог np.matmul(a, b)
Умножение вектора на матрицу
Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:
или
Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:
a = np.array([1,2,3]) b = np.arange(4,10).reshape(3,2) # матрица 3x2
И, затем, воспользуемся уже знакомой нам функцией dot:
np.dot(a, b) # array([40, 46])
При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.
Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:
np.dot(b, a) # несогласованность размеров
Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:
Определим массивa в два элемента и умножим на матрицу b:
a = np.array([1, 2]) np.dot(b, a) # array([14, 20, 26])
Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде:
a.shape = -1, 1 # вектор-столбец 2x1
Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:
np.dot(b, a) # вектор-столбец 3x1
Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):
a @ b # вектор-столбец 3x1
Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.
Элементы линейной алгебры
Из высшей
математики хорошо известно, что матрицы можно использовать для решения систем
линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте
рассмотрим некоторые из его функций.
Для этого в NumPyсуществует модуль linalg. Давайте
рассмотрим некоторые из его функций.
Предположим, имеется квадратная матрица 3×3:
a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])
Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:
np.linalg.matrix_rank(a) # рангравен 3
Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:
Здесь - некие числа линейного уравнения. Например, возьмем их равными:
y = np.array([10, 20, 30])
Тогда корни уравнения можно вычислить с помощью функции solve:
np.linalg.solve(a, y) # array([-5. , 10. , -1.66666667])
Другой способ
решения этой же системы линейных уравнений возможен через вычисление обратной
матрицы. Изначально, уравнение можно записать в векторно-матричном виде:
Изначально, уравнение можно записать в векторно-матричном виде:
Откуда получаем решения :
На уровне пакета NumPy это делается так:
invA = np.linalg.inv(a) # вычисление обратной матрицы invA @ y # вычисление корней
Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.
|
Функция |
Описание |
|
linalg.cholesky() |
Разложение Холецкого |
|
linalg. |
QR-разложение матрицы |
|
linalg.svd() |
Сингулярное (SVD) разложение матрицы |
|
linalg.norm() |
Норма матрицы или вектора |
|
linalg.cond() |
Число обусловленности матрицы |
|
linalg.det() |
Определитель (детерминант) матрицы |
|
linalg.matrix_rank() |
Вычисление ранга матрицы по алгоритму SVD |
|
np.trace() |
Сумма диагональных элементов массива |
|
linalg. |
Вычисление собственных значений и правых собственных векторов |
|
linalg.eigvals() |
Вычисление собственных значений матрицы |
|
linalg.solve() |
Решение линейного матричного уравнения |
|
linalg.tensorsolve() |
Решение линейного тензорного уравнения |
|
linalg.lstsq() |
Решает задачу поиска наименьших квадратов для линейного матричного уравнения |
|
linalg.inv() |
Вычисление обратной матрицы |
|
linalg. |
Вычисление псевдообратной (Мура-Пенроуза) матрицы |
|
linalg.tensorinv() |
Вычисление обратного тензора (N-мерного массива) |
Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:
https://numpy.org/doc/stable/
Видео по теме
#1. Пакет numpy — установка и первое знакомство | NumPy уроки
#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки
#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки
#4. Свойства и представления массивов, создание их копий | NumPy уроки
#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки
#6. Объединение и разделение массивов | NumPy уроки
Объединение и разделение массивов | NumPy уроки
#7. Индексация, срезы, итерирование массивов | NumPy уроки
#8. Базовые математические операции над массивами | NumPy уроки
#9. Булевы операции и функции, значения inf и nan | NumPy уроки
#10. Базовые математические функции | NumPy уроки
#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки
#12. Множества (unique) и операции над ними | NumPy уроки
#13. Транслирование массивов | NumPy уроки
Векторы и матрицы в квантовых вычислениях — Azure Quantum
- Статья
- Чтение занимает 5 мин
Для понимания квантовых вычислений нужно хотя бы в общих чертах разбираться в векторах и матрицах. {*} v_n.
$$
{*} v_n.
$$
Такая нотация позволяет выразить норму вектора $v$ как $\sqrt{\langle v, v\rangle}$.
При умножении вектора на число $c$ мы получим новый вектор, все элементы которого умножены на $c$. При сложении двух векторов $u$ и $v$ мы получим новый вектор, все элементы которого являются суммами соответствующих элементов $u$ и $v$. К этим операциям относятся:
$$\mathrm{Если}~u =\begin{bmatrix} u_1\\ u_2\\ \vdots\\ u_n \end{bmatrix}~\mathrm{and}~ v =\begin{bmatrix} v_1\\ v_2\\ \vdots\\ v_n \end{bmatrix},~\mathrm{то}~ au+bv =\begin{bmatrix} au_1+bv_1\\ au_2+bv_2\\ \vdots\\ au_n+bv_n \end{bmatrix}. $$
Матрица размером $m \times n$ представляет собой набор из $mn$ комплексных чисел, организованных в $m$ строк и $n$ столбцов, как показано ниже:
$$M =\begin{bmatrix} M_{11}~~ M_{12}~~\cdots~~ M_{1n}\\ M_{{21}~~ M_{22}~~\cdots~~ M_{2n}\\\ddots\\ M_{m1}~~ M_{m2}~~\cdots~~ M_{mn}\\\end{bmatrix}.$$
Обратите внимание, что вектор с размерностью $n$ полностью идентичен матрице $n \times 1$.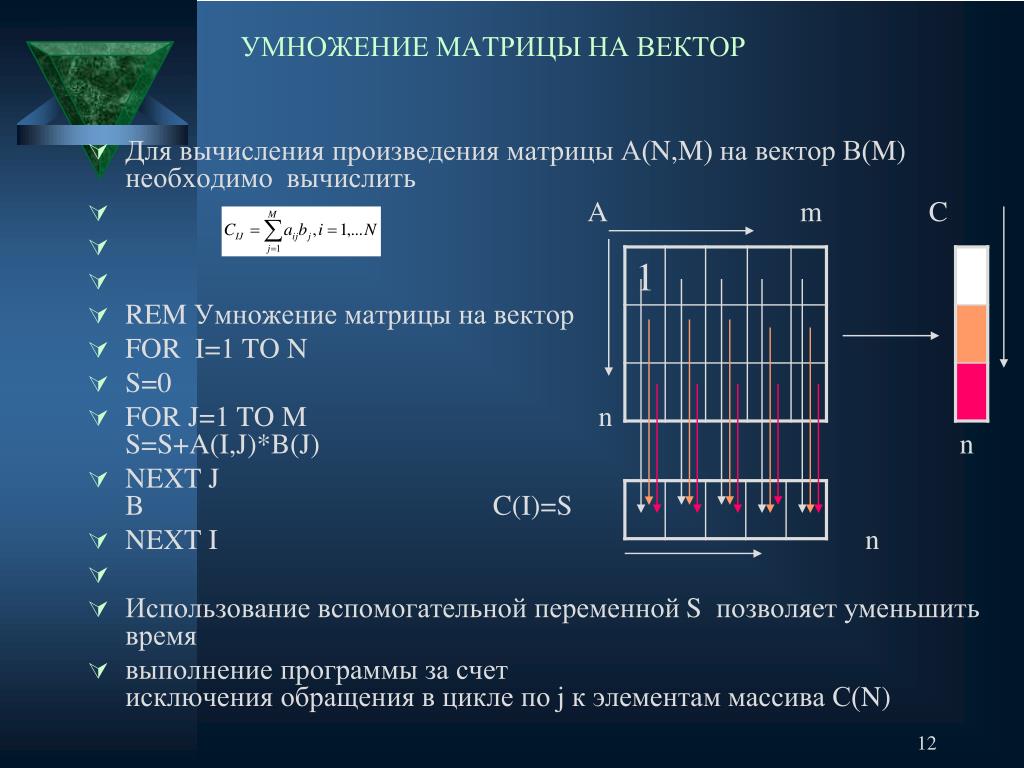 Как и для векторов, при умножении матрицы на число $c$ мы получим новую матрицу, в которой все элементы умножены на $c$, а при сложении двух матриц одинаковых размеров мы получим новую матрицу, все элементы которой являются суммой соответствующих элементов двух исходных матриц.
Как и для векторов, при умножении матрицы на число $c$ мы получим новую матрицу, в которой все элементы умножены на $c$, а при сложении двух матриц одинаковых размеров мы получим новую матрицу, все элементы которой являются суммой соответствующих элементов двух исходных матриц.
Умножение матриц
При умножении двух матриц $M$ с размером $m\times n$ и $N$ с размером $n \times p$ мы получим новую матрицу $P$ с размером $m \times p$ по такой формуле:
\begin{\begin{align}&\begin{bmatrix} M_{{11}~~ M_{12}~~\cdots~~ M_{1n}\\ M_{21}~~ M_{22}~~\cdots~~ M_{2n}\\\ddots\\ M_{m1}~~ M_{m2}~~\cdots~~ M_{mn}\end{bmatrix}\begin{bmatrix} N_{{11}~~ N_{12}~~\cdots~~ N_{1p}\\ N_{{21}~~ N_{{22}~~\cdots~~ N_{2p}\\\ddots\\ N_{n1}~~ N_{n2}~~\cdots~~ N_{np}\end{bmatrix}=\begin{bmatrix} P_{{11}~~ P_{{12}~~\cdots~~ P_{1p}\\ P_{{21}~~ P_{22}~~\cdots~~ P_{2p}\\\ddots\\ P_{m1}~~ P_{m2}~~\cdots~~ P_{mp}\end{bmatrix}\end{align}
где элементы $P$ обозначены как $P_{ik}=\sum_j M_{ij}N_{jk}$. Например, элемент $P_{11}$ является скалярным произведением первой строки $M$ и первого столбца $N$. \dagger$.
\dagger$.
Тензорное произведение
Еще одной важной операцией является кронекерово произведение, также именуемое прямым произведением матриц или тензорным произведением. Обратите внимание, что кронекерово произведение коренным образом отличается от обычного умножения матриц. В теории квантовых вычислений для обозначения кронекерового произведения широко применяется термин тензорное произведение.
Для примера рассмотрим два вектора $v=\begin{bmatrix}a \\ b \end{bmatrix}$ и $u =\begin{bmatrix} c \\ d \\ e \end{bmatrix}$. Тензорное произведение этих векторов обозначается как $v \otimes u$, а его результатом является блочная матрица. $$\begin{bmatrix} a \\ b \end{bmatrix}\otimes\begin{bmatrix} c \\ d \\ e \end{bmatrix}=\begin{bmatrix} a \begin{bmatrix} c \\ d \\ e \end{bmatrix}\\[1.5em] b \begin{bmatrix} c \\ d \\ e\end{bmatrix}\end{bmatrix}=\begin{bmatrix} a c \\ a d \\ a e \\ b c \\ b d \\ be\end{bmatrix}$$
Обратите внимание, что операцию для получения тензорного произведения можно применить к любым матрицам и (или) векторам произвольных размеров.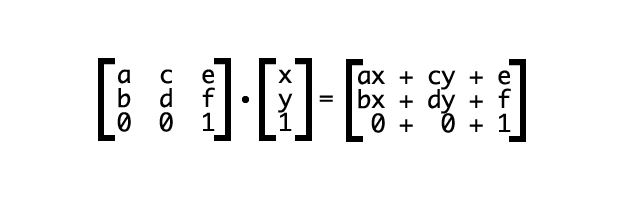 Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле:
Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле:
\begin{align} M \otimes N &=\begin{bmatrix} M_{11}~~\cdots~~ M_{1n}\\\ddots\\ M_{m1}~~\cdots~~ M_{mn}\end{bmatrix}\otimes\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\\&=\begin{bmatrix} M_{{11}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}~~\cdots~~ M_{1n}\begin{bmatrix} N_{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\\\ddots\\ M_{m1}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}~~\cdots~~ M_{mn}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\end{bmatrix}. \end{align}
Лучше всего продемонстрировать это на конкретном примере: $$\begin{bmatrix} a\ b \\ c\ d \end{bmatrix}\otimes\begin{bmatrix} e\ f\\g\ h \end{bmatrix}=\begin{bmatrix} a\begin{bmatrix} e\ f\\ g\ h \end{bmatrix} b\begin{bmatrix} e\ f\\ g\ h \end{bmatrix}\\[1em] c\begin{bmatrix} e\ f\\ g\ h \end{bmatrix} d\begin{bmatrix} e\ f\\ g\ h \end{bmatrix}\end{bmatrix}=\begin{bmatrix} ae\ af\ be\ bf \\ ag\ ah\ bg\ bh \\ ce\ cf\ de\ df \\ cg\ ch\ dg\ dh \end{bmatrix}. {\otimes 2}=\begin{bmatrix} 0 &0&0&1 \\ 0 &0&1&0 \\ 0 &1&0&0\\ 1 &0&0&0\end{bmatrix}.
\end{align}
{\otimes 2}=\begin{bmatrix} 0 &0&0&1 \\ 0 &0&1&0 \\ 0 &1&0&0\\ 1 &0&0&0\end{bmatrix}.
\end{align}
Next Steps
- Расширенные концепции матриц
- Кубит в квантовых вычислениях
- Операции с несколькими кубитами
- Нотация Дирака
- Измерения Паули
- Квантовые схемы
- Квантовые оракулы
Умножение комплексного вектора на матрицу
|
|
|
|||||||||||||||||||||||||||||||||||
Умножение матриц и векторов — Math Insight
Произведение матриц и векторов
Для определения умножения между матрицей $A$ и вектором $\vc{x}$
(т. е. произведение матрицы на вектор), нам нужно просмотреть вектор
как матрица-столбец.
Определим матрично-векторное произведение только для случая, когда число
столбцов в $A$ равно количеству строк в $\vc{x}$. Итак, если $A$
матрица $m \times n$ (т.е. с $n$ столбцами), то произведение $A
\vc{x}$ определено для $n \times 1$ векторов-столбцов $\vc{x}$. Если мы
пусть $A \vc{x} = \vc{b}$, тогда $\vc{b}$ — столбец $m \times 1$
вектор. Другими словами, количество строк в $A$ (которое может быть
что угодно) определяет количество строк в произведении $\vc{b}$.
е. произведение матрицы на вектор), нам нужно просмотреть вектор
как матрица-столбец.
Определим матрично-векторное произведение только для случая, когда число
столбцов в $A$ равно количеству строк в $\vc{x}$. Итак, если $A$
матрица $m \times n$ (т.е. с $n$ столбцами), то произведение $A
\vc{x}$ определено для $n \times 1$ векторов-столбцов $\vc{x}$. Если мы
пусть $A \vc{x} = \vc{b}$, тогда $\vc{b}$ — столбец $m \times 1$
вектор. Другими словами, количество строк в $A$ (которое может быть
что угодно) определяет количество строк в произведении $\vc{b}$.
Общая формула для матрично-векторного произведения:
\начать{выравнивать*}
А\ВК{х}=
\оставил[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{с}
х_1\\
х_2\\
\vdots\\
х_n
\конец{массив}
\Правильно]
знак равно
\оставил[
\начать{массив}{с}
a_{11}x_1+a_{12}x_2 + \cdots + a_{1n} x_n\\
a_{21}x_1+a_{22}x_2 + \cdots + a_{2n} x_n\\
\vdots\\
a_{m1}x_1+a_{m2}x_2 + \cdots + a_{mn} x_n\\
\конец{массив}
\Правильно]. \конец{выравнивание*}
Хотя поначалу это может показаться запутанным, процесс матрично-векторного
умножение на самом деле очень просто. Берется скалярное произведение
$\vc{x}$ с каждой строкой $A$. (Вот почему количество
столбцов в $A$ должно быть равно количеству компонентов в $\vc{x}$.)
первый компонент матрично-векторного произведения является скалярным произведением
$\vc{x}$ с первой строкой $A$ и т. д. На самом деле, если $A$ имеет только один
row, произведение матрицы на вектор на самом деле является замаскированным точечным произведением.
\конец{выравнивание*}
Хотя поначалу это может показаться запутанным, процесс матрично-векторного
умножение на самом деле очень просто. Берется скалярное произведение
$\vc{x}$ с каждой строкой $A$. (Вот почему количество
столбцов в $A$ должно быть равно количеству компонентов в $\vc{x}$.)
первый компонент матрично-векторного произведения является скалярным произведением
$\vc{x}$ с первой строкой $A$ и т. д. На самом деле, если $A$ имеет только один
row, произведение матрицы на вектор на самом деле является замаскированным точечным произведением.
Например, если
\начать{выравнивать*}
А = \ влево[
\начать{массив}{ррр}
1 и -1 и 2\\
0 и -3 и 1
\конец{массив}
\Правильно]
\конец{выравнивание*}
и $\vc{x} = (2,1,0)$, то
\начать{выравнивать*}
A \vc{x} &= \left[
\начать{массив}{ррр}
1 и -1 и 2\\
0 и -3 и 1
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{л}
2\\1\\0
\конец{массив}
\Правильно]\\
знак равно
\оставил[
\начать{массив}{г}
2 \cdot 1 — 1\cdot 1 + 0 \cdot 2\\
2 \cdot 0 — 1 \cdot 3 +0 \cdot 1
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{г}
1\\
-3
\конец{массив}
\Правильно]. \конец{выравнивание*}
\конец{выравнивание*}
Произведение матрицы на матрицу
Поскольку мы рассматриваем векторы как матрицы-столбцы, произведение матрицы на вектор равно просто частный случай матрично-матричного произведения (т. е. произведения между двумя матрицами). Так же, как и для матрично-векторного произведения, Произведение $AB$ между матрицами $A$ и $B$ определено, только если количество столбцов в $A$ равно количеству строк в $B$. Говоря математическим языком, мы говорим, что можем умножить матрицу $m \times n$ $A$ на $n \times p$-матрицу $B$. (Если $p$ равно 1, то $B$ будет вектор-столбец $n\times 1$, и мы вернемся к матрично-векторное произведение.)
Произведение $AB$ представляет собой матрицу $m \x p$, которую мы будем называть $C$, т.е.
$АВ=С$. Чтобы вычислить произведение $B$, мы рассматриваем $B$ как группу из $n
\times 1$ векторов-столбцов, выстроенных рядом друг с другом:
\начать{выравнивать*}
\оставил[
\begin{массив}{cccc}
b_{11} & b_{12} & \ldots & b_{1p}\\
b_{21} & b_{22} & \ldots & b_{2p}\\
\vdots & \vdots & \vdots & \vdots\\
b_{n1} & b_{n2} & \ldots & b_{np}
\конец{массив}
\Правильно]
знак равно
\оставил[
\оставил[
\начать{массив}{с}
б_{11}\\
б_{21}\\
\vdots\\
b_{n1}\\
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{с}
б_{12}\\
б_{22}\\
\vdots\\
b_{n2}\\
\конец{массив}
\Правильно]
\cdots
\оставил[
\начать{массив}{с}
б_{1п}\\
б_{2п}\\
\vdots\\
b_{np}\\
\конец{массив}
\Правильно]
\Правильно]
\конец{выравнивание*}
Тогда каждый столбец таблицы $C$ является векторным произведением матрицы $A$ с
соответствующий столбец $B$. Другими словами, компонент в $i$th
строка и $j$-й столбец $C$ — это скалярное произведение между $i$-й строкой
$A$ и $j$-й столбец $B$. В математике мы пишем этот компонент
$C$ как $c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots +
a_{in}b_{nj}$.
Другими словами, компонент в $i$th
строка и $j$-й столбец $C$ — это скалярное произведение между $i$-й строкой
$A$ и $j$-й столбец $B$. В математике мы пишем этот компонент
$C$ как $c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots +
a_{in}b_{nj}$.
Пример справки делает процесс понятным. Пусть $A$ будет $2 \times 3$
матрица
\начать{выравнивать*}
А=\влево[
\начать{массив}{ррр}
0 и 4 и -2\\
-4 и -3 и 0
\конец{массив}
\Правильно]
\конец{выравнивание*}
и $B$ — матрица $3 \times 2$
\начать{выравнивать*}
B= \влево[
\begin{массив}{rr}
0 &1\\
1 и -1\\
2 и 3
\конец{массив}
\Правильно].
\конец{выравнивание*}
Затем,
\начать{выравнивать*}
АБ &=\влево[
\начать{массив}{ррр}
0 и 4 и -2\\
-4 и -3 и 0
\конец{массив}
\Правильно]
\оставил[
\begin{массив}{rr}
0 &1\\
1 и -1\\
2 и 3
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{ррр}
0 \cdot 0+4 \cdot 1-2\cdot 2 && 0 \cdot 1 +4 \cdot (-1) -2\cdot 3\\
-4 \cdot 0-3\cdot 1 + 0 \cdot 2 && -4 \cdot 1 -3 \cdot (-1) + 0\cdot 3
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{ррр}
0+4-4 && 0-4-6\\
0-3+0 && -4 +3 +0
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\begin{массив}{rr}
0 и -10\\
-3 и -1
\конец{массив}
\Правильно]. \конец{выравнивание*}
\конец{выравнивание*}
Хотите больше примеров?
Умножение матрицы на вектор — Мэтью Н. Бернштейн
5 минут чтения
Опубликовано:
Введение
В предыдущем посте мы обсуждали три способа просмотра матрицы: как таблицу значений, как список векторов и, наконец, как функцию. Это третий способ просмотра матриц, который действительно придает матрицам их силу. Здесь мы представим операцию между матрицами и векторами, называемую умножением матрицы на вектор , которая позволит нам использовать матрицы как функции.
Умножение матрицы на вектор — это операция между матрицей и вектором, в результате которой получается новый вектор. Примечательно, что умножение матрицы на вектор определяется только между матрицей и вектором, где длина вектора равна количеству столбцов матрицы. Он определяется следующим образом: 9n$ матрично-векторное умножение $\boldsymbol{A}$ и $\boldsymbol{x}$ определяется как
Примечательно, что умножение матрицы на вектор определяется только между матрицей и вектором, где длина вектора равна количеству столбцов матрицы. Он определяется следующим образом: 9n$ матрично-векторное умножение $\boldsymbol{A}$ и $\boldsymbol{x}$ определяется как
, где $\boldsymbol{a}_{*, i}$ — $i$-й вектор-столбец $\boldsymbol{A}$.
Как и большинство математических понятий, умножение матрицы на вектор можно рассматривать с разных точек зрения на разных уровнях абстракции. Эти взгляды пригодятся, когда мы попытаемся концептуализировать различные способы использования матричного умножения на вектор для моделирования реальных проблем. Ниже приведены три способа, которые я считаю полезными для концептуализации умножения матрицы на вектор в порядке от наименее к наиболее абстрактному:0005
- Как «построчный» процесс генерации вектора: Умножение матрицы на вектор определяет процесс создания нового вектора с использованием существующего вектора, где каждый элемент нового вектора «генерируется» путем взятия взвешенной суммы каждой строки матрицы с использованием элементов вектора в качестве коэффициентов
- Как взятие линейной комбинации столбцов матрицы: Умножение матрицы на вектор — это процесс взятия линейной комбинации пространства столбцов матрицы используя элементы вектора в качестве коэффициентов
- Как вычисление функции между векторными пространствами: Умножение матрицы на вектор позволяет матрице определить отображение между двумя векторными пространствами.

Я считаю полезными все три перспективы. Первые две перспективы обеспечивают способ понимания механизма умножения матрицы на вектор, тогда как третья перспектива обеспечивает суть умножения матрицы на вектор. Именно эта третья перспектива умножения матрицы на вектор позволяет нам рассматривать матрицы как функции, как мы обсуждали в предыдущем посте.
Умножение матрицы на вектор как «построчный» процесс генерации вектора
Полезный способ просмотра механизма умножения матрицы на вектор между матрицей $\boldsymbol{A}$ и вектором $\boldsymbol{x }$ заключается в том, чтобы рассматривать его как своего рода «процесс» (или даже как компьютерную программу), который создает каждый элемент выходного вектора итеративным образом, когда мы перебираем каждую строку $A$. В частности, для каждой строки $i$ матрицы $\boldsymbol{A}$ мы берем $\boldsymbol{x}$ и вычисляем скалярное произведение между $\boldsymbol{x}$ и $i$-й строкой матрицы, тем самым производя $i$-й элемент выходного вектора (см. n$, считается, что
n$, считается, что
, где $\boldsymbol{a}_{i,* }$ — это $i$-й вектор-строка в $\boldsymbol{A}$.
Доказательство:
\[\begin{align*} \boldsymbol{A}\boldsymbol{x} &:= x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{* ,2} + \dots + x_n\boldsymbol{a}_{*,n} \\ &= x_1 \begin{bmatrix}a_{1,1} \\ a_{2,1} \\ \vdots \\ a_ {m, 1} \end{bmatrix} + x_2\begin{bmatrix}a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m, 2} \end{bmatrix} + \ точки + x_n\begin{bmatrix}a_{1,n} \\ a_{2,n} \\ \vdots \\ a_{m, n} \end{bmatrix} \\ &= \begin{bmatrix}x_1a_{ 1,1} \\ x_1a_{2,1} \\ \vdots \\ x_1a_{m, 1} \end{bmatrix} + \begin{bmatrix}x_2a_{1,2} \\ x_2a_{2,2} \ \ \vdots \\ x_2a_{m, 2} \end{bmatrix} + \dots + \begin{bmatrix}x_na_{1,n} \\ x_na_{2,n} \\ \vdots \\ x_na_{m, n } \end{bmatrix} \\ &= \begin{bmatrix} x_1a_{1,1} + x_2a_{1,2} + \dots + x_na_{1,n} \\ x_1a_{2,1} + x_2a_{2 ,2} + \dots + x_na_{2,n} \\ \vdots \\ x_1a_{m,1} + x_2a_{m,2} + \dots + x_na_{m,n} \\ \end{bmatrix} \ \ &= \begin{bmatrix} \sum_{i=1}^n a_{1,i}x_i \\ \sum_{i=1}^n a_{2,i}x_i \\ \vdots \\ \sum_ {i=1}^n a_{m,i}x_i \\ \end{bmatrix} \\ &= \begin{bma trix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a }_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\end{align*}\]$\square$
Теги: линейная алгебра, линейное преобразование, математика, матрицы, учебник
Умножение вектора на матрицу
Горячая математика Чтобы умножить вектор-строку на вектор-столбец, вектор-строка должен иметь столько столбцов, сколько строк имеет вектор-столбец.
Определим произведение матрицы А и вектор Икс в котором количество столбцов в А равно количеству строк в Икс .
Так что если А является м × н матрица, то произведение А Икс определяется для н × 1 столбцы векторов Икс . Если мы позволим А Икс знак равно б , тогда б является м × 1 вектор-столбец. Другими словами, количество строк в А определяет количество рядов в изделии б .
Общая формула для матрично-векторного произведения:
А Икс знак равно [ а 11 а 12 ⋯ а 1 н а 21 а 22 ⋯ а 2 н ⋮ ⋮ ⋮ ⋮ а м 1 а м 2 ⋯ а м н ] [ Икс 1 Икс 2 ⋮ Икс н ] знак равно [ а 11 Икс 1 + а 12 Икс 2 + ⋯ + а 1 н Икс н а 21 Икс 1 + а 22 Икс 2 + ⋯ + а 2 н Икс н ⋮ а м 1 Икс 1 + а м 2 Икс 2 + ⋯ + а м н Икс н ]
Пример :
Находить
А
у
куда
у
знак равно
[
2
1
3
]
а также
А
знак равно
[
1
2
3
4
5
6
7
8
9
]
.
По определению количество столбцов в А равно количеству строк в у .
А у знак равно [ 1 2 3 4 5 6 7 8 9 ] [ 2 1 3 ]
Сначала умножьте ряд 1 матрицы по столбцу 1 вектора.
[ 1 2 3 ] [ 2 1 3 ] знак равно [ 1 ⋅ 2 + 2 ⋅ 1 + 3 ⋅ 3 ] знак равно 13
Далее умножить ряд
2
матрицы по столбцу
1
вектора.
[ 4 5 6 ] [ 2 1 3 ] знак равно [ 4 ⋅ 2 + 5 ⋅ 1 + 6 ⋅ 3 ] знак равно 31
Наконец, умножьте ряд 3 матрицы по столбцу 1 вектора.
[ 7 8 9 ] [ 2 1 3 ] знак равно [ 7 ⋅ 2 + 8 ⋅ 1 + 9 ⋅ 3 ] знак равно 49
Записав произведение матрицы на вектор, мы получим:
А у знак равно [ 13 31 49 ]
Загрузите наши бесплатные приложения для обучения и книги для подготовки к экзаменам
Умножение вектора
Умножение вектора на вектор дает интересные результаты. известный как векторный внутренний продукт и как векторный внешний продукт.
известный как векторный внутренний продукт и как векторный внешний продукт.
Требование: Этот материал предполагает знакомство с умножение матриц.
Внутреннее произведение вектора
Предположим, что a и b равны векторы, каждый с одинаковым количеством элементов. Затем внутренний продукт из и и б это с .
а’ б = b’ a = с
где
а и б — векторы-столбцы,
каждый из n элементов,
a’ является транспонированием a , что делает a’ вектор-строка,
b’ является транспонированием b , что делает b’ вектор-строка и
s — скаляр; то есть s — это действительное число, а не матрица.
Обратите внимание на этот интересный результат. Произведение двух матриц обычно другая матрица. Однако внутренний продукт двух векторов различен. В результате получается действительное число, а не матрица. Это показано ниже.
| A = | B = |
Then
9000. 10 + 18 = 32
Таким образом, внутренний продукт a’ b равен равно 32.
Примечание. Внутренний продукт также известен как скалярное произведение или как скалярное произведение .
Реклама
Векторный внешний продукт
Предположим, что a и b являются векторы. Затем внешний продукт из и и б это С .
а b’ = С
где
a — вектор-столбец, содержащий м элементов,
b — вектор-столбец, содержащий n элементов,
b’ является транспонированием b , что делает б’ вектор-строка и
C представляет собой прямоугольник m x n матрица
В отличие от внутреннего произведения, внешнее произведение двух векторов дает
прямоугольная матрица, а не скаляр. Это показано ниже.
Это показано ниже.
| A = | B = |
THEN,
THEN,
.0269
| v * x | v * y | v * z | ||
| w * x | w * y | w * z |
Notice that the элементы Matrix C состоят из произведение элементов из Vector A , скрещенных с элементы из Vector B . Таким образом, Matrix C оказывается матрицей перекрестных произведений двух векторов.
Проверьте свое понимание
Проблемы
Рассмотрим векторы, показанные ниже — a , b , и c
Используя a , b и c ,
ответить на вопросы ниже.
1. Найти a’ b ,
внутренний продукт a и b .
2. Найдите b c’ ,
внешний продукт b и c .
3. Верно или неверно: б в’ = c b’
Решения
что равно 3. Решение приведено ниже.
a’ b = * a’ b = 0*2 + 1*3 = 3 Термин b c’ является внешним продуктом. Вот матрица 2 x 3, как показано ниже.
b c’ = * b c’ = 2*4 2 *5 2*6 3*4 3*5 3*6 = 8 10 12 12 15 18 The statement b с’ = с b’ ложно.

Обратите внимание, что b является вектором 2 x 1, а c представляет собой вектор 3 x 1. Следовательно, б с’ представляет собой матрицу 2 x 3, а c b’ представляет собой Матрица 3 х 2. Потому что b c’ и c b’ отличаются Габаритные размеры, они не могут быть равны.
Последний урок Следующий урок
Умножение матрицы на вектор
Видео академии Хана выше называет внутренний продукт просто скалярным произведением и использует обозначение
x.yвместоНачиная с
, яшироко используется в качестве указателя в этом примечании.видео на самом деле является 2D-DFT, а не точно таким же DFT, как определено выше.

Я намеренно не даю понять, что именно я имею в виду под цифрами. Но для этого раздела подойдет практически любой разумный набор чисел (например, целые числа, действительные числа, комплексные числа). Если вы спросите, множество чисел, для которых выполняется этот закон (плюс некоторые другие требования), называется полукольцом 9.0670 .
Если проблема кажется слишком эзотерической, просто держитесь за своих (оценочных) лошадей. Вскоре мы увидим, что эта сумма произведений соответствует очень естественной задаче.
Для этой заметки мы будем предполагать, что числа достаточно малы, так что все основные операции (сложение, умножение, вычитание и деление) занимают постоянное время.
В этой заметке мы будем работать с матрицами и векторами. Проще говоря, матрицы — это двумерные массивы, а векторы — одномерные массивы (или «обычное» понятие массивов). Мы будем использовать нотацию, совместимую с нотацией массива. Так, например. матрица $\mathbf{A}$ с $m$ строками и $n$ столбцами (также обозначаемая как матрица $m\times n$) будет в коде определена как
Так, например. матрица $\mathbf{A}$ с $m$ строками и $n$ столбцами (также обозначаемая как матрица $m\times n$) будет в коде определена как int [][] A = new int[m][n] (при условии, что матрица хранит целые числа). Также вектор $\mathbf{x}$ размера $n$ в коде будет объявлен как int [] x = new int[n] (опять же при условии, что вектор содержит целые числа). Чтобы соответствовать обозначениям массива, мы будем обозначать запись в $\mathbf{A}$, соответствующую $i$-й строке и $j$-му столбцу, как $A[i][j]$ (или A[ я][j] ). Точно так же $i$-я запись в векторе $\mathbf{x}$ будет обозначаться как $x[i]$ (или x[i] ). Мы будем следовать соглашению о массивах, предполагая, что индексы $i$ и $j$ начинаются с $0$.
Если вы хотите освежить знания о матрицах, вы можете начать с этого видео Академии Хана (хотя, если вы знакомы с приведенной выше аналогией с массивом, вам не нужно больше для этой заметки):
Умножение матрицы на вектор
Даны $n\times n$ матрица $\mathbf{A}$ и вектор $\mathbf{x}$ длины $n$, их произведение обозначается
\[\mathbf{y} =\mathbf{A}\cdot \mathbf{x},\]
где $\mathbf{y}$ также является вектором длины $n$, а его $i$-й элемент для $0\le i\lt n$ определяется следующим образом:
\[y_i =\sum_{j=0}^{n-1} A[i][j]\cdot x[j]. \]
\]
Упрощение
Обратите внимание, что в приведенном выше определении задачи у нас одинаковое количество строк и столбцов, т. е. $m=n$. Я использую это упрощение, чтобы уменьшить количество переменных, которые нужно держать в голове. Большинство рассуждений в этой заметке можно довольно легко обобщить на случай $m\neq n$.
Если вы еще не видели эту операцию, в этом видео Академии Хана есть несколько примеров (или прочитайте следующий раздел): 9{n-1} х[я]\cdot у[я].\]
Ниже приведена анимация, показывающая скалярное произведение двух случайных векторов размера $n=6$ (нажмите «Далее», чтобы продолжить вычисление внутреннего произведения: анимация начинается с двух новых случайных векторов, если «Далее» нажата после того, как внутренний продукт уже был вычислен):
Вооружившись определением скалярного произведения, вот эквивалентное определение задачи умножения матрицы на вектор:
Умножение матрицы на вектор (переопределено)
Для матрицы $\mathbf{A}$ размером $n\times n$ и вектора $\mathbf{x}$ длины $n$ их произведение $\mathbf{y }=\mathbf{A}\cdot\mathbf{x}$ также можно определить следующим образом. Его $i$-я запись для $0\le i\lt n$ определяется следующим образом:
\[y_i =\left\langle \mathbf{A}[i],\mathbf{x}\right\rangle,\]
где $\mathbf{A}[i]$ обозначает $i$-ю строку $\mathbf{A}$.
Его $i$-я запись для $0\le i\lt n$ определяется следующим образом:
\[y_i =\left\langle \mathbf{A}[i],\mathbf{x}\right\rangle,\]
где $\mathbf{A}[i]$ обозначает $i$-ю строку $\mathbf{A}$.
Ниже приведен один пример умножения матрицы на вектор: \[ \begin{pmatrix} 1 и 2 и -3\\ 2 и 9 &0\\ 6 и -1 и -2 \end{pматрица} \ раз \begin{pматрица} 2\\ 3\\ -1 \end{pматрица} знак равно \begin{pматрица} 1\умножить на 2 + 2\умножить на 3 + (-3)\раз(-1)\\ 2\умножить на 2+ 9\умножить на 3+0\раз (-1)\\ 6\умножить на 2+(-1)\умножить на 3+ (-2)\раз(-1) \end{pматрица} знак равно \begin{pmatrix} 11\\ 31\\ 11 \end{pматрица}. \] 92)$ время. Проиллюстрируем этот момент конкретным семейством структурированных матриц:
Внешний продукт
Для двух векторов $\mathbf{s}$ и $\mathbf{t}$ их внешний продукт определяется как $n\times n$ матрица $\mathbf{A}$ такая, что для любой записи $(i,j)$ имеем
\[A[i][j]=s[i]\cdot t[j]. {n-1} s[i]\cdot t[j]\cdot x[j].\]
{n-1} s[i]\cdot t[j]\cdot x[j].\]
Детали алгоритма
//Ввод: s[i], t[i], x[i] для 0 сначала
IP=0;
для (j = 0; j < n; j ++)
ip+=t[j]*x[j];
//Теперь вычисляем выходной вектор
у = новый интервал [n];
для (я = 0; я < п; я ++)
y[i] = s[i]*ip;
вернуть у;
Анализ во время выполнения остается в качестве упражнения:
Упражнение 3
Докажите, что приведенный выше алгоритм работает за время $\Theta(n)$.
Дискретное преобразование Фурье
В этом разделе мы рассмотрим, возможно, наиболее широко используемое в мире умножение матрицы на вектор: дискретное преобразование Фурье (или ДПФ). Для приложений и больше математики (чем ниже), посмотрите его страницу Википедии . Вот определение дискретного преобразования Фурье:
Дискретное преобразование Фурье
Сначала определим дискретную матрицу Фурье. $n\times n$ (дискретная) матрица Фурье $\mathbf{F}$ определяется следующим образом. {-2\pi \iota \cdot \frac{i\cdot j}{n}},\]
где $\iota$ — мнимое число. 2
{-2\pi \iota \cdot \frac{i\cdot j}{n}},\]
где $\iota$ — мнимое число. 2
Наконец, для вектора $\mathbf{x}$ длины $n$ его преобразование Фурье задается выражением \[\mathbf{F}\cdot \mathbf{x}.\]
Прежде чем углубиться в математику ДПФ, вот видео, показывающее ДПФ 3 изображения скатерти:
Игра с ДПФ может вызвать привыкание:
Не знаю почему, но мне нравится проводить преобразование Фурье повседневных вещей. Вот крышка слива. pic.twitter.com/31RqNK52bo
— Аатиш Бхатия (@aatishb) 25 августа 2015 г.Комплексное число
Как вы, должно быть, заметили, ДПФ использует комплексные числа. Вот видео о том, почему комплексные числа действительно полезны (и почему «мнимое число» — одна из PR-ошибок математики):
youtube.com/embed/-IJuqR6nz_Q" allowfullscreen="">И, извините, не удержался от этого видео на "воображаемое число Эрдоса" (пропустите, если не хотите отвлекаться):
Итак, получается, что комплексные числа, используемые в дискретной матрице Фурье, являются корнями из единицы 9m$ за время $O(nm)$.
Подсказка: Используйте предложение 1.
В этом разделе мы представим простое наблюдение, которое окажется очень полезным при разработке эффективных алгоритмов (особенно тех, которые включают сложение и умножение чисел). В частности, эту идею (правильно реализованную) можно использовать и для решения упражнения 4, приведенного выше.
Начнем с утверждения распределительного закона:
Распределительный закон
Даны три числа $a,b,c$, мы имеем 9{n-1} b_i\право).\]
Вышеизложенное означает, что вместо $n$ умножений в левой части мы можем обойтись одним умножением в правой части. {n-1} s[i]\cdot t[j]\cdot x[j]$ с помощью дистрибутивного закона. Потом мы заметили, что если бы мы сохранили "общий" терм $\left\langle \mathbf{t},\mathbf{x}\right\rangle$, то можно было бы избежать перевычисления этого терма для разных $i$. Мы резюмируем эту стратегию следующим образом:
9{n-1} б_и.\]
В дальнейшем сохраните все промежуточные результаты для возможного использования в будущем.
{n-1} s[i]\cdot t[j]\cdot x[j]$ с помощью дистрибутивного закона. Потом мы заметили, что если бы мы сохранили "общий" терм $\left\langle \mathbf{t},\mathbf{x}\right\rangle$, то можно было бы избежать перевычисления этого терма для разных $i$. Мы резюмируем эту стратегию следующим образом:
9{n-1} б_и.\]
В дальнейшем сохраните все промежуточные результаты для возможного использования в будущем.
Вычисление сумм произведений
Оказывается, стратегия дистрибутивного закона особенно хороша для эффективного вычисления сумм произведений. Вместо более формального определения того, что я имею в виду под суммами произведений, позвольте мне проиллюстрировать мою точку зрения на конкретной задаче: 5
Пример суммы произведения
Даны $n\times n$ матриц $\mathbf{A} ,\mathbf{B},\mathbf{C}$ и вектор $\mathbf{x}$ рассмотрим следующие суммы произведений. В частности, мы хотим вычислить вектор $\mathbf{y}$ такой, что для каждого $0\le i\lt n$:
\[y[i]=\sum_{j=0}^{n-1}\sum_{k=0}^{n-1}\sum_{\ell=0}^{n-1} A[i ][j]\cdot B[j][k]\cdot C[k][\ell]\cdot x[\ell]. \]
92)$.
\]
92)$.
Что здесь только что произошло?
Вернемся теперь к нерешенному вопросу о том, почему рассмотренные выше суммы произведений сами по себе являются естественным вопросом. Нетрудно заметить, что суммы произведений также можно представить в виде \[\mathbf{y}= \mathbf{A}\cdot \mathbf{B}\cdot \mathbf{C}\cdot \mathbf{x}.\] Кроме того, рассмотренный выше алгоритм в основном следует очевидному способу вычисления $\mathbf{y}$. То есть вычислить RHS как \[\ mathbf{A}\cdot \underbrace{\left(\mathbf{B}\cdot \underbrace{\left(\mathbf{C}\cdot \mathbf{x}\right)} _{\mathbf{z }}\right)}_{\mathbf{u}}.\]
Умножение правой и левой матриц | Джошуа Пикард | Geek Culture
Умножение матриц — одна из самых важных операций в математике и вычислениях. В этой статье представлены 2 лучших способа думать об умножении матриц по сравнению с тем, как вы, вероятно, его выучили.
Изображение найдено в Википедии Все сначала изучают умножение матриц, когда каждый элемент произведения вычисляется отдельно. Для A×b=c , где A — матрица, а b и c являются векторами, каждый член в c вычисляется путем умножения i -й строки A на вектор-столбец b . Члены c вычисляются по одному, что делает это быстрым и простым способом изучения умножения матриц на вектор. Однако этот метод плохо отражает структуру матричного преобразования.
Для A×b=c , где A — матрица, а b и c являются векторами, каждый член в c вычисляется путем умножения i -й строки A на вектор-столбец b . Члены c вычисляются по одному, что делает это быстрым и простым способом изучения умножения матриц на вектор. Однако этот метод плохо отражает структуру матричного преобразования.
Умножение матрицы на вектор лучше представить как линейную комбинацию строк и столбцов в А . Вместо того, чтобы вычислять каждый член в c по одному, вычисляется ряд векторов размером c , которые затем складываются вместе для получения окончательного результата. Это может дать представление о типе преобразования, которое выполняет матричное умножение. Будь то строки или столбцы A , зависит от того, на какой стороне матрицы b . В следующих разделах описываются 2 отличных подхода к умножению матриц на вектор.
Чаще всего люди умножают матрицу на вектор как A×b , где b находится на правой стороне A . Это более распространенный способ увидеть умножение, потому что он хорошо подходит для решения линейных систем, что обычно является мотивацией для матричной алгебры. Если A является матрицей m × n , так что она имеет m строк и n столбцов, то b должен быть вектор-столбцом с n строк.
Это более распространенный способ увидеть умножение, потому что он хорошо подходит для решения линейных систем, что обычно является мотивацией для матричной алгебры. Если A является матрицей m × n , так что она имеет m строк и n столбцов, то b должен быть вектор-столбцом с n строк.
Произведение умножения на представляет собой линейную комбинацию n векторов-столбцов A . Поскольку, когда вектор находится справа от A , выход представляет собой линейную комбинацию столбцов A , правое умножение использует пространство столбца.
Умножение справа на пространство столбца. Изображение Эли Бендерски на сайте thegreenplace.net На приведенном выше рисунке A представляет собой матрицу 3×3 со столбцами разных цветов. Вектор b состоит из 3 элементов. Произведение, расположенное справа, представляет собой линейную комбинацию столбцов A, где элементы из b — коэффициенты линейной комбинации.
Левое умножение работает по тем же принципам, что и правое умножение, но поскольку вектор находится на другой стороне A , пространство столбцов переключается на пространство строк. Настройка аналогична: A — это m×n , а b — вектор с m элементами. При умножении справа или по столбцам b имеет столько же элементов, сколько A имеет столбцов, но при умножении слева или по строкам b имеет столько же элементов, сколько A имеет строк.
Произведение числа b×A представляет собой линейную комбинацию m строк числа A , где элементы числа b являются коэффициентами линейной комбинации.
Умножение влево с пробелом строки. Изображение Эли Бендерски на сайте thegreenplace.net На приведенном выше рисунке A — это матрица со строками разных цветов, а b содержит ровно столько элементов, сколько строк в А . Произведение, показанное справа, представляет собой линейную комбинацию строк A с элементами b в качестве коэффициентов.
Ниже приведены две функции, написанные на Python, которые выполняют правое и левое умножение матрицы на вектор. Эти функции настроены на работу на основе описанной выше интуиции. Этот код и некоторые примеры можно найти в этом файле colab.
def right_multiplication (A, b):
C = np.zeros (b.shape)
m, n = A.shape
для i в диапазоне (n):
C += np.reshape(b[i,0] * A[:,i], (m,1))
return Cdef left_multiplication(b, A):
C = np.zeros(b.shape)
m, n = A.shape
для i в диапазоне (m):
C += np.reshape(b[0,i] * A[i,:], (1,n))
return C
Вышеуказанные 2 функции имеют очень похожую структуру, отличаясь только циклом для . Для правостороннего умножения строк цикл повторяется по строкам A, а для левого умножения столбцов цикл повторяется по столбцам A. Внутри цикла обе функции увеличиваются на c на строку или столбец соответственно, умноженные на соответствующий i -й элемент из b .

 ones(9)
np.dot(a, b) # значение 45
ones(9)
np.dot(a, b) # значение 45 resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b)
resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b) array([1, 2])
np.dot(b, a) # array([14, 20, 26])
array([1, 2])
np.dot(b, a) # array([14, 20, 26]) qr()
qr()
 eig()
eig()
 pinv()
pinv()
 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.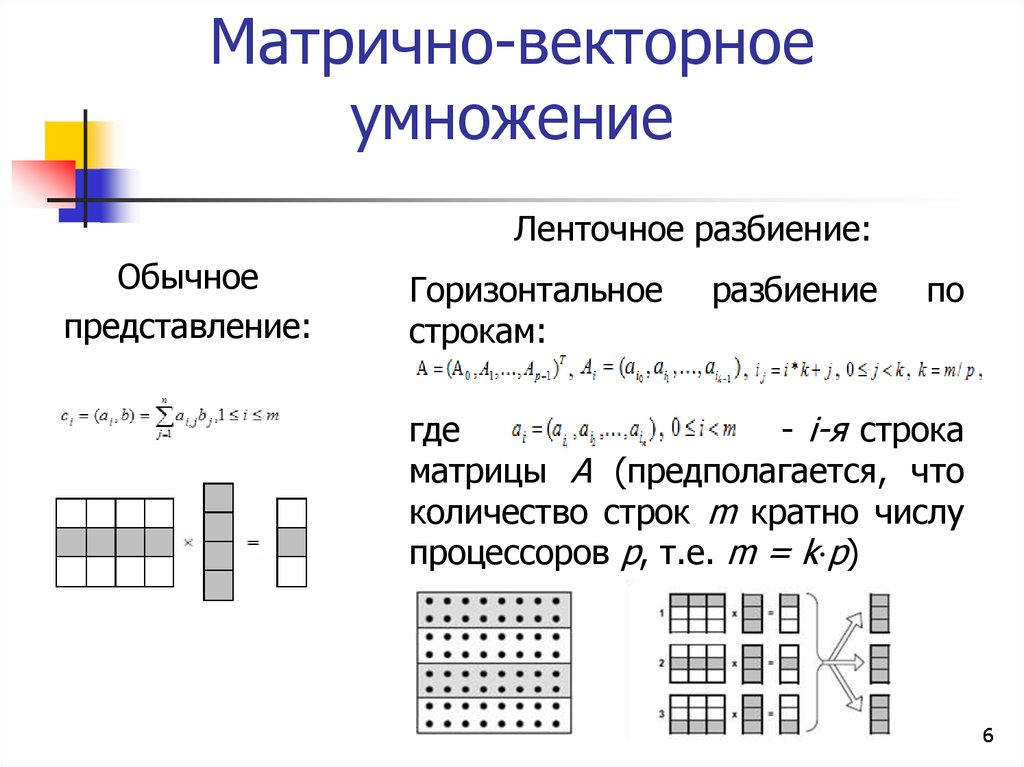 Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн