Матрица метод гаусса калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Примеры решения системы линейных алгебраических уравнений 4-ого порядка методом Гаусса, пример № 4

СЛАУ 3-его порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12
СЛАУ 4-ого порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12

---

Условие

3x 1  + x 2  — 2x 3  — 2x 4   =   -2  2x 1  — x 2  + 2x 3  + 2x 4   =   2  2x 1  + x 2  — x 3  — x 4   =   -1  x 1  + x 2  — 3x 3  + 2x 4   =   -3

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса.

Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!

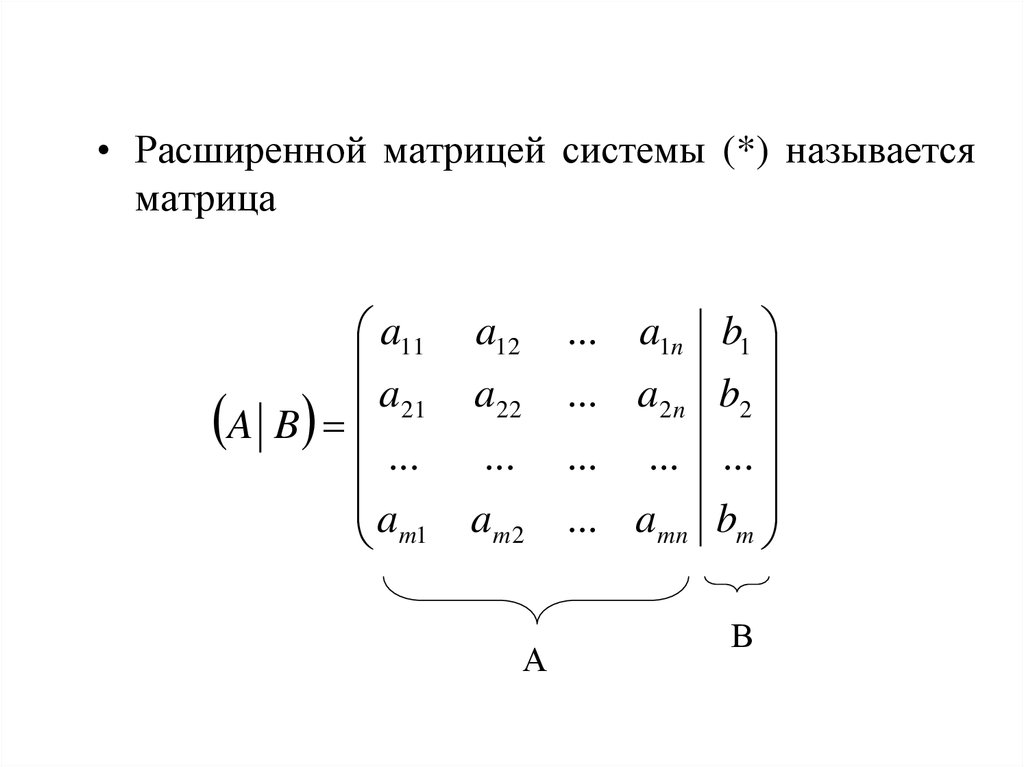
Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.

Проведём следующие действия:

• Поменяем местами строку № 1 и строку № 4

Получим:

Проведём следующие действия:

• Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 — 2 × строка 1)
• Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
• Из строки № 4 вычтем строку № 1 умноженную на 3 (Строка 4 — 3 × строка 1)

Получим:

Проведём следующие действия:

• Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)
• Поменяем местами строку № 2 и строку № 3

Получим:

Проведём следующие действия:

• К строке № 3 прибавим строку № 2 умноженную на 3 (Строка 3 + 3 × строка 2)
• К строке № 4 прибавим строку № 2 умноженную на 2 (Строка 4 + 2 × строка 2)

Получим:

Проведём следующие действия:

• Строку № 4 поделим на -3 (Строка 4 = строка 4 / -3)
• Поменяем местами строку № 3 и строку № 4

Получим:

Проведём следующие действия:

• К строке № 4 прибавим строку № 3 умноженную на 7 (Строка 4 + 7 × строка 3)

Получим:

Проведём следующие действия:

• Строку № 4 поделим на 55 (Строка 4 = строка 4 / 55)
• Из строки № 3 вычтем строку № 4 умноженную на 6 (Строка 3 — 6 × строка 4)
• Из строки № 2 вычтем строку № 4 умноженную на 5 (Строка 2 — 5 × строка 4)
• Из строки № 1 вычтем строку № 4 умноженную на 2 (
  Строка 1 — 2 × строка 4)

Получим:

Проведём следующие действия:

• К строке № 2 прибавим строку № 3 умноженную на 5 (Строка 2 + 5 × строка 3)
• К строке № 1 прибавим строку № 3 умноженную на 3 (Строка 1 + 3 × строка 3)

Получим:

Проведём следующие действия:

• Из строки № 1 вычтем строку № 2 (Строка 1 — строка 2)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:

х₁ = 0
х₂ = 0
х₃ = 1
х₄ = 0

Вы поняли, как решать? Нет?

Другие примеры

Мэтуэй | Популярные задачи

Популярные задачи

Базовая математикаПредварительная алгебраАлгебраТригонометрияПредварительный исчислениеИсчислениеКонечная математикаЛинейная алгебраХимияФизика

92+9х+3 , х=х+2 94

Ранг	Тема	Проблема	Проблема с форматированием
1	Решение с использованием обратной матрицы	х+2у=1 , 4х+5у=13	,
2	Умножение матриц	[[1/(квадратный корень из 17),-4/(квадратный корень из 17)]][[1/(квадратный корень из 17)],[-4/(квадратный корень из 17)]]
3	Найти домен	х+у=3
4	Найти домен	х-у=3
5	Найти домен	у=-2х+3
6	Найти домен	у=2х+1
7	Записать как векторное равенство	,
8	Найти домен	у=2х
9	Найти домен	г=-3x
10	Найти домен	у=3х-2
11	Найти домен	у=4х
12	Найти домен	3x+2y=6
13	Найдите матрицу идентичности 5×5	5
14	Найдите матрицу идентичности 6×6	6
15	Найдите матрицу идентичности 4×4	4
16	Решение с использованием обратной матрицы	2х+у=-2, х+2у=2	,
17	Решение с использованием обратной матрицы	4х+4=у, у=6х	,
18	Решение с использованием обратной матрицы	4х+2=5у-3, у=3х-1	,
19	Найдите силовой набор	(3,4)
20	Оценка	кубический корень из 216
21	Найдите силовой набор	(1,3)
22	Найти домен	3x-2y=12
23	Найти домен	у=5х+2
24	Найти домен	у=2х-3
25	Найти домен	у=2х-4
26	Найти домен	у=2х+5
27	Найти домен	у=1/2х
28	Найти домен	у=1/2x-3
29	Найти домен	у=2/3х-2
30	Найти домен	х=2у
31	Найти домен	х-2у=2
32	Найти домен	х-2у=6
33	Найти домен	2г+х
34	Найти домен	2х+у=0
35	Найти домен	у=5х+6
36	Найти домен	у=х+3
37	Решить с помощью матрицы путем исключения	у=4х+3х-2, у=6	,
38	Определить, является ли линейно зависимым	В={[[-10,2],[5,-2,5]]}
39	Добавить	[[2,4],[6,-4]]+[[-3,-7],[20,10]]
40	Определить, является ли линейно зависимым	В={[[-1,2],[0,-2,5]]}
41	Умножение матриц	[[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1, 1],[1,0,1,0],[0,0,0,1],[0,1,0,0]]
42	Найти домен	у=5х
43	Найти домен	у=7х
44	Найти домен	у=-х-2
45	Найти домен	у=х-2
46	Найти домен	у=х-3
47	Найти сокращенную форму эшелона строк	[[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]]
48	Записать как векторное равенство	х+у+г=2, 4х+5у+г=12, 2х=-4	, ,
49	Найти определитель	[[0,-1,а],[3,-а,1],[1,-2,3]]
50	Найти домен	у=-х+2
51	Найдите определитель	[[2,5,0],[1,0,-3],[2,-1,2]]
52	Найти определитель	[[7,5,0],[4,5,8],[0,-1,5]]
53	Найдите обратное	[[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]]
54	Найдите обратное	[[1,2,3],[2,5,7],[3,7,9]]
55	Найти сокращенную форму Echelon Row	[[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]]
56	Найти сокращенную форму эшелона строк	[[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]]
57	Найти сокращенную форму эшелона строк	[[1,2,3],[4,5,6],[7,8,9]]
58	Найти сокращенную форму эшелона строк	[[7,8]]
59	Найти домен	2х+у=1
60	Записать как векторное равенство	2х+у=-2, х+2у=2	,
61	Найти домен	х-2у=4
62	Найти домен	х-у=-1
63	Найти домен	х+у=5
64	Найти домен	х=-3у-8
65	Найти домен	х=-2у-8
66	Найти домен	х+у=6
67	Найти домен	х+у=4
68	Найти домен	х+2у=4
69	Найти домен	х+у
70	Найти домен	у=7х+9
71	Найти домен	у=1/2x-5
72	Найти домен	у=1/2х+2
73	Найти домен	у=1/2х+3
74	Найти домен	х-у=-3
75	Найти домен	х-у=4
76	Найти домен	г=-2x
77	Найти домен	у=-2х+1	92
80	Найти домен	у=2х-6
81	Найти домен	у=-2x-3
82	Найти домен	у=3х-8
83	Найти домен	у=3х
84	Найти домен	у=-3х+1
85	Найти домен	у=4х+3
86	Найти домен	у=3х-4
87	Найти домен	у=4х-2
88	Найти домен	у=-6х
89	Найти домен	у=х-4
91	Найти домен	с=5/9*(ф-32)
92	Найти домен	ф=9/5с+32
93	Оценка	квадратный корень из 4
94	Найти сокращенную форму эшелона строк	[[-6,7],[2,6],[-4,1]]
95	Найдите собственные значения	[[2,1],[3,2]]
96	Найдите собственные значения	[[4,0,1],[2,3,2],[49,0,4]]
97	Найдите силовой набор	А=(2,3,4,5)
98	Найти мощность	(2,1)
99	Решение с использованием обратной матрицы	-3x-4y=2 , 8y=-6x-4	,
100	Решение с использованием обратной матрицы	2x-5y=4 , 3x-2y=-5	,

jacobian-matrix-calculator — Google Suche

AlleBilderVideosShoppingMapsNewsBücher

Suchoptionen

Wolfram|Alpha Widgets: «Jacobian matrix and determinant»

www. wolframalpha.com › widgets › view

16.08.2016 · Вычисляет матрицу Якоби (матрицу частных производных) заданной вектор-функции по соответствующему списку …

Калькулятор Якобиана — AllMath

www.allmath.com › jacobian-matrix-calculator

Калькулятор Якобиана используется для нахождения матрицы Якобиана и определителя после взятия производной заданной функции. Калькулятор матрицы Якоби …

Калькулятор Якоби — eMathHelp

www.emathhelp.net › калькуляторы › исчисление-3 › jaco…

Калькулятор найдет матрицу Якоби набора функций и якобиан определитель (если возможно) с указанием шагов.

Калькулятор Якобиана — Найдите якобиан с двумя и тремя переменными три переменные быстро.

Как рассчитать якобиан? · Критические точки

Ähnliche Fragen

Пример матрицы Якоби?

Какова формула якобиана?

Калькулятор Якобиана

www.antiderrivativecalculator.net › jacobian-calculator

Загрузите наше приложение для Android из Google Play Store и приложение для iOS из Apple App Store. … Антипроизводный (интегральный) калькулятор — это инструмент исчисления. Он выполняет шаг за шагом …

Онлайн-калькулятор якобиана — comnuan.com

comnuan.com › cmnn04 › cmnn04003

Онлайн-калькулятор для нахождения якобиана системы вещественных функций с использованием … значений f1 ,f2,…,fm и матрица Якоби размера m × n: [∂f1∂x1∂f1∂x2…

Калькулятор матрицы Якобиана

www.meracalculator.com › math › jacobian-matrix-…

Калькулятор матрицы Якобиана. У меня есть: 2 переменные 3 переменные. Функция 1: Функция 2: Функция 3: Расчет сброса. Результат …

Калькулятор Якобиана с тремя переменными — Бесплатная онлайн-помощь по домашнему заданию

www.geekandnerd.org › с тремя переменными-якобианом-cal…

Калькулятор Якобиана с тремя переменными вычисляет матрицу Якобиана для четырех входных данных переменные и одна выходная переменная. Матрица Якоби — это матрица …

▷ Как вычислить матрицу Якоби (и определитель)

www.