Матрица нахождение определителя: Определитель матрицы онлайн

Вычисляем определитель матрицы на Хаскелле / Хабр

Решил выложить код вычисления определителей. Код рабочий, хотя и не претендует на виртуозность. Просто было интересно решить эту задачу именно на Хаскелле. Рассмотрены два подхода к решению задачи: простая рекурсия и метод Гаусса.

Немного теории

Как известно, определитель квадратной матрицы n*n — это сумма n! слагаемых, каждое из которых есть произведение, содержащее ровно по одному элементу матрицы из каждого столбца и ровно по одному из каждой строки. Знак очередного произведения:

определяется чётностью подстановки:

Прямой метод вычисления определителя состоит в разложении его по элементам строки или столбца в сумму произведений элементов какой-либо строки или столбца на их алгебраические дополнения. В свою очередь, алгебраическое дополнение элемента матрицы

есть

при этом

— есть минор элемента (i,j), т. е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.

Такой метод порождает рекурсивный процесс, позволяющий вычислить любой определитель. Но производительность этого алгоритма оставляет желать лучшего — O(n!). Поэтому применяется такое прямое вычисление разве что при символьных выкладках (и с определителями не слишком высокого порядка).

Гораздо производительнее оказывается метод Гаусса. Его суть основывается на следующих положениях:

1. Определитель верхней треугольной матрицы \begin{pmatrix}{a}_{1,1} & {a}_{1,2} &… & {a}_{1,n} \\ 0 & {a}_{2,2} &… & {a}_{2,n} \\ 0 & 0 &… & …\\ 0 & 0 &… & {a}_{n,n} \\\end{pmatrix} равен произведению ее диагональных элементов. Этот факт сразу же следует из разложения определителя по элементам первой строки или первого столбца.

2. Если в матрице к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то значение определителя не изменится.

3. Если в матрице поменять местами две строки (или два столбца), то значение определителя изменит знак на противоположный.

Мы можем, подбирая коэффициенты, складывать первую строку матрицы со всеми остальными и получать в первом столбце нули во всех позициях, кроме первой. Для получения нуля во второй строке, нужно прибавить ко второй строке первую, умноженную на

Для получения нуля в третьей строке, нужно к третьей строке прибавить первую строку, умноженную на

и т.д. В конечном итоге, матрица приведется к виду, в котором все элементы

при n>1 будут равны нулю.

Если же в матрице элемент

оказался равным нулю, то можно найти в первом столбце ненулевой элемент (предположим, он оказался на k-м месте) и обменять местами первую и k-ю строки. При этом преобразовании определитель просто поменяет знак, что можно учесть.

Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.

Далее, действуя аналогично, можно получить нули во втором столбце, затем в третьем и т.п. Важно, что при сложении строк полученные ранее нули не изменятся. Если для какой-либо строки не удастся найти ненулевой элемент для знаменателя, то определитель равен нулю и процесс можно остановить. Нормальное завершение процесса Гаусса порождает матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю. Как говорилось выше, определитель такой матрицы равен произведению диагональных элементов.

Перейдем к программированию.

Мы работаем с данными с плавающей точкой. Матрицы представляем списками строк. Для начала определим два типа:

type Row    = [Double]
type Matrix = [Row]

Простая рекурсия

Ничтоже сумняшеся, мы будем раскладывать определитель по элементам первой (т.е. нулевой) строки. Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.

-- Удаление k-го элемента изо всех строк матрицы
deln :: Matrix -> Int -> Matrix
deln matrix k = map (\ r -> (take (k) r)++(drop (k+1) r)) matrix

А вот и минор:

-- Минор k-го элемента нулевой строки
minor :: Matrix -> Int -> Double
minor matrix k = det $ deln (drop 1 matrix) k

Обратите внимание: минор — это определитель. Мы вызываем функцию det, которую еще не реализовали. Для реализации det, нам придется сформировать знакочередующуюся сумму произведений очередного элемента первой строки на определитель очередного минора. Чтобы избежать громоздких выражений, создадим для формирования знака суммы отдельную функцию:

sgn :: Int -> Double
sgn n = if n `rem` 2 == 0 then 1.0 else (-1.0)

Теперь можно вычислить определитель:

-- Определитель квадратной матрицы
det :: Matrix -> Double
det [[a,b],[c,d]] = a*d-b*c
det matrix = sum $ map (\c -> ((matrix !! 0)!!c)*(sgn c)*(minor matrix c))  [0. .n]
             where n = length matrix - 1

Код очень прост и не требует особых комментариев. Чтобы проверить работоспособность наших функций, напишем функцию main:

main = print $ det [[1,2,3],[4,5,6],[7,8,(-9)]]

Значение этого определителя равно 54, в чем можно убедиться.

Метод Гаусса

Нам понадобится несколько служебных функций (которые можно будет использовать и в других местах). Первая из них — взаимный обмен двух строк в матрице:

-- Обмен двух строк матрицы
swap :: Matrix -> Int -> Int -> Matrix
swap matrix n1 n2 = map row [0..n]
                    where n=length matrix - 1
                          row k | k==n1 = matrix !! n2
                                | k==n2 = matrix !! n1
                                | otherwise = matrix !! k

Как можно понять по приведенному выше коду, функция проходит строку за строкой. При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.

Следующая функция вычисляет строку r1 сложенную со строкой r2, умноженной поэлементно на число f:

-- Вычислить строку r1+f*r2
comb :: Row -> Row -> Double -> Row
comb r1 r2 f = zipWith (\ x y -> x+f*y) r1 r2

Здесь все предельно прозрачно: действия выполняются над строками матрицы (т.е. над списками [Double]). А вот следующая функция выполняет это преобразование над матрицей (и, естественно, получает новую матрицу):

-- прибавить к строке r1 строку r2, умноженную на f
trans :: Matrix -> Int -> Int -> Double -> Matrix
trans matrix n1 n2 f = map row [0..n]
                       where n=length matrix - 1
                             row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
                                   | otherwise = matrix !! k

Функция getNz ищет номер первого ненулевого элемента в списке. Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.

-- Номер первого ненулевого в списке
getNz :: Row -> Int
getNz xs = if length tmp == 0 then (-1) else snd $ head tmp
           where tmp=dropWhile (\ (x,k) -> (abs x) <= 1.0e-10) $ zip xs [0..]

Если все элементы списка равны нулю, функция вернет -1.

Функция search проверяет, подходит ли матрица для очередного преобразования (у нее должен быть ненулевым очередной диагональный элемент). Если это не так, матрица преобразовывается перестановкой строк.

-- Поиск ведущего элемента и перестановка строк при необходимости
search :: Matrix -> Int -> Matrix
search matrix k | (abs ((matrix !! k) !! k)) > 1.0e-10 = matrix
                | nz < 0 = matrix  -- матрица вырождена    
                | otherwise = swap matrix k p 
                           where n   = length matrix
                                 lst = map (\ r -> r !! k) $ drop k matrix
                                 nz  = getNz lst
                                 p   = k + nz

Если ведущий (ненулевой) элемент найти невозможно (матрица вырождена), то функция вернет ее без изменений. Функция mkzero формирует нули в очередном столбце матрицы:

-- получение нулей в нужном столбце
mkzero :: Matrix -> Int -> Int -> Matrix
mkzero matrix k p | p>n-1 = matrix
                  | otherwise = mkzero (trans matrix p k (-f)) k (p+1)
                    where n = length matrix
                          f = ((matrix !! p) !! k)/((matrix !! k) !! k)

Функция triangle формирует верхнюю треугольную форму матрицы:

-- Получение верхней треугольной формы матрицы
triangle :: Matrix -> Int -> Matrix
triangle matrix k | k>=n = matrix
                  | (abs v) <= 1.0e-10 = [[0.0]] -- матрица вырождена
                  | otherwise = triangle (mkzero tmp k k1) k1 
                    where n   = length matrix
                          tmp = search matrix k
                          v   = (tmp !! k) !! k -- диагональный элемент
                          k1  = k+1

Если на очередном этапе не удалось найти ведущий элемент, функция возвращает нулевую матрицу 1-го порядка. Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:

-- Парадная функция
gauss :: Matrix -> Matrix
gauss matrix = triangle matrix 0 

Для вычисления определителя нам нужно перемножить диагональные элементы. Для этого составим отдельную функцию:

-- Произведение диагональных элементов
proddiag :: Matrix -> Double
proddiag matrix = product $ map (\ (r,k) -> r !!k) $ zip matrix [0,1..]

Ну, и «бантик» — собственно вычисление определителя:

-- Вычисление определителя
det :: Matrix -> Double
det matrix = proddiag $ triangle matrix 0

Проверим, как работает эта функция:

main = print $ det  [[1,2,3],[4,5,6],[7,8,-9]]
[1 of 1] Compiling Main             ( main.hs, main.o ) 
Linking a.out ...                                                                                 
54.0     

Спасибо тем, кто дочитал до конца!

Код можно скачать здесь

Вычисление определителя матрицы в EXCEL.

Примеры и описание

Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).

Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.

Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).

Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как массив констант , например =МОПРЕД({5;4:3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на именованный диапазон .

Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.

Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).

В файле примера для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.

Свойства определителя

Теперь о некоторых свойствах определителя (см. файл примера ):

• Определитель транспонированной матрицы равен определителю исходной матрицы
• Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
• Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
• Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на k
• Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
• det(А)=1/det(А ^-1 ), где А ^-1 — матрица обратная матрице А (А — квадратная невырожденная матрица).

Вычисление определителя матрицы по определению (до 6 порядка включительно)

СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .

Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:

Определителем квадратной матрицы порядка n х n является сумма, содержащая n! слагаемых ( =ФАКТР(n) ). Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А . Перед k-ым слагаемым появляется коэффициент (-1) , если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий в k-ой перестановке множества номеров столбцов нечетно.

где ( α ₁ , α ₂ ,…, α _n ) — перестановка чисел от 1 до n , N( α ₁ , α ₂ ,…, α _n ) — число инверсий в перестановке , суммирование идёт по всем возможным перестановкам порядка n .

Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.

Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:

• а21*а12*а33
• а21*а32*а13
• а11*а32*а23
• а11*а22*а33
• а31*а22*а13
• а31*а12*а23

а21, а12 и т. д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее транспонированной матрицы равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).

Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения ( в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А ), а в нашем слагаемом нет элемента из строки 3.

Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью Перестановки без повторений: Комбинаторика в MS EXCEL

Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).

СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье Перебор всех возможных Перестановок в MS EXCEL .

Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.

Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье Перестановки без повторений: Комбинаторика в MS EXCEL

Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т. д.

Сложив все слагаемые:  (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.

В файле примера на листе 4+, и зменяя порядок матрицы с помощью элемента управления Счетчик , можно вычислить определитель матрицы до 6 порядка включительно.

Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).

Найти определитель матрицы с примерами решения

Содержание:

1. Определители. Основные определения и теоремы
2. Примеры с решением

Определение 1. Матрицей называется прямоугольная таблица, состоящая из строк и столбцов, заполненная некоторыми математическими объектами, которые называются элементами матрицы.

Мы будем рассматривать матрицы, элементами которых будут действительные или комплексные числа.

Матрицы обозначаются прописными латинскими буквами, а их элементы — строчными латинскими или греческими буквами с двумя нижними индексами: . Здесь первый индекс указывает на номер строки, а второй — на номер столбца, на пересечении которых расположен данный элемент. Число строк и столбцов матрицы называется ее размерностью. Так, если матрица имеет строк и столбцов, то ее размерность записывается в виде , а сама матрица имеет вид:

. (3.1)

Если все элементы матрицы равны :

, (3.2)

то такая матрица называется нулевой соответствующей размерности. Особое значение имеют матрицы, в которых число строк и столбцов одинаково. Такие матрицы называются квадратными. Как правило, размерность квадратной матрицы записывают одним числом, которое называется порядком матрицы.

Все элементы квадратной матрицы, имеющие одинаковые индексы образуют главную диагональ. Другая диагональ квадратной матрицы называется побочной. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны , то такая матрица называется диагональной.

Диагональные матрицы, в которых все элементы главной диагонали равны между собой, называются скалярными.

Скалярная матрица, в которой все элементы главной диагонали равны единице, называется единичной матрицей соответствующей размерности.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Определители. Основные определения и теоремы

Далее в этой главе будут рассматриваться только квадратные матрицы. С каждой квадратной матрицей связано вполне определенное число, которое называется ее определителем. Существует несколько подходов к построению теории определителей. Классический подход использует понятие перестановок и подстановок. А поскольку учебными программами основных технических специальностей высшей школы в курсе математики не предусмотрено изучение понятий перестановок и и подстановок, то здесь мы будем использовать индуктивный подход к введению понятия определителя и при будем избегать громоздких доказательств известных фактов — читатель может с ними ознакомиться в других известных учебниках.

Вначале рассмотрим квадратные матрицы небольших порядков. Если порядок матрицы равен единице, то матрица состоит из одного элемента и определителем такой матрицы будем называть число .Вообще для любой квадратной матрицы ее определитель чаще всего будем обозначать . Для обозначения определителя будем применять также следующие символы: (иногда с индексами). Таким образом, для матрицы первого порядка .

Если, далее, порядок матрицы равен двум, т. е. если эта матрица имеет вид , (3. 8) то определителем этой матрицы назовем число, равное . Записывать определитель матрицы будем следующим образом: . (3.9) Окончательно сформулируем следующее определение.

Возможно вам будут полезны данные страницы:

Умножение матрицы на вектор

Собственные значения матрицы

Нахождение обратной матрицы

Как найти ранг матрицы: пример решения

Определение 2. Определителем матрицы второго порядка называется число, получаемое следующим образом: . (3.10)

Будем применять термин порядок определителя, подразумевая под этим порядок исходной матрицы.

В дальнейшем мы будем говорить об элементах, строках, столбцах или диагоналях определителя, подразумевая под этими терминами соответственно элементы, строки, столбцы или диагонали соответствующей матрицы.

Перейдем теперь к формулированию понятия определителя любого порядка , где . Понятие такого определителя мы введем индуктивно, предполагая, что нам уже известно, как находятся определители всех квадратных матриц, порядок которых строго меньше . Рассмотрим произвольную квадратную матрицу порядка : . (3.11)

Выберем в любой элемент и вычеркнем из -ю строку и -й столбец. Из оставшихся элементов, не меняя их взаимного расположения, составим матрицу. Это будет квадратная матрица порядка (). По индуктивному предположению, мы умеем находить определитель полученной матрицы. Обозначим его и назовем минором элемента .  

Определение 3. Определителем порядка , соответствующим матрице (3.11), называется число, равное . (3.12) Итак, по определению

. (3.13)

Формула (3.13) при вычислении определителя использует все элементы первой строки (разложение определителя по первой строке). Заметим, что формула вычисления определителя второго порядка (3. 10) является частным случаем формулы (3.13).

Возникает вопрос, почему первая строка определителя имеет отличительные особенности по сравнению с другими его строками? Так ли это?

На самом деле это не так: все строки определителя равнозначны в смысле возможности вычисления определителя, но для формулировки определения необходимо выбрать какую-либо конкретную строку.

Чтобы поставить точку в этом вопросе, сформулируем основную теорему, доказательство которой читатель может найти, например, в [2].

Теорема 3.1. При любом номере строки , для определителя -го порядка матрицы (3.11) справедлива формула

. (3.14) называемая разложением этого определителя по -й строке.

Теорема 3.1 установила возможность вычисления определителя с помощью разложения его по любой строке. Здесь возникает вопрос о возможности применения столбцов определителя для его вычисления. Ответ на этот вопрос дает следующая основная теорема.

Теорема 3.2. При любом номере столбца , для определителя -го порядка матрицы (3.11) справедлива формула , (3.15)

называемая разложением этого определителя по -му столбцу. Нетрудно понять, что формулы (3.14) и (3.15) позволяют вычислить определитель любой квадратной матрицы. Действительно, применение любой из этих формул сводит вычисление определителя -го порядка к вычислению миноров, которые в свою очередь являются определителями порядка . Применяя формулы (3.14) или (3.15) к каждому из этих миноров, мы сведем вычисление исходного определителя к вычислению определителей уже порядка . Продолжая этот процесс, мы придем к вычислению вполне определенного числа определителей порядка 2, которые вычисляются по формуле (3.10).

Теперь очевидно, что непосредственное применение формул (3.14) и (3.15) к вычислению определителей (особенного высоких порядков) приведет к громоздким вычислениям. С другой стороны, понятно, что если в какой-то строке (или в столбце) определителя имеется «достаточно большое» количество нулей, то процесс вычисления определителя с помощью этих формул станет заметно проще. Далее будут приведены свойства определителей, применение которых позволяет, не изменяя численного значения определителя, так его предварительно преобразовать, что вычисление его значения с помощью вышеуказанных формул существенно упростится.

Чтобы не доводить вычисление определителя до второго порядка, приведем формулу вычисления определителя третьего порядка, которая называется правилом треугольников; ее доказательство оставляем читателю в качестве упражнения. Итак, справедлива формула

(3.16)

В правой части равенства (3.16) находится шесть слагаемых. Первые три из них записываются со знаком плюс, остальные со знаком минус. Рассмотрим первую группу слагаемых. Первое слагаемое — это произведение всех элементов главной диагонали определителя, а в каждом из следующих множители образуют в определителе треугольники, у которых одна сторона параллельна главной диагонали: . Слагаемые, которые в формуле (3.16) имеют знак минус, иллюстрируются аналогично, только вначале перемножаются все элементы побочной диагонали, а затем выбираются такие тройки элементов определителя, которые образуют треугольники со стороной, параллельной его побочной диагонали:

.

В заключение этого параграфа познакомим читателя с теоремой Лапласа, которая является обобщением теорем 3.1 и 3.2. Применение теоремы Лапласа позволяет вычислять определители, разлагая их по нескольким выделенным строкам или столбцам. Для формулировки этой теоремы нам потребуются понятия минора -ro порядка и его алгебраического дополнения.

Определение 4. Пусть дан определитель порядка . Выберем целое число , удовлетворяющее условию , и в определителе выберем произвольные строк и столбцов. Элементы, стоящие на пересечениях выбранных строк и столбцов, очевидно составляют квадратную матрицу порядка . Определитель этой матрицы называется минором -го порядка определителя . Пусть в определителе порядка выбран минор -го порядка.

Вычеркнем те строки и столбцы, на пересечениях которых расположен этот минор. Оставшиеся элементы образуют квадратную матрицу порядка , определитель которой называется дополнительным к минору и обозначается . Если мы вычеркнем, наоборот, те строки и столбцы, в которых расположены элементы минора , то, очевидно, останется минор . Таким образом можно говорить о паре взаимно дополнительных миноров определителя. В частности, определенный выше минор является дополнительным к минору первого порядка и наоборот.

Определение 5. Если минор -го порядка расположен в строках с номерами и в столбцах с номерами то образуем сумму . Алгебраическим дополнением для минора будем называть число . В частности, алгебраическим дополнением элемента будет число . С учетом определения 11 перепишем иначе формулы (3.14) и (3.15): . (3.17) Здесь — квадратная матрица порядка (3.11). Теперь приведем формулировку теоремы.

Теорема 3.3 (Лапласа). Пусть в определителе порядка произвольно выбраны строк (или столбцов), . Тогда сумма произведений всех миноров -го порядка, содержащихся в выбранных строках (или столбцах), на их алгебраические дополнения равна определителю . Таким образом, применяя теорему Лапласа, вычисление определителя, например, четвертого порядка можно свести к вычислению нескольких определителей порядка 2, а определитель пятого порядка можно вычислить через несколько определителей третьего и второго порядков. Доказательство теоремы Лапласа в стиле нашего изложения теории определителей можно найти в [2].

Примеры с решением

Пример 1.

Вычислить определитель третьего порядка по правилу треугольников

Пример 2.

Вычислить определитель третьего порядка, разложив его по первой строке:

Пример 3.

Вычислить определитель пятого порядка, применяя теорему Лапласа:

.

Решение. Разлагая определитель по первому и третьему столбцам, содержащим „удачно» расположенные нули, мы получим:

Определитель матрицы — 2×2, 3×3, 4×4, нахождение определителя

Определитель матрицы — это функция, которая отображает каждую квадратную матрицу в уникальное число (действительное число или комплексное число). Если A — множество всех квадратных матриц (всех порядков), а B — множество всех чисел (как вещественных, так и комплексных), то определяющая функция f равна f : A → B и определяется как f(x) = y, где «у» — определитель матрицы «х».

Давайте изучим процесс нахождения определителя матрицы для матриц порядка 1×1, 2×2, 3×3 и т. д. вместе с несколькими примерами. Также остановимся на свойствах определителей.

1.	Что такое определитель матрицы?
2.	Определитель матрицы 3×3
3.	Определители матричных формул
4.	Свойства определителя матрицы
5.	Часто задаваемые вопросы об определителе матрицы

Что такое определитель матрицы?

Определитель матрицы представляет собой сумму произведений элементов любой строки или столбца и их соответствующих коэффициентов . Определитель матрицы определен только для квадратных матриц. Для любой квадратной матрицы A определитель A обозначается det A (или) |A|. Иногда обозначается символом Δ . Процесс вычисления определителей матриц 1×1 и 2×2 довольно прост, тогда как процесс усложняется по мере увеличения порядка матрицы. В процессе нахождения определителя матрицы участвуют миноры и кофакторы. Напомним сначала, как найти миноры и кофакторы элементов матрицы.

Определитель матрицы 2×2

Определитель матрицы 2×2 A = \(\left[\begin{array}{cc}a & b \\ \\ c & d\end{array}\right]\) |А| = объявление — до н.э. Это просто получается путем перекрестного умножения элементов, начиная с верхнего левого угла, а затем вычитания произведений.

Минор элемента матрицы

Минор элемента \((a_{ij})\) квадратной матрицы любого порядка – это определитель матрицы, полученный удалением строки (i ^th ряд) и столбец (j ^{-й столбец} ), содержащий элемент. Мы можем понять это на примере.

Пример: Для матрицы A = \(\left[\begin{array}{ccc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right ]\),

• Минор числа 6 есть,
  \(\left|\begin{array}{ccc}1 & 2 & ̶3̶ \\ ̶4̶ & ̶5̶ & { ̶6̶} \\ 7 & 8 & ̶9̶\end{массив}\right|\) = \(\left| \begin{массив}{cc}1 и 2 \\ \\ 7 и 8\end{массив}\right|\)
  = 1(8) — 2(7) = 8 — 14 = -6.
• Младший 9,
  \(\left|\begin{массив}{ccc}1 & 2 & ̶3̶ \\ 4 & 5 & ̶6̶ \\ ̶7̶ & ̶8̶ & ̶9̶\end{массив}\right|\) = \(\left|\begin {массив}{cc}1 и 2 \\ \\ 4 и 5\конец{массив}\справа|\)
  = 1(5) — 2(4) = 5 — 8 = -3.

Кофактор элемента матрицы

Кофактор элемента \(a_{ij}\) квадратной матрицы любого порядка равен его минору, умноженному на (-1) ^{i + j} . то есть

• Кофактор элемента = (-1) ^{номер строки + номер столбца} (младший элемент)

Мы нашли миноры элементов 6 и 8 в предыдущем примере. Теперь вычислим кофакторы тех же элементов.

Пример: Для той же матрицы A = \(\left[\begin{array}{ccc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\ right]\),

• Так как 6 находится во 2 ^й строке и 3 ^й столбце,
  Сомножитель 6 = (-1) ^{2 +3} (минор 6) = (-1) ⁵ (-6) = 6
• Поскольку 9 находится в строке 3 ^nd и столбце 3 ^rd ,
  Сомножитель 9 = (-1) ^{3 +3} (младшая из 9) = (-1) ⁶ (-3) = -3

Сомножители элементов любой матрицы есть не что иное, как миноры, но умноженные на альтернативные знаки + и — (начиная со знака + для первого элемента первой строки).

Определитель матрицы 3×3

В предыдущем разделе мы видели, что определитель матрицы представляет собой сумму произведений элементов любой строки (или любого столбца) и соответствующих им коэффициентов. Итак, вот шаги для нахождения определителя матрицы (матрицы 3 × 3 или любой другой матрицы).

• Шаг 1: Выберите любую строку или столбец. Обычно мы выбираем первую строку, чтобы найти определитель.
• Шаг 2: Найдите кофакторы каждого из элементов строки/столбца, которые мы выбрали в Шаге 1.
• Шаг 3: Умножить элементы строки/столбца из Шаг 1 на соответствующие коэффициенты, полученные из Шаг 2
• Шаг 4: Сложите все произведения из Шага 3 , что даст определитель матрицы.

Пример: Используйте описанные выше шаги для вычисления определителя матрицы 3×3 A = \(\left[\begin{array}{ccc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{массив}\right]\).

Решение:

Шаг 1: Выбираем первую строку с элементами 1, 2 и 3.

Шаг 2: Вычислим сомножители этих элементов: = (-1) ¹⁺¹ Минор от 1 = (-1) ² \(\left|\begin{array}{cc}5 & 6 \\ \\ 8 & 9\end{array}\ вправо |\) = 5(9) — 6(8) = -3
Сомножитель 2 = (-1) ¹⁺² Минор 2 = (-1) ³ \(\left|\begin{array}{cc}4 & 6 \\ \\ 7 & 9\end{массив}\right|\) = -1 (4(9) — 6(7)) = -1(-6) = 6
Сомножитель 3 = (-1) ¹⁺³ Минор 1 = (-1) ⁴ \(\left|\begin{array}{cc}4 & 5 \\ \\ 7 & 8\ end{array}\right|\) = 4(8) — 5(7) = -3

Шаг 3: Умножьте элементы на их кофакторы.

1(коэффициент 1) = 1 (-3) = -3
2(сомножитель 2) = 2(6) = 12
3(сомножитель 3) = 3(-3) = -9

Шаг 4: Сложите их, чтобы получить определитель.

det A = -3 + 12 — 9 = 0.

Все эти шаги можно суммировать в одном шаге следующим образом:

det A = 1(кофактор 1) + 2(кофактор из 2) + 3 (сомножитель 3)

= 1 \(\left|\begin{array}{cc}5 & 6 \\ \\ 8 & 9\end{array}\right|\) — 2 \(\left|\begin{array}{cc}4 & 6 \\ \\ 7 & 9\end{array}\right|\) + 3 \(\left|\begin{array}{cc}4 & 5 \\ \\ 7 & 8\end{массив}\right|\)

= 1 [5(9) — 6(8)] — 2 [4(9) — 6(7)] + 3 [ 4(8) — 5(7)]

= 1 (-3) — 2 (-6) + 3 (-3)

= -3 + 12 — 9

= 0

Примечание: Здесь мы использовали отрицательный знак с 2 в второй шаг, потому что мы получаем знак минус при нахождении сомножителя 2.

Определители матричных формул

Процесс нахождения определителя матрицы, описанный в предыдущем разделе, можно использовать для нахождения определителя матрицы любого порядка. Но есть некоторые хитрости, чтобы найти определители матриц 1×1, 2×2 и 3×3. Эти уловки очень полезны, так как большую часть времени при решении задач мы сталкиваемся с нахождением определителей матриц этих порядков.

Определитель матрицы 1×1

Матрица 1×1 представляет собой строку, состоящую всего из 1 строки и 1 столбца, следовательно, она содержит только один элемент. Определитель любой матрицы 1×1 всегда равен элементу матрицы. т. е.

• Если A = [x] _1×1 , то |A| (или) det A = x

Определитель матрицы 2×2

Как мы обсуждали ранее, ее определитель получается путем вычитания произведения элементов неглавной диагонали из произведения элементов главной диагонали. то есть

• Если A = \(\left[\begin{array}{cc}a & b \\ \\ c & d\end{array}\right]\), то |A| (или) det A = ad — bc

Определитель матрицы 3×3 (ярлык)

Быстрый способ найти определитель матрицы 3×3: просто напишите матрицу дважды и примените следующий трюк. Вот ярлык (самый простой способ) найти определитель матрицы 3×3 A = \(\left[\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\ конец{массив}\справа]\).

Свойства определителя матрицы

Свойства определителей полезны при нахождении определителя матрицы без фактического использования процесса его нахождения. Они полезны при оценке сложных детерминант. К ним относятся изменения определителя по отношению к элементарным операциям со строками.

Свойство 1

«Определитель матрицы равен определителю ее транспонирования.»

Пример:

\(\left|\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array}\right|\) = \ (\left|\begin{array}{ccc}a & p & x \\ b & q & y \\ c & r & z\end{array}\right|\)

Попробуйте проверить.

Свойство 2

«Если поменять местами любые две строки (или столбца) определителя, то знак определителя изменится.»

Пример:

\(\left|\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array}\right|\) = — \(\left|\begin{array}{ccc}p & q & r \\ a & b & c \\ x & y & z\end{array}\right|\)

Здесь первая и вторая строки определителя левой части переставлены местами. В этом легко убедиться, найдя оба определителя.

Свойство 3

«Если любые две строки (или столбца) определителя идентичны, то определитель равен 0.»

Пример:

\(\left|\begin{array}{ccc}a & b & c \\ a & b & c \\ x & y & z\end{array}\right|\) = 0

Свойство 4

«Если все элементы строки (или столбца) матрицы определителя равны нулю, то значение определителя равно 0».

Пример:

\(\left|\begin{array}{ccc}0 & 0 & 0 \\ p & q & r \\ x & y & z\end{массив}\right|\) = 0

Свойство 5

«Если каждый элемент строки (или столбца) определителя умножить на скаляр k, то значение результирующего определителя в k раз больше значения исходного определителя».

Пример:

\(\left|\begin{array}{ccc}ka & kb & kc \\ p & q & r \\ x & y & z\end{array}\right|\) = k \(\left|\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array}\right|\)

Свойство 6

«Если каждый элемент строки (или столбца) определителя выразить в виде суммы двух (или более) чисел, то определитель можно разбить на сумму двух (или более) определителей. »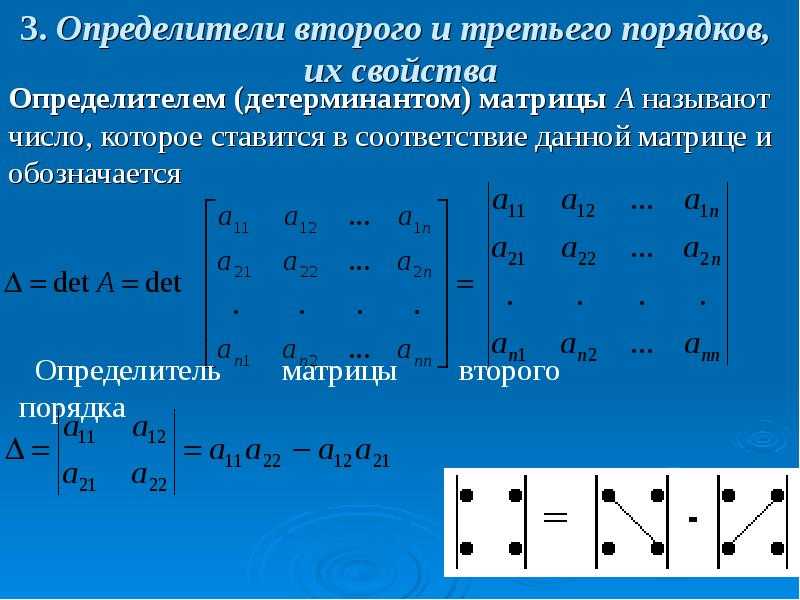

Пример:

\(\left|\begin{array}{ccc}a + k & b + l & c + m \\ p & q & r \\ x & y & z\ end{array }\right|\) = \(\left|\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array}\right|\) + \(\left|\begin{array}{ccc}k & l & m \\ p & q & r \\ x & y & z\end{array}\right|\)

Свойство 7

«Если каждый элемент строки (или столбца) умножить на константу и прибавить к соответствующим элементам другой строки (или столбца), то определитель останется неизменным.»

Пример:

\(\left|\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array}\right|\) = \(\left|\begin{array}{ccc}a+kp & b+kq & c+kr \\ p & q & r \\ x & y & z\end{array}\right|\)

Важные замечания по определителю матрицы:

• Определитель единичной матрицы всегда равен 1.
• Определитель диагональной матрицы всегда является произведением элементов ее главной диагонали.
• Определитель ортогональной матрицы равен либо +1, либо -1.
• Определитель матрицы может быть положительным, отрицательным или нулевым.
• Определитель матрицы используется в правиле Крамера, которое используется для решения системы уравнений.
• Также используется для нахождения обратной матрицы. Если определитель матрицы не равен 0, то это обратимая матрица, поскольку мы можем найти ее обратную.
• Если A — квадратная матрица порядка 3×3, то |kA| = k ³ |A|, для любого скаляра k.
• Квадратная матрица A называется вырожденной, если |A| = 0 и неособой, если |A| ≠ 0,
• Определитель полезен при вычислении собственных значений и собственных векторов матрицы.

☛ Связанные темы:

• Определитель матричного калькулятора
• Матричный калькулятор
• Калькулятор умножения матриц
• Типы матриц

Часто задаваемые вопросы об определителе матрицы

Что такое определение определителя матрицы?

Определитель матрицы получается путем умножения элементов любой из ее строк или столбцов на соответствующие коэффициенты и сложения всех произведений. Определитель квадратной матрицы A обозначается через |A| или дет (А).

Как найти определитель матрицы?

Чтобы найти определитель квадратной матрицы:

• Выберите любую строку или столбец
• Найдите кофакторы всех элементов строки или столбца, которые вы выбрали
• Умножить элементы строки или столбца на соответствующие им коэффициенты
• Добавьте продукты из последнего шага. Эта сумма дает определитель.

Что такое определитель матричного произведения?

Произведение определителей двух квадратных матриц равно произведению определителей отдельных матриц. т. е. для любых двух квадратных матриц A и B порядка nxn каждая, det(AB) = det(A) × det(B).

Что такое определитель квадрата матрицы?

Для любых двух квадратных матриц A и B одного порядка det(AB) = det A det B. Таким образом, det(A ² ) = det(AA) = detA det A = (det A) ² . Таким образом, определитель квадрата матрицы равен квадрату определителя матрицы.

Каково применение определителя матрицы?

Определители используются для:

• поиска обратной матрицы.
• решить систему уравнений
• по правилу Крамера.

Какой определитель матрицы, если все ее элементы равны?

Используя одно из свойств определителей, когда любые две строки или столбца матрицы равны, ее определитель равен нулю. Используя это, определитель матрицы, все элементы которой равны, равен 0,

Какой определитель матрицы, если все ее элементы равны нулю?

Используя одно из свойств определителей, когда все элементы любой строки или столбца равны нулю, его определитель равен нулю. Отсюда определитель матрицы, все элементы которой равны нулю, равен 0.

Как проще всего найти определитель матрицы?

Вот несколько самых простых способов/формул для нахождения определителя матрицы.

• Определитель матрицы 1×1: Если A = [x] _1×1 , тогда |A| = х.
• Определитель матрицы 2×2: если A = \(\left[\begin{array}{cc}a & b \\ \\ c & d\end{array}\right]\), то |A| = объявление — до н. э.
• Определитель матрицы 3 × 3: если A = \(\left[\begin{array}{ccc}a & b & c \\ p & q & r \\ x & y & z\end{array} \право]\), то |А| = а (qz — ry) — b (pz — rx) + c (py — qx).

Определители 2 на 2 | Purplemath

3 на 3

Purplemath

Определитель основан на квадратной матрице, но он заключен в столбцы абсолютного значения, а не в квадратные скобки. Вы можете многое сделать с детерминантами (и научиться у них), но вам, скорее всего, придется подождать продвинутого курса, чтобы узнать о них. В этом уроке я просто покажу вам, как вычислить определители 2×2 и 3×3. (Возможно вычисление определителей большего размера, но этот процесс намного сложнее, поэтому я не буду здесь этим заниматься.)

Содержание продолжается ниже

MathHelp.com

Для матрицы с именем « B «, определитель B обозначается как «det( B )», произносится как «детерминант B «, или просто «det -пчела».

Определитель можно получить только из квадратной матрицы. (Некоторые люди пытались определить различные псевдодетерминанты для неквадратных матриц, но я не думаю, что они приживаются. Все, о чем вы когда-либо слышали, это определители для квадратных матриц. Потому что причины.) Если ваша матрица не квадрат, у него нет определителя.

Как получить определитель матрицы?

Если у вас есть квадратная матрица, ее определитель записывается путем взятия той же сетки чисел, удаления квадратных скобок «[]» и замены этих скобок полосами абсолютного значения «||», как показано ниже:

Если это
«матрица A «…

…тогда это «детерминант A »

на той же клавише клавиатуры, что и символ «обратная косая черта».)

Точно так же, как абсолютные значения могут быть вычислены и упрощены для получения единого числа, то же самое можно сказать и о определителях. Процесс оценки определителей довольно запутан, поэтому давайте начнем с простого, со случая 2×2.

---

Как найти определитель матрицы 2 на 2?

Для матрицы 2×2 ее определитель находится путем вычитания произведений ее диагоналей, что является причудливым способом выразить словами то, что следующее говорит на картинках:

матрица A с переменными:

Определяющая среда A (или «DET A »):

Матрица A с числами:

. Определитель A (OR «DET» 656565666666666666666666666666 гг.

Другими словами, чтобы найти определитель матрицы 2×2, выполните следующие действия:

1. Умножьте значения по диагонали слева вверху и справа внизу
2. Умножить значения по диагонали от левого нижнего угла к правому верхнему
3. Вычесть второе произведение из первого
4. Упростите, чтобы получить значение определителя 2 на 2

«Но подождите!» Я слышу, как ты плачешь; «Разве абсолютные значения не всегда должны быть положительными? Численная матрица выше показана как имеющая отрицательный определитель. Что с этим не так?» Ты делаешь доброе дело.

Может ли определитель быть отрицательным?

Да, определители могут быть отрицательными! Детерминанты похожи на абсолютные значения и используют те же обозначения, но они не идентичны, и одно из отличий состоит в том, что определители действительно могут быть отрицательными.

---

Какой пример нахождения определителя 2 на 2?

• Оцените следующий определитель:

В этом упражнении мне дали определитель (а не матрицу), чтобы я мог сразу приступить к работе. Я умножаю диагонали (выделены фиолетовыми стрелками в моей работе ниже) и вычитаю:

Тогда мой ответ:

det( A ) = 3

---

• Найдите определитель следующей матрицы:

Вот, мне дали матрицу и попросили найти ее определитель.

Во-первых, я переведу матрицу в определитель, заменив квадратные скобки столбцами абсолютного значения.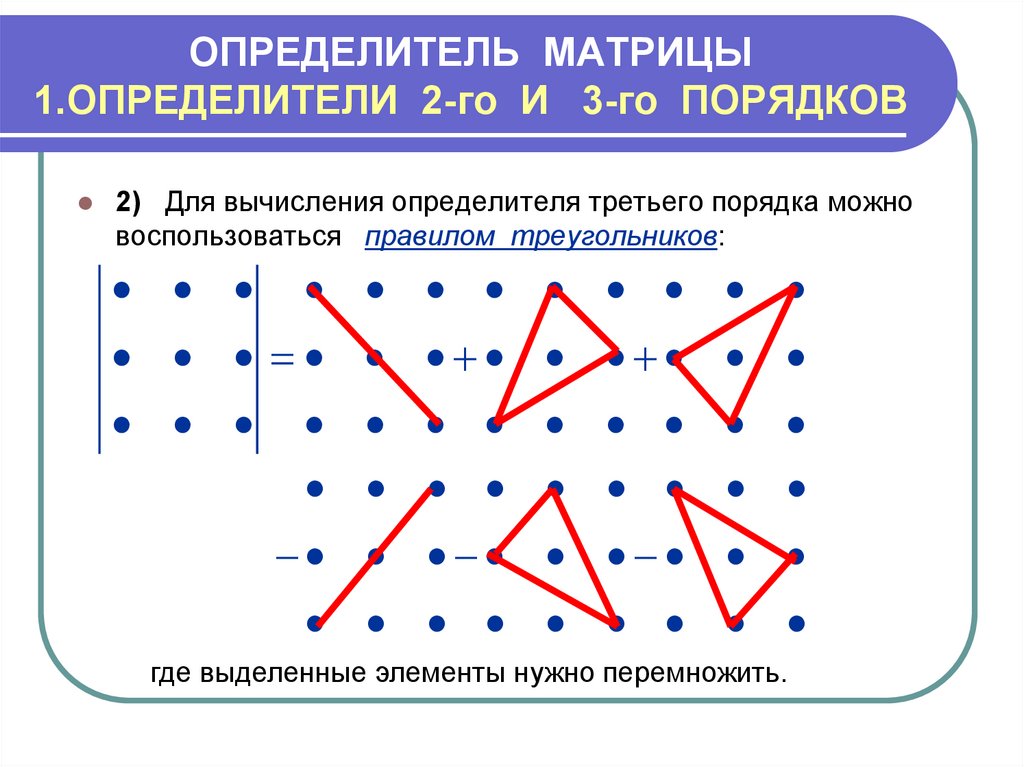 Затем я умножаю по диагоналям (синие стрелки внизу), вычитаю произведения и упрощаю, чтобы получить числовой ответ:

Тогда мой ответ:

det( A ) = 7

---

Вот и все равно 2 на 2 определителям. Просто убедитесь, что вы умножаете и вычитаете в правильном порядке, и все будет в порядке.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске значений определителей матриц 2 на 2 (или пропустить виджет и перейти к следующей странице). Попробуйте введенное упражнение или введите свое собственное упражнение. (Используйте их кнопку «матрица», чтобы ввести свою собственную матрицу, или же используйте запись в квадратных скобках «[[a b], [c d]]. Если вы опустите запятую, программа не поймет, что вы имеете в виду.) Затем нажмите кнопку и выберите «Найти определитель», чтобы сравнить свой ответ с ответом Mathway.0002 Чтобы активировать этот виджет, примите файлы cookie настроек.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )

---

URL: https://www.purplemath.com/modules/determs.htm 2

Обнаружение определителя матрицы | by Marvin Lanhenke

Fundamentals

Разблокировка ключевого элемента собственного разложения

Фото Ricardo Gomez Angel на Unsplash

В линейной алгебре есть понятия, которые легко понять с первого раза. Вероятно, потому что их приложения и варианты использования относительно очевидны, а концепции несколько осязаемы.

Представление о определителе матрицы , однако, сделало для меня полную противоположность — я больше запутался, чем просветился. Мое замешательство в основном было связано с тем, что у меня резко отсутствовала интуиция — я не мог визуализировать или представить себе значение и назначение определителя.

В следующих разделах мы построим часть этой интуиции, изучим несколько процедур вычисления определителя и получим первое представление о его применении.

Определитель описывает функцию, которая отображает матрицы в скаляр. Он определяется произведением всех собственных значений, что допускает несколько менее абстрактную, более геометрическую интерпретацию.

В зависимости от размеров матрицы определитель также может быть интерпретирован как площадь или том соответственно. Грубо говоря, он говорит нам, насколько умножение на данную матрицу растягивает или сжимает пространство.

Пример геометрической интерпретации [Изображение автора]

Предположим, у нас есть матрица с определителем, равным нулю. Умножение на эту матрицу сожмет пространство и сожмет все в одну строку. Следовательно, площадь также будет равна нулю.

Теперь, когда мы приобрели базовую интуицию, мы можем перечислить некоторые факты об определителе, чтобы углубить наше понимание:

1. Определитель определен только для квадратных матриц (M x M).
2. Матрица имеет ровно один определитель, так как это скаляр, содержащий информацию о матрице.
3. Определитель равен нулю для сингулярных матриц. Или, говоря иначе, матрицы с линейными зависимостями, рангом r < M , имеют нулевой определитель.
4. Определитель часто обозначается одним из следующих символов:

Примечание . Следует иметь в виду одну вещь: определитель великолепен в теории, но его трудно вычислить на практике из-за численной нестабильности при расчете для ' большие' матрицы.

В предыдущем разделе мы узнали некоторые основные сведения об определителе и о том, как его интерпретировать. Но как мы это вычисляем?

Процедура вычисления определителя довольно утомительна. К счастью, есть несколько сокращений, применимых только к маленьким матрицам (2x2, 3x3). Сначала мы поговорим о ярлыках, прежде чем говорить об общей процедуре.

Примечание : К счастью, нам не нужно вычислять определитель вручную, так как встроенная функция NumPy numpy.linalg.det(a) сделает всю работу за нас.

2x2 ярлык

Определитель матрицы 2 на 2 относительно легко вычислить. Нам просто нужно умножить каждый элемент вдоль главной диагонали и вычесть произведение недиагональных элементов.

Давайте рассмотрим несколько числовых примеров:

В первом примере мы использовали ярлык для вычисления определителя единичной матрицы 2 на 2, который равен единице. Мы также можем визуализировать это решение как площадь плоскости, где одна сторона определяется единичным вектором v=[1, 0], а другая — единичным вектором w=[0, 1].

Определитель единичной матрицы 2x2 [Изображение автора]

Сингулярная матрица имеет нулевой определитель — и это именно то, что мы можем видеть во втором примере. Поскольку оба столбца линейно зависят друг от друга, у нас есть матрица с недостаточным рангом, в результате чего определитель равен нулю. Думая о решении более геометрически, мы должны представить два вектора, образующих всего одну линию с нулевой площадью.

Определитель для единственной матрицы 2x2 [Изображение автора]

3x3 ярлык

Вычисление определителя для матрицы 3 на 3 уже сложнее, но относительно похоже на сокращение 2 на 2.

Суммируем все произведения диагональных элементов от верхнего левого до нижнего правого и вычитаем сумму всех произведений недиагональных элементов от верхнего правого до нижнего левого. Мы можем визуализировать эту процедуру двумя различными способами.

1. Одним из способов является увеличение матрицы путем конкатенации:

Дополненная визуализация матрицы [Изображение автора]

2. Другой способ — представить «обход» по диагоналям:

Визуализация матрицы обтекания [Изображение автора]

Общая процедура

Теперь все очень быстро усложняется. Таким образом, следующий пример будет основан только на матрице 4 на 4.

В целом, процедура состоит в переборе каждого элемента первой строки, создании подматрицы (3x3) путем исключения столбца текущего элемента первой строки, вычислении определителя подматрицы и умножении на текущую первую строку элемент. Это даст четыре числа, которые мы будем складывать и вычитать в чередующемся порядке [+,-,+,-].

Мы должны визуализировать процедуру, чтобы распутать сложное описание:

Мы видим, что процедура намного сложнее. Для относительно небольшой матрицы 4 на 4 нам нужно вычислить 4 определителя 4 подматриц, из которых нам также необходимо вычислить определители подматриц и т. д. Таким образом, алгоритм можно применять рекурсивно и, таким образом, он требует больших вычислительных ресурсов.

Однако эта общая процедура может масштабироваться до матрицы любого размера — и, к счастью, нам не нужно вычислять ее вручную.

Теперь мы знаем, что такое определитель, как его интерпретировать и как его вычислять, но один вопрос остается без ответа — для чего он используется?

Некоторые из его приложений, например, предоставляют способ найти обратную заданную матрицу или найти собственные значения. Последнее особенно важно, поскольку собственные значения и, следовательно, собственное разложение играют центральную роль в анализе главных компонент.

Внедрение PCA с нуля

Улучшите свои навыки линейной алгебры, используя только Python и NumPy

в направлении datascience. com

Предположим, у нас есть матрица 2 на 2, и мы уже знаем определитель. Помещение элементов матрицы в одну сторону и определителя в другую часть уравнения позволяет нам найти конкретный элемент матрицы.

Давайте подумаем о числовом примере, чтобы сделать все более очевидным.

Теперь, если мы продолжим эту идею и вычтем несколько неизвестных из действительных чисел по главной диагонали и обобщим уравнение, мы получим характеристический полином матрицы.

Характеристический многочлен полезен, поскольку он позволяет не только выразить матрицу в терминах полиномиального выражения, но и вычислить собственные значения матрицы. Если характеристический полином равен нулю, λ, являющиеся корнями полинома, описывают собственные значения матрицы.

В этой статье мы узнали о понятии определителя матрицы. Как его интерпретировать и вычислить, а также некоторые его приложения.

Два наиболее важных приложения — вычисление обратной матрицы и, возможно, даже более интересное — определение собственных значений.

Как мы вкратце упомянули ранее, определитель матрицы — отличная концепция в теории, но ее трудно вычислить на практике, особенно для «больших» матриц из-за численной нестабильности. Чтобы избежать таких проблем, например, при вычислении собственных значений, существует целое семейство итерационных алгоритмов (например, степенной метод).

Несмотря на практические проблемы, определитель по-прежнему является великой и фундаментальной концепцией, которую нужно знать и понимать.

Спасибо за прочтение! Обязательно оставайтесь на связи и следите за мной здесь на Medium, Kaggle или просто скажите «Привет» на LinkedIn

Понравилась статья? Станьте участником Medium и продолжайте учиться без ограничений. Я получу часть вашего членского взноса, если вы воспользуетесь следующей ссылкой, без каких-либо дополнительных затрат для вас.

Присоединяйтесь к Medium по моей реферальной ссылке - Марвин Ланхенке

Как участник Medium, часть вашего членского взноса идет авторам, которых вы читаете, и вы получаете полный доступ ко всем историям…

medium.

No related posts.