Тригонометрические функции от матрицы
Тригонометрические функции от матрицы — обобщения тригонометрических функций для квадратных матриц.
Тригонометрические функции (особенно часто синус и косинус) от квадратных матриц возникают в решениях систем дифференциальных уравнений второго порядка. Они определяются через те же ряды Тейлора, через которые определяются тригонометрические функции от вещественного или комплексного аргумента:
sin X = X − X 3 3 ! + X 5 5 ! − X 7 7 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n ( 2 n + 1 ) ! X 2 n + 1 cos X = I − X 2 2 ! + X 4 4 ! − X 6 6 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! X 2 n {displaystyle {egin{aligned}sin X&=X-{frac {X^{3}}{3!}}+{frac {X^{5}}{5!}}-{frac {X^{7}}{7!}}+cdots &=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}X^{2n+1}cos X&=I-{frac {X^{2}}{2!}}+{frac {X^{4}}{4!}}-{frac {X^{6}}{6!}}+cdots &=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}X^{2n}end{aligned}}}
где Xn означает матрицу X в степени n, а I — единичную матрицу той же размерности.
Также тригонометрические функции матричного аргумента могут быть определены через матричную экспоненту с учётом матричного аналога формулы Эйлера eiX = cos X + i sin X:
sin X = e i X − e − i X 2 i cos X = e i X + e − i X 2 . {-iX} over 2}.end{aligned}}}
{-iX} over 2}.end{aligned}}}
Например, пусть X — стандартная матрица Паули:
σ 1 = σ x = ( 0 1 1 0 ) , {displaystyle sigma _{1}=sigma _{x}={egin{pmatrix}0&11&0end{pmatrix}}~,}
Тогда
sin ( θ σ 1 ) = sin ( θ ) σ 1 , cos ( θ σ 1 ) = cos ( θ ) I , {displaystyle sin( heta sigma _{1})=sin( heta )~sigma _{1},qquad cos( heta sigma _{1})=cos( heta )~I~,}
Можно вычислить и кардинальный синус:
sinc ( θ σ 1 ) = sinc ( θ ) I . {2}X=I}
{2}X=I}
Если X является диагональной матрицей, sin X и cos X также являются диагональными матрицами, причём (sin X)nn = sin(Xnn) и (cos X)nn = cos(Xnn), то есть синус и косинус диагональной матрицы могут быть вычислены путём вычисления соответственно синусов и косинусов элементов аргумента на главной диагонали.
Матричные аналоги формул синуса и косинуса суммы справедливы тогда и только тогда, когда матрицы коммутируют, то есть XY = YX:
sin ( X ± Y ) = sin X cos Y ± cos X sin Y cos ( X ± Y ) = cos X cos Y ∓ sin X sin Y {displaystyle {egin{aligned}sin(Xpm Y)=sin Xcos Ypm cos Xsin Ycos(Xpm Y)=cos Xcos Ymp sin Xsin Yend{aligned}}}
Другие функции
Тангенс, обратные тригонометрические функции, гиперболические функции и обратные гиперболические функции так же могут быть определены и для матриц:
arcsin X = − i ln ( i X + I − X 2 ) {displaystyle arcsin X=-iln left(iX+{sqrt {I-X^{2}}}
ight)} (см. Обратные тригонометрические функции#Связь с натуральным логарифмом, Матричный логарифм, Квадратный корень из матрицы) sinh X = e X − e − X 2 cosh X = e X + e − X 2 {displaystyle {egin{aligned}sinh X&={e^{X}-e^{-X} over 2}cosh X&={e^{X}+e^{-X} over 2}end{aligned}}}
Обратные тригонометрические функции#Связь с натуральным логарифмом, Матричный логарифм, Квадратный корень из матрицы) sinh X = e X − e − X 2 cosh X = e X + e − X 2 {displaystyle {egin{aligned}sinh X&={e^{X}-e^{-X} over 2}cosh X&={e^{X}+e^{-X} over 2}end{aligned}}}
и так далее.
Как найти детерминант матрицы онлайн · Как пользоваться Контрольная Работа РУ
Пример использования сервиса по нахождению определителя матрицы
1. Попробуем сначала матрицу с обычными неизвестными a, b и q и числами:
Введём здесь матрицу, как изображено на рис. ниже
После того, как вы нажмёте кнопку «Далее», вы получите следующее подробное решение:
| Дана матрица А= |
[q 0 -q] [ ] [3 4 -b] [ ] [a q 0 ] |
Вычисляем последовательно детерминант det(A):
[q 0 -q] [ ] [3 4 -b] [ ] [a q 0 ] |
= | + (q) *( |
[4 -b] [ ] [q 0 ] |
) | — (0) *( |
[3 -b] [ ] [a 0 ] |
) | + (-q) *( |
[3 4] [ ] [a q] |
) |
[4 -b] [ ] [q 0 ] |
= | + (4) *( | [0] |
) | — (-b) *( |
[q] |
) |
[3 -b] [ ] [a 0 ] |
= | + (3) *( |
[0] |
) | — (-b) *( |
[a] |
) |
[3 4] [ ] [a q] |
= | + (3) *( |
[q] |
) | — (4) *( |
[a] |
) |
Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,
| получаем det(A) = det( |
[q 0 -q] [ ] [3 4 -b] [ ] [a q 0 ] |
) = |
4*a*q + b*q^2 — 3*q^2
2. Второй пример с использованием функций синус и косинус: sin(x) и cos(x):
Второй пример с использованием функций синус и косинус: sin(x) и cos(x):
Нажмёте кнопку «Далее», получите ответ:
| Дана матрица А= |
[sin(x) cos(x) 0] [ ] [-cos(x) sin(x) 0] [ ] [ 0 0 1] |
Вычисляем последовательно детерминант det(A):
[sin(x) cos(x) 0] [ ] [-cos(x) sin(x) 0] [ ] [ 0 0 1] |
= | + (sin(x)) *( |
[sin(x) 0] [ ] [ 0 1] |
) | — (cos(x)) *( |
[-cos(x) 0] [ ] [ 0 1] |
) | + (0) *( |
[-cos(x) sin(x)] [ ] [ 0 0 ] |
) |
[sin(x) 0] [ ] [ 0 1] |
= | + (sin(x)) *( |
[1] |
) | — (0) *( |
[0] |
) |
[-cos(x) 0] [ ] [ 0 1] |
= | + (-cos(x)) *( |
[1] |
) | — (0) *( |
[0] |
) |
[-cos(x) sin(x)] [ ] [ 0 0 ] |
= | + (-cos(x)) *( |
[0] |
) | — (sin(x)) *( |
[0] |
) |
Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,
| получаем det(A) = det( |
[sin(x) cos(x) 0] [ ] [-cos(x) sin(x) 0] [ ] [ 0 0 1] |
) = | = sin(x)^2 + cos(x)^2 |
3. Ещё один пример — с простыми и отрицательными числами и определителем квадратной матрицей 2×2 (предыдущие примеры были с матрицей 3×3):
Ещё один пример — с простыми и отрицательными числами и определителем квадратной матрицей 2×2 (предыдущие примеры были с матрицей 3×3):
Сначала изменим размер матрицы до 2 на 2, после введём заданные числа, так, как на рис. ниже:
Результат решения детерминанта матрицы 2 на 2:
| Дана матрица А= |
[1 9 ] [ ] [2 -4] |
Вычисляем последовательно детерминант det(A):
[1 9 ] [ ] [2 -4] |
= | + (1) *( |
[-4] |
) | — (9) *( |
[2] |
) |
Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,
| получаем det(A) = det( |
[1 9 ] [ ] [2 -4] |
) = | = -22 |
— для чего нужен косинус/синус матрицы?
спросил
Изменено 4 года, 8 месяцев назад
Просмотрено 832 раза
$\begingroup$
На уроке расширенной линейной алгебры мы недавно узнали о косинусе, экспоненте и синусе матрицы — как их определить, как найти и т. д. Однако мы не узнали о приложениях и необходимости их определения. концепции.
Я где-то читал о том, как экспонента матрицы используется в робототехнике (экспоненциальные координаты), но зачем определять косинус и синус? Это просто для удовольствия?
д. Однако мы не узнали о приложениях и необходимости их определения. концепции.
Я где-то читал о том, как экспонента матрицы используется в робототехнике (экспоненциальные координаты), но зачем определять косинус и синус? Это просто для удовольствия?
- линейная алгебра
- мягкий вопрос
- матрично-экспоненциальный
$\endgroup$
2
$\begingroup$
Прежде чем я начну, просто учтите, что когда мы оцениваем функцию в матрице, мы не имеем в виду поэлементную оценку (за исключением Octave и Matlab):
$$\text{Если } A=[A_{i,j}] \text{, то } f(A)\neq[f(A_{i,j})].$$
Для вещественной функции $f$ с разложением Тейлора мы сначала определяем матричный эквивалент $f$ для диагональных матриц:
$$\text{Если } D=\begin{bmatrix}d_1\\&d_2\\&&\ddots\\&&&d_n\end{bmatrix} \qquad \text{то } f(D):=\begin{bmatrix}f (d_1)\\&f(d_2)\\&&\ddots\\&&&f(d_n)\end{bmatrix}.
Теперь я просто упомяну, что матрицы, такие как дискретные косинусные преобразования и дискретные синусоидальные преобразования (которые на самом деле построены как поэлементные вычисления $[\cos(a_{i,j}) ]$, $[\sin(b_{i,j})]$) полезны, поскольку их столбцы представляют собой собственные векторы некоторых специальных трехдиагональных матриц (Британак, Ип и Рао; Дискретные косинусные и синусоидальные преобразования: общие свойства, быстрые алгоритмы). и Integer Approximations , $2006$), которые возникают при численном решении некоторых дифференциальных уравнений.
$\endgroup$
$\begingroup$ КОММЕНТАРИЙ ( отклонен как комментарий, потому что «слишком длинный на 75 символов» ).- В функциональном анализе понятие функции, которая действует в алгебре, определяется следующим образом: Пусть $ y = f (x) $ функция, скажем, от $\mathbb R$ в $\mathbb R$. x$, действующая в алгебре $\mathcal A_n$ матриц $n\space\text {x} n$. Я не знаю, действуют ли функции sinus и cosinus на $ \mathcal A_n $ ( , возможно, не из-за $|\sin(x)|\le 1$). Французские математики называют это «символическим исчислением» (см. теорему Кацнельсона, которая является экстраординарным случаем, касающимся всех аналитических функций на окружности $\mathbb T$).
x$, действующая в алгебре $\mathcal A_n$ матриц $n\space\text {x} n$. Я не знаю, действуют ли функции sinus и cosinus на $ \mathcal A_n $ ( , возможно, не из-за $|\sin(x)|\le 1$). Французские математики называют это «символическим исчислением» (см. теорему Кацнельсона, которая является экстраординарным случаем, касающимся всех аналитических функций на окружности $\mathbb T$).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 92(A)=I_n$ для диагонализируемых матриц.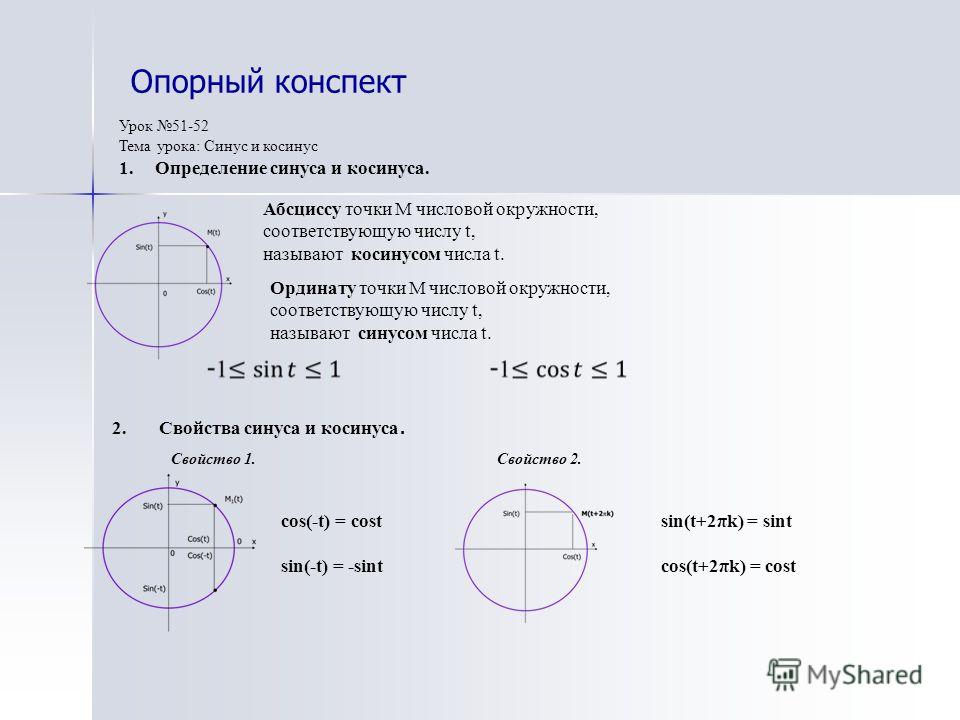 Я также думаю, что это верно в целом, но я не могу сейчас придумать доказательство.
Я также думаю, что это верно в целом, но я не могу сейчас придумать доказательство.
Функции матриц весьма важны. Матричная экспонента появляется повсюду в математике. Он соединяет алгебры Ли и группы Ли. Я не знаю никаких очевидных применений или геометрической интерпретации матричного синуса и косинуса. Я видел, как квадратный корень матрицы несколько раз появлялся в контексте числовой линейной алгебры.
$\endgroup$
4
$\begingroup$
Чтобы расширить ответ Билла: как я уже упоминал здесь, можно использовать разложение Жордана вместо собственного разложения при вычислении синуса матрицы (или косинуса, или любой матричной функции). Таким образом, нужен метод вычисления синуса для скаляров и жордановых блоков; для блока Жордана
$$\mathbf J=\begin{pmatrix}\lambda&1&&\\&\lambda&\ddots&\\&&\ddots&1\\&&&\lambda\end{pmatrix}$$ 9{(p)}(x)=\sin\left(x+p\frac{\pi}{2}\right)$, довольно легко вычислить синус жордановой клетки.
В неточной арифметике разложение Жордана чрезвычайно сложно вычислить стабильно. В этом случае приходится использовать разные методы. Один из способов — заменить разложение Жордана разложением Шура; существует метод Бересфорда Парлетта для вычисления матричных функций для общих треугольных матриц, но я не буду обсуждать это дальше, а вместо этого сосредоточусь на другом методе вычисления. Суть в том, что синус и косинус удовлетворяют аккуратной формуле умножения: 92 x-1\end{align*}$$
Таким образом, как и в случае скаляра, можно использовать сокращение аргумента: делить матрицу пополам достаточное количество раз, пока ее норма не станет крошечной (и помнить, сколько раз $ m$ это деление пополам было выполнено), оценить некоторую хорошую аппроксимацию для синуса и косинуса в этой преобразованной матрице (хорошо работает усеченный ряд Маклорена или Паде, с небольшим преимуществом для аппроксимаций Паде) и, наконец, применить две формулы дублирования в тандеме $m $ раз, чтобы получить синус и косинус исходной матрицы.
Тогда существует единственный непрерывный морфизм $\mathbb C[X]$-алгебры из $B$ в $\mathbb C[A]$.
Обозначим его через $f\mapsto f(A)$.
Для каждого $f$ из $B$ существует единственный многочлен $P(X)\in\mathbb C[X]$ степени меньше $\deg M(X)$, удовлетворяющий условию $P(A) =f(А)$. 9{m_j}}\quad, $$ где $T_j(g)$ или $T_j(g(X))$ обозначает степень меньше $m_j$ полинома Тейлора $g$ в $\lambda_j$, рассматриваемого как элемент $\mathbb C[X]$ .
Матрица $A$ диагонализируема тогда и только тогда, когда все $m_j$ равны $1$. В этом случае мы имеем $$ P(X)=\sum_j\ \prod_{k\neq j}\ \frac{X-\lambda_k}{\lambda_j-\lambda_k}\quad. $$
Тот же ответ с меньшим количеством индексов
Пусть $A$ — комплексная матрица размером $n$ на $n$, пусть
$$
M (X) = \ prod _ {\ lambda \ in \ Lambda} \ (X- \ lambda) ^ {m_ \ lambda} \ \ in \ mathbb C [X]
$$
— ее минимальный многочлен ($m_\lambda$ положительна), пусть $U\subset\mathbb C$ — открытое множество, содержащее $\Lambda$, пусть $B$ — $\mathbb C[X]$-алгебра голоморфных функций на $U$.