Что такое матрица? Понятие матрицы
Матрицы — традиционная головная боль для очень многих студентов. Я бы даже сказал, подавляющего большинства. Ну вот не любят студенты матрицы, хоть ты убей!
Но высшая математика на то и высшая, что работает с более сложными объектами, чем привычная школьная. От этого никуда не деться.) И матрица — один из первых таких объектов, с которым студенты знакомятся уже на первом курсе ВУЗа. И мы тоже познакомимся.)
Итак, ключевые причины, почему же студенты не любят матрицы и всячески стараются избегать работы с ними. Перечислю их.
Причина первая — визуальное восприятие. Оно… непривычно, да.) С формулами, уравнениями, графиками у народа обычно всё более-менее ясно и прозрачно: в школе всё худо-бедно решалось, строилось, ощущалось. Всё знакомо. А тут… Какая-то табличка, какие-то малопонятные буковки с индексами (аж двумя!), которые так и норовят путаться перед глазами. Всё это поначалу очень смущает и даже пугает, да…
Всё это поначалу очень смущает и даже пугает, да…
Причина вторая — это действия с матрицами. Их очень и очень много. Сложение матриц, умножение матриц, транспонирование матриц, поиск обратной матрицы, вычисление определителя, вычисление миноров матрицы, ранга матрицы… Причём все эти операции тоже весьма специфичны и имеют очень мало общего с действиями над обычными числами и алгебраическими выражениями из школьной математики. Эти фишки тоже очень здорово выбивают из колеи.
Причина третья — это рутина. Спору нет, работа с матрицами порой бывает весьма занудной. И скучной. А вместе с рутиной неизбежно возрастает и вероятность глупых арифметических ошибок, да… Особенно при работе с матрицами больших размерностей и/или в процессе элементарных преобразований. Где-то минус теряется, где-то вместо нуля единица пишется, где-то 3+4 двенадцать получается… Эти ляпы на общем фоне рутинной работы просто-напросто не замечаются. И лечатся только лишь предельным вниманием. К сожалению.
И лечатся только лишь предельным вниманием. К сожалению.
И даже после прочтения всех этих ужасов отчаиваться и впадать в панику рано. Прорвёмся!) Для начала успокою: матрица сама по себе — понятие очень простое. Да-да! И главное — полезное и очень мощное в высшей математике. Такое же полезное и мощное, как, скажем, формулы сокращённого умножения в школьной алгебре.) Сомневаетесь? Не надо.) Всё сами дальше увидите. Нужно лишь собраться с духом, рискнуть и… почитать.)
Итак, начнём с первой проблемы — с визуального восприятия.)
Что такое матрица? Устройство матрицы.
Так что же такое матрица? Нет, ничего общего с известным американским научно-фантастическим боевиком данное понятие не имеет. Ну… очень-очень отдалённое сходство всё же есть.)
Итак, удивляемся, но запоминаем:
Матрица — это просто прямоугольная таблица каких-либо элементов.
И всё! Ничего хитрого за этим страшным понятием больше не кроется.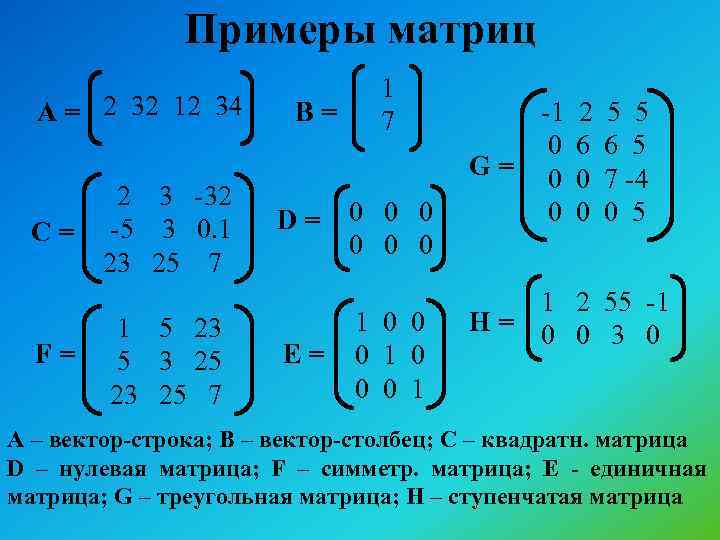 ) Разумеется, каждое слово в определении несёт свой собственный смысл, да. Разберёмся?)
) Разумеется, каждое слово в определении несёт свой собственный смысл, да. Разберёмся?)
Слова «прямоугольная таблица» вопросов ни у кого не вызывают (надеюсь).
Например, можно сочинить что-нибудь типа такого:
Чем не прямоугольная табличка?) Но матрицы в высшей математике изображаются и выглядят немножко по-другому, нежели то что мы называем таблицей в привычном восприятии.
Чаще всего матрица в математике записывается вот так:
Всё очень просто и компактно, правда? Никаких рамок, никаких ячеек — ничего чертить и рисовать не нужно. Любая матрица записывается просто набором каких-то чисел в скобочках. Скобочки, кстати, могут быть не только круглыми. Могут быть и квадратными:
Или даже в виде вот таких двойных прямых палочек:
Это всё одно и то же. В большинстве учебников обычно используются круглые скобки. Квадратные скобки чаще встречаются в технических дисциплинах — в сопромате, строительной механике, теории упругости и т. п. Двойные — почти нигде не встречал. Я всё-таки буду следовать традициям и рисовать круглые скобки. Надеюсь, возражений нет.)
п. Двойные — почти нигде не встречал. Я всё-таки буду следовать традициям и рисовать круглые скобки. Надеюсь, возражений нет.)
Итак, с таблицей разобрались. Что же такое «элемент»? Тоже элементарно (сорри за тавтологию). Любое число, стоящее в матрице на определённом месте, и будет её элементом! Для нашей матрицы число 1 — элемент, 5 — тоже элемент, и 10 — тоже элемент. В общем, вы поняли…
Кстати, слова «на определённом месте» я выделил не зря. И вот почему. Дело всё в том, что любую матрицу следует воспринимать именно как таблицу! А вовсе не как простое множество или набор чисел. Поясняю в чём суть. Рассматривая простое множество чисел, скажем, {1; 2; 3}, мы имеем полное право переставлять элементы множества как попало.
Например, мы можем переставить единичку и двойку. Получим:
{2; 1; 3}
Или переставить двойку и тройку:
{1; 3; 2}
И так далее. Перестановки элементов множества на его сути никак не сказываются. А вот матрицы более чувствительны к перестановкам. И переставлять элементы матрицы просто так нельзя! Каждый элемент строго на своём месте, в своей ячейке. И если переставить местами хотя бы два элемента, то получится, вообще говоря, уже другая матрица. С другими свойствами, да.
Перестановки элементов множества на его сути никак не сказываются. А вот матрицы более чувствительны к перестановкам. И переставлять элементы матрицы просто так нельзя! Каждый элемент строго на своём месте, в своей ячейке. И если переставить местами хотя бы два элемента, то получится, вообще говоря, уже другая матрица. С другими свойствами, да.
Элементами матрицы, кстати, могут быть не только числа. Могут быть и буквенные выражения, и даже функции. Всякое может быть.) Матрицы с функциями в качестве элементов так и называются — функциональными. Это — довольно сложная штука. И встречается уже в серьёзных разделах высшей математики — в дифференциальных уравнениях, в теории функций нескольких переменных и т.п. Этих ужасов пока не будет.)
Мы же пока будем работать только с матрицами, элементами которых являются числа. Или с числовыми матрицами. Намёк понятен?)
Откуда взялись матрицы, зачем они нужны и в чём их смысл?
Итак, мы выяснили, что матрица — это какая-то табличка.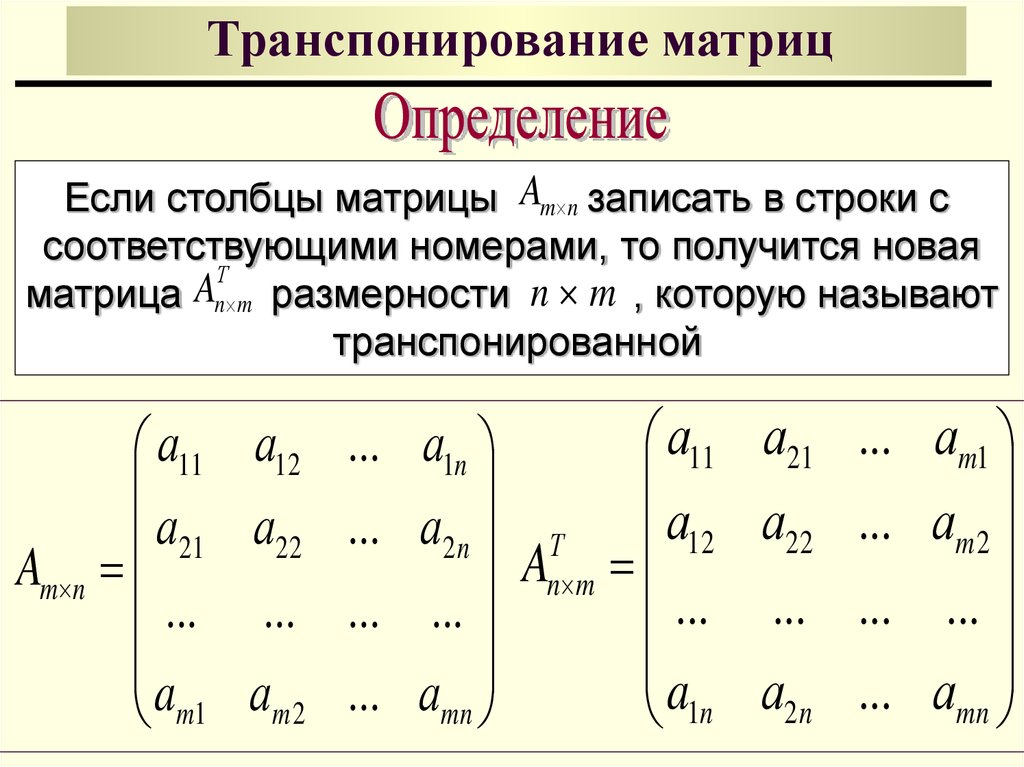 Чаще всего с какими-то числами. Ну и что из этого — спросите вы? Табличка и табличка… Что с ней делать-то? Просто пучить глазки? А делать можно очень много полезного! В соответствующих уроках сами увидите.)
Чаще всего с какими-то числами. Ну и что из этого — спросите вы? Табличка и табличка… Что с ней делать-то? Просто пучить глазки? А делать можно очень много полезного! В соответствующих уроках сами увидите.)
На самом деле с матрицами вы постоянно сталкивались ещё в школе. Сами того не подозревая. Не верите? Сейчас удивитесь.)
Слова «система уравнений» вам знакомы?
Например, такая простенькая системка из двух линейных уравнений:
Решив её (например, подстановкой), получим ответ:
х=1; у=2.
Или, кратенько: (1; 2).
Можно изменить коэффициенты при икс и игрек и получить какую-то новую систему. Например, такую:
Решив её, получим новый ответ: (1; 3).
А можно, например, коэффициенты при переменных не трогать, зато как-то поменять свободные члены. Вместо 8 и 3 записать, скажем, 1 и 2. Получим снова какую-то систему и какое-то решение…
Вместо 8 и 3 записать, скажем, 1 и 2. Получим снова какую-то систему и какое-то решение…
Короче говоря, меняя в системе уравнений коэффициенты при неизвестных и/или свободные члены, можно получать какие-то решения для конкретной системы. Для каждого набора чисел — свои. Кстати, можно и такое наподбирать, что система вообще не будет иметь решений или будет иметь бесконечно много решений.)
Например:
Эта система имеет бесконечно много решений. И (1; 1) — решение, и (0; 2) — решение, и (0,5; 1,5) — тоже решение. Можно перечислять до посинения…)
А теперь я изменю в этой системе всего одно число и получу систему, которая вообще не имеет решений:
Кому интересно, можете решить подстановкой. Получите забавный результат 6=5. Попробуйте.)
Итак, что мы видим? Мы видим, что решение системы колоссальным образом зависит от этого самого набора чисел. Причём только от него! Этот факт настолько важен, что математики даже придумали этот самый набор чисел (коэффициентов и свободных членов системы) оформлять в виде таблички. Или, говоря математическим языком, в виде матрицы.
Причём только от него! Этот факт настолько важен, что математики даже придумали этот самый набор чисел (коэффициентов и свободных членов системы) оформлять в виде таблички. Или, говоря математическим языком, в виде матрицы.
Вот так:
Меняя содержимое табличек (матриц) коэффициентов и свободных членов, мы будем получать различные системы линейных уравнений. С различными решениями, да.)
Кстати, вот вам и ответ на вопрос, почему мы не можем просто так переставлять элементы в матрице. Не догадались? Да! Переставив местами хотя бы два элемента, мы получим уже другую матрицу, соответствующую другой системе уравнений. И с другими решениями…
Ну ладно, системы из двух уравнений — это ещё легко. При их решении про матрицы можно особо не вспоминать: выражай себе по-школьному икс через игрек (или наоборот), делай подстановку, решай — и дело с концом. А вот система из трёх линейных уравнений с тремя неизвестными уже гораздо злее.) Заниматься явным выражением одной переменной через другую, подстановкой и прочим школьным занудством уже неохота, да… А если уравнений и/или неизвестных ещё больше? Скажем, четыре или пять…)
А вот система из трёх линейных уравнений с тремя неизвестными уже гораздо злее.) Заниматься явным выражением одной переменной через другую, подстановкой и прочим школьным занудством уже неохота, да… А если уравнений и/или неизвестных ещё больше? Скажем, четыре или пять…)
И вот тут возникает вполне закономерный вопрос: а можно ли, как-то работая напрямую только с матрицами (коэффициентов и свободных членов), попробовать выяснить:
1) Есть у системы решение или нет его? Или решений вообще бесконечно много?
2) Если решение есть и единственно, то отыскать его быстро и легко.
Новость хорошая: да, можно! Добро пожаловать в новый раздел высшей математики! Под названием линейная алгебра.)
Именно этот раздел и занимается решением систем линейных алгебраических уравнений. Сокращённо — СЛАУ.) Эта страшная аббревиатура будет мозолить вам глаза на протяжении почти всех уроков этого раздела. Привыкаем.)
Привыкаем.)
Причём прошу обратить особое внимание на слово «линейных». Это слово означает, что все неизвестные (x, y, z, …) входят во все уравнения максимум в первой степени и нигде не должно быть деления на неизвестное.
Например:
Это система двух линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. Все неизвестные (x, y, z) в только первой степени, деления на неизвестное ни в одном из уравнений нету. То что число неизвестных больше числа уравнений — вопрос другой. В соответствующем уроке мы научимся с такими злыми системами расправляться.) Главное, что оба уравнения — линейные. Это важно.)
А теперь я изменю в этой системе всего одно слагаемое. Нарисую, например, квадратик над иксом во втором уравнении:
А вот такая система уравнений будет уже нелинейна, да… Именно из-за этого самого квадратика, нарушающего базовый принцип «все неизвестные только в первой степени». К нелинейным системам имеется свой индивидуальный подход, и линейная алгебра перед ними бессильна… С такими системами мы в этом разделе работать не будем. На радость студентам.)
К нелинейным системам имеется свой индивидуальный подход, и линейная алгебра перед ними бессильна… С такими системами мы в этом разделе работать не будем. На радость студентам.)
Итак, запоминаем:
Матрицы — очень мощный инструмент для решения систем линейных алгебраических уравнений (СЛАУ).
Намёк понятен?)
Но не одними лишь системами уравнений ограничивается применение матриц! Матрица — это ещё и своего рода математический оператор. Или преобразователь. Который что-то куда-то преобразует. Или отображает. Как фотоаппарат.) Скажем, один вектор через матрицу можно отобразить в другой. Мощная штука.) Об этом в более серьёзных темах линейной алгебры будет. А системы — так, частный случай. Для начального знакомства.
Как обозначать матрицу и её элементы?
Очень просто. Любые матрицы в математике обозначаются большими буквами латинского алфавита: A, B, C и так далее.
Например, нашу матрицу, приведённую в начале урока, можно обозначить вот так:
И все дела. Слева от знака равенства — название матрицы, справа — её содержимое. В скобочках.)
Но это ещё не все обозначения. Есть и другие, более специфические. Разберём и их.
Любая матрица — это ведь табличка, не так ли? А из чего у нас состоит любая табличка? Правильно, из строчек и колонок! Только это в обиходе.) А в математике те же самые названия звучат более научно — строки и столбцы! Зацените.)
Количество этих самых строк и столбцов коротко записывают в виде произведения m x n и называют размерностью матрицы. Которая дополнительно может указывается в виде подстрочного знака.
Вот так:
Am x n
Читается эта запись очень просто: «матрица A размерности m на n». И вот тут студентов могут подстерегать первые проблемы. Какое число (буква) за что отвечает?
И вот тут студентов могут подстерегать первые проблемы. Какое число (буква) за что отвечает?
Запоминаем:
В размерности матрицы m x n первое число (m) — это (всегда!) количество СТРОК в матрице. Второе число (n) — количество СТОЛБЦОВ.
Именно в таком порядке. Сначала строки, а потом — столбцы. А не наоборот. Например, наша матрица — это матрица размера «два на три»:
У неё две строки (m=2) и три столбца (n=3).
Размерность — ключевая характеристика любой матрицы. Почему? А потому, что на некоторые операции с матрицами (например, на сложение, умножение, взятие определителя и обратной матрицы) существуют очень жёсткие ограничения по размерности! Сами увидите. В соответствующих уроках. )
)
А как кратко в общем виде обозначать элементы матрицы? Тоже просто. Маленькими латинскими буквами с двойным индексом.
Например, вот так:
aij
И всё. Читается эта закорючка так: «а и-жи». Или: «а итое-житое». Забавно, да? Тем не менее вполне себе научно.)
И снова могут быть проблемы с расшифровкой индексов. В школе ведь мы привыкли работать с одиночными индексами. В прогрессиях, например. А тут — двойной! Какой индекс что означает? Не беда! Принцип расшифровки индексов тот же самый — сначала строка, а потом столбец. Первый индекс «i» («и»)– это номер строки, где находится интересующий нас элемент. Второй индекс «j« («жи») – номер столбца.
Например, нам дана такая матрица A:
Размерности какой, кстати? Правильно, «три на три». Или A3x3. Пусть нам надо обратиться, скажем, к элементу матрицы a23.
Здесь первый индекс «и» равен двойке (i=2), а второй индекс «жи» – тройке (j=3). Вот и пересекаем (мысленно!) вторую строку и третий столбец. На пересечении получаем нужный нам элемент a23 = 3.
Вот так:
Точно так же на пересечении первой строки и первого столбца мы получим элемент матрицы a11 = 0, на пересечении третьей строки и второго столбца — элемент a32 = 7 и так далее. Чем-то похоже на игру в кораблики или морской бой, не находите?) Вроде бы, всё элементарно. И что, думаете не ошибаются люди? Ошибаются, ещё как! Ещё один источник дурацких ошибок при работе с элементами матриц — это неправильная нумерация строк и столбцов. Со столбцами обычно всё ясно — нумеруем и читаем привычно, слева направо. Не арабы, чай…) А вот со строками могут случаться и непонятки — сверху вниз их нумеровать или снизу вверх…
И что, думаете не ошибаются люди? Ошибаются, ещё как! Ещё один источник дурацких ошибок при работе с элементами матриц — это неправильная нумерация строк и столбцов. Со столбцами обычно всё ясно — нумеруем и читаем привычно, слева направо. Не арабы, чай…) А вот со строками могут случаться и непонятки — сверху вниз их нумеровать или снизу вверх…
Запоминаем:
В элементе матрицы aij первый индекс (i) — номер строки, второй индекс (j) — номер столбца. Нумерация строк (всегда!) — сверху вниз. Нумерация столбцов (всегда!) — слева направо.
А теперь, разобравшись с загадочными индексами i и j, мы подходим к самому научному способу задания матрицы — через элемент матрицы в общем виде и диапазон изменения индексов.
Вот она, эта запись:
Расшифровываются эти страшные иероглифы так:
Задана матрица А с элементами aij, где индекс «i» принимает все натуральные значения от единицы до «эм» включительно, а индекс «j» — все натуральные значения от единицы до «эн» включительно.
Солидно, да… Куда проще не заморачиваться и написать кратко и точно Amxn, правда? Но будьте готовы и к такой супернаучной форме записи. Особенно в каких-нибудь продвинутых учебниках.)
Внимание! Запись элемента a23 читается и произносится как «а два три«. Именно так, вы не ослышались.) Ни в коем случае не «a двадцать три«! Или b11 — это элемент «бэ один один« (а не «бэ одиннадцать«)! Такое чтение — это… гм… серьёзный вызов преподавателю.) И говорит о полном отсутствии хоть какого-то понимания. О «зачёте» (или «удовл») даже и не мечтайте после этого. Вот так.
Основы высшей математики — Матрицы — Высшая математика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Матрицы
- Обратная матрица
- Матрицы.
 Вся теория и задачи с решениями или ответами
Вся теория и задачи с решениями или ответами
Основные теоретические сведения
Матрицы
К оглавлению…
Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.
Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a14 есть элемент матрицы, стоящий в первой строке и четвертом столбце, a32 стоит в третьей строке и втором столбце.
Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали.
Побочная диагональ идет «перпендикулярно» главной диагонали.
Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.
Простейшие действия с матрицами
1. Умножение матрицы на число. Для этого необходимо умножить каждый элемент матрицы на данное число.
2. Сложение матриц. Складывать можно только матрицы одинакового размера, то есть имеющие одинаковое число строк и одинаковое число столбцов. При сложении матриц соответствующие их элементы складываются.
3. Транспонирование матрицы. При транспонировании у матрицы строки становятся столбцами и наоборот. Полученная матрица называется транспонированной и обозначается A
Полученная матрица называется транспонированной и обозначается A
4. Умножение матриц. Для произведения матриц существуют следующие свойства:
- Умножать можно матрицы, если число столбцов первой матрицы равно числу строк второй матрицы.
- В результате получится матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
- Умножение матриц некоммутативно. Это значит, что от перестановки местами матриц в произведении результат меняется. Более того, если можно посчитать произведение A∙B, это совсем не означает, что можно посчитать произведение B∙A.
- Пусть C = A∙B. Для определения элемента матрицы С, стоящего в i-той строке и k-том столбце необходимо взять i-тую строку первой умножаемой матрицы и k-тый столбец второй. Далее поочередно брать элементы этих строки и столбца и умножать их.
 Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.
Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.
Свойства произведения матриц:
Определитель матрицы
Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается detA, реже |A| или просто Δ, и вычисляется определённым образом. Для матрицы размера 1х1 определителем является сам единственный элемент матрицы. Для матрицы размера 2х2 определитель находят по следующей формуле:
Миноры и алгебраические дополнения
Рассмотрим матрицу А. Выберем в ней s строк и s столбцов. Составим квадратную матрицу из элементов, стоящих на пересечении полученных строк и столбцов. Минором матрицы А порядка s называют определитель полученной матрицы.
Рассмотрим квадратную матрицу А. Выберем в ней s строк и s столбцов. Дополнительным минором к минору порядка s называют определитель, составленный из элементов, оставшихся после вычеркивания данных строк и столбцов.
Алгебраическим дополнением к элементу aik квадратной матрицы А называют дополнительный минор к этому элементу, умноженный на (–1)i+k, где i+k есть сумма номеров строки и столбца элемента aik. Обозначают алгебраическое дополнение Aik.
Вычисление определителя матрицы через алгебраические дополнения
Рассмотрим квадратную матрицу А. Для вычисления ее определителя необходимо выбрать любую ее строку или столбец и найти произведения каждого элемента этой строки или столбца на алгебраическое дополнение к нему. А дальше надо просуммировать все эти произведения.
Когда будете считать алгебраические дополнения, не забывайте про множитель (–1)i+k. Чтобы счет был более простым, выбирайте ту строку или столбец матрицы, который содержит наибольшее число нулей.
Чтобы счет был более простым, выбирайте ту строку или столбец матрицы, который содержит наибольшее число нулей.
Расчет алгебраического дополнения может сводиться к расчету определителя размером более чем 2х2. В этом случае такой расчет также нужно проводить через алгебраические дополнения, и так далее до тех пор, пока алгебраические дополнения, которые нужно будет считать, не станут размером 2х2, после чего воспользоваться формулой выше.
Обратная матрица
К оглавлению…
Рассмотрим квадратную матрицу А. Матрица A–1 называется обратной к матрице А, если их произведения равны единичной матрице. Обратная матрица существует только для квадратных матриц. Обратная матрица существует, только если матрица А невырождена, то есть ее определитель не равен нулю. В противном случае обратную матрицу посчитать невозможно. Для построения обратной матрицы необходимо:
- Найти определитель матрицы.
- Найти алгебраическое дополнение для каждого элемента матрицы.

- Построить матрицу из алгебраических дополнений и обязательно транспонировать ее. Часто про транспонирование забывают.
- Разделить полученную матрицу на определитель исходной матрицы.
Таким образом, в случае, если матрица А имеет размер 3х3, обратная к ней матрица имеет вид:
Матрицы. Вся теория и задачи с решениями или ответами
К оглавлению…
Решение матричных уравнений. Подробные примеры решений
Предварительно рекомендуется изучить основные действия над матрицами.Даны матричные уравнения
A·X = B, (1)
Y·A = B, (2)
Нельзя ли определить деление матриц?
Вспомним, что в числовой области частное от деления b на a определяется как решение уравнения a∙x=b (или x∙a=b) и существует не всегда.
 Можно попытаться определить «деление» матриц, рассматривая уравнения (1) и (2), в которых, согласно правилу умножения, матрицы A, B, X, Y не могут иметь произвольную структуру. Так, в первом уравнении матрицы A и B должны иметь одинаковое число строк, а во втором – одинаковое число столбцов. Уже отсюда ясно, что если даже оба эти уравнения однозначно разрешимы (а это далеко не всегда так), то их решения вполне могут быть матрицами не только разными, но и разной структуры. Таким образом, для матриц оказывается невозможным определить деление с привычными свойствами.
Можно попытаться определить «деление» матриц, рассматривая уравнения (1) и (2), в которых, согласно правилу умножения, матрицы A, B, X, Y не могут иметь произвольную структуру. Так, в первом уравнении матрицы A и B должны иметь одинаковое число строк, а во втором – одинаковое число столбцов. Уже отсюда ясно, что если даже оба эти уравнения однозначно разрешимы (а это далеко не всегда так), то их решения вполне могут быть матрицами не только разными, но и разной структуры. Таким образом, для матриц оказывается невозможным определить деление с привычными свойствами.
Матричные уравнения вида (1) и (2) решаются следующим образом. Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения (1) на A-1: A-1·A·X = A-1·B, тогда получим E·X = A
X = A-1·B. (3)
Аналогично, умножая справа обе части равенства (2) на A-1, будем иметь: Y·A· A-1 = B· A-1, откуда находим, чтоY = B· A-1. (4)
(4)
Пример 1. Решить матричное уравнение .
Решение. Обозначим , . Тогда матричное уравнение запишется в виде A·X = B. Найдем A-1: ; A11 = 4; A21 = -3; A12 = -2; A22 = 1, . Воспользуемся формулой (3):
Пример 2. Решить матричное уравнение .
Решение. (в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет.
Пример 3. Решить уравнение .
Решение . Данное уравнение записываем в виде A∙X∙B = C. Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1∙A∙X∙B∙B-1 = A-1∙C∙B-1. Так как A∙A-1 = B∙B-1 = E и E∙X = X∙E = X, то X = A-1∙C∙B-1.
Находим обратные матрицы , , тогда
.
Проверка.
Перейти к онлайн решению своей задачи
Пример 6
Вариантов записей матричных уравнений может быть достаточно много, однако, все их можно свести к двум видам:- A·X = B
- Y·A = B
- умножение матриц (
A*B): соответствующие элементы матриц умножаем и складываем: ; - сложение матриц (
C+B): складываются соответствующие элементы матриц C и B ; - разница (вычитание) матриц (
A-B): из каждого элемента матрицы A вычитается соответствующий элемент матрицы B ; - умножение матрицы на число (
2*C): число умножается на каждый элемент матрицы ;
Пример 1. Решить матричные уравнения и сделать проверку.
Решить матричные уравнения и сделать проверку.
A·X - B = 3C. Его можно записать как A·X = 3C + B. Найдем сумму матриц:
| 3C + B = |
|
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 2*(4*4 — (-2)*(-2)) — 3*(1*4 — (-2)*1) + 3*(1*(-2) — 4*1) = -12
Определитель матрицы А равен detA=-12
Так как A невырожденная матрица, то существует обратная матрица A
 Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
Алгебраические дополнения
| A1,1 = (-1)1+1 |
|
∆1,1 = (4*4 — (-2)*(-2)) = 12
| A1,2 = (-1)1+2 |
∆1,2 = -(1*4 — 1*(-2)) = -6
| A1,3 = (-1)1+3 |
∆1,3 = (1*(-2) — 1*4) = -6
| A2,1 = (-1)2+1 |
∆2,1 = -(3*4 — (-2)*3) = -18
| A2,2 = (-1)2+2 |
∆2,2 = (2*4 — 1*3) = 5
| A2,3 = (-1)2+3 |
∆2,3 = -(2*(-2) — 1*3) = 7
| A3,1 = (-1)3+1 |
| A3,2 = (-1)3+2 |
| A3,3 = (-1)3+3 |
Обратная матрица A-1.

| A-1 = 1/12 |
|
| X= 1/12 |
| · |
| = |
|
| X = |
|
Пример 2.
Данное выражение в матричной форме имеет вид: X·A - B = 2C. Преобразуем к виду: X·A = 2C + B или X·A = D, где D = 2C + B
Пример 3.
Пример 4.
Здесь имеем следующий тип матричного уравнения:A - X·B = 2C. Сводим его к типу X·B = A + 2C или X·B = D, где D = A + 2C.
| A + 2C = |
Обозначим:
| A = |
|
Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 3*(3*3 — 1*1) — 2*(2*3 — 1*2) + 1*(2*1 — 3*2) = 12
Определитель матрицы А равен detA=12
Так как A невырожденная матрица, то существует обратная матрица A-1.
 Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
| A1,1 = (-1)1+1 |
| A1,2 = (-1)1+2 |
| A1,3 = (-1)1+3 |
| A2,1 = (-1)2+1 |
| A2,2 = (-1)2+2 |
| A2,3 = (-1)2+3 |
| A3,1 = (-1)3+1 |
| A3,2 = (-1)3+2 |
| A3,3 = (-1)3+3 |
Обратная матрица A-1.

| A-1 = 1/12 |
|
| X = | 1/12 |
| = |
|
| X = |
|
Пример 2.
Перейти к онлайн решению своей задачи
Пример №5. Решение матричных уравнений.
Обозначим:
| A = |
|
| C = |
|
Вычислим определитель матрицы А:
∆ = 3*(-2) — 5*(-1) = -1
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.

Транспонированная матрица AT.
| AT = |
|
A11 = (-1)1+1·-2 = -2; A12 = (-1)1+2·-1 = 1; A21 = (-1)2+1·5 = -5; A22 = (-1)2+2·3 = 3;
Обратная матрица A-1.
| A-1 = 1/-1 |
|
∆ = 5*8 — 7*6 = -2
Определитель матрицы B равен detB=-2
Найдем обратную матрицу B-1.
Транспонированная матрица BT.
Алгебраические дополнения:
A11 = (-1)1+1·8 = 8; A12 = (-1)1+2·6 = -6; A21 = (-1)2+1·7 = -7; A22 = (-1)2+2·5 = 5;
Обратная матрица B-1.

| B-1 = 1/-2 |
|
|
Решение одновременных уравнений с использованием матриц
Матрицы используются во многих сферах жизни, от шифрования данных до разработки трехмерных игр, но они также чрезвычайно полезны в других математических контекстах, таких как решение одновременных уравнений. Набор одновременных уравнений (также известный как система уравнений) может быть решен с помощью различных приложений матричной алгебры с использованием обратных матриц и таких методов, как сокращение строк.
В этой статье мы рассмотрим решение одновременных уравнений с использованием матриц, сначала записав их в матричной форме, а затем изучив различные методы их решения, такие как использование обратных матриц и сокращение строк.
Система уравнений в матричной форме
Чтобы решить систему уравнений с использованием матриц, вы должны иметь возможность переписать эти уравнения в виде матриц.
Следующий пример подробно объясняет процесс.
Перепишите следующий набор уравнений в матричной форме (также известной как \(Ax = b\)):
\begin{equation}\begin{split}-4x + 4y + z & = 3 \\11y — 7x + z & = 4 \\-5x + 3y + 2z & = 5 \\\end{split}\qquad\begin{matrix}(1) \\ (2) \\ (3)\end{matrix}\ конец {уравнение}
Решение
ШАГ 1 : Убедитесь, что переменные находятся в одном и том же порядке для каждого уравнения (т.е. если порядок, который вы выбрали для первого уравнения, \(x, y, z\) тогда переменные в каждом последующем уравнении также должны быть в порядке \(x, y, z\)).
Для этого примера мы выберем порядок \(x, y, z\).
Переменные во втором уравнении не в правильном порядке. Мы исправим это, просто перестроив уравнение так, чтобы порядок переменных был таким же, как и в двух других уравнениях.
Таким образом, второе уравнение будет выглядеть следующим образом:
\[-7x + 11y + z = 4\]
ШАГ 2 : Перепишите уравнения в матричной форме .
Первая матрица, которая нам нужна, это матрица коэффициентов. Это квадратная матрица, содержащая коэффициенты каждой переменной, и ее размер зависит от количества переменных в данных уравнениях.
Каждый столбец в матрице коэффициентов содержит коэффициенты для определенной переменной. Например, столбец 1 содержит коэффициенты \(x\). Столбцы 2 и 3 содержат коэффициенты для \(y\) и \(z\) соответственно. Вот почему так важен порядок переменных в данных уравнениях; если они в неправильном порядке, то коэффициенты будут в неправильных столбцах.
Каждая строка в матрице коэффициентов соответствует одному из заданных уравнений. Все коэффициенты в строке 1 взяты из уравнения 1, в строке 2 содержатся коэффициенты из уравнения 2 и т. д. {bmatrix}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{bmatrix}\]
Как видите, столбцы 1, 2 и 3 содержат коэффициенты для \ (x, y\) и \(z\) соответственно, а строки 1, 2 и 3 содержат коэффициенты для уравнений 1, 2 и 3 соответственно.
Вторая матрица, которая нам нужна, представляет собой матрицу 3 x 1, содержащую переменные, и она известна как матрица переменных. Он всегда должен располагаться справа от матрицы коэффициентов.
Переменные в матрице перечислены сверху вниз в том порядке, который вы выбрали для них, и это должно выглядеть следующим образом:
\[\begin{bmatrix}x \\ y \\ z\end{bmatrix} \]
Последняя необходимая матрица — это матрица 3 x 1, расположенная справа от знака равенства. Она называется постоянной матрицей, и, как и в матрице коэффициентов, каждая строка содержит постоянное значение, принадлежащее соответствующему уравнению.
Это будет выглядеть так:
\[\begin{bmatrix}3 \\ 4 \\ 5\end{bmatrix}\]
Наш окончательный ответ состоит из всех трех матриц, и он будет выглядеть следующим образом:
\[\begin{bmatrix}-4 & 4 & 1 \\11 & -7 & 1 \\-5 & 3 & 2 \\\end{bmatrix}\begin{bmatrix}x \\ y \\ z\ end{bmatrix}=\begin{bmatrix}3 \\ 4 \\ 5 \\\end{bmatrix}\]
Что произойдет, если вы перемножите матрицы?
\[\begin{align}\begin{bmatrix}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}& = \begin{bmatrix}3 \\ 4 \\ 5\end{bmatrix} \\\hspace{1cm} \\\begin{bmatrix}-4x & 4y & z \\ 11x & -7y & z \\ -5x & 3y & 2z\end{bmatrix} & = \begin{bmatrix}3 \\ 4 \\ 5 \end{bmatrix} \\\end{align}\]
Результат дает нам исходные уравнения. Именно по этой причине эти конкретные матрицы изложены таким особым образом.
Расширенные матрицы
Наиболее распространенный метод решения одновременных уравнений с матрицами включает использование сокращения строк. Чтобы выполнить сокращение строк, нужно уметь записывать данные уравнения в расширенной матрице.
Чтобы выполнить сокращение строк, нужно уметь записывать данные уравнения в расширенной матрице.
Используя те же уравнения, что и в предыдущем примере, перепишите их в расширенной матрице.
\begin{equation}\begin{split}-4x + 4y + z & = 3 \\-7x +11y + z & = 4 \\-5x + 3y + 2z & = 5 \\\end{split} \end{уравнение}
Решение
ШАГ 1 : Сначала убедитесь, что все ваши уравнения имеют одинаковый порядок. В этом случае нет никакого уравнения, которое нужно переставлять.
ШАГ 2 : Запишите коэффициенты переменных, чтобы начать матрицу.
\[\left[\begin{array}{rrr}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{array}\right.\]
ШАГ 3 : Проведите вертикальную линию справа от коэффициентов.
\[\left[\begin{array}{rrr|}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{array}\right.\]
ШАГ 4 : Запишите константы в правой части строки и закройте скобки
Ваш ответ должен выглядеть следующим образом:
\[\left[\begin{array}{rrr|r}-4 & 4 & 1 & 3 \\11 & -7 & 1 & 4 \\-5 & 3 & 2 & 5 \end{массив}\right]\]
Решение одновременных линейных уравнений с использованием матриц
Интерпретация систем уравнений
Система уравнений может не иметь единственного решения. Можно использовать расширенные матрицы для определения количества решений, если таковые имеются, в системе уравнений.
Можно использовать расширенные матрицы для определения количества решений, если таковые имеются, в системе уравнений.
Если дана система уравнений с тремя уравнениями с тремя неизвестными, мы можем смоделировать эти три уравнения как плоскости. Одним из уникальных решений было бы пересечение всех плоскостей. Если система имеет бесконечное число решений, то это означает, что все три плоскости пересекаются на линии пересечения. Система без решений не будет иметь точки пересечения всех трех плоскостей.
Бесконечное множество решений
Некоторые системы уравнений могут иметь бесконечное число решений. Это происходит в результате того, что свободная переменная является частью уравнений.
Свободная переменная — это переменная, значение которой может свободно изменяться.
В следующем примере показано, как определить бесконечное количество решений, которые может иметь система уравнений.
Рассчитайте решение следующей системы уравнений:
\[\begin{align}x + 5y — z & = 1 \\2x + 7y — 4z & = 0 \\4x + 11y -10z & = -2\end{align}\]
Решение
ШАГ 1 : Запишите расширенную матрицу.
\[\left[\begin{array}{rrr|r}1 & 5 & -1 & 1 \\ 2 & 7 & -4 & 0 \\ 4 & 11 & -10 & -2\end{массив }\right]\]
ШАГ 2 : Выполнение вычислений строк.
Выполняем следующие операции со строками:
\[\begin{align}R_{3} — 2R_{2} & \to R_{3} \\R_{2} — 2R_{1} & \to R_{ 2} \\R_{3} — R_{2} & \to R_{3} \end{align}\]
для получения расширенной матрицы:
\[\left[\begin{array}{rrr|r}1 & 5 & -1 & 1 \\ 0 & -3 & -2 & -2 \\ 0 & 0 & 0 & 0\end{array}\right]\]
В форме \(Ax = B\) это будет выглядеть следующим образом:
\[\begin{bmatrix}1 & 5 & -1 \\ 0 & -3 & -2 \\ 0 & 0 & 0\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}=\begin{bmatrix}1 \\ -2 \\ 0\ end{bmatrix}\]
Отсюда мы знаем, что \(x + 5y — z = 1\) и \(-3y — 2z = -2\).
Теперь упростим уравнения, чтобы получить следующее:
\[\begin{align}y & = \frac{2}{3} -\frac{2}{3}z \\\hspace{1cm} \ \x & = -5y + 1 + z \qquad \text{Подстановка} \; у \; \текст{в} \; x \\\hspace{1cm} \\\поэтому x & = -\frac{7}{3} + \frac{7}{3}z\end{align}\]
Пусть \(\frac{z {3}\) — свободная переменная \(t\).
Таким образом, уравнения будут выглядеть следующим образом:
\[\begin{align}x & = -\frac{7}{3} + 7t \\y & = \frac{2}{3} — 2t\end {выравнивание}\]
и когда в матричной форме даст нам:
\[\begin{bmatrix}x \\ y \\ z \end{bmatrix} =\begin{bmatrix}-\frac{7}{3} \\ \ frac{2}{3} \\ 0\end{bmatrix} +\begin{bmatrix}7 \\ -2 \\ 3\end{bmatrix} t\]
Оба \(x\) и \(y\ ) зависят от \(z\), поэтому мы можем ввести их в систему. \(z\) — свободная переменная, то есть она может свободно изменять свое значение, а поскольку \(x\) и \(y\) зависят от \(z\), это означает, что существует бесконечное число решений к этой системе уравнений.
Помните, что мы обозначили \(\frac{z}{3} = t\), поэтому \(z = 3t\).
Пример того, как может выглядеть система уравнений с бесконечным числом решений, показан ниже:
Система уравнений с бесконечным числом решений, смоделированных как плоскости. Плоскости пересекаются на линии пересечения — StudySmarter Originals
Нет решений
В следующем примере показано, как определить, не имеет ли система уравнений решений.
Покажите, что следующая система уравнений не имеет решений:
\[\begin{align}x + 2y — z = -8 \\ 2x — y + z = 4 \\ 8x + y + z = 2\end{align}\]
Решение
ШАГ 1 : Запишите расширенную матрицу.
\[\begin{array}{rrr|r}1 & 2 & -1 & -8 \\ 2 & -1 & 1 & 4 \\ 8 & 1 & 1 & 2\end{array}\]
ШАГ 2 : Выполняйте вычисления строк до тех пор, пока не будут получены необходимые нули.
\(R_{3} — R_{2} \к R_{3}, \; R_{2} + R_{1} \к R_{2}, \; R_{3} — 2R_{2} \ до R_{3}\) выполняются для получения:
\[\left[\begin{array}{rrr|r}1 & 2 & -1 & -8 \\ 3 & 1 & 0 & 4 \\ 0 & 0 & 0 & -6\end {массив} \right]\]
Когда вы посмотрите на последнюю строку, вы увидите, что в ней указано, что \(0 = -6\). Это заведомо неверно, и поэтому система не имеет решений.
При моделировании с использованием плоскостей система без решений может выглядеть следующим образом:
Система трех одновременных уравнений без решений, смоделированных как плоскости — StudySmarter Originals 9{-1}\), должен быть на левой стороне других матриц; в противном случае вы не сможете их умножить.
В следующем примере показано, как решать одновременные уравнения с использованием обратных матриц.
Решите следующие уравнения одновременно, используя матричную алгебру:
\[\begin{align}4x + y & = -7 \\3x-2y & = 3 \\\end{align}\]
Решение
ШАГ 1 : Перепишите два уравнения в виде матричного уравнения. Ваш ответ должен выглядеть так:
\[\begin{bmatrix}4 & 1 \\3 & -2 \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix}-7 \\ 3\end {bmatrix}\]
ШАГ 2 : Вычислить обратную матрицу коэффициентов.
Мы хотим найти \(x\) и \(y\), поэтому мы должны изолировать эти две переменные на одной стороне уравнения. Для этого мы должны задействовать единичную матрицу. Мы делаем это, умножая обе части уравнения на обратную матрицу коэффициентов.
9{-1}\) слева, чтобы получить это.Ваш результат будет выглядеть следующим образом:
\[\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} =-\frac{ 1}{11}\begin{bmatrix}-2 & -1 \\ -3 & 4\end{bmatrix}\begin{bmatrix}-7 \\ 3 \end{bmatrix} \]
ШАГ 4 : Упростите, чтобы получить решения для \(x\) и \(y\).
\[\begin{align}\begin{bmatrix}x \\ y\end{bmatrix}& =-\frac{1}{11} \times\begin{bmatrix}11 \\ 33\end{bmatrix} \\\hspace{1cm}\\\begin{bmatrix}x \\ y \end{bmatrix}& = \begin{bmatrix} -1 \\ -3 \end{bmatrix}\end{align}\]
\(\следовательно, \quad x = -1\) и \(y = -3\)
В следующем примере показано, как использовать обратные матрицы для решения одновременных уравнений, содержащих три переменные.
Используйте обратные матрицы для решения следующей системы одновременных уравнений:
\[\begin{align}x — y — z & = 4 \\2x + 3y — z & = 2 \\- x — 2y + 3z & = -3\end{align}\]
Решение
ШАГ 1 : Перепишите уравнения в матричной форме.
9{-1}\) слева от обеих частей уравнения.\[\frac{1}{13} \begin{bmatrix}7 & 5 & 4 \\-5 & 2 & -1 \\-1 & 3 & 5\end{bmatrix}\begin{bmatrix}1 & -1 & -1 \\ 2 & 3 & -1 \\-1 & -2 & 3 \\\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix} =\frac {1}{13} \begin{bmatrix}7 & 5 & 4 \\-5 & 2 & -1 \\-1 & 3 & 5\end{bmatrix} \begin{bmatrix}4 \\ 2 \\ — 3\end{bmatrix}\]
ШАГ 4 : Упрощение.
\[\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}= \frac{1}{13} \begin{bmatrix}26 \\ -13 \\ -12 \end{bmatrix}\]
\[\begin{bmatrix}x \\ y\\z \end{bmatrix} = \begin{bmatrix} 2 \\ -1 \\ -1 \end{bmatrix}\]
\(\следовательно \quad x = 2,\quad y = -1\quad\) и \(\quad z = -1\).
Хотя можно решить для трех неизвестных с помощью обратных матриц (как показано выше), этот метод не рекомендуется, так как он быстро становится утомительным и чрезмерно сложным. Вместо этого следует использовать сокращение строк, которое будет подробно рассмотрено в следующем разделе.
Решение одновременных уравнений с использованием сокращения строк
Сокращение строк — это еще один метод решения одновременных уравнений с использованием матриц. Также известное как Исключение Гаусса , редукция строк использует вычисления строк в расширенной матрице для решения неизвестных в наборе одновременных уравнений.
Вы хотите получить строку с двумя нулями, чтобы можно было вычислить значение одной из переменных, а затем вам нужна строка с одним нулем, чтобы можно было вычислить значение второй переменной.
При выполнении этих вычислений строк следует помнить несколько важных моментов:
В приведенном ниже примере показано, как это сделать.
Используйте сокращение строк для решения следующей системы уравнений:
\[\begin{align}2x + y — 3z = -11 \\x — 2y + z = -3 \\-3x + 4y — 2z = 9 \end{align}\qquad \quad \quad \begin{matrix}(1) \\ (2) \\ (3) \end{matrix}\]
Решение
ШАГ 1 : Запишите расширенная матрица для этих уравнений. Это должно выглядеть следующим образом:
\[\left[\begin{array}{rrr|r}2 & 1 & -3 & -11 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {array}\right]\qquad \quad \quad \begin{array}{r}(1) \\ (2) \\ (3)\end{array}\]
ШАГ 2 : Выполнение вычислений строк .
Сначала запишите расширенную матрицу.
\[\left[\begin{array}{rrr|r}2 & 1 & -3 & -11 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {массив}\right]\]
Какое вычисление мы можем сделать, чтобы получить наш первый ноль?
\[\left[\begin{array}{rrr|r}5 & 0 & -5 & -25 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {array}\right]\quad \begin{array}{r}2 \times R_{1} + R_{2} \to R_{1} \\ \hspace{1cm} \\ \hspace{1cm}\end {массив}\]
Мы всегда записываем вычисляемые строки рядом с матрицей.
Второй ноль должен находиться в том же столбце, что и первый.
\[\left[\begin{array}{rrr|r}5 & 0 & -5 & -25 \\ -1 & 0 & 0 & 3 \\ -3 & 4 & -2 & 9\end{массив}\right]\quad \begin{array}{r}\hspace{1cm} \\ 2 \times R_{2} + R_{3} \to R_{2} \\ \hspace{1cm} \end{array}\]
Так уж получилось, что и второй, и третий нуль были получены с помощью этого вычисления второй строки. Это не всегда так, и вам часто придется выполнять вычисление третьей строки, чтобы получить третий ноль.
ШАГ 3 : Рассчитать значения неизвестных.
Из строки 2: \[\begin{align}-x & = 3 \\\поэтому \qquad x & = -3 \end{align}\]
Из строки 1 (замените \(x\) в): \[\begin{align}5x — 5z & = -25 \\5(-3) — 5z & = -25 \\-5z & = -10 \\\поэтому \qquad z & = 2\end{align}\]
Из строки 3 (подставьте \(x\) и \(z\) в):
\[\begin{align}-3x + 4y — 2z & = 9 \\-3(-3) + 4y — 2(2) & = 9 \\4y & = 4 \\\поэтому \qquad y & = 1 \end{align}\]
\ (\поэтому \qquad x = -3; \; y = 1\) и \(z = 2\)
Существует множество различных способов решения одновременных уравнений с использованием редукции строк, и расчеты строк, которые вы выберете, могут быть отличаются от используемых здесь.
Примеры решения одновременных уравнений с использованием матриц 2×2
В следующих примерах основное внимание уделяется решению одновременных уравнений 2-го порядка, то есть вам придется использовать матрицы 2 x 2.
Найдите \(x\) и \(y\), используя обратные матрицы.
\[\begin{align}6x — 5y & = 7 \\12x + 20y & = -4 \end{align}\]
Решение
Сначала мы должны переписать уравнения в матричной форме.
\[\begin{bmatrix}6 и -5 \\ 12 и 20 \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix}7 \\ -4\end {bматрица}\] 9{-1}=\frac{1}{180}\begin{bmatrix}20 & 5 \\ -12 & 6\end{bmatrix}\end{align}\]
Умножить на обратную матрицу слева от обе части уравнения, чтобы получить:
\[\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \end{bmatrix}= \frac{1} {180} \begin{bmatrix}20 и 5 \\ -12 и 6\end{bmatrix}\begin{bmatrix}7 \\ -4\end{bmatrix}\]
Упростите дальше, чтобы получить окончательный результат:
\[\begin{bmatrix}x \\ y\end{bmatrix}=\frac{1}{180}\begin{bmatrix}120 \\ -108\end{bmatrix}\]
\(\следовательно \qquad x = \frac{2}{3} \; \text{and} \; y = -\frac{3}{5}\)
Можно также решить множество одновременного только с 2 неизвестными с использованием сокращения строк. Следующий пример показывает, как это делается.
Найдите \(x\) и \(y\), используя сокращение строк.
\[\begin{align}8x — 3y & = 6 \\-16x + y & = -\frac{31}{3}\end{align}\]
Решение
Запишите дополненное матрица для системы.
\[\left[\begin{array}{rr|r}8 & -3 & 6 \\ -16 & 1 & -\frac{31}{3}\end{array}\right]\]
Далее выполнять операции со строками до тех пор, пока в одной из строк не будет получен ноль. Поскольку есть только две переменные для решения, нам нужен только один ноль, так как это позволит нам вычислить значение одной из переменных. Затем мы можем использовать вычисленную переменную, чтобы найти значение другой неизвестной, подставив ее обратно в уравнение.
\[\left[\begin{array}{rr|r}8 & -3 & 6 \\ 0 & -5 & \frac{5}{3}\end{array}\right]\qquad\begin {matrix}\hspace{1cm} \\ R_{2} + 2R_{1} \to R_{2}\end{matrix}\]
Найдите \(x\) и \(y\).
\[\begin{align}-5y & = \frac{5}{3} \\y & = -\frac{1}{3} \\\hspace{1cm} \\\поэтому \qquad8x — 3y & = 6 \\8x — 3(-\frac{1}{3}) & = 6 \\x & = \frac{5}{8}\end{align}\]
Решение одновременных уравнений с использованием матриц 3×3 примеры
В некоторых случаях невозможно избежать вычислений, которые приводят к большим числам. Следующий пример иллюстрирует это.
Следующий пример иллюстрирует это.
Решите следующую систему уравнений, используя сокращение строк:
\[\begin{align}-4x — 5y +3z & = 7\\-2x + 3y — z & = -25 \\3x — 2y — 4z & = -6\end{align}\]
Решение
ШАГ 1 : Запишите расширенную матрицу.
\[\left[\begin{array}{rrr|r}-4 & — 5 & 3 & 7 \\ -2 & 3 & -1 & -25 \\ 3 & -2 & -4 & -6 \end{массив}\right]\]
ШАГ 2 : Выполнение вычислений строк.
\[\left[\begin{array}{rrr|r}-10 & 4 & 0 & -68 \\ -2 & 3 & -1 & -25 \\ 3 & -2 & -4 & -6 \end{массив}\right]\quad\begin{array}{r}R_{1} + 3R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{ массив}\]\[\left[\begin{array}{rrr|r}-10 и 4 и 0 и -68 \\ -11 и 14 & 0 и -94 \\ 3 & -2 & -4 & -6\end{массив}\right]\quad\begin{массив}{r}4R_{2} — R_{3} \to R_{2}\end{массив }\]\[\left[\begin{array}{rrr|r}-48 & 0 & 0 & -288 \\ -11 & 14 & 0 & -94 \\ 3 & -2 & -4 & -6 \end{массив}\right]\quad\begin{массив}{r}7R_{1} — 2R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{ array}\]
ШАГ 3 : Вычислите значения переменных.
\[\begin{align}-48x & = — 288 \\x & = 6\end{align}\]
\[\begin{align}-11x + 14y & = -94 \\\qquad -11(6) + 14y & = -94 \\14y & = -28 \\y & = -2\end{align}\]
\[\begin{align}3x — 2y — 4z & = -6 \\3(6) — 2(-2) — 4z & = -6 \\-4z & = -28 \\z &= 7\end{align}\]
\(\поэтому \qquad x = 6, \; y = -2\) и \(z = 7\)
Некоторые уравнения могут содержать только две переменные. В этих случаях вы просто используете ноль в качестве коэффициента для отсутствующей переменной.
Решите следующие одновременные уравнения, используя сокращение строк:
\[\begin{align}2b + c & = — 8 \\a — 2b — 3c & = 0 \\-a + b + 2c & = 3\end{align}\]
Решение
ШАГ 1 : Запишите расширенную матрицу.
\(2b + c= — 8\) — это то же самое, что сказать \(0a + 2b + c\), поэтому мы говорим, что коэффициент \(a\) равен 0 для уравнения 1.
\[\ left[\begin{array}{rrr|r}0 & 2 & 1 & -8 \\ 1 & -2 & -3 & 0 \\ -1 & 1 & 2 & 3\end{массив}\right]\ ]
ШАГ 2 : Выполните вычисления строк.
Ноль на самом деле упрощает решение системы уравнений, так как требуется меньше шагов для получения трех необходимых нулей.
\[\left[\begin{array}{rrr|r}0 & 2 & 1 & -8 \\ 0 & -1 & -1 & 3 \\ -1 & 1 & 2 & 3 \end{array }\right]\quad\begin{array}{r}\hspace{1cm} \\R_{2} + R_{3} \to R_{2} \\\hspace{1cm}\end{array}\] \[\left[\begin{array}{rrr|r}0 & 1 & 0 & -5 \\ 0 & -1 & -1 & 3 \\ -1 & 1 & 2 & 3\end{array}\ right]\quad\begin{array}{r}R_{1} + R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{array}\]
ШАГ 3 : Рассчитать значения переменных.
\[\begin{align}b & = -5 \end{align}\]
\[\begin{align}-b — c & = 3 \\-(-5) — c & = 3 \ \c & = 2 \end{align}\]\[\begin{align}-a + b + 2c & = 3 \\-a + (-5) + 2(2) & = 3 \\a & = -4 \end{align}\]
\( \следовательно \qquad a = -4, \; b = -5\) и \(c = 2\)
Решение одновременных уравнений с использованием матриц — основные выводы
- Чтобы записать одновременные уравнения в матричной форме, вы должны сначала написать квадратную матрицу, содержащую коэффициенты, затем переменную матрицу, а справа от знака равенства вы должны написать постоянную матрицу.

- Расширенные матрицы содержат только коэффициенты и константы.
- Обратные матрицы можно использовать для решения одновременных уравнений путем умножения обратной матрицы коэффициентов слева от обеих частей матричного уравнения и упрощения.
- Сокращение строк является предпочтительным методом решения одновременных уравнений с тремя неизвестными и включает использование операций со строками для вычисления значений переменных.
- Уравнения могут иметь бесконечно много решений, не иметь решений и иметь одно единственное решение, и все они могут быть смоделированы с помощью плоскостей.
Объяснение: Матрицы | Новости Массачусетского технологического института
Среди наиболее распространенных инструментов в электротехнике и информатике — прямоугольные сетки чисел, известные как матрицы. Числа в матрице могут представлять данные, а также математические уравнения. Во многих инженерных приложениях, чувствительных ко времени, умножение матриц может дать быстрые, но хорошие приближения к гораздо более сложным вычислениям.
Матрицы изначально возникли как способ описания систем линейных уравнений, задачи, знакомой всем, кто изучал алгебру в начальной школе. «Линейный» просто означает, что переменные в уравнениях не имеют показателей, поэтому их графики всегда будут прямыми линиями.
Уравнение x — 2y = 0, например, имеет бесконечное число решений как для x, так и для y, которые можно изобразить в виде прямой линии, проходящей через точки (0,0), (2,1), (4,2) и так далее. Но если вы объедините его с уравнением x — y = 1, тогда будет только одно решение: x = 2 и y = 1. Точка (2,1) также находится там, где пересекаются графики двух уравнений.
Матрица, изображающая эти два уравнения, будет представлять собой сетку чисел два на два: верхняя строка будет [1-2], а нижняя строка будет [1-1], чтобы соответствовать коэффициентам переменные в двух уравнениях.
В различных приложениях, от обработки изображений до генетического анализа, компьютеры часто используются для решения систем линейных уравнений — обычно с более чем двумя переменными. Еще чаще им приходится перемножать матрицы.
Еще чаще им приходится перемножать матрицы.
Умножение матриц можно рассматривать как решение линейных уравнений для конкретных переменных. Предположим, например, что выражения t + 2p + 3h; 4т+5п+6ч; и 7t + 8p + 9h описывают три разные математические операции, включающие измерения температуры, давления и влажности. Их можно представить в виде матрицы с тремя строками: [1 2 3], [4 5 6] и [7 8 9].
Теперь предположим, что в два разных момента времени вы измеряете температуру, давление и влажность за пределами своего дома. Эти показания также могут быть представлены в виде матрицы с первым набором показаний в одном столбце, а вторым — в другом. Перемножение этих матриц вместе означает сопоставление строк из первой матрицы — той, что описывает уравнения, — и столбцов из второй — той, которая представляет измерения, — умножение соответствующих членов, их сложение и ввод результатов в новую матрицу. Числа в окончательной матрице могут, например, предсказывать траекторию системы низкого давления.
Конечно, сведение сложной динамики моделей погодных систем к системе линейных уравнений само по себе является трудной задачей. Но это указывает на одну из причин, по которой матрицы так распространены в компьютерных науках: они позволяют компьютерам, по сути, заранее выполнять большую вычислительную тяжелую работу. Создание матрицы, которая дает полезные результаты вычислений, может быть трудным, но выполнение матричного умножения, как правило, не так сложно.
Одной из областей информатики, в которой умножение матриц особенно полезно, является графика, поскольку цифровое изображение, по сути, представляет собой матрицу: Строки и столбцы матрицы соответствуют строкам и столбцам пикселей, а числовые элементы соответствуют значениям цвета пикселей. Декодирование цифрового видео, например, требует матричного умножения; Ранее в этом году исследователи Массачусетского технологического института смогли создать один из первых чипов для реализации нового стандарта высокоэффективного кодирования видео для телевизоров сверхвысокой четкости, отчасти благодаря закономерностям, которые они обнаружили в матрицах, которые он использует.
Точно так же, как умножение матриц может помочь в обработке цифрового видео, оно может помочь в обработке цифрового звука. Цифровой аудиосигнал в основном представляет собой последовательность чисел, представляющую изменение во времени давления воздуха акустического аудиосигнала. Многие методы фильтрации или сжатия цифровых аудиосигналов, такие как преобразование Фурье, основаны на умножении матриц.
Другая причина, по которой матрицы так полезны в компьютерных науках, заключается в том, что графы. В этом контексте граф представляет собой математическую конструкцию, состоящую из узлов, обычно изображаемых в виде кругов, и ребер, обычно изображаемых в виде линий между ними. Сетевые диаграммы и генеалогические деревья — знакомые примеры графов, но в информатике они используются для представления всего, от операций, выполняемых во время выполнения компьютерной программы, до отношений, характерных для логистических задач.
Однако любой график можно представить в виде матрицы, где каждый столбец и каждая строка представляют узел, а значение на их пересечении представляет силу связи между ними (которая часто может быть равна нулю). Часто наиболее эффективным способом анализа графов является сначала преобразование их в матрицы, а решения задач, связанных с графами, часто являются решениями систем линейных уравнений.
Часто наиболее эффективным способом анализа графов является сначала преобразование их в матрицы, а решения задач, связанных с графами, часто являются решениями систем линейных уравнений.
линейная алгебра — Простые, логические методы решения матриц?
Исключение Гаусса на матрице — это алгоритмическая процедура, которую вы должны уметь применять к любой матрице, не «думая» слишком много. А именно, вы не должны применять операции со случайными строками, но вы должны применять их определенным образом, который гарантированно приведет к простой системе, из которой решения могут быть считаны немедленно. Когда задействованы параметры, следует как можно дольше откладывать использование параметров для исключения строк, чтобы не обрабатывать разные случаи (что-то равно нулю, что-то не равно нулю). Позвольте мне продемонстрировать это на вашей первой матрице:
- Первое, что нужно сделать, это выполнить операцию со строкой, которая сделает элемент $(1,1)$ матрицы ненулевым (и, желательно, не параметром).
 2 — 2a & a \end{массив}\right]. $$ 92 + 2a}$, поэтому существует единственное значение $x_3$, удовлетворяющее уравнению. Если $a = 0$, то мы получаем уравнение $0 \cdot x_3 = 0$, которое имеет бесконечно много решений. Если $a = 2$, то получается уравнение $0 \cdot x_3 = 2$, не имеющее решений. Теперь выполняем обратную замену. Учитывая $x_3$, мы видим, что второе уравнение имеет единственное решение, если $a \neq 2$, и нам не нужно беспокоиться о случае $a = 2$, потому что третье уравнение не может быть решено. Наконец, мы переходим к первому уравнению, в котором мы видим, что при заданных $x_3,x_2$ мы видим, что $x_1$ определяется однозначно. Подведем итоги:
2 — 2a & a \end{массив}\right]. $$ 92 + 2a}$, поэтому существует единственное значение $x_3$, удовлетворяющее уравнению. Если $a = 0$, то мы получаем уравнение $0 \cdot x_3 = 0$, которое имеет бесконечно много решений. Если $a = 2$, то получается уравнение $0 \cdot x_3 = 2$, не имеющее решений. Теперь выполняем обратную замену. Учитывая $x_3$, мы видим, что второе уравнение имеет единственное решение, если $a \neq 2$, и нам не нужно беспокоиться о случае $a = 2$, потому что третье уравнение не может быть решено. Наконец, мы переходим к первому уравнению, в котором мы видим, что при заданных $x_3,x_2$ мы видим, что $x_1$ определяется однозначно. Подведем итоги:- Если $a = 0$, то решений бесконечно много (размерность пространства решений будет равна единице).
- Если $a = 2$, то решений нет.
- Если $a \neq 0,2$, то система будет иметь единственное решение.
Это требует некоторой практики, но после нескольких упражнений такого рода вы увидите, что сможете выполнять операции быстро и систематически.
 Для практики предлагаю вам попробовать описанный выше подход со второй матрицей и опубликовать свои результаты. Я буду рад проголосовать и прокомментировать вашу попытку.
Для практики предлагаю вам попробовать описанный выше подход со второй матрицей и опубликовать свои результаты. Я буду рад проголосовать и прокомментировать вашу попытку.Для второй матрицы имеем
$$ \left[\begin{array}{rrr|r} 1 и -2 и 0 и 1 \\ 1 & -1 & \лямбда &2\\ 0 & \ лямбда & 9 & \ мю \end{массив}\right] \xrightarrow{R_2 = R_2 — R_1} \left[\begin{массив}{rrr|r} 1 и -2 и 0 и 1 \\ 0 & 1 & \ лямбда & 1 \\ 0 & \ лямбда & 9 & \ мю \end{массив}\right] \xrightarrow{R_3 = R_3 — \lambda R_1} \left[\begin{массив}{rrr|r} 1 и -2 и 0 и 1 \\ 0 & 1 & \ лямбда & 1 \\ 0 и 0 и 92$ (так что $\lambda = \pm 3$) уравнение выглядит так: $0 \cdot x_3 = \mu — \lambda$. Это уравнение имеет бесконечно много решений, если $\mu = \lambda$, и не имеет решений в противном случае. Переходя ко второму уравнению, мы видим, что при $x_3$, $x_2$ определяется однозначно, а при $x_3,x_2$ первое уравнение определяет $x_1$ однозначно. Отсюда три случая:
- Если $\lambda \neq \pm 3$, то система имеет единственное решение.


 Вся теория и задачи с решениями или ответами
Вся теория и задачи с решениями или ответами Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.
Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.