решаем системы линейных алгебраических уравнений (слау)
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8.
Решить систему линейных уравнений методом Крамера:Решение. Находим определитель системы:
Находим определители при неизвестных
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать?
Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать?
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя
определители 3-го порядка, решение такой
системы можно записать в таком же виде,
как и для системы двух уравнений, т. е.
е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где
– определитель
основной матрицы ,
i – определитель
матрицы , полученной
из основной, заменой i -го
столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя
понятие алгебраического дополнения
можно сформулировать теорему
о разложении определителя n -го
порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.
 5. Основные свойства определителей
5. Основные свойства определителейРазлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство
1 . Определитель
не изменится, если в нем поменять местами
строки и столбцы, т. е. при транспонировании
матрицы :
е. при транспонировании
матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство
4 . Определитель
не изменится, если к элементам одной
строки (столбца), прибавить элементы
другой строки (столбца), умноженной на
какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$.
 Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса. - Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус.
 B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель.
 Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
Метод Крамера . Применение для систем линейных уравнений
Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится.
Если определитель матрицы не равен нулю
то система линейных алгебраических уравнений имеет единственное решение.
Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.
Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой.
Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.
Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:
— определители, образованные с заменой -го столбца, столбцом из свободных членов.
Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
—————————————————————
Задача 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера
Решение.
Найдем определитель матрицы коэффициентов при неизвестных
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:
По формулам Крамера находим неизвестные
Итак единственное решение системы.
Задача 2.
Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.
Решение.
Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.
Найдем составляющие определителя:
Подставим найденные значения в определитель
Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:
Разложим каждый из определителей по столбцу в котором есть больше нулей.
По формулам Крамера находим
Решение системы
Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.
Фрагмент программы и результаты вычислений наведены ниже.
——————————
МЕТОД К Р А М Е Р А
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Посмотреть материалы:
- Матричный метод решения системы линейных уравнений
- Метод Гаусса
- Решение методом Крамера СЛАУ 3-4-го порядка
- Решение СЛАУ 3-4 порядка матричным методом
- Решение методом Гаусса СЛАУ 3-5-ого порядка
{jcomments on}
Пример решения методом Крамера
Задание. Дана система линейных уравнений. Найти неизвестные xi методом Крамера.
Дана система линейных уравнений. Найти неизвестные xi методом Крамера.
2 x 1 + 5x2 + 4x3+ x4= 20
x 1 + 3x2 + 2x3+ x4= 11
2 x 1 + 10x2 + 9x3+ 9x4= 40
3 x 1 + 8x2 + 9x3+ 2x4= 37
Решение находим с помощью калькулятора. Запишем систему в виде:
BT = (20,11,40,37)
Найдем главный определитель:
Минор для (1,1):
Найдем определитель для этого минора.
∆1,1 = 3∙(9∙2-9∙9)-10∙(2∙2-9∙1)+8∙(2∙9-9∙1)= -67
Минор для (2,1):
∆2,1 = 5∙(9∙2-9∙9)-10∙(4∙2-9∙1)+8∙(4∙9-9∙1)= -89
Минор для (3,1):
∆3,1 = 5∙(2∙2-9∙1)-3∙(4∙2-9∙1)+8∙(4∙1-2∙1)= -6
Минор для (4,1):
∆4,1 = 5∙(2∙9-9∙1)-3∙(4∙9-9∙1)+10∙(4∙1-2∙1)= -16
Главный определитель:
∆ = 2∙(-67)-1∙(-89)+2∙(-6)-3∙(-16) = -9
Заменим 1-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
Минор для (1,1):
∆1,1 = 3∙(9∙2-9∙9)-10∙(2∙2-9∙1)+8∙(2∙9-9∙1)= -67
Минор для (2,1):
∆2,1 = 5∙(9∙2-9∙9)-10∙(4∙2-9∙1)+8∙(4∙9-9∙1)= -89
Минор для (3,1):
∆3,1 = 5∙(2∙2-9∙1)-3∙(4∙2-9∙1)+8∙(4∙1-2∙1)= -6
Минор для (4,1):
∆4,1 = 5∙(2∙9-9∙1)-3∙(4∙9-9∙1)+10∙(4∙1-2∙1)= -16
Определитель минора:
∆1 = 20∙(-67)-11∙(-89)+40∙(-6)-37∙(-16)
Заменим 2-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
Минор для (1,1):
∆1,1 = 11∙(9∙2-9∙9)-40∙(2∙2-9∙1)+37∙(2∙9-9∙1)= -160
Минор для (2,1):
∆2,1 = 20∙(9∙2-9∙9)-40∙(4∙2-9∙1)+37∙(4∙9-9∙1)= -221
Минор для (3,1):
∆3,1 = 20∙(2∙2-9∙1)-11∙(4∙2-9∙1)+37∙(4∙1-2∙1)= -15
Минор для (4,1):
∆4,1 = 20∙(2∙9-9∙1)-11∙(4∙9-9∙1)+40∙(4∙1-2∙1)= -37
Определитель минора:
∆2 = 2∙(-160)-1∙(-221)+2∙(-15)-3∙(-37)
Заменим 3-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
Минор для (1,1):
∆1,1 = 3∙(40∙2-37∙9)-10∙(11∙2-37∙1)+8∙(11∙9-40∙1)= -137
Минор для (2,1):
∆2,1 = 5∙(40∙2-37∙9)-10∙(20∙2-37∙1)+8∙(20∙9-40∙1)= -175
Минор для (3,1):
∆3,1 = 5∙(11∙2-37∙1)-3∙(20∙2-37∙1)+8∙(20∙1-11∙1)= -12
Минор для (4,1):
∆4,1 = 5∙(11∙9-40∙1)-3∙(20∙9-40∙1)+10∙(20∙1-11∙1)= -35
Определитель минора:
∆3 = 2∙(-137)-1∙(-175)+2∙(-12)-3∙(-35)
Заменим 4-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
Минор для (1,1):
∆1,1 = 3∙(9∙37-9∙40)-10∙(2∙37-9∙11)+8∙(2∙40-9∙11)= 17
Минор для (2,1):
∆2,1 = 5∙(9∙37-9∙40)-10∙(4∙37-9∙20)+8∙(4∙40-9∙20)= 25
Минор для (3,1):
∆3,1 = 5∙(2∙37-9∙11)-3∙(4∙37-9∙20)+8∙(4∙11-2∙20)= 3
Минор для (4,1):
∆4,1 = 5∙(2∙40-9∙11)-3∙(4∙40-9∙20)+10∙(4∙11-2∙20)= 5
Определитель минора:
∆4 = 2∙17-1∙25+2∙3-3∙5
Выпишем отдельно найденные переменные Х:
см. также Вычисление определителя разложением по столбцу.
также Вычисление определителя разложением по столбцу.
Пример №2. Решение находим с помощью калькулятора. Запишем систему в виде:
| A = |
|
Главный определитель:
∆ = 1 • (5 • 0-8 • 6)-4 • (2 • 0-8 • 3)+7 • (2 • 6-5 • 3) = 27 = 27
Заменим 1-ый столбец матрицы А на вектор результата В.
| ∆ 1 = |
|
∆1 = 6 • (5 • 0-8 • 6)-9 • (2 • 0-8 • 3)+(-6 • (2 • 6-5 • 3)) = -54
x1 = -54/27 = -2
Заменим 2-ый столбец матрицы А на вектор результата В.
| ∆ 2 = |
|

∆2 = 1 • (9 • 0-(-6 • 6))-4 • (6 • 0-(-6 • 3))+7 • (6 • 6-9 • 3) = 27
x2 = 27/27 = 1
Заменим 3-ый столбец матрицы А на вектор результата В.
| ∆ 3 = |
|
∆3 = 1 • (5 • (-6)-8 • 9)-4 • (2 • (-6)-8 • 6)+7 • (2 • 9-5 • 6) = 54
x3 = 54/27 = 2
Выпишем отдельно найденные переменные Х
x1 = -54/27 = -2
x2 = 27/27 = 1
x3 = 54/27 = 2
Проверка.
1•-2+2•1+3•2 = 6
4•-2+5•1+6•2 = 9
7•-2+8•1+0•2 = -6
Пример №2. Запишем систему в виде:
| A = |
|
Найдем главный определитель:
Минор для (1,1):
| ∆ 1,1 = |
|

∆1,1 = -1 • (-2 • (-1)-(-9 • (-5)))-(-2 • (-5 • (-1)-(-9 • 0)))+(-5 • (-5 • (-5)-(-2 • 0))) = -72
Минор для (2,1):
| ∆ 2,1 = |
|
∆2,1 = -1 • (-2 • (-1)-(-9 • (-5)))-(-2 • (12 • (-1)-(-9 • (-5))))+(-5 • (12 • (-5)-(-2 • (-5)))) = 279
Минор для (3,1):
| ∆ 3,1 = |
|
Минор для (4,1):
| ∆ 4,1 = |
|
Главный определитель:
∆ = 2 • (-72)-1 • 279+3 • 63-7 • (-45) = 81
Заменим 1-ый столбец матрицы А на вектор результата В.

| ∆ 1 = |
|
| ∆ 1,1 = |
|
Минор для (2,1):
| ∆ 2,1 = |
|
Минор для (3,1):
| ∆ 3,1 = |
|
Минор для (4,1):
| ∆ 4,1 = |
|
Определитель минора:
∆1 = 1 • (-72)-0 • 279+3 • 63-(-4 • (-45))
x1 = -63/81 = -0.
 78
78Заменим 2-ый столбец матрицы А на вектор результата В.
| ∆ 2 = |
|
| ∆ 1,1 = |
|
Минор для (2,1):
| ∆ 2,1 = |
|
Минор для (3,1):
| ∆ 3,1 = |
|
Минор для (4,1):
| ∆ 4,1 = |
|
Определитель минора:
∆2 = 2 • (-115)-1 • 408+3 • 105-7 • (-50)
x2 = 27/81 = 0.
 33
33Заменим 3-ый столбец матрицы А на вектор результата В.
| ∆ 3 = |
|
| ∆ 1,1 = |
|
∆1,1 = -1 • (3 • (-1)-(-4 • (-5)))-(-2 • (0 • (-1)-(-4 • 0)))+(-5 • (0 • (-5)-3 • 0)) = 23
Минор для (2,1):
| ∆ 2,1 = |
|
Минор для (3,1):
| ∆ 3,1 = |
|
Минор для (4,1):
| ∆ 4,1 = |
|
Определитель минора:
∆3 = 2 • 23-1 • (-69)+3 • (-21)-7 • 10
x3 = -18/81 = -0.
 22
22Заменим 4-ый столбец матрицы А на вектор результата В.
| ∆ 4 = |
|
| ∆ 1,1 = |
|
Минор для (2,1):
| ∆ 2,1 = |
|
Минор для (3,1):
| ∆ 3,1 = |
|
Минор для (4,1):
| ∆ 4,1 = |
|
Определитель минора:
∆4 = 2 • 80-1 • (-303)+3 • (-84)-7 • 43
x4 = -90/81 = -1.
 11
11Выпишем отдельно найденные переменные Х
x1 = -63/81 = -0.78
x2 = 27/81 = 0.33
x3 = -18/81 = -0.22
x4 = -90/81 = -1.11
Проверка.
2•-0.78+-1•0.33+12•-0.22+-5•-1.11 = 1
1•-0.78+-1•0.33+-5•-0.22+0•-1.11 = 0
3•-0.78+-2•0.33+-2•-0.22+-5•-1.11 = 3
7•-0.78+-5•0.33+-9•-0.22+-1•-1.11 = -4
Пример №3. Запишем систему в виде:
| A = |
|
Главный определитель:
∆ = 2 • (-2 • 1-1 • 2)-1 • (1 • 1-1 • (-1))+3 • (1 • 2-(-2 • (-1))) = -10 = -10
Заменим 1-ый столбец матрицы А на вектор результата В.
| ∆ 1 = |
|
x1 = 10/-10 = -1
Заменим 2-ый столбец матрицы А на вектор результата В.

| ∆ 2 = |
|
x2 = 20/-10 = -2
Заменим 3-ый столбец матрицы А на вектор результата В.
| ∆ 3 = |
|
x3 = 30/-10 = -3
Выпишем отдельно найденные переменные Х
x1 = 10/-10 = -1
x2 = 20/-10 = -2
x3 = 30/(-10) = -3
Проверка.
2•-1+1•-2+-1•-3 = -1
1•-1+-2•-2+2•-3 = -3
3•-1+1•-2+1•-3 = -8
Пример №4. Запишем систему в виде:
| A = |
|
Главный определитель:
∆ = 1 • (3 • 5-(-1 • (-2)))-4 • (-1 • 5-(-1 • 1))+2 • (-1 • (-2)-3 • 1) = 27 = 27
Заменим 1-ый столбец матрицы А на вектор результата В.

| ∆ 1 = |
|
x1 = -27/27 = -1
Заменим 2-ый столбец матрицы А на вектор результата В.
| ∆ 2 = |
|
x2 = 54/27 = 2
Заменим 3-ый столбец матрицы А на вектор результата В.
| ∆ 3 = |
|
x3 = 81/27 = 3
Выпишем отдельно найденные переменные Х
x1 = -27/27 = -1
x2 = 54/27 = 2
x3 = 81/27 = 3
Проверка.

1•-1+-1•2+1•3 = 0
4•-1+3•2+-2•3 = -4
2•-1+-1•2+5•3 = 11
Пример №5. Запишем матрицу в виде:
| A = |
|
∆ = 1 • (-2 • (-1)-1 • 1)-2 • (2 • (-1)-1 • 2)+3 • (2 • 1-(-2 • 2)) = 27
Пример №6. При решении системы линейных уравнений с квадратной матрицей коэффициентов А можно применять формулы Крамера, если:
- столбцы матрицы А линейно независимы;
- определитель матрицы А не равен нулю;
Пример №7. Дана система трех линейных уравнений с тремя неизвестными. Найти ее решение с помощью формул Крамера. Выполнить проверку полученного решения.
-75x 1 + 35 x 2 + 25 x 3 = -4,5
25x 1 — 70x 2 + 25 x 3 = -20
15x 1 + 10x 2 — 5 5 x 3 = -30
- Решение
- Видеоинструкция
Решение получаем через калькулятор. Запишем систему в виде:
Запишем систему в виде:
BT = (-4.5,-20,-30)
Главный определитель:
∆ = -75∙(-70∙(-55)-10∙25)-25∙(35∙(-55)-10∙25)+15∙(35∙25-(-70∙25))= -176250 = -176250
Заменим 1-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
∆1 = -4.5∙(-70∙(-55)-10∙25)-(-20∙(35∙(-55)-10∙25))+(-30∙(35∙25-(-70∙25)))= -138450
Заменим 2-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
∆2 = -75∙(-20∙(-55)-(-30∙25))-25∙(-4.5∙(-55)-(-30∙25))+15∙(-4.5∙25-(-20∙25))= -157875
Заменим 3-ый столбец матрицы А на вектор результата В .
Найдем определитель полученной матрицы.
∆3 = -75∙(-70∙(-30)-10∙(-20))-25∙(35∙(-30)-10∙(-4.5))+15∙(35∙(-20)-(-70∙(-4.5)))= -162600
Выпишем отдельно найденные переменные Х
Пример №8. Решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
Решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
Скачать решение
Перейти к онлайн решению своей задачи
Объяснение урока: Правило Крамера | Nagwa
В этом объяснителе мы узнаем, как использовать правило Крамера для решения система линейных уравнений.
Это будет включать использование определителей для решения систем двойки и тройки линейные уравнения.
Правило Крамера дает нам полезный способ решения одновременные уравнения; например, это позволяет нам решить систему уравнения для одной переменной независимо без необходимости решать для всех переменные.
Правило Крамера было разработано Габриэлем Крамером, женевским математиком, в 1750 году, и то, что он изобрел, было способ решения системы линейных уравнений с использованием матричного уравнения и определители соответствующих матриц.
Теперь мы рассмотрим правило Крамера и то, как оно используется. Начнем с системы двух линейных уравнений.
Начнем с системы двух линейных уравнений.
Определение: правило Крамера для системы двух линейных уравнений в двух неизвестных
Если у нас есть следующая система два линейных уравнения с двумя неизвестными 𝑥 и 𝑦 с константами 𝑎–𝑓, 𝑎𝑥+𝑏𝑦=𝑒𝑐𝑥+𝑑𝑦=𝑓, которое можно преобразовать в матричное уравнение 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓, Правило Крамера говорит нам, что если определитель коэффициента матрица отлична от нуля, то 𝑥 = ||| 𝑒𝑏𝑓𝑑 |||||| 𝑎𝑏𝑐𝑑 ||| = 𝑒𝑑 — 𝑏𝑓𝑎𝑑- = ||| является единственным решением этой системы уравнений.
Это часто упрощается до
𝑥=ΔΔ,𝑦=ΔΔ,
где Δ=|||𝑒𝑏𝑓𝑑|||, Δ=|||𝑎𝑒𝑐𝑓||| и Δ=|||𝑎𝑏𝑐𝑑||| являются определителями матриц, найденных
заменив элементы матрицы констант элементами из
столбцы 𝑥- и 𝑦-коэффициентов и
определитель матрицы коэффициентов. Правило Крамера можно распространить на любое
ряд линейных уравнений. Например, для системы из трех уравнений в трех
неизвестных, получаем следующее.
Определение: правило Крамера для системы трех уравнений в Три неизвестных
Если у нас есть следующая система из трех линейных уравнений с тремя неизвестными, 𝑥, 𝑦 и 𝑧, с константами 𝑎–𝑙, 𝑎𝑥+𝑏𝑦+𝑐𝑧=𝑗,𝑑𝑥+𝑒𝑦+𝑓𝑧=𝑘,𝑔𝑥+ℎ𝑦+𝑖𝑧=𝑙, которое можно преобразовать в матричное уравнение 𝑎𝑏𝑐𝑑𝑒𝑓𝑔ℎ𝑖𝑥𝑦𝑧=𝑗𝑘𝑙, Правило Крамера говорит нам, что если Δ не равно нулю, то 𝑥=ΔΔ,𝑦=ΔΔ,𝑧=ΔΔ является единственным решением этой системы уравнений, где Δ=||||𝑗𝑏𝑐𝑘𝑒𝑓𝑙ℎ𝑖||||, Δ=|||||𝑎𝑗𝑐𝑑𝑘𝑓𝑔𝑙𝑖|||||, Δ=||||𝑎𝑏𝑗𝑑𝑒𝑘𝑔ℎ𝑙||||, и Δ=||||𝑎𝑏𝑐𝑑𝑒𝑓𝑔ℎ𝑖|||| являются определителями матриц, найденных заменив элементы матрицы констант элементами из столбцы 𝑥-, 𝑦-, и 𝑧-коэффициенты и определитель коэффициента матрица.
Однако стоит отметить, что правило Крамера можно обобщить на
𝑛 линейные уравнения с 𝑛 неизвестными и различные
обозначение можно увидеть; например, для определителя матрицы вы можете увидеть
𝐷 или |Δ|. В этом объяснении мы будем использовать обозначение в форме Δ
и мы будем иметь дело только с системами линейных уравнений с не более чем тремя неизвестными.
В этом объяснении мы будем использовать обозначение в форме Δ
и мы будем иметь дело только с системами линейных уравнений с не более чем тремя неизвестными.
Теперь мы знаем, что такое правило Крамера и как его использовать, но где это откуда?
Чтобы понять, откуда взялось правило Крамера, попробуем решить следующую систему линейных уравнений: 𝑎𝑥+𝑏𝑦=𝑟,𝑐𝑥+𝑑𝑦=𝑟.
Мы хотим удалить переменную; предполагая как 𝑏, так и 𝑑 отличны от нуля, мы умножаем верхнее уравнение на 𝑑 и нижнее уравнение на 𝑏, а затем вычтите: 𝑎𝑑𝑥+𝑏𝑑𝑦=𝑑𝑟𝑏𝑐𝑥+𝑏𝑑𝑦=𝑏𝑟𝑎𝑑𝑥−𝑏𝑐𝑥=𝑑𝑟−𝑏𝑟.2900 (𝑎𝑑−𝑏𝑐)𝑥=𝑑𝑟−𝑏𝑟.
Наконец, если 𝑎𝑑−𝑏𝑐≠0, 𝑥=𝑑𝑟−𝑏𝑟𝑎𝑑−𝑏𝑐.
В наших обозначениях это ΔΔ; мы могли бы сделать точно так же для 𝑦. Фактически, мы можем сделать то же самое для матрицы более высокого порядка, если определитель отличен от нуля.
Теперь в качестве первого примера мы рассмотрим вопрос, объясняющий условие правила.
Пример 1.
 Определение применимости правила Крамера к решению системы линейных уравнений с бесконечным набором решений
Определение применимости правила Крамера к решению системы линейных уравнений с бесконечным набором решенийПолезно ли правило Крамера для поиска решений систем линейные уравнения, в которых существует бесконечное множество решения?
Ответ
Короткий ответ на этот вопрос — нет, так как правило Крамера не работает. применимо, когда система линейных уравнений имеет бесконечное число решения.
Давайте разберемся, почему. Есть два пути для системы линейных уравнений
иметь бесконечное число решений. Во-первых, может быть больше переменных
чем уравнения. В этом случае правило Крамера неприменимо, так как
нам нужно, чтобы матрица коэффициентов была квадратной. Во-вторых, если определитель
матрица коэффициентов равна нулю, то может быть бесконечное число
решения или нулевые решения. Однако, как мы видим из нашей формулы для
Правило Крамера, делим на определитель коэффициента
матрица; мы не можем этого сделать, если он равен нулю. Следовательно, Крамер
правило не применимо.
Следовательно, Крамер
правило не применимо.
Таким образом, мы можем сделать вывод, что правило Крамера не может быть использовано для нахождение решений систем линейных уравнений, в которых есть бесконечное множество решений.
Мы рассмотрели условия правила, но прежде чем перейти к Глядя на примеры использования правила, мы быстро повторим, как найти определитель 2×2 и 3×3 матрицы.
Практическое руководство. Нахождение определителя матрицы 2 × 2 и 3 × 3
Если мы начнем с матрицы 2×2, 𝑎𝑏𝑐𝑑, затем
Мы получаем этот результат, вычитая произведение диагоналей.
Теперь для матрицы 3×3 𝑎𝑏𝑐𝑑𝑒𝑓𝑔ℎ𝑖, затем, используя первую строку, чтобы найти определитель, мы получаем
. Если посмотреть на определитель матрицы 3 × 3,
важно помнить, что коэффициенты, которые вы умножаете
миноры матрицы 2 × 2 по шаблону
+, -, +
как показано выше.
Здесь мы также помним, что определитель можно вычислить используя любую строку или столбец.
Давайте вспомним, как мы нашли кофактор 2×2:
Если мы возьмем элемент a, а затем удалим столбец и строку, в которых он находится, тогда четыре оставшихся элемента образуют наш кофактор.
Напомнив себе, как находить определители, мы теперь рассмотрим некоторые примеры использования правила Крамера для решения систем линейных уравнений.
Пример 2. Решение системы двух уравнений с использованием определителей
Использование определителей для решения системы −8𝑥−4𝑦=−8,9𝑥−6𝑦=−9.
Ответ
Первым шагом является составление матричного уравнения для нашей системы уравнений: −8−49−6𝑥𝑦=−8−9.
Теперь, когда мы пытаемся решить систему уравнений с помощью определителей, вспомним правило Крамера.
Если Δ не равно нулю, 𝑥=ΔΔ,𝑦=ΔΔ является единственным решением этой системы уравнений, где Δ и Δ определители матриц, найденные подстановкой элементов матрица констант с элементами из столбцов 𝑥- и 𝑦-коэффициенты, следующим образом:
Чтобы применить правило Крамера, нам нужно определить
Δ, Δ,
и Δ. Начнем с Δ:
Δ=||−8−49−6||=(−8×−6)−(−4×9)=48+36=84.
Начнем с Δ:
Δ=||−8−49−6||=(−8×−6)−(−4×9)=48+36=84.
С этим результатом мы не только нашли Δ, но так как Δ отличен от нуля, мы показали, что можем найти единственное решение нашей системы уравнений.
Далее рассчитаем Δ: Δ=||−8−4−9−6||=(−8×−6)−(−4×−9)=48−36=12.
Наконец, вычислим Δ: Δ=||−8−89−9||=(−8×−9)−(−8×9)=72+72=144.
Теперь подставим значения наших определителей в решение по правилу Крамера, чтобы найти значения 𝑥 и 𝑦: 𝑥=ΔΔ,Δ=12,Δ=84; следовательно, 𝑥=1284=17.
Теперь, если мы посмотрим на 𝑦, 𝑦=ΔΔ,Δ=144,Δ=84; следовательно, 𝑦=14484=127.
В заключение можно сказать, что единственное решение системы линейных уравнения 𝑥=17𝑦=127.и
На этом этапе мы можем выполнить быструю проверку, подставив значения
из 𝑥 и 𝑦 в исходный набор
уравнения, чтобы проверить, что оба уравнения удовлетворены, следующим образом:
−8𝑥−4𝑦=−8,✓9𝑥−6𝑦=−9. ✓
✓
В первом уравнении −817−4127=−87−487=−567=−8.✓
Во втором уравнении 917−6127=97−727=−637=−9.✓
В нашем следующем примере мы рассмотрим задачу, в которой система уравнений нужно будет переставить перед решением.
Пример 3. Решение системы двух уравнений с использованием определителей
Использование определителей для решения системы −9𝑥=−8+8𝑦,6𝑦=7+3𝑥.
Ответ
В этом вопросе нас просят решить систему двух линейных уравнения с двумя переменными. Мы могли бы сделать это, исключив переменную; однако мы будем использовать правило Крамера.
Для системы уравнений с двумя неизвестными правило Крамера утверждает что если Δ отличен от нуля, то 𝑥=ΔΔ,𝑦=ΔΔ является единственным решением системы.
Таким образом, первый шаг — преобразовать наши уравнения в форму, которая
можно легко преобразовать в матричное уравнение:
−9𝑥−8𝑦=−8, −3𝑥+6𝑦=7.
Теперь, когда у нас есть наша система в этой форме, мы составим матричное уравнение: −9−8−36𝑥𝑦=−87.
Здесь мы помним, что Δ и Δ – определители матриц, найденных как результат замены элементов матрицы констант на элементы из столбцов 𝑥- и 𝑦-коэффициенты, как показано ниже: Δ=||−8−876||Δ=||−9−8−37||.и
Следующим этапом является вычисление искомых определителей. Начнем с Δ: Δ=||-9-8-36||=(-9×6)-(-8×-3)=-54-24=-78.
С этим результатом мы не только нашли Δ, но и мы также показали, что можем решить нашу систему уравнений, так как определитель матрицы коэффициентов не равен нулю.
Далее рассчитаем Δ: Δ=||−8−876||=(−8×6)−(−8×7)=−48+56=8.
Наконец, вычислим Δ: Δ=||−9−8−37||=(−9×7)−(−8×−3)=−63−24=−87.
У нас есть все, что нужно, чтобы использовать правило Крамера для решения нашей системы уравнений. уравнения. Теперь подставим значения определителей, чтобы найти
значения 𝑥 и 𝑦:
𝑥=ΔΔ,Δ=8,Δ=−78;
следовательно,
𝑥=−878=−439.
уравнения. Теперь подставим значения определителей, чтобы найти
значения 𝑥 и 𝑦:
𝑥=ΔΔ,Δ=8,Δ=−78;
следовательно,
𝑥=−878=−439.
Теперь, если мы посчитаем 𝑦, 𝑦=ΔΔ,Δ=−87,Δ=−78; следовательно, 𝑦=−87−78=2926.
В заключение можно сказать, что единственное решение системы уравнений является 𝑥=−439𝑦=2926.and
В предыдущих двух примерах мы рассмотрели задачи с двумя неизвестными. В следующем примере мы рассмотрим систему трех линейных уравнений с три неизвестных.
Пример 4. Решение системы трех уравнений с использованием определителей
Использование определителей для решения системы 5𝑥=−2𝑦−5+3𝑧,−3𝑥−𝑦+1=2𝑧,2𝑦−𝑧=−5𝑥+3.
Ответ
Чтобы решить систему из трех уравнений с тремя неизвестными с помощью определителей,
можно использовать правило Крамера при условии, что определитель
матрица коэффициентов отлична от нуля.
Тогда единственное решение определяется выражением 𝑥=ΔΔ,𝑦=ΔΔ,𝑧=ΔΔ.
Первый шаг — изменить наши уравнения так, чтобы у нас была константа условия самостоятельно. Мы делаем это для того, чтобы систему можно было легко конвертировать в матричное уравнение: 5𝑥+2𝑦−3𝑧=−5,−3𝑥−𝑦−2𝑧=−1,5𝑥+2𝑦−𝑧=3.
Теперь, когда у нас есть наша система в этой форме, мы составим матричное уравнение: 52−3−3−1−252−1𝑥𝑦𝑧=−5−13.
Далее по правилу Крамера запоминаем, что Δ, Δ, и Δ – определители матриц, которые результат замены элементов матрицы констант на элементы из столбцов 𝑥-, 𝑦-, и 𝑧-коэффициенты следующим образом: Δ=||||−52−3−1−1−232−1||||.
Следующим этапом является вычисление необходимых определителей; мы начнем с Δ: Δ=||||52−3−3−1−252−1||||=5||−1−22−1||−2||−3−25−1||−3||− 3−152||=5(1+4)−2(3+10)−3(−6+5)=2.
С этим результатом мы не только нашли Δ, но и
также показали, что мы можем найти единственное решение нашей системы уравнений. Это связано с тем, что значение Δ отлично от нуля.
Это связано с тем, что значение Δ отлично от нуля.
Далее рассчитаем Δ: Δ=||||−52−3−1−1−232−1||||=−5||−1−22−1||−2||−1−23−1||−3| |−1−132||=−5(5)−2(7)−3(1)=−42.
Затем рассчитаем Δ: Δ=||||5−5−3−3−1−253−1||||=5||−1−23−1||+5||−3−25−1||−3| |−3−153||=5(7)+5(13)−3(−4)=112.
Наконец, вычислим Δ: Δ=||||52−5−3−1−1523||||=5||−1−123||−2||−3−153||−5||−3−152||= 5(−1)−2(−4)−5(−1)=8.
Теперь у нас есть все, что нужно, чтобы использовать правило Крамера для решения задачи. система уравнений; мы подставляем наши значения для определителей в единственное решение, даваемое правилом Крамера, для нахождения значений 𝑥, 𝑦 и 𝑧 следующим образом: 𝑥=ΔΔ,Δ=−42,Δ=2; следовательно, 𝑥=−422=−21.
Теперь вычисляем 𝑦: 𝑦=ΔΔ,Δ=112,Δ=2; следовательно, 𝑦=1122=56.
Наконец, вычисляем 𝑧:
𝑧=ΔΔ,Δ=8,Δ=2;
следовательно,
𝑧=82=4.
В заключение можно сказать, что единственное решение системы линейных уравнения 𝑥=−21,𝑦=56,𝑧=4.и
В качестве последнего примера рассмотрим вопрос, где система уравнений задается через определители.
Пример 5. Решение системы трех уравнений с помощью определителей
Решите, используя правило Крамера, одновременные уравнения |||−1𝑧−4𝑦|||=23, |||2𝑦−5𝑥|||=13, ||3𝑥5𝑧||=51.
Ответ
Чтобы мы могли использовать правило Крамера в этой задаче, первым шагом будет для оценки определителей матриц 2 × 2: |||−1𝑧−4𝑦|||=(−1×𝑦)−(𝑧×(−4))=−𝑦+4𝑧,|||2𝑦−5𝑥|||=(2×𝑥)−(𝑦 ×(−5))=2𝑥+5𝑦,||3𝑥5𝑧||=(3×𝑧)−(𝑥×5)=−5𝑥+3𝑧.
Теперь, когда у нас есть определители, мы можем составить систему из трех уравнений затем его можно использовать для составления матричного уравнения: −𝑦+4𝑧=23,2𝑥+5𝑦=13,−5𝑥+3𝑧=51.
Поскольку нас попросили решить систему уравнений с помощью определителей,
вспомним правило Крамера: если определитель
матрица коэффициентов отлична от нуля, то существует единственное решение системы
данный
𝑥=ΔΔ,𝑦=ΔΔ,𝑧=ΔΔ.
Чтобы применить правило Крамера, перепишем систему в виде матрицы уравнение; однако мы должны быть осторожны, чтобы включить нулевые коэффициенты в наш матрица коэффициентов. Чтобы помочь нам в этом, мы можем переписать нашу систему уравнений чтобы включить нулевые коэффициенты перед записью в виде матричного уравнения: 0𝑥−𝑦+4𝑧=23,2𝑥+5𝑦+0𝑧=13,−5𝑥+0𝑦+3𝑧=51.
При записи в виде матричного уравнения получаем 0−14250−503𝑥𝑦𝑧=231351.
Здесь мы помним, что Δ, Δ и Δ, по правилу Крамера, являются определителями матриц, которые образованный в результате замены элементов матрицы констант на элементы из столбцов 𝑥-, 𝑦- и 𝑧-коэффициенты следующим образом: Δ=||||23−1413505103||||.
Следующим этапом является вычисление искомых определителей; мы начнем
с Δ:
Δ=||||0−14250−503||||=0||5003||+1||20−53||+4||25−50||=0+1(6−0)+ 4(0+25)=106.
Далее рассчитаем Δ: Δ=||||23−1413505103||||=23||5003||+1||130513||+4||135510||=23(15)+1(39)+4(−255) =−636.
Тогда рассчитаем Δ: Δ=||||02342130−5513||||=0||130513||−23||20−53||+4||213−551||=0−23(6)+4(167) =530.
Наконец, рассчитаем Δ: Δ=||||0−1232513−5051||||=0||513051||+1||213−551||+23||25−50||=0+1(167)+23( 25)=742.
Теперь подставим наши значения определителей в уникальные решение из правила Крамера, чтобы найти наши значения 𝑥, 𝑦 и 𝑧: 𝑥=ΔΔ,Δ=−636,Δ=106; следовательно, 𝑥=−636106=−6.
Теперь вычисляем 𝑦: 𝑦=ΔΔ,Δ=530,Δ=106; следовательно, 𝑦=530106=5.
Наконец, мы рассмотрим 𝑧: 𝑧=ΔΔ,Δ=742,Δ=106; следовательно, 𝑧=742160=7.
В заключение можно сказать, что единственное решение системы линейные уравнения 𝑥=−6,𝑦=5,𝑧=7.и
Давайте закончим, повторив некоторые основные моменты.
Ключевые моменты
- Для следующей системы уравнений с двумя неизвестными 𝑎𝑥+𝑏𝑦=𝑒𝑐𝑥+𝑑𝑦=𝑓, Правило Крамера говорит нам, что если Δ не равно нулю, то система имеет единственное решение, заданное формулой 𝑥=ΔΔ,𝑦=ΔΔ.
- Для следующей системы уравнений с тремя неизвестными 𝑎𝑥+𝑏𝑦+𝑐𝑧=𝑗,𝑑𝑥+𝑒𝑦+𝑓𝑧=𝑘,𝑔𝑥+ℎ𝑦+𝑖𝑧=𝑙, Правило Крамера говорит нам, что если Δ не равно нулю, то система имеет единственное решение, заданное формулой 𝑥=ΔΔ,𝑦=ΔΔ,𝑧=ΔΔ.
- Правило Крамера можно распространить на 𝑛 линейные уравнения в 𝑛 неизвестных.
- Чтобы найти Δ, Δ или Δ, мы подставляем значения в матрице констант для столбца в матрице коэффициентов, который идентифицируется и находится определитель вновь образованной матрицы.
- Необходимое условие правила Крамера состоит в том, что определитель матрица коэффициентов ∆ не равна нулю.
, использующие правило Крамера Решающие системы
, использующие правило Крамера 5
5Мы встретили операцию нахождения определителя. Теперь мы видим, что мы можем найти определитель любой квадратной матрицы.
Определение:
| Несовершеннолетний | Определитель формируется, когда строка и столбец, содержащие этот элемент удаляются. Примеры следуют. |
| В матрице слева минор b: | |
| В матрице слева минор а: | |
| В матрице слева минор e: | |
| В матрице слева минор до: | |
| В матрице слева минор ре: |
 Определители можно найти только для квадрата
матрицы.
Определители можно найти только для квадрата
матрицы. | Определитель матрицы 2-го порядка. | |
| Определитель матрицы 3-го порядка. | |
| а умножить на меньшую — b умножить на меньшую + с умножить на меньшую | Другой способ описания определителя матрицы 3-го порядка. |
| Данная проблема. | |
| Раскройте выражение, используя определение определителя матрицы 3-го порядка и миноров. | |
Найдите определители
Матрицы 2-го порядка. | |
| -60 — это решение. |
До сих пор мы решали линейные системы с помощью 1) построения графиков; 2) замена; а также 3) Ликвидация. В этом уроке мы изучим четвертую технику. На самом деле, это Техника является разновидностью Метода исключения. Правило о коэффициентах будет развиваться. Это правило называется правилом Крамера . Правило . Мы начнем с решения общей системы линейных уравнений в стандартной форме.
| Решите данную систему общих линейных уравнений. | |
| Умножить уравнение A на e. Умножьте уравнение B на -b. Добавьте уравнения устранить ю. Решите для х. | |
Подставьте решение x из последнего шага в уравнение A. Решите для
у. | |
| Решение | |
| Проверьте значения в уравнении A. | |
| Проверьте значения в уравнении B. |
| Значения x и y, которые мы нашли выше, всегда будут давать нам решение системы двух линейных уравнений (если уравнения записаны в стандартной форме). С помощью этой формулы мы может игнорировать переменные x и y и алгебраические методы решения и сосредоточиться на коэффициентах а, б, в, г, д, и ф. Мы можем взять эти коэффициенты и поместите их в матрицу или сетку, и сконцентрируйтесь на расчетах с ними. |
| Матрица | Прямоугольный массив чисел со столбцами и строками. Матрица 2 на 2
означает 2 строки и 2 столбца. Матрица коэффициентов из системы выше
было бы: ,
который представляет собой матрицу 2 на 3. Матрица 2 на 2
означает 2 строки и 2 столбца. Матрица коэффициентов из системы выше
было бы: ,
который представляет собой матрицу 2 на 3. |
| Определитель | Определен определитель матрицы 2 на 2 (определитель второго порядка) на примере. Этот операция может быть выполнена только на квадратной матрице. |
| Крамерс Правило |
| Определите коэффициенты | |
 | |
Изучите правила для матриц 2×2 и 3×3, формулы здесь
0
Сохранить
Скачать публикацию в формате PDF Правило Крамера в матрицах представляет решение в терминах определителей матрицы коэффициентов и матриц, полученных заменой одного столбца на вектор-столбец правых частей уравнений. Правило Крамера возникает в матрицах и определителях. Всякий раз, когда система имеет единственное решение, правило Крамера будет самым надежным способом определить решение системы линейных уравнений, в которой столько уравнений, сколько неизвестных. По мере чтения статьи вы узнаете о формуле правила Крамера, концепции определителей, линейных уравнениях, условиях единственного решения в матрице, отсутствии условий решения и многом другом. Прежде чем перейти к обсуждению правила Крамера и его методов с решенными примерами, давайте узнаем о некоторых ключевых терминах.
Правило Крамера возникает в матрицах и определителях. Всякий раз, когда система имеет единственное решение, правило Крамера будет самым надежным способом определить решение системы линейных уравнений, в которой столько уравнений, сколько неизвестных. По мере чтения статьи вы узнаете о формуле правила Крамера, концепции определителей, линейных уравнениях, условиях единственного решения в матрице, отсутствии условий решения и многом другом. Прежде чем перейти к обсуждению правила Крамера и его методов с решенными примерами, давайте узнаем о некоторых ключевых терминах.
Правило Крамера — это явный метод решения системы линейных уравнений с несколькими уравнениями и неизвестными, т. е. квадратной матрицы, действующий, когда система имеет единственное решение. Правило Крамера — это дополнительный подход, позволяющий решать системы линейных уравнений с помощью определителей. Он представляет решение через определители (квадратной матрицы) матрицы коэффициентов и матриц, полученных из нее заменой одного столбца на вектор правых частей уравнений.
Система линейных уравнений с двумя и тремя переменными может быть эффективно решена путем применения определителей. Ниже приведены формулы и шаги для определения решения системы линейных уравнений вместе с решенными примерами.
\(\begin{array}{l} Рассмотрим\ линейную\ систему:\\
ax+by=p\ и\ cx+dy=q\ \\
\ эквивалентную\ матрицу\ form=\begin {bmatrix}a&b\\
c&d\end{bmatrix}\begin{bmatrix}x\\
y\end{bmatrix}=\begin{bmatrix}p\\
q\end{bmatrix}\\
Здесь,\ D=\begin{bmatrix}a&b\\
c&d\end{bmatrix}\\
Рассмотрим \det er\min ant\ отличен от нуля.\\
Тогда\ x\ и\ y\ можно\ вычислить\ по\ правилу Крамера\:\\
x=\frac{\begin{ vmatrix}p&b\\
q&d\end{vmatrix}}{\begin{vmatrix}a&b\\
c&d\end{vmatrix}}=\frac{\left(pd-bq\right)}{\left(ad- bc\right)}\\
Здесь,\ \left|D_x\right|=\begin{vmatrix}p&b\\
q&d\end{vmatrix}\\
y=\frac{\begin{vmatrix}a&p\\
c&q\end{vmatrix}}{\begin{vmatrix}a&b\\
c&d\end{vmatrix}}=\frac{\left(aq-pc\ right)}{\left(ad-bc\right)}\\
Здесь,\ \left|D_y\right|=\begin{vmatrix}a&p\\
c&q\end{vmatrix}\end{array}
\ )
Узнайте больше о линейных неравенствах здесь.
\(\begin{array}{l}Рассмотрим\ линейную\ систему:\\
4x-3y=11\ и\6x+5y=7\\
\эквивалентная\матрица\форма=\begin{bmatrix}4&-3\\
6&\ 5\end{bmatrix}\begin{bmatrix}x\\
y\end{bmatrix}=\begin{bmatrix}11\\
7\end{bmatrix}\\
D=\begin{bmatrix} 4&-3\\
6&\ 5\end{bmatrix}\стрелка вправо\влево|D\вправо|=\begin{vmatrix}4&-3\\
6&\ 5\end{vmatrix}=\left(4\times5 \right)-\left(-3\times6\right)\\
\left|D\right|=20+18=38\\
For\ x\\
D_x=\begin{bmatrix}11&-3\ \
7&\ 5\end{bmatrix}\Стрелка вправо\влево|D_x\right|=\begin{vmatrix}11&-3\\
7&\ 5\end{vmatrix}=55+21\\
\left|D_x\right|=76\\
x=\frac{\left|D_x\right|}{\left|D\right|}=\frac{76}{38}=2\\
Для \ y\\
D_y=\begin{bmatrix}4&11\\
6&\ 7\end{bmatrix}\Стрелка вправо\влево|D_y\right|=\begin{vmatrix}4&11\\
6&\ 7\end{vmatrix }=28-66=-38\\
y=\frac{\left|D_y\right|}{\left|D\right|}=\frac{-38}{38}=-1\\
( x,y)=(2,−1)\end{array}
\)
Ознакомьтесь с этой статьей о системах счисления.
\(\begin{array}{l}Рассмотрим\ линейную\ систему:\\
ax+by+cz=p\ ,\ dx+ey+fz=q\ and\ gx+hy+iz=r\\
\ эквивалентная\ матрица\ form=\begin{bmatrix}a&b&c\\
d&e&f\ \
g&h&i\end{bmatrix}\begin{bmatrix}x\\
y\\
z\end{bmatrix}=\begin{bmatrix}p\\
q\\
r\end{bmatrix}\\
Здесь \ D=\begin{bmatrix}a&b&c\\
d&e&f\\
g&h&i\end{bmatrix}and\ \left|D\right|=\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end {vmatrix}\\
Тогда\ значение\ x\, y\ и\ z\ вычисляется\ по\ правилу Крамера\:\\
x=\frac{\begin{vmatrix}p&b&c\\
q&e&f\\
r&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}}\\
Здесь \ \left|D_x\right|=\begin{vmatrix}p&b&c\\
q&e&f\\
r&h&i\end{vmatrix}\\
y=\frac{\begin{vmatrix}a&p&c\\
d&q&f\\
g&r&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}}\\
Здесь,\ \left|D_y\right|=\begin{vmatrix}a&p&c\ \
d&q&f\\
g&r&i\end{vmatrix}\\
z=\frac{\begin{vmatrix}a&b&p\\
d&e&q\\
g&h&r\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f \\
g&h&i\end{vmatrix}}\\
Здесь,\ \left|D_z\right|=\begin{vmatrix}a&b&p\\
d&e&q\\
g&h&r\end{vmatrix}\end{array}
\ )
\(\begin{array}{l}Для\ упрощения\\
x=\frac{\begin{vmatrix}p&b&c\\
q&e&f\\
r&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}}=\frac{\left|D_x\right|}{\left|D\right|} \\
Где\ D=\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix},\ D_x=\begin{vmatrix}p&b&c\\
q&e&f\\
r&h&i\end{vmatrix}\ \
y=\frac{\begin{vmatrix}a&p&c\\
d&q&f\\
g&r&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}}=\frac{\left|D_y\right|}{\left|D\right|}\\
Где\ D=\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i \end{vmatrix}\ ,\ D_y=\begin{vmatrix}a&p&c\\
d&q&f\\
g&r&i\end{vmatrix}\\
z=\frac{\begin{vmatrix}a&b&p\\
d&e&q\\
g&h&r\end{vmatrix}}{\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}}=\frac{\left|D_z\right|}{\left|D\right|}\ \
Где\ D=\begin{vmatrix}a&b&c\\
d&e&f\\
g&h&i\end{vmatrix}\ ,\ D_z=\begin{vmatrix}a&b&p\\
d&e&q\\
g&h&r\end{vmatrix}\end {массив}
\)
Изучите концепции трехмерной геометрии здесь.
\(\begin{array}{l}Рассмотрим\ линейную\ систему:\\
x+2y+3z=-5\ ,\ 3x+y-3z= 4\ и\ -3x+4y+7z=-7\\
\ Эквивалентная\ матрица\ form=\begin{bmatrix}1&2&3\\
3&1&-3\\
-3&4&7\end{bmatrix}\begin{bmatrix}x\\
y\\
z\end{bmatrix}=\begin{bmatrix}-5\\
4\\
-7 \end{bmatrix}\\
Здесь,\ D=\begin{bmatrix}1&2&3\\
3&1&-3\\
-3&4&7\end{bmatrix}\\
\left|D\right|=\begin{vmatrix }1&2&3\\
3&1&-3\\
-3&4&7\end{vmatrix}=40\\
D_x=\begin{bmatrix}-5&2&3\\
4&1&-3\\
-7&4&7\end{bmatrix}\\
\влево|D_x\вправо|=-40\\
D_y=\begin{bmatrix}1&-5&3\\
3&4&-3\\
-3&-7&7\end{bmatrix}\\
\left|D_y\right|=40\\
D_z=\begin{bmatrix }1&2&-5\\
3&1&4\\
-3&4&-7\end{bmatrix}\\
\left|D_z\right|=-80\\
Тогда\ значение\ x\ ,y\ и\ z \ быть\ рассчитано\ по\ правилу Крамера\:\\
x=\frac{\left|D_x\right|}{\left|D\right|}=-\frac{40}{40}=-1\ \
y=\frac{\left|D_y\right|}{\left|D\right|}=\frac{40}{40}=1\\
z=\frac{\left|D_z\right| }{\left|D\right|}=\frac{-80}{40}=-2\\
(x,y,z)=(−1,1,−2)\end{array}
\)
Условия для правила Крамера
Правило Крамера эффективно для решения небольших систем и может быть вычислено довольно быстро; но по мере роста системы определение новых детерминант может быть утомительным. Например, для системы уравнений с единственным решением определитель матрицы должен быть невырожденным, то есть его значение должно быть ненулевым.
Например, для системы уравнений с единственным решением определитель матрицы должен быть невырожденным, то есть его значение должно быть ненулевым.
\(\begin{array}{l}
Рассмотрим\ два\ уравнения:\\
ax_1+by_1=c_1\\
ax_2+by_2=c_2\\
Одно\ или\бесконечно\ много\ решений\ называются\ непротиворечивым\ решением.\\
Для\ единственного\ решения\левого (непротиворечивого\ и\независимого\правого)\ :\ \frac{a_1}{a_2}\ne\frac{b_1}{b_2}\ или\ \ a_1b_2-a_2b_1=0\\
Единственное\ решение\ представляет собой\ пересекающиеся\секущие\ линии.\\
Для\ Бесконечно\много\решений\слева(непротиворечивых\ и\зависимых\справа):\\\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\\
Бесконечно\ много \решения\ представляют\ совпадающие\ линии.\\
Нет\ решения\ (несовместимые\ и\ независимые):\ \frac{a_1}{a_2}=\frac{b_1}{b_2}\ne\frac{c_1}{ с_2}\\
Нет\ решения\ представляют\ параллельные\ непересекающиеся\ линии.\end{массив}\)
Если вы читаете Правило Крамера, вам также следует прочитать о Множествах здесь.
Мы надеемся, что приведенная выше статья о правиле Крамера поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о правиле КрамераВ.1 Как работает правило Крамера?
Ответ 1 Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, содержащих то же количество уравнений, что и переменных. То есть он работает только с квадратными матрицами, имеющими ненулевой определитель и единственное решение.
Q.2 Какие преимущества имеет правило Крамера?
Ответ 2 Правило Крамера позволяет определить только одну искомую переменную, например, если у вас есть система с тремя переменными и тремя уравнениями и вы хотите найти только одну. Это позволяет нам делать это очень быстро и легко.
Это позволяет нам делать это очень быстро и легко.
Q.3 Что утверждает правило Крамера?
Ответ 3 Правило Крамера в матрицах представляет решение через определители матрицы коэффициентов и матриц, полученных из нее заменой одного столбца на вектор-столбец правых частей уравнений.
В.4 Как проверить правило Крамера?
Ответ 4 Для получения n-го решения системы линейных уравнений по правилу Крамера заменяет n-й столбец основной матрицы вектором решения и оценивает его определитель. Затем разделите этот определитель на главный.
В.5 Каковы ограничения правила Крамера?
Ответ 5 Поскольку для получения результата мы делим на определитель, правило Крамера работает только в том случае, если det(A) не равно нулю. Если det(A) = 0, правило Крамера не может быть использовано, потому что единственного решения не существует, поскольку было бы бесконечно много решений или вообще не было бы решений.

 Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.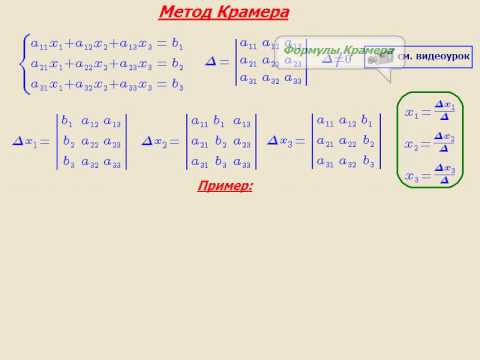 B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.