Площадь наружной поверхности цилиндра онлайн калькулятор. Радиус цилиндра, онлайн расчет
Цилиндр – это фигура, состоящая из цилиндрической поверхности и двух окружностей, расположенных параллельно. Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто. Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Как найти площадь цилиндра – правила вычисления
- Чтобы узнать площадь цилиндра, необходимо две площади основания сложить с площадью боковой поверхности: S= Sбок.+ 2Sосн. В более развернутом варианте данная формула выглядит так: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Площадь боковой поверхности данного геометрического тела можно высчитать, если известны его высота и радиус окружности, лежащей в основании. В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте.
 Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
Формула боковой поверхности данного тела выглядит так: S= 2 π rh. - Площадь основания считается по формуле нахождения площади круга: S osn= π r 2 . В некоторых задачах может не даваться радиус, но задаваться длина окружности. С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
- При выполнении всех этих расчетов число π обычно не переводится в 3,14159… Его нужно просто дописывать рядом с числовым значением, которое было получено в результате проведения вычислений.
- Далее необходимо лишь умножить найденную площадь основания на 2 и прибавить к полученному числу вычисленную площадь боковой поверхности фигуры.
- Если в задаче указывается, что в цилиндре есть осевое сечение и это – прямоугольник, то решение будет немного другим. В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра.
 Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π. - Можно высчитать площадь данного геометрического тела через его объем. Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
- В вычислении площади цилиндра нет ничего сложного. Нужно только знать формулы и уметь выводить из них величины, необходимые для проведения расчетов.
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H.
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.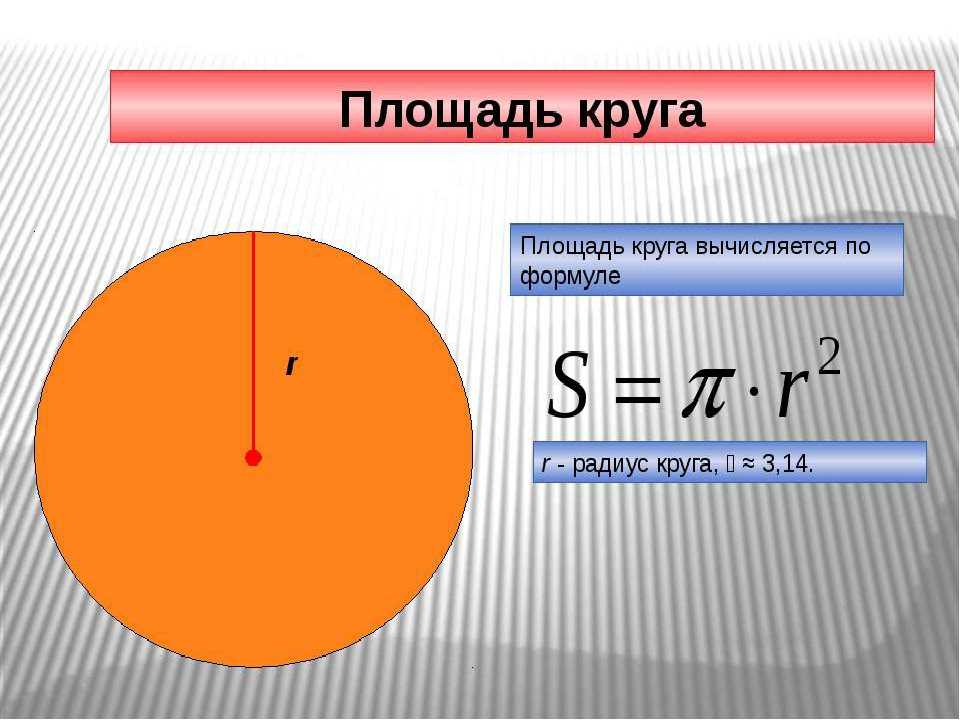
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3. 14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом.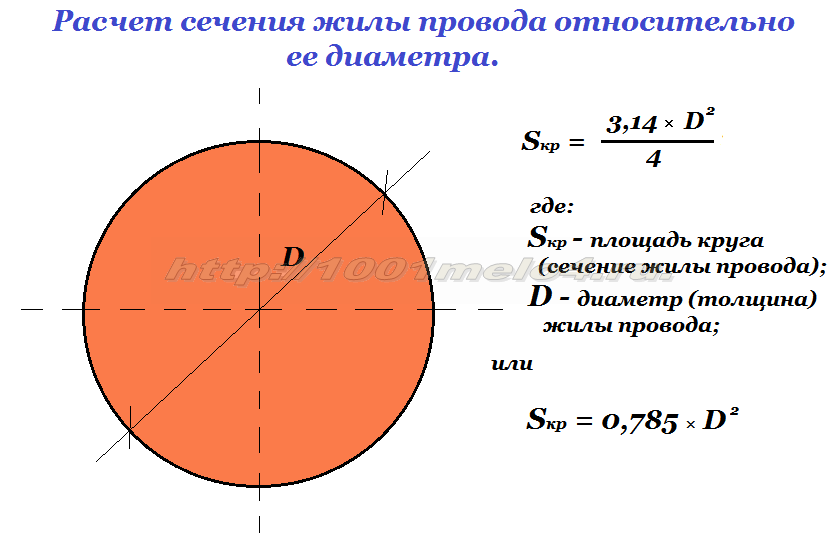 Точность – вежливость королей.
Точность – вежливость королей.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
|
Random converter |
Конвертер площадиКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Исходная величина квадратный метрквадратный километрквадратный гектометрквадратный декаметрквадратный дециметрквадратный сантиметрквадратный миллиметрквадратный микрометрквадратный нанометргектарарбарнквадратная милякв. миля (США, геодез.)квадратный ярдквадратный фут²кв. фут (США, геодез.)квадратный дюймкруговой дюймтауншипсекцияакракр (США, геодезический)рудквадратный чейнквадратный родрод² (США, геодезический)квадратный перчквадратный родкв. Преобразованная величина квадратный метрквадратный километрквадратный гектометрквадратный декаметрквадратный дециметрквадратный сантиметрквадратный миллиметрквадратный микрометрквадратный нанометргектарарбарнквадратная милякв. миля (США, геодез.)квадратный ярдквадратный фут²кв. фут (США, геодез.)квадратный дюймкруговой дюймтауншипсекцияакракр (США, геодезический)рудквадратный чейнквадратный родрод² (США, геодезический)квадратный перчквадратный родкв. тысячнаякруговой милхомстедсабинарпанкуэрдаквадратный кастильский локотьvaras conuqueras cuadпоперечное сечение электронадесятина (казенная)десятина хозяйственная круглаяквадратная верстаквадратный аршинквадратный футквадратная саженьквадратный дюйм (русский)квадратная линияПланковская площадь Температурный интервалЗнаете ли вы, что температурный интервал в 1 градус Фаренгейта равен 5/9 градуса Цельсия? В Мьянме и в Северной Америке для измерения площади земельных владений используют акры Общие сведения Единицы Квадратные Метры Единичный квадрат Ар Гектар Акр Барн Расчет площади Формулы для вычисления площади Вычисление площади поверхности Планиметр Интересные факты о площади Теорема о свойствах площадей Географические объекты с самой большой площадью Изучайте технический русский язык с этим видео! — Learn technical Russian with this video! Общие сведенияВ ряде Европейских стран и в Индонезии площадь земельных участков измеряют в арах Площадь — это величина геометрической фигуры в двумерном пространстве. ЕдиницыКвадратные МетрыПлощадь измеряется в системе СИ в квадратных метрах. Один квадратный метр — площадь квадрата, со стороной в один метр. Единичный квадратЕдиничный квадрат это квадрат со сторонами в одну единицу. Площадь единичного квадрата тоже равна единице. В прямоугольной системе координат этот квадрат находится в координатах (0,0), (0,1), (1,0) и (1,1). На комплексной плоскости координаты — 0, 1, i и i+1, где i — мнимое число. АрАр или сотка, как мера площади, используется в странах СНГ, Индонезии и некоторых других странах Европы, для измерения небольших городских объектов таких как парки, когда гектар слишком велик. ГектарВ гектарах измеряют недвижимость, особенно земельные участки. Один гектар равен 10 000 квадратных метров. Он используется со времен Французской революции, и применяется в Европейском Союзе и некоторых других регионах. Так же как и ар, в некоторых странах гектар называется иначе. В южной части провинции Онтарио, Канада АкрВ Северной Америке и Бирме площадь измеряется в акрах. Гектары там не используются. Один акр равен 4046,86 квадратным метрам. Изначально акр определялся как площадь, которую за один день мог вспахать крестьянин с упряжкой из двух волов. БарнБарны используются в ядерной физике для измерения поперечного сечения атомов. Один барн равен 10⁻²⁸ квадратным метрам. Барн не является единицей в системе СИ, но принят к использованию в этой системе. Один барн приблизительно равен площади поперечного сечения ядра урана, которое физики в шутку называли «огромным, как амбар». Расчет площадиПлощадь простейших геометрических фигур находят, сравнивая их с квадратом известной площади. Это удобно тем, что площадь квадрата легко вычислить. Некоторые формулы вычисления площади геометрических фигур, приведенные ниже, получены именно таким путем. Также для вычисления площади, особенно многоугольника, фигуру делят на треугольники, вычисляют площадь каждого треугольника по формуле, а потом складывают. Площадь более сложных фигур вычисляют с помощью математического анализа. Формулы для вычисления площади
Площадь поверхности Луны равна приблизительно 3,793 x 10⁷ квадратным километрам Вычисление площади поверхностиНайти площадь поверхности простых объемных фигур, таких как призмы, можно по развертке этой фигуры на плоскости. Площади поверхности некоторых астрономических объектов: Солнце — 6,088 x 10¹² квадратных километров; Земля — 5,1 x 10⁸; таким образом, площадь поверхности Земли примерно в 12 раз меньше площади поверхности Солнца. Площадь поверхности Луны приблизительно равна 3,793 x 10⁷ квадратных километров, что примерно в 13 раз меньше площади поверхности Земли. ПланиметрПлощадь также можно вычислить с помощью специального прибора — планиметра. Существуют несколько видов этого прибора, например полярный и линейный. Также, планиметры бывают аналоговыми и цифровыми. В дополнение к другим функциям, в цифровые планиметры можно вводить масштаб, что облегчает измерение объектов на карте. Планиметр измеряет расстояние, пройденное по периметру измеряемого объекта, а также направление. Интересные факты о площадиТеорема о свойствах площадейСогласно изопериметрической теореме, из всех фигур с одинаковым периметром, самая большая площадь у круга. Если, наоборот, сравнить фигуры с одинаковой площадью, то у круга самый маленький периметр. Периметр — это сумма длин сторон геометрической фигуры, или линия, которая обозначает границы этой фигуры. Географические объекты с самой большой площадьюВид на вечерний Нью-Йорк с 35-го этажа из окна гостиницы ONE UN New York Hotel Страна: Россия, 17 098 242 квадратных километров, включая сушу и водное пространство. Вторая и третья по площади страны — это Канада и Китай. Город: Нью-Йорк — это город с самой большой площадью в 8683 квадратных километров. Второй по площади город — Токио, занимающий 6993 квадратных километров. Третий — Чикаго, с площадью в 5498 квадратных километров. Городская площадь: Самая большая площадь, занимающая 1 квадратный километр, находится в столице Индонезии Джакарте. Это площадь Медан Мердека. Вторая по величине площадь в 0,57 квадратного километра — Праса-дуз-Жирасойс в городе Палмас, в Бразилии. Третья по величине — площадь Тяньаньмэнь в Китае, 0,44 квадратного километра. Озеро: Географы спорят, является ли Каспийское море озером, но если это так, то это — самое большое озеро в мире с площадью 371 000 квадратных километров. Второе по площади озеро — озеро Верхнее в Северной Америке. Это одно из озер системы Великих озер; его площадь составляет 82 414 квадратных километров. Третье по площади — озеро Виктория в Африке. Оно занимает площадь 69 485 квадратных километров. Список литературы Автор статьи: Kateryna Yuri Перевести единицы: квадратный метр в квадратный фут² Перевести единицы: квадратный метр в квадратный миллиметр Перевести единицы: квадратный километр в квадратная миля Перевести единицы: гектар в квадратный километр Перевести единицы: квадратный метр в квадратный сантиметр Перевести единицы: гектар в акр Перевести единицы: квадратный дюйм в квадратный метр Перевести единицы: акр в квадратный метр Перевести единицы: гектар в квадратный километр Вас могут заинтересовать и другие конвертеры из группы «Популярные конвертеры единиц»:Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления. Конвертер единиц измерения количества информации Конвертер десятичных приставок Передача данных Курсы валют Размеры мужской одежды и обуви Размеры женской одежды и обуви Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ. |
Расчет площади пола — онлайн калькулятор
Содержание
- Как рассчитать площадь пола?
- Расчет площади помещения с несколькими уровнями
- Как рассчитать квадратные метры стен комнаты, расчет площади стен
- Калькулятор расчёта площади стен
- Пол оригинальной формы
- Треугольники
- Круги и овалы
- Многоуровневый пол
- Как высчитать квадратный метр: нюансы, которые следует обязательно знать
- Измеряем площадь неправильной фигуры
- Окружность
- Треугольник
- Похожие самоделки
- Площадь комнаты в квадратных метрах
- Прямоугольная комната
- Помещение неправильной формы
- Виды треугольников
- Пример вычислений в помещениях с нестандартной формой
- Заключение
Как рассчитать площадь пола?
Итак, как же рассчитать квадратные метры? Самыми простыми для формулировки площади пола, является дом квадратной и прямоугольной формы. Чтобы провести расчет площади подобного помещения, необходимо измерить длину и ширину комнаты (измеряем в метрах), а потом умножить эти два числа друг на друга, получив интересующее нас число.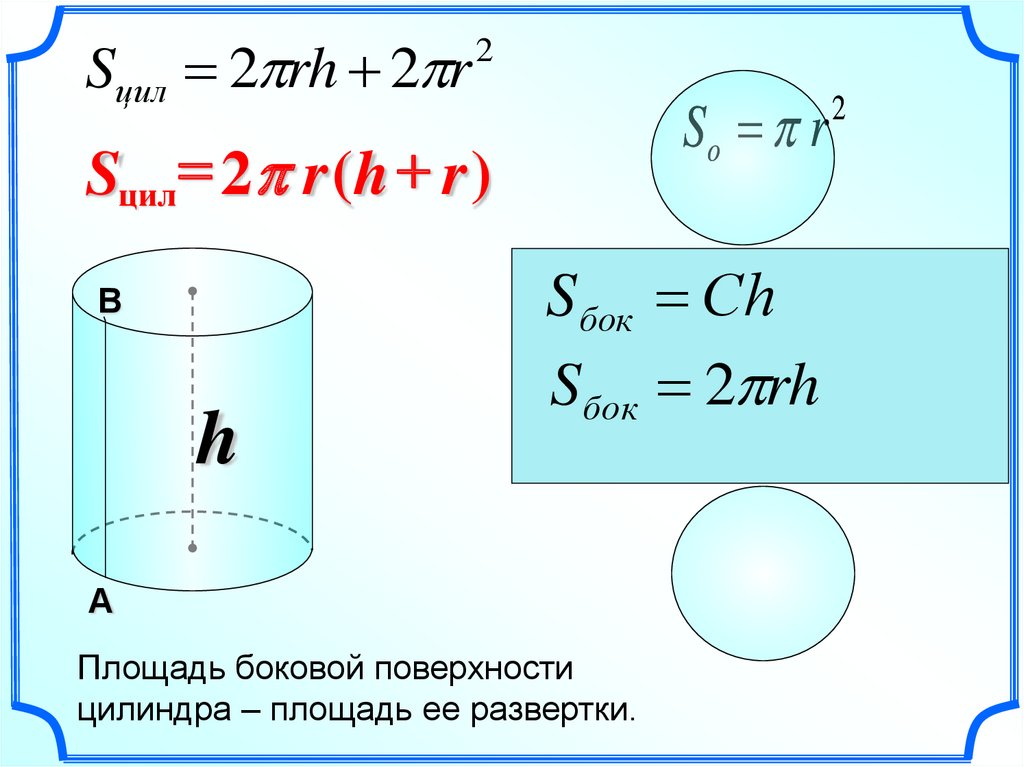 Такой вариант не трудно осуществить, не требуется перестановка дивана, шкафа и прочей мебели – хватит всего лишь, посчитать расстояние. Единственной проблемой, будет камин (если он, конечно же, есть) в таком случае от итоговой цифры, необходимо будет вычесть S (площадь) камина.
Такой вариант не трудно осуществить, не требуется перестановка дивана, шкафа и прочей мебели – хватит всего лишь, посчитать расстояние. Единственной проблемой, будет камин (если он, конечно же, есть) в таком случае от итоговой цифры, необходимо будет вычесть S (площадь) камина.
Комнаты неправильной формы, представляют более сложный расчет S пола. Квартира, имеющая форму прямоугольника или квадрата, называют стандартной, однако, если есть наличие декоративных изменений (арок, ниш), то подсчет более сложный, поскольку требует вычисление S фигур входящих в состав комнаты.
Сначала план нужно разделить на два прямоугольника, а затем суммировать их площади
Вычисляя итоговую площадь «нестандартных фигур», например, Г-образную комнату, можно «разбить» помещение на два квадрата или треугольника и суммировать их сумму, такая небольшая хитрость позволяет в считаные минуты без каких-либо математических формул расчета, узнать S данного участка. В некоторых случая, угол Г-образной комнаты переходит не под углом 90º, что является небольшой, но решаемой загвоздкой.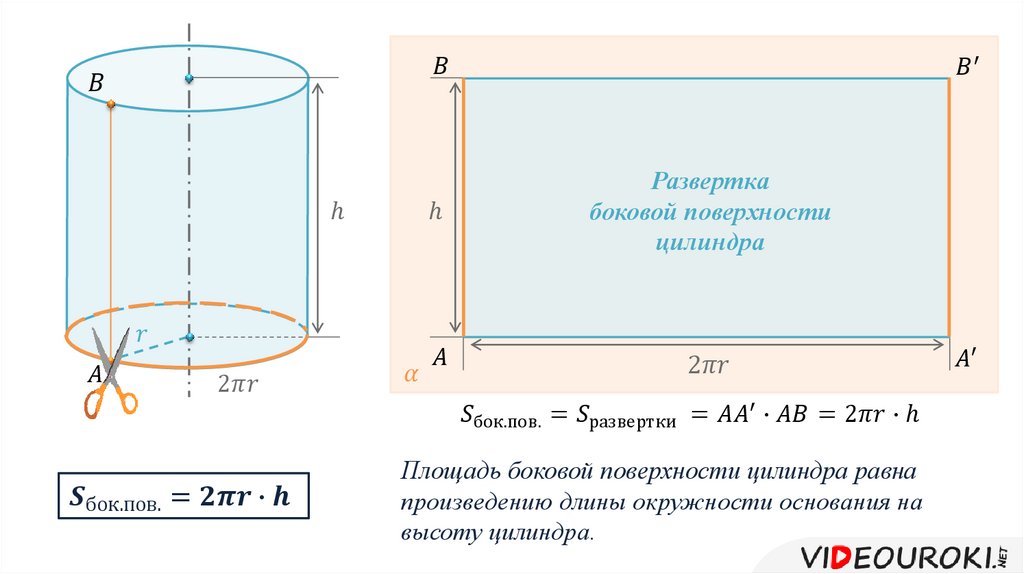 Пересекаясь под непрямым углом, переход имеет вид треугольника, расчет нужно провести, по знакомому геометрическому закону: «Площадь треугольника, равна первому катету умноженному на второй».
Пересекаясь под непрямым углом, переход имеет вид треугольника, расчет нужно провести, по знакомому геометрическому закону: «Площадь треугольника, равна первому катету умноженному на второй».
Цилиндрические и полусигментные частицы, но как же вычислить квадратные метры исходя из базового курса алгебры и геометрии? Гораздо легче, разделить участок на условные треугольники и квадраты, а затем сделать расчет и суммирование результатов каждого отдельного элемента.
Формулы площади, геометрических фигур
Существуют гостиные комнаты в частных домах, имеющие различную высоту пола (выступы, возвышенности, уклоны). Чтобы выполнить расчет, необходимо, как и прошлом случае разделить области на отдельные элементы, измеряв каждый по отдельности суммировав результаты.
Рулетка – это лучший инструмент, который поможет высчитать S пола. Однако, помимо рулетки необходимо взять листик и карандаш и записать замеры, а лишь потом проводить математические вычисления (чтобы не запутать и не перемерять все по десять раз).
Совет
Не осуществляйте замеры по стене, поскольку, она может иметь дефекты и привести к неточности измерения. Места, имеющие выступы в виде полукругов или зигзагов – следует считать по отдельности.
Расчет площади помещения с несколькими уровнями
Думаете, что таких комнат не бывает? Совершенно напрасно, дом, построенный на склоне, вполне может иметь в планировке уступы, например, так гостиная или кухня может быть поделена на зоны. Впрочем, совершенно не обязательно смотреть на пол, ведь и потолок может состоять из нескольких ярусов в самом обычном типовом помещении. Допустим, вам нужно купить краску для его окраски. Разумеется, в целом площади потолка и пола равны, но вот в местах перепада высот вертикальные откосы тоже имеют некоторую квадратуру. И даже с учетом 10 % запаса к закупаемым материалам их может не хватить. Поэтому считаем.
Если уровни у вас простой формы, с прямоугольными элементами, никаких сложностей не возникнет. Достаточно измерить линейкой высоту вертикальных участков, найти их длину и, использовав формулу S = a . b, определить площадь, с которой суммируется квадратура горизонтальных поверхностей. Если край уступа нависает над более низкой площадкой в виде карниза, суммировать результаты измерений каждого яруса недостаточно, поскольку получится, что не учтена нижняя сторона нависающей части. Для настилания паркета или облицовки плиткой эти места особой роли играть не будут, а вот при окраске могут остаться «белые пятна». Так что при подобном положении дел следует обмерить линеечкой и скрытые участки.
b, определить площадь, с которой суммируется квадратура горизонтальных поверхностей. Если край уступа нависает над более низкой площадкой в виде карниза, суммировать результаты измерений каждого яруса недостаточно, поскольку получится, что не учтена нижняя сторона нависающей части. Для настилания паркета или облицовки плиткой эти места особой роли играть не будут, а вот при окраске могут остаться «белые пятна». Так что при подобном положении дел следует обмерить линеечкой и скрытые участки.
Обмеры рулеткой или иным приспособлением лучше выполнять ближе к основанию, поскольку стены могут иметь небольшую кривизну, что даст определенную погрешность в результате.
Сложнее всего выполнять расчет площади помещения при наличии уступов округлой или более сложной формы. В этом случае нужно точно измерить каждую дугу по краю, либо короткими отрезками, либо сразу целиком посредством рулетки и воспользовавшись чьей-нибудь помощью. Затем, найдя радиусы и раздробив поверхности на отдельные геометрические фигуры, используем приведенные выше формулы и находим площадь каждого уступа. Что касается вертикальных участков, о них также было сказано выше, разницы между прямым вариантом и изогнутым нет никакой, если известен периметр.
Что касается вертикальных участков, о них также было сказано выше, разницы между прямым вариантом и изогнутым нет никакой, если известен периметр.
Как рассчитать квадратные метры стен комнаты, расчет площади стен
Приведу пример расчета пола и стен комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты. В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б. и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Чтобы рассчитать площадь комнаты по стенам:
Надо с начало сложить длины всех четырех сторон комнаты А + Б + Г + В и умножить на высоту потолка комнаты h, ( А + Б + Г + В)* h — если у нас длина комнаты 5 метра, а ширина 3 метров, а высота потолка комнаты к примеру 2,5 метра, тогда надо ((5+3+5+3)*2,5= 40 кв. м.), в итоге получаем 40 кв.м. по стенам.
м.), в итоге получаем 40 кв.м. по стенам.
Но это еще не все, для того чтобы получить чистые квадратные метры стен комнаты для ремонта и отделки квартиры. надо из полученного вычесть двери и окно.
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров. — а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м. в итоге окно получаем 2,4 кв.м., Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Осталось вычесть от (40-2,4-1,64)= 35,96 кв.м., ИТОГО: Получили 35,96 кв.м. по стенам комнаты.
Если вы не хотите в ручную рассчитывать площадь стен или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь стен автоматически.
Для расчёта необходимо измерить в метрахдлину, ширину комнаты и высоту потолка и внести данные по порядку заполнив форму и вы автоматически получите расчет площади стен в квадратных метрах.
Калькулятор расчёта площади стен
Обращаем ваше внимание, что измерения необходимо проводить в метрах.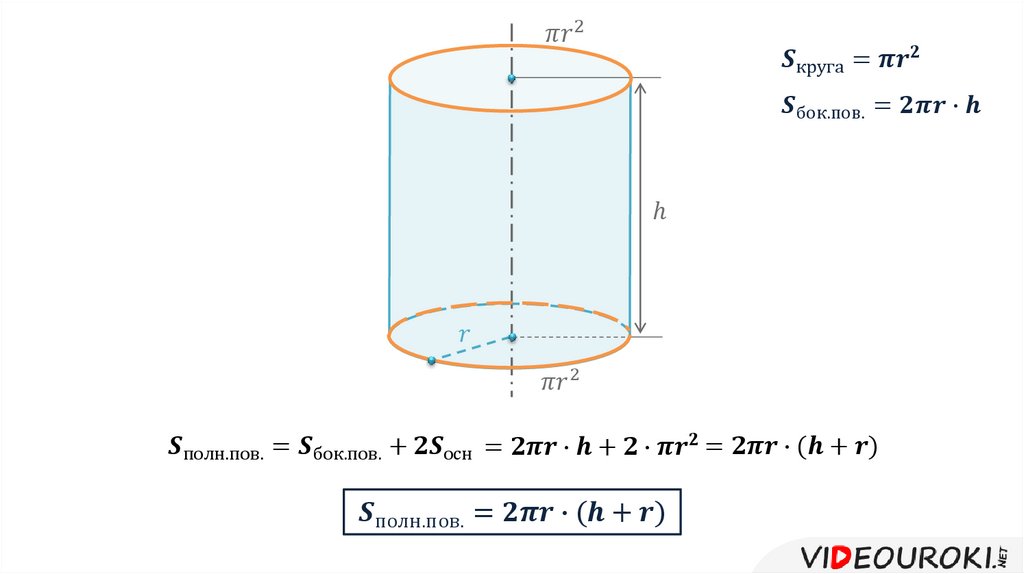 Т.е
Т.е
если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой. а не с запятой!
Калькулятор рассчитывает только площадь стен. но без учета и вычета площади окон и дверей, для этого надо еще раз повторить расчеты на площадь окон и дверей описанные выше.
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров. — а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м. в итоге окно получаем 2,4 кв.м., Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Осталось вычесть от (от полученных расчетов автоматического калькулятора (площадь чистых стен) -2,4-1,64 (Окно и двери)= получим площадь стен с учетом вычета Окон и двери помещения (комнаты) в кв.м.
Чтобы рассчитать площадь комнаты по полу. воспользуйтесь нашим Калькулятором. чтобы расчитать площадь пола или потолка .
Калькулятор рассчитывает не только площадь пола или потолка. а также данный калькулятор можно использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей .
а также данный калькулятор можно использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей .
Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола
Пол оригинальной формы
Первое, что следует сделать при подсчёте площади пола неправильной формы — мысленно или на бумаге расчленить его на простые фигуры. После чего высчитать отдельно площадь каждой из них и суммировать результаты.
По ходу выполнения этого задания вы обязательно заметите, что фигуры сами по себе простые, а вот процесс вычисления их площади не всегда. Для каждой отдельной части придётся применять свою формулу в зависимости от её геометрии. Некоторые из них мы сейчас рассмотрим.
Треугольники
Проще всего иметь дело с прямоугольными представителями этого семейства.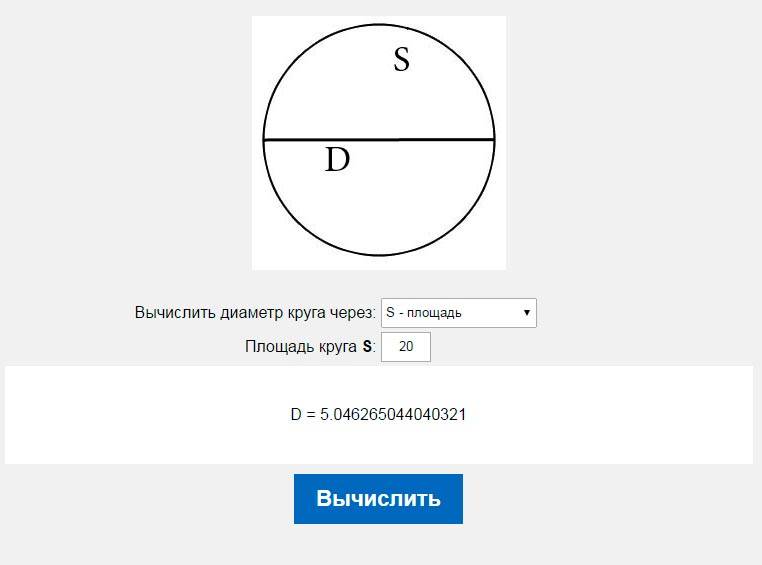 Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).
Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).
Если треугольник не имеет прямых углов, необходимо провести следующие действия:
- принять одну из его сторон за основание;
- провести от вершины к нему высоту;
- умножить одно на другое;
- результат разделить на 2.
В итоге формула будет иметь такой вид: S=a*h/2. Где a и h — длина основания и высота соответственно.
Для любителей экзотики существуют и другие варианты. Например, формула Герона, или подсчёт с помощью радиуса вписанной в треугольник окружности. Но проще всё-таки будет считать через основание и высоту.
Круги и овалы
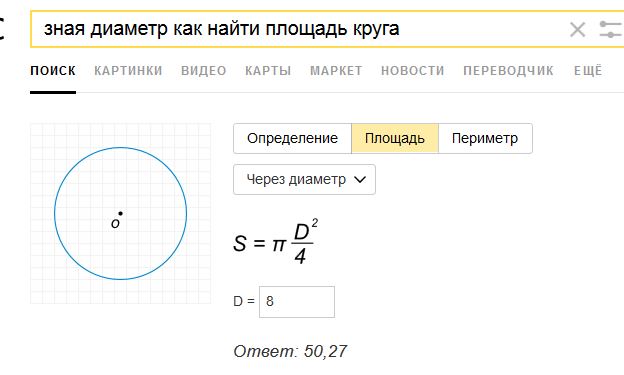
Такие геометрические формы в строительстве встречаются редко, но всё же встречаются. Чтобы рассчитать площадь круга достаточно найти его радиус и подставить в уравнение: S=πr2.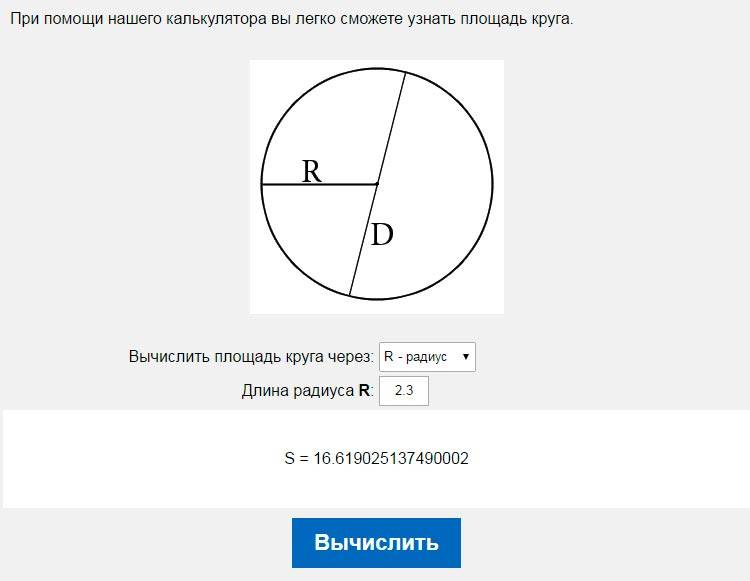 Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.
Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.
Площадь овала (эллипса) вычисляется похожим образом. Только вместо радиуса необходимо найти длину двух его полуосей — длинной (a) и короткой (b). Дальше — по той же схеме: S=π*a*b.
Но чаще можно столкнуться с полукруглыми или «полуовальными» помещениями. Для подсчёта размеров такой комнаты к формулам для круга и овала в конце дописываем /2. На латыни это будет выглядеть так: S=πr2/2 и S=π*a*b/2.
Многоуровневый пол
Встречается ещё реже. И посчитать его площадь можно так, как и в примере с прилегающими помещениями — сложить показатели каждого фрагмента. Но, если вам нужно такой пол покрасить, то не забудьте учесть и вертикальные плоскости. В противном случае краски на них может не хватить.
В конце хотелось бы отметить, что главное в любых расчётах — точность. Поэтому будьте внимательны при выполнении замеров и тщательно проверяйте результаты вычислений. Это значительно упростит дальнейшие, более сложные действия во время ремонта.
Поэтому будьте внимательны при выполнении замеров и тщательно проверяйте результаты вычислений. Это значительно упростит дальнейшие, более сложные действия во время ремонта.
Как высчитать квадратный метр: нюансы, которые следует обязательно знать
Чаще всего при указании квадратуры упаковки того или иного строительного материала производитель приводит квадратные метры. Система СИ принята во многих странах. Как рассчитать квадратный метр? Можно вычертить квадрат с метровой стороной. В этом случае поверхность, очерченная данным квадратом, и будет равна квадратному метру. Большинство измерительных приборов позволяют получить результаты измерения сразу в квадратных метрах.
Квадратный метр найти несложно
Кроме квадратных метров можно использовать и другие единицы измерения. При наличии онлайн-калькулятора расчет квадратных метров значительно упрощается. Однако при желании перевод можно выполнить самостоятельно, умножив имеющееся значение на соответствующий коэффициент, можно найти искомое значение. Для начала следует определить с новой единицей измерения. Если это:
При наличии онлайн-калькулятора расчет квадратных метров значительно упрощается. Однако при желании перевод можно выполнить самостоятельно, умножив имеющееся значение на соответствующий коэффициент, можно найти искомое значение. Для начала следует определить с новой единицей измерения. Если это:
Для перевода из квадратных футов в метры умножаем на 0,093
- Ярды. Коэффициент равен 0,84. Перевод ядров в квадратные метры выполняется по алгоритму, описанному выше. Для более точных расчетов можно использовать поправочный коэффициент 0,83613;
- Акры. При расчете квадратуры помещения такие единицы измерения используются редко, так как один акр равен 4050 квадратным метрам. Однако при необходимости перевод можно сделать с помощью поправочного коэффициента 4050 (4046,9 при более точном расчете).
Акр используется при определении квадратуры земли
Возможно использование и других единиц
При переводе площади важно помнить, что речь идет о квадратах, а потому используется не соотношение линейных размеров, а площадей. Найти поправочный коэффициент в этом случае достаточно просто
Найти поправочный коэффициент в этом случае достаточно просто
Если известно, что метр и искомая единица измерения соотносятся как коэффициент К, то поправочный коэффициент будет численно равен К².
Измеряем площадь неправильной фигуры
Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.
С квадратами и прямоугольниками совмещают части круга и треугольники.
Окружность
Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.
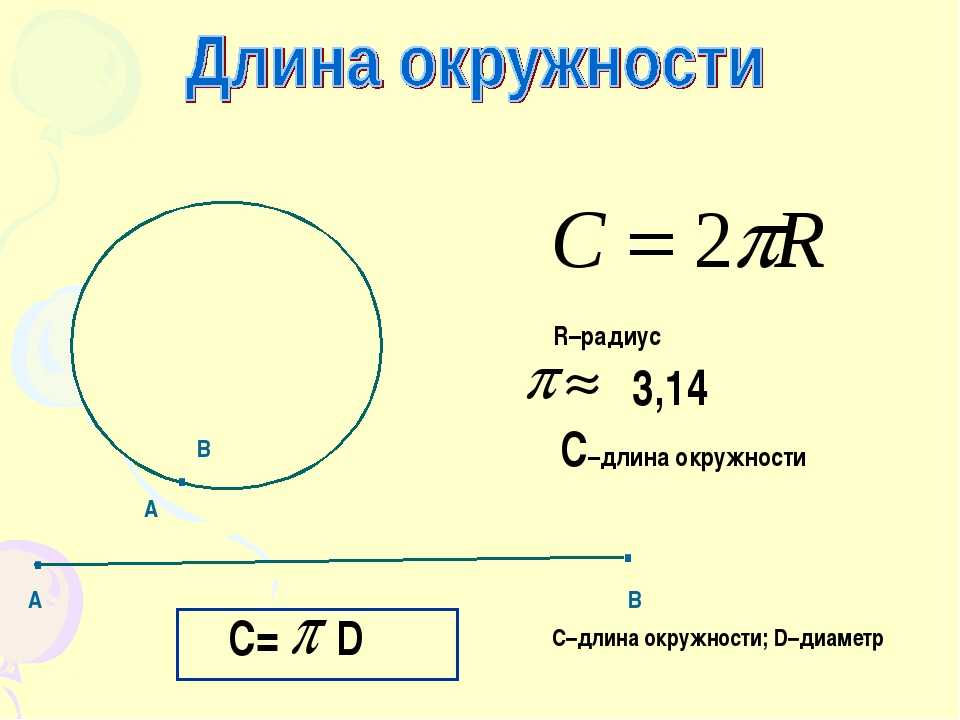
Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.
Подсчёт площади круга производят по формуле S = π*R², где:
- R – радиус;
- S – площадь круга;
- π – постоянная математическая величина, округлённая до значения 3,14.

Числовое значение площади полукруга получают делением полученного результата на 2.
Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.
Треугольник
Формула площади треугольника S=1/2*Н*А, где:
- S – площадь треугольника;
- Н – высота;
- А – сторона треугольника.
Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.
Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:
Статья полезна? Сохраните закладку или отметьте для друзей!
”
Похожие самоделки
Самодельные строительные блоки: «теплый» кирпич
Фундамент из автомобильных покрышек: делаем своими руками за один день
Фундамент за один день: делаем своими руками
Самодельный утеплитель: оригинальные блоки из соломы
Самодельная опалубка для фундамента своими руками: легко и просто
Как одному легко переносить большие листы фанеры: простая самоделка
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту
Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка
Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Виды треугольников
Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:
- Равносторонний треугольник имеет равные стороны и равные углы.
- Равнобедренный треугольник имеет две равные стороны и два равных угла.

- Разносторонний треугольник имеет три неравные стороны и три неравных угла.
- Прямоугольный треугольник имеет один прямой угол 90 градусов.
- Остроугольный треугольник имеет все углы меньше 90 градусов.
- Тупоугольный треугольник имеет один угол больше 90 градусов.
Площадь любого треугольника определяется по формулам.
1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:
- S=1⁄2×a×h, где: h – высота, a — основание.
- S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
- S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.
Площадь равностороннего треугольника:
S=a2х√3 ⁄4 , где a=b= c.
Площадь равнобедренного треугольника:
S=1⁄4xbx√(4a2-b2).
2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:
S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.
Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.
Решение: b=14 см, h=10 см, A=1⁄2х14х10=70
Ответ: 70 см2.
Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.
Решение: Площадь треугольника =1⁄2xaxbxsin 45.
Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)
Площадь =1⁄2×24,745=12,3725
Ответ: 12,3725 см2.
Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.
Решение: Площадь равнобедренного треугольника определяется:
A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48
Ответ: 48 м2.
Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).
Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.
Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50
Ответ: 35,50 м2.
Пример вычислений в помещениях с нестандартной формой
Такую комнату предстоит условно разбить на несколько правильных фигур: квадратов, прямоугольников, треугольников. После этого, проведя все операции, выполнить расчет, пользуясь известными формулами.
Перед тем, как посчитать общую площадь, сделайте замеры. При проведении работ с нестандартными помещениями количество получаемых цифр удваивается, к стандартным двум показателям добавляют длину и ширину выступа. Габариты каждой из условных доль считаются отдельно, а в результате суммируются.
Пример: если требуется посчитать площадь образованных двух прямоугольников, получившихся в результате планировки комнаты, площадь считают по той же формуле, только найденную цифру или отнимают (если это окно в потолке), или добавляют к размеру помещения, что зависит от конфигурации.
Как посчитать площадь комнаты в квадратных метрах с выступом, разберем на примере:
- Квадратура без выступа: 3,7*8,7=32,9 м2.
- Габариты выступающего потолка или стены: 4,25*0,75=3,2 м2.
- Общая площадь: 32,9+3,2=36,1 м2.
Из нестандартных планировок выделяют еще и категорию помещений со скошенными стенами. В этом случае площадь разбивают на несколько прямоугольников и треугольный участок. Для данной схемы потребуется провести пять этапов вычислений. Разбивку можно проводить по своему плану — так, как вам удобнее
Это не столь важно, требуется набор фигур, а способ их выделений можно брать любой. Главное, правильно посчитать
Как посчитать площадь стен в этом случае:
- Сначала измеряют большую прямоугольную часть: 6,9*1,7=11,7 м2.
- Высчитайте малый треугольник с параметрами 2,3*1,4=3,3 м2.
- Просчитайте площадь прямоугольного треугольника, равного половине площади треугольника с такими же параметрами (2,3*1,4)/2=1,65 м2.

- Сложите все полученные цифры, чтобы получить итоговое значение: 11,7+3,3+1,65=16,65 м2.
Планировки бывают самыми разнообразными, но общий принцип нахождения искомого понятен: все сложное подразделяем на простое, измеряем все требуемые параметры фигур, высчитываем квадратуру каждого фрагмента, соединяем все в одно число.
Обратите внимание на важное замечание: площадь комнаты, напольной и потолочной поверхностей – это одинаковые величины. Отличия бывают, если в проекте присутствуют полуколонны, не доходящие до потолка — тогда из общей суммы вычитывают этот показатель, в результате получая площадь пола. Не забывайте при работе посчитать площадь в метрах и следите, чтобы все показатели прописывались в одном значении (метрах, сантиметрах, миллиметрах), в зависимости от необходимости
Не забывайте при работе посчитать площадь в метрах и следите, чтобы все показатели прописывались в одном значении (метрах, сантиметрах, миллиметрах), в зависимости от необходимости.
Заключение
Теперь мы знаем, как правильно рассчитать площадь стен и можем, согласно полученным данным, закупить необходимое количество отделочного материала. Даже если ремонт будут осуществлять специальные квалифицированные бригады, то вы всегда сможете проверить правильность их расчетов.
Поскольку клиент оплачивает стоимость ремонта за каждый квадрат, а сторонние подрядчики частенько считают в свою пользу, не учитывая окон и дверей, то эти знания помогут вам существенно сократить стоимость ремонта, особенно при использовании дорогих отделочных материалов. Для полной уверенности рекомендуется проводить все замеры дважды, что позволит избежать возможной ошибки.
Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.
Для расчетов понадобятся:
- уровень строительный;
- рулетка с ограничителем;
- длинная линейка и угольник;
- карандаш и бумага;
- калькулятор.

Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.
Sphere Calculator — Найдите объем и площадь поверхности сферы
Онлайн-калькулятор сфер предназначен исключительно для расчета радиуса, объема, площади поверхности и окружности сферического тела со 100% точностью. Вы можете проанализировать любую сферу с точки зрения ее параметров, используя этот калькулятор объема свободной сферы. Так хотите получить больше знаний об этом? Мы организовали этот контент так, чтобы вы не чувствовали проблем при исследовании сферы.
Продолжайте читать!
9{2}\)?Решение:
Мы знаем, что:
$$ r = \sqrt{\frac{A}{4π} $$
$$ r = \sqrt{\frac{4}{4π} $$
$$ r = \sqrt{\frac{4}{4*3,14} $$
$$ r = \sqrt{\frac{4}{12,56} $$
$$ r = \sqrt{0,318 } $$
$$ r = 0,564 см $$
Хотите больше абсолютных результатов? Попробуйте бесплатно воспользоваться нашим калькулятором свободного радиуса сферы. Мы заверяем, что вы, люди, не будете разочарованы.
Мы заверяем, что вы, люди, не будете разочарованы.
Как работает калькулятор сфер?
Калькулятор объема свободной поверхности поможет вам лучше оценить параметры сферы. Давайте подскажем, как правильно его использовать:
Ввод:
Выберите один из следующих вариантов в раскрывающемся списке.
- Радиус
- Том
- Площадь поверхности
- Окружность
После выбора;
- Запишите значение выбранного параметра
- Нажмите кнопку расчета
Вывод:
Калькулятор площади свободной поверхности сферы вычисляет:
- Радиус сферы
- Объем сферы
- Площадь поверхности сферы
- Окружность сферы
Независимо от того, какой параметр вы выберете в качестве входных данных, калькулятор радиуса сферы точно рассчитает все эти параметры. Кроме того, вся информация отображается в виде четкой таблицы, чтобы вы могли легко ее прочитать.
Часто задаваемые вопросы:
Круг и сфера — это одно и то же?
Нет, круг — это двумерная геометрическая форма, а сфера — трехмерный объект. На плоскости точки окружности равноудалены от ее центра. С другой стороны, точки на поверхности сферы находятся на одинаковом расстоянии от центра по любой из присутствующих осей.
Что означает дуга окружности?
Термин дуга относится к части окружности. Он имеет только два типа, которые обозначаются как малая дуга и большая дуга. 9\text{o}\)
Вывод:
Сфера имеет широкое применение в области геометрии. Кроме того, ученые и профессионалы широко используют бесплатный онлайн-калькулятор площади поверхности сферы для получения точных результатов, чтобы избежать каких-либо препятствий во время расчетов. Так что вперед и воспользоваться возможностью.
Литература:
Из источника википедии: Уравнения в трехмерном пространстве, Замкнутый объем, Площадь поверхности, Геометрические свойства, Терминология, Сферическая геометрия, Кривые на сфере
Из источника академии хана: Объем сфер, Объем конуса
Из источника изучения просвета: Площадь поверхности, призмы, цилиндры, сферы
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах, которые обеспечивают чувствительность к регистру 9Пример 0011 e и пример E не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Неработающее изображениеЕсли на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным X , где отсутствует изображение. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотр информации о странице» и перейдите на вкладку «Мультимедиа».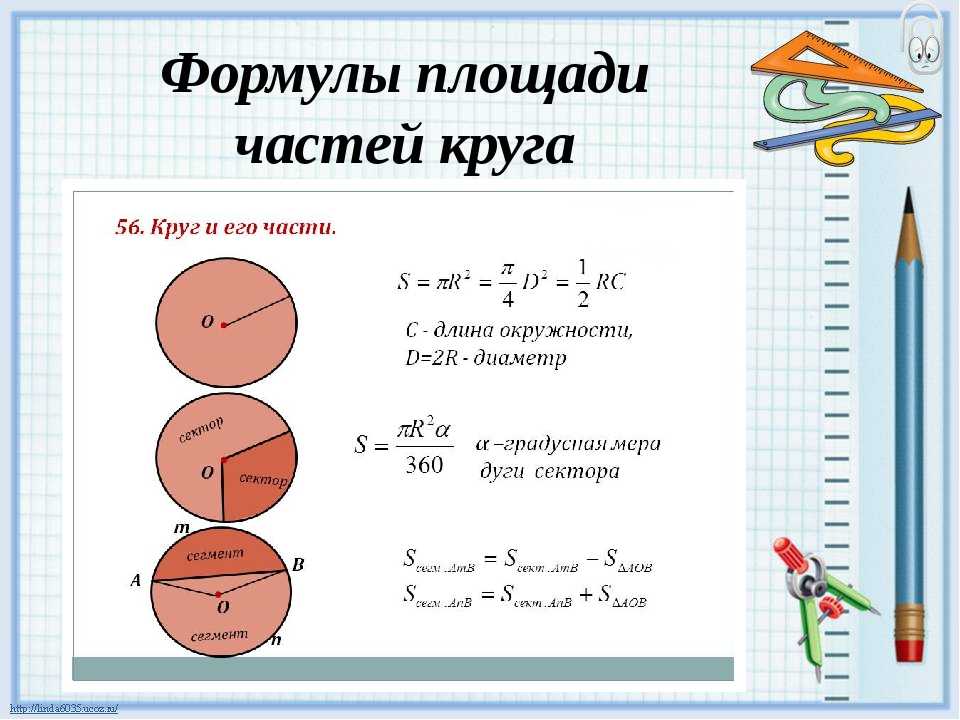
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/ пример. На платформах с учетом регистра символов PNG и png не совпадают.
Ошибки 404 после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать, когда была активирована новая тема или когда были изменены правила перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .

- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки . 9index.php$ — [L]
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Использование файлового менеджера в cPanel
- Войдите в cPanel.

- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.

- При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
- После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
- Площадь квадрата : area_square.
 Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны.
Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны. - Площадь круга : area_circle. Онлайн-калькулятор площади, который может рассчитать площадь круга по его радиусу или по диаметру.
- Площадь прямоугольника : area_rectangle. Онлайн-калькулятор площади, который может рассчитать площадь прямоугольника по его длине и ширине.
- Найти уравнение прямой из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
- Калькулятор периметра: периметр. Онлайн-калькулятор периметра, который вычисляет периметр прямоугольника, периметр квадрата, периметр треугольника или периметр круга.
- Периметр квадрата: perimeter_square. Онлайн-калькулятор позволяет рассчитать периметр квадрата по длине стороны.
- Периметр круга: perimeter_circle. Онлайн-калькулятор, вычисляющий периметр круга по его радиусу.
- Периметр прямоугольника : perimeter_rectangle.
 Онлайн-калькулятор позволяет вычислить периметр прямоугольника по его длине и ширине.
Онлайн-калькулятор позволяет вычислить периметр прямоугольника по его длине и ширине. - Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Вычисление площади геометрической фигуры. : область. Онлайн-калькулятор площади, позволяющий вычислить площадь прямоугольника, квадрата, треугольника или круга.
- Объем куба : volume_cube. Онлайн-калькулятор позволяет рассчитать объем куба по длине стороны.
- Объем прямоугольного параллелепипеда : volume_rectangle. Онлайн-калькулятор позволяет рассчитать объем прямоугольника по его длине, ширине и высоте.
- Объем сферы : volume_sphere. Онлайн-калькулятор позволяет рассчитать объем сферы по ее радиусу.
- Вычисление площади диска.

RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле . htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccessСамый простой способ редактирования файла .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджерКалькулятор — area_circle(3) — Солуматы
Площадь круга, расчет онлайн
Резюме:
площадь онлайн калькулятор, который может вычислить площадь круга от его радиуса или от его диаметра.
area_circle онлайн
Описание :
Калькулятор имеет несколько функций, позволяющих сделать поверхностные расчеты .
Таким образом, можно вычислить поверхность круга, также называемую
область диска с помощью функции area_circle, но и
поверхность прямоугольника
, или
поверхность квадрата
(который представляет собой конкретный прямоугольник).
Вычисление площади круга может быть выполнено из его радиус или его диаметр.
Вычисление площади круга по его радиусу 92`, где r представляет радиус
окружности .Таким образом, вычисление площади круга с радиусом 3 выполняется путем ввода следующей формулы area_circle(`3`) , после вычисления возвращается результат `9pi`.
Также можно сделать символическое вычисление и вычислить площадь круга с радиусом 1+x, набрав следующая формула area_circle(`1+x`) , после вычисления возвращается результат. 92`, где d – диаметр окружности.
Таким образом, расчет площади круга с диаметром 5 выполняется путем ввода следующей формулы area_circle(`5/2`) , после вычисления возвращается результат `25/4*pi`.
Игры и викторины по вычислению площадей обычных геометрических фигур
Чтобы применить различные формулы расчета, несколько
викторины по вычислению площади квадрата, прямоугольника и круга
предлагаются.
Синтаксис:
area_circle(радиус) или area_circle(диаметр/2)
Примеры:
area_circle(`3`) возвращает `9pi`
Список связанных калькуляторов:
Список связанных упражнений:

 Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
Формула боковой поверхности данного тела выглядит так: S= 2 π rh. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π. Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева тысячнаякруговой милхомстедсабинарпанкуэрдаквадратный кастильский локотьvaras conuqueras cuadпоперечное сечение электронадесятина (казенная)десятина хозяйственная круглаяквадратная верстаквадратный аршинквадратный футквадратная саженьквадратный дюйм (русский)квадратная линияПланковская площадь
тысячнаякруговой милхомстедсабинарпанкуэрдаквадратный кастильский локотьvaras conuqueras cuadпоперечное сечение электронадесятина (казенная)десятина хозяйственная круглаяквадратная верстаквадратный аршинквадратный футквадратная саженьквадратный дюйм (русский)квадратная линияПланковская площадь Она используется в математике, медицине, инженерных и других науках, например, в вычислении поперечного сечения клеток, атомов, или труб, таких как кровеносные сосуды или водопроводные трубы. В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади.
Она используется в математике, медицине, инженерных и других науках, например, в вычислении поперечного сечения клеток, атомов, или труб, таких как кровеносные сосуды или водопроводные трубы. В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади. Один ар равен 100 квадратным метрам. В некоторых странах эта единица называется иначе.
Один ар равен 100 квадратным метрам. В некоторых странах эта единица называется иначе.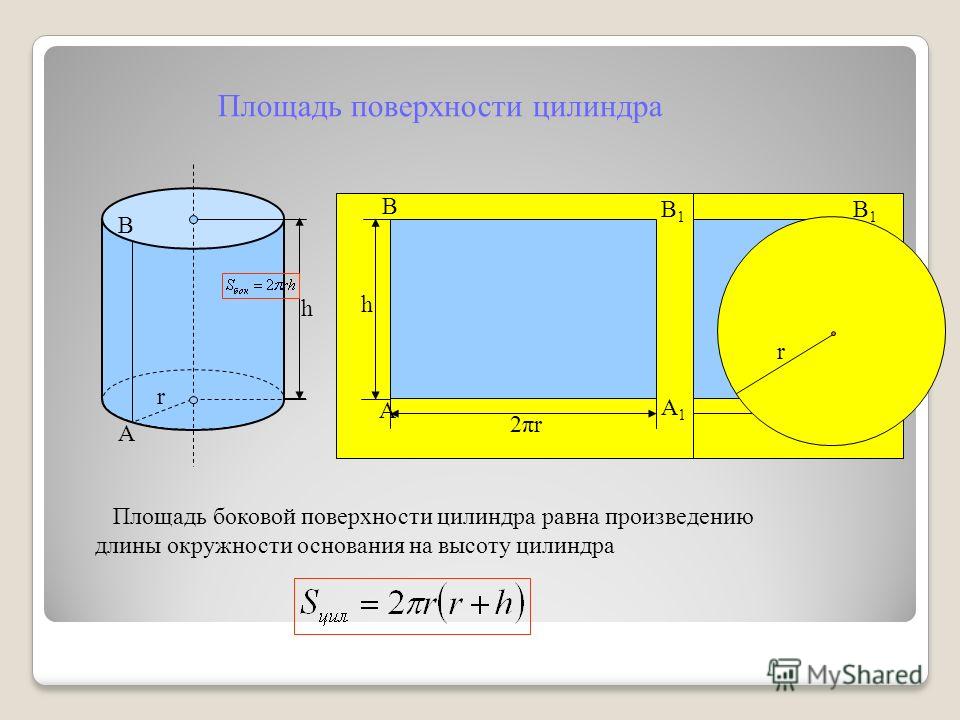 Амбар по-английски «barn» (произносится барн) и из шутки физиков это слово стало названием единицы площади. Эта единица возникла во время Второй мировой войны, и понравилась ученым, потому что ее название можно было использовать как кодовое в переписке и телефонных разговорах в рамках Манхэттенского проекта.
Амбар по-английски «barn» (произносится барн) и из шутки физиков это слово стало названием единицы площади. Эта единица возникла во время Второй мировой войны, и понравилась ученым, потому что ее название можно было использовать как кодовое в переписке и телефонных разговорах в рамках Манхэттенского проекта.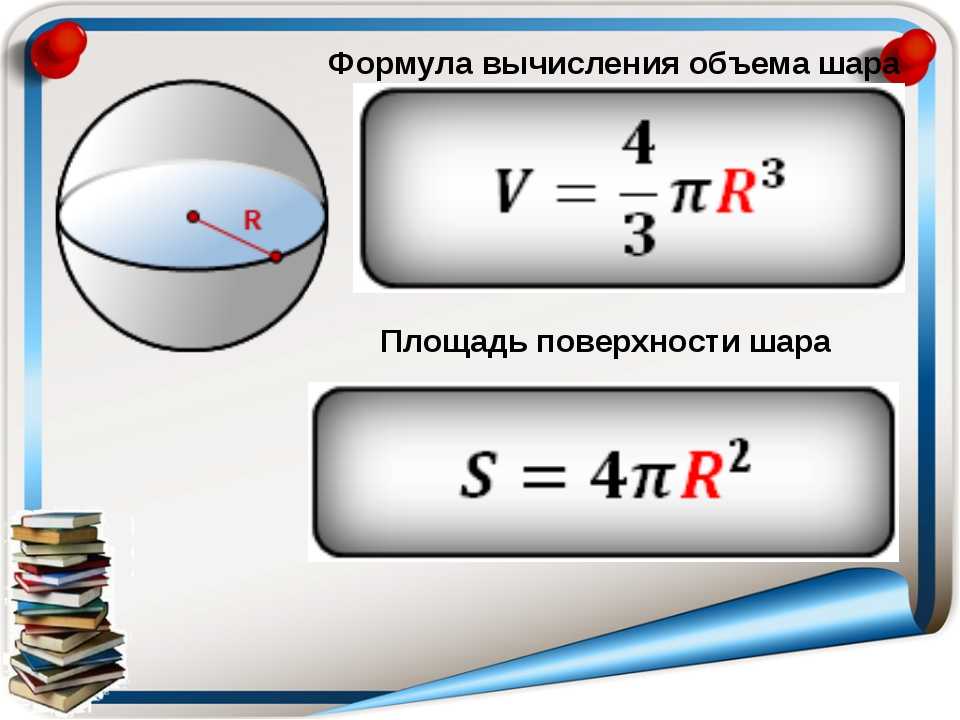 Формула: A = ½ah, где A — площадь, a — сторона, и h — высота.
Формула: A = ½ah, где A — площадь, a — сторона, и h — высота.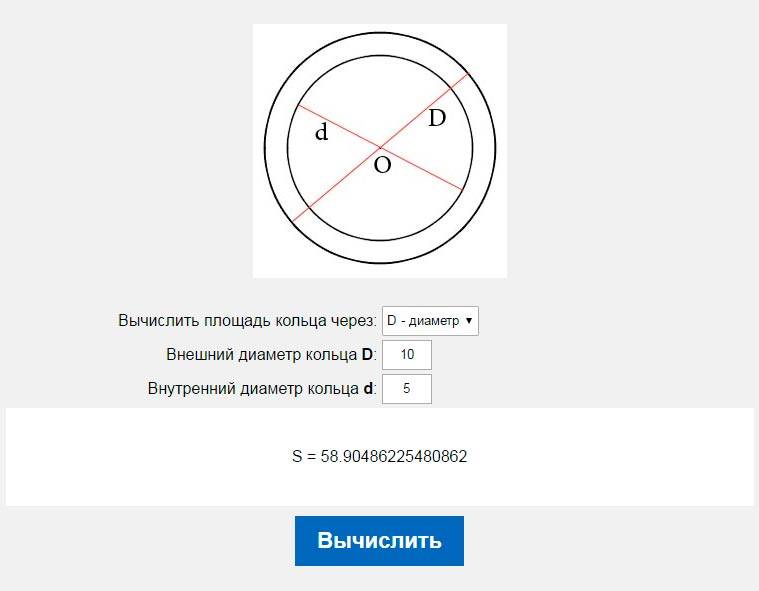 Развертку шара получить таким образом невозможно. Площадь поверхности шара находят с помощью формулы, умножая квадрат радиуса на 4π. Из этой формулы следует, что площадь круга в четыре раза меньше площади поверхности шара с таким же радиусом.
Развертку шара получить таким образом невозможно. Площадь поверхности шара находят с помощью формулы, умножая квадрат радиуса на 4π. Из этой формулы следует, что площадь круга в четыре раза меньше площади поверхности шара с таким же радиусом. Расстояние, пройденное планиметром параллельно его оси, не измеряется. Эти устройства используются в медицине, биологии, технике, и сельском хозяйстве.
Расстояние, пройденное планиметром параллельно его оси, не измеряется. Эти устройства используются в медицине, биологии, технике, и сельском хозяйстве.


 », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube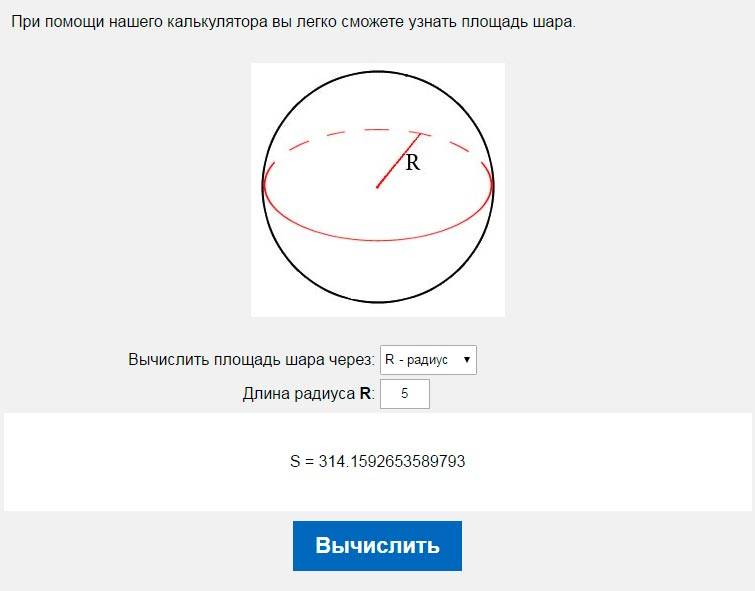
 м.
м.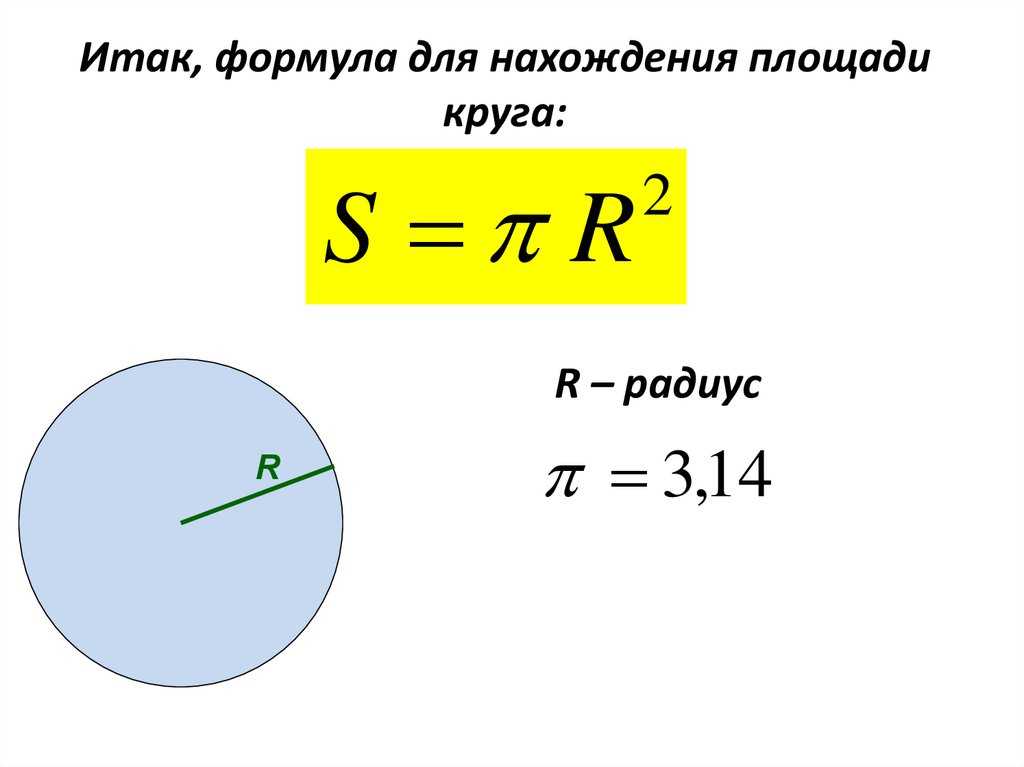 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.




 Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны.
Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны. Онлайн-калькулятор позволяет вычислить периметр прямоугольника по его длине и ширине.
Онлайн-калькулятор позволяет вычислить периметр прямоугольника по его длине и ширине.