Возведение в степень суммы двух чисел. Формулы степеней и корней
можно найти с помощью умножения. Например: 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5 6 .
То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».
Выражение 5 6 — это степенью числа, где:
5 — основание степени;
6 — показатель степени.
Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.
В общем виде степень с основанием «a» и показателем «n» записывается так
Возвести число a в степень n — значит найти произведение n множителей, каждый из которых равен а
Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1.
Если возвести число «а» возвести в первую степень , то получим само число a: a 1 = a
Если возвести любое число в нулевой степень , то в результате вычислений получим один. a 0 = 1
Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа , третью — кубом этого числа.
В степень можно возводить любое число — положительное, отрицательное или нуль. При этом не пользуются следующими правилами:
При нахождении степени положительного числа получается положительное число .
При вычислениях нуля в натуральной степени получаем ноль.
х m · х n = х m + n
например: 7 1.7 · 7 — 0.9 = 7 1.7+(- 0.9) = 7 1.7 — 0.9 = 7 0.8
Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем :
х m / х n = х m — n
, где, m > n,например: 13 3. 8 / 13 -0.2 = 13 (3.8 -0.2) = 13 3.6
8 / 13 -0.2 = 13 (3.8 -0.2) = 13 3.6
При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.
(у m ) n = у m · n
например: (2 3) 2 = 2 3·2 = 2 6
(х · у) n = х n · у m ,
например:(2·3) 3 = 2 n · 3 m ,
При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби
(х / у) n = х n / у n
например: (2 / 5) 3 = (2 / 5) · (2 / 5) · (2 / 5) = 2 3 / 5 3 .
Последовательность выполнения расчетов при работе с выражениями содержащими степень.
При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.
Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.
Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени (0 , 5) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1
Условие: возведите — 2 в степень 4 .
Решение
Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Пример 2
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Разберем пример.
Пример 3
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Пример 4
Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
Пример 5
5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1
0 0 — не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Пример 6
Возведите 2 в степень — 3 .
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3
Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8
Пример 7
Возведите 1 , 43 в степень — 2 .
Решение
Переформулируем: 1 , 43 — 2 = 1 (1 , 43) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1 , 43) — 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1 , 43) — 2 = 10000 20449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .
Пример 8
Пример: 3 − 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Определение 2
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Пример 9
Вычислите 8 — 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11
Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.
Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.
Калькулятор степеней
Возвести в степень
Возведений в степень: 94722
Что такое натуральная степень числа?
Число p называют n -ой степенью числа a , если p равно числу a , умноженному само на себя n раз: p = a n = a·…·a
n — называется показателем степени , а число a — основанием степени .
Как возвести число в натуральную степень?
Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:
Пример 1 . Возвести число три в четвёртую степень. То есть необходимо вычислить 3 4
Решение : как было сказано выше, 3 4 = 3·3·3·3 = 81 .
Ответ : 3 4 = 81 .
Пример 2 . Возвести число пять в пятую степень. То есть необходимо вычислить 5 5
Решение : аналогично, 5 5 = 5·5·5·5·5 = 3125 .
Ответ : 5 5 = 3125 .
Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.
Что такое отрицательная степень числа?
Отрицательная степень -n числа a — это единица, поделённая на a в степени n: a -n = .
При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.
Как возвести число в целую отрицательную степень?
Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.
Пример 1 . Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2 -4
Решение : как было сказано выше, 2 -4 = = = 0. 3 = 8
.
3 = 8
.
Примеры для решения:
Возведение в степень презентация
Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Когда число умножается само на себя , произведение называется степенью .
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель . Это число или буква называется показателем степени или степенью числа. Так, а 2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a 3 означает aaa, то есть здесь a повторяется три раза как множитель.
Показатель первой степени есть 1, но он обычно не записывается. Так, a 1 записывается как a.
Так, a 1 записывается как a.
Вы не должны путать степени с коэффициентами . Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a 4 = a.a.a.a
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква . В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a x , показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень . Так, b m и d n возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b m = b 3 ; но если m = 5, тогда b m =b 5 .
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d) 3 есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a 3 + 3a 2 b + 3a 2 d + 3ab 2 + 6abd + 3ad 2 + b 3 + d 3 .
Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель , и этот множитель или делитель есть первоначальным числом, которое возводится в степень.
Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a 5 , a 4 , a 3 , a 2 , a 1 ;
показатели, если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножать на a, мы успешно получим несколько значений.
Tак a.a = a 2 , второй член. И a 3 .a = a 4
a 2 .a = a 3 , третий член. a 4 .a = a 5 .
a 4 .a = a 5 .
Если мы начнем слева делить на a,
мы получим a 5:a = a 4 и a 3:a = a 2 .
a 4:a = a 3 a 2:a = a 1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a 5 , a 4 , a 3 , a 2 , a, 1, 1/a, 1/a 2 , 1/a 3 .
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a 3) = a 3 .
Тот же самый план записи может применяться к многочленам . Так, для a + b, мы получим множество,
(a + b) 3 , (a + b) 2 , (a + b), 1, 1/(a + b), 1/(a + b) 2 , 1/(a + b) 3 .
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a 1 = a -1 . И 1/aaa или 1/a 3 = a -3 .
1/aa или 1/a 2 = a -2 . 1/aaaa или 1/a 4 = a -4 .
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a 0 .
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a 4 , a 3 , a 2 , a 1 , a 0 , a -1 , a -2 , a -3 , a -4 .
Или a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa) 2 есть второй степенью aa.
И aa.aa.aa или (aa) 3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a 4 или aaaa. (Art. 195.)
Шестая степень y есть y 6 или yyyyyy.
N-ая степень x есть x n или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay) 2 =a 2 y 2 ; (ay) 2 = ay.ay.
Но ay.ay = ayay = aayy = a 2 y 2 .
Так, (bmx) 3 = bmx.bmx.bmx = bbbmmmxxx = b 3 m 3 x 3 .
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy) 4 , или d 4 h 4 y 4 .
Пример 2. Третья степень 4b, есть (4b) 3 , или 4 3 b 3 , или 64b 3 .
Пример 3. N-ая степень 6ad есть (6ad) n или 6 n a n d n .
Пример 4. Третья степень 3m.2y есть (3m.2y) 3 , или 27m 3 .8y 3 .
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b) 1 = a + b, первая степень.
(a + b) 1 = a 2 + 2ab + b 2 , вторая степень (a + b).
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 , третья степень.
(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 , четвертая степень.
Квадрат a — b, есть a 2 — 2ab + b 2 .
Квадрат a + b + h есть a 2 + 2ab + 2ah + b 2 + 2bh + h 2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.
Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a 2 + 2ah + h 2 также, (a — h)(a — h) = a 2 — 2ah + h 2 .
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a 2 + 4ab + b 2 .
Пример 2. Квадрат ab + cd, есть a 2 b 2 + 2abcd + c 2 d 2 .
Пример 3. Квадрат 3d — h, есть 9d 2 + 6dh + h 2 .
Пример 4. Квадрат a — 1 есть a 2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b) 2 .
N-ая степень bc + 8 + x есть (bc + 8 + x) n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей , скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)] 2 или (a + b) 2 .(c + d) 2 .
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a.(b + d), есть 3 , или a 3 .(b + d) 3 .
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a 2
Третья степень (-a) есть -a 3
Четвёртая степень (-a) есть +a 4
Пятая степень (-a) есть -a 5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a 2
И -a.-a = +a 2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a 2 есть a 2.3 = a 6 .
Для a 2 = aa; куб aa есть aa.aa.aa = aaaaaa = a 6 ; что есть шестой степенью a, но третьей степенью a 2 .
Четвертая степень a 3 b 2 есть a 3.4 b 2.4 = a 12 b 8
Третья степень 4a 2 x есть 64a 6 x 3 .
Пятая степень (a + b) 2 есть (a + b) 10 .
N-ая степень a 3 есть a 3n
N-ая степень (x — y) m есть (x — y) mn
(a 3 .b 3) 2 = a 6 .b 6
(a 3 b 2 h 4) 3 = a 9 b 6 h 12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a -2 есть a -3.3 =a -6 .
Для a -2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a 6 = a -6
Четвертая степень a 2 b -3 есть a 8 b -12 или a 8 /b 12 .
Квадрат b 3 x -1 , есть b 6 x -2 .
N-ая cтепень ax -m есть x -mn или 1/x .
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a 3 есть +a 6 . Квадрат -a 3 есть -a 3 .-a 3 , которое, согласно правилам знаков при умножении, есть +a 6 .
2. Но куб -a 3 есть -a 9 . Для -a 3 .-a 3 .-a 3 = -a 9 .
3. N-ая степень -a 3 есть a 3n .
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a 2 /b 2 . Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a 2 b 2
Вторая, третья и n-ая степени 1/a есть 1/a 2 , 1/a 3 и 1/a n .
Примеры двочленов , в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2) 2 = x 2 + 2.x.(1/2) + 1/2 2 = x 2 + x + 1/4
(x — 1/2) 2 = x 2 — 2.x.(1/2) + 1/2 2 = x 2 — x + 1/4
2. Квадрат a + 2/3 есть a 2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x 2 + bx + b 2 /4.
4 Квадрат x — b/m есть x 2 — 2bx/m + b 2 /m 2 .
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени .
Так, в дроби ax -2 /y, мы можем переместить x из числителя в знаменатель.
Тогда ax -2 /y = (a/y).x -2 = (a/y).(1/x 2 = a/yx 2 .
В дроби a/by 3 мы можем переместить у из знаменателя в числитель.
Тогда a/by 2 = (a/b).(1/y 3) = (a/b).y -3 = ay -3 /b.
Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.
Так, ax 3 /b = a/bx -3 . Для x 3 обратным есть x -3 , что есть x 3 = 1/x -3 .
Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.
Так, a/b = 1/ba -1 , or ab -1 .
Пятые степени цифр : Школьная алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| main.c |
| ||
22/07/12 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
main. c c |
| ||
22/07/12 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| VAL |
| |||
27/06/08 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| VAL |
| |||
27/06/08 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| VAL |
| |||
27/06/08 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Одночлены и многочлены /qualihelpy
Одночленом называют алгебраическое выражение, представленное в виде произведения чисел и переменных величин.
Например, , и – одночлены. Действительное число, например, число 5 также одночлен, так как его можно записать в виде или, например, в виде .
Одночлен имеет стандартный вид, если он имеет только один числовой множитель, а каждая из переменных встречается в его записи только один раз. Числовой множитель называют коэффициентом одночлена.
Если коэффициент одночлена равен 0, то его называют нулевым одночленом. Например, – нулевой одночлен.
Одночлены, которые имеют одинаковую переменную часть, называются подобными.
Чтобы сложить подобные одночлены, необходимо сложить их коэффициенты, а переменную часть переписать.
Например, одночлены и подобные, а их сумма равна .
Степенью одночлена называют сумму показателей степеней всех входящих в него переменных.
Например: степень одночлена равна 1; степень одночлена равна 5.
Если одночлен представлен отличным от нуля числом, то его степень равна 0.
Например, числа –260 и 0,5 – одночлены, степень которых равна 0.
Нулевым одночленам не приписывают никакую степень.
Многочленом называют алгебраическое выражение, представленное в виде суммы нескольких одночленов.
Например, и – многочлены.
Многочлен имеет стандартный вид, если все одночлены имеют стандартный вид, и среди них нет подобных.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в него одночленов.
Например, степень многочлена равна 4.
Чтобы умножить одночлен на многочлен, необходимо умножить одночлен на каждый член многочлена и полученные произведения сложить.
Например, .
При умножении многочлена на число 1, многочлен не изменится, а при умножении многочлена на число –1, получим многочлен, каждый член которого будет иметь противоположный коэффициент.
Например, ;.
Это утверждение часто формулируют, как правило раскрытия скобок. Говорят, что если перед скобкой стоит знак «+» (этот знак не ставят), то скобки опускают, а выражение, стоящее в скобках, переписывают без изменений. Если перед скобкой стоит знак «–», то скобки опускают, а выражение, стоящее в скобках, умножают на число –1.
Например, .
Чтобы умножить многочлен на многочлен, необходимо каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Например: .
Многочленом степени от одной переменной называют выражение вида при и .
Числа называют коэффициентами многочлена, при этом число называют старшим коэффициентом многочлена, а число – свободным членом. Коэффициенты многочлена за исключением его старшего коэффициента, могут быть равны нулю.
Например: – многочлен первой степени, а – многочлен третьей степени.
Многочлен вида называют многочленом нулевой степени, а если , то имеем нулевой многочлен.
Например, – многочлен нулевой степени, а – нулевой многочлен.
Корнем многочлена называют такое число , что .
Например, число является корнем многочлена , так как .
Число называют корнем кратности многочлена , если справедливо равенство , где – многочлен степени , и – натуральные числа и .
Деление многочленов. Деление многочленов выполняют аналогично делению целых чисел: делят старший член многочлена-делимого на старший член многочлена-делителя, затем частное умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого. Многочлен-первый остаток аналогичным образом делят на многочлен-делитель. Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
Многочлен-первый остаток аналогичным образом делят на многочлен-делитель. Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
Например,
Результат деления записывают так: .
Теорема Безу. Остатокот деления многочлена на двучлен равен значению многочлена при , то есть .
Следствие 1. Для делимости многочлена на двучлен необходимо и достаточно, чтобы число было корнем многочлена .
Следствие 2. Если – все корни многочлена , то этот многочлен можно разложить на множители следующим образом: .
Если – корень кратности многочлена , то разложение этого многочлена на множители примет вид: .
Теорема о целых корнях. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
Следствие. При отыскании целых корней многочлена с целыми коэффициентами достаточно рассмотреть делители свободного члена.
Пример 1. Приведем одночлен к стандартному виду: .
Пример 2. Приведем многочлен к стандартному виду: .
Пример 3. Найдите корни многочлена .
Решение. Найдем целые корни многочлена. Согласно теореме о целых корнях многочлена, ими могут быть только делители свободного члена, то есть числа –1 и 1.
,.
Так как , то число –1 не является корнем многочлена, а так как , то число 1 – целый корень многочлена.
Тогда, согласно следствию из теоремы Безу, многочлен делится на двучлен .
Выполним деление многочленов:
Запишем результат деления: .
Найдем корни квадратного трехчлена . Получим: , , .
Следовательно, многочлен имеет три корня: .
Ответ: .
Пример 4. Найдем остаток от деления многочлена на двучлен .
Решение. Вычислим значение многочлена при :
.
Ответ: .
Пример 5. Найдите все целые значения , при которых дробь является целым числом.
Решение. Упростим дробь: .
Разделим числитель дроби на ее знаменатель:
Запишем результат деления: . Очевидно, что дробь будет целым числом, если 49 разделится без остатка на , то есть если число будет делителем числа 49.
Запишем делители числа 49: . Решим уравнения:
Решим уравнения:
1) ,;
2) ;
3) ;
4) ;
5) ;
6) .
Поскольку, согласно условию задачи, – целое число, то , и .
Ответ: .
1. Если коэффициент одночлена равен 1 или –1, то цифру 1, как правило, не записывают, а пишут только его переменную часть. Например: ;.
2. Одночлены также являются многочленами.
020: Пятые степени (4 или 6 терминов)
◄ Вернуться к оглавлению
III. Сумма / суммы пятых полномочий 5.1 Четыре термина 5,2 шесть терминов 5,3 Семь терминов 5,4 восемь терминов 5,5 Десять терминов 5,6 9 5,1 5 термины 9006 5,1 5 термины 5. Хотя предполагается, что x 1 K + x 2 K = Y 1 K + Y 2 K не имеет необразны квадратичные уравнения для k = 5.
А. Десбовес
(a√2+b) 5 + (-b+c√-2) 5 = (a√2-b) 9 9 + (b+c√-2) 5
где a 2 +b 2 = c 2 . Piezas (√p + √q) 5 + (√p-√q) 5 = (√r + √s) 5 + (√r-√s) 5
{p,q,r,s} = {5vw 2 , -1+uw 2 , 5v, -(u+10v)+w 3 }, где w = u 2 +10мкВ+5В 2 .
Затем можно установить v = 5t 2 , чтобы {p,r} были квадратами. Можно ли тогда {q, s} сделать нетривиальными квадратами, это другой вопрос. В более общем случае приведенное выше уравнение для k = 5, 6, 7, 8 имеет полиномиальное решение, и первые два можно привести к общему виду. √p (стр 2 +10pq +5q 2 ) = √r (r 2 +10RS +5S 2 ) Тогда {p, Q, R, S} = = {5(bc-ad)v 2 , u 3 -(10bc+w)v 2 , 5(bc-ad)u 2 , -v 3 +(10ad+w)u 2 }
where {u,v,w} = {a 2 +10ab+5b 2 , c 2 +10cd+5d 2 , ac+5bd}
с четырьмя свободными переменными {a,b,c,d}. Для к = 6,
(√p+√q) 6 + (√p-√q) 6 = (√r+√s) 6 + (√r-√s) 6
или после расширения, (P+Q) (P 2 +14PQ+Q 2 ) = (R+S) (R 2 +14RS+S 2 ) +14RS+S 2 )+14RS+S )тогда {p,q,r,s} = {-u 2 +vw, u 2 -vx, v 2 -ux, -v 2 +uw}
где {u ,v,w,x} = {a 2 +14ab+b 2 , c 2 +14cd+d 2 , ac+bc+13ad+bd, ac+13bc+ad+bd} p Форма )(p 2 +apq+bq 2 ) k = (r+cs)(r 2 +ars+bs 2 ) k 6 Это обобщает две приведенные выше формы 7 и, как уже обсуждалось в разделе о третьих степенях , требуется лишь небольшое преобразование, чтобы принять с = 0 без потери общности. , а затем для k = 6 Рао, Брудно и др. Ли, , а затем для k = 6 Рао, Брудно и др. Ли, Шеру, Э. Зайдлу) Шеру, Э. Зайдлу) радиус 17700, и это единственные солны, у которых есть единичный член. Тем не менее, это также включает в себя один с ноль терм, найденный Бобом Шером и Эдом Зайдлом в 1997 году, радиус 17700, и это единственные солны, у которых есть единичный член. Тем не менее, это также включает в себя один с ноль терм, найденный Бобом Шером и Эдом Зайдлом в 1997 году, См. здесь.) См. здесь.) ) ) 744, хотя это свойство 744 5 , вероятно, не связан.) 744, хотя это свойство 744 5 , вероятно, не связан.) 4. 40006 40006 4. 40006 . +2c 4 = d 4 , наименьший из которых пифагорейский: [2, 2, 3, 4, 4] = [5]. Существует также одна для пятой степени, пока единственная, представленная в базе данных Уолдби как: [526, 526, 1349, 1349, 1355] = [1685] e) x 1 k +x 2 k +x 3 k = x 4 k +x 5 k +x 6 k The наименьшее решение оказывается подходящим для обоих k = 1,5: [24, 28, 67] = [3, 54, 62]. Для шестых степеней наименьшее подходит для обоих k = 2,6: [3, 19, 22] = [10, 15, 23]. Фактически, из 198 солнов в базе данных Томиты для [5. [344, 902, 1112, 1555] = [479, 662, 1237, 1535], для k = 1,3,7 и другие, найденные А. Дж. Чоудри всякий раз, когда некоторая многомерная кубика имеет рациональный корень. А также [51, 253, 412, 600, 624] = [100, 187, 429, 603, 621], для k = 1,3,9 , найденное Вроблевским и единственное уже. Известен только один для [8.4.4], найденный Куосой, но я держу пари, что в конечном итоге он будет найден хорошим для k = 2,8 или, если он подписан, даже хорошим для k = 1,2,8, как некоторые к = 1,2,6. (Update, 11/3/09): f) x 1 k +x 2 k +x 3 k = x 4 K +x 5 K +x 6 K , с x 1 +x 2 +x 3 = x 4 +x 5 +x 6 4 +x 5 +x 6 4 +x 5 +x 6 40 +x 5 +x 6 40 +x 5 +x 6 + +x 5 . = 0 Внизу этой веб-страницы я спросил, имеет ли эта система для k = 1,5 нетривиальные решения, поскольку аналогичная версия для 7-й степени с восемью членами и дополнительным условием x 1 +x 2 +x 3 +x 4 = x 5 +x 6 +x 7 +x 8 = 0 ,3,7 и сведен Чоудри к нахождению рационального корня кубического уравнения с несколькими переменными. [105, 1153, -1258] = [455, 582, -1037] [31, 47242, -47273] = [5681, 9717, — 15398] [3914, 51858, — 55772] = [19264, 25403, -44667] [12292, 59070, -71362] = [27745, 37983, -65728] Система, по сути, тоже сводится к нахождению нетривиального рационального корня кубического. Используйте форму L 1 , (a+bp+q) k + (b-bp+q) k + (c+ap+q) k = (a+cp+q) k + (b+ap+ q) k + (c-cp+q) k , что уже верно для k = 1, общая форма будет доказана позже. Пусть p = q/a+1, и это будет равняться x 1 + х 2 = х 5 . Расширение для k = 5 и после удаления тривиальных факторов приведет к кубическому виду q с коэффициентами в {a,b,c}. ( End update )
(обновление от 26.
(Обновление от 17.07.09): Просматривая Интернет, я наткнулся (снова) на страницу Тома Вомака. Я читал его диссертацию много лет назад и, перечитав ее, понял, что он заметил ту же самую точку об изобилии k = 2,6 (и Питер Монтгомери, а также другие до него). На самом деле Вомак провел поиск и обнаружил, что из 207 солнов с общей суммой < 5717 6 , почти 90% были для k = 2,6 (только 22 были только для k = 6), что намного выше, чем тот, который дает меньший набор решений Томиты.
(Обновление от 07.10.09): Дункан Мур, проделавший обширную работу над номерами такси и такси , имеет большую базу данных, которая включает [5.3.3] и [6.3.3]. Ниже определенной границы, для 5-й степени, он нашел почти 5400 солнов, из которых около 59% являются всеградусными для k = 1,5. Для 6-й степени их было 405, из них 92% многостепенных для k = 2,6, больше из базы данных Вомака. Неизвестно, приближаются ли эти проценты асимптотически к определенному значению. ( Конец обновления .)
После приведения к симметричной форме были найдены различные тождества для 5-х степеней, где { x i , y i } не обязательно положительны, которые принадлежат четырем классам: x 900 7. 9006 1 5 +x 2 5 +x 3 5 = Y 1 5 +Y 2 5 +y 3 2 5 +y 3 2 5 +y 3 2 . + х 2 = у 1 +у 2 , 9006 1 5 +x 2 5 +x 3 5 = Y 1 5 +Y 2 5 +y 3 2 5 +y 3 2 5 +y 3 2 . + х 2 = у 1 +у 2 , x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +y 3 k , x 1 -x 2 = y 1 -y 2 , k = 1,5 x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +y 3 k , x 1 -x 2 = y 1 -y 2 , k = 1,5 1.5) со всеми положительными членами. Вне этого диапазона оно превращается в (5.2.4), но не существует {u,v} такого, что оно дает (5.3.3) со всеми положительными членами. Это имеет базовую форму: 1.5) со всеми положительными членами. Вне этого диапазона оно превращается в (5.2.4), но не существует {u,v} такого, что оно дает (5.3.3) со всеми положительными членами. Это имеет базовую форму: В: Существуют ли другие, не просто кратные этим двум числам в пятой степени или другие малые m,n? В: Существуют ли другие, не просто кратные этим двум числам в пятой степени или другие малые m,n?  Для r = 2 это дает (5,4,6) тождество — (у 5 +200В 5 ) 5 — (u 5 -200v 5 ) 5 = 2(2u 3 v 2 ) 5 + 4(4uv 4 ) 5 Для r = 2 это дает (5,4,6) тождество — (у 5 +200В 5 ) 5 — (u 5 -200v 5 ) 5 = 2(2u 3 v 2 ) 5 + 4(4uv 4 ) 5   ) 4 = ) 4 = ) Хотя существуют тождества для k = 6, , ни одно не известно с такими малыми коэффициентами. ( Кто-нибудь может найти? ) Другие личности 5-й степени можно найти с помощью ff. два метода Чоудри. Учитывая, ) Хотя существуют тождества для k = 6, , ни одно не известно с такими малыми коэффициентами. ( Кто-нибудь может найти? ) Другие личности 5-й степени можно найти с помощью ff. два метода Чоудри. Учитывая, Уравнение 1 можно сократить всего до 6 членов, если x 4 = y 4 . Таким образом, если Уравнение 1 можно сократить всего до 6 членов, если x 4 = y 4 . Таким образом, если Примечание : Чоудри также использовал уравнение 1 и его замены для решения k = 1,3,7. Примечание : Чоудри также использовал уравнение 1 и его замены для решения k = 1,3,7.
как,
{x, y, z} = {(P 1 T 2 -P 1 T+Q 1 ) R 1 , (P 2 T 2 -P 2 0 2 T 2 -P 2 0 t+q 2 )r 2 , (p 3 t 2 -p 3 t+q 3 )r 3 } {u, v, w} = {(Q 1 T 2 -P 1 T+P 1 ) R 1 , (Q 2 T 2 -P 2 0 2 T 2 -P 2 0 t+p 2 )r 2 , (q 3 t 2 -p 3 t+p 3 )r 3 }
где.
{стр 1 , стр 2 , стр 3 } = {17A 2 +14AB +14B 2 , 14A 2 +14AB +17B 2 , 17A 2 +20AB +17B 2 } 9007 +20AB +17B 2 } 9007 9007 +20AB +17B 2 } . {Q 1 , Q 2 , Q 3 } = {2A 2 -AB -B 2 , -A 2 -AB +2B 2 , 2A 2 +5AB +5B 2 , 2A 2 +2b 2 } {r 1 , r 2 , r 3 } = {a+2b, -2a-b, ab} задана константа {a,b} для произвольных т . Затем можно установить t = v 5 , чтобы удовлетворить уравнению 1. Например, для {a,b,c} = {1,2,-3} после перестановки членов мы получаем решение x 5 +2y 5 +3z 5 = u 5 +2v 5 +3w 5 {x, y, z} = {101t 10 -101T 5 -4, 4T 12 -88T 7 +88T 2 , 25T 10 -25T 5 +477777777777 гг. {u, v, w} = {-4t 12 -101T 7 +101, 88T 10 -88T 5 +4, 4T 12 -25T 7 +25T 2 -25T 7 +25T 2 }
( Конец обновления .)
(обновление от 03.02.10): Чоудри
(-8M 6 + 2MN 5 ) K + (8M 5 N + N 6 ) K + 2 (8M 6 ) K = (8m + + + + + + + + + + ) K = (8m 6 ). 2мн 5 ) к + (8m 5 n-n 6 ) k + 2(n 6 ) k , для k = 1,5
Раствор в положительном выражении можно получить, если n > m и находится в диапазоне 2 2/5 < n/m < 2 3/5 , или прибл.
(-8m 6 +2mn 5 ) k + (8m 5 n+n 6 ) K — (8M 6 + 2MN 5 ) K — (8M 5 N -N 6 ) K + 2 (8M 6 ) K + 2 (8M 6 ) K + 2 (8M 6 ) K = 2 (8M 6 ) K = 2 (8M 6 ) K + 2 (8M 6 ) K + 2 (8M 6 ) K + 2 (8M 6 ) K + 2 (8M 6 ) 6 ) к
Для n = 1 тождество доказывает, что целое число 2 является суммой/разностью шести целых пятых степеней бесконечным числом способов. Источник: Диофантово уравнение x 1 5 +x 2 5 +2x 3 5 = y 1 5 +y 2 5 +2y 3 5 , Ганита, Vol.
Примечание : В каком-то смысле это версия числа в пятой степени.
(-6x 3 +Y 3 ) 3 +(6x 3 +Y 3 ) 3 — (6x 2 Y) 3 = 2 (Y 3 )) 3
, где для y = 1 доказывает, что 2 бесконечно есть сумма, равная сумме/разности трех целых 3-х степеней.
Q : Кто-нибудь может дать аналогичную идентичность, выражающую 2 в виде целых 7-х степеней? ( Конец обновления .) Ландер позже найдет трехпараметрическое семейство, которое в общем случае будет включать полиномы 9-й степени. Этот автор обнаружил, что для особых случаев его можно уменьшить до 7-й или 8-й степени. Есть ли 6й град неизвестно. Мы уже видели, что при начальном решении a 1 k +a 2 k = b 1 k +b 2 k для любого k = 2, 3 или 4, можно использовать это, чтобы найти больше решений.  Оказывается, существует квинтик версия этого, хотя и с небольшим условием, Оказывается, существует квинтик версия этого, хотя и с небольшим условием,
Теорема (Ландер): «Дано рациональное решение 1 k +a 1 +a 3 k = b 1 k +b 2 k +b 3 k для оба k = 1,5, назовите эту систему S 5 , тогда это может породить последующие. Равные суммы одинаковых степеней », Ландер начал с формы (u+x) k + z k + (v+y) k = (v+x) k + y k + (u+z) k , (назовем это L 0 )
общее решение для k = 1. Это также может быть верно для k = 5 с использованием соответствующих значений. ( Примечание : Кстати, следует отметить, что уравнение, x 1 k + x 2 k + …+ x k+1 k = 0 одновременно справедливо для трех нечетных степени k = 1,3, n имеет тривиальные решения только при n = 5. Во всяком случае, L 0 при расширении для k = 5 имеет красивый симметричный вид,
(x-z)u 4 +2 (x 2 -z 2 )u 3 +2(x 3 -z 3 )u 2 +(x 4 -y 4) 4 +2(х 2 -у 2 )v 3 +2(x 3 -y 3 )v 2 +(x 4 -y 4 )v 4 )v После умного геометрического анализа Ландер предложил метод получения полиномиальных выражений для всех переменных. Учитывая первоначальный раствор {a i , b i } до L 0 , это приводит к новому, обычно намного большему, двумя способами.
1. Используя пункт P 1 (x 1 , Y 1 , Z 1 ) DEFIN , A 2 -B 2 , x 0 +(x 1 -x 0 ) T, Y 0 +(Y 1 -Y 0 ) T, Z 0. +(z 1 -Z 0 ) T}, Где, x 1 = Y 1 = Z 1 = (x 0 D 1 +Y 0 D 2 +Z 0 D 3 )/(D 1 +D 2 +D 3 ) +D 3 )6. , d 2 , d 3 } = {a 1 4 -b 1 4 , a 2 4 -b 2 4 , a 3 4 -b 3 4 }
{x 0 , y 0 , z 0 } = {a 1 +a 3 -b 3 , b 2 , a 3 } 5 Однако остается найти 1 . Когда все эти выражения подставлены в L 0 , если {a i , b i } является решением, то уравнение представляет собой квартику с четырьмя корнями {0,0,1,t}, так что это просто линейное уравнение в t , которое затем легко решается. Можно также использовать второй подход, Когда все эти выражения подставлены в L 0 , если {a i , b i } является решением, то уравнение представляет собой квартику с четырьмя корнями {0,0,1,t}, так что это просто линейное уравнение в t , которое затем легко решается. Можно также использовать второй подход,
2. Используя точку P 2 (x 2 ,y 2 ,z 2 )
Определить 4 0 9 {09 3a} +B 3 , A 2 -B 2 , x 0 +(x 2 -x 0 ) T, Y 0 +(Y 2 -Y 0 ). T, Z 0 +(Z 2 -Z 0 ) T}, Где, {x 2 , Y 2 , z 0039 2 } = {x 1 -d 0 , x 1 -d 0 +u, x 1 -d 0 +v}
x 1 = ( x 0 d 1 +y 0 d 2 +z 0 d 3 )/(d 1 +d 2 +d 3 )
d 0 = (d 2 u+d 3 v)/(d 1 +d 2 +d 3 )
и {d 1 , d 2 , d 3 }, {x 0 , y 0 , z 0 } определяются так же, как и в первом пункте. {а 1 , а 2 , a 3 , b 1 , b 2 , b 3 } = {p, -p, q, r, q, -r} для первой и второй 9000 точек соответственно, и они дадут полиномы 9-й степени.
Theorem (Piezas): «The complete soln to S 5 , or x 1 k +x 2 k +x 3 k = y 1 к +у 2 к +y 3 k , для k = 1,5 включает решение только квадратного уравнения с дискриминантом D , который является полиномом четвертой степени от одной переменной. Тогда задачу преобразования D в квадрат можно рассматривать как эллиптическую кривую.
(a+bp+q) k + (b-bp+q) k + (c+ap+q) k = (a+cp+q) k + (b+ap+q) k + (c-cp+q) k
, с которым мы сталкивались раньше.
(u+x) k + z k + (0v+9041 k ) 9 + (0v+x) = (v+x) k + y k + (u+z) k
, исключая случай uv(u-v) = 0. Чтобы убедиться в этом, просто приравняйте первые пять членов L 1 с L 0 , и всегда можно найти рациональные {a,b,c,p,q} с помощью,
{a,b,c,p,q} = {(1+ t)(st+y-z)/(2t), -(1+t)(st-y+z)/(2t), (1+t)(y+tu-tx+ty-z)/(2t) , t/(1+t), (st-y+z+2tz)/(2t)}, где {s,t} = {u+x-y, -(u-v)/u}
, следовательно, случаи со знаменателем (1+t)t = uv(u-v) = 0 следует исключить, иначе имеет место деление на ноль. Используя эти выражения, также видно, что шестые члены L 1 и L 0 равны. Тот факт, что Л 1 менее общий, чем L 0 не имеет значения, так как в исключительном случае L 0 сводится к четырехчленной форме,
n 1 k 90 + + (n 29003 n 3 ) k = (n 1 +n 2 ) k + n 3 k
which, after expanding, is easily seen to have trivial solns for k < 6, кроме k = 1, поэтому не представляет интереса.
без учета тривиального множителя p(p-1). Poly i находятся в {a,b,c,q}, а полиномы в q имеют степень 1,1,3 соответственно. (К сожалению, явно записывать их утомительно.) Дискриминант D равен 9.0007
D:= (Poly2) 2 -4(Poly1)(Poly3)
степени 1+3 и, следовательно, является квартикой в q , что доказывает теорему. Чтобы найти полиномиальное решение, есть два способа: 1-й метод : Поскольку Poly1 является линейным относительно q , все, что нам нужно сделать, это установить Poly1 = 0 и найти q , с уравнение
2(b+c)(b 2 +c 2 ) q = (a 4 -c 4 )-(a+b)(b+c)(b 2 +c 2 )
и (уравнение 1) сводится к уравнению 1.
(a+bp+q) + (b-bp+q) = (a 4 -c 4 )/((b+c)(b 2 +c 2 )) ( a+cp+q) + (c-cp+q) = (a 4 -b 4 )/((b+c)(b 2 +c 2 ))
для {p,q}, как определено выше. Этот автор обнаружил, что степень полиномов может быть уменьшена на до , если мы предположим некоторые линейные отношения между членами. Известно, что система при k = 1,5 может иметь боковое условие x 1 -х 2 = у 1 -у 2 . Пусть
(a+bp+q) — (b-bp+q) = (a+cp+q) — (b+ap+q)
, что верно, если c = a+ 2б .
c = a+2 t = 4a(a-2 )(a+3)(a 2 +4a+5) 2 p = (a 2 +1)(a 2 +8a+11)(a 3 +15a 2 +33a+31) q = -2a(a+1)(a-2)(a 2 +4a+5)(a 3 +15a 2 +33a+31)
, где общий множитель (a+1) терминов должен быть удален. (А. Месснер также нашел седьмой градус солнца в 1951, но я не знаю, совпадает ли это, поскольку Ландер указал источник как итальянский журнал.) В качестве альтернативы, если используется c = a-2b, они уменьшаются до восьмых градусов, хотя я не смог найти линейная зависимость между терминами. В: Итак, есть 5-й, 7-й, 8-й и 9-й градусы солнца.
(Обновление от 13.07.09) 2-й метод : Напрямую находим q такое, что дискриминант D является квадратом. Чтобы найти тривиальное решение, нужно начать с разложения L 1 для k = 5,7 и исключения p между ними. Разлагая результат на множители, можно найти линейную зависимость между {a,b,c,q}, заданную формулой -ab-ac-bc
Использование этого Q , D становится простым квадратом, D: = (A 2 -B 2 ) 2 (A 2 -C 2 ) 2 (2 -C 2 ) 2 (2 -C 2 ) b-c) 2 /(b+c) 2
Это тривиальное решение, но, как было показано в первом методе, D является квартикой в q , из этой начальной точки можно затем найти бесконечное число нетривиальных единиц.
Piezas
The complete criterion to solve the system x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +y 3 k для k = 1,5 уже было дано выше, с подмножеством, также удовлетворяющим x 1 -x 2 = у 1 -у 2 . Мы также можем изучить другие методы ради упражнения. Это подмножество может быть полностью определено любой из двух хороших форм. Пусть
(а+г) к + (б+г) к + (в-2г) к = (а-г) к + (б-г) к + (в+ 2d) k
уже верно для k = 1, а если разложить для k = 5, сводится к простому уравнению
(a 4 +b 4 -2C 4 ) + 2 (A 2 + B 2 -8C 2 ) D 2 -6D 4 = 0 Один из способов, чтобы речь его как квадратное в d 2 и сделать его дискриминант (многочлен четвертой степени) квадратом, хотя это нелегко сделать для этой конкретной четвертой степени.
(p+r) k + (pr-r) k + (2q+s) k = (q+r) k + (q-r) k + (2p+s) k
что для удобства после масштабирования можно принять s = 1 без ограничения общности. Расширяя это при k = 5, это всего лишь квадратичное число по r 2 . Решение для R 2 , R 2 = -P 2 -PQ -Q 2 ± Y, , где Y -квадратный корень дискриминантного, 77777 y -квадратный корень дискриминантного,7777777777777 Y . y 2 = 4q 4 +(8+5p)q 3 +2(4+4p+3p 2 )q 2 +(4+8p+8p 2 p 0 +5 1 0 )q+(1+2p+2p 2 ) 2 (ур.1)
Это более легко сделать квадратом, являющимся полиномом с квадратом в начале и постоянным членом, и иллюстрирует, как использование соответствующей формы может упростить задачу.
(p+r) k + (p-r) k + (2q+1) k = (q+r) k + (q-r) k + (2p+1) к , к = 1,5
имеет соль,
q = – (80p+40)/(57p+80), r = z/(57p+80), 40 2
q = 3(13p 2 +10p+8)/(9p-16), r = z/(9p-16), 8 2 +656p+1999p 2 +2922p 3 +9041p 4 = г 2
q = (13p 2 +14p+8)/(3p+16), r = z/(3p+16), 24 2 +1232p+1183p 2 +542p 3 +181p 4 = z 2
где нужно решить эллиптическую кривую в p .
U 1 P 4 +U 2 P 3 +U 3 P 2 +U 4 P +U 5 = (V 1 P 2 . 2 p+v 3 ) 2 Поскольку u i выражаются через {a,b}, то неизвестные равны {a,b,v 1 ,v 2 ,v 3 }.
Добавив еще одно ограничение, можно также найти простую форму для S 5 . Например,
(v+8) k + (u-8) k + (-u+2v+7) k = (-u+2v+8) k + (v-8) k + (u+7) k
Это уже верно для k = 1. Разложение для k = 5 дает только квадратичное значение v и легко решается. Для Rational V , нужно сделать его дискриминантом, квартирный полином в U , в качестве квадрата, Y 2 = -43281 +40110U -4597U 2 +39041 3 4141414141414141414141414141414141414.3114141414141414141414141414141414141414.3111110U -4597U 2 +39041 3 414141414141414141414141.
с одним малым решением при u = 3/2, что дает [389, -208, 442] = [474, -123, 272]. Из этой начальной точки можно затем вычислить бесконечное число рациональных точек. Это, по сути, полное решение для системы, назовите это M 1 ,
x 1 -x 2 = у 1 -у 2 x 2 -nx 3 = -ny 1 +y 3 x 1 k +x 2 k +x 3 k = y 1 к +у 2 к +у 3 к
для k = 1,5 и n = 15. Кроме случая n = 1, который тривиален, я еще не проверял, для каких других n эта система разрешима.
(Обновление от 12.07.09): Еще один, подчиняющийся системе M 1 , но с n = 2,
(1-2q+2r) k + (-3-2q) k + (1+2q) к = (2+q+r) к + (-2+q-r) к + (-1-4q+2r) к
Опять же, это уже верно для k = 1 и, будучи расширено для k = 5, дает квадратное выражение в r .
у 2 = -(384+1112q+1297q 2 +738q 3 +171q 4 )
с малой рациональной точкой при q = -16/15. В: Есть ли другое простое решение для системы M 1 для некоторого целого числа n ? ( Конец примечания .) Примечание 1 : к случайному, учитывая монический квартик формы, y 2 = x 4 +(Poly1) x 3 +(Poly2 (Poly1) x 3 +(Poly2 (Poly1). )x 2 +(Poly3)x+(Poly4)
сделать квадратом и где Poly_i являются полиномами от переменной p степени 1,2,3,4 соответственно (подобно уравнению 1 выше), каково максимально возможное количество линейных решений вида x = (ap+b) или x = (ap+b)/(cp+d)?
Note 2 : The complete criterion of x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +x 3 k , k = 1,5, где x 1 -x 2 = y 1 -y 2 также было дано Бремнером, хотя я этого не видел.
Примечание 3 : Можно доказать, что k = 1,2,5 дает только тривиальные рациональные результаты. Полное решение k = 1,2 принадлежит Л. Диксону (форма 4 в суммах трех квадратов )
(ad+e) k + (bc+e) k + (ac +bd+e) k = (ac+e) k + (bd+e) k + (ad+bc+e) k
, и разложение этого на k = 5 дает просто квадратичный многочлен от e с дискриминантом D , D = -2 (A 2 -AB+B 2 ) (C 2 -CD+D 2 ) , который должен быть изготовлен квадрат. Но пусть {a,b,c,d} = {u+v, 2v, x+y, 2y}, тогда
D = -2(u 2 +3v 2 )(x 2 +3y 2 )
и очевидно, что не существует действительных значений, таких, что D становится положительным действительным квадратом.
Примечание 4 : Is a 5 +b 5 +c 5 = d 5 +e 5 = ad2+e+c+f , что при расширении равно pq(p+q)(p 2 +pq+q 2 ) = rs(r+s)(r 2 +rs+s 2 ) хотя кажется, что быть неизвестным, если это нетривиально разрешимо. 105 5 + 1153 5 + (-105-1153) 5 = 455 5 + 582 5 + (-455-582) 95. См. обновление от 03.11.09 выше.) ◄ Предыдущая страница Следующая страница ► |
Сумма и разность степеней
Содержание | Дом
вернуться к разделу 1
Форма ( a + b ) ( a − b )
Факторинг по группировке
Сумма и разность нечетных степеней
разница четных степеней
Пример 2. Форма ( a + b )( a − b ).
Нижеследующее имеет форму ( a + b ) ( a − b ):
( х + у + 8)( х + у — 8)
Мы можем просматривать x + y в качестве первого члена. 8 это второй. Следовательно, будет получена разница двух квадратов:
8 это второй. Следовательно, будет получена разница двух квадратов:
| ( х + у + 8)( х + у — 8) | = | ( х + у ) 2 − 64 |
| = | х 2 + 2 ху + у 2 − 64 | |
— при применении правила квадрата двучлена.
Задача 7. Каждый из них даст разность двух квадратов. Умножить.
| а) ( p + 3 q + 2)( p + 3 q − 2) | = | ( р + 3 к ) 2 − 4 |
| = | p 2 + 6 pq + 9 q 2 − 4 | |
| b) ( x − y − 1)( x − y + 1) | = | ( х — у ) 2 — 1 |
| = | x 2 − 2 xy + y 2 − 1 | |
Пример 3. Факторизация по группировке.
Факторизация по группировке.
x 3 + 2 x 2 − 25 x − 50.
Давайте разложим это по группам (Урок 15), а затем распознаем разность двух квадратов:
| x 3 + 2 x 2 − 25 x − 50 | = | х 2 ( х + 2) − 25 ( х + 2) |
| = | ( х 2 − 25)( х + 2) | |
| = | ( х + 5)( х — 5)( х + 2) | |
Проблема 8. Фактор по группировке.
| а) x 3 + 3 x 2 − 4 x − 12 | = | x 2 ( x + 3) − 4 ( x + 3) |
| = | ( х 2 − 4)( х + 3) | |
| = | ( х + 2)( х — 2)( х + 3) | |
| б) x 3 − 4 x 2 − 9 x + 36 | = | х 2 ( х — 4) — 9( х — 4) |
| = | ( х 2 − 9)( х − 4) | |
| = | ( х + 3)( х — 3)( х — 4) | |
| c) 2 x 3 − 3 x 2 − 50 x + 75 | = | x 2 (2 x − 3) − 25 (2 x − 3) |
| = | ( x 2 − 25)(2 x − 3) | |
| = | ( х + 5)( х — 5)(2 х — 3) | |
| d) 3 x 3 + x 2 − 3 x − 1 | = | x 2 (3 x + 1) − (3 x + 1) |
| = | ( x 2 − 1)(3 x + 1) | |
| = | ( х + 1)( х — 1)(3 х + 1) | |
Сумма и разность нечетных степеней
Сумму и разность пятых степеней можно разложить следующим образом:
a 5 + b 5 = ( a + b )( a 4 − a 3 b + a 2 b 2 − аб 3 + б 4 )
a 5 − b 5 = ( a − b )( a 4 + 0015 3 B + A 2 B 2 + A B 3 + B 4 )
+ B 4 ) + B 4 )2 + B 4 )
+ B 4 ) Можно убедиться, что это множители, умножив на правых частей. При умножении множителей на 5 + b 5 вы найдете десять членов: пять при умножении на на и пять при умножении на b . Однако восемь из них должны быть отменены, чтобы остаться только с a 5 + b 5 .
При умножении множителей на 5 + b 5 вы найдете десять членов: пять при умножении на на и пять при умножении на b . Однако восемь из них должны быть отменены, чтобы остаться только с a 5 + b 5 .
На самом деле они попарно сокращаются, поэтому знаки во втором множителе должны чередоваться.
Например, при умножении на − a 3 b , произведение равно − a 4 b . Но когда b умножается на a 4 , произведение равно +9.0014 a 4 b , и они отменяются.
Таким образом, терминысокращаются парами, оставляя a 5 + b 5 .
Однако важно изучить форму факторов.
( a + b ) является коэффициентом a 5 + b 5 ; в то время как ( a − b ) является коэффициентом a 5 − b 5 .
В каждом втором множителе первый член равен a 4 . (Умножение на дает на 5 .) Затем показатель степени на уменьшается по мере увеличения показателя степени b , но сумма показателей в каждом члене равна 4.
(Мы говорим, что степень каждого члена равна 4.)
Во втором множителе a 5 − б 5 , все знаки являются +. Это гарантирует отмену.
Доказательство факторизации на основе теоремы о факторах см. в разделе 13 Precalculus .
Задача 9. Учтите следующее.
[ Подсказка : 32 = 2 5 . Следовательно, x 5 + 32 имеет вид a 5 + b 5 , где b = 2.,]
| а) x 5 + 32 | = | ( х 5 + 2 5 ) = ( x + 2)( x 4 − 2 x 3 + 4 x 2 − 8 x + 63 16) |
| б) х 5 − 32 | = | ( x − 2)( x 4 + 2 x 3 + 4 x 2 + 8 x + 16) |
x n − 1 всегда можно разложить на множители, потому что 1 = 1 n , и все степени 1 равны 1.
Задача 10. Учтите следующее.
| а) x 5 − 1 | = | ( x 5 − 1 5 ) = ( x − 1)( x 4 + x 3 + x 2 + x + 1) |
| б) x 5 + 1 | = | ( x + 1)( x 4 − x 3 + x 2 − x + 1) |
Задача 11. Сумма и разность двух кубов. Фактор.
а) а 3 + б 3 = ( a + b )( a 2 − ab + b 2 )
б) а 3 − б 3 = ( a − b )( a 2 + ab + b 2 )
На практике чаще всего всплывают именно они.
Задача 12. Фактор.
| а) x 3 + 8 | = | x 3 + 2 3 |
| = | ( x + 2)( x 2 − x · 2 + 2 2 ) | |
| = | ( х + 2)( х 2 — 2 х + 4) | |
| б) x 3 − 1 | = | x 3 − 1 3 |
| = | ( x − 1)( x 2 + x · 1 + 1 2 ) | |
| = | ( х — 1)( х 2 + х + 1) | |
| x 3 + 1 | = | ( х + 1)( х 2 − х + 1) |
разность четных степеней
Вот вам сумма и разность нечетных степеней. Что касается даже степеней, то только их разность может быть учтена. (Если вы сомневаетесь в этом, попробуйте разложить на 2 + b 2 или на 4 + b 4 . 70 умножьте вашу попытку на .
Что касается даже степеней, то только их разность может быть учтена. (Если вы сомневаетесь в этом, попробуйте разложить на 2 + b 2 или на 4 + b 4 . 70 умножьте вашу попытку на .
Если показатель степени четный, то мы всегда можем распознать разницу двух квадратов:
A 4 — B 4 = ( A 2 + B 2 ) ( A 2 – ) ( A 2 – ).
, но также, когда N ровно, A N — B N может быть учтено любого с ( A — B ) как коэффициент или ( A — B ) как коэффициент ( A — B ). б ).
a 4 − b 4 = ( a − b )( a 3 + a 2 b + a b 2 + б 3 )
A 4 — B 4 = ( A + B ) ( A 3 — A 2 — A 2 B44. B 2 2 — A 2 — A 2 — A 2 — A — A — A .0015 2 − б 3 )
B 2 2 — A 2 — A 2 — A 2 — A — A — A .0015 2 − б 3 )
[если N нечетный, то A N — B N можно учитывать только с фактором
( A — B
Когда n четно, то по следующей причине нельзя разложить a n + b n .
Начало факторинга:
( a + b )( a n −1 − a n −2 b.
При продолжении чередования знаков последний член будет — b n -1 . Следовательно, при умножении этого на + b произведение будет — b n , а не + b n .
Задача 13. Множитель x 4 − 81 с ( x + 3) в качестве множителя.
| x 4 − 81 | = | x 4 − 3 4 |
| = | ( х + 3)( x 3 − x 2 · 3 + x · 3 2 − 3 93 5 3 9) | |
| = | ( х + 3)( х 3 — 3 х 2 + 9 х — 27). | |
Задача 14. x 4 − 1 = ( x − 1)( х 3 + х 2 + х + 1)
вернуться к разделу 1
Следующий урок: Экспоненты II
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Как сложить последовательные степени числа 2
Вам не нужно быть гением математики, чтобы быть хорошим программистом, но есть несколько приемов, которые вы захотите добавить в свой набор решений проблем, чтобы повысить производительность своих алгоритмов и произвести впечатление на технических собеседованиях. В этом уроке вы узнаете, как суммировать последовательные степени двойки с помощью простого и легко запоминающегося уравнения.
Be O (# 1). Возьмите свою копию Маленькой книги Большого О. 9п = ?
Как бы вы решили это?
Программирование — это решение проблем
Что такое программирование?
Программирование — это решение проблем.
Какие проблемы мы решаем?
Есть две основные категории проблем, которые мы решаем как программисты:
- Автоматика
- Алгоритмы
Мы могли бы написать цикл for, чтобы автоматизировать сложение наших степеней 2:
const sumPowers2 = мощность => {
пусть сумма = 0;
for (пусть я = 0; я <мощность; я++) {
сумма += 2**i;
}
сумма возврата;
}
Будет ли он масштабироваться?
Что такое большое О?
О(н).
Почему?
Наша функция должна выполнять одну операцию для каждого входа, поэтому порядок нашего алгоритма равен O(n) или линейной временной сложности.
Должен быть лучший способ!
Вместо того, чтобы автоматизировать подход грубой силы, как мы можем решить эту проблему алгоритмически ?
Часы математики 🧮 🕐
Я собираюсь взорвать ваш мозг.
Проверьте это:
😐
Потерпите меня.
🐻
Если 1 равно 1 , то отсюда следует, что
1 = 2 - 1
А если
1 + 2 = 3
Отсюда следует, что
1 + 2 = 4 - 1
Давайте сделаем еще один шаг. Если
1 + 2 + 4 = 7
Затем
1 + 2 + 4 = 8 - 1
Круто?
😎
Включаем!
Что такое x в этом уравнении? 96 , результат тоже 127:
1 + 2 + 4 + 8 + 16 + 32 + 64 = 127
💥 Доказательство!
Сумма степеней двойки на единицу меньше произведения следующей степени.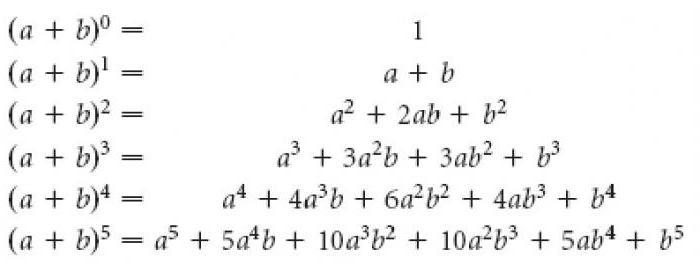
Не верьте мне на слово. Попробуйте с большим значением.
Программирование — это решение проблем
Давайте еще раз посмотрим на нашу функцию сверху. Как мы можем реорганизовать это, чтобы улучшить его временную сложность?
const sumPowers2 = мощность => {
пусть сумма = 0;
for (пусть я = 0; я <мощность; я++) {
сумма += 2**i;
}
сумма возврата;
} Мы просто переводим наше уравнение в JavaScript!
const sumPowers2 = мощность => 2**(мощность + 1) - 1;
Каков порядок нашей новой функции?
О(1).
Независимо от размера входных данных наша функция всегда будет выполнять одинаковое количество операций.
Как сложить последовательные степени числа 2
Вам не нужно быть гением математики, чтобы быть хорошим программистом, но есть несколько уравнений, которые вы захотите добавить в свой набор инструментов для решения задач. В этом уроке вы узнали, как суммировать последовательные степени двойки с помощью простого и легко запоминающегося уравнения.


 2016, 12:23
2016, 12:23  01.2016, 13:15
01.2016, 13:15  01.2016, 13:29
01.2016, 13:29  01.2016, 16:01
01.2016, 16:01  01.2016, 16:46
01.2016, 16:46  01.2016, 18:36
01.2016, 18:36  01.2016, 19:50
01.2016, 19:50  01.2016, 20:13
01.2016, 20:13  01.2016, 22:32
01.2016, 22:32  01.2016, 12:21
01.2016, 12:21  1
1 Для k = 5 это сводится к
Для k = 5 это сводится к Этот автор нашел решение с c=0 as,
Этот автор нашел решение с c=0 as, 3.3], приведенной выше, которая полна для терминов < 1000, почти 2/3 (66%) подходят для k = 1,5. Должно быть интересно проверить процент [6.3.3] с членами ниже границы, которая подходит для k = 2,6. Почему они внезапно становятся хорошими для двух степеней , это пища для размышлений, но может быть просто из-за увеличения количества членов и симметричного характера уравнения. Для более высоких степеней также с минимальным числом членов существуют решения, действительные для трех степеней , например,
3.3], приведенной выше, которая полна для терминов < 1000, почти 2/3 (66%) подходят для k = 1,5. Должно быть интересно проверить процент [6.3.3] с членами ниже границы, которая подходит для k = 2,6. Почему они внезапно становятся хорошими для двух степеней , это пища для размышлений, но может быть просто из-за увеличения количества членов и симметричного характера уравнения. Для более высоких степеней также с минимальным числом членов существуют решения, действительные для трех степеней , например, ( End note )
( End note ) Вроблевски проверил свою базу данных за 2002 год и нашел четыре, а именно:
Вроблевски проверил свою базу данных за 2002 год и нашел четыре, а именно: 06.09): В ответ на электронное письмо Томита любезно создал полную таблицу [6.3.3] с терминами < 1000. Действительно, из 59 solns, почти 3/4 (75%) были хорошими для k = 2,6, что больше, чем для k = 1,5. Для [7.4.4] в базе данных Вроблевского (что составляет , а не полный список ниже определенной границы), и исключая 18 солнов в кубе Чоудри, рассчитанном на получение k = 1,3,7, осталось 40 и почти 1/4 для k = 1,7 . Если можно предоставить полный список с терминами < 10 000, я полагаю, что процент будет больше. Но , почему есть эта склонность к всесезонности неизвестно. ( Конец примечания )
06.09): В ответ на электронное письмо Томита любезно создал полную таблицу [6.3.3] с терминами < 1000. Действительно, из 59 solns, почти 3/4 (75%) были хорошими для k = 2,6, что больше, чем для k = 1,5. Для [7.4.4] в базе данных Вроблевского (что составляет , а не полный список ниже определенной границы), и исключая 18 солнов в кубе Чоудри, рассчитанном на получение k = 1,3,7, осталось 40 и почти 1/4 для k = 1,7 . Если можно предоставить полный список с терминами < 10 000, я полагаю, что процент будет больше. Но , почему есть эта склонность к всесезонности неизвестно. ( Конец примечания ) Насколько выше будет этот процент для полного списка с намного большей общей суммой ? И что это означает для восьми 90 259 положительных 90 260 членов, действительных для k = 1,7 или k = 2,8? (Учитывая, что единственный известный до сих пор для k = 8 не является всесезонным.) ( Конец примечания .)
Насколько выше будет этот процент для полного списка с намного большей общей суммой ? И что это означает для восьми 90 259 положительных 90 260 членов, действительных для k = 1,7 или k = 2,8? (Учитывая, что единственный известный до сих пор для k = 8 не является всесезонным.) ( Конец примечания .)

 1,32 < н/м < 1,51. С терминами, перенесенными на одну сторону,
1,32 < н/м < 1,51. С терминами, перенесенными на одну сторону, 48, № 2, 1997, 115-116.
48, № 2, 1997, 115-116. Используя приведенную выше форму и функцию Mathematica Resultant[] для исключения одной переменной при k = 3 и 5, можно увидеть, что существует являются лишь тривиальными решениями. Напротив, существует — это нетривиальных решений при k = 1,3,7, найденных Чоудри, и k = 1,3,9, найденных Вроблевски. Остается выяснить, существует ли k = 1,3,11.)
Используя приведенную выше форму и функцию Mathematica Resultant[] для исключения одной переменной при k = 3 и 5, можно увидеть, что существует являются лишь тривиальными решениями. Напротив, существует — это нетривиальных решений при k = 1,3,7, найденных Чоудри, и k = 1,3,9, найденных Вроблевски. Остается выяснить, существует ли k = 1,3,11.)  Во-первых,
Во-первых, Используя их, уравнение 0 снова сводится к линейному уравнению в t . Также возможно найти полиномиальное решение, используя тривиальное начальное решение. пусть -r}
Используя их, уравнение 0 снова сводится к линейному уравнению в t . Также возможно найти полиномиальное решение, используя тривиальное начальное решение. пусть -r} Это уже верно для k = 1. Это подмножество Ландера L 0 ,
Это уже верно для k = 1. Это подмножество Ландера L 0 , С этим из пути, расширив L 1 при k = 5, это сводится к многочлену от p , который является просто квадратичным формы, .1)
С этим из пути, расширив L 1 при k = 5, это сводится к многочлену от p , который является просто квадратичным формы, .1) линейное уравнение (Poly2)p+(Poly3) = 0, где p легко вычисляется. В соответствии с результатом Ландера это дает девятый полином градусов по одной из переменных {a,b,c}. Между прочим, суммы слагаемых x 1 + x 2 , y 1 + y 3 имеют простой вид:
линейное уравнение (Poly2)p+(Poly3) = 0, где p легко вычисляется. В соответствии с результатом Ландера это дает девятый полином градусов по одной из переменных {a,b,c}. Между прочим, суммы слагаемых x 1 + x 2 , y 1 + y 3 имеют простой вид: Используя это ограничение, полиномы уменьшаются до седьмых градусов. Поскольку уравнение является однородным, его можно положить b = 1 без ограничения общности, и мы имеем тождество ct+ap+q) k = (at+cp+q) k + (t+ap+q) k + (ct-cp+q) k , k = 1,5,
Используя это ограничение, полиномы уменьшаются до седьмых градусов. Поскольку уравнение является однородным, его можно положить b = 1 без ограничения общности, и мы имеем тождество ct+ap+q) k = (at+cp+q) k + (t+ap+q) k + (ct-cp+q) k , k = 1,5, Есть для 6 степени? (Примечание: Как уже обсуждалось, форма L 1 также может быть использована для соответствующих высших степеней k. Позже она будет использована для доказательства того, что система k = 1,2,6 также может быть приведена, опять же, к простому решению квадратного уравнения.)
Есть для 6 степени? (Примечание: Как уже обсуждалось, форма L 1 также может быть использована для соответствующих высших степеней k. Позже она будет использована для доказательства того, что система k = 1,2,6 также может быть приведена, опять же, к простому решению квадратного уравнения.) Для простоты можно положить c = a+2b, а следующая точка дает члены для x i , y i как полиномы 13-й степени после удаления общих множителей.
Для простоты можно положить c = a+2b, а следующая точка дает члены для x i , y i как полиномы 13-й степени после удаления общих множителей. Однако мы можем использовать альтернативную форму:
Однако мы можем использовать альтернативную форму: Эта квартика также довольно специфична, поскольку ее растворы достаточно многочисленны, чтобы их можно было параметризовать линейно за три способов, а именно {q 1 , q 2 , q 3 } = {-(80p+40)/(57p+80), -(p+2), -(3p+2) /3}, хотя последние два тривиальны по отношению к исходному уравнению. Однако мы всегда можем вывести нетривиальные точки. Затем будут заданы три параметрических решения, каждое из которых включает отдельную эллиптическую кривую. Таким образом,
Эта квартика также довольно специфична, поскольку ее растворы достаточно многочисленны, чтобы их можно было параметризовать линейно за три способов, а именно {q 1 , q 2 , q 3 } = {-(80p+40)/(57p+80), -(p+2), -(3p+2) /3}, хотя последние два тривиальны по отношению к исходному уравнению. Однако мы всегда можем вывести нетривиальные точки. Затем будут заданы три параметрических решения, каждое из которых включает отдельную эллиптическую кривую. Таким образом, Первое найденное q было найдено методом Ферма. Существуют тривиальные значения p, такие как {-1/2, -80/57, 0}, но они могут привести к нетривиальным, например, p = -15/38 и т. д. Следующие два значения q были найдены с помощью метода Ферма на два тривиальных линейных решения. Они не полностью дают все значения, которые делают дискриминант квадратом, но можно показать, что три q как линейные многочлены являются только единиц вида q = (ap+b) или q = (ap+b)/(cp+d) для некоторого рационального {a,b,c,d}. Чтобы показать это, по уравнению 1 подставьте q = (ap+b) в уравнение и предположите, что полученный полином представляет собой квадрат,
Первое найденное q было найдено методом Ферма. Существуют тривиальные значения p, такие как {-1/2, -80/57, 0}, но они могут привести к нетривиальным, например, p = -15/38 и т. д. Следующие два значения q были найдены с помощью метода Ферма на два тривиальных линейных решения. Они не полностью дают все значения, которые делают дискриминант квадратом, но можно показать, что три q как линейные многочлены являются только единиц вида q = (ap+b) или q = (ap+b)/(cp+d) для некоторого рационального {a,b,c,d}. Чтобы показать это, по уравнению 1 подставьте q = (ap+b) в уравнение и предположите, что полученный полином представляет собой квадрат, Расширяя вышеизложенное и собирая степени p , можно получить систему из пяти уравнений с пятью неизвестными, а окончательное уравнение в этом случае имеет два рациональных решения. Аналогичный подход для q = (ap+b)/(cp+d) даст единственное рациональное решение.
Расширяя вышеизложенное и собирая степени p , можно получить систему из пяти уравнений с пятью неизвестными, а окончательное уравнение в этом случае имеет два рациональных решения. Аналогичный подход для q = (ap+b)/(cp+d) даст единственное рациональное решение. 4
4  Его дискриминант представляет собой квартику q , а если сделать квадрат, то
Его дискриминант представляет собой квартику q , а если сделать квадрат, то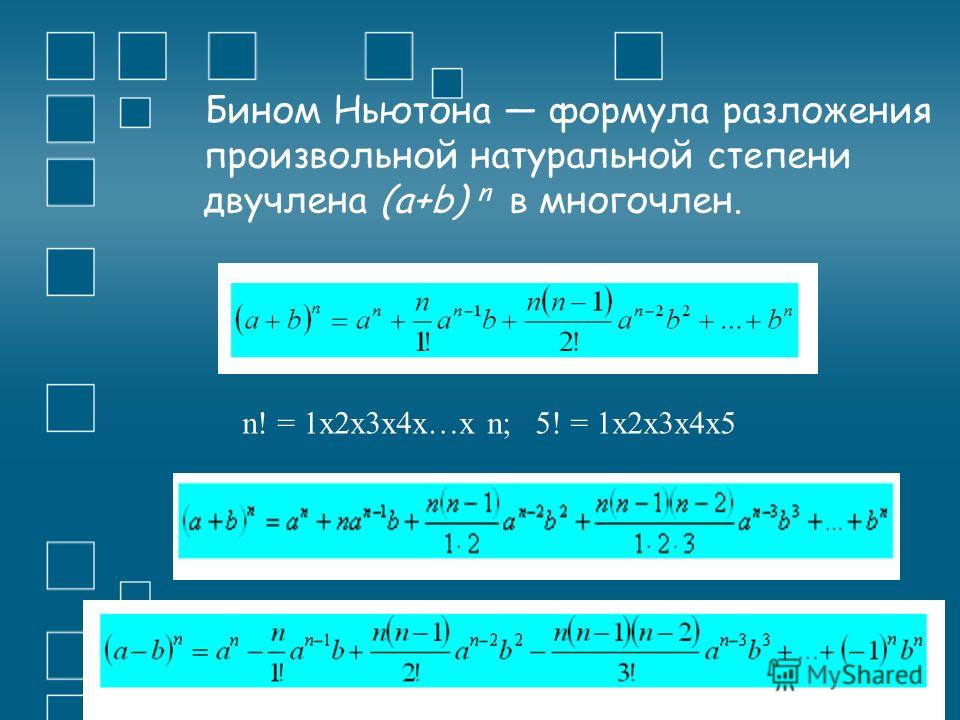 работать еще. Я обновлю этот раздел, чтобы сравнить методы, когда прочитаю его.
работать еще. Я обновлю этот раздел, чтобы сравнить методы, когда прочитаю его. К такому же выводу пришел Чоудри в своей статье 9.0014 The system of simultaneous equations x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +y 3 k , k = 1,2,5 не имеет нетривиальных решений в целых числах , The Mathematics Student, Vol 70, 2001. (Однако неизвестно, имеет ли случай k = 2,5 решение или нет, хотя с помощью базы данных Мура легко доказать, что в радиусе 17000 их нет.)
К такому же выводу пришел Чоудри в своей статье 9.0014 The system of simultaneous equations x 1 k +x 2 k +x 3 k = y 1 k +y 2 k +y 3 k , k = 1,2,5 не имеет нетривиальных решений в целых числах , The Mathematics Student, Vol 70, 2001. (Однако неизвестно, имеет ли случай k = 2,5 решение или нет, хотя с помощью базы данных Мура легко доказать, что в радиусе 17000 их нет.) ( Обновление : Вроблевски доказал, что это имеет нетривиальные решения, наименьшим из которых является {p,q,r,s} = {105, 1153, 455, 582}, что дает,
( Обновление : Вроблевски доказал, что это имеет нетривиальные решения, наименьшим из которых является {p,q,r,s} = {105, 1153, 455, 582}, что дает,