Суть метода Ньютона — презентация онлайн
Похожие презентации:
Метод хорд
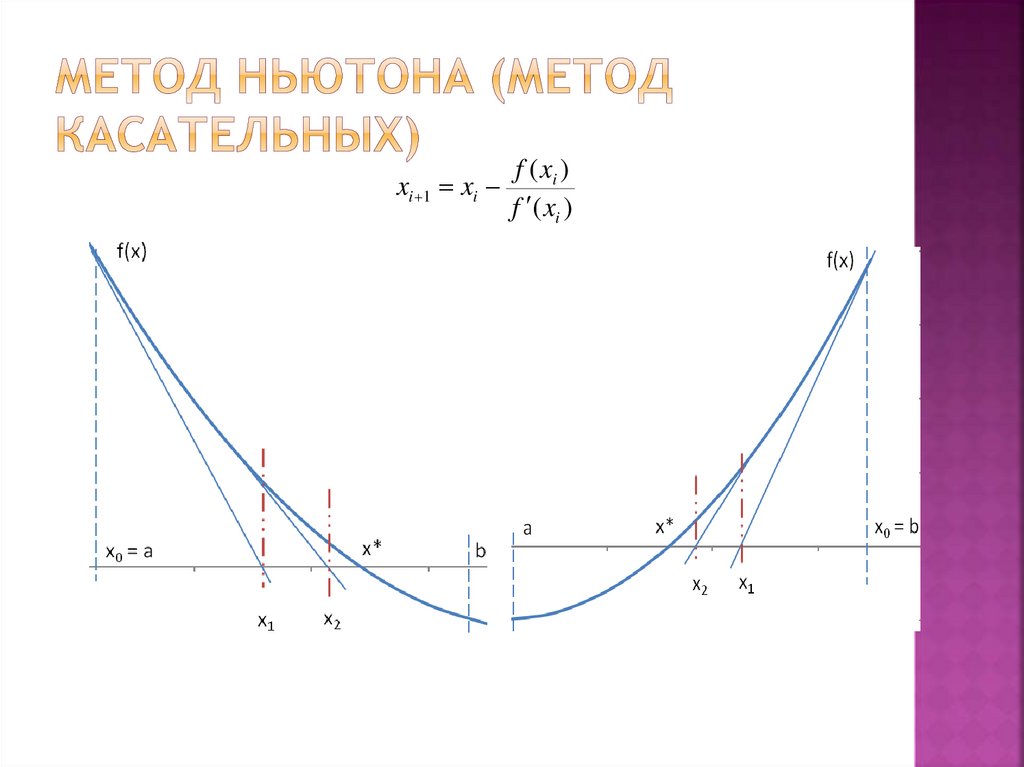
Метод Ньютона (метод касательных)
Метод деления отрезка пополам
Геометрическая интерпретация метода простых итераций
Решение нелинейных уравнений
Геометрическая интерпретация метода простых итераций
Математическое моделирование. Форма и принципы представления математических моделей
Численные методы решения инженерных задач
Численные методы
Лекция 5. Численные методы решения нелинейных уравнений
1. Лекция 7
1. Метод Ньютона (методкасательных)
2. Метод хорд
3. Сравнение методов уточнения
корней нелинейных уравнений
2. Суть метода Ньютона
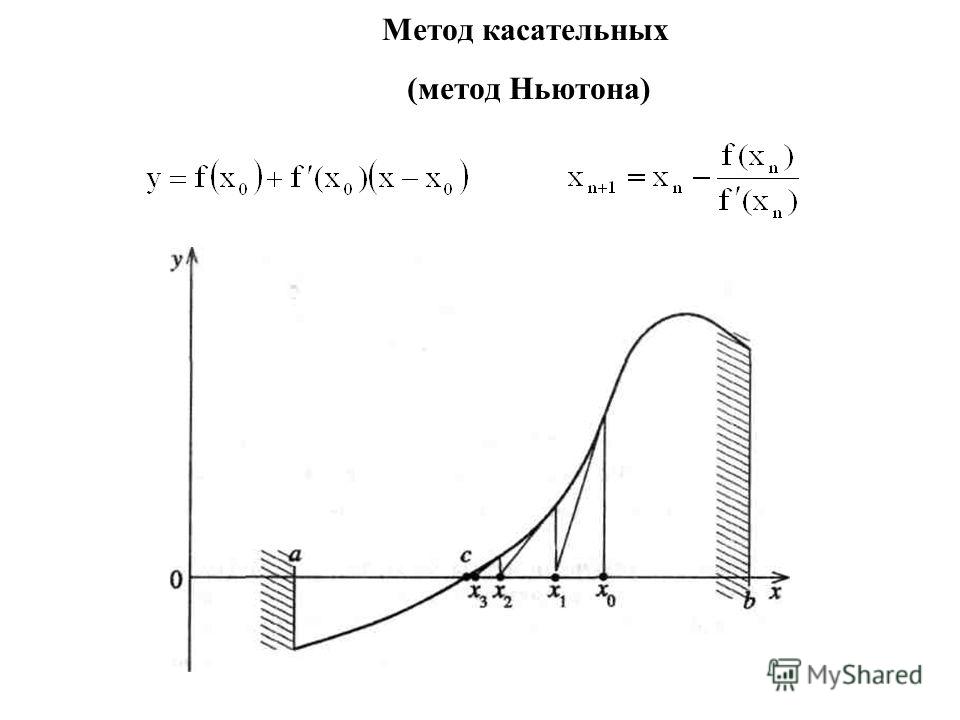
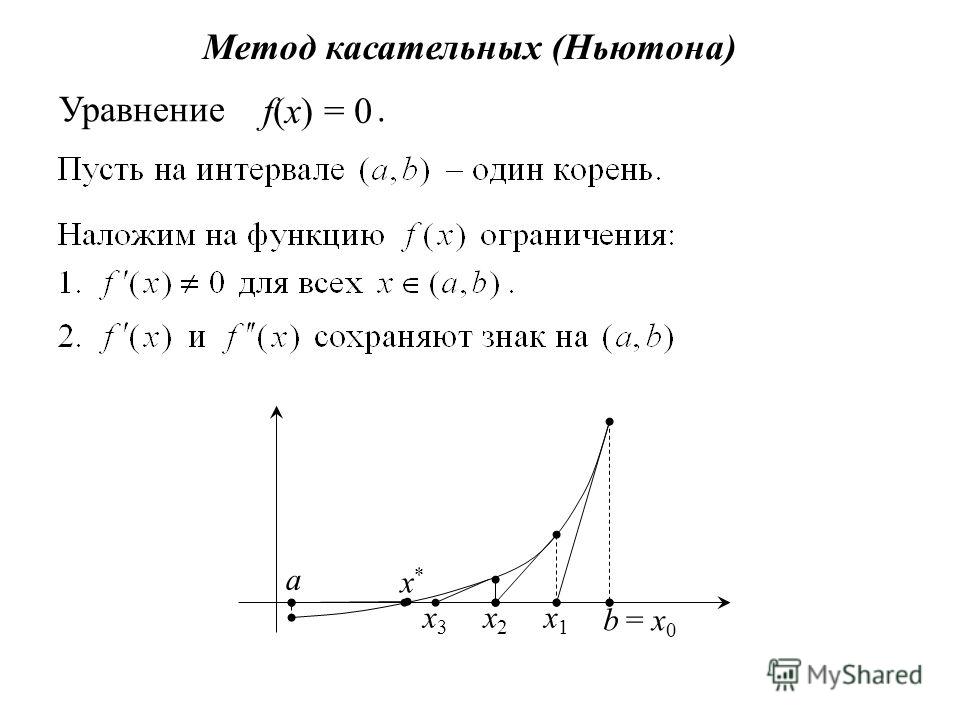
Пусть корень уравнения f(x)=0 отделен на отрезке [a;b], причем перваяи вторая производные f’(x) и f»(x) непрерывны и знакопостоянны при х
[a;b].
В этом случае для построения последовательности приближений к
корню может быть использован метод Ньютона: каждое следующее
приближение xn вычисляется через предыдущее приближение xn–1 по
формуле:
f(x n 1 )
x n x n 1
f’ (x n 1 )
Таким образом, задавшись начальным приближением x0 можно
получить первое приближение
f(x 0 )
x1 x 0
f’ (x 0 )
затем второе
f(x 1 )
x 2 x1
f’ (x1 )
и так далее до получения приближения, погрешность которого не превышает
заданную.

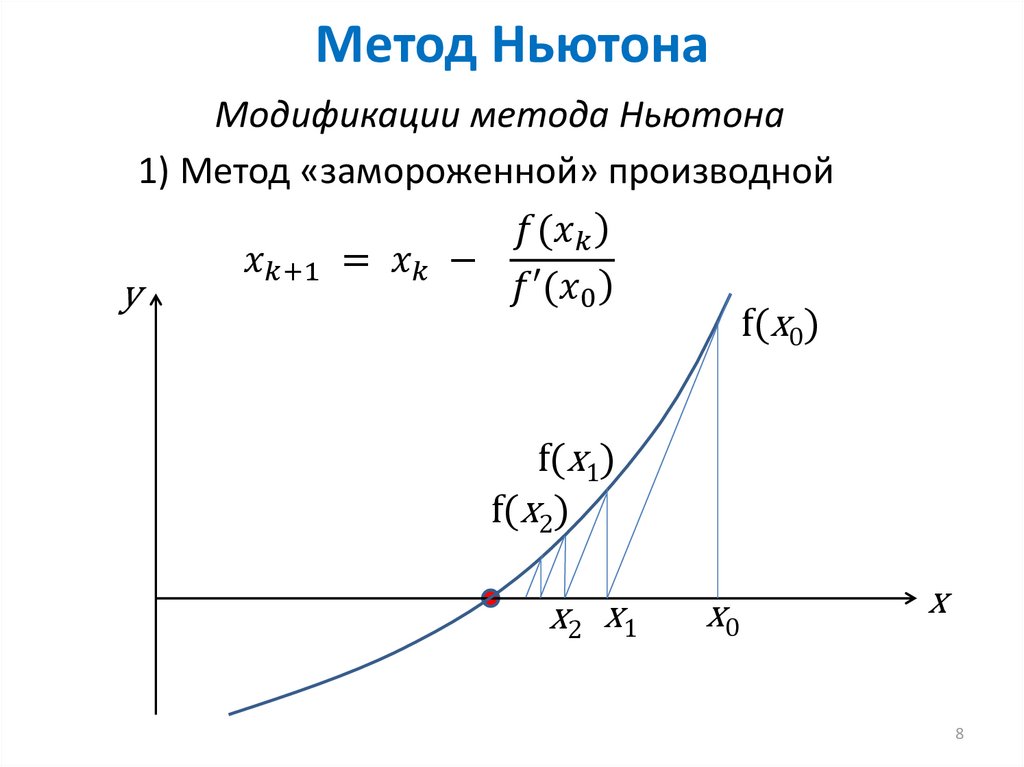
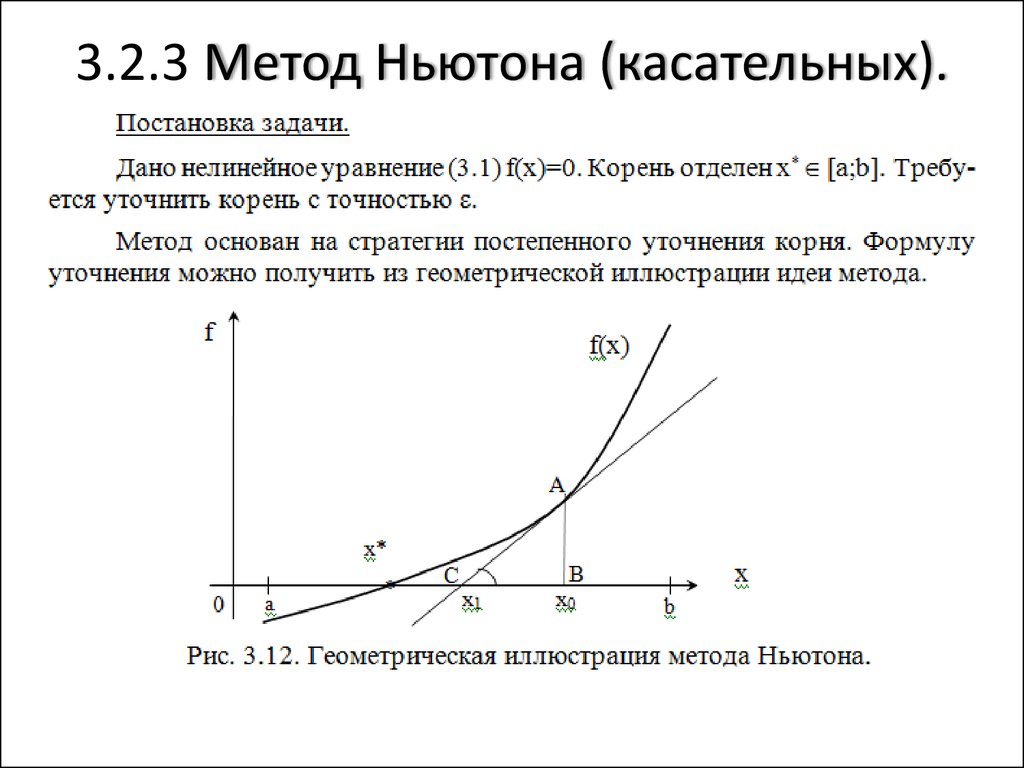
3. Геометрическая иллюстрация метода Ньютона
5. f'(x) и f»(x) не знакопостоянны
6. Выбор начального приближения
7. Теорема о сходимости метода Ньютона
Пусть корень уравнения f(x) = 0 отделен на отрезке [a;b] (функция f(x)непрерывна на [a;b] и на концах его принимает разные знаки), а производные
f'(x) и f»(x) отличны от нуля и сохраняют постоянные знаки на [a;b]. Тогда,
если выбрать начальное приближение х0 [a;b] так, чтобы f'(x0) ∙ f»(x0) > 0, то
последовательность приближений, определяемая формулой
f(x n 1 )
x n x n 1
f’ (x n 1 )
сходится.
8. Проверка условий сходимости метода Ньютона
Проверим условия сходимости метода Ньютона и выберем начальноеприближение для уравнения cos (x) – 3x + 1 = 0, корень которого отделен на
отрезке [0;1] на прошлой лекции.
Первая производная f'(x) = –sin(x) – 3 < 0 при любых значениях x.
Вторая производная f»(x) = –cos(x) < 0 на отрезке [0;1]. Следовательно,
последовательность приближений по методу Ньютона будет сходящейся при
выборе начального приближения так, чтобы f(x0) < 0.
 Это условие
Это условиевыполняется на правом конце отрезка: x0 = 1.
9. Последовательность приближений по методу Ньютона
Получим несколько последовательных приближений по итерационнойформуле Ньютона
f(x n 1 )
x n x n 1
f’ (x n 1 )
из начального приближения x0 = 1:
x1 = x0 – (cos(x0) – 3×0 + 1)/(-sin(x0) – 3) = 1 – (0.54 – 3 + 1)/(-0.84 — 3) = 0.62
x2 = x1 – (cos(x1) – 3×1 + 1)/(-sin(x1) – 3) = 0.62 – (0.814 – 1.86 + 1)/(-0.581 — 3) =
=0.607
x3 = x2 – (cos(x2) – 3×2 + 1)/(-sin(x2) – 3)=0.607 – (0.821 – 1.821 + 1)/(-0.57 — 3)=
=0.607
Как видно, процесс последовательных приближений сходится.
10. Оценка погрешности приближения для метода Ньютона
Можно показать, что погрешность n–го приближения| x n x* |
M2
(x n x n 1 ) 2
2 m1
где m1 – наименьшее значение |f'(x)| при x [a; b];
M2 – наибольшее значение |f’’(x)| при x [a; b].
Таким образом, если задана допустимая погрешность приближения к корню
ε, то процесс последовательных приближений можно прекратить при
выполнении условия:
2 m 1ε
| x n x n 1 |
M2
Существует и другой, универсальный способ оценки погрешности
приближения и соответствующее ему правило останова.
 Этот способ
Этот способприменим к любому методу уточнения корня, но требует дополнительного
вычисления функции в точке очередного приближения:
| f(x n ) |
ε
m1
где m1 – наименьшее значение |f'(x)| при x [a; b].
11. Схема алгоритма метода Ньютона
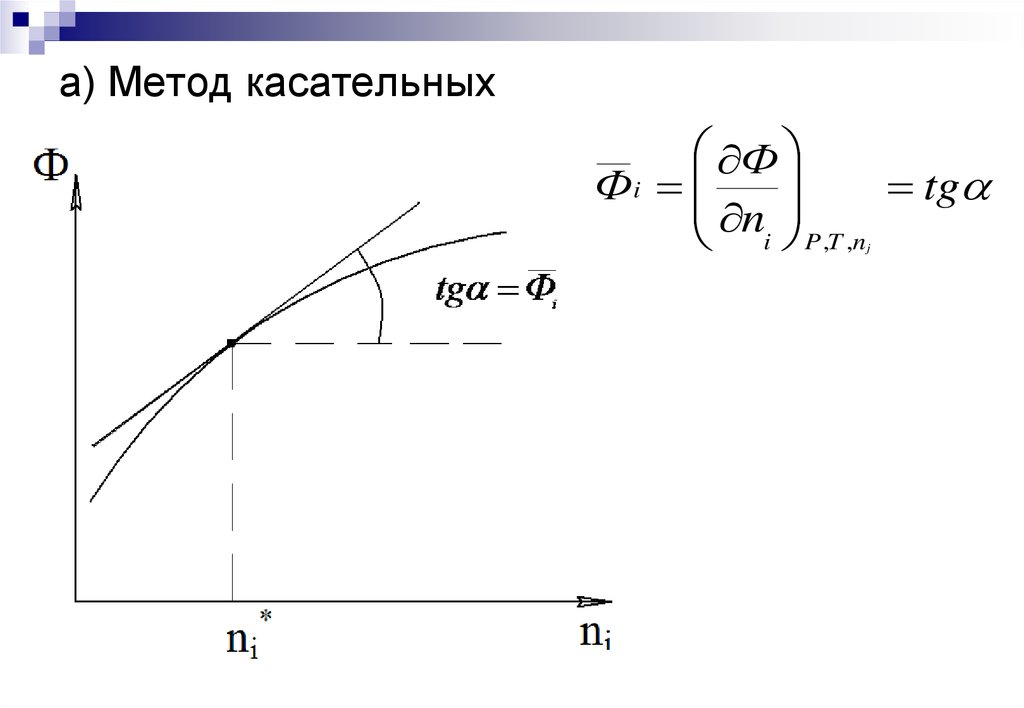
12. Геометрическая иллюстрация метода хорд. Случай f'(x) > 0 и f»(x) > 0
Геометрическая иллюстрация методахорд. Случай f'(x) > 0 и f»(x) > 0
x a
y f(a)
b a f(b) f(a)
a = x0
y=0
f(x o )
(b x 0 )
f(b) f(x 0 )
f(x1 )
x 2 x1
(b x1 )
f(b) f(x1 )
x1 x 0
………………………………………………
x n x n 1
f(x n 1 )
(b x n 1 )
f(b) f(x n 1 )
13. Геометрическая иллюстрация метода хорд. Случай f'(x) > 0 и f»(x) < 0
Геометрическая иллюстрация методахорд. Случай f'(x) > 0 и f»(x) < 0
b x
f(b) y
b a f(b) f(a)
b = x0
y=0
f(x o )
(x 0 a)
f(x 0 ) f(a)
f(x1 )
x 2 x1
(x1 a)
f(x1 ) f(a)
x1 x 0
………………………………………………
x n x n 1
f(x n 1 )
(x n 1 a)
f(x n 1 ) f(a)
14.
 Выбор неподвижной точки и начального приближенияИз рассмотренных построений видно, что один из
Выбор неподвижной точки и начального приближенияИз рассмотренных построений видно, что один изконцов отрезка отделения корня в процессе итераций
остается неподвижным, а противоположный конец
вначале принимается за начальное приближение, а
затем постепенно смещается в сторону корня,
образуя последовательность приближений. Общее
правило таково:
за неподвижную точку в методе хорд
выбирается тот конец отрезка [a;b], на котором
знак функции совпадает со знаком второй
производной: f(x)∙f’’(x)>0; в качестве начального
приближения выбирается
противоположный
конец отрезка.
15. Последовательность приближений по методу хорд
Получим несколько последовательных приближений методом хорд дляуравнения cos (x) – 3x + 1 = 0, корень которого отделен на отрезке [0;1].
Условия сходимости метода для этого уравнения совпадают с условиями
сходимости метода Ньютона и были нами проверены ранее. Так как вторая
производная f»(x)<0, за неподвижную точку принимаем правую границу
отрезка b=1, где f(b)=-1.
 4597<0, за начальное приближение – x0=a=0, и
4597<0, за начальное приближение – x0=a=0, ииспользуем итерационную формулу
f(x n 1 )
xn xn 1
(b xn 1 )
f(b) f(x n 1 )
В результате получаем:
x1 = x0 – (cos (x0) – 3×0 + 1)/(-1.4597- cos (x0) – 3×0 + 1)∙(1- x0) =
= 0 – 2/(-1.4597-2)∙1 = 0.5781
x2 = x1 – (cos (x1) – 3×1 + 1)/(-1.4597- cos (x1) – 3×1 + 1)∙(1- x1) =
= 0.5781 – 0.1028/(-1.4597-0.1028)∙(1-0.5781) = 0.6059
x3 = x2 – (cos (x2) – 3×2 + 1)/(-1.4597- cos (x2) – 3×2 + 1)∙(1- x2) =
= 0.6059 – 0.0043/(-1.4597-0.0043)∙(1-0. 6059) = 0.6070
16. Оценка погрешности приближения для метода хорд
Можно показать, что погрешность n–го приближения метода хордM 1 m1
| x n x n 1 |
| x n x |
m1
*
где m1 – наименьшее значение |f'(x)| при x [a; b];
M1 – наибольшее значение |f’(x)| при x [a; b].
Таким образом, если задана допустимая погрешность приближения к корню
ε, то процесс последовательных приближений можно прекратить при
выполнении условия:
m1
ε
| x n x n 1 |
M 1 m1
17.
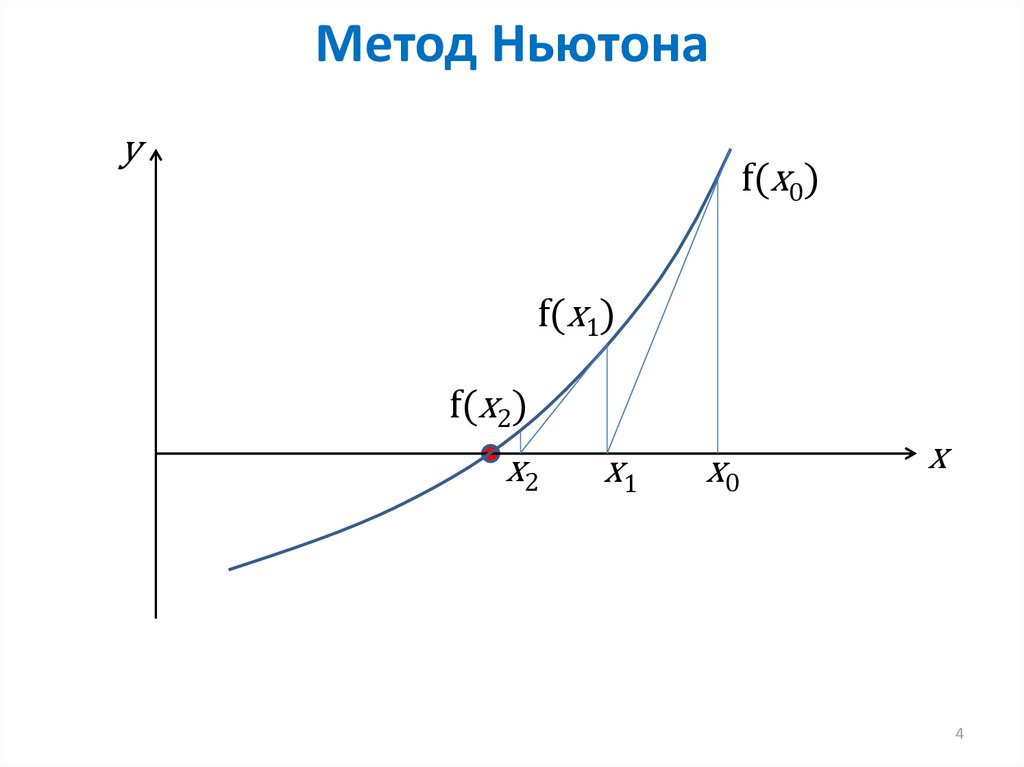 Схема алгоритма метода хорд
Схема алгоритма метода хорд18. Сравнение методов уточнения корней НЛУ
Методполовинного
деления
Метод
простой
итерации
Метод
Ньютона
Метод
хорд
Требования к 1–й
производной
–
+
+
+
Требования к 2–й
производной
–
–
+
+
Необходимость
проверки сходимости
–
+
+
+
Специальные
требования к выбору x0
–
–
+
+
низкая
высокая при
q<0.5
очень
высокая
высокая
одно значение
одно
значение
функции
значение
функции и
значение
производной
одно
значение
функции
Характеристика
Скорость сходимости
Объем вычислений на
каждой итерации
English Русский Правила
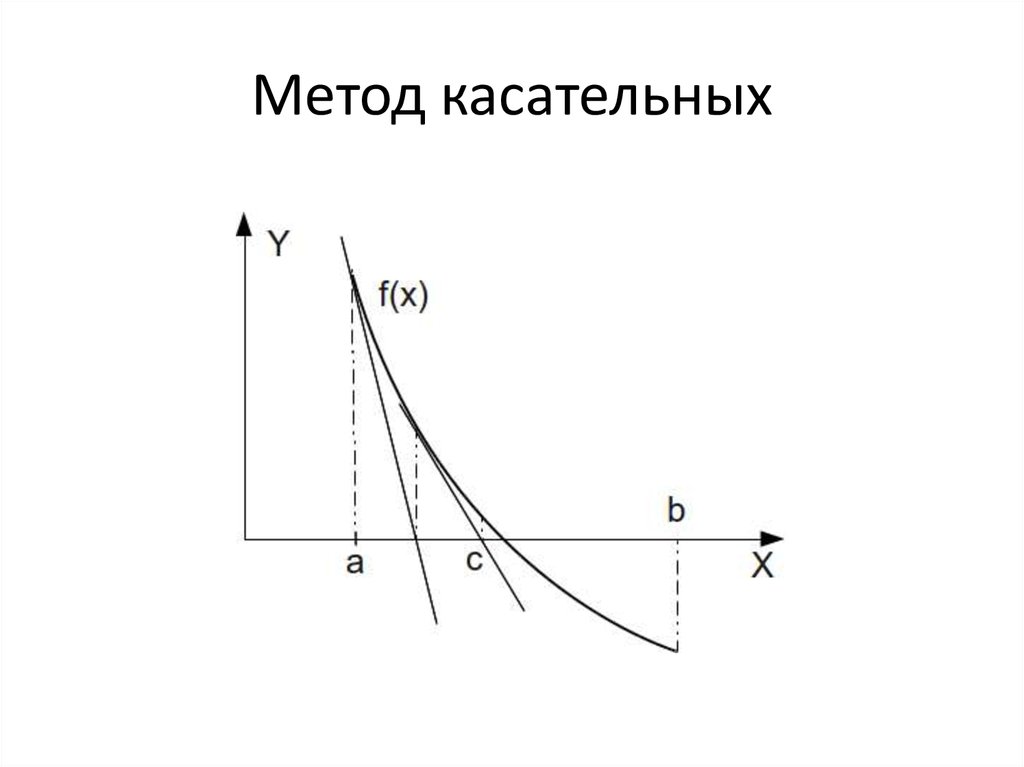
3. Метод касательных (Ньютона)
» В отличие от метода хорд, в методе касательных вместо хорды на каждом шаге проводится касательная к кривой y=F(x) при x=xn и ищется точка пересечения касательной с осью абсцисс:
Формула для (n+1) приближения имеет вид:
Если F(a)*F»(a)>0, x0=a,
в противном случае x0=b.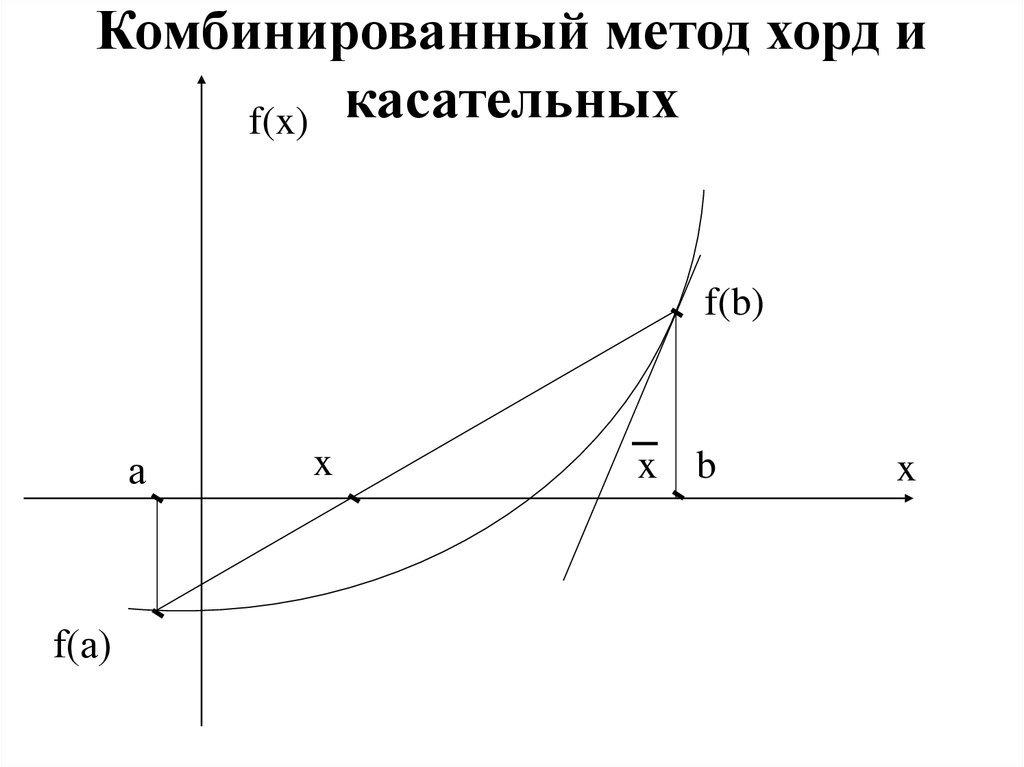
Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что:
.
Пример:
Пусть дана задача следующего характера: Уточнить корни уравнения cos(2x)+x-5=0 методом касательных с точностью до 0,00001.
Для решения такой задачи, используя Excel, необходимо выполнить следующие действия:
Изначально необходимо определиться с тем, чему равно x0: либо a, либо b. Для этого необходимо выполнить следующие действия:
Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.
Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).
Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении — они должны быть такими же, как на рисунке):
В итоге получается следующее:
Так как x0=b, то необходимо выполнить следующие действия:
Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении — они должны быть такими же, как на рисунке):
В
ячейку A6 ввести формулу =D5.
Выделить диапазон ячеек B5:E5 и методом протягивания заполнить диапазон ячеек B6:E6.
Выделить диапазон ячеек A6:E5 и методом протягивания заполнить диапазон нижерасположенных ячеек до получения в одной из ячеек столбца E результата (диапазон ячеек A6:E9).
В итоге получаем следующее:
Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.
Для того чтобы достичь наиболее точной погрешности, нужно одновременно использовать методы хорд и касательных. «По формуле хорд находят xn+1 , а по формуле касательных — zn+1 . Процесс нахождения приближенного корня прекращается, как только:
В качестве приближенного корня берут значение, равное (11):»[2]
Пример:
Пусть
требуется уточнить корни уравнения
cos(2x)+x-5=0 комбинированным методом с
точностью до 0,00001.
Для решения такой задачи, используя Excel, необходимо выполнить следующие действия:
Так как в комбинированном методе необходимо использовать одну из формул хорд и формулу касательных, то для упрощения следует ввести следующие обозначения:
— xn как mn.
— Переменная c будет играть роль a или b в зависимости от ситуации.
— Остальные обозначения аналогичны приведенным в формулах хорд, только учитывая выше введенные переменные.
— xn как nn.
— Остальные обозначения аналогичны приведенным в формуле касательных, только учитывая выше введенные переменные.
Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.
Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).

Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении — они должны быть такими же, как на рисунке):
В итоге получается следующее:
В ячейку G1 ввести e, а в G2 ввести число 0,00001.
В ячейку h2 ввести c, а в h3 ввести число 6, так как c=b (см. ячейку F2).
В ячейку I1 ввести f(c), а в I2 ввести формулу =COS(2*h3)+h3-5.
Заполнить ячейки последовательно следующим образом (обратить внимание на названия и номера столбцов при заполнении — они должны быть такими же, как на рисунке):
В ячейку A6 ввести формулу =E5.
В ячейку F6 ввести формулу =I5.
Выделить диапазон ячеек B5:E5 и маркером автозаполнения заполнить диапазон ячеек B6:E6.

Выделить диапазон ячеек G5:K5 и маркером автозаполнения заполнить диапазон ячеек G6:K6.
Выделить диапазон ячеек A6:K6 и методом протягивания заполнить все нижестоящие ячейки до получения ответа в одной из ячеек столбца K (диапазон ячеек A6:K9).
В итоге получаем следующее:
Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.
Калькулятор касательной — Solumaths
Уравнение касательной линии, расчет онлайн
Сводка:
Калькулятор уравнения касательной линии используется для расчета уравнения касательной к кривой в заданной точке абсцисс с поэтапным расчетом.
уравнение_тангента_линия онлайн
Описание:
C — график дифференцируемой функции f в точке a.
Касательная к C в точке A (a, f (a)) — это прямая, проходящая через A, коэффициент директора которой равен `f'(a)`.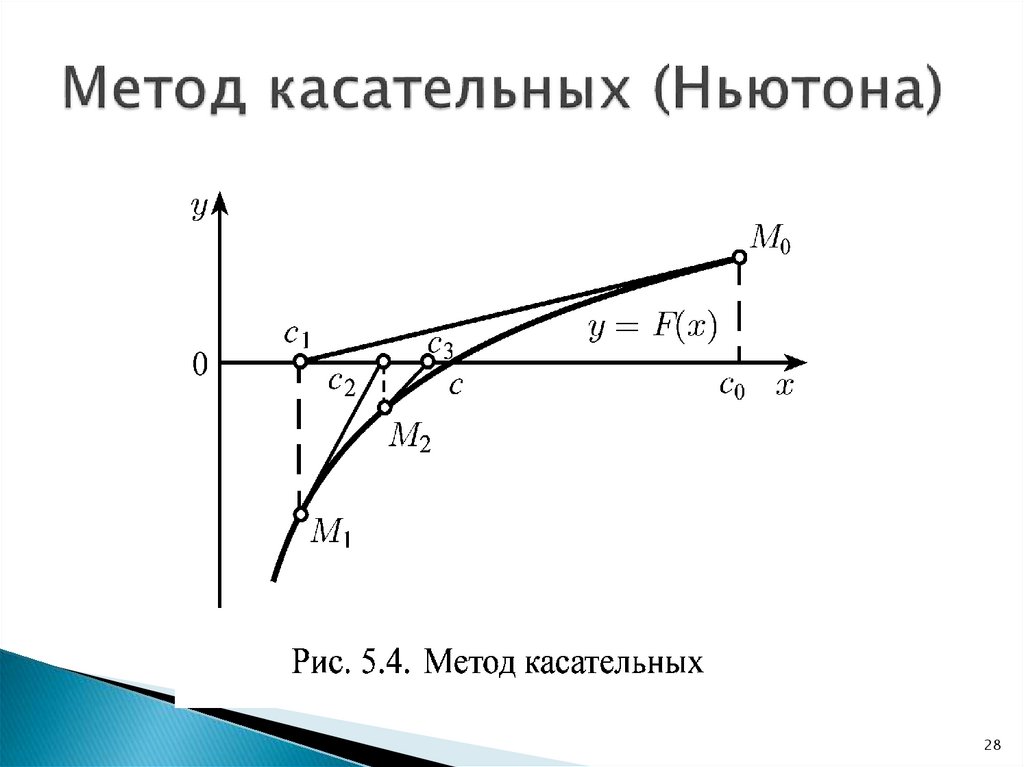 92+3;1`) , после вычисления возвращается результат `[y=2+2*x]`.
92+3;1`) , после вычисления возвращается результат `[y=2+2*x]`.
Калькулятор показывает этапы определения уравнения касательной.
Из уравнения репрезентативной кривой функции можно использовать онлайн-калькулятор для построения касательной функции в точке.
Синтаксис:
уравнение_касательной_линии(функция;число)
Примечание: x всегда должен использоваться как переменная
92+3;1`), возвращает [y=2+2*x]
Вычислите онлайн с уравнением_касательной_линии (найдите уравнение касательной линии)
См. также
Список связанных калькуляторов:
 Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.- Расчет дискриминанта онлайн: дискриминант. Калькулятор, который позволяет вычислить дискриминант квадратного уравнения онлайн.
- Найти уравнение прямой линии из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
- Найдите уравнение касательной линии: уравнение_касательной_линии. Калькулятор уравнения касательной используется для расчета уравнения касательной к кривой в заданной точке абсцисс с поэтапным вычислением.
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Калькулятор решения для x: уравнение_решателя. Решатель уравнений позволяет решать уравнения с неизвестным с шагами расчета: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.

- Калькулятор неравенства: неравенство_решатель. Решатель неравенств, который решает неравенство с деталями расчета: линейное неравенство, квадратное неравенство.
- Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.
Прочие ресурсы
- Упражнение по уравнениям
- Бесплатные математические игры с уравнениями
- Научитесь решать уравнения
92+2у_0у)+\\
+ 2 gx
+2 фу + с =0.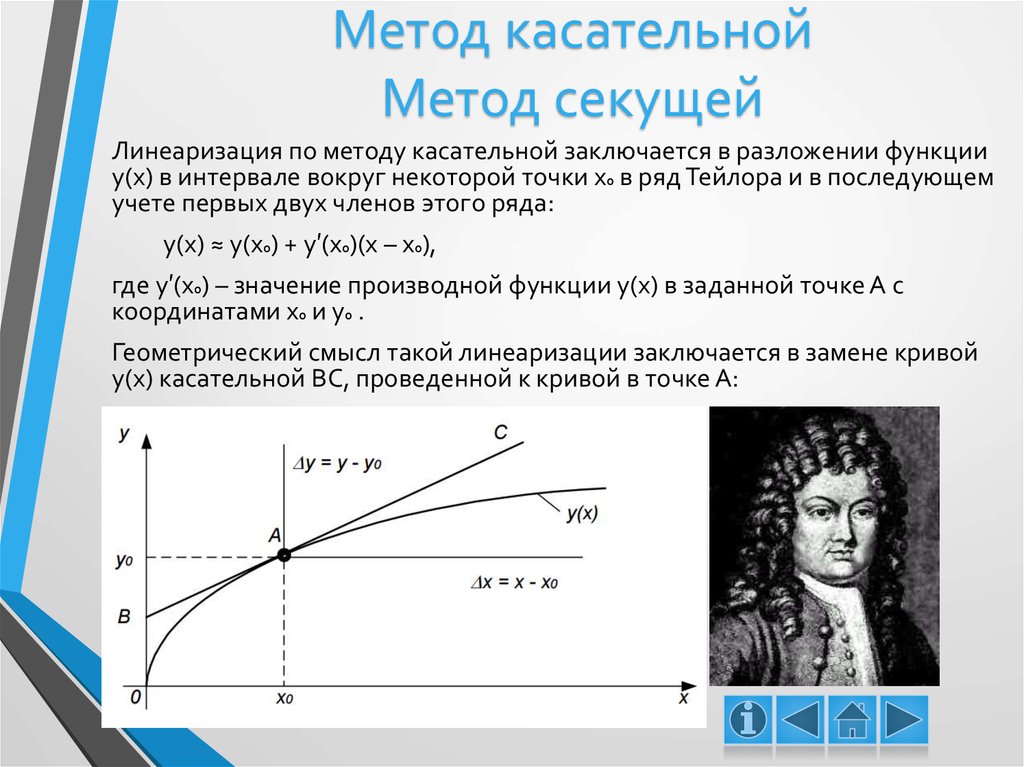

 Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.