Роды и зрение — статьи от специалистов клиники «Мать и дитя»
Бритцова (Мартынова) Оксана Александровна
Логопед
Клиника «Мать и дитя» Кунцево,
Миопия и роды
Говоря, что плохое зрение может повлиять на роды, врачи чаще всего имеют в виду миопию (близорукость). Миопия – это нарушение фокуса зрения, при котором ухудшается видимость вдаль. Отсюда – второе название болезни: близорукость, так как люди с миопией гораздо лучше видят вблизи. Есть три степени миопии: до 3 диоптрий – слабая степень; от 3,25 до 6 диоптрий – средняя степень; свыше 6 диоптрий – сильная степень.
Если миопия слабой или средней степени, то роды на нее никак не повлияют. Но при близорукости высокой степени есть риск того, что во время родов и без того плохое зрение станет еще хуже. Почему? Во время родов весь организм женщины испытывает сильнейшую нагрузку и глаза в том числе.
Идем к врачу
Если у будущей мамы есть проблемы с глазами, то ей стоит посетить окулиста как минимум 3 раза: в начале, середине и в конце беременности. Зачем так часто? Надо следить за состоянием сетчатки, чтобы не упустить момент, когда на ней появятся какие-то изменения или даже надрывы. И сделать это можно, только регулярно наблюдаясь у врача.
В конце беременности окулист дает заключение о состоянии зрения и рекомендует тактику родоразрешения. Если доктор напишет, что «рекомендуется исключить потужной период в связи с возможным повреждением сосудов на сетчатке», то это значит, что, скорее всего, надо будет делать кесарево сечение. Если же состояние сетчатки нормальное, то офтальмолог просто напишет: «Противопоказаний к естественным родам нет».
Как это будет
Многие считают, что наличие миопии – прямой путь исключительно к кесареву сечению. Но это не так. Есть инструкция Минздравсоцразвития, составленная совместно окулистами и акушерами-гинекологами. Согласно этому документу, оперативное вмешательство необходимо только при близорукости свыше минус 7 диоптрий. В остальных случаях предлагается действовать, исходя из конкретной ситуации. А это значит, что решая, как женщине лучше родить, врач учтет не только остроту зрения, но еще и общее самочувствие будущей мамы, ее возраст, состояние сетчатки, различные осложнения во время беременности. Например, если к миопии (пусть и слабой степени) добавляется высокое давление, отеки и прочие осложнения – без кесарева здесь не обойтись. Кстати, сейчас многие врачи вообще считают, что острота зрения на способ родов влиять не должна и рожать можно даже при минус 10–12, главное – чтобы состояние сетчатки было хорошим.
Естественные роды
Если естественные рода разрешены, то самое главное во время них – правильно тужиться. А что это значит? Тужиться надо исключительно тем местом, из которого и выходит ребенок. То есть не надо напрягать лицо, зажмуривать глаза – толку от этого не будет. Все усилие должно идти в промежность. Именно мышцы тазового дна вместе с мышцами живота и помогут ребенку появиться на свет. Если же напрягать лицо (тужиться лицом), то и ребенку помощи никакой не будет, и силы зря потратятся, и глаза могут пострадать. Из-за ненужного перенапряжения внутриглазное давление возрастет, из-за чего мелкие кровеносные сосуды могут лопнуть. При обычном состоянии глаз или при незначительной миопии это не страшно, но при сильной ее степени в сетчатке может произойти кровотечение, разрыв, а в самом плохом варианте она начнет отслаиваться.
Очки и линзы
Можно ли рожать в очках? Можно ли взять их в родблок? Конечно, можно, ведь без очков многие люди чувствуют себя крайне неудобно.
А вот можно ли рожать в линзах, здесь даже у окулистов нет однозначного мнения. С одной стороны, ничего такого страшного в линзах на родах нет, ведь занимаются же в линзах спортом и даже спят в них. Но линзы у всех разные, и чувствуют себя в них женщины тоже по-разному. Кто-то может носить линзы всего один день и вечером обязательно должен снять их. Другие предпочитают носить линзы месяц и прекрасно с ними себя чувствуют. Поэтому решать надо, учитывая каждую конкретную ситуацию. Почему часто рекомендуют снять линзы на роды? Если женщина неправильно тужится, то линзы могут еще больше усугубить состояние глаз. К тому же если потребуется какое-то экстренное вмешательство с наркозом, то линзы надо будет снять. А куда их деть в родблоке? Поэтому, если хотите рожать в линзах, в роддом надо взять с собой специальный раствор и емкость для хранения линз. И обязательно предупредить врачей о том, что вы рожаете с линзами.
Приятные нюансы
Есть женщины, у которых зрение после родов не только не ухудшается, а даже улучшается. Происходит это потому, что проблемы со зрением возникли вследствие определенных нарушений в организме – спазмов мышц, защемления нервов, застойных явлений. В процессе родов эти проблемы исчезают, и в результате молодая мама начинает видеть все действительно в новом свете.
Происходит это потому, что проблемы со зрением возникли вследствие определенных нарушений в организме – спазмов мышц, защемления нервов, застойных явлений. В процессе родов эти проблемы исчезают, и в результате молодая мама начинает видеть все действительно в новом свете.
К родам у женщин с проблемным зрением отношение врачей сейчас уже изменилось. Естественным путем рожают и с высокой миопией, и после некоторых операциях на глазах. Если есть какие-то сомнения – обратитесь в крупную офтальмологическую клинику, там уж точно знают, какой способ родов в какой ситуации лучше выбрать.
Записаться на приём
к доктору — Бритцова (Мартынова) Оксана Александровна
Клиника «Мать и дитя» Кунцево
ДетямДиспансеризацияНаблюдение детей на домуНаблюдение детей с особенностями развития
Нажимая на кнопку отправить, я даю согласие на обработку персональных данных
Внимание! Цены на услуги в разных клиниках могут отличаться. Для уточнения актуальной стоимости выберите клинику
Администрация клиники принимает все меры по своевременному обновлению цен на программы, однако во избежание возможных недоразумений, рекомендуем уточнять стоимость услуг по телефону/у менеджеров клиники
 Одинцово (филиал)Клиника «Мать и дитя» Ходынское полеКлиника «Мать и дитя» КунцевоКлиника «Мать и дитя» СавёловскаяКлиника «Мать и дитя» Юго-ЗападКлиника «Мать и дитя» НовогиреевоКлиника «Мать и дитя» Лефортово
Одинцово (филиал)Клиника «Мать и дитя» Ходынское полеКлиника «Мать и дитя» КунцевоКлиника «Мать и дитя» СавёловскаяКлиника «Мать и дитя» Юго-ЗападКлиника «Мать и дитя» НовогиреевоКлиника «Мать и дитя» ЛефортовоВсе направленияКонсультации специалистов (взрослые)Консультации специалистов (детские)Лаборатория молекулярной генетикиОбщеклинические исследованияПроцедурный кабинетТелемедицина для взрослыхТерапевтические исследованияУльтразвуковые исследования взрослых
01.
Консультации специалистов (взрослые)
02.
Консультации специалистов (детские)
03.
Лаборатория молекулярной генетики
04.
Общеклинические исследования
05.
Процедурный кабинет
06.
Телемедицина для взрослых
07.
Терапевтические исследования
08.
Ультразвуковые исследования взрослых
Ничего не найдено
Администрация клиники принимает все меры по своевременному обновлению размещенного на сайте прайс-листа, однако во избежание возможных недоразумений, советуем уточнять стоимость услуг и сроки выполнения анализов по телефону
Чему равно 7 в 3-й степени?
Математика касается не только чисел, но и различных вычислений с использованием чисел и переменных. Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Показатели и степени
Экспоненты и степени — это основные операторы, используемые в математических вычислениях, экспоненты используются для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя. Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 5 . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 3 , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 3 равно 1331.
Показатель степени определяется как степень, заданная числу, сколько раз оно умножается само на себя. Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
p × p × p × p … n раз = p n
Основные правила экспоненты наряду с другими математическими операциями, например, если есть произведение двух показателей, его можно упростить, чтобы упростить вычисления, и оно известно как правило произведения, давайте рассмотрим некоторые из основных правил показателей,
- Правило произведения ⇢ a n + a m = a n + m
- Частное правило ⇢ a n / a m 90 0 – = a 038
- Силовое правило ⇢ (a n ) m = a n × m или m √a n = a n/m
- Правило отрицательного показателя степени = 1 7/0 a — 80 9000 007 м
- Нулевое правило ⇢ a 0 = 1
- Одно правило ⇢ a 1 = a
Сколько будет 7 в степени 3
rd ?Решение:
Любое число, имеющее степень 3, можно представить в виде куба этого числа.
Куб числа числа — это число, умноженное само на себя трижды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728.
Давайте вернемся к постановке задачи и поймем, как она будет решаться, постановка задачи просила упростить 7 в 3-й степени. Это означает, что вопрос требует решить куб 7, который представлен как 7 3 ,
7 3 = 7 × 7 × 7
= 49 × 7
= 343
Следовательно, 343 3 rd степень числа 7.
Пример задачи
Вопрос 1: Решите выражение 3 3 – 2 3 .
Решение:
Чтобы решить выражение, сначала решите третью степень чисел, а затем вычтите второй член из первого.
Однако ту же проблему можно решить проще, просто применив формулу, формула: xy)
3 3 – 2 3 = (3 – 2)(3 2 + 2 2 + 3 × 2)
= 1 × (9 + 4 + 6)
= 1 × 19
= 19
Вопрос 2. Решите выражение 10 0 9 0 9 0 0 8 – 5 9 0 0 08 .
Решение:
Чтобы решить выражение, сначала решите 2 -й степени чисел, а затем вычтите второй член из первого члена. Однако ту же проблему можно решить проще, просто применив формулу, формула
x 2 – y 2 = (x + y)(x – y)
10 2 – 5 2 = (10 + 5)(10 – 5)
= 905 105= 225
Вопрос 3: Решите выражение 2 3 + 9 3 .
Решение:
Чтобы решить выражение, сначала решите 3 -й степени чисел, а затем вычтите второй член из первого члена.
Однако ту же проблему можно решить проще, просто применив формулу, формула
x 3 + y 3 = (x + y)(x 2 + y 2 – xy)
2 3 + 9 = (2) 9 3 007 2 + 9 2 — 2 × 9)
= 11 × (4 + 81 — 18)
= 11 × 67
= 737
Основные вставки и ауты экспонентов
Негативы. Not’nEng. Not’nFractional
Purplemath
Что такое экспоненты?
Экспоненты, также называемые степенями или порядками, являются сокращением для многократного умножения одного и того же самого на себя. Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5)(5)(5) = 5 3 . «Показатель степени», равный 3 в этом примере, означает, сколько раз значение умножается. То, на что умножается число 5 в этом примере, называется «базой».
Содержание продолжается ниже
MathHelp.com
Показатели: Основные правила: Правило произведения
Этот процесс использования показателей называется «возведением в степень», где показатель степени — это «степень». Выражение 5 3 произносится как «пять в третьей степени», «пять в третьей степени» или «пять в третьей степени».
Выражение 5 3 произносится как «пять в третьей степени», «пять в третьей степени» или «пять в третьей степени».
Есть две специально названные степени: «во второй степени» обычно произносится как «квадрат», а «в третьей степени» обычно произносится как «куб». Таким образом, 5 3 обычно произносится как «пять в кубе».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы бы предпочли иметь дело с 27, чем с 3 3 . Но с переменными нам нужны показатели степени, потому что мы скорее будем иметь дело с x 6 , чем с xxxxxx .
Каковы правила упрощения с показателями степени?
Правила упрощения с показателями следующие:
- ( x m ) ( x n ) = x m0 3 8 9007 m0 3 8 9007 m0
- ( x м ) n = x м × n
- ( x m )/( x n ) = x m − n
Итак, что означают эти правила? Далее я проиллюстрирую каждое правило, чтобы вы могли понять, как и почему они работают.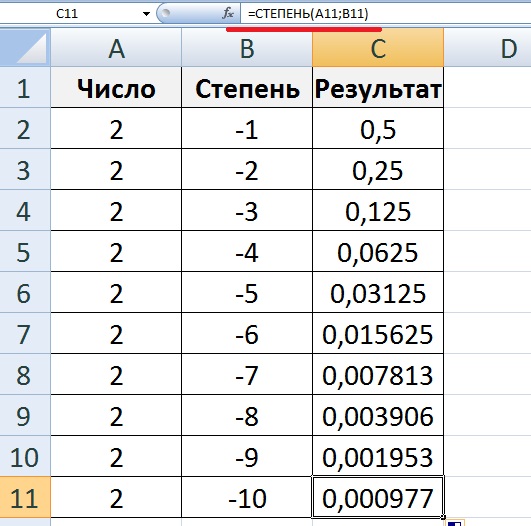
Упростить (
x 3 )( x 4 ).
Чтобы упростить это, я могу думать о том, что означают эти показатели степени. «К третьему» означает «умножение трех копий», а «к четвертому» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме.
Сначала расширяю:
( x 3 )( x 4 ) = ( xxx )( xxxx ) и сложим все множители вместе:
( xxx )( xxxx ) = xxxxxxx
Подсчитав, я вижу, что это семь копий переменной. «Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
xxxxxxx = x 7
Собираем все вместе, шаги следующие:
( x 3 )( x 4 ) 2 x9 261 хххх )
= ххххххх
= х 7
Тогда упрощенная форма ( х 38 ) (
х 08 ) составляет:
x 7
Обратите внимание, что x 7 также равно x (3+4) . Это демонстрирует первое основное правило экспоненты:
Это демонстрирует первое основное правило экспоненты:
Всякий раз, когда вы умножаете два термина с одним и тем же основанием, вы можете упростить, добавляя показатели степени:
Однако обратите внимание, что мы НЕ МОЖЕМ упростить ( x 4 )( y 3 ) путем сложения показателей степени, потому что основания разные: ( x 4 )( y 3 ) = xxxxyyy = ( x 4 7 2 )( 90 ) 0008). Ничего не совмещает.
Теперь, когда я знаю правило (а именно, что я могу добавлять способности к одной и той же базе), я могу начать с перемещения баз, чтобы все одинаковые базы располагались рядом друг с другом:
( a 5 б 3 ) ( а б 7 ) = ( а 5 ) ( a ) ( b 3 ) ( b 7 )
Теперь я хочу добавить мощность на и 9026 62 с. Однако второй и , похоже, не обладают силой. Что мне делать с этим фактором?
Однако второй и , похоже, не обладают силой. Что мне делать с этим фактором?
Все, что не имеет явной силы, в техническом смысле «возводится в степень 1». Все, что в степени 1, является просто самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:
( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( ) ( и 1 ) ( b 3 ) ( b 7 )
Теперь я могу объединить:
( a 5 ) ( 7 8 ) ( б 3 ) ( б 7 ) = а 5+1 б 3+7 = a 6 b 10
Если сложить все вместе, то моя работа сдачи будет выглядеть так: 62 3 ) ( а б 7 ) = ( а 5 а 1 ) ( б
23 007 7 ) =
а 6 б 10
В следующем примере есть две силы, причем одна сила в некотором смысле находится «внутри» другой.
Упростить (
x 2 ) 4
Для упрощения я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, которое находится внутри круглых скобок. В этом случае основание четвертой степени равно x 2 . Умножение четырех копий этого основания дает мне:
( х 2 ) 4 = ( х 2 )( х 2 )( 70 0 8 х ) )( x 2 )
Каждый фактор в приведенном выше расширении «умножение двух копий» переменной. Это расширяется как:
( x 2 )( x 2 )( x 2 )( x 8 0 29000 ) 1 хх )( хх )( хх )( хх )
Сняв скобки, я получаю:
( хх )( хх )( хх )( хх )( хх 90 хх 90 xxxxxxx
Это строка из восьми копий переменная. «Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
xxxxxxxx = x 8
Собираем все вместе:
3
3 62 2 ) 4 = ( х 2 )( х 2 )( х 2 )( х 2 )
1 = ( 2 2 х
) ( хх )( хх )( хх )
= хххххххх
= х 8
Обратите внимание, что (
) 4 = x 8 , и что 2 × 4 = 8. Это демонстрирует второе правило экспоненты:
Всякий раз, когда у вас есть выражение экспоненты, которое само возводится в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:
( x m ) n = x m n
Если у вас есть произведение внутри круглых скобок и мощность в скобках, то мощность передается каждому элементу внутри. Например:
Например:
( ху 2 ) 3 = ( ху 2 )( ху 2 007 х )( 002 )( 2 )
= ( ххх )( г 2 г 2 y 2 )
= ( xxx )( гггггг )
= x
8 2 30007 6
= ( х ) 3 ( у 2 ) 3
Другой пример:
Примечание. Это правило НЕ работает, если в скобках указана сумма или разность. Экспоненты, в отличие от умножения, НЕ «распределяют» над сложением.
Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильно. На самом деле, (3 + 4) 2 = (7) 2 = 49, а не 25.
Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x − 2) 2 , не пытайтесь сделать это в уме. Вместо этого напишите это; «квадрат» означает «умножение двух копий», поэтому:
Например, учитывая ( x − 2) 2 , не пытайтесь сделать это в уме. Вместо этого напишите это; «квадрат» означает «умножение двух копий», поэтому:
( х − 2) 2 = ( х − 2)( х − 2)
= xx — 2 x — 2 x + 4= x 2 — 4 x + 4.
пытаются все делать в уме, вместо того, чтобы показывать свои работы. Делайте все аккуратно, и вероятность того, что вы совершите эту ошибку, снизится.Упрощение (
a 2 b 3 c ) 4
Теперь, когда я знаю правило о силах на силах, я могу применить 4 к каждому из внутренних факторов. (Мне нужно помнить, что число c в скобках, не имеющее явной силы над ним, следует рассматривать как возведенное «в степень 1».)
( а 2 ) 4 ( б 3 ) 4 ( с 7 90 0 9 0007 8 ) 008
= ( a 2×4 ) ( б 3×4 ) ( с 1×4 )
= 4
- Упрощение a 5 / а 2
Чтобы упростить это, я сначала расширю числитель и знаменатель.
( aaaaa )/( aa )
Очевидно, две копии множителя a дублируются, поэтому я могу отменить их:
( 90 261) )
(Помните, что, когда «все» сокращается, остается понятный, но обычно игнорируемый множитель 1, который остается.) окончательный ответ:
aaa = a 3
Обратите внимание, что ( a 5 )/( a 22 5−2 = a 3 , и что 5 − 2 = 3. Это иллюстрирует правило третьей степени:
Всякий раз, когда у вас есть одно и то же основание в числителе и знаменателе дроби, вы можете упростить, вычитая степени:
( x м ) / ( x n ) = x m − n
(Да, это правило может привести к отрицательным показателям степени. На следующей странице вы узнаете, как с ними работать.)
На следующей странице вы узнаете, как с ними работать.)
Есть еще одно правило. которые могут или не могут быть рассмотрены в вашем классе на данном этапе:
Все, что в нулевой степени равно 1 (до тех пор, пока «что угодно» само по себе не является нулем).
Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем могут показаться на первый взгляд:
Кого волнует то, что заключено в квадратные скобки? Уж точно нет, потому что нулевая мощность снаружи означает, что значение всего этого всего равно 1. Ха!
[(3 x 4 y 7 z 12 ) 5 (−5 900 0 x 9 8 y 3 z 4 ) 2 ] 0 = 1
Кстати, как только ваш класс перейдет «в нулевую степень», вы должны ожидать упражнение, подобное приведенному выше, на следующем тесте.

 Куб числа числа — это число, умноженное само на себя трижды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728.
Куб числа числа — это число, умноженное само на себя трижды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728.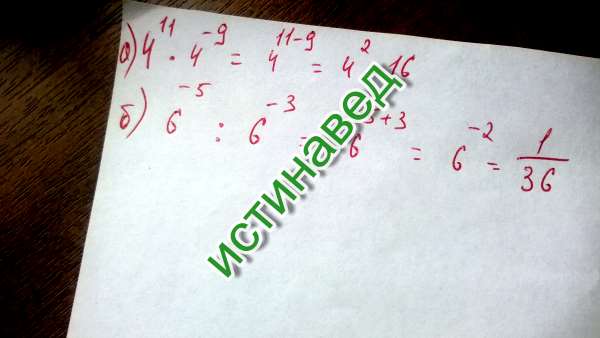 Однако ту же проблему можно решить проще, просто применив формулу, формула: xy)
Однако ту же проблему можно решить проще, просто применив формулу, формула: xy) Однако ту же проблему можно решить проще, просто применив формулу, формула
Однако ту же проблему можно решить проще, просто применив формулу, формула