Онлайн калькулятор: Определение ранга матрицы
УчебаМатематика
Калькулятор, определяющий ранг матрицы
Ниже калькулятор, вычисляющий ранг матрицы. Под ним, как водится, немного теории.
Определение ранга матрицы
3 2 -1 2 -1 5 1 7 -1
Матрица
Ранг матрицы
Update: Меня тут попросили сформулировать попроще, что такое ранг матрицы. Если попроще, то это максимальное число линейно-независимых строк/столбцов матрицы (число строк и число столбцов совпадает), то есть таких строк/столбцов, которые нельзя получить друг из друга элементарными преобразованиями.
Например, у этой матрицы
3 -1 1
6 -2 2
ранг равен 1, потому что вторая строка есть первая, умноженная на 2.
Итак, несколько определений.
Пусть дана матрица А размеров n x m и число k, не превосходящее наименьшего из чисел m и n. Выберем произвольно k строк матрицы и k столбцов (номера строк могут отличаться от номеров столбцов).
Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных k строк и k столбцов, называется
Рангом матрицы А называется наибольший из порядков миноров матрицы А, отличных от нуля. Ранг нулевой матрицы считается равным нулю.
Ненулевой минор наибольшего порядка называется базисным минором. Или, что тоже самое, минор матрицы А является ее базисным минором, если он не равен нулю, и его порядок равен рангу матрицы А.
Теорема о базисном миноре
Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из базисного минора.
Минор Mок матрицы А называют окаймляющим минором для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А.
Понятно, что ранг матрицы можно вычислить, перебирая все миноры, но в данном калькуляторе для вычисления ранга матрицы применяется метод окаймляющих миноров, основанный на следующей теореме.
Теорема: Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным. (А порядок, его, соответственно, равен рангу матрицы).
Метод окаймляющих миноров заключается в нахождении одного из базисных миноров матрицы и состоит в следующем:
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Определитель (детерминант) матрицы
- • Обратная матрица по модулю
- • Обратная матрица
- • Решение неоднородной системы линейных алгебраических уравнений матричным методом
- • Метод Крамера с подробным решением
- • Раздел: Математика ( 265 калькуляторов )
детерминант линейная алгебра Математика матрица минор ранг
PLANETCALC, Определение ранга матрицы
Timur2020-11-03 14:19:29
Обратная матрица онлайн
е. такой определитель которой отличен от нуля), существует
обратная матрица,
такая, что её произведение на исходную матрицу равно единичной:
A∙A−1 = A−1∙A = E
Наш калькулятор поддерживает два различных способа вычисления обратной матрицы: по методу Гаусса-Жордана и при помощи построения алгебраических дополнений к исходной матрице.
Для нахождения обратной матрицы по методу Гаусса-Жордана, к исходной матрице справа дописывают единичную матрицу:
( A | E )
Затем, с помощью элементарных преобразований приводят исходную матрицу к единичной, выполняя теже самые операции и над единичной матрицей, записанной справа. В результате таких действий исходная матрица приводится к единичной, а единичная к обратной:
( A | E) → ( E | A−1 )
Метод довольно простой, удобный и не очень трудоемкий.
Для нахождения обратной матрицы при помощи метода алгебраических дополнений используют следующую формулу:
где
| A |
— определитель матрицы
A,
Ai j
— алгебраическое дополнение элемента
ai j
матрицы
A.
По определению:
Ai j = (-1) i+j Mi j
где
M
По определению — минор элемента ai j матрицы A — это определитель, полученный путем вычеркивания i строки, j столбца матрицы A.
Таким образом, метод алгебраических дополнений для вычисления обратной матрицы порядка
n
является достаточно трудоемким, поскольку помимо определителя исходной матрицы, нужно вычислить
n2
определителей
n-1
порядка.
Калькулятор обратной матрицы
Установить калькулятор на свой сайт
Другие полезные разделы:
Найти определитель матрицы онлайнНайти ранг матрицы онлайн
Умножение матриц онлайн
Оставить свой комментарий:
Миноры и кофакторы матрицы
Миноры и кофакторы матрицыНавигация по страницам:
- Миноры матрицы
- Кофакторы матрицы
- Кофакторы матрицы — свойства
Определение.
Минор M ij к элементу a ij определителя n-го порядка, называемого определителем (n — 1)-го порядка, полученного из исходного определителя вычеркиванием i-й строки и j -й столбец.
Пример 1.
Найти миноры матрицы A
| А = |
|
Решение:
| M 11 = |
| = |
|
| М 11 = |
| = 1·3 — 0·0 = 3 – 0 = 3 |
| М 12 = |
| = -4·3 — 0·2 = -12 -0 = -12 |
| М 13 = |
| = -4·0 — 1·2 = 0 — 2 = -2 |
| М 21 = |
| = 7·3 — 1·0 = 21 – 0 = 21 |
| М 22 = |
| = 5·3 — 1·2 = 15 – 2 = 13 |
| М 23 = |
| = 5·0 — 7·2 = 0 – 14 = -14 |
| М 31 = |
| = 7·0 — 1·1 = 0 – 1 = -1 |
| М 32 = |
| = 5·0 — 1·(-4) = 0 + 4 = 4 |
| М 33 = |
| = 5·1 — 7·(-4) = 5 + 28 = 33 |
Определение.
Кофактор C ij к элементу a ij определителя число
С ij = (-1) i + j · M ij
Сумма произведений элементов строки (столбца) определителя на сомножители на элементы этой строки (столбца) равна определителю матрицы:
п Σ a ij ·A ij = det(A) j = 1 Сумма произведений элементов строки (столбца) определителя на сомножители на элементы другой строки (столбца) равна нулю: = 0
j = 1
Пример 2.
Найдите кофакторы матрицы A
| A = |
|
Решение:
| А 11 = (-1) 1 + 1 · М 11 = (-1) 2 · |
| = 1·3 — 0·0 = 3 – 0 = 3 |
| А 12 = (-1) 1 + 2 ·М 12 = (-1) 3 · |
| = -(-4·3 — 0·2) = -(-12 -0) = 12 |
| А 13 = (-1) 1 + 3 ·М 13 = (-1) 4 · |
| = -4·0 — 1·2 = 0 – 2 = -2 |
| А 21 = (-1) 2 + 1 · М 21 = (-1) 3 · |
| = -(7·3 — 1·0) = -(21 — 0) = -21 |
| А 22 = (-1) 2 + 2 · М 22 = (-1) 4 · |
| = 5·3 — 1·2 = 15 – 2 = 13 |
| А 23 = (-1) 2 + 3 ·М 23 = (-1) 5 · |
| = -(5·0 — 7·2) = -(0 — 14) = 14 |
| А 31 = (-1) 3 + 1 ·М 31 = (-1) 4 · |
| = 7·0 — 1·1 = 0 – 1 = -1 |
| А 32 = (-1) 3 + 2 ·М 32 = (-1) 5 · |
| = -(5·0 — 1·(-4)) = -(0 + 4) = -4 |
| А 33 = (-1) 3 + 3 · М 33 = (-1) 6 · |
| = 5·1 — 7·(-4) = 5 + 28 = 33 |
Онлайн-калькуляторы с матрицами
Онлайн упражнения с матрицами
Ранг матрицы по минорному методу
Ранг матрицы по минорному методу :
Здесь мы рассмотрим несколько примеров задач, чтобы узнать метод нахождения ранга матрицы по минорному методу.
Ранг матрицы A определяется как порядок старшего ненулевого минора матрицы A. Он обозначается символом ρ (A). Ранг нулевой матрицы определяется равным 0.
Примечание
(i) Если матрица содержит хотя бы один ненулевой элемент, то ρ (A) ≥ 1
(ii) Ранг единичной матрицы I n равен n.
(iii) Если ранг матрицы A равен r, то существует по крайней мере один минор матрицы A порядка r, который не равен нулю, и каждый минор матрицы A порядка r + 1 и выше (если есть) равен нулю .
(iv) Если A является матрицей размера m × n, то ρ (A) ≤ min {m, n} = минимум m, n.
(v) Квадратная матрица A порядка n имеет обратную тогда и только тогда, когда ρ (A) = n.
Вопрос 1 :
Решение :
Тогда A — матрица порядка 2×2. Итак, ρ (A) min {2, 2} = 2. Наивысший порядок миноров A равен 2 . Существует только один минор третьего порядка A .
= 4 — 4
|A| = 0
Ранг данной матрицы будет меньше 2.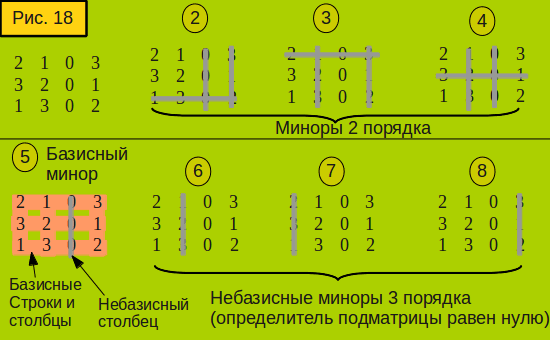
Следовательно, ранг данной матрицы равен 1.
Вопрос 2 :
Решение :
Тогда A — матрица порядка 3 × 2. Значит, ρ (A) min {3, 2} = 2. Наивысший порядок миноров матрицы A равен 2 .
В приведенной выше матрице есть четыре второстепенные матрицы 2 x 2. Находя определители, получаем
Поскольку минор матрицы 2 x 2 не равен нулю, ранг данной матрицы равен 2. матрица порядка 2 × 4. Итак, ρ (A) min {2, 4} = 2. Наивысший порядок миноров матрицы A равен 2 .
В приведенной выше матрице есть четыре второстепенные матрицы 2 x 2.
Ранг данной матрицы равен 2.
Вопрос 4 :
Решение:
Тогда A — матрица порядка 3 × 3. Значит, ρ (A) min {3, 3} = 3. Высший порядок миноров A равен 3 .
Найдя определитель данной матрицы, получим
= 1(-4 + 6) + 2(-2 + 30) + 3(2 — 20)
= 1(2) + 2(28) + 3 (-18)
= 2 + 56 — 54
= 58 — 54
|А| = 4 ≠ 0
Следовательно, ранг данной матрицы равен 3.