Множества. Операции над множествами
Цели урока: обобщить и систематизировать знания студентов по теме «Множества. Операции над множествами», используя мультимедиа технологии.
Задачи урока:
- Образовательные:
- закрепить теоретические знания: понятие множества, элемент множества, виды множеств, отношения между множествами, операции над множествами;
- сформировать умения применять полученные теоретические знания определения множества и его элементов, умения охарактеризовать множество, выполнять действия над множествами (объединение и пересечение), изображать множества с помощью диаграмм Эйлера-Венна, применять данные знания для решения прикладных задач;
- формировать информационно-коммуникативную компетенцию;
- развивать познавательный интерес, интеллектуальные и творческие способности учащихся;
- формировать информационную культуру, овладение навыками контроля и самоконтроля;
- осуществлять исследовательскую деятельность.
- Воспитательные:
- обучать самостоятельной деятельности по овладению знаниями;
- формировать осознанные мотивы учения, самосовершенствования, самовоспитания;
- воспитывать целеустремленность и настойчивость в достижении цели;
- воспитывать взаимопомощь.
ЗУН + опыт деятельности. Мультимедиа
технологии позволяют работать в индивидуальном
темпе, осуществить дифференцированный подход,
способствуют закреплению полученных знаний, а
также выступают как источник дополнительной
информации по предмету. Использование на уроке
опорных конспектов – фрагментов рабочих
тетрадей для студентов позволяют
совершенствовать навыки контроля и
самоконтроля, как способ самоорганизации труда и
самообразования.
- систематизируют свои знания по данной теме;
- закрепят теоретические знания: понятие множества, элемент множества, виды множеств, отношения между множествами, операции над множествами;
- закрепят умения применять полученные теоретические знания;
- осуществят исследовательскую деятельность.
Оборудование урока. ПК учителя, мультимедиа проектор, персональные компьютеры учащихся.
Программное обеспечение
Презентация иллюстрирует основную информационную составляющую урока по теме «Множества. Операции над множествами», содержит задания для самостоятельной работы, занимательные задачи.
ХОД И СОДЕРЖАНИЕ УРОКА
Этапы урока
I. Повторение и закрепление теоретических знаний
В начале занятия проводится актуализация знаний, умений и навыков: учащиеся повторяют основные понятия теории множеств. Ответы учащихся сопровождаются показом слайдов презентации с четкими формулировками, определениями. (Слайды 1, 2, 4, 5, 6)
II. Историческая справка
В качестве дополнительного материала можно
предложить студентам подготовить материал об
основателе теории множеств Георге Канторе
(слайд 6), и Леонарде Эйлере —
швейцарском, немецком и российском математике,
внёсшем значительный вклад в развитие
математики, а также механики, физики, астрономии
и ряда прикладных наук (слайд 28).
(как домашнее
задание к уроку).
III. Практикум решения упражнений
Данный урок является заключительным на этапе
изучения темы «Теория множеств». По ходу урока
студентам предлагается выполнение различных
заданий по теме, которые выполняются в
подготовленных фрагментах рабочих тетрадей (Приложение 1), частично с
проверкой и обсуждением. На этапе применения
теоретических знаний для решения задач
демонстрируются слайды с условиями для устного и
письменного решения упражнений, идет обсуждение
алгоритмов решения, в целях контроля и
формирования навыков самоконтроля
демонстрируются слайды с ответами и пояснениями.
Вторая часть урока посвящена решению
прикладных задач, демонстрации наиболее
рационального способа решения с использованием
теории множеств. (Слайды 29-39)IV. Контроль знаний и умений
Самый важный этап урока. Студенты на протяжении урока работают в рабочих тетрадях, выполняя предложенные задания. Частично в ходе урока производится проверка выполнения части упражнений и обсуждения способа решения, выявление пробелов и коррекция знаний. На заключительных этапах урока студентам предоставляется возможность реализовать в рамках самостоятельной работы, полученные на предыдущих этапах знания и умения, накопленный опыт. Отдельную часть заданий студентам предлагается выполнить самостоятельно, в конце урока дать оценку своей работе.
V. Рефлексия деятельности на уроке
Оценка своего участия в работе на уроке по 10
бальной
шкале: 0/__________________/10 по критериям
самооценки.
САМООЦЕНКА
10 – хорошо знаю весь фактический материал, и
участвовал в организации группы;
9 – хорошо знаю свой вопрос, и участвовал в
работе на уроке;
8 – хорошо знаю весь фактический материал;
7 – хорошо знаю свой вопрос;
5 – знаю свой вопрос, но был пассивен;
4 – плохо знаю свой вопрос, но был активен в обсуждении других вопросов;
3 – плохо знаю свой вопрос, и был пассивен;
1,2 – не знаю свой вопрос, и был пассивен.
Оценка валеологической составляющей урока по Бланку рефлексивной оценки.
Бланк рефлексивной оценки
Уважаемый студент! Для того, чтобы обучение
приносило Вам больше пользы, радости, здоровья,
мы просим вас выразить свое мнение об этом
занятии при помощи ответов на вопросы данной
анкеты. Внимательно прочитайте утверждения и
предложенные варианты ответов, выберите
наиболее подходящий и поставьте напротив его ?
палочку ? ( \ ).
Заранее благодарим за искренние
и точные ответы.
| Вопросы анкеты | ||||||||
| 1. После занятия я чувствую себя | ||||||||
| а) заряженным новой энергией | ||||||||
| б) работоспособным, бодрым | ||||||||
| в) самочувствие не изменилось | ||||||||
| г) утомленным | ||||||||
| д) подавленным | ||||||||
| е) несколько возбужденным, взвинченным | ||||||||
ж) апатичным, сонливым. |
||||||||
| 2. В конце занятия я испытал состояние | ||||||||
| а) восхищения | ||||||||
| б) благодарности | ||||||||
| в) удовлетворения | ||||||||
| г) впустую потраченного времени | ||||||||
| д) скуки | ||||||||
| е) раздражения | ||||||||
| ж) гнева | ||||||||
3. После занятия мне захотелось |
||||||||
| а) творить добро, совершать благородные поступки | ||||||||
| б) изобретать что-то новое, сочинять | ||||||||
| в) совершенствовать свои качества | ||||||||
| г) самостоятельно пополнять свои знания | ||||||||
д) чтобы материал данной темы никогда не ?попал?
мне на к. р., зачете, экзамене |
||||||||
| е) никогда о нем не вспоминать | ||||||||
| ж) поделиться с кем-нибудь о неприятных ощущениях от этого урока |
Обсуждение со студентами, какой урок они считают более эффективным – обычный или электронный, на каком они достигли лучших результатов: больше узнали, больше решили.
VI. Заключение
Презентация – наиболее удачная форма подачи
мультимедиа материала. Использование
презентации на данном уроке позволяет провести
обобщение изученного материала, демонстрировать
способы решения задач с применением теории
множеств, диаграмм Эйлера, показать поэтапное
решение прикладных задач, преимущества
использования графического способа решения.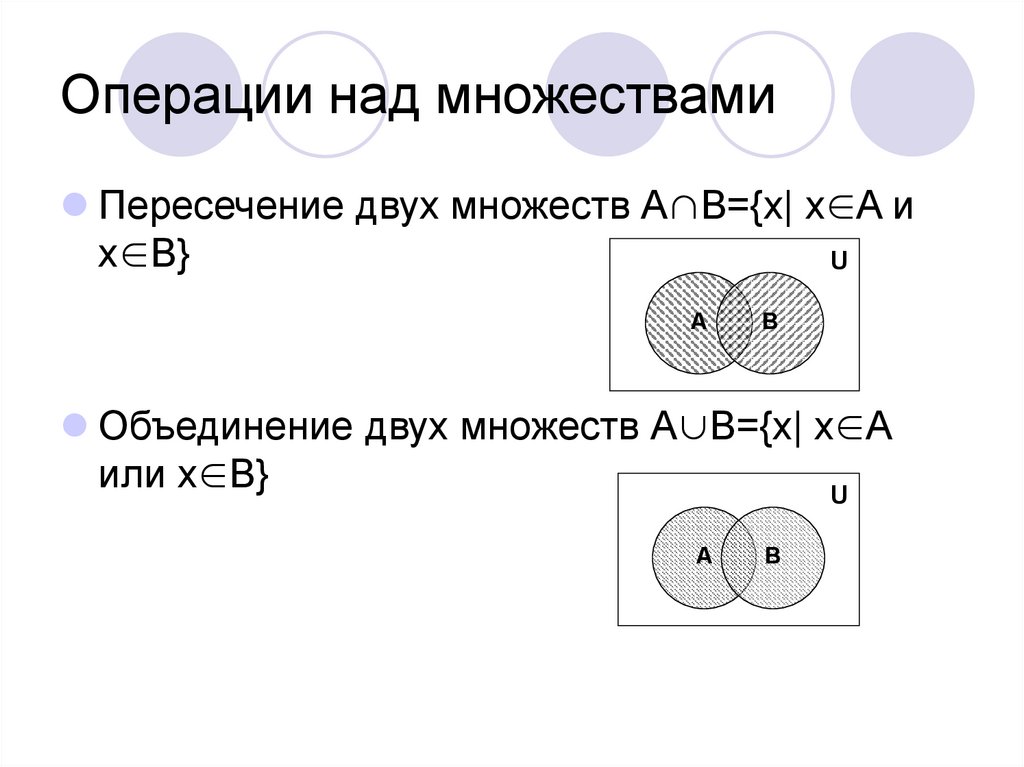
Все, это вызывает интерес, активизирует
память, обеспечивает более эффективное усвоение
материала, дает возможность организовать
интересную самостоятельную работу, развивает
образное мышление и способствует закреплению
учебного материала.
Урок проходит в быстром темпе, экономия во
времени позволяет выполнить большой объем
разнообразной работы: рассмотреть виды множеств,
отношения между множествами (не иметь общих
элементов, быть подмножеством, быть равными,
иметь общие элементы), организовать работу
учащихся на уровне, соответствующем уровню уже
сформированных знаний.
Данный электронный материал можно
использовать и на уроках, и на внеурочных
занятиях. Презентация используется учащимися
для самостоятельного повторения, закрепления
или углубления своих знаний по теме «Теория
множеств». Это особенно удобно для учащихся,
пропустивших занятия по уважительной причине и
желающим ликвидировать пробелы в знаниях.
Использованные источники и литература:
- Спирина М.С., Спирин П.А. Дискретная математика. – М.: Издательский центр «Академия», 2011.
- Виленкин Н.Я. Рассказы о множествах. – М.: Наука, 1965.
- Жарковская Н.А. Георг Кантор и теория множеств. //»Курсор. Международный математический конкурс-игра «Кенгуру»». 2011, выпуск 5
- Тюрин Ю.Н. и др. Теория вероятностей и статистика, – Москва, МЦНМО, 2008.
Множества и операции над множествами
Тема урока: Множества и операции над ними.
Учитель Рыкова Л.Г.
Цели урока:
образовательные: повторить основные понятия множества, подмножества, операции над множествами;
развивающие: развитие логического мышления через решение нестандартных задач, систематизацию и обобщение, развитие математической речи,
воспитательные: воспитание внимательности, интереса к предмету, расширение кругозора, воспитывать грамотную математическую речь.
Тип урока: комбинированный урок — изучение и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения, совершенствование вычислительных навыков.
Формы работы учащихся: фронтальная работа, групповая технология, ИКТ.
Необходимое техническое оборудование: компьютер, мультимедийный проектор, доска, экран
Ход урока:
I этап. Сообщение темы, цели, задач урока и мотивация учебной деятельности.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
«Множество есть многое, мыслимое нами как единое» ( Г. Кантор)
(слайд 2)
Историческая справка 1 (сообщение обучающихся)
Понятие множество связано с таким известным в математике именем как Кантор (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.
В семидесятые годы ХIX века немецкий математик Георг Кантор, исследуя тригонометрические ряды и числовые последовательности, встал перед необходимостью сравнить между собой бесконечные совокупности чисел. Для решения возникших при этом проблем Кантор и выдвинул понятие множества. Это понятие, введенное в достаточно узкой области математики для довольно специальных целей, вскоре стало с успехом применяться в других ее областях. Посвященные ему исследования приобрели самостоятельный интерес и выделились в особый раздел математики – теорию множеств.
Теория множеств появилась на свет 7 декабря 1873 года.
Кантора заинтересовал вопрос, каких чисел больше – натуральных или действительных?
В одном из писем адресованных к своему приятелю Рихарду Дедекинду, Кантор писал, что ему удалось доказать посредством множеств, что действительных чисел больше, чем натуральных. День, которым было датировано это письмо, математики считают днем рождения теории множеств.
(слайд 3,4)
II этап. Проверка домашнего задания, уточнение направлений актуализации изученного материала.
Учитель. — Множество — одно из основных понятий современной математики, используемое почти во всех её разделах. К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству. Понятие множества поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.. Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C, … , X, Y, … ,A1,B1, …
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи.
Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ. Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c, … , x, y, … , a1, b1, … Если элемент х принадлежит множеству М, то записывают х М, если не принадлежит – x M.
Множества можно задать, перечислив все его элементы или указав характеристическое свойство элементов, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.
Примеры множеств:
множество дней недели;
множество планет солнечной системы;
множество месяцев;
множество знаков зодиака;
числовые множества.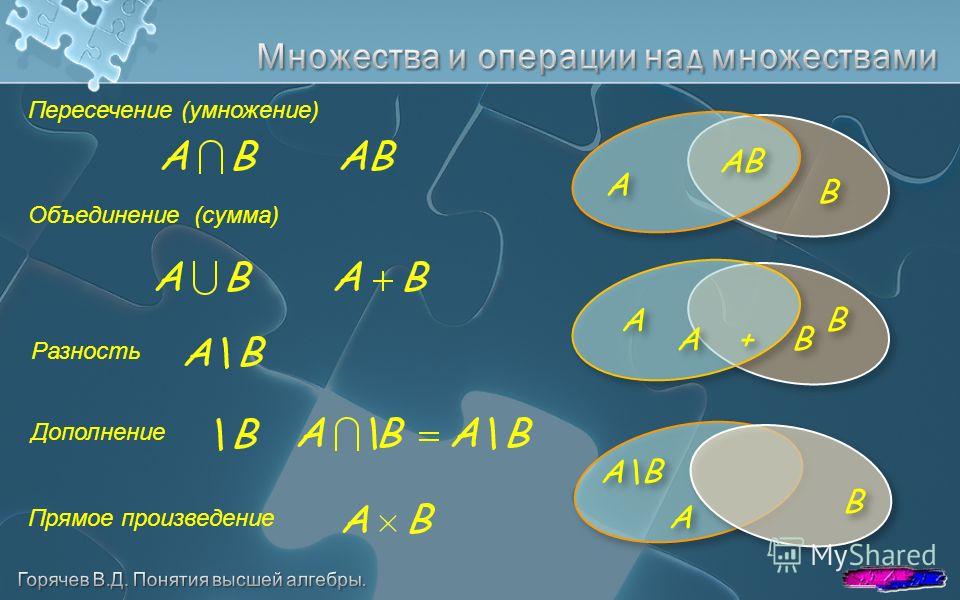
Приведите свой пример множества.
ТЕОРЕТИЧЕСКАЯ РАЗМИНКА:
(слайд 5- 12)
1. Что означает слово «множество»? (Множество – это набор или совокупность предметов одинаковой природы).
2. Как различаются множества по числу элементов? (Множества бывают конечные, бесконечные и пустое множество).
4. Какими способами можно задать множество? (Множество можно задать перечислением, с помощью характеристического свойства, графически).
5. Какое свойство называется характеристическим свойством? (Характеристическим свойством называется такое свойство, которым обладают все элементы данного множества и не обладают никакие другие объекты).
(Слайд 13-17)
Леонард Эйлер (1707-1783) – швейцарский, немецкий и российский математик и механик, внесший огромный вклад в развитие этих наук.
Жизнь Леонарда Эйлера была полна удивительных открытий, принесших человечеству огромную пользу. Его масштабный вклад в развитие математики, механики, физики и астрономии невозможно переоценить, а его познания в самых разнообразных отраслях науки вызывают восхищение. За всю свою жизнь он издал более 850 трудов, в которых содержатся глубокие исследования ботаники, химии, медицины, древних языков. Имел членство во многих Академиях наук по всему миру.
Круги Эйлера — это геометрическая схема, которую можно применять для наглядного отображения отношений между множествами. Диаграммы разработал известный математик и механик, чьим именем и назван метод. Учёный считал, что его подход облегчает размышления человека.
Какие операции можно выполнять над множествами? (объединение, пересечение, вычитание).
III этап. Изучение нового материала.
Повторение.
(Слайды 17, 18)
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.
Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством В. Обозначение: А Ì В. Знак « Ì » — знак включения.
Рассмотрим некоторые операции над множествами.
(Слайды 20- 23)
Какие операции можно выполнять над множествами? (объединение, пересечение, вычитание).
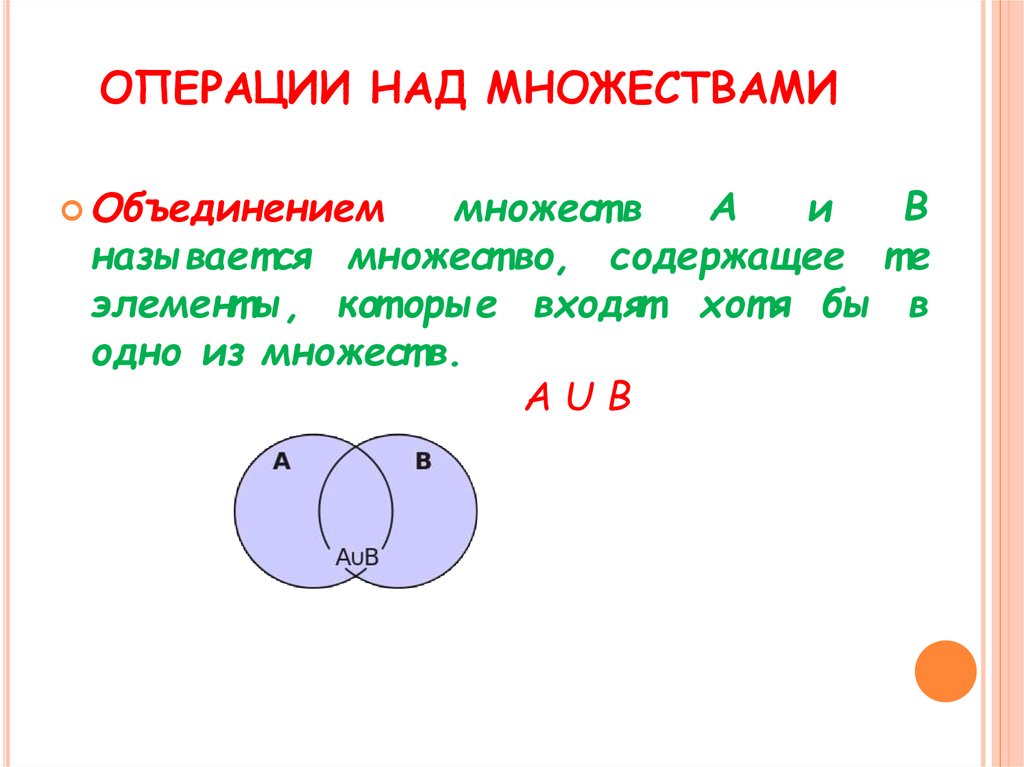
Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.
Символически объединение двух множеств А и В обозначается так:
А В, где — символ объединения множеств. Определение можно записать с помощью характеристического свойства:
С = А В={x xA или xB}.
(Слайды 21)
Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Символически пересечение множеств А и В обозначается так: АВ, где символ — знак пересечения множеств. Используя характеристическое свойство, определение можно записать следующим образом:
Р = А В= {x xA и xB}.
(Слайд 22)
Вычитание множеств.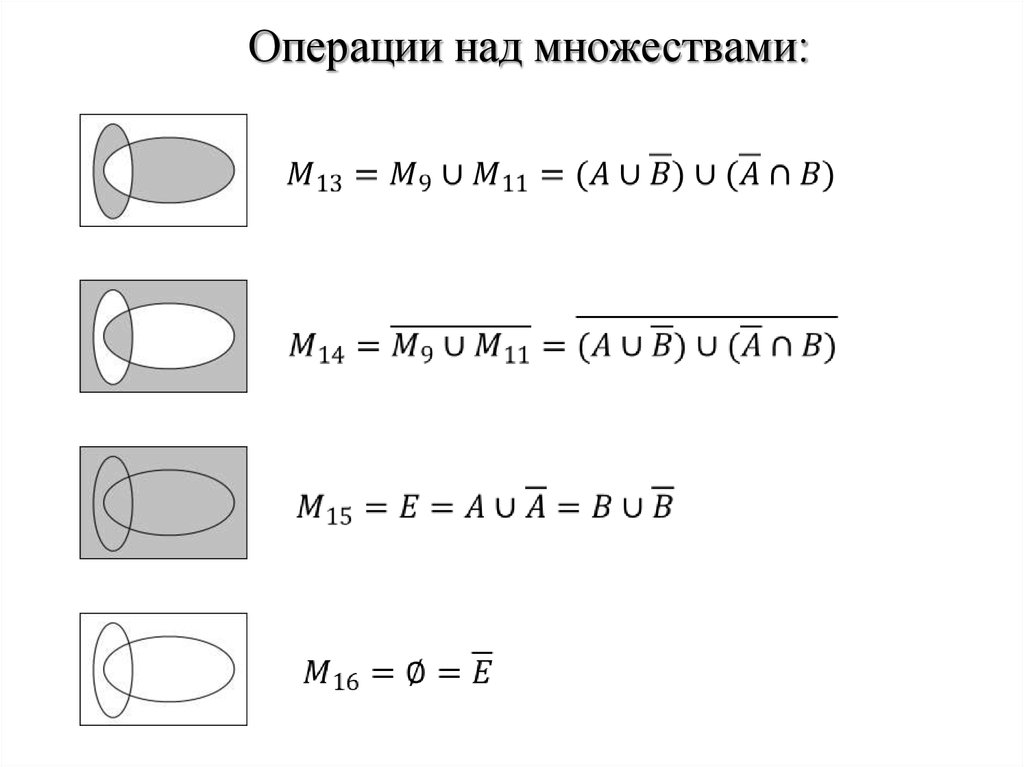
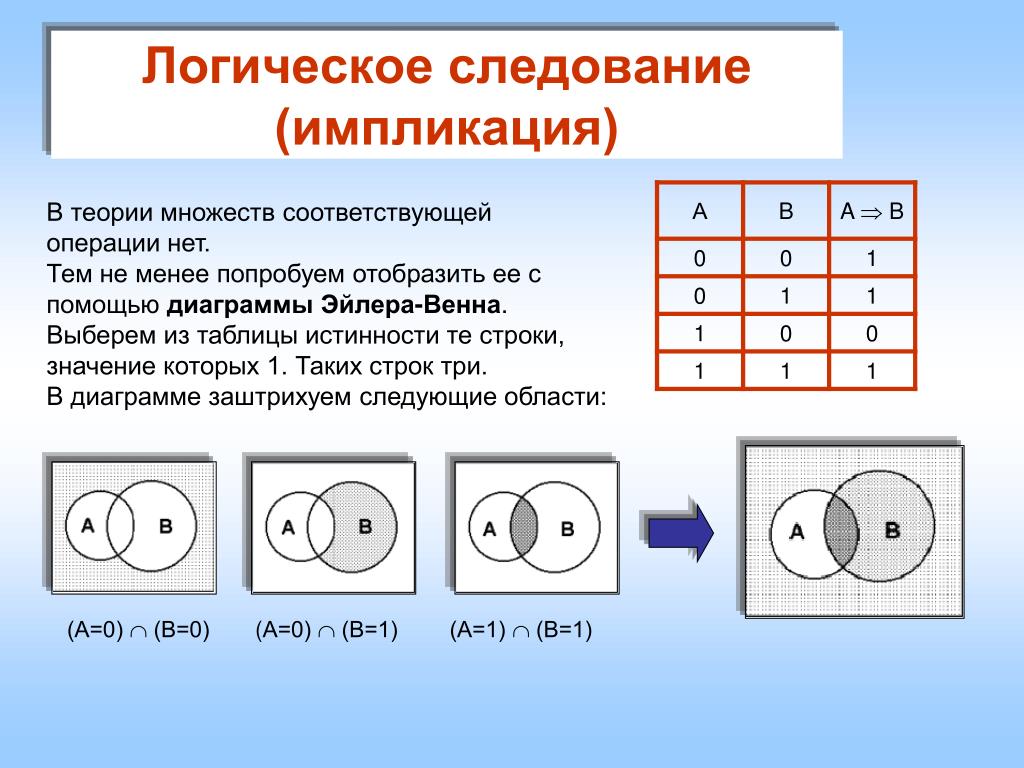
Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
А\В={х|х Є А и х ∉ В}
(Слайд 23)
IV этап. Воспроизведение изученного и его применение в стандартных условиях.
(Слайд 24)
УПРАЖНЕНИЕ № 1. (Слайд 25)
Множество задано путем перечисления своих элементов. Придумайте какое-нибудь его словесное описание.
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
{A, B, C, D, E, … X, Y, Z};
{0, 2, 4, 6, 8}.
УПРАЖНЕНИЕ № 2. (Слайд 26)
Даны множества:
А = {2, 5, 0, 11, 12, 19}, В = {2, 7, 8, 12, 13, 9, 0}.
Найдите множества A Ç В, А È В, А\В, В\А.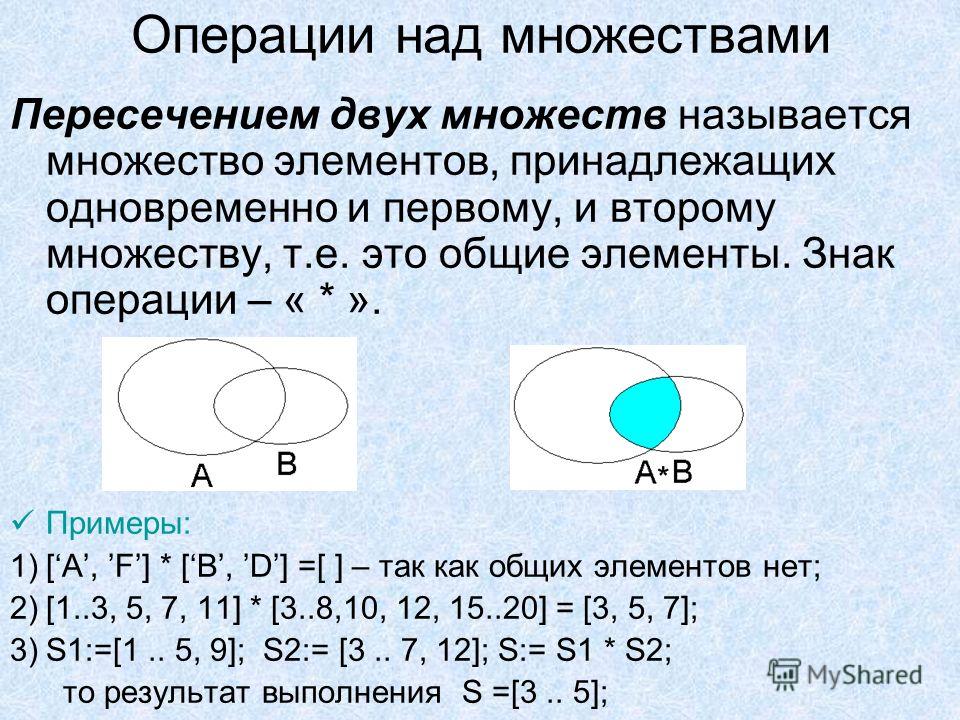
Ответы:
A В= {2, 0, 12},
А В= {2, 5, 0, 11, 12, 19, 7, 8, 13, 9},
А\В = { 5, 11, 19},
В\А = { 7, 8, 13, 9}.
УПРАЖНЕНИЕ № 3. (Слайд 27)
Задайте множество груш, растущих на берёзе.
Задайте множество чисел, которые делятся на 0.
УПРАЖНЕНИЕ № 4. (Слайд 28)
Даны множества: М = {5, 4, 6}, Р = {4, 5, 6}, Т = {5, 6, 7}, S = {4, 6}. Какое из утверждений неверно?
а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.
УПРАЖНЕНИЕ № 5. (Слайд 29)
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 11;
б) множество делителей числа 5;
в) множество океанов;
г) множество натуральных чисел;
д) множество рек России;
е) множество корней уравнения х — 3 = 10.
УПРАЖНЕНИЕ № 6. (Слайд 30)
Даны множества:
А – множество фруктов в корзине;
В – множество яблок в этой корзине;
С – множество груш в этой корзине;
Д – множество слив в этой корзине.
Чем являются множества В, С и Д для множества А?
УПРАЖНЕНИЕ № 7. (Слайд 31 -35)
Изобразите с помощью кругов Эйлера пересечение множеств A и В, если: а) А Ç В; б) А È В; в) А = В; г) А Ç В = ᴓ .
УПРАЖНЕНИЕ № 8 (Слайд 36)
Расположите 4 элемента a, b, c, d в двух множествах так, чтобы в каждом из них было по 3 элемента.
УПРАЖНЕНИЕ № 9 (Слайд 37)
Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В?
V этап.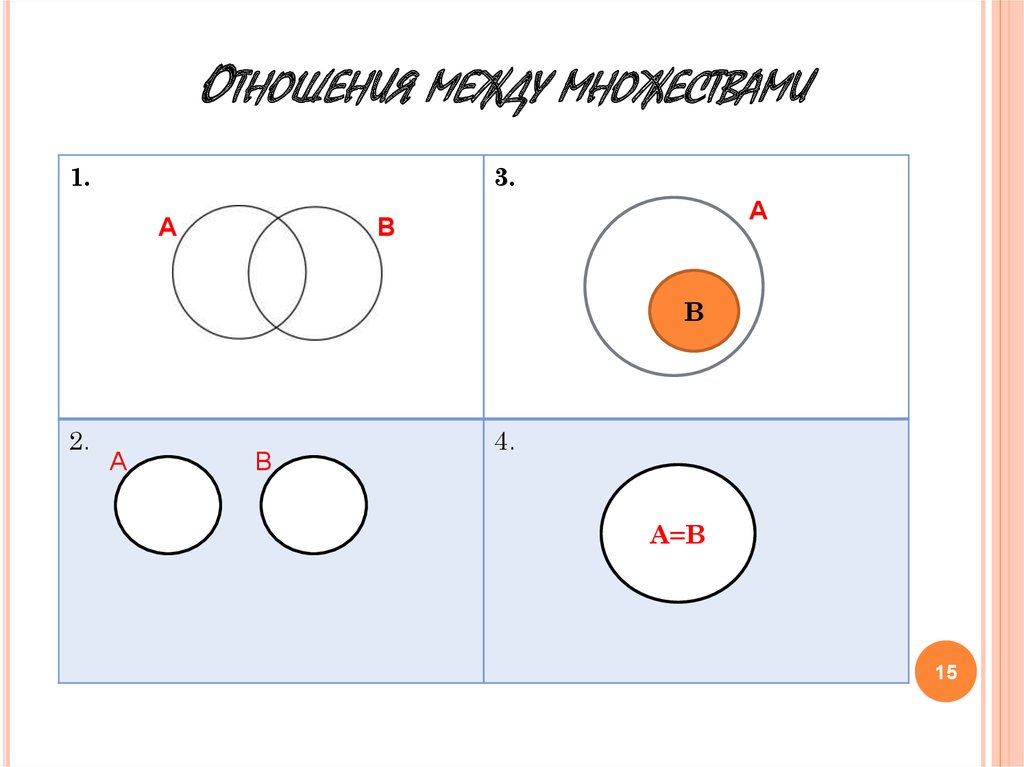
Перенос приобретенных знаний и их первичное применение в новых или измененных условиях с целью формирования умений.
ЗАДАЧА 1 (Слайд 38)
Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
ЗАДАЧА 2 (Слайд 39)
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
Ответить на вопросы теста:
Тест по теме «Множества»
1. Определить какое из множеств является подмножеством
А = {5, 15, 25, 35, 45, 55}
a) {55} б) {5, 25, 50} в) {25, 55, 75}
2.
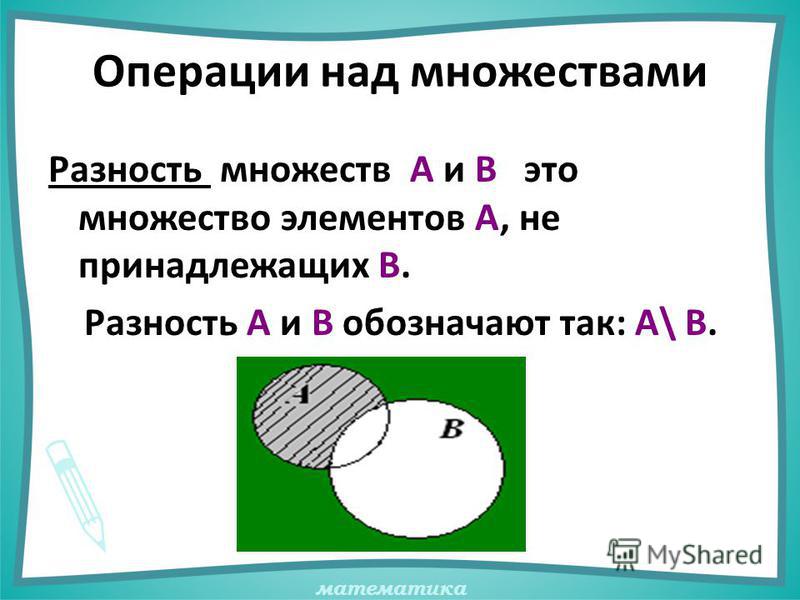Какое из множеств определяет , если А = {2, 4, 6, 8, 10}, B = {8, 10, 12, 14}
a) {2, 4, 6, 8, 10, 12, 14} б) {8, 10, 12, 14} в) {8, 10}
3. Какое из множеств определяет , если A = {2, 4, 6, 8, 10}, B = {2, 4, 8, 9}
а) {2, 4, 6, 8, 10} б) {2, 4, 8, 9} в) {2, 4, 8}
4. На каком рисунке изображено пересечение множеств А и В ( )?
Сообщение на тему «Фракталы». (Слайды 45-54)
Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
Множество, обладающее свойством самоподобия. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность.
VI этап. Рефлексия.
Подведение итогов урока.
Продолжите слова:
сегодня я узнал… теперь я могу… я научился… было интересно…
меня удивило… я приобрел… мне захотелось…
VII этап. Постановка задания на дом. (Слайды 55-58)
ТЕСТ.
Тест по теме «Множества»
Тест с выбором правильного ответа.
ИНСТРУКЦИЯ: Выберите букву с правильным ответом и занесите её в бланк ответов.
1. Определить какое из множеств является подмножеством А = {10, 20, 30, 40, 50, 60}
a) {10, 20, 30, 40, 50, 60, 70} б) {10} в) {10, 35}
2. Какое из множеств определяет , если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
a) {1, 4, 5} б) {1, 2, 3, 4, 5} в) {1, 2, 3, 4, 5, 6, 7}
3.
Какое из множеств определяет , если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
а) {1, 3, 5, 7} б) {1, 2, 3, 4, 5, 7, 9} в) {1, 3}
4. На каком рисунке изображено объединение множеств А и В ( )?
Задача для любознательных (Слайд 40)
Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые — даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:
Сколько всего человек в классе?
Сколько человек умеют играть в футбол?
Сколько человек умеют играть в волейбол?
9
Математический обзор операций с множествами
Математический обзор операций с множествами https://schooltutoring.
com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg
150
150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
Обзор
Операции с множествами включают объединение множеств, пересечение множеств и дополнение множеств. Эти операции можно применять для решения геодезических задач с помощью множеств.
Специальные типы наборов
Некоторые специальные типы наборов включают нулевой или пустой набор, универсальный набор, а также правильные и неправильные подмножества. Нулевой или пустой набор ⦰ не имеет элементов. Его установленное обозначение { }. Напротив, универсальный набор U содержит все элементы каждого набора в операции. В то время как пустой набор всегда один и тот же, набор без элементов, универсальный набор меняется с каждой задачей.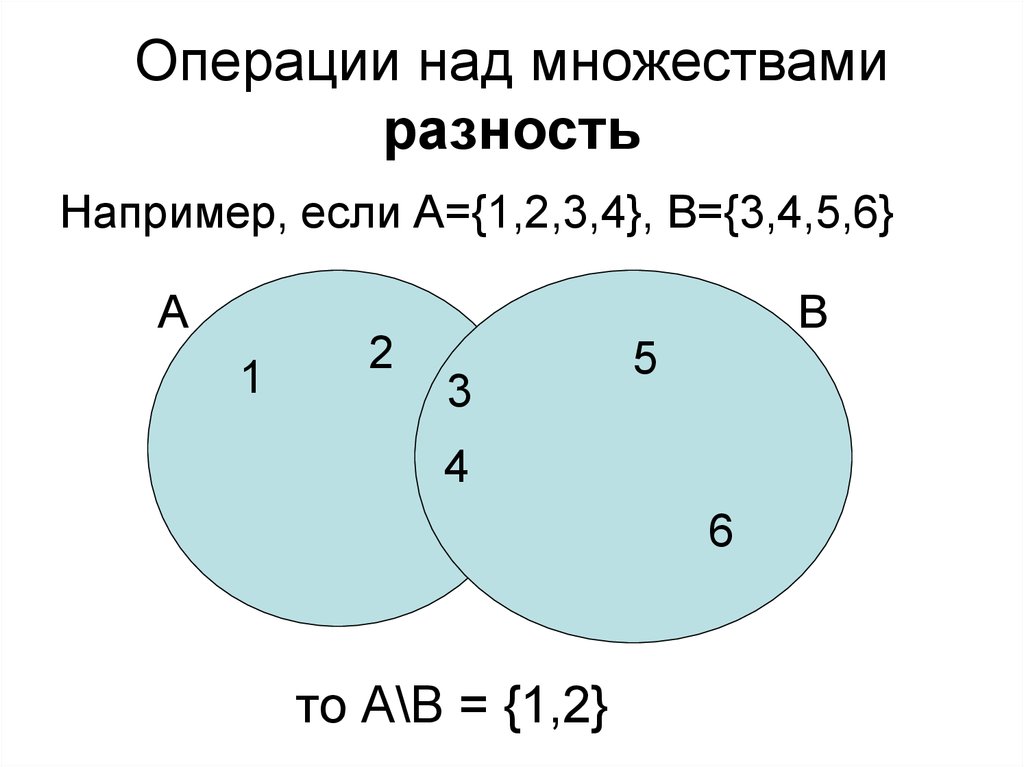
Он определяется до выполнения каких-либо операций. Предположим, что множество F является универсальным множеством для задачи. Он содержит элементы {2, 4, 6, 8, 10, 12}. Следовательно, все операции над множеством F будут содержать только эти элементы. Надлежащие подмножества множества F будут включать в себя некоторые элементы множества F, такие как множество G {2, 4, 6} или множество H {8, 10}. На языке множеств сокращение символов G ⊂ F. Несобственные подмножества множества F будут содержать все члены множества F. Множество I {12, 10, 8, 6, 4, 2} является неправильным подмножеством множества F.
Рисунок 1: Набор F является универсальным набором для этой задачи; Множества G, H и M являются собственными подмножествами.
Объединение и пересечение множеств
Объединение множеств обозначается символом ⋃, поэтому если множество G {2,4,6} и множество H {8, 10} G ⋃ H = {2, 4, 6, 8, 10}. Пересечение множеств состоит из элементов, общих для двух или более множеств.
Предположим, что Set J {1, 2, 3, 4, 5} и Set K {a, 3, d, 4, q}. Пересечение множеств J⋂K равно {3, 4}. Это единственные точки, общие для множеств J и K.
Рисунок 2: Диаграммы Венна как рабочие определения множеств и операций.
Дополнения наборов
Дополнение набора связано с универсальным набором для этой задачи. Помните универсальное множество F с элементами {2, 4, 6, 8, 10, 12}? Если множество O {6, 8, 10}, дополнение O (Ō) равно {2, 4, 12}. Если универсальный набор для задачи равен I , набор целых чисел и набор L равен {1, 3, 5, 7…}, дополнение L будет {0, 2, 4, 6…}.
Рисунок 3: Некоторые символы и терминология наборов.
Решение задач опроса с наборами
Предположим, что 100 человек спросили, какие передачи они любят смотреть по телевизору. Предположим, что 15 человек смотрят спорт, 15 — детективы и детективы, 12 — реалити-шоу, 20 — реалити-шоу и детективы, 28 — спорт и детективы и 3 — спорт, детективы и реалити-шоу.
Сколько людей не смотрят ни спорт, ни детективы, ни реалити-шоу? Это можно решить, используя диаграмму Венна и логику. Пусть Set S — это спорт, Set M — детективы, а Set R — реалити-шоу. Пересечение S⋂M⋂R равно 3, поэтому дополнение будет 15 -3 или 12. Другими словами, есть еще 12 людей, которые смотрят спорт. Кто-то из них смотрит только спорт, кто-то смотрит спорт и детективы, а кто-то смотрит спорт и реалити-шоу. Мы уже знаем, что есть 15 человек, которые смотрят детективы, но некоторые из них также смотрят спорт, а некоторые еще и реалити-шоу. Точно так же пересечение S⋂M⋂R равно 3, поэтому дополнение будет 15 -3 или 12. Есть 12 человек, которые смотрят реалити-шоу, но 3 из них также смотрят спорт и детективы, поэтому дополнение 12-3 равно 9. Часть множества M, которая не является частью множества S, равна (15–3) или 12, а часть множества M, которая не является частью множества R, равна 12-3 или 9. Наконец, часть множества R, которая 15 -9 или 6 не входит в набор S. 15 + 9 + 3 = 27.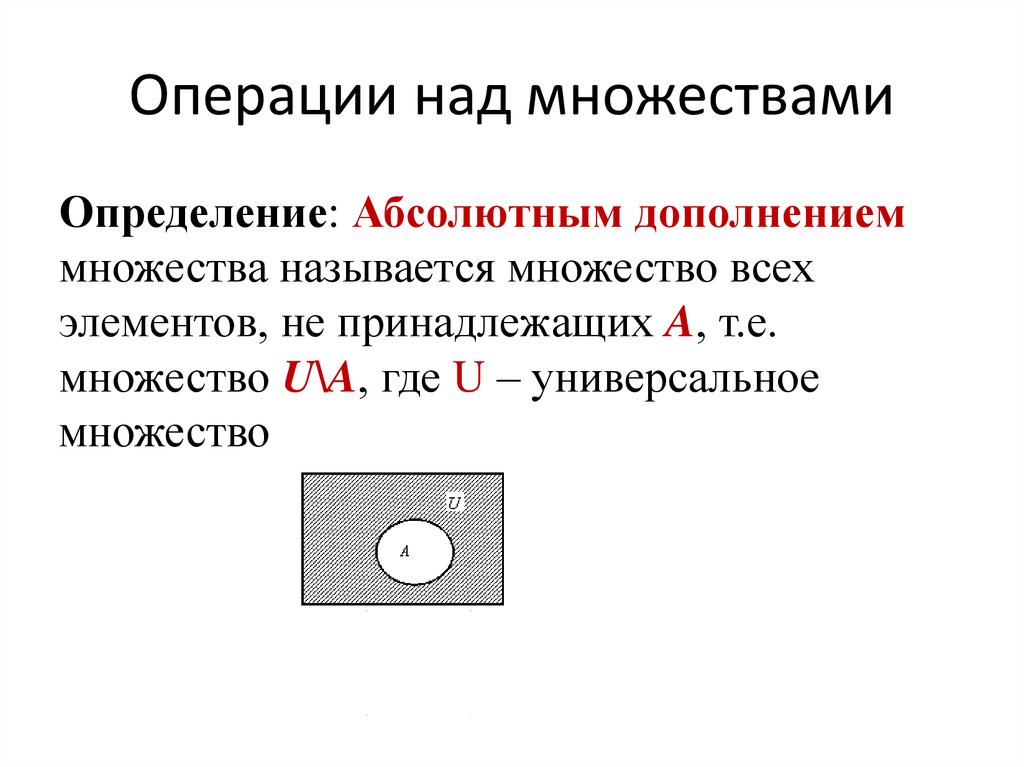
100 – 27 = 73, или 73 человека не смотрят ни спорт, ни детективы, ни реалити-шоу.
Рисунок 4: Диаграмма Венна, показывающая области и взаимосвязи 3 различных наборов.
Заинтересованы в услугах репетитора по алгебре? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — это первоклассная компания, предоставляющая образовательные услуги для учащихся K-12 и колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и учащимся в Линчбурге, штат Вирджиния, посетите веб-сайт Tutoring in Lynchburg, VA
NumPy ufuncs — Set Operations
❮ Предыдущая Далее ❯
Что такое множество
Множество в математике — это набор уникальных элементов.
Наборы используются для операций, включающих частые операции пересечения, объединения и разности.
Создание наборов в NumPy
Мы можем использовать метод NumPy unique() для поиска уникальных элементов из любого массива.
Например. создайте массив наборов, но помните, что массивы наборов должны быть только одномерными массивами.
Пример
Преобразование следующего массива с повторяющимися элементами в набор:
импортировать numpy как np
arr = np.array([1, 1, 1, 2, 3, 4, 5, 5, 6, 7])
x = np.unique(arr)
print(x)
Попробуйте сами »
Поиск объединения
Чтобы найти уникальные значения двух массивов, используйте метод union1d() .
Пример
Найти объединение следующих двух массивов наборов:
импортировать numpy как np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([3, 4, 5, 6])
newarr = np.union1d(arr1, arr2 )
print(newarr)
Попробуйте сами »
Поиск пересечения
Чтобы найти только те значения, которые присутствуют в обоих массивах, используйте Метод intersect1d() .
Пример
Найти пересечение следующих двух наборов массивов:
импортировать numpy как np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([3, 4, 5, 6])
newarr = np.intersect1d (arr1, arr2 , accept_unique=True)
print(newarr)
Попробуйте сами
который, если установлено значение True, может ускорить вычисления. При работе с наборами всегда следует устанавливать значение True.
Поиск различий
Чтобы найти только значения в первом наборе, которые НЕ присутствуют в наборе секунд, используйте метод setdiff1d() .
Пример
Найти отличие набора 1 от набора 2:
импортировать numpy как np
set1 = np.array([1, 2, 3, 4])
set2 = np.array([3, 4, 5, 6])
newarr = np.setdiff1d (set1, set2 , accept_unique=True)
print(newarr)
Попробуйте сами »
Примечание: метод setdiff1d() принимает необязательный аргумент accept_unique ,
который, если установлено значение True, может ускорить вычисления.
При работе с наборами всегда следует устанавливать значение True.
Поиск симметричной разницы
Чтобы найти только те значения, которые НЕ присутствуют в ОБОИХ наборах, используйте метод setxor1d() .
Пример
Найдите симметричную разность множества1 и множества2:
импортировать numpy как np
set1 = np.array([1, 2, 3, 4])
set2 = np.array([3, 4, 5, 6])
newarr = np.setxor1d(set1, set2, accept_unique = True )
print(newarr)
Попробуйте сами »
Примечание: метод setxor1d() принимает необязательный аргумент
который, если установлено значение True, может ускорить вычисления. При работе с наборами всегда следует устанавливать значение True.
❮ Предыдущий Следующий ❯
ВЫБОР ЦВЕТА
Лучшие учебники
Учебник HTMLУчебник CSS
Учебник JavaScript
How To Tutorial
Учебник SQL
Учебник Python
Учебник W3.
CSS Учебник Bootstrap
Учебник PHP
Учебник Java
Учебник C++
Учебник jQuery 902 Top30 Reference 902 Top30s Reference 902 900 Справочник по HTML
Справочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery
Основные примеры
Примеры HTMLПримеры CSS
Примеры JavaScript
Примеры инструкций
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery
FORUM | О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.