НОУ ИНТУИТ | Лекция | Базисные средства манипулирования реляционными данными: реляционная алгебра Кодда
< Лекция 10 || Лекция 3: 12345
Аннотация: В предыдущей лекции упоминались три составляющих реляционной модели данных. Две из них – структурную и целостную части – мы рассмотрели более или менее подробно, а манипуляционной части реляционной модели данных посвящается эта и следующие две лекции. Мы уделяем данной теме такое большое внимание, поскольку понимание формальных механизмов манипулирования реляционными данными исключительно важно для понимания технологии баз данных вообще. В этой лекции после небольшого введения будет рассмотрен вариант реляционной алгебры, предложенный Кристофером Дейтом около 15 лет тому назад. Мне этот вариант алгебры кажется наиболее понятным, хотя предлагаемый набор операций несколько избыточен. В следующей лекции мы обсудим новый «минимальный» вариант алгебры, предложенный Дейтом и Дарвеном в конце 1990-х гг. Возможно, новая алгебра не очень практична, но зато красива и элегантна.
После этого в лекции 5 мы перейдем к реляционному исчислению, достаточно подробно рассмотрим один из вариантов реляционного исчисления кортежей и кратко обсудим особенности исчисления доменов.
Ключевые слова: механизм манипулирования реляционными данными, реляционная алгебра, реляционное исчисление, очередь, исчисление кортежей, исчисление доменов, механизмы, БД, выражение, модель данных, реляционно-полный язык баз данных, логические выражения, запрос, интерпретация, SQL, знание, операция дополнения, реляционная алгебра Кодда, теоретико-множественные операции, реляционные операции, операции, операция объединения отношений, операция пересечения отношений, операция взятия разности отношений, операция взятия расширенного декартова произведения отношений, операция ограничения отношения, операция проекции отношения, операция соединения отношений, операция деления отношений, операция присваивания отношений, операция переименования атрибутов, кортеж отношения, заголовок отношения, именованный атрибут, разность множеств, замкнутость реляционной алгебры, совместимость отношений по объединению, декартово произведение множества, совместимость отношений относительно операции расширенного декартова произведения, трехзначная логика, тело отношения, эквисоединение, естественное соединение, точечная нотация, ключ отношения, множества, путь, семантика
Введение
intuit.ru/2010/edi»>Как мы отмечали в предыдущей лекции, в манипуляционной составляющей реляционной модели данных определяются два базовых механизма манипулирования реляционными данными – основанная на теории множеств реляционная алгебра и базирующееся на математической логике (точнее, на исчислении предикатов первого порядка) реляционное исчисление. В свою очередь, обычно выделяются два вида реляционного исчисления – исчисление кортежей и исчисление доменов.Все эти механизмы обладают одним важным свойством: они замкнуты относительно понятия отношения. Это означает, что выражения реляционной алгебры и формулы реляционного исчисления определяются над отношениями реляционных БД и результатом их «вычисления» также являются отношения (конечно, здесь имеются в виду значения-отношения). В результате любое выражение или формула могут интерпретироваться как отношения, что позволяет использовать их в других выражениях или формулах.
intuit.ru/2010/edi»>Как мы увидим, алгебра и исчисление обладают большой выразительной мощностью: очень сложные запросы к базе данных могут быть выражены с помощью одного выражения реляционной алгебры или одной формулы реляционного исчисления. Именно по этой причине такие механизмы включены в реляционную модель данных. Конкретный язык манипулирования реляционными БД называется реляционно-полным, если любой запрос, формулируемый с помощью одного выражения реляционной алгебры или одной формулы реляционного исчисления, может быть сформулирован с помощью одного оператора этого языка.Известно (и мы не будем это доказывать), что механизмы реляционной алгебры и реляционного исчисления эквивалентны, т. е. для любого допустимого выражения реляционной алгебры можно построить эквивалентную (т. е. производящую такой же результат) формулу реляционного исчисления и наоборот. Почему же в реляционной модели данных присутствуют оба эти механизма?
intuit.ru/2010/edi»>Дело в том, что они различаются уровнем процедурности. Выражения реляционной алгебры строятся на основе алгебраических операций (высокого уровня), и подобно тому, как интерпретируются арифметические и логические выражения, выражение реляционной алгебры также имеет процедурную интерпретацию. Другими словами, запрос, представленный на языке реляционной алгебры, может быть вычислен на основе выполнения элементарных алгебраических операций с учетом их приоритетности и возможного наличия скобок. Для формулы реляционного исчисления однозначная вычислительная интерпретация, вообще говоря, отсутствует. Формула только ставит условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются в большей степени непроцедурными, или декларативными.Поскольку механизмы реляционной алгебры и реляционного исчисления эквивалентны, в конкретной ситуации для проверки степени реляционности некоторого языка БД можно пользоваться любым из этих механизмов.
Заметим, что крайне редко алгебра или исчисление принимается в качестве полной основы какого-либо языка БД. Обычно (например, в случае языка SQL) язык основывается на некоторой смеси алгебраических и логических конструкций. Тем не менее знание алгебраических и логических основ языков баз данных часто применяется на практике.
Для экономии времени и места мы не будем вводить какие-либо строгие синтаксические конструкции, а в основном ограничимся рассмотрением материала на содержательном уровне.
Обзор реляционной алгебры Кодда
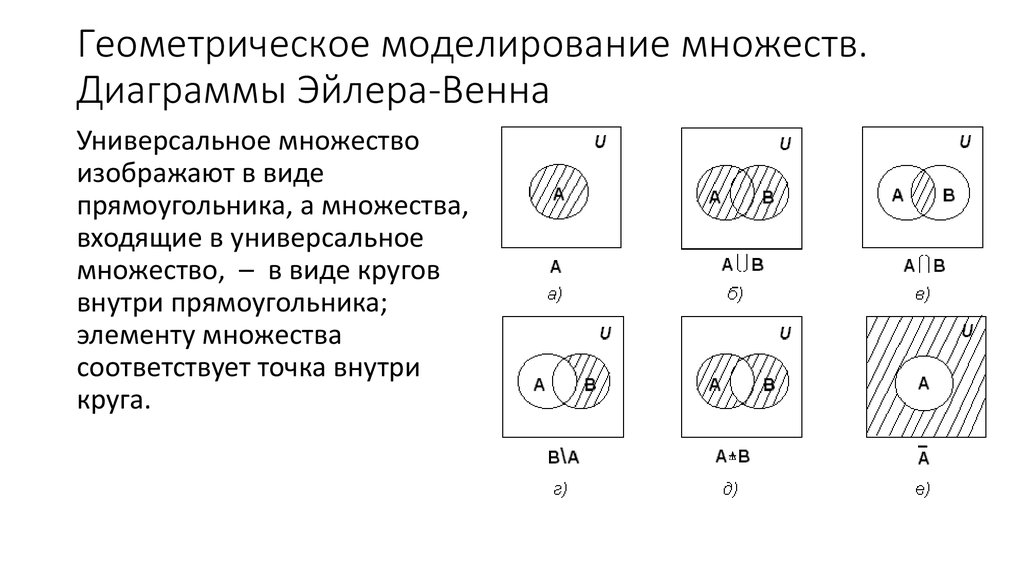
Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для реляционных баз данных.
intuit.ru/2010/edi»>Существует много подходов к определению реляционной алгебры, которые различаются наборами операций и способами их интерпретации, но, в принципе, являются более или менее равносильными. В данном разделе мы опишем немного расширенный начальный вариант алгебры, который был предложен Коддом (будем называть ее » алгеброй Кодда «). В этом варианте набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса – теоретико-множественные операции и специальные реляционные операции. В состав теоретико-множественных операций входят операции:- объединения отношений ;
- пересечения отношений ;
- взятия разности отношений ;
- взятия декартова произведения отношений.
Специальные реляционные операции включают:
- проекцию отношения ;
- соединение отношений ;
- деление отношений.
intuit.ru/2010/edi»>
ограничение отношения ;Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения.
Общая интерпретация реляционных операций
Если не вдаваться в некоторые тонкости, которые мы рассмотрим в следующих разделах, то почти для всех операций предложенного выше набора имеется очевидная и простая интерпретация.
- При выполнении операции объединения ( UNION ) двух отношений с одинаковыми заголовками производится отношение, включающее все кортежи, которые входят хотя бы в одно из отношений-операндов.
- Операция пересечения ( INTERSECT ) двух отношений с одинаковыми заголовками производит отношение, включающее все кортежи, которые входят в оба отношения-операнда.
- Отношение, являющееся разностью ( MINUS ) двух отношений с одинаковыми заголовками, включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, которое является вторым операндом.
- При выполнении декартова произведения ( TIMES ) двух отношений, пересечение заголовков которых пусто, производится отношение, кортежи которого производятся путем объединения кортежей первого и второго операндов.
- Результатом ограничения ( WHERE ) отношения по некоторому условию является отношение, включающее кортежи отношения-операнда, удовлетворяющее этому условию.
- При соединении ( JOIN ) двух отношений по некоторому условию образуется результирующее отношение, кортежи которого производятся путем объединения кортежей первого и второго отношений и удовлетворяют этому условию.
- У операции реляционного деления ( DIVIDE BY ) два операнда – бинарное и унарное отношения. Результирующее отношение состоит из унарных кортежей, включающих значения первого атрибута кортежей первого операнда таких, что множество значений второго атрибута (при фиксированном значении первого атрибута) включает множество значений второго операнда.
- Операция переименования ( RENAME ) производит отношение, тело которого совпадает с телом операнда, но имена атрибутов изменены.
- Операция присваивания ( := ) позволяет сохранить результат вычисления реляционного выражения в существующем отношении БД.
ru/2010/edi»>При выполнении проекции ( PROJECT ) отношения на заданное подмножество множества его атрибутов производится отношение, кортежи которого являются соответствующими подмножествами кортежей отношения-операнда. 
Поскольку результатом любой реляционной операции (кроме операции присваивания, которая не вырабатывает значения) является некое отношение, можно образовывать реляционные выражения, в которых вместо отношения-операнда некоторой реляционной операции находится вложенное реляционное выражение. В построении реляционного выражения могут участвовать все реляционные операции, кроме операции присваивания. Вычислительная интерпретация реляционного выражения диктуется установленными приоритетами операций:
RENAME >= WHERE = PROJECT >= TIMES = JOIN = INTERSECT = DIVIDE BY >= UNION = MINUS
В другой форме приоритеты операций показаны на рис. 3.1. Вычисление выражения производится слева направо с учетом приоритетов операций и скобок.
Рис. 3.1. Таблица приоритетов операций традиционной реляционной алгебры
Замкнутость реляционной алгебры и операция переименования
Как мы отмечали в предыдущей лекции, каждое значение-отношение характеризуется заголовком (или схемой) и телом (или множеством кортежей). Поэтому, если нам действительно нужна алгебра, операции которой замкнуты относительно понятия отношения, то каждая операция должна производить отношение в полном смысле, т. е. оно должно обладать и телом, и заголовком. Только в этом случае можно будет строить вложенные выражения.
Заголовок отношения представляет собой множество пар <имя-атрибута, имя-домена>. Если посмотреть на общий обзор реляционных операций, приведенный в предыдущем подразделе, то видно, что домены атрибутов результирующего отношения однозначно определяются доменами отношений-операндов.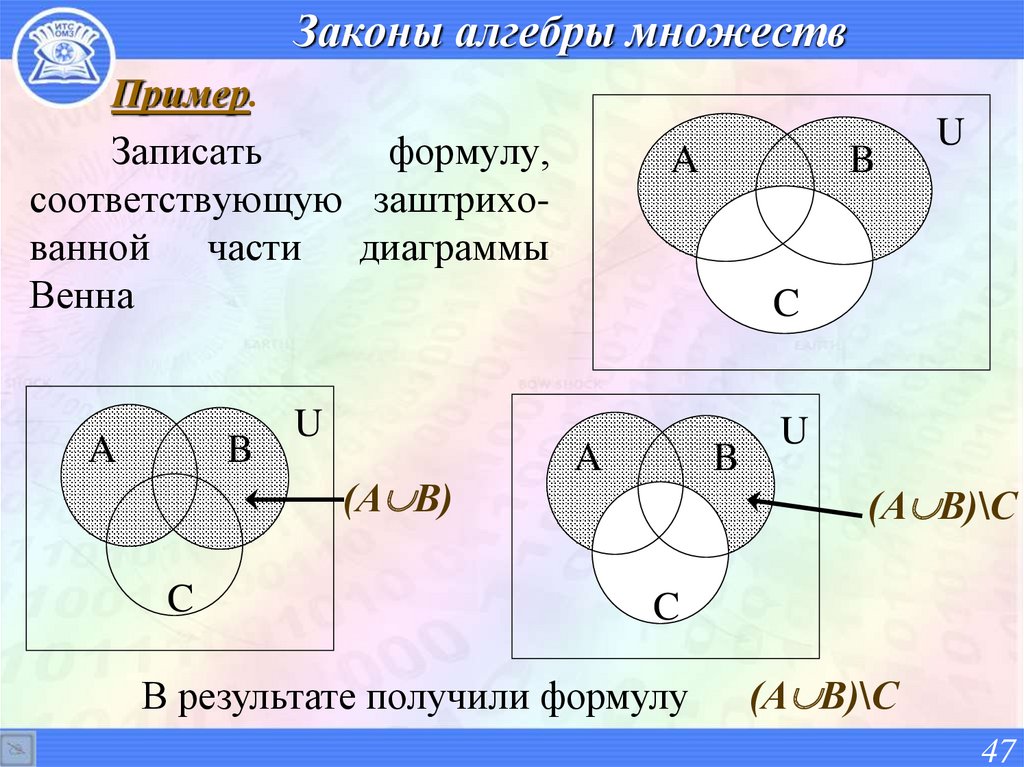
Однако с именами атрибутов результата не всегда все так просто.
Например, представим себе, что у отношений-операндов операции декартова произведения имеются одноименные атрибуты с одинаковыми доменами. Каким был бы заголовок результирующего отношения? Поскольку это множество, в нем не должны содержаться одинаковые элементы. Но и потерять атрибут в результате недопустимо. А это значит, что в таком случае вообще невозможно корректно выполнить операцию декартова произведения.
Аналогичные проблемы могут возникать и в случаях других двуместных операций. Для разрешения проблем в число операций реляционной алгебры вводится операция переименования. Ее следует применять в том случае, когда возникает конфликт именования атрибутов в отношениях-операндах одной реляционной операции. Тогда к одному из операндов сначала применяется операция переименования, а затем основная операция выполняется уже без всяких проблем.
Более строго мы определим операцию переименования в следующей лекции, а пока лишь заметим, что результатом этой операции является отношение, совпадающее во всем с отношением-операндом, кроме того, что имя указанного атрибута изменено на заданное имя.
В дальнейшем изложении мы будем предполагать применение операции переименования во всех конфликтных ситуациях.
Дальше >>
< Лекция 10 || Лекция 3: 12345
Элементы теории множеств | Виктор Осипов
Что же такое множество? Как таковое, данное понятие не имеет определения. Его можно интерпретировать как совокупность объектов определенного свойства, природы. Например, множество точек на плоскости, множество равных геометрических фигур и тд.
Множество состоит из элементов. Само множество принято обозначать заглавной латинской буквой (А, B, C и тд.), а элементы – строчными латинскими буквами (а, b, c и тд).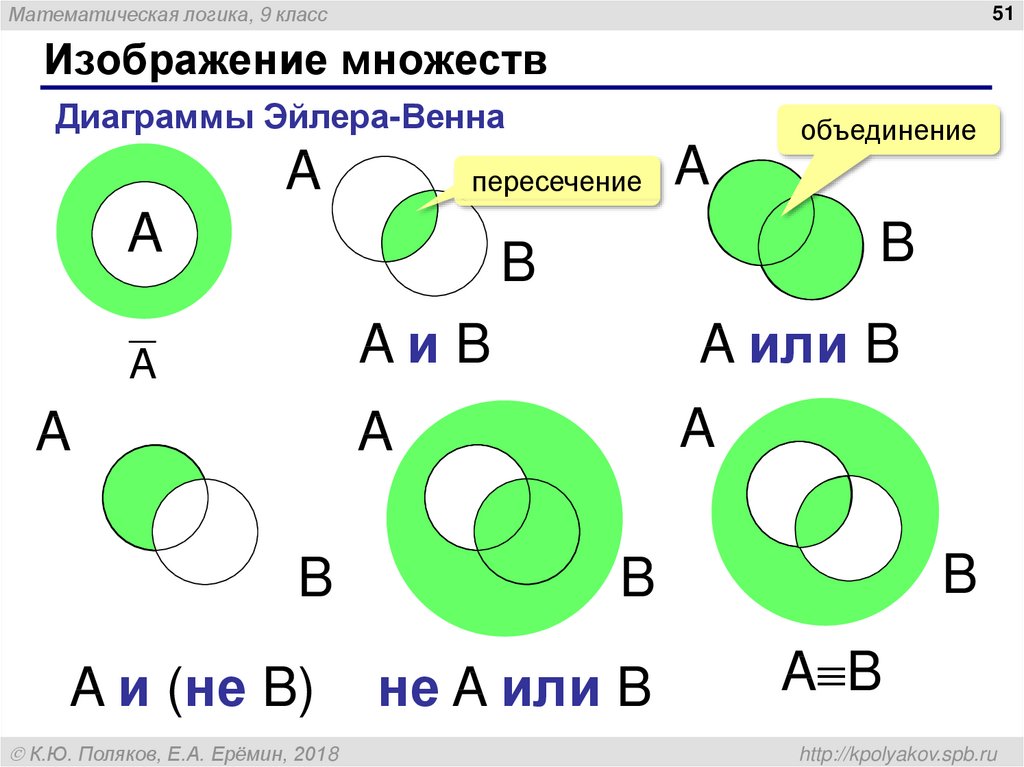
Если элемент входит в какое-либо множество (или принадлежит) , то используется следующий знак: $$\in $$
Например, элемент x принадлежит множеству A, на математическом языке будет выглядеть как: $$x\in A$$
Если же элемент не входит в множество, то используется знак ∉, например элемент x не принадлежит множеству A: $$x\notin A$$
В математике используются следующие числовые множества:
N – множество натуральных чисел
Z – множество целых чисел
Q – множество рациональных чисел
R – множество действительных чисел
K ( или С) – множество комплексных чисел
Если множество не содержит никаких элементов, то его обозначают как пустое множество: ∅
Иногда множество можно записать с помощью перечисления элементов, в него входящих. В таком случае, элементы берутся в фигурные скобки, например: A={1;2;3}. В данном случае мы указали множество А, состоящее из элементов 1, 2 и 3.
Если же в множестве используется перечисление всех чисел с отрезка или промежутка, то используются квадратные и круглые скобки, например, множество чисел на отрезке от 1 до 4 будет выглядеть A=[1;4]
Иногда невозможно задать все элементы множества в силу их бесконечности, тогда в фигурных скобках указывается характеристика этих элементов: A={x ,x<2}.
То есть мы задали множество A, состоящее из действительных чисел, каждое их которых меньше двух.
Если два множества состоят из одинаковых элементов, то можно говорить о равенстве множеств и обозначается это c знака равенства: A = B. Например, если множество A = {1; 2; 3} и множество B = {1; 2 ;3 }, тогда можно говорить о равенстве множеств A и B.
При этом следует учитывать, что если есть расхождение хотя в одном элементе, то равенства уже не будет. Так, если множество A = {1; 2; 3} и множество B = {1; 2; 3; 4}, то A ≠ B.
При этом вводится понятие подмножества и принадлежности. Так, если все элементы одного множества входят в элементы другого множества, то первое является подмножеством второго множества. В приведенном примере множество A является подмножеством множества B, и записывается это (множество A принадлежит множеству B или же множество B включает множество А).
Знак ⊂ называется знаком включения.
Основными операциями над множествами являются операции пересечения и объединения.
Пусть даны множества A и B. Тогда множество C будет пересечением множеств A и B в том случае, если оно состоит только из элементов, которые входят одновременно и в множество А и в множество B. Знак пересечения выглядит как: ⋂. Например:
А={1;2;3;4} и B={1;3;5}. Тогда A⋂B=C={1;3}
Число 1 и 3 содержится и в множестве A и в множестве B, именно поэтому они попадают в множество C.
Рисунок 1. Геометрическая интерпретация пересечения множеств A и B.
На рисунке 1 показано, как может быть изображено пересечение множеств. Заштрихованная область и есть результатом действия пересечения.
Кстати, пересечение множеств, математически задается как знак системы ( { ). Но об этом позже
Надо понимать, что если в двух множествах нет одинаковых элементов, то результатом их пересечения будет пустое множество:
A={1;2;3;4} и B={11;30;50}.
Тогда A⋂B=C=∅
Замечу, что данное действие подходит как для трех множеств, четырех и более. Смысл остается в нахождении всех элементов, которые принадлежали бы каждому из начальных множеств.
Пусть даны множества A и B. Тогда множество C будет объединением множеств A и B в том случае, если оно состоит из всех элементов, которые входят и в множество А, и в множество B. Знак пересечения выглядит как: ∪ . Например:
A={1;2;3;4} и B={1;3;5}. Тогда A⋂B=C={1;2;3;4;5}
При этом не нужно перечислять дважды (трижды и тд) элемент, если он входит одновременно в оба подмножества, то есть 1 и 3 в нашем примере записывается один раз.
Рисунок 2. Геометрическая интерпретация объединения множеств A и B.
Аналогично с пересечением, данные правила действуют для объединения двух, трех и более множеств.
Вообще, частенько понятие множества и операций над ними используется при решении уравнения и неравенств, и именно здесь бывают обидные и распространенные ошибки на ЕГЭ, когда при правильном решении задания, конечная фаза нахождения объединения или пересечения корней (решений) делалась неправильно.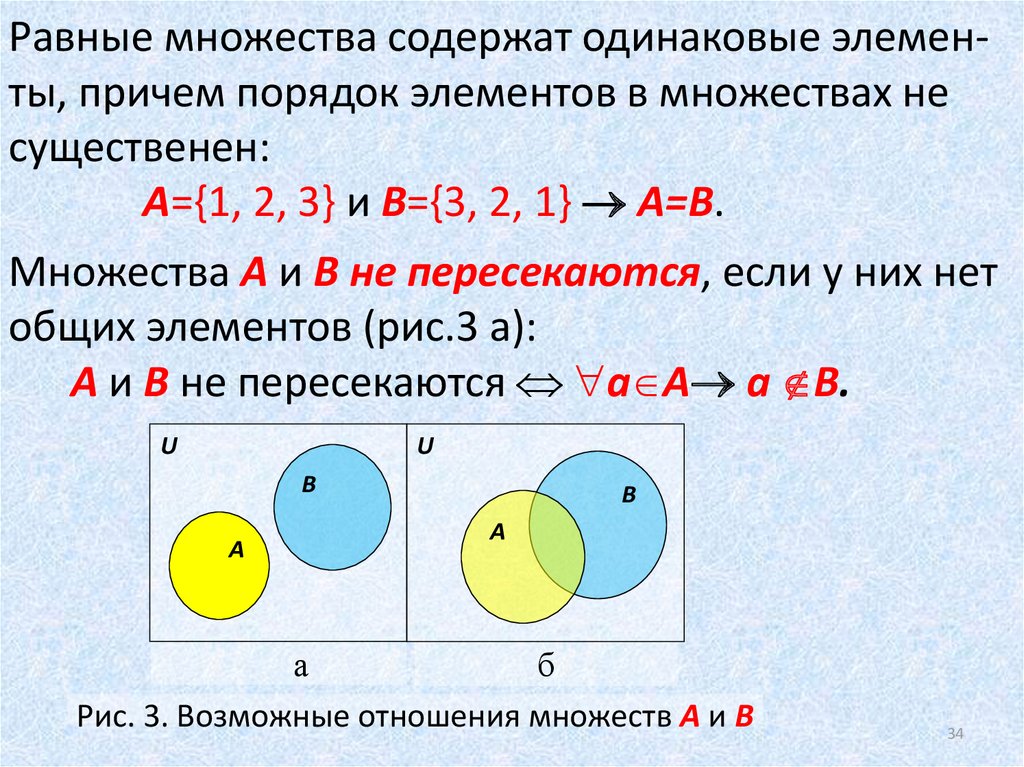
Так же следует указать еще некоторые математические символы, используемые для решения заданий:
Знак следствия: ⇒. Если вам даны два утверждения а и b, и из истинности a следует истинность b, то используем этот знак. Часто встречается при доказательствах в геометрии. Например, в треугольнике ABC два угла при основании равны ⇒ данный треугольник равнобедренный.
Знак равносильности: ⇔. Если два высказывания a и b, так что из a следует b и наоборот, то используют этот знак. Часто используется при решении уравнений. Например: 2x = 6 ⇔ x = 3
Знак существования: ∃. Как следует из названия, данным знаком можно заменить слово “существует”.
Знак всеобщности: ∀. Ну а этим знаком можно заменить слова “для любого”, “всякий”.
Например, если мы возьмем множество целых чисел B без нуля (x≠0), и множество обратных чисел A, то мы можем записать ∀ x ∈ B ∃ y ∈ A, что означает для всякого числа x, которое принадлежит множеству B, найдется число y, принадлежащее множеству A.
Но это лирика, и крайние два вам встретятся ближе к матанализу.
У крайних символов, естественно, существует собственное название с использованием такого страшного слова, как квантор, но для понимания школьной математики вам оно не нужно.
std :: set — cppreference.com
Библиотека контейнеров
Std :: Set
. > набор классов; | (1) | |
| (2) | (начиная с С++ 17) | |
std::set — это ассоциативный контейнер, содержащий отсортированный набор уникальных объектов типа 
Операции поиска, удаления и вставки имеют логарифмическую сложность. Наборы обычно реализуются в виде красно-черных деревьев.
Везде, где стандартная библиотека использует требования сравнения, уникальность определяется с помощью отношения эквивалентности. Говоря неточно, два объекта a и b считаются эквивалентными, если ни один из них сравнивается меньше, чем другой: !comp(a, b) && !comp(b, a).
std::set соответствует требованиям Container, AllocatorAwareContainer, AssociativeContainer и ReversibleContainer.
|
[править] Параметры шаблона
[править] Типы элементов
| Тип элементов | Определение | ||||
key_type | Ключ [править] | ||||
значение_тип | Ключ [править] | ||||
размер_тип | Беззнаковый целочисленный тип (обычно std::size_t)[править] | ||||
тип_различия | Целочисленный тип со знаком (обычно std::ptrdiff_t) [править] | ||||
key_compare | Сравнить [править] | ||||
сравнение значений | Сравнить [править] | ||||
allocator_type | Распределитель [править] | ||||
номер | value_type& [править] | ||||
const_reference | const value_type&[править] | ||||
указатель |
| ||||
константный_указатель |
| ||||
итератор | Константа LegacyBidirectionalIterator to value_type [править] | ||||
const_iterator | LegacyBidirectionalIterator в const value_type[править] | ||||
реверс_итератор | std::reverse_iterator<итератор>[править] | ||||
const_reverse_iterator | std::reverse_iterator | ||||
node_type (начиная с C++17) | специализация дескриптора узла, представляющая узел-контейнер [править] | ||||
insert_return_type (начиная с C++17) | Тип, описывающий результат вставки node_type , специализация template |
[править] Функции-члены
(конструктор) | создает набор (открытая функция-член) [править] |
(деструктор) | уничтожает набор (открытая функция-член) [править] |
оператор= | присваивает значения контейнеру (открытая функция-член) [править] |
get_allocator | возвращает связанный распределитель (открытая функция-член) [править] |
Итераторы | |
начало cначало (С++ 11) | возвращает итератор в начало (открытая функция-член) [править] |
конец конец (С++ 11) | возвращает итератор в конец (открытая функция-член) [править] |
rbegincrbegin (С++ 11) | возвращает обратный итератор в начало (открытая функция-член) [править] |
rendcrend (С++ 11) | возвращает обратный итератор в конец (открытая функция-член) [править] |
Вместимость | |
| проверяет, пуст ли контейнер (открытая функция-член) [править] | |
| возвращает количество элементов (открытая функция-член) [править] | |
макс_размер | возвращает максимально возможное количество элементов (открытая функция-член) [править] |
Модификаторы | |
| очищает содержимое (открытая функция-член) [править] | |
вставка | вставляет элементы или узлы (начиная с C++17) (открытая функция-член) [править] |
вставить (С++ 11) | создает элемент на месте (открытая функция-член) [править] |
emplace_hint (С++ 11) | создает элементы на месте, используя подсказку (открытая функция-член) [править] |
| стирает элементы (открытая функция-член) [править] | |
| меняет содержимое местами (открытая функция-член) [править] | |
экстракт (С++ 17) | извлекает узлы из контейнера (открытая функция-член) [править] |
слияние (С++ 17) | объединяет узлы из другого контейнера (общедоступная функция-член) [править] |
Поиск | |
| возвращает количество элементов, соответствующих определенному ключу (открытая функция-член) [править] | |
| находит элемент с определенным ключом (открытая функция-член) [править] | |
содержит (C++20) | проверяет, содержит ли контейнер элемент с определенным ключом (открытая функция-член) [править] |
равный_диапазон | возвращает диапазон элементов, соответствующих определенному ключу (открытая функция-член) [править] |
нижняя граница | возвращает итератор к первому элементу не менее , чем заданный ключ (открытая функция-член) [править] |
верхняя граница | возвращает итератор к первому элементу большему , чем заданный ключ (открытая функция-член) [править] |
Наблюдатели | |
key_comp | возвращает функцию сравнения ключей (открытая функция-член) [править] |
значение_комп | возвращает функцию, которая сравнивает ключи в объектах типа value_type (открытая функция-член) [править] |
[править] Функции, не являющиеся членами
оператор==оператор!=оператор<оператор<=оператор>оператор>=оператор<=> ++20)(удалено в C++20)(удалено в C++20)(удалено в C++20)(C++20) | лексикографически сравнивает значения в наборе (шаблон функции) [править] |
станд::своп(стд::набор) | специализируется на алгоритме std::swap (шаблон функции) [править] |
erase_if(std::set) (С++ 20) | Удаляет все элементы, удовлетворяющие определенным критериям (шаблон функции) [править] |
[править] Руководства по дедукции (начиная с C++17)
[править] Примечания
Типы-члены iterator и const_iterator могут быть псевдонимами одного и того же типа.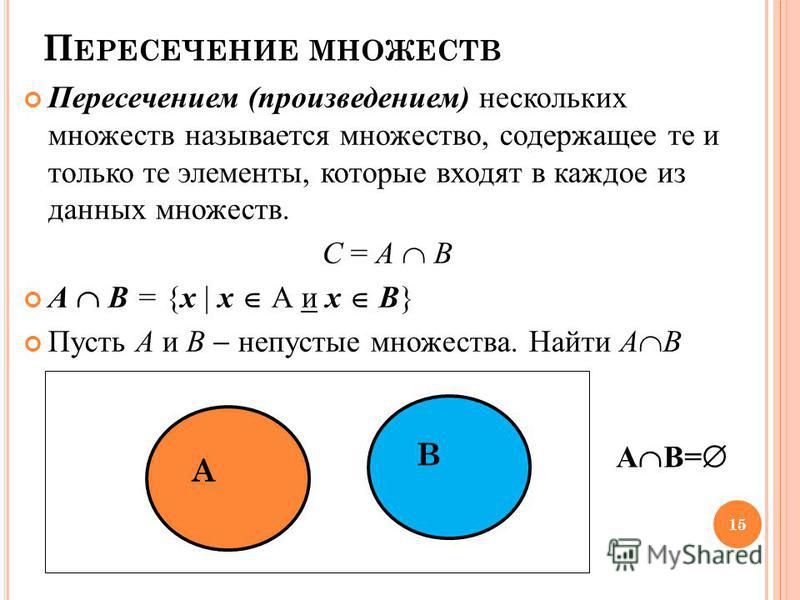
Это означает, что определение пары перегруженных функций с использованием двух типов в качестве типов параметров может нарушить правило единого определения. Поскольку iterator можно преобразовать в const_iterator , вместо этого будет работать одна функция с const_iterator в качестве типа параметра.
[править] Пример
[править] Отчеты о дефектах
Следующие отчеты о дефектах, изменяющих поведение, были применены задним числом к ранее опубликованным стандартам C++.
| ДР | Применяется к | Поведение после публикации | Правильное поведение |
|---|---|---|---|
| LWG 103 | С++ 98 | Итераторпозволяет изменять ключи | итератор сделан постоянным |
| LWG 230 | С++ 98 | Ключ не должен быть CopyConstructible (ключ типа Ключ может быть не создан) | Ключ также требуется, чтобы был CopyConstructible |
STD :: SET — CPPREEFERENCEAR.
comБиблиотека контейнеров
Std :: SET
Template <
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
