Подмножество | это… Что такое Подмножество?
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
На диаграмме кругов Эйлера видно, что является подмножеством , а является надмножеством
Подмно́жество в теории множеств — это понятие части множества.
Содержание
|
Определение
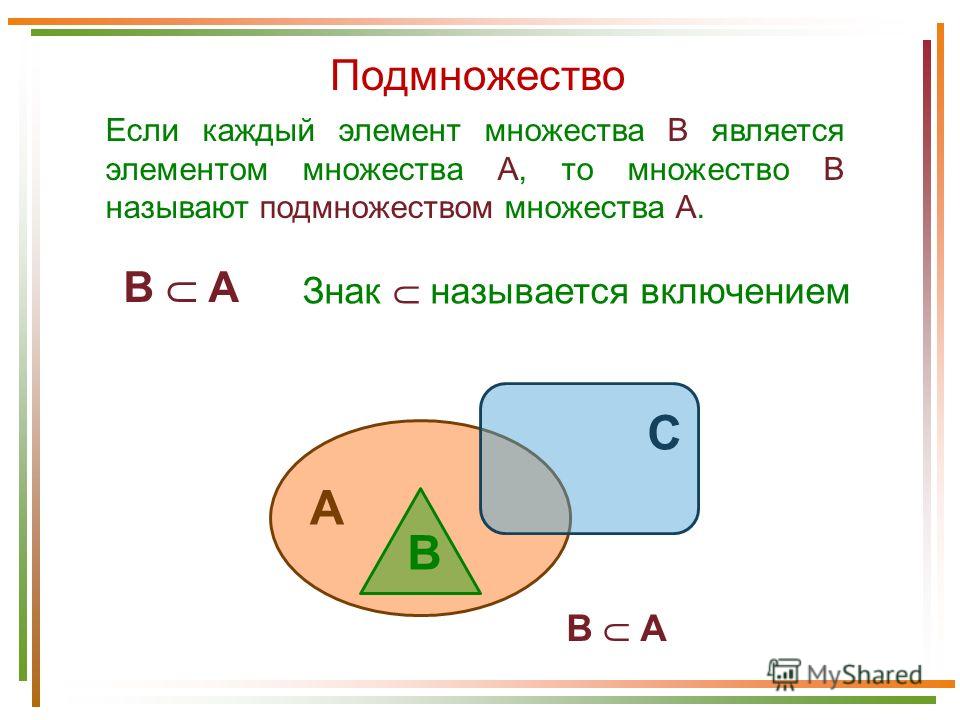
Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:
Формальное определение:
Множество называется надмно́жеством множества , если — подмножество .
Существует два символических обозначения для подмножеств:
| « является подмножеством » обозначается | « является собственным подмножеством » обозначается | Примечание |
|---|---|---|
| Внешний вид символа намекает, что если , то . | ||
| Для понятия «подмножество» используется более простой символ, так как это понятие является более «фундаментальным». |
К сожалению, обе системы обозначений используют символ в разных смыслах, что может привести к путанице. В данной статье мы будем использовать последнюю систему обозначений.
То, что называется надмножеством , часто записывают .
Множество всех подмножеств множества обозначается и называется множеством-степенью.
Собственное подмножество
Любое множество является своим подмножеством.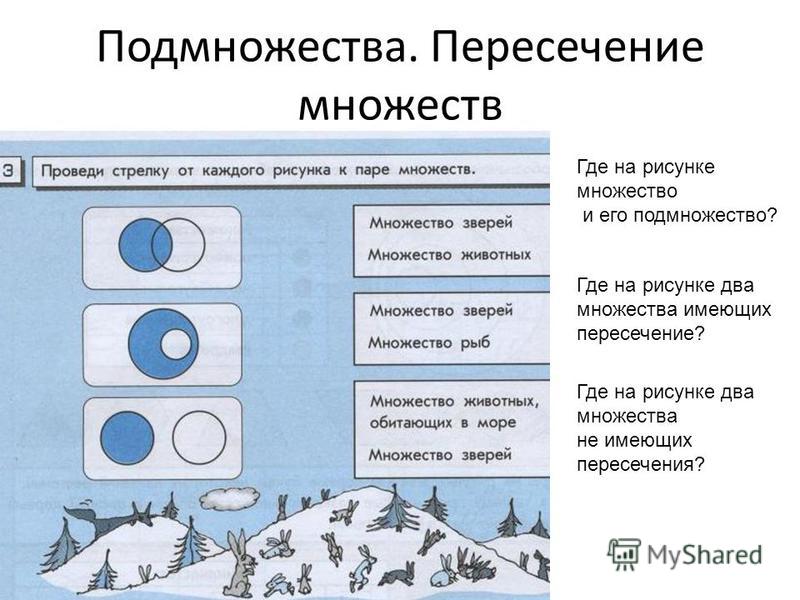
- Множество является собственным подмножеством множества , если и .
Пустое множество является подмножеством любого множества. Если мы вдобавок хотим исключить из рассмотрения пустое множество, мы пользуемся понятием нетривиа́льного подмножества, которое определяется так:
- Множество является нетривиальным подмножеством множества , если является собственным подмножеством и .
Примеры
- Множества являются подмножествами множества
- Множества являются подмножествами множества
- Пусть , тогда .
- Пусть . Тогда .
Свойства
Отношение подмножества обладает целым рядом свойств[1].
- Отношение подмножества является отношением частичного порядка:
- Отношение подмножества рефлексивно:
- Отношение подмножества антисимметрично:
- Отношение подмножества транзитивно:
- Отношение подмножества рефлексивно:
- Пустое множество является подмножеством любого другого, поэтому оно является наименьшим множеством относительно отношения подмножества:
- Для любых двух множеств и следующие утверждения эквивалентны:
Подмножества конечных множеств
Если исходное множество конечно, то у него существует конечное количество подмножеств. А именно, у -элементного множества существует подмножеств (включая пустое). Чтобы убедиться в этом, достаточно заметить, что каждый элемент может либо входить, либо не входить в подмножество, а значит, общее количество подмножеств будет -кратным произведением двоек. Если же рассматривать только подмножества -элементного множества из элементов, то их количество выражается биномиальным коэффициентом . Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать способами, второй способом, и так далее, и, наконец, -й элемент можно выбрать способом. Таким образом мы получим последовательность из элементов, и ровно таким последовательностям соответствует одно подмножество. Значит, всего найдется таких подмножеств.
А именно, у -элементного множества существует подмножеств (включая пустое). Чтобы убедиться в этом, достаточно заметить, что каждый элемент может либо входить, либо не входить в подмножество, а значит, общее количество подмножеств будет -кратным произведением двоек. Если же рассматривать только подмножества -элементного множества из элементов, то их количество выражается биномиальным коэффициентом . Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать способами, второй способом, и так далее, и, наконец, -й элемент можно выбрать способом. Таким образом мы получим последовательность из элементов, и ровно таким последовательностям соответствует одно подмножество. Значит, всего найдется таких подмножеств.
Примечания
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т.
 1. — С. 65. — 672 с. — ISBN 5-482-00445-7
1. — С. 65. — 672 с. — ISBN 5-482-00445-7
См. также
- Булеан
Ссылки
Определение и значение подмножества — Merriam-Webster
подмножество ˈsəb-ˌset
1
: множество, каждый элемент которого является элементом включающего множества
2
: подразделение, часть
подмножество нашего сообщества
Примеры предложений
Набор {1,2,3} является подмножеством набора {1,2,3,4,5}. Эти побочные эффекты наблюдались только у небольшой группы из пациентов, участвовавших в исследовании, из
Эти побочные эффекты наблюдались только у небольшой группы из пациентов, участвовавших в исследовании, из
Недавние примеры в Интернете
С тех пор, как был принят Закон о лекарствах для лечения редких заболеваний, сотрудники FDA регулярно предоставляли компаниям эксклюзивные права на лекарства для лечения редких заболеваний, предназначенные для лечения подмножества пациентов, таких как педиатрия.
— Сара Джейн Триббл, USA TODAY , 19 февраля 2023 г.
Доброкачественный фасцикуляционный синдром Хотя у большинства людей фасцикуляции возникают лишь изредка,Подгруппа 0021 постоянно испытывает подергивания мышц — редкое состояние, известное как синдром доброкачественной фасцикуляции или BFS.
 — Кэтрин Фолдерс, ABC News , 24 января 2023 г.
Исследователи обнаружили, что у подмножества было стойкое воспаление.
— Стефани Сазерленд, Scientific American , 14 февраля 2023 г.
Кроме того, подмножество населения страдают заболеваниями крови, требующими многократных переливаний крови в течение года.
— Уильям А. Хазелтин, Forbes , 10 февраля 2023 г.
Узнать больше
— Кэтрин Фолдерс, ABC News , 24 января 2023 г.
Исследователи обнаружили, что у подмножества было стойкое воспаление.
— Стефани Сазерленд, Scientific American , 14 февраля 2023 г.
Кроме того, подмножество населения страдают заболеваниями крови, требующими многократных переливаний крови в течение года.
— Уильям А. Хазелтин, Forbes , 10 февраля 2023 г.
Узнать больше Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «подмножество». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Первое известное использование
1881, в значении, определенном в смысле 1
Путешественник во времени
Первое известное использование подмножество было в 1881 году
Посмотреть другие слова того же года лежачий
подмножество
субсексуальный
Посмотреть другие записи поблизости
Процитировать эту запись0003
«Подмножество.» Словарь Merriam-Webster.com , Merriam-Webster, https://www. merriam-webster.com/dictionary/subset. По состоянию на 25 февраля 2023 г.
существительное
merriam-webster.com/dictionary/subset. По состоянию на 25 февраля 2023 г.
существительное
подмножество ˈsəb-ˌset
: математический набор, являющийся частью другого математического набора
множество четных чисел является подмножеством множества всех чисел для говорящих на арабском языке
Britannica.com: статья в энциклопедии о подмножество
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
воспитывать
 Определения и примеры »
Определения и примеры »Получайте ежедневно по электронной почте Слово дня!
Модные слова
- Какой из этих предметов назван в честь смертоносного оружия?
- хенли рубашка Каблук-шпилька
- Броги шляпа Федора
Вы знаете, как это выглядит… но как это называется?
ПРОЙДИТЕ ТЕСТ
Сможете ли вы составить 12 слов из 7 букв?
ИГРАТЬ
Наборы — Подмножества | Brilliant Math & Science Wiki
Карли Мур, Праншу Габа, Махиндра Джейн, и
способствовал
Содержимое
- Правильные подмножества
- Вычисление количества подмножеств в наборе
- Также см
\(A\) является правильным подмножеством \(B\), если \(A\) является подмножеством \(B\) и \(A\) не равно \(B\). Это обозначается \( A \subset B \). Пустое множество \(\emptyset\) является правильным подмножеством каждого непустого множества.
Это обозначается \( A \subset B \). Пустое множество \(\emptyset\) является правильным подмножеством каждого непустого множества.
Подмножество по сравнению с правильным подмножеством:
Возьмем следующие множества: \(A = \{a,b,c,d,e\}\), \(B = \{a,b,c,d,e\}\) и \(C = \{а,г,е\}\).
- \( A \subseteq B \), потому что каждый элемент в \(A\) также находится в \(B\).
- \( B \subseteq A \), потому что каждый элемент в \(B\) также находится в \(A\).
- \( C \subseteq A \) и \( C \subseteq B \), потому что каждый элемент в \(C\) также находится в \(A\) и \(B\).
- \( C \subset A \) и \( C \subset B \), потому что все элементы в \(C\) находятся в \(A\) и \(B\), но \(C\) не равны на \(A\) или \(B\).
Если \(A\) не является подмножеством \(B\), то \(A \не\подмножество B\).
\[\{1,2,3\}\] \[\{6,5,2,1\}\] \[\{2\}\] \[\{1,2,4,5\}\]
\(A = \{6,2,4,1,5\}\).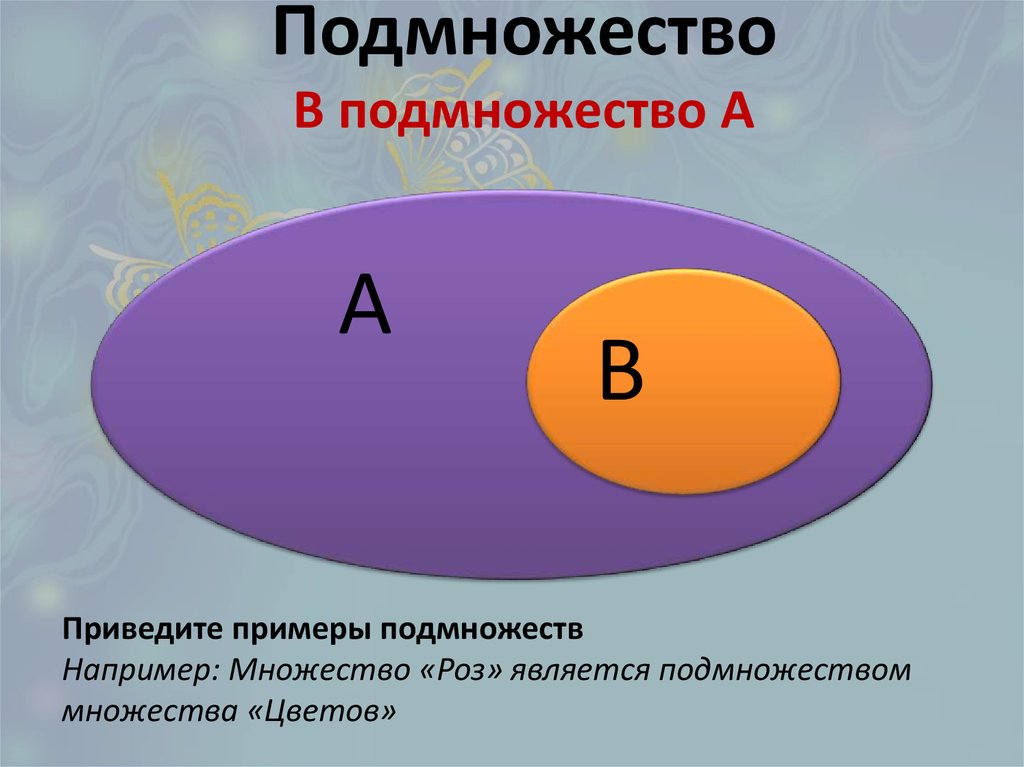

 1. — С. 65. — 672 с. — ISBN 5-482-00445-7
1. — С. 65. — 672 с. — ISBN 5-482-00445-7