Модуль 2 равен: Чему равен модуль числа –2,3 ?

Физические основы механики

Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.

Средняя скорость за время от t₁ до t₂ равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:

Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <…> , как это сделано выше.

Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:

Действительно

Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю.

По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t₂ – t₁ к нулю. Сделаем переобозначения: t₁ = t и t₂ = t + и перепишем верхнее соотношение в виде:

Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю

Рис. 2.5. К определению мгновенной скорости.

В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости

есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде

Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:

По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.

Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.

Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения , , или , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки

Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени

С другой стороны, разложение по базису вектора скорости имеет вид

опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть

Модуль вектора скорости равен

Получим ещё одно, важное, выражение для модуля вектора скорости.

Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому

и в пределе (>0)

Иными словами, модуль скорости — это производная пройденного пути по времени.

Окончательно имеем:

Средний модуль вектора скорости, определяется следующим образом:

Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:

Здесь s(t₁, t₂) — путь за время от t₁ до t₂ и, соответственно, s(t₀, t₂) — путь за время от t₀ до t₂ и s(t₀

, t₂) — путь за время от t₀ до t₁.

Средний вектор скорости или просто средняя скорость, как указано выше, равен

Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.

Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.

Рис. 2.6. Определение мгновенной и средней скорости тела

Модуль скорости в данный момент времени

будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается

Противоположные числа. Модуль числа 6 класс онлайн-подготовка на Ростелеком Лицей

Противоположные числа. Модуль числа.

Построим координатную прямую. Понадобится начало отсчета, положительное направление, единичный отрезок.

На координатной прямой отметим точки с координатами 5 и -5, они одинаково удалены от точки О и находятся по разные стороны от неё. Чтобы попасть из точки О в эти точки, надо пройти одинаковые расстояния, но в противоположных направлениях. Поэтому числа 5 и -5 называются противоположными числами, т. е. число 5 противоположно числу -5, а число -5 противоположно числу 5.

 

 

Два числа, отличающихся друг от друга только знаками, называют противоположными числами.

Например, противоположными числами будут 8 и -8; 2,6 и -2,6.

Для каждого числа есть только одно противоположное ему число.

Число 0 противоположно самому себе.

Число, противоположное числу а, обозначают -а.

Если а = -7,8, то -а = 7,8. Если а = 8,3, то -а = -8,3. Если а = 0, то -а = 0. Запись «-(-15)» означает число, противоположное числу -15, то есть, -(-15)=15.

-(-а)=а.

Пример 1. Отметим на координатной прямой точки А(4), В(-5). Найдем расстояние от начала отсчета до каждой из точки.

 

 

точка	координата	отрезок	расстояние (в единичных отрезках)
А	4	ОА	4
В	-5	ОВ	5

Для такого расстояния придумано специальное название – модуль.

Модулем числа a называют расстояние (в единичных отрезках) от начала отсчета до точки А(а).

Пишут: |3|=3;|-7|=7. Читают: «Модуль числа 3 равен 3. Модуль числа -7 равен 7».

Модуль числа 0 равен 0, т. к. точка с координатой 0 совпадает с началом отсчета О. т. е. удалена от нее на 0 единичных отрезков.

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Другими словами, модуль положительного числа равен самому числу; модуль отрицательного числа равен положительному числу. Модуль нуля равен нулю.

Противоположные числа имеют равные модули: |-а| = а.

Например, |-7|=7; |0|=0; |- 47 |=47.

Натуральные числа, противоположные им числа и нуль называют целыми числами.

Объединение множества натуральных чисел, множества чисел, им противоположных, и нуля, образует

множество целых чисел.

Множество целых чисел обозначают заглавной латинской буквой Z.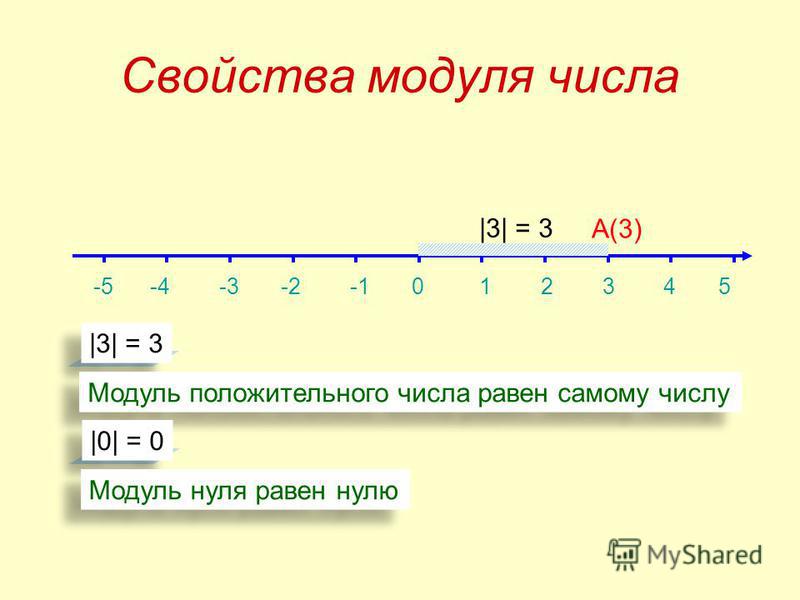

5 ∈ Z ; -3 ∈ Z; 0 ∈ Z.

Числа 47∉Z и -10,7 ∉ Z, то есть не являются целыми числами. Множество натуральных чисел является подмножеством целых чисел.

Пример 2. Найдем значение выражений:

|-8| — |-5|= 8-5 = 3

|-2,3| + |3,7| = 2,3+3,7 = 6

Что такое 7 мод 2? (7 по модулю 2)

Вам нужно знать, что означает 7 по модулю 2? Может надо посчитать? В этом небольшом руководстве мы покажем вам, как точно вычислить мод числа. Вы также можете увидеть, что это называется модулем или модулем.

Хотите быстро научиться или показать учащимся, как считать 7 по модулю 2? Включи это очень быстрое и веселое видео прямо сейчас!

Так что же такое модуль или модуль? Проще говоря, по модулю — это математическая операция нахождения остатка при делении двух чисел. Если вы спрашиваете «что такое 7 мод 2?» тогда вам действительно нужно знать: «Каков остаток при делении 7 на 2?».

Существует множество причин, по которым вы хотели бы использовать модуль по модулю, в том числе проверка того, является ли число четным или нечетным, подсчет чего-либо определенное количество раз, и даже обычные часы в вашем доме будут использовать модуль для определения времени. .

Давайте рассмотрим два метода вычисления 7 по модулю 2. Мы назовем их методом по модулю и методом по модулю.

Примечание: первое число (7) называется Дивидендом, а второе число (2) называется Делителем. Когда вы делите дивиденд на делитель, ответ, который у вас остается, это частное. Это частное имеет целую числовую часть (называемую целым) и десятичную часть, которая называется дробной.

Метод по модулю

Сначала нужно разделить дивиденд на делитель:

7 / 2 =  3,50

Затем мы берем целую часть частного (3) и умножаем ее на делитель (2):

3 x 2 = 6

И, наконец, мы берем ответ на втором шаге и вычитаем его из Делимое для получения ответа на 7 по модулю 2:

7 — 6 = 1

Как видите, ответ на 7 по модулю 2 равен 1 .

Модульный метод

Модульный метод требует, чтобы мы сначала выяснили, каково наибольшее общее кратное Делителя (2), которое меньше или равно Делимому (7).

Мы видим, что числа, кратные 2, равны 0, 2, 4, 6 и т. д. Наибольшее кратное, меньшее или равное 7, равно 6.

Итак, последний шаг в методе модуля здесь — вычесть делитель наибольшего кратного из Дивиденда и ответьте на вопрос «чему равно 7 по модулю 2?»:

7 — 6 = 1

Как мы видим, это тот же ответ, что и метод по модулю, и ответ равен 1 .

Надеюсь, вы поняли это краткое, но увлекательное путешествие по модулю и модульному методу вычислений. Если вам интересно, возьмите ручку и бумагу и сделайте пару таких упражнений сами, чтобы посмотреть, действительно ли вы чему-то научились.

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Что такое 7 mod 2?

• «Что такое 7 мод 2?». VisualFractions.com . По состоянию на 24 ноября 2022 г. http://visualfractions.com/calculator/modulo/what-is-7-mod-2/.

• «Что такое 7 мод 2?». VisualFractions.com , http://visualfractions.com/calculator/modulo/what-is-7-mod-2/. По состоянию на 24 ноября 2022 г.

• Что такое 7 мод 2?. VisualFractions.com. Получено с http://visualfractions.com/calculator/modulo/what-is-7-mod-2/.

Калькулятор модуля

Хотите решать больше задач на модуль? Введите свои числа ниже и нажмите рассчитать.

Введите задачу по модулю

Следующий расчет по модулю

• Что такое 8 по модулю 2?

арифметика — запутался в XOR и сложении по модулю $2$

спросил 7 лет, 7 месяцев назад

Изменено 1 год, 4 месяца назад

Просмотрено 32к раз

$\begingroup$

Насколько я понимаю, когда вы что-то выполняете XOR, результатом является сумма двух чисел по модулю $2$.

Почему тогда $4\oplus 2 = 6$, а не $0$? $4+2=6$, $6%2$ не равно $6$. Должно быть, я что-то упускаю из того, что означает «сложение по модулю 2», но что?

100 // 4

010 // Исключающее ИЛИ против 2

110 = 6 // почему не ноль, если xor = sum mod 2?

• арифметика

$\endgroup$

0

$\begingroup$

Путаница здесь происходит из-за пропущенного слова. Правильное утверждение: «Результат операции XOR двух бит такой же, как и при добавлении этих двух бит mod 2».

Например, $(0+1)\bmod 2 = 1\bmod 2 = 1=(0\text{ XOR }1)$

и

$(1+1) \bmod 2= 2\bmod 2 = 0 = (1\текст{исключающее ИЛИ}1)$

$\endgroup$

$\begingroup$

Вы путаете операции над одним битом с операциями над байтом или словом.