ОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если у мы знаем функцию f(x) и нам нужно построить функцию f(–x) (то есть заменить все иксы в функции на противоположные), тогда нужно отразить график симметрично относительно оси Оу, т.е. все ординаты останутся неизменными, а абсциссы поменяют знак.
Например:
Четная функция при таком изменении не изменяется, т.к. это следует из определения четной функции.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если у мы знаем функцию f(x) и нам нужно построить функцию –f(x) (то есть заменить все значения функции на противоположные), тогда нужно отразить график симметрично относительно оси Ох, т.е. все абсциссы останутся неизменными, а ординаты поменяют знак.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
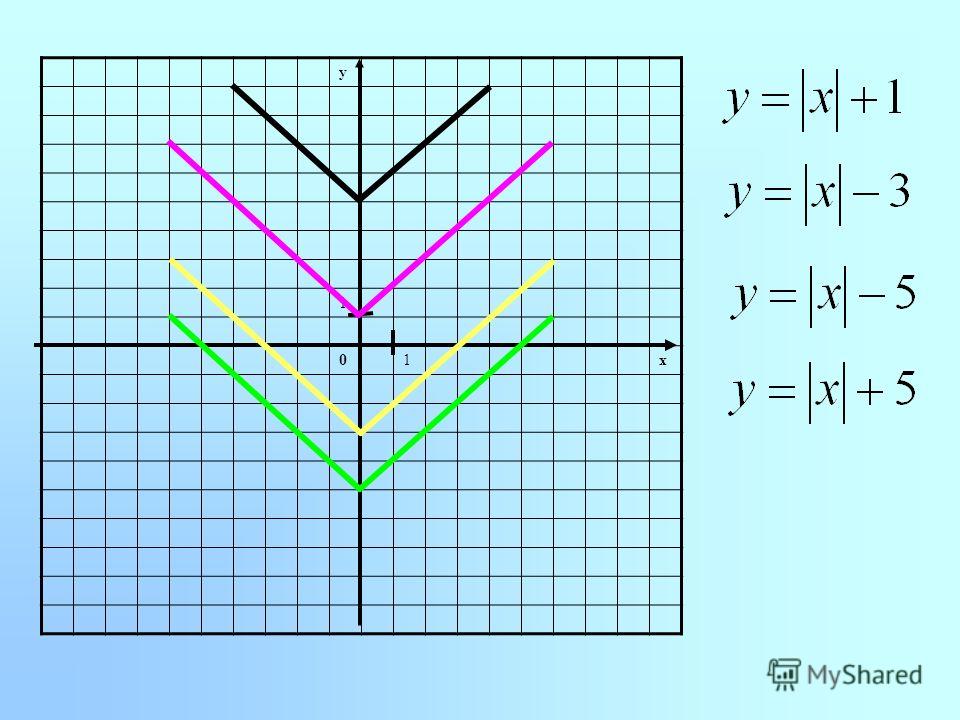
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(x)\ \pm \ a\ \)(то есть прибавить к получившимся значениям функции \(\pm\) a), тогда f(x) будет двигаться по оси Оу.
– Если нужно построить \(f(x)\ + \ a\), то функция поднимется на a единичных отрезков вверх.
– Если нужно построить \(f(x)\ –\ a\), то функция опуститься на a единичных отрезков вниз.
Например:
Функция \(y = \frac{1}{x} + 5\) будет выше функции \(y = \frac{1}{x}\) на 5 единичных отрезков, а функция \(\frac{1}{x}\ –\ 4\) ниже на 4 единичных отрезка:
ПРОИЗВЕДЕНИЕ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(\text{ax})\ \)(то есть заменяем все иксы на выражение ax), тогда функция \(f(x)\) будет «сжиматься» и «растягиваться» вдоль оси Ох.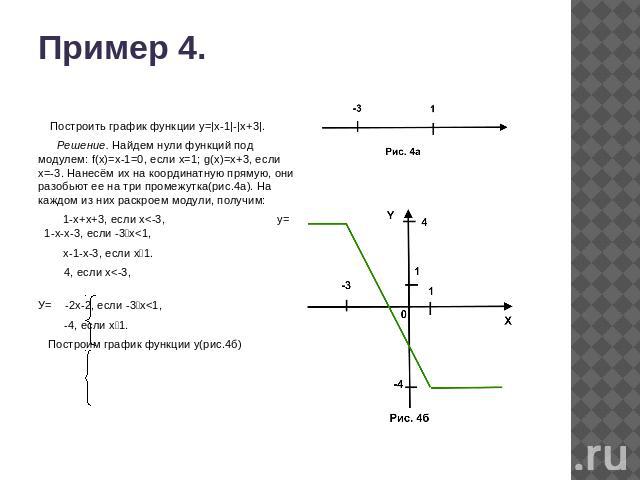
МОДУЛЬ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(f(|x|)\) (то есть заменяем все иксы на модуль икс), тогда график в области с отрицательными абсциссами стирается, а график в области с положительными абсциссами отражается относительно оси Оу. Функция становится четной.
Например:
ИЗЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
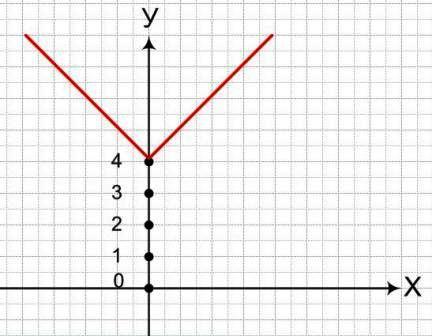
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(|f\left( x \right)|\) (то есть берем под модуль значение функции). Тогда график в области с отрицательными ординатами отражается относительно оси Ох.
Например:
Лямбда-функция в Python простыми словами / Хабр
В этой статье вы подробнее изучите анонимные функции, так же называемые «лямбда-функции». Давайте разберемся, что это такое, каков их синтаксис и как их использовать ( с примерами).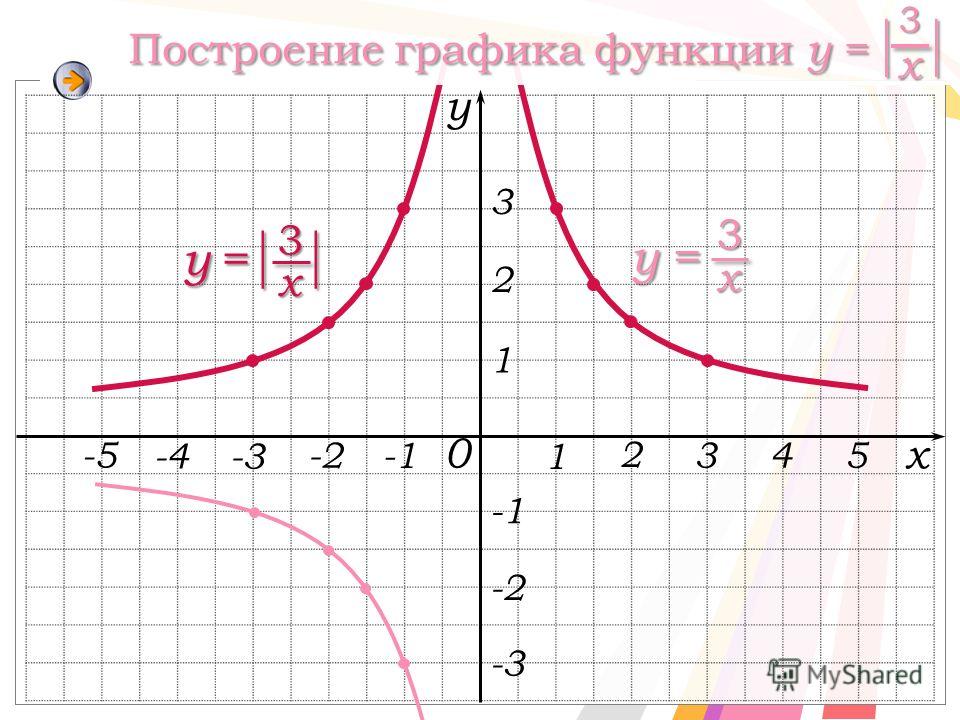
Лямбда-функции в Python являются анонимными. Это означает, что функция безымянна. Как известно, ключевое слов def используется в Python для определения обычной функции. В свою очередь, ключевое слово lambda используется для определения анонимной функции.
Лямбда-функция имеет следующий синтаксис.
Lambda аргументы: выражение
Лямбда-функции могут иметь любое количество аргументов, но у каждой может быть только одно выражение. Выражение вычисляется и возвращается. Эти функции могут быть использованы везде, где требуется объект-функция.
1.1. Пример лямбда-функции.
Ниже представлен пример лямбда-функции, удваивающей вводимое значение.
double = lambda x: x*2 print(double(5))
Вывод:
10
В вышеуказанном коде lambda x: x*2 — это лямбда-функция. Здесь x — это аргумент, а x*2 — это выражение, которое вычисляется и возвращается.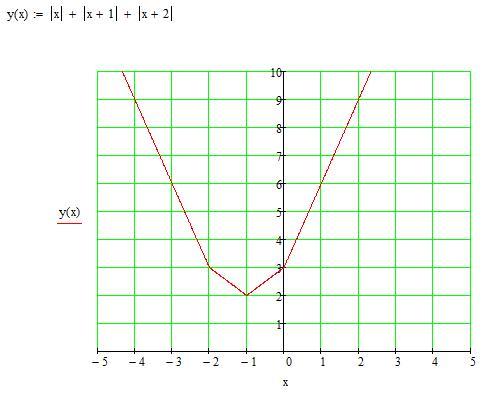
Эта функция безымянная. Она возвращает функциональный объект с идентификатором double. Сейчас мы можем считать её обычной функцией.
Инструкция:
double = lambda x: x*2
Эквивалентна:
def double(x): return x * 2
Эта функция может иметь любое количество аргументов, но вычисляет и возвращает только одно значение
Лямбда-функции применимы везде, где требуются объекты-функции
Вы должны помнить, что синтаксически лямбда-функция ограничена, позволяет представить всего одно выражение
Они имеют множество вариантов применения в конкретных областях программирования, наряду с другими типами выражений, используемых в функциях.
2. Различие между обычной функцией и лямбда-функцией
Рассмотрим пример и попробуем понять различие между определением (Def) для обычной функции и lambda—функции. Этот код возвращает заданное значение, возведенное в куб:
def defined_cube(y):
return y*y*y
lambda_cube = lambda y: y*y*y
print(defined_cube(2))
print(lambda_cube(2))Вывод:
8 8
Как показано в примере выше, обе представленные функции, defined_cube() и lambda_cube(), ведут себя одинаково, как и предполагалось.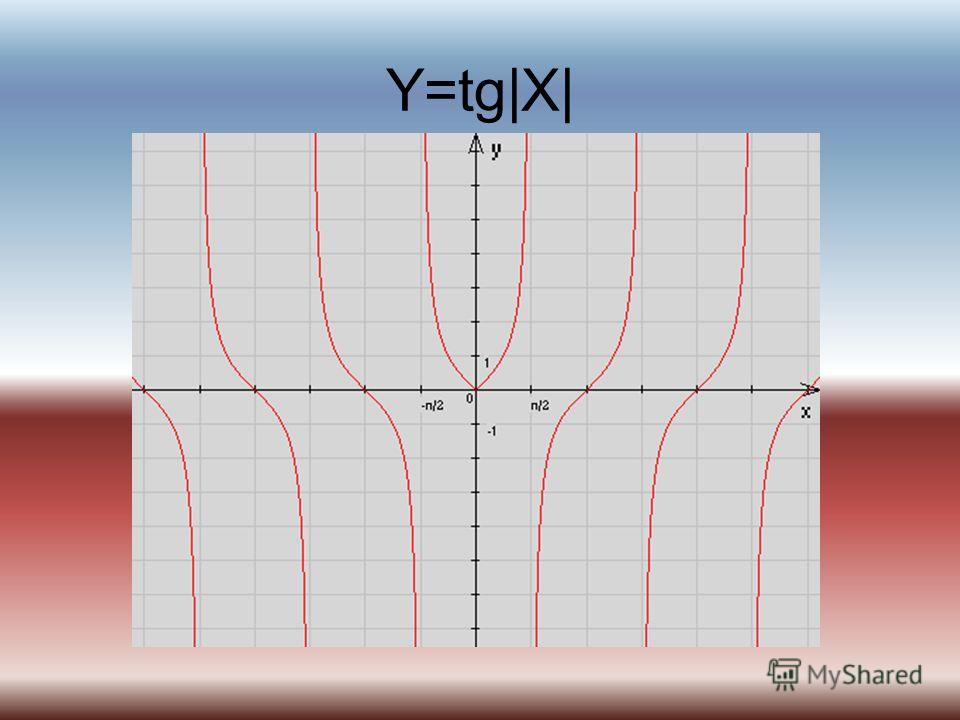
Разберем вышеуказанный пример подробнее:
Без использования лямбды: Здесь обе функции возвращают заданное значение, возведенное в куб. Но при использовании
defined_cube()дать ей входную величину. После выполнения нам также понадобилось возвратить результат, из того места, откуда была вызвана функция, и мы сделали это, используя ключевое словоreturn.С применением лямбды: Определение лямбды не включает оператор
return, а всегда содержит возвращенное выражение. Мы также можем поместить определение лямбды в любое место, где ожидается функция, и нам не нужно присваивать его переменной. Так выглядят простые лямбда-функции.
3. Лямбда-функции и функции высшего порядка
Мы используем лямбда-функцию, когда нам ненадолго требуется безымянная функция.
В Python мы часто используем их как аргумент функции высшего порядка (функции, которая принимает другие функции в качестве аргументов).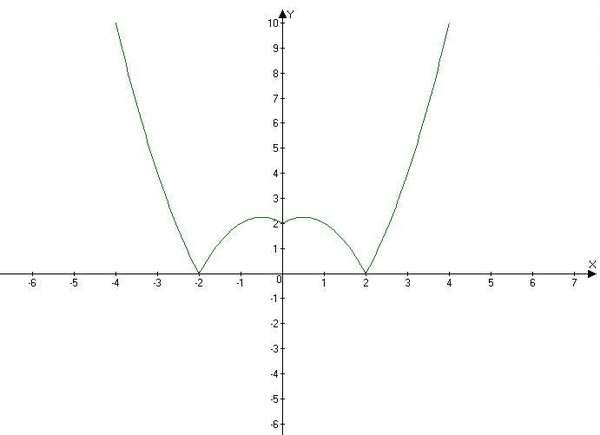
Лямбда-функции используют вместе с такими встроенными функциями как filter(), map(),reduce() и др.
Давайте рассмотрим еще несколько распространенных вариантов использования лямбда-функций.
3.1. Пример с filter()
Функция filter() в Python принимает в качестве аргументов функцию и список .
Функция вызывается со всеми элементами в списке, и в результате возвращается новый список, содержащий элементы, для которых функция результирует в True
Вот пример использования функции filter() для отбора четных чисел из списка.
my_list = [1, 3, 4, 6, 10, 11, 15, 12, 14] new_list = list(filter(lambda x: (x%2 == 0) , my_list)) print(new_list)
Вывод:
[4, 6, 10, 12, 14]
3.2. Пример с map()
Функция map() принимает в качестве аргументов функцию и список.
Функция вызывается со всеми элементами в списке, и в результате возвращается новый список, содержащий элементы, возвращенные данной функцией для каждого исходного элемента.
Ниже пример использования функции map() для удвоения всех элементов списка.
current_list = [1, 3, 4, 6, 10, 11, 15, 12, 14] new_list = list(map(lambda x: x*2 , current_list)) print(new_list)
Вывод:
[2, 6, 8, 12, 20, 22, 30, 24, 28]
3.3. Пример с reduce()
Функция reduce()
reduce() входит в состав модуля functools.from functools import reduce current_list = [5, 15, 20, 30, 50, 55, 75, 60, 70] summa = reduce((lambda x, y: x + y), current_list) print(summa)
Вывод:
380
Здесь результаты предыдущих двух элементов суммируются со следующим элементом, и это продолжается до конца списка, вот так:
5+15+20+30+50+55+75+60+70
4.
Лямбда и списковое включениеВ этом примере мы будем использовать лямбда-функцию со списковым включением и лямбда-функцию с циклом for. Мы выведем на экран таблицу из 10 элементов.
tables = [lambda x = x: x*10 for x in range(1, 11)]
for table in tables:
print(table())Вывод:
10 20 30 40 50 60 70 80 90 100
5. Лямбда и условные операторы
Давайте рассмотрим использование условий if-else в лямбда-функции. Как вы знаете, Python позволяет нам использовать однострочные условия, и именно их мы можем помещать в лямбда-функцию для обработки возвращаемого результата.
Например, есть две цифры, и вы должны определить, какая из них представляет наибольшее число.
max_number = lambda a, b: a if a > b else b print(max_number(3, 5))
Вывод:
5
Этот метод позволяет вам добавлять условия в лямбда-функции.
6. Лямбда и множественные операторы
Лямбда-функции не допускают использования нескольких операторов, однако мы можем создать две лямбда-функции, а затем вызвать вторую лямбда-функцию в качестве параметра для первой функции.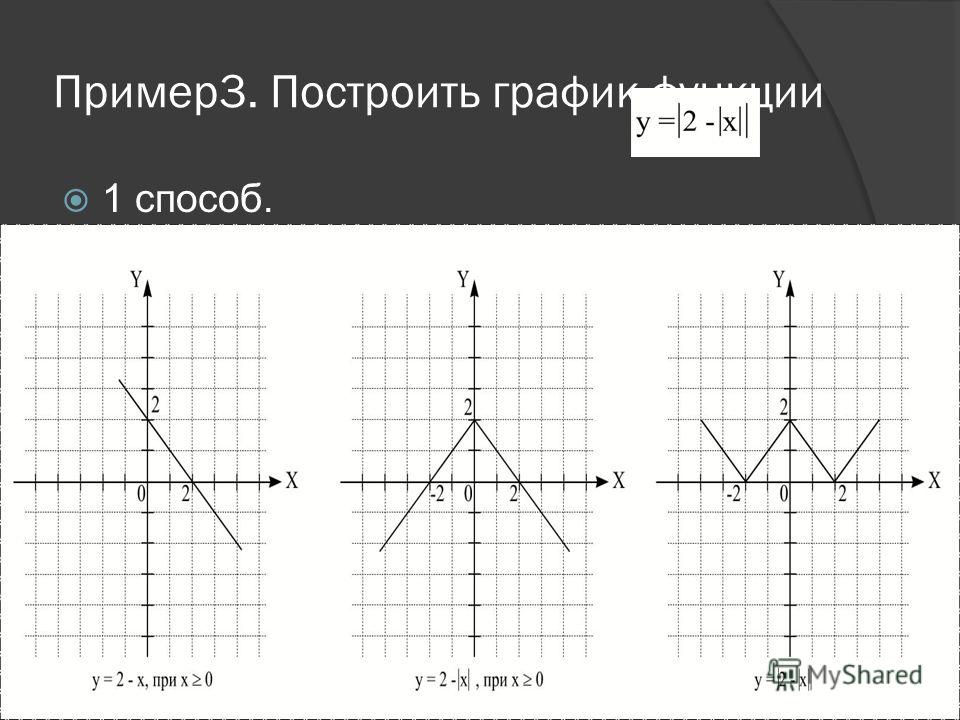
Давайте попробуем найти второй по величине элемент, используя лямбду.
current_list = [[10,6,9],[0, 14, 16, 80],[8, 12, 30, 44]] sorted_list = lambda x: (sorted(i) for i in x) second_largest = lambda x, func: [y[len(y)-2] for y in func(x)] result = second_largest(current_list, sorted_list) print(result)
Вывод:
[9, 16, 30]
В предыдущем примере, мы создали лямбда-функцию, которая сортирует каждый вложенный список в заданном списке. Затем этот список проходит как параметр для второй лямбда-функции, которая возвращает элемент n-2 из отсортированного списка, где n — длина вложенного списка.
Заключение
Теперь вы знаете как использовать в Python lambda-функции и можете:
Писать и использовать лямбда-функции.
Рационально выбирать между обычными и лямбда-функциями в Python.
Использовать лямбды с функциями высшего порядка или ключевыми функциями.
Использовать лямбды с абстракциями списков.
Добавлять условия к лямбда-функциям.
— Mathematica: построение модуля с FindRoot
Задавать вопрос
спросил
Изменено 10 лет, 6 месяцев назад
Просмотрено 1к раз
Время от времени я сталкиваюсь с этой проблемой, и я не нашел способа ее обойти. Обычно это происходит, когда я нахожу корень уравнения и хочу максимизировать/минимизировать/построить этот корень в соответствии с некоторым параметром. Поэтому я пытаюсь заключить код в модуль, чтобы его можно было выполнить только с входным числом, но он не будет работать внутри таких функций, как Plot. Например:
f[din_] := Модуль[{d = din},
sol = NDSolve[{y'[x] == y[x], y[0] == 1}, y[x], {x, 0, 10}];
t1 = Flatten[FindRoot[y[x] - d /. соль, {х, 1}]];
Икс /. т1
]
ф[2]
f[2.5]
ф[3]
График [ф [х], {х, 2, 3}]
соль, {х, 1}]];
Икс /. т1
]
ф[2]
f[2.5]
ф[3]
График [ф [х], {х, 2, 3}]
Все вызовы f с числом работают, как и ожидалось, но f в функции Plot, похоже, оценивается с символом «x» или что-то в этом роде и просто выдает много текста об ошибке.
Как это обойти?
Просматривая форумы, я нашел несколько предложений для подобных проблем — например, сделать определение следующим образом:
f[din_?NumericQ]:=
, и я перепробовал все, что мог, но ничего не изменилось. Я использую Mathematica 8.0
- функция
- модуль
- сюжет
- wolfram-mathematica
- отложенное выполнение
Основное исправление состоит в том, чтобы взять модуль ... Сам модуль также можно упростить, как показано ниже:
sol = NDSolve[{y'[x] == y[x], y[0] == 1}, y[x], {x, 0, 10 }];
f[din_] := х /. FindRoot[y[x] - дин /. соль, {х, 1}]
График [ф [х], {х, 2, 3}]
Попробуйте:
f[din_?NumericQ] := Module[{LocalDummy, Localy, LocalSol},
Локально = у/. NDSolve[{y'[LocalDummy] == y[LocalDummy], y[0] == 1}, y, {LocalDummy, 0, 10}][[1]];
LocalSol = FindRoot[Localy[LocalDummy] - din == 0, {LocalDummy, 1}][[1, 2]]]
NDSolve[{y'[LocalDummy] == y[LocalDummy], y[0] == 1}, y, {LocalDummy, 0, 10}][[1]];
LocalSol = FindRoot[Localy[LocalDummy] - din == 0, {LocalDummy, 1}][[1, 2]]]
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
non-proportional-relationships-module-4-quiz-b - Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
[PDF] Nonproportionen Relationships
›Domains › Centricity › 40002.
goldenrams.com.goldenramsВикторина модуля: D. 1. В этой таблице показаны пропорциональные отношения. Икс. −4. −2. 0. 2. 4 г. −14. −7. 0. 7. 14. Чему равно постоянное отношение y x ? А-4. Б-7.
[PDF] Модуль 4 Викторина D Ответы.pdf
www.goldenrams.com › cms › lib › Centricity › Domain › Module 4 ...
MODULE. Дата. Сорт. Непропорциональные отношения. Тест модуля: D. 1. В этой таблице показаны пропорциональные отношения. источник. Х.-4-2.
Обзор Модуля 4 - Викторина по непропорциональным отношениям - Викторина
quizizz.com › admin › module-4-review-non-propo...
Сыграйте в эту игру, чтобы повторить Алгебру I. Определите наклон.
Обзор Модуля 4 — Непропорциональные отношения — Тест
quizizz.com › admin › викторина › модуль-4-обзор-непропорциональные-отношения...
Модуль 4 Обзор - Непропорциональные отношения... СЕССИЯ ПОД РУКОВОДСТВОМ ПРЕПОДАВАТЕЛЯ Начать живую викторину... Какой график не- пропорциональный? варианты ответа.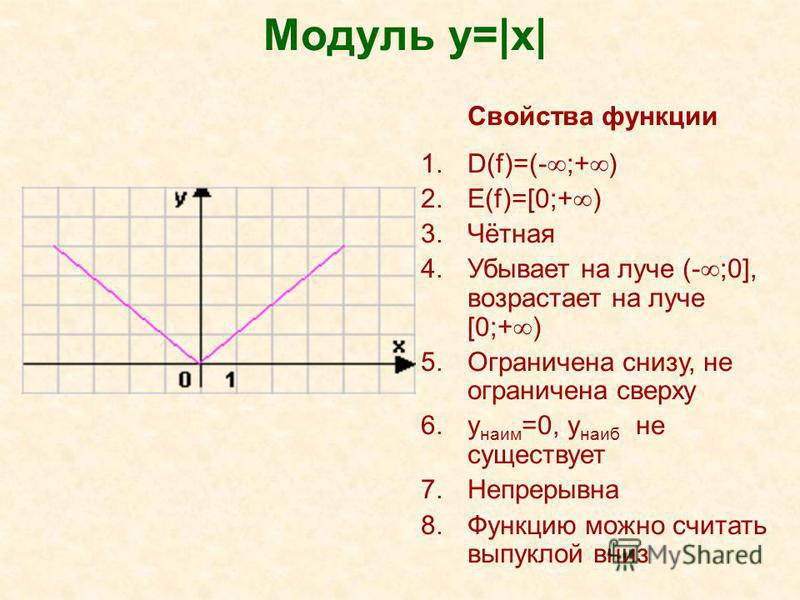
A. B.
[PDF] Класс
www.bwls.net › CourseFiles
МОДУЛЬ Соотношения и пропорциональность. 4. Викторина по модулю: B ... в этой строке показаны пропорциональные отношения? Выберите Верно или Ложно. A Он не изогнут.
Карточки Модуль 4: Непропорциональные отношения — Quizlet
quizlet.com › 444606151 › модуль-4-непропорциональн... ⁻1/3 b = -8 и более.
Карточки Модуль 4 Непропорциональные отношения - Quizlet
quizlet.com › модуль-4-непропорциональные-отношения...
Y-координата точки пересечения графика с осью y (0, b). Непропорциональные отношения. Связь между двумя величинами, в которой отношение ...
Bilder
Alle anzeigen
Alle anzeigen
[PDF] Пропорциональные отношения
vazquezmath.weebly.com Викторина по модулю: B. Используйте таблицу для 1–3. ... В у = 30х. Д у = х. 15. 4. Какая таблица показывает постоянную скорость изменения? Время (ч).
[PDF] Ответы
pillig.