Четные и нечетные числа. Понятие о десятичной записи числа
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два.
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа
— те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел
, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел
, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел.
———————————————————————————————
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.
При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9
213.
Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.
При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32
214.
Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.
Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.
215.
Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?
2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).
216. Выпиши чётные числа в один столбик, а нечётные — в другой.
2844 57893
67586 9231
10050 9929
217.
Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?
Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.
218.
Запиши самое большле чётное шестизначное число.
0 четное или нечетное число. Нечетные числа
В разделе Гуманитарные науки на вопрос Ноль -четное или нечетное? И почему заданный автором КАТЕРИНА лучший ответ это Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится на два, оно называется чётным (примеры: 2, 28, -8, 40), если нет — нечётным (примеры: 1,3, 75, -19). Нуль считается чётным числом.
Нуль считается чётным числом.
Чётное число — целое число, которое делится на 2 без остатка: …−4,-2,0,2,4,6,8…
Нечётное число — целое число, которое не делится на 2 без остатка: …−3,−1,1,3,5,7,9…
Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов и по модулю 2.
Ответ от Валентина Дубковская [гуру]
Четное. Потому что на 2 делится.
Ответ от Ёофья Ерина [гуру]
Да. Но мат-ка, между прочим, точная наука, а не гуманитарная!
Ответ от Пользователь удален [гуру]
Все четные числа делятся на 2, в том числе и 0.
Ответ от James Lukash [гуру]
Видимо, нуль все-таки четное число, если вики так говорит на пару с БСЭ, хотя я считал, что нуль стоит особняком от всего остального числового ряда и не является ни четным, ни нечетным
Ответ от Л [активный]
ноль абсолютное и самодостаточное. нах его делить?
Ответ от Ёергей Сергеев [активный]
Ваще, по моему, ноль это не число и то, что выбран раздел гуманитарных наук — эо верно. Ноль — это понятие, определение и то, что он делится на 2 ни о чем не говорит. Ноль — это таже бесконечность, только наоборот. И размышлять на эту тему можно бесконечно. А если кому-то охота, то может поискать мои «Размышления о вечности», да в инете меня Гринго зовут
Ноль — это понятие, определение и то, что он делится на 2 ни о чем не говорит. Ноль — это таже бесконечность, только наоборот. И размышлять на эту тему можно бесконечно. А если кому-то охота, то может поискать мои «Размышления о вечности», да в инете меня Гринго зовут
Ответ от Данил «stager» Воронов [активный]
Соня Ерина Меню пользователя Знаток (307)1 минуту назад (ссылка)ПожаловатьсяПожаловатьсяДа. Но мат-ка, между прочим, точная наука, а не гуманитарная!о_0
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
- Маарду
- Сверхпроводимость
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Нечётные числа
Чётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечётное — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечётное число — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Четные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточные числа — Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Совершенные числа — целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Квантовые числа — целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. … … Большая советская энциклопедия
… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42 , 104 , 11110 , 9115817342 — чётные числа.
31 , 703 , 78527 , 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
- Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
- Деление:
- Ч ётное / Ч ётное — однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное = если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное = если результат целое число , то оно Н ечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
В разных странах существуют связанные с количеством даримых цветов традиции, например в США , Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье . В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
Wikimedia Foundation . 2010 .
- Нечетность
- Нечетные и четные функции
Смотреть что такое «Нечетные числа» в других словарях:
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ЧИСЛА — ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Пифагор и пифагорейцы — Пифагор родился на Самосе. Расцвет его жизни приходится на 530 е годы до н.э., а смерть на начало V в. до н.э. Диоген Лаэртский, один из известных биографов античных философов, сообщает нам: Молодой и жадный до знаний, он покинул отечество,… … Западная философия от истоков до наших дней
сорит — (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров
НУМЕРОЛОГИЯ — и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь
Случайное простое число — В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов, на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является… … Википедия
Получение случайных простых чисел является… … Википедия
Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия
Книги
- Занимаюсь математикой. Для детей 6-7 лет , Сорокина Татьяна Владимировна. Основные задачи пособия — ознакомление ребенка с математическими понятиями «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «однозначные/двузначные числа», «четные/нечетные…
- Нечётное число — целое число , которое не делится на без остатка : …, −3, −1, 1, 3, 5, 7, 9, …
Если m чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные — «ян » .
В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные — «ян » .
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США , Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье . В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов , у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Практика
В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.
Напишите отзыв о статье «Чётные и нечётные числа»
Примечания
Ссылки
- Последовательность A005408 в OEIS : нечётные числа
- Последовательность A005843 в OEIS : чётные числа
- Последовательность A179082 в OEIS : чётные числа с чётной суммой цифр в десятичной записи
Отрывок, характеризующий Чётные и нечётные числа
– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
– И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
Чётность нуля — вопрос, считать ли ноль чётным или нечётным числом . Ноль — чётное число . Однако чётность нуля вызывает сомнения в среде людей, недостаточно знакомых с математикой. Большинство людей задумываются дольше, прежде чем идентифицировать 0 как чётное число, по сравнению с идентификацией обычных чисел вроде 2, 4, 6 или 8. Некоторые студенты, изучающие математику, и даже некоторые преподаватели, ошибочно считают ноль нечётным числом, или чётным и нечётным одновременно, или не относят его ни к одной категории.
Некоторые студенты, изучающие математику, и даже некоторые преподаватели, ошибочно считают ноль нечётным числом, или чётным и нечётным одновременно, или не относят его ни к одной категории.
По определению, чётное число — такое целое число , которое делится на без остатка. Ноль обладает всеми свойствами, которые присущи чётным числам, например, 0 с обеих сторон граничит с нечетными числами, каждое десятичное целое число имеет такую же чётность, как и последняя цифра этого числа, поэтому, поскольку 10 является чётным, то 0 также будет чётным. Если y {\displaystyle y} является четным числом, тогда y + x {\displaystyle y+x} имеет такую чётность, что имеет x {\displaystyle x} , а x {\displaystyle x} и 0 + x {\displaystyle 0+x} всегда имеют одинаковую чётность.
Ноль также соответствует закономерностям, которые образуют другие чётные числа. Правила чётности в арифметике, такие как чётное−чётное=чётное , предполагают, что 0 также должно быть чётным числом. Ноль является аддитивным нейтральным элементом группы чётных чисел, и он является началом, с которого рекурсивно определены другие чётные натуральные числа . Применение такой рекурсии по теории графов к вычислительной геометрии полагается на то, что ноль является чётным. Ноль делится не только на 2, он делится на все степени двойки. В этом смысле, 0 является «наиболее чётным» числом из всех чисел.
Ноль является аддитивным нейтральным элементом группы чётных чисел, и он является началом, с которого рекурсивно определены другие чётные натуральные числа . Применение такой рекурсии по теории графов к вычислительной геометрии полагается на то, что ноль является чётным. Ноль делится не только на 2, он делится на все степени двойки. В этом смысле, 0 является «наиболее чётным» числом из всех чисел.
Почему ноль является чётным
Чтобы доказать, что ноль является чётным, можно непосредственно использовать стандартное определение «чётного числа». Число называют чётным, если это число кратно 2. Например, причиной того, что число 10 является чётным, является то, что оно равно 5 × 2 . В то же время, ноль также является целым кратным 2, то есть 0 × 2 , следовательно ноль является чётным .
Кроме того, можно объяснить, почему ноль является чётным, не применяя формальных определений.
Простые объяснения
Числа можно изобразить с помощью точек на числовой оси . Если на ней нанести чётные и нечётные числа, их общая закономерность становится очевидной, особенно если добавить и отрицательные числа:
Чётные и нечётные числа чередуются между собой. Нет причины пропустить число ноль .
Нет причины пропустить число ноль .
Математический контекст
Численные результаты теории обращаются к основной теореме арифметики и алгебраическим свойствам чётных чисел, поэтому вышеупомянутая конвенция имеет далеко идущие последствия. Например, факт, что положительные числа имеют уникальную факторизацию , означает, что для отдельного числа можно определить, имеет ли оно чётное или нечётное количество различных простых множителей. Поскольку 1 не является простым числом, а также не имеет простых множителей, оно является пустым произведением простых чисел; поскольку 0 — чётное число, 1 имеет чётное количество простых множителей. Из этого следует, что функция Мёбиуса принимает значение μ (1) = 1, что необходимо, чтобы она была мультипликативной функцией и работала формула вращения Мёбиуса .
В образовании
Вопрос, является ли ноль чётным числом, поднимался в системе школьного образования Великобритании. Проводились многочисленные опросы мнения школьников по данному вопросу. Выяснилось, что ученики по-разному оценивают чётность нуля: некоторые считают его чётным, некоторые — нечётным, иные полагают, что он является особым числом — и тем и другим одновременно или ни тем ни другим. Причём ученики пятых классов дают правильный ответ чаще, чем ученики шестых классов .
Выяснилось, что ученики по-разному оценивают чётность нуля: некоторые считают его чётным, некоторые — нечётным, иные полагают, что он является особым числом — и тем и другим одновременно или ни тем ни другим. Причём ученики пятых классов дают правильный ответ чаще, чем ученики шестых классов .
Как показали исследования, даже преподаватели в школах и вузах недостаточно осведомлены о чётности нуля. Так, например, порядка 2/3 преподавателей Университета Южной Флориды ответили «нет» на вопрос «Является ли ноль чётным числом?» .
Примечания
Литература
- Anderson, Ian (2001), A First Course in Discrete Mathematics , London: Springer, ISBN 1-85233-236-0
- Anderson, Marlow & Feil, Todd (2005), A First Course in Abstract Algebra: Rings, Groups, And Fields , London: CRC Press, ISBN 1-58488-515-7
- Andrews, Edna (1990), Markedness Theory: the union of asymmetry and semiosis in language , Durham: Duke University Press, ISBN 0-8223-0959-9
- Arnold, C.
 L. (January 1919), «The Number Zero «, The Ohio Educational Monthly Т. 68 (1): 21–22,
. Проверено 11 апреля 2010.
L. (January 1919), «The Number Zero «, The Ohio Educational Monthly Т. 68 (1): 21–22,
. Проверено 11 апреля 2010. - Arsham, Hossein (January 2002), Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives , . Проверено 24 сентября 2007. Архивная копия от 25 сентября 2007 на Wayback Machine
- Ball, Deborah Loewenberg; Hill, Heather C. & Bass, Hyman (2005), «Knowing Mathematics for Teaching: Who Knows Mathematics Well Enough To Teach Third Grade, and How Can We Decide? «, American Educator , . Проверено 16 сентября 2007.
- Ball, Deborah Loewenberg; Lewis, Jennifer & Thames, Mark Hoover (2008), «Making mathematics work in school «, Journal for Research in Mathematics Education Т. M14: 13–44 and 195–200, . Проверено 4 марта 2010.
- Barbeau, Edward Joseph (2003), Polynomials , Springer, ISBN 0-387-40627-1
- Baroody, Arthur & Coslick, Ronald (1998), Fostering Children»s Mathematical Power: An Investigative Approach to K-8 , Lawrence Erlbaum Associates, ISBN 0-8058-3105-3
- Berlinghoff, William P.
 ; Grant, Kerry E. & Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rev. ed.), Rowman & Littlefield, ISBN 0-7425-0202-3
; Grant, Kerry E. & Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rev. ed.), Rowman & Littlefield, ISBN 0-7425-0202-3 - Border, Kim C. (1985), Fixed Point Theorems with Applications to Economics and Game Theory , Cambridge University Press, ISBN 0-521-38808-2
- Brisman, Andrew (2004), Mensa Guide to Casino Gambling: Winning Ways , Sterling, ISBN 1-4027-1300-2
- Bunch, Bryan H. (1982), Mathematical Fallacies and Paradoxes , Van Nostrand Reinhold, ISBN 0-442-24905-5
- Caldwell, Chris K. & Xiong, Yeng (27 December 2012), «What is the Smallest Prime? «, Journal of Integer Sequences Т. 15 (9),
- Column 8 readers (10 March 2006a), Column 8 (First ed.), с. 18, Factiva SMHH000020060309e23a00049
- Column 8 readers (16 March 2006b), Column 8 (First ed.), с. 20, Factiva SMHH000020060315e23g0004z
- Crumpacker, Bunny (2007), Perfect Figures: The Lore of Numbers and How We Learned to Count , Macmillan, ISBN 0-312-36005-3
- Cutler, Thomas J.
 (2008), The Bluejacket»s Manual: United States Navy (Centennial ed.), Naval Institute Press, ISBN 1-55750-221-8
(2008), The Bluejacket»s Manual: United States Navy (Centennial ed.), Naval Institute Press, ISBN 1-55750-221-8 - Dehaene, Stanislas; Bossini, Serge & Giraux, Pascal (1993), «The mental representation of parity and numerical magnitude «, Journal of Experimental Psychology: General Т. 122 (3): 371–396, doi :10.1037/0096-3445.122.3.371 , . Проверено 13 сентября 2007.
- Devlin, Keith (April 1985), «The golden age of mathematics», New Scientist Т. 106 (1452)
- Diagram Group (1983), The Official World Encyclopedia of Sports and Games , Paddington Press, ISBN 0-448-22202-7
- Dickerson, David S & Pitman, Damien J (July 2012), Tai-Yih Tso, ed., «Advanced college-level students» categorization and use of mathematical definitions «, Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education Т. 2: 187–195,
- Dummit, David S. & Foote, Richard M. (1999), Abstract Algebra (2e ed.
 ), New York: Wiley, ISBN 0-471-36857-1
), New York: Wiley, ISBN 0-471-36857-1 - Educational Testing Service (2009), Mathematical Conventions for the Quantitative Reasoning Measure of the GRE® revised General Test , Educational Testing Service, . Проверено 6 сентября 2011.
- Freudenthal, H. (1983), Didactical phenomenology of mathematical structures , Dordrecht, The Netherlands: Reidel
- Frobisher, Len (1999), Anthony Orton, ed., Primary School Children»s Knowledge of Odd and Even Numbers , London: Cassell, с. 31–48
- Gouvêa, Fernando Quadros (1997), p-adic numbers: an introduction (2nd ed.), Springer-Verlag, ISBN 3-540-62911-4
- Gowers, Timothy (2002), Mathematics: A Very Short Introduction , Oxford University Press , ISBN 978-0-19-285361-5
- Graduate Management Admission Council (September 2005), The Official Guide for GMAT Review (11th ed.), McLean, VA: Graduate Management Admission Council, ISBN 0-9765709-0-4
- Grimes, Joseph E.
 (1975), The Thread of Discourse , Walter de Gruyter, ISBN 90-279-3164-X
(1975), The Thread of Discourse , Walter de Gruyter, ISBN 90-279-3164-X - Hartsfield, Nora & Ringel, Gerhard (2003), Pearls in Graph Theory: A Comprehensive Introduction , Mineola: Courier Dover, ISBN 0-486-43232-7
- Hill, Heather C.; Blunk, Merrie L.; Charalambous, Charalambos Y. & Lewis, Jennifer M. (2008), «Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study «, Cognition and Instruction Т. 26 (4): 430–511, DOI 10.1080/07370000802177235
- Hohmann, George (25 October 2007), Companies let market determine new name , с. P1C, Factiva CGAZ000020071027e3ap0001l
- Kaplan Staff (2004), Kaplan SAT 2400, 2005 Edition , Simon and Schuster, ISBN 0-7432-6035-X
- Keith, Annie (2006), Mathematical Argument in a Second Grade Class: Generating and Justifying Generalized Statements about Odd and Even Numbers , IAP, ISBN 1-59311-495-8
- Krantz, Steven George (2001), Dictionary of algebra, arithmetic, and trigonometry , CRC Press, ISBN 1-58488-052-X
- Levenson, Esther; Tsamir, Pessia & Tirosh, Dina (2007), «Neither even nor odd: Sixth grade students» dilemmas regarding the parity of zero «, The Journal of Mathematical Behavior Т.
 26 (2): 83–95, DOI 10.1016/j.jmathb.2007.05.004
26 (2): 83–95, DOI 10.1016/j.jmathb.2007.05.004 - Lichtenberg, Betty Plunkett (November 1972), «Zero is an even number», The Arithmetic Teacher Т. 19 (7): 535–538
- Lorentz, Richard J. (1994), Recursive Algorithms , Intellect Books, ISBN 1-56750-037-4
- Lovas, William & Pfenning, Frank (22 January 2008), «A Bidirectional Refinement Type System for LF «, Electronic Notes in Theoretical Computer Science Т. 196: 113–128, doi :10.1016/j.entcs.2007.09.021 , . Проверено 16 июня 2012.
- Lovász, László ; Pelikán, József & Vesztergombi, Katalin L. (2003), Discrete Mathematics: Elementary and Beyond , Springer, ISBN 0-387-95585-2
- Morgan, Frank (5 April 2001), Old Coins , The Mathematical Association of America, . Проверено 22 августа 2009.
- Nipkow, Tobias; Paulson, Lawrence C. & Wenzel, Markus (2002), Isabelle/Hol: A Proof Assistant for Higher-Order Logic , Springer, ISBN 3-540-43376-7
- Nuerk, Hans-Christoph; Iversen, Wiebke & Willmes, Klaus (July 2004), «Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect «, The Quarterly Journal of Experimental Psychology A Т.
 57 (5): 835–863, DOI 10.1080/02724980343000512
57 (5): 835–863, DOI 10.1080/02724980343000512 - Partee, Barbara Hall (1978), Fundamentals of Mathematics for Linguistics , Dordrecht: D. Reidel,
Что такое четное число. Чёт и нечет
О таинственном влиянии чисел, которые нас окружают, известно с древнейших времен. Каждая цифра имеет свое особое значение и обладает своим воздействием. И деление чисел на четные и нечетные является очень важным для определения нашей дальнейшей судьбы.
Чет и нечет
В нумерологии (науке о связях чисел с жизнью людей) нечетные числа (1, 3, 5, 7, 9, 11 и так далее) считаются выразителями мужского начала, которое в восточной философии называется — ян. Их также называют солнечными, потому что они несут энергию нашего светила. Такие цифры отражают поиск, стремление к чему-то новому.
Четные же числа (которые без остатка делятся на 2) говорят о женской природе (в восточной философии — инь) и энергетике Луны. Их суть в том, что они изначально тяготеют к двойке, поскольку делятся на нее. Эти цифры говорят о стремлении к логическим правилам отображения действительности и нежелании выйти за их пределы.
Эти цифры говорят о стремлении к логическим правилам отображения действительности и нежелании выйти за их пределы.
Другими словами: четные цифры более правильны, но в то же время более ограничены и прямолинейны. А нечетные способны помочь выбраться из скучного и серого бытия.
Нечетных чисел больше (ноль в нумерологии имеет собственное значение и не считается четным числом) — пять (1, 3, 5, 7, 9) против четырех (2,4,6, 8). Их более сильная энергия выражается в том, что при их сложении с четными числами снова получается нечетное число.
Противопоставление четных и нечетных чисел входит в общую систему противоположностей (один -много, мужчина — женщина, день -ночь, правый — левый, добро — зло и т.п.). При этом с нечетными числами связаны первые понятия, а с четными-вторые.
Таким образом, всякое нечетное число обладает мужскими характеристиками: властностью, резкостью, способностью к восприятию чего-то нового, а любое четное наделено женскими свойствами: пассивностью, стремлением сгладить любой конфликт.
Значения цифр
Всем цифрам в нумерологии свойственны определенные значения: Единица несет в себе активность, целеустремленность, инициативу. Двойка — восприимчивость, слабость, готовность подчиняться. Тройка — веселье, артистизм, удачливость. Четверка — трудолюбие, однообразие, скуку, безвестность, поражение. Пятерка — предприимчивость, успехи в любви, движение к цели. Шестерка — простоту, спокойствие, тяготение к домашнему уюту. Семерка — мистику, таинственность. Восьмерка — материальные блага. Девятка — интеллектуальное и духовное совершенство, высокие достижения. Как видим, нечетные цифры обладают гораздо более яркими свойствами. Согласно учению знаменитого древнегреческого математика Пифагора, именно они являлись олицетворением добра, жизни и света, а также символизировали правую от человека сторону — сторону удачи.
Четные же цифры ассоциировались с неудачной левой стороной, злом, тьмой и смертью. Эти взгляды пифагорейцев позже отразились в некоторых приметах (например, что нельзя живому человеку дарить четное количество цветов или что встать с левой ноги — к неудачному дню), хотя у разных народов они могут быть разными.
Влияние четных и нечетных чисел на нашу жизнь
Со времен Пифагора было принято считать, что «женские» четные числа ассоциируются со злом потому, что легко расщепляются на две половины — и значит, можно говорить, что внутри них пустое пространство, первобытный хаос. А нечетное число расщепить на равные части без остатка не получится, следовательно, оно содержит внутри себя нечто цельное и даже священное (в Средние века некоторые философы-теологи утверждали, что внутри нечетных чисел живет Бог).
В современной нумерологии принято учитывать многие окружающие нас цифры — например, номера телефонов или квартир, даты рождения и знаменательных событий, числа имени и фамилии и т.п.
Наибольшее значение для нашей жизни имеет так называемое число судьбы, которое высчитывается по дате рождения. Нужно сложить все цифры этой даты и «свернуть» их до простого числа.
Скажем, вы родились 28 сентября 1968 года (28.09.1968). Складываем цифры: 2+8+0+9+1+9+ 6 -I- 8 = 43; 4 + 3 = 7. Следовательно, ваше число судьбы — 7 (как было сказано выше — число мистики и таинственности).
Следовательно, ваше число судьбы — 7 (как было сказано выше — число мистики и таинственности).
Точно так же можно проанализировать даты важных для вас событий. В этом отношении очень показательна судьба знаменитого Наполеона. Он родился 15 августа 1769 года (15.08.1769), следовательно, его число судьбы равно единице:
1 + 5 + 0 + 8 + 1 + 7 + 6 + 9 = 37; 3 + 7 = 10; 1 + 0 = 1.
Это нечетное число, согласно современной нумерологии, несет в себе активность, целеустремленность, инициативу -качества, благодаря которым Наполеон проявил себя. Он стал французским императором 2 декабря 1804 года (02.12.1804), число этой даты — девятка (0 + 2+1 + 2 + 1 + 8 + 0 + 4 = 18; 1 + 8 = 9), которая является числом высоких достижений. Он скончался 5 мая 1821 года (05.05.1821), число этого дня — четверка (0 + 5 + 0 + 5 + 1+ 8 + 2 + 1 = 22; 2 + 2 = 4), которая означает безвестность и поражение.
Древние люди не зря говорили, что цифры правят миром. Пользуясь знаниями нумерологии, вы легко можете подсчитать, какие события сулит та или иная дата — и в каких случаях следует воздержаться от ненужных действий.
Что означают чётные и нечётные числа в духовной нумерологии. В изучении языка чисел это очень важная тема! Чем по своей сути чётные числа отличаются от нечётных чисел?
Нечётные числа в нумерологии – солнечные, мужской природы, кислотные, электрические, динамичные. При группировании нечётных чисел, одно число останется без своей пары (1 и 3; 5 и 7; 9). Эти числа являются слагаемые (их складывают с чем-либо).
Чётные числа – лунные, женской природы, щелочные, магнетические, статичные. Числа данной группы вычитаемые или уменьшаемые. Они статичны и остаются без движения, потому что имеют чётные группы пар (2 и 4; 6 и 8).
Чётные числа в нумерологии
Общеизвестно, что чётные числа – те числа которые делятся на два. А что означают чётные числа относительно духовной нумерологии? Какова нумерологическая суть «деления на два»? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У цифры 2 несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств – точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств – точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа в нумерологии
Нечётными называют числа, которые не делятся на два. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого – чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера число 3 – число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность – вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия – один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены – область нечётных чисел…
Нечётные числа – взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42 , 104 , 11110 , 9115817342 — чётные числа.
31 , 703 , 78527 , 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
- Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
- Деление:
- Ч ётное / Ч ётное — однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное = если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное = если результат целое число , то оно Н ечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные — Ян .
В разных странах существуют связанные с количеством даримых цветов традиции, например в США , Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье . В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
Wikimedia Foundation . 2010 .
- Нечетность
- Нечетные и четные функции
Смотреть что такое «Нечетные числа» в других словарях:
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ЧИСЛА — ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Пифагор и пифагорейцы — Пифагор родился на Самосе. Расцвет его жизни приходится на 530 е годы до н.э., а смерть на начало V в. до н.э. Диоген Лаэртский, один из известных биографов античных философов, сообщает нам: Молодой и жадный до знаний, он покинул отечество,… … Западная философия от истоков до наших дней
сорит — (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики
«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров
НУМЕРОЛОГИЯ — и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь
Случайное простое число — В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов, на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является… … Википедия
Получение случайных простых чисел является… … Википедия
Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия
Книги
- Занимаюсь математикой. Для детей 6-7 лет , Сорокина Татьяна Владимировна. Основные задачи пособия — ознакомление ребенка с математическими понятиями «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «однозначные/двузначные числа», «четные/нечетные…
· Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K, подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).
·
Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 +
1, 5 = 2 х 2 + 1, и т. д.).
д.).
- Сложение и вычитание:
- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
- Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
- Деление:
- Ч ётное / Ч ётное — однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное -— если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное —если результат целое число , то оно Н ечётное
Сумма любого числа четных чисел –
четно.
Сумма нечетного числа нечетных чисел – нечетно.
Сумма четного числа нечетных чисел – четно.
Разность двух
чисел имеет ту же четность, что и их сумма .
(напр. 2+3=5 и 2-3=-1 оба нечетные)
Алгебраическая (со знаками + или -) сумма целых чисел имеет ту же четность, что и их сумма .
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)
Идея
четности имеет много разных применений. Самые простые из них:
1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).
2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу переходов между ними и наоборот !!! )
2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны , то периодов пребывания объекта в том или ином состоянии — четное число, если исходное и конечное состояния совпадают — то нечетное . (переформулировка п.2)
(переформулировка п.2)
3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.
3″. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным. (переформулировка п.3)
4. Если предметы можно разбить на пары, то их количество четно.
5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).
(!) Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.
Примеры:
Задача 1. На плоскости расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей… 9-я с первой). Могут ли они вращаться одновременно?
Решение: Нет, не могут. Если бы
они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка ! ) Тогда всего должно быть
четное число шестеренок, а их 9 штук?! ч. и.т.д. (знак «?!» обозначает получение противоречия)
и.т.д. (знак «?!» обозначает получение противоречия)
Задача 2. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы
получилось выражение, равное нулю?
Решение: Нет, нельзя. Четность
полученного выражения всегда будет совпадать с четностью суммы 1+2+…+10=55, т.е. сумма всегда будет нечетной . А 0
— четное число?! ч.т.д.
Прежде чем говорить про четные и нечетные числа, стоит уяснить несколько моментов о том, какие вообще группы чисел бывают. Это необходимо для того, чтобы не пытаться выяснять четность дроби.
С каких чисел начинается изучение в основной школе?
Первыми идут натуральные. Они также сначала появились исторически. Человечеству было необходимо подсчитывать предметы. Причем при счете ноль не используется, поэтому он не входит в группу натуральных чисел. Здесь все целые, которые больше единицы.
Именно для них впервые дается определение четности. Чтобы понять, какое число нечетное, нужно запомнить признак четного. Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.
Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.
Какие числа идут дальше?
Целые. В их множество входит уже ноль и все отрицательные числа. Цепочка натуральных чисел была ограничена слева, а вправо продолжалась бесконечно. С целыми оказывается бесконечное количество чисел и слева от нуля.
В этот момент немного меняется определение четности. Оно теперь должно делиться на два без остатка. Значит, нечетные числа при делении на два дают ответ с остатком.
Причем даже вводится общая запись: для четных — 2n, нечетные — (2n+1). Если для натуральных не существует только максимального четного или нечетного, то у целых нет и минимального.
А что потом?
Рациональные (другое название — вещественные) числа. Кроме уже упомянутых, в это множество входят еще и дроби. То есть числа, которые можно представить в виде двух. Первое из них является числителем и представляется в виде целого числа. Второе — знаменатель, который никогда не равен нулю.
Второе — знаменатель, который никогда не равен нулю.
Кстати, для них не вводится понятие четности. Поэтому нечетные числа, записанные в виде дроби, не существуют вовсе.
Какие результаты дают действия с четными и нечетными числами?
Их можно рассмотреть в порядке усложнения арифметического действия. Тогда первым и вторым пойдут сложение и вычитание. Неважно, какое из них выполняется, ответ будет зависеть только от начальной пары чисел. К примеру, если исходные числа четные, то результат действия будет делиться на два. Такой же итог будет, если стоит разность или сумма нечетных чисел. Чтобы получить нечетное число, придется складывать или вычитать четное с нечетным.
Это легко можно проверить, используя их общую запись. Например, сложение двух четных чисел: 2n+2n = 4n = 2*2n. Здесь 2n — четное число, которое еще умножается на два. Значит, оно точно будет делиться нацело на двойку. То есть ответ — четный.
При сложении четного с нечетным имеем такую запись: 2n + (2n + 1) = 4n + 1. Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.
Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.
Третье действие — умножение. При его выполнении всегда будет четный ответ, если есть хотя бы один множитель четный. В ситуации, когда перемножаются два нечетных числа, результатом окажется нечетное.
Для иллюстрации последнего потребуется сделать такую запись: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Опять первое слагаемое представляет собой четное число, а единица сделает его нечетным.
С четвертым действием — делением — все не так однозначно. Начать можно с двух четных. Во-первых, может получиться дробь, тогда о четности речи не идет. Во-вторых, результатом бывает целое число. Но и тогда однозначного ответа на вопрос о будущей четности получить невозможно. Оценить ее можно только после выполнения деления. Ответ может быть как четным, так и нечетным.
Если делится нечетное число на четное, то ответ оказывается всегда дробным. Значит, его четность не определяется.
Значит, его четность не определяется.
Когда в делении участвуют нечетные числа, то результатом также может оказаться дробь. Но если ответ целый, то он обязательно будет нечетным.
При делении четного на нечетное, как в предыдущей ситуации, возможно два варианта: дробь или целое число. Во втором случае оно всегда будет четным.
Определите нечетное и четное число
Несколько дней назад, когда пользователи вводили основную информацию, чтобы посмотреть, какой метод заполнения у пользователя выше при заполнении информации, был проведен тест: он разделен на два случая: обязательное заполнение и пропуск, если он не завершен. По конечному номеру мобильного телефона пользователя определите четность, чтобы различить сцену, поэтому выходит тема этой статьи, метод определения нечетного и четного числа (всего два):
Метод 1: Найдите оставшийся%
1.if( x % 2 == 0)
//Четный
else
//Странный
2. (x% 2 == 0)? Четное число: нечетное число
анализ:
Согласно определению нечетных и четных чисел, если целое число делится на 2 без остатка, это четное число, в противном случае — нечетное число.
Следовательно, остаток от четного числа равен 0, а остаток от нечетного числа не равен нулю.
В суждении if (условие), если условие не равно нулю, это означает, что условие выполнено, в противном случае это означает, что условие не выполняется (то есть оператор после if () не выполняется)
?: ситуация аналогичная.
Метод 2: И 1 фаза и (& 1)
1.if( x & 1 == 0)
//Четный
else
//Странный
2. (x & 1 == 0)? Четное число: нечетное число
анализ:
Во-первых, вы должны знать, как использовать побитовую операцию И &
побитовая операция И a & b
Соответствующими двоичными битами двух чисел, участвующих в операции, является И, только если оба соответствующих двоичных бита равны 1, бит результата равен 1, в противном случае — 0. Число, участвующее в операции, отображается в виде дополнения.
Например: 9 и 5 можно записать следующим образом:
Сначала преобразуйте два числа в двоичные, а затем выполните операции. 0, то есть десятичное число является нечетным числом Четный он или нет, зависит от того, является ли младшая цифра в двоичном коде 0 или 1.
0, то есть десятичное число является нечетным числом Четный он или нет, зависит от того, является ли младшая цифра в двоичном коде 0 или 1.
Наконец, в этой статье упоминаются:http://blog.csdn.net/u013162593/article/details/17473331
Интеллектуальная рекомендация
Решите java.err.nojdk при доступе к JSP на странице Jetty
При попытке использовать архетип jetty7 + cometd + spring для создания проекта сегодня, обычные результаты доступа, ожидаемые по ссылке, не могли появиться, и появилось org.apache.jasper.JasperExcepti…
Уточнить взаимосвязь между сервлетом, Tomcat, веб -сервером, интерпретацией отношений между содержанием сервиса
Уточнить взаимосвязь между сервлетом, Tomcat, веб -сервером 1. Что такое веб -сервер? В: Как мы можем получить доступ к ресурсу, отображаемому с помощью картирования веб -сервера? Во -вторых, что тако…
Простое руководство по созданию надстроек для пошаговых мобильных игр на Python (часть 2)
Простое руководство по созданию надстроек для пошаговых мобильных игр на Python (часть 2) Вводить: Продолжить с предыдущегоСообщение блога, Сегодня мы поговорим о том, как помочь другим Предварительна. ..
..
Создайте среду выполнения на основе среды Express.
Во-первых, установить экспресс-генератор глобально npm install -g express-generator // Установите генератор экспресс-генератора, вы можете быстро создавать экспресс-проекты, команду express * нельзя и…
1039 Покупать или нет (на основе Python)
Хахаха, директор внезапно хочет приехать посмотреть наш VR-проект, и я с радостью добавлю еще один вопрос. Код этого вопроса не очень похож на Python, я чувствую, что его можно оптимизировать, хе-хе Я…
Вам также может понравиться
Как писать файлы кеша
В проекте, помимо написания необходимых документов api, необходимо описать другие структуры данных, и документ кеша является одной из них. По моему инженерному опыту, Redis используется относительно ч…
IOS XIB изменить кадр
// Динамические изменения рамы // Casonry Изменить кадр…
Советы Swagger-ui не могут выводить базовый URL.
Unable to infer base url. This is common when using dynamic servlet registration or when the API is behind an API Gateway. The base url is the root of where all the swagger resources are served. For e…
This is common when using dynamic servlet registration or when the API is behind an API Gateway. The base url is the root of where all the swagger resources are served. For e…
Анализ самого всеобъемлющего и основательного принципа BFC в истории
В этой статье рассказывается о том, что такое концепция BFC: правила ограничения BFC, как мы можем инициировать генерацию нового BFC; применение BFC в макете: предотвращение перекрытия полей (коллапс,…
Python-отформатированный выход
…
5 класс. Математика. Никольский. Учебник. Ответы к стр. 143
Делимость натуральных чисел
Простые и составные числа
Ответы к стр. 143
Доказываем
640. Докажите, что, кроме числа 2, не существует других чётных простых чисел.
Чётное число — это число, которое делится на 2. Число 2 делится на 1 и на само себя, а любое другое чётное число будет делится на 1, на само себя, а также на 2. Поэтому любое чётное число, кроме 2 — составное.
Исследуем
641. Можно ли простое число записать в виде суммы:
а) двух чётных чисел;
б) двух нечётных чисел;
в) чётного и нечётного чисел?
а) Простое число нельзя записать в виде суммы двух чётных чисел, так как эта сумма чётная и больше 2 и поэтому не равная простому числу.
б) Только одно простое число можно записать в виде суммы двух нечётных чисел: 2 = 1 + 1. Сумма любых других нечётных чисел чётная и больше 2 и поэтому не равна простому числу.
в) Любое простое число, большее 2, — это нечётное число, его можно представить в виде суммы чётного и нечётного чисел. Например, 5 = 4 + 1; 37 = 34 + 3, а простое число 2 нельзя записать в виде суммы чётного и нечётного чисел.
642. а) Может ли сумма двух простых чисел быть простым числом?
б) Верно ли, что сумма любых двух простых чисел является простым числом?
а) Да, может. Например: 2 + 3 = 5 — все числа простые.
б) Нет, не верно. Например: 3 + 5 = 8 — число 8 составное.
643. Некто пообещал дать 99 конфет тому, кто сумеет их разделить между четырьмя людьми так, чтобы каждому досталось нечетное число конфет. Почему этот приз до сих пор никому не удалось получить?
Количество людей — чётное число, а сумма чётного числа нечётных слагаемых — чётное число. Поэтому разделить конфеты заданным способом невозможно, и приз до сих пор никому не удалось получить.
644. В следующих записях замените буквы цифрами так, чтобы полученные числа делились на 3:
а) 35α25; б) 4αb40;
в) 5α2b5; г) 72αb8.
Какие из полученных чисел делятся на 5; делятся на 2; делятся на 10; делятся на 4?
Число делится на 3, если сумма его цифр делится на 3 (в этом задании в каждом пункте нужно выбрать только одно число).
а) 3 + 5 + 2 + 5 = 15 — делится на 3. Значит нужно добавить цифру, которая делится на 3, это 3 или 6 или 9: 35325 или 35625 или 35925.
б) 4 + 4 + 0 = 8, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 8 + 9 + 9 = 26, которая не делится на 3. В промежутке от 8 до 26 следующие числа делятся на 3: 9, 12, 15, 18, 21, 24.
Самое большое число — 9, если добавить две 9, то получим сумму 8 + 9 + 9 = 26, которая не делится на 3. В промежутке от 8 до 26 следующие числа делятся на 3: 9, 12, 15, 18, 21, 24.
9 — 8 = 1, значит, числа могут быть 0 и 1: 40 140 или 41 040;
12 — 8 = 4, значит, числа могут быть 0 и 4 или 1 и 3 или 2 и 2: 40 440 или 44 040 или 41 340 или 43 140 или 42 240;
15 — 8 = 7, значит, числа могут быть 0 и 7 или 1 и 6 или 2 и 5 или 3 и 4: 40 740 или 47 040 или 41 640 или 46 140 или 42 540 или 45 240 или 43 440 или 44 340;
18 — 8 = 10, значит, числа могут быть 1 и 9 или 2 и 8 или 3 и 7 или 4 и 6 или 5 и 5: 41 940 или 49 140 или 42 840 или 48 240 или 43 740 или 47 340 или 44 640 или46 440 или 45 540;
21 — 8 = 13, значит, числа могут быть 4 и 9 или 5 и 8 или 6 и 7: 44 940 или 49 440 или 45 840 или 48 540 или 46 740 или 47 640;
24 — 8 = 16, значит, числа могут быть 7 и 9 или 8 и 8: 47 940 или 49 740 или 48 840.
в) 5 + 2 + 5 = 12, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 12 + 9 + 9 = 30, которая делится на 3. Также в промежутке от 12 до 30 следующие числа делятся на 3: 12, 15, 18, 21, 24, 27, 30.
Также в промежутке от 12 до 30 следующие числа делятся на 3: 12, 15, 18, 21, 24, 27, 30.
12 — 12 = 0, значит, числа могут быть 0 и 0: 50 205;
15 — 12 = 3, значит, числа могут быть 0 и 3 или 1 и 2: 50 235 или 53 205 или 51 225 или 52 215;
18 — 12 = 6, значит, числа могут быть 0 и 6 или 1 и 5 или 2 и 4 или 3 и 3: 50 265 или 56 205 или 51 255 или 55 215 или 52 245 или 54 225 или 53 235;
21 — 12 = 9, значит, числа могут быть 0 и 9 или 1 и 8 или 2 и 7 или 3 и 6 или 4 и 5: 50 295 или 59 205 или 51 285 или 58 215 или 52 275 или 57 225 или 53 265 или 56 235 или 54 255 или 55 245;
24 — 12 = 12, значит, числа могут быть 3 и 9 или 4 и 8 или 5 и 7 или 6 и 6: 53 295 или 59 235 или 54 285 или 58 245 или 55 275 или 57 255 или 56 265;
27 — 12 = 15, значит, числа могут быть 6 и 9 или 7 и 8: 56 295 или 59 265 или 57 285 или 58 275;
30 — 12 = 18, значит, числа могут быть 9 и 9: 59 295.
г) 7 + 2 + 8 = 17, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 17 + 9 + 9 = 35, которая не делится на 3. В промежутке от 17 до 35 следующие числа делятся на 3: 18, 21, 24, 27, 30, 33.
В промежутке от 17 до 35 следующие числа делятся на 3: 18, 21, 24, 27, 30, 33.
18 — 17 = 1, значит, числа могут быть 0 и 1: 72 018 или 72 108;
21 — 17 = 4, значит, числа могут быть 0 и 4 или 1 и 3 или 2 и 2: 72 048 или 72 408 или 72 138 или 72 318 или 72 228;
24 — 17 = 7, значит, числа могут быть 0 и 7 или 1 и 6 или 2 и 5 или 3 и 4: 72 078 или 72 708 или 72 168 или 72 618 или 72 258 или 72 528 или 72 348 или 72 438;
27 — 17 = 10, значит, числа могут быть 1 и 9 или 2 и 8 или 3 и 7 или 4 и 6 или 5 и 5: 72 198 или 72 918 или 72 288 или 72 828 или 72 378 или 72 738 или 72 468 или 72 648 или 72 558;
30 — 17 = 13, значит, числа могут быть 4 и 9 или 5 и 8 или 6 и 7: 72 498 или 72 948 или 72 588 или 72 858 или 72 678 или 72 768;
33 — 17 = 16, значит, числа могут быть 7 и 9 или 8 и 8: 72 798 или 72 978 или 72 888.
На 5 делятся числа, оканчивающиеся на цифру 0 и 5, поэтому все числа в пунктах а), б) и в) будут делиться на 5.
На 2 делятся числа, оканчивающиеся на цифру 0, 2, 4, 6, 8, поэтому все числа в пунктах б) и г) будут делиться на 2.
На 10 делятся числа, оканчивающиеся на цифру 0, поэтому все числа в пункте б) будут делиться на 10.
На 4 делятся числа, последние две цифры которых образуют число, кратное 4. Поэтому все числа в пункте б) и числа 72 108, 72 048, 72 408, 72 228, 72 708, 72 168, 72 528, 72 348, 72 288, 72 828, 72 468, 72 648, 72 948, 72 588, 72 768, 72 888 из пункта г) будут делиться на 4.
645. а) Напишите четырехзначное число, которое делится на 9. Может ли оно не делится на 3?
б) Напишите четырехзначное число, которое делится на 3, но не делится на 9.
а) 9333 делится на 9, поскольку 9 + 3 + 3 + 3 = 18, а 18 кратно 9. Не может, так как любое число обязательно делится на 3, если оно делится на 9, так как 9 кратно 3.
б) 2112 делится на 3, поскольку 2 + 1 + 1 + 2 = 6, а 6 кратно 3, но не делится на 9, так как 6 не кратно 9.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А. В.
В.
Математика. 5 класс
Четные и нечетные числа — определение, признаки и свойства
Одной из характеристик числа является его кратность двум. Простое арифметическое свойство стало основой для мистических верований древних людей, служит фундаментом для быстрых алгебраических вычислений и геометрических формул. Нечетные и четные числа широко используются современным человеком в повседневной жизни.
Содержание
- Арифметические свойства
- Характеристика парности у ноля
- Свойства группы для вычислений
- История и значение в культуре
- Практическое применение
Арифметические свойства
Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.
Метод работает для любых многозначных чисел.
Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.
Закономерности арифметических операций с целыми числами:

Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.
При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.
Характеристика парности у ноля
Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.
В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.
Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.
Признаки четности ноля:
Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.
Свойства группы для вычислений
Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.
Алгоритм оптимизированного решения:
Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.
Примеры логических задач для решения через характеристику парности:
 Сколько всего малышей, если известно, что соблюдено чередование девочек и ребят?
Сколько всего малышей, если известно, что соблюдено чередование девочек и ребят?Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.
com/embed/3e0AQyCr08U»>Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.
История и значение в культуре
Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.
Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.
Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.
У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.
Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.
Практическое применение
Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.
В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.
В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.
Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.
Предыдущая
МатематикаПараллельность плоскостей — способы, модели и примеры решения и построения
Следующая
МатематикаЧетырехугольник, вписанный в окружность — основные свойства, признаки и формулы
Тест на простоту. Может ли нечетное число делиться без остатка на целое число, большее, чем его квадратный корень?
Спросил
Изменено 3 года, 2 месяца назад
Просмотрено 150 раз
$\begingroup$
Я уже видел это раньше на веб-сайте по программированию. Это был эффективный алгоритм проверки того, является ли число простым. Я никогда не видел никаких доказательств для этого алгоритма, поэтому я хотел бы, чтобы кто-нибудь предоставил его здесь. Алгоритм работы следующий:
Это был эффективный алгоритм проверки того, является ли число простым. Я никогда не видел никаких доказательств для этого алгоритма, поэтому я хотел бы, чтобы кто-нибудь предоставил его здесь. Алгоритм работы следующий:
Шаг №1 : Проверить, делится ли число на 2. Если да, перейти к шагу №2 ; В противном случае это не премьер. (кроме 2, конечно.)
Шаг #2 : Проверить, делится ли число на любое нечетное число от 3 до квадратного корня из числа . Если это не так, это простое число; В противном случае это не премьер.
Пример №1. Проверить, является ли число 55 простым:
- Делится ли 55 на 2? нет, иди дальше.
- Мы ищем в диапазоне ($3: \sqrt{55}$), который равен ($3: 7,41$). Итак, мы проверяем каждое нечетное число от 3 до 7:
- 55 делится на 3? Нет, иди дальше.
- Делится ли 55 на 5? Да. Это не простое число.
- Мы не продолжаем поиск, так как мы уже нашли число, которое делит 55.

Пример #2. Проверка, является ли число 181 простым:
- Делится ли 181 на 2? нет, иди дальше.
- Мы ищем в диапазоне ($3: \sqrt{181}$), который равен ($3: 13,45$). Итак, мы проверяем каждое нечетное число от 3 до 13:
- Делится ли 181 на 3? Нет, иди дальше.
- Делится ли 181 на 5? Нет, иди дальше.
- Делится ли 181 на 7? Нет, иди дальше.
- Делится ли 181 на 9? Нет, иди дальше.
- Делится ли 181 на 11? Нет, иди дальше.
- Делится ли 181 на 13? Число 181 — это простое число .
Итак, мне нужно строгое доказательство следующего утверждения:
Учитывая нечетное простое число $n$, $n$ никогда не может делиться нацело на целое число $x$; для $x\geq\sqrt{n}$
- тест на простоту
$\endgroup$
2
$\begingroup$
То, что вы хотите доказать, является ложным. $$
15 = 3 х 5
$$
и $5$ больше, чем квадратный корень из $15$. Верно то, что если $n$ не простое число, то его нетривиальный множитель не больше его квадратного корня. Чтобы увидеть это, напишите
$$
п = аб
$$
и обратите внимание, что у вас не может быть $a$ и $b$ больше, чем $\sqrt{n}$.
$$
15 = 3 х 5
$$
и $5$ больше, чем квадратный корень из $15$. Верно то, что если $n$ не простое число, то его нетривиальный множитель не больше его квадратного корня. Чтобы увидеть это, напишите
$$
п = аб
$$
и обратите внимание, что у вас не может быть $a$ и $b$ больше, чем $\sqrt{n}$.
Вот почему вам нужно только проверить простые числа до квадратного корня, чтобы определить, является ли само $n$ простым.
$\endgroup$
3
$\begingroup$
Возьмем, к примеру, $39$. Квадратный корень из $39$ находится между $6$ и $7$, но $39$ делится на $13$.
$\endgroup$
$\begingroup$
Очевидно, что нечетное число больше 1 само по себе является одним из своих делителей, превышающих квадратный корень. Для правильного делителя, большего, чем квадратный корень, рассмотрим делитель 5 из 15.
$\endgroup$
$\begingroup$
Верно (и на это опирается алгоритм) вот что:
Лемма . $(i)\,$ Пусть $n$ — натуральное число. Наименьшее целое число $p>1$, на которое делится $n$, простое.
$(ii)\,$ Если $n$ не простое число, $1
Доказательство простое:
$(i)$ если бы $p$ не было простым, у него был бы нетривиальный делитель; поскольку этот делитель также будет делителем $n$, $p$ не будет наименьший делитель $>1$ числа $n$.
$(ii)$ пусть $m=\smash{\dfrac np}$; это еще один делитель $n$, и если мы предположим, что $p>\sqrt n$, так как $p $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Почему два — единственное четное число, которое является простым?
Спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 72k раз
$\begingroup$
Все остальные простые числа являются нечетными, например, $5, 11, 127, $ и $37$. Так почему же $2$ — единственное простое четное число?
Это потому, что он имеет только 1 и сам такой, хотя он четный? Проверьте это на этой превосходной математической странице, расположенной на четверть снизу.
- элементарная теория чисел
$\endgroup$
7
$\begingroup$
Почему двойка — единственное четное число $($binary$)$, которое является простым?
По той же причине, что три — единственное простое троичное число. По той же причине пятерка — единственное простое пятерное число. И т.д.
По той же причине пятерка — единственное простое пятерное число. И т.д.
$\endgroup$
3
$\begingroup$
Потому что каждое четное число, отличное от 2 , равно , которое, очевидно, делится на 2 , и поэтому по определению не может быть простым.
$\endgroup$
$\begingroup$
(положительное) четное число — это такое число $n$, что $n = 2 \cdot k$ для некоторого (положительного) целого числа $k$. Простое число имеет только себя и $1$ в качестве (положительных) делителей.
Что произойдет, если $n \not = 2$ в нашем определении четных чисел?
$\endgroup$
0
$\begingroup$
Выберите простое число $p$. Назовем число $n$ $p$-делимым, если $p\mid n$. Тогда $p$ — единственное простое число, делимое на $p$, что тривиально. В частности, $2$ — это единственное $2$-кратное или даже простое число.
Назовем число $n$ $p$-делимым, если $p\mid n$. Тогда $p$ — единственное простое число, делимое на $p$, что тривиально. В частности, $2$ — это единственное $2$-кратное или даже простое число.
$\endgroup$
1
$\begingroup$
В целых числах $-2$ — еще одно четное простое число.
Для разнообразия в целых числах Гаусса $2$ не является простым: например. факторы как $(1+i)(1-i)$. Четные простые числа гауссовых целых чисел равны $\pm 1 \pm i$, хотя все они являются «одними и теми же» простыми числами в том же смысле, что и в целых числах $2$ и $-2$ являются «одними и теми же» простыми числами.
(я определяю «четность» в числовом поле как эквивалент четности его нормы)
В кольце всех рациональных чисел с нечетным знаменателем $2/7$ является четным простым числом. На самом деле, $2/n$ простое число для каждого нечетного целого числа $n$. (но опять же, это все «одинаковые» простые числа)
(но опять же, это все «одинаковые» простые числа)
Существуют также числовые кольца, в которых есть разные четные простые числа, которые не являются «одними и теми же» в смысле, подразумеваемом выше.
$\endgroup$
$\begingroup$
Простое число таково, что на оно делится только на и на единицу. Включение 1 в качестве простого числа нарушило бы фундаментальную теорию арифметики, поэтому в современной математике это исключено. Два — простое число, потому что оно делится только на два и один. Все остальные четные числа не являются простыми, потому что все они делятся на два. Остаются только нечетные числа. Конечно, не все нечетные числа являются простыми (например, девять делится на три).
$\endgroup$
$\begingroup$
Слово «прайм» происходит от латинского слова primus , что означает «первый». Два (2) — первое четное число. Другими словами, он начинает все четные числа. Существует более одного нечетного простого числа, потому что нечетные числа никогда не делятся на 2.
Два (2) — первое четное число. Другими словами, он начинает все четные числа. Существует более одного нечетного простого числа, потому что нечетные числа никогда не делятся на 2.
$\endgroup$
3
$\begingroup$
Число $2$ имеет только два целых числа: $1$ и само себя. Вот и все после этого: все остальные числа, которые больше двух, все каким-то образом делятся на это число. Это также известно как «самое нечетное простое число», потому что это единственное четное простое число, поэтому оно также известно как нечетное. Я предполагаю, что теперь это в значительной степени касается вопроса о том, почему это может произойти.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как делить нечетные числа
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ИСАТ
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- Французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Арифметика » Целые числа » Четные/нечетные числа » Как делить нечетные числа
Выберите ответ, который лучше всего решает следующее уравнение:
Возможные ответы:
Правильный ответ:
Объяснение:
Есть два способа решить эту проблему. Сначала вы можете сделать это алгебраически, разделив обе части на 13:
Сначала вы можете сделать это алгебраически, разделив обе части на 13:
Но есть и другой способ, который, если вы понимаете нечетные числа, еще быстрее. Из всех ответов выше только один нечетный. Вы знаете, что данное уравнение должно быть нечетным — любое нечетное число, умноженное на нечетное число, даст нечетное число. Если вы умножите нечетное число на четное число, вы получите четное число.
Сообщить об ошибке
Найдите в следующем уравнении:
Возможные ответы:
Правильный ответ:
5 Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (29), которое даст другое нечетное число (493) при умножении на заданное нечетное число (17).
2. Решить алгебраически:
Отчет о ошибке
Решение для уравнения в Фоллвинге:
Возможные ответы:
Правильный ответ:
9Правильный ответ:
. Правильный ответ:
Правильный ответ:
9. Правильный ответ:
. Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (85), которое дает другое нечетное число (7,735) при умножении на заданное нечетное число (91).
2. Решить алгебраически:
Отчет о ошибке
Уведомление об авторском праве
Посмотреть акт математики
Mary Paige
Сертифицированный Tutor
Университет Оклахомы Норманский камм, Bachelor of Ncience, Образование. Северо-восточный государственный университет, магистр искусств, советник…
View ACT Math Tutors
Lloyd
Сертифицированный репетитор
Университет Рочестера, бакалавр наук, экономика. Университет Рочестера, бакалавр наук, математика.
View ACT Math Tutors
Monica
Сертифицированный преподаватель
Главный кампус Университета Пердью, бакалавр наук, подготовка учителей математики. Университет Конкордия, Анн-Арбор, магистр …
Университет Конкордия, Анн-Арбор, магистр …
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Можно ли разделить нечетное число на четное?
Согласно правилу №3, невозможно получить четное число путем умножения двух нечетных чисел ; хотя бы одно число должно быть четным. … Не существует общего правила, согласно которому четное число (ab), деленное на другое четное число, всегда будет целым числом. Может ли адресат оферты отозвать акцепт? случаи отзыва приемки .
При умножении нечетного числа на нечетное число ответ всегда будет нечетным?
: Так как нечетно, то также нечетно, так как и нечетное число, умноженное на нечетное число, дает нечетное произведение . Поскольку оно тоже нечетное, умножение его на снова даст нечетное произведение, поэтому это выражение всегда нечетное.
Что такое P нечетная математика?
В математике четность — это свойство целого числа быть четным или нечетным . Четность целого числа четна, если оно делится на два без остатка, и его четность нечетна, если это не так; то есть его остаток равен 1,
На какие числа можно делить нечетные числа?
Нечетные числа — это числа, не кратные 2, такие как 3, 5, 7 и 9. Поскольку нечетное число нельзя разделить пополам без остатка, такой расчет может оказаться сложным. Важно помнить, что нечетное число будет иметь остаток 1 при делении на 2 .
Почему нечетные числа нельзя делить поровну?
Почему? Нет, ноль — это не нечетное число , а четное число, потому что при делении 0 на 2 получается частное равное 0, а также после деления не остается остатка. Итак, 0 делится на 2 без остатка.
Что такое четные и нечетные числа?
Что такое четные и нечетные числа? Четные числа делятся на 2 без остатка . Они заканчиваются на 0, 2, 4, 6 или 8. Нечетные числа не делятся на 2 без остатка и оканчиваются на 1, 3, 5, 7 или 9.
Нечетные числа не делятся на 2 без остатка и оканчиваются на 1, 3, 5, 7 или 9.
Что такое нечетное деление на нечетное?
Правильный ответ: 1. Воспользуйтесь правилом, согласно которому любые два нечетных числа , умноженные вместе, дадут еще одно нечетное число. Используя это правило, только один ответ является нечетным числом (29), которое даст другое нечетное число (49).3) при умножении на заданное нечетное число (17).
На какое целое число всегда делится четное число?
Четные числа — это числа, которые можно без остатка разделить на 2 .
Все ли кратны 3 Нечетные?
Всегда ли числа, кратные 3, нечетны? … Нет , числа, кратные 3, не всегда нечетны. Например, 6, 12 и 18 — четные числа, кратные 3. Если 3 умножить на четное число, произведение будет четным числом.
Какова нечетная вероятность P?
P(нечетные числа) Малонда, Вероятности выражаются как десятичных знаков от 0 до 1 . Таким образом, вероятность P(орел) при подбрасывании монеты равна 0,5. Вероятность Р(високосный год) родиться в високосный год равна 0,25.
Вероятность Р(високосный год) родиться в високосный год равна 0,25.
Почему нечетные числа называются нечетными?
Нечетные числа — это числа , которые нельзя расположить парами . Древние греки считали нечетными числа, которые нельзя расположить в два ряда. Эта концепция менялась на протяжении тысячелетий.
Какие нечетные числа можно разделить на 2?
Нечетное число не делится на два . Нечетные числа определяются как те числа, которые имеют вид 2*n+1, где n — целое число. Ответ на вопрос: есть ли нечетные числа, которые делятся на 2? Все нечетные числа делятся на 2 или любое другое число (например, 1,7, 2,3 400 и т. д.).
Все ли нечетные числа можно разделить на 3?
Существует бесконечно много нечетных чисел с 3 простыми делителями: 105, 165, 195, 255, … Конечно, другие простые числа (которые, за исключением 2, все нечетные), конечно, не делятся на 3 (это в определении). Никакое нечетное число не делится на 3, например. 3,9,15,21,27,33…. А какое-то нечетное число не делится на 3e.
3,9,15,21,27,33…. А какое-то нечетное число не делится на 3e.
Можно ли делить четные числа на 2?
Все четные числа делятся на 2 . Следовательно, число делится на 2, если в нем стоят 0, 2, 4, 6 или 8 на месте единиц. Например, 54 и 2870 делятся на 2, а 2221 не делится на 2.
Почему два нечетных числа равны четному?
простой ответ заключается в том, что между каждым нечетным числом есть разница в одну цифру. поэтому , когда вы добавляете один и один, становится двумя, то есть даже . Вот почему сложение нечетных чисел становится четным.
Можно ли разделить на 4 нечетные числа?
34,807 – последняя цифра 7. Это означает, что число НЕЧЕТНОЕ и 2 не делится на него без остатка. … Правило для 4 : Если две последние цифры целого числа делятся на 4, то и все число делится на 4 .
При сложении двух нечетных чисел сумма будет четной или нечетной?
Сумма двух нечетных чисел всегда четна . Произведение двух и более нечетных чисел всегда нечетно.
Является ли 2 нечетным числом?
2 нечетное число.
Что называют нечетным числом?
Определение нечетного числа: целое число, которое нельзя разделить на два на два равных целых числа Числа 1, 3, 5 и 7 являются нечетными числами.
Что произойдет, если разделить нечетное число на нечетное число?
Правильный ответ: В качестве проверки, если вы разделите нечетное число на другое нечетное число, ваш результат должен быть нечетное .
По какой формуле разделить нечетное количество команд?
Количество команд в верхней половине = n/2 Когда количество команд нечетное, например, 3,5,7,9 и т. д. Тогда применяется следующая формула: n=общее количество. команд (где n=3,5,7,9)
Почему сумма четного и нечетного числа всегда нечетна?
четное число нечетное. При сложении двух слагаемых одновременно ответ меняется между четным и нечетным. Когда последние два числа складываются вместе , одно четное, а другое нечетное. Следовательно, сумма нечетна, что делает произведение нечетным, поскольку оно эквивалентно сумме.
Следовательно, сумма нечетна, что делает произведение нечетным, поскольку оно эквивалентно сумме.
Является ли произведение трех нечетных чисел нечетным?
Произведение трех нечетных чисел равно нечетному . Если четное число разделить на 2, то частное всегда будет нечетным. Все простые числа нечетные. Простые числа не имеют делителей.
Чему кратно 4?
Кратность 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48 , …
Является ли ноль четным числом?
Итак, давайте рассмотрим 0 так же, как и любое другое целое число. Когда 0 делится на 2, результирующее частное также оказывается равным 0 — целому числу, таким образом, классифицируется как четное число .
Чему кратно 6?
Здесь снова кратные 6, 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96 ,… Если мы разделим любое из этих множителей на 6, мы получаем частное с нулевым остатком.
Как число может быть четным?
Четные числа — это те числа, которые можно разделить на две равные группы или пары и которые точно делятся на 2 . Например, 2, 4, 6, 8, 10 и так далее. … Следовательно, 10 — четное число.
Например, 2, 4, 6, 8, 10 и так далее. … Следовательно, 10 — четное число.
Как найти вероятность нечетного числа?
Для любого вопроса, подобного этому, вы берете количество способов, которыми может произойти событие (нечетное число) , и делите на общее количество возможностей (граней игральной кости) . Если вы предполагаете, что у шестигранного кубика есть 3 нечетных числа, 1,3, 5. И всего 6 граней, поэтому 3/6 = 1/2 или 50%.
Какова вероятность получить нечетную сумму?
∴ Вероятность выпадения нечетной суммы равна 1/2 .
Что из перечисленного не может быть вероятностью события?
Правильный вариант (б) : – 1,5 Вероятность события не может быть – 1,5, т.к. Вероятность события никогда не может быть отрицательной. Вероятность наступления события всегда лежит в пределах от 0 до 1 (от 0 до 1 включительно), т. е. 0 ≤ P(E) ≤ 1.
Какова вероятность получить два четных числа?
Таким образом, шанс выпадения четного числа на двух кубиках равен 1/2 x 1/2… что равно 1/4, или 25% .
Чему равно P больше 5 )?
Значение p выше 0,05 (> 0,05) не является статистически значимым и указывает на убедительные доказательства нулевой гипотезы . Это означает, что мы сохраняем нулевую гипотезу и отвергаем альтернативную гипотезу. Вы должны отметить, что вы не можете принять нулевую гипотезу, мы можем только отвергнуть нулевую гипотезу или не отвергнуть ее.
Почему он называется нечетным и четным?
Число, которое делится на 2 и дает в остатке 0 , называется четным числом. Нечетное число — это число, которое не делится на 2. Свойство, по которому мы классифицируем целое число в математике как четное или нечетное, также известно как четность. …
Чему равна сумма любых двух нечетных чисел?
Сумма любых двух нечетных чисел равна , всегда четное число .
Как найти нечетность двух чисел?
- Если L или R нечетные, то количество нечетных чисел будет N/2 + 1, а четных чисел = N – countofOdd.

- В противном случае количество нечетных чисел будет N/2, а четных = N – countofOdd.
Какие целые числа не делятся на 2?
Полное пошаговое решение: Целые числа, которые не делятся на 2, называются нечетными числами . Например. 1, 3, 5, 7 и т. д.
Как разделить на 2?
Чтобы разделить число на 2 с помощью многократного вычитания, вычтите из него 2 снова и снова, пока не получите 0. Количество раз, которое вы вычитаете, является ответом на задачу деления.
[ИКС]
Четные и нечетные числа – Made Easy
В вашем браузере деактивирован JavaScript.
Чтобы получить доступ ко всем функциям нашего веб-сайта,
активируйте JavaScript для вашего браузера.
Попробуйте 30 дней бесплатно
Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!
Рейтинг
Ø 4,6 / 5 оценок
Вы должны войти в систему, чтобы иметь возможность дать оценку.
Вау, спасибо!
Оцените нас и в Google! Мы с нетерпением ждем этого!
Перейти в Google
Авторы
Юджин Ли
Основы по теме
Четные и нечетные числа Число называется четным тогда и только тогда, когда оно делится на 2; в противном случае это считается странным. Еще один способ узнать, является ли число четным или нечетным, просто посмотреть на его последнюю цифру. Если число оканчивается на 0, 2, 4, 6 или 8, то оно четное, а если на 1, 3, 5, 7 или 9, то оно нечетное. Например, глядя на числа 125 и 236, мы видим, что, поскольку 5 — последняя цифра числа 125, оно нечетное, а 236 оканчивается на 6, которое делится на 2, поэтому оно четное. Узнайте, как определить число, четное оно или нечетное, помогая Нечетной Осени и Четный Стивену, двум бесстрашным друзьям, которые отправляются в лес Сплиткипарис, чтобы найти Пуфстрича, разделить свою добычу или еду поровну. Общий основной справочник: CCSS.MATH.CONTENT.4.OA.C.5
Если число оканчивается на 0, 2, 4, 6 или 8, то оно четное, а если на 1, 3, 5, 7 или 9, то оно нечетное. Например, глядя на числа 125 и 236, мы видим, что, поскольку 5 — последняя цифра числа 125, оно нечетное, а 236 оканчивается на 6, которое делится на 2, поэтому оно четное. Узнайте, как определить число, четное оно или нечетное, помогая Нечетной Осени и Четный Стивену, двум бесстрашным друзьям, которые отправляются в лес Сплиткипарис, чтобы найти Пуфстрича, разделить свою добычу или еду поровну. Общий основной справочник: CCSS.MATH.CONTENT.4.OA.C.5
Стенограмма
Четные и нечетные числаНечетная Осень и Четный Стивен несколько месяцев назад отправился на поиски Сплиткипарисового леса, чтобы найти Пуффстриха. Каждый день они ищут пищу на ночь — и каждую ночь пара делит дневной улов. Чтобы эти бесстрашные друзья могли поровну разделить свою добычу, им нужно знать о четных и нечетных числах.
Посмотрим, что они сегодня нашли. Двое друзей выгружают свои тележки в небольшую кучу между собой. У Отэм в тележке 11 очаровательных ягод. Прежде чем решить, смогут ли они разделить одиннадцать ягод поровну, им нужно знать: Является ли 11 числом 9?0016 четное или нечетное число ? делится на 2 ?
У Отэм в тележке 11 очаровательных ягод. Прежде чем решить, смогут ли они разделить одиннадцать ягод поровну, им нужно знать: Является ли 11 числом 9?0016 четное или нечетное число ? делится на 2 ?
Понимание делимости
Прежде чем мы ответим на этот вопрос, нам нужно понять делимость . В математике мы говорим, что число делится на другое число, если частное или ответ представляет собой целое число без остатка . Четные числа — это все целые числа , которые делятся на на число 2 , а нечетные числа — все остальные (не делящиеся на 2 без остатка). Осень смотрит с помощью длинного деления. Остаток 1! 11 не должно быть четным числом! Итак, если они поделят ягоды шарма поровну, у них останется одна.
Определение четности или нечетности
Но должен быть более быстрый способ, чем деление в длину , чтобы определить, является ли число четным или нечетным. К счастью, даже Стивен знает, что вам нужно только посмотреть на последнее число, чтобы определить 9.0016 четность — четность или нечетность числа. Если число заканчивается на 1, 3, 5, 7 или 9, оно нечетное. В противном случае это даже.
К счастью, даже Стивен знает, что вам нужно только посмотреть на последнее число, чтобы определить 9.0016 четность — четность или нечетность числа. Если число заканчивается на 1, 3, 5, 7 или 9, оно нечетное. В противном случае это даже.
Отэм достает из своей тележки следующие предметы. Вау! У нее 15 больших фруктов! Она следует совету Стивена и просто смотрит на последнюю цифру — 5. Поскольку последняя цифра равна нечетному , Отэм неохотно признает, что 15 тоже должно быть нечетным. Таким образом, после того, как они поделились поровну, у них снова остался один.
Теперь, когда тележка Странной Осени пуста, пришло время осмотреть тележку Стивена. Стивен производит 128 семян вивизии из своей тележки. Поскольку Стивен так привык просто смотреть на последнее число, чтобы определить, четное оно или нечетное, он концентрируется на 8.
За всю свою практику Стивен запомнил, что четные цифры равны 9. 0016 0, 2, 4, 6 и 8 . Поскольку 8 — это последняя цифра из 128, и она есть в списке, который он запомнил, 128 должно быть четным числом ! Таким образом, они могут равномерно распределить семена без каких-либо остатков.
0016 0, 2, 4, 6 и 8 . Поскольку 8 — это последняя цифра из 128, и она есть в списке, который он запомнил, 128 должно быть четным числом ! Таким образом, они могут равномерно распределить семена без каких-либо остатков.
Теперь, когда двое друзей поровну поделили свой дневной улов между собой, что им делать с оставшимися чармберри и магнезией? О, посмотри! Наконец-то Паффстрих! Им повезло! Говорят, что Puffstriches любят очаровательные ягоды и фрукты. Может быть, этот захочет быть их домашним животным.
Упражнение с четными и нечетными числами
Хотите применить полученные знания? Вы можете повторить и потренироваться с заданиями к видео Четные и нечетные числа .
Определить, является ли число 11 четным или нечетным.
Подсказки
Четное число делится на 2 и не имеет остатка.

Нечетное число дает остаток при делении на 2.
Решение
Осень знает, что четное число делится на 2 без остатка. Нечетные числа имеют остаток при делении на два.
Таким образом, Отэм знает, что если она разделит 11 на 2, то сможет выяснить, четное это число или нечетное. Она знает, что если она получит остаток, то 11 должно быть нечетным. Если она не получает остатка, то 11 должно быть четным.
Отэм делит 11 на два с помощью длинного деления. Вы можете увидеть ее расчеты на изображении.
Она находит, что 11 разделить на 2 равно 5 с остатком 1.
Поскольку остаток равен 1, 11 должно быть нечетным.
Обобщите свои знания о четных и нечетных числах.
Подсказки
Число делится на два, если при делении этого числа на два не получается остатка.
Четные числа делятся на два.
Решение
Четный Стивен изучает некоторые ключевые факты о четных и нечетных числах, прежде чем приступить к составлению утверждений Отем.

Число делится на два, если при делении этого числа на два не получается остатка.
Четные числа делятся на два. Нечетные числа не делятся на два.
Итак, Стивен знает, что:
«Нечетные числа… это все числа, которые не делятся без остатка на два».
«Все числа, которые… делятся на два, являются четными числами.»
«Четные числа… все делятся на два без остатка.»
«Числа, дающие остаток при делении на два… нечетные.»
Определите, какие числа четные, а какие нечетные.
Подсказки
Если вы разделите число на $2$ и получите остаток, это число будет нечетным.
Если вы разделите число на $2$ и не получите остатка, это число будет четным.
Число является четным, если его последняя цифра — $0$, $2$, $4$, $6$ или $8$.
Решение
Если вы разделите число на $2$ и получите остаток, это число будет нечетным. Если вы разделите число на $2$ и не получите остатка, это число будет четным.

Но даже у Стивена есть хитрость: он знает, что число четное, если его последняя цифра — $0$, $2$, $4$, $6$ или $8$. Число является нечетным, если его последняя цифра равна $1$, $3$, $5$, $7$ или $9.$.
Используя трюк Стивена, мы можем увидеть, что:
$6$ груш, $14$ грецких орехов и $26$ листьев базилика — все четные числа.
Лесные орехи по 19$, яблоки по 7$ и вишни по 11$ — все это нечетные числа.
Определите, какие числа четные, а какие нечетные.
Подсказки
Если число заканчивается на $1$, $3$, $5$, $7$ или $9$, то оно нечетное.
Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное.
Решение
Если число оканчивается на $1$, $3$, $5$, $7$ или $9$, то оно нечетное.
Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное.
Таким образом, 283$, 8247$, 921$ и 3011$ нечетны.
И у нас есть четные 926$, 4822$, 9740$ и 2734$.

Объясните, что значит, если одно число делится на другое число.
Подсказки
Число является четным, если его последняя цифра — $0$, $2$, $4$, $6$ или $8$.
Если число делится на $3$, вы не получите остатка при делении этого числа на $3$.
Решение
Если вы разделите число на $2$ и получите остаток, это число будет нечетным, а не четным.
Число делится на два, если при делении этого числа на два не получается остатка. Итак, третье утверждение верно.
Число является четным, если его последняя цифра — $0$, $2$, $4$, $6$ или $8$. Итак, четвертое утверждение верно.
Выберите четные числа.
Подсказки
Если число заканчивается на $1$, $3$, $5$, $7$ или $9$, то оно нечетное.
Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное.
Решение
Если число оканчивается на $1$, $3$, $5$, $7$ или $9$, то оно нечетное.
 Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное. Эти правила всегда верны, независимо от того, сколько цифр в числе.
Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное. Эти правила всегда верны, независимо от того, сколько цифр в числе.Таким образом, из заданных чисел четными являются только следующие числа:
$134$ — $624$ — $938$ — $836$
$7298$ — $2084$ — $3942$ — $3094$
$20932$ — $83584$ — $65692$ — $89264$
Еще видео по теме Характеристики номеров
Четные и нечетные числа
Правила делимости — 3, 6, 9
Правила делимости — 7
Правила делимости — 4, 5, 8, 10
Простые числа
Компания
- Наша команда
- Цены
- Вакансии
Платформа
Как это работает
- Обучающие видео
- Упражнения
- Диван-герой
- Рабочие листы
- Чат
Справка
- Часто задаваемые вопросы
- Дайте нам отзыв
Юридический
- Условия
- Право на отзыв
- Политика конфиденциальности
- Свяжитесь с нами
- Не продавать мою личную информацию
Есть вопросы? Свяжитесь с нами!
help@sofatutor. com
com
- дивантутор.com
- диван-репетитор.ch
- диван-репетитор.ат
- дивантутор.com
- ru.sofatutor.co.uk
Есть вопросы? Свяжитесь с нами!
Четные и нечетные числа, Свойства, Как найти, Примеры решения
Четные и нечетные числа — это два типа классификации целых чисел. Это означает, что при сложении четных и нечетных чисел мы получаем множество целых чисел.
В этой статье мы изучим, что такое четные и нечетные числа, их определения, как определить, является ли число четным или нечетным с примерами, их различиями и сходствами, а также их свойствами с помощью решенных примеров и часто задаваемых вопросов.
Что такое четные и нечетные числа?
Четные и нечетные числа являются частью системы счисления. Понимание четных и нечетных чисел является базовой математикой и важной темой алгебры.
Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9.
Числа, которые нельзя разделить на пары без остатка, называются нечетными. Когда вы делите нечетные целые числа на два, вы получаете остаток от единицы. Вместо единиц в нечетных числах стоят цифры 1, 3, 5, 7 или 9.. Нечетные числа — это целые числа, которые при делении на два всегда оставляют остаток. Это целые числа типа n = 2k + 1, где k — натуральное число. К нечетным числам относятся такие числа, как 51, 733, 55, 97 и так далее.
Определение нечетных и четных чисел
Определения нечетных и четных чисел приведены ниже:
Определение четных чисел
Четное число — это целое число, которое можно разделить на два на два равных целых числа. числа 0, 2, 4, 6 и 8 — четные числа. Список четных чисел бесконечен, потому что счет продолжается до бесконечности. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом.
числа 0, 2, 4, 6 и 8 — четные числа. Список четных чисел бесконечен, потому что счет продолжается до бесконечности. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом.
Определение нечетных чисел
Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два.
Например, 13 не делится точно на два, так как при делении на два остается единица. В результате 13 — необычное число. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9, 11, 13, 15,……, 51, 53,…… и так далее. Это нечетное число. Таким образом, нечетные числа оканчиваются на 1, 3, 5, 7 и 9..
Таблица четных и нечетных чисел
Нечетные числа выделены синим цветом, а четные — фиолетовым в таблице чисел. Любое число, оканчивающееся на 1, 3, 5, 7 или 9, является нечетным числом, на что указывает синяя подсветка. Целые числа, оканчивающиеся на 2, 4, 6, 8 и 0, выделены фиолетовым цветом, что указывает на то, что все они являются четными числами.
Целые числа, оканчивающиеся на 2, 4, 6, 8 и 0, выделены фиолетовым цветом, что указывает на то, что все они являются четными числами.
Как найти нечетные и четные числа?
Существует два способа определить, является число четным или нечетным. Они следующие:
1 . В месте нахождения единицы проверьте цифру числа:
Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа.
Нечетные числа — это те, которые заканчиваются цифрами 1,3,5,7 и 9.
7,11,283,5735,9859 и так далее.
Данное число является нечетным, так как число 2835 оканчивается цифрой 5 (нечетное число).
Кроме того, четными считаются числа, оканчивающиеся цифрами 0, 2, 4, 6 и 8.
Данное число является четным, так как число 2838 заканчивается цифрой 8 (четное число).
2. По группировке:
Всего на этом изображении 11 точек. Все точки не связаны. На картинке не хватает одной точки.
Все точки не связаны. На картинке не хватает одной точки.
Нечетные числа — это числа, которые нельзя поставить вместе парами.
Нечетные числа — это любые числа, которые не делятся точно на два.
Теперь 12 точек. Поскольку все точки парные и не осталось ни одной непарной точки, мы можем заключить, что 12 — четное число.
Мы можем сделать вывод, что четные числа — это все те, которые можно разделить на пары.
Свойства четных и нечетных чисел
Некоторые из важных свойств четных чисел приведены ниже: четное число. Например: 10 + 4 = 14
- Свойство вычитания двух четных чисел гласит, что когда мы вычитаем два четных числа, результатом всегда будет четное число. Например: 10 – 4 = 6
- Свойство сложения одного нечетного и одного четного числа гласит, что , когда мы складываем четное число и нечетное число, результат всегда будет нечетным.
 Например: 9 + 4 = 13
Например: 9 + 4 = 13
- Свойство вычитания одного нечетного и одного четного числа гласит, что w когда мы вычитаем четное число и нечетное число, результат всегда будет нечетным. Например: 9– 4 = 5
- Свойство сложения двух нечетных чисел гласит, что при сложении двух нечетных чисел всегда получается четное число. Например: 7 + 3 = 10
- Свойство вычитания двух нечетных чисел гласит, что при вычитании двух нечетных чисел всегда получается четное число. Например: 7 – 3 = 4
- Свойство умножения двух четных чисел гласит, что при умножении двух четных чисел результатом всегда будет четное число. Например: 10 × 4 = 40
- Свойство умножения одного нечетного и одного четного числа гласит, что когда мы умножаем четное число на нечетное число, результатом всегда будет четное число. Например: 7 × 6 = 42
- Свойство умножения двух нечетных чисел гласит, что при умножении двух нечетных чисел всегда получается нечетное число.
 Например: 7 × 5 = 35
Например: 7 × 5 = 35
Разница между нечетными и четными числами
Разница между нечетным числом и четным числом следующая:
| Нечетные числа | Четные числа |
| При делении на нечетные числа остается напоминание 1 | При делении на четные числа остается напоминание 0 |
| Все числа, оканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными. | Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными. |
| Нечетные числа не могут быть сгруппированы в пары. | Четные числа можно объединять в пары. |
| Если последняя цифра данного числа нечетная, число нечетное. | Если последняя цифра заданного числа четная, то и число четное. |
Решенные примеры нечетных и четных чисел
Решенный пример: Здесь объясняются примеры четных и нечетных чисел. Являются ли следующие числа четными или нечетными 18, 22, 35, 165
Являются ли следующие числа четными или нечетными 18, 22, 35, 165
Решение:
Мы знаем, что четные числа делятся на 2. Итак, давайте проверим приведенные выше числа для теста на делимость.
18: Мы знаем, что 9 х 2 = 18. Следовательно, 18 четно.
22: Мы знаем, что 11 х 2 = 22. Следовательно, 22 четно.
35 : 35 не делится на 2. Следовательно, 35 нечетно.
165: 165 не делится на 2. Следовательно, 165 нечетно.
Решено Пример: Какова медиана 1, 2, 3, 4, 5, 6, 7, 8, 9, 10?
Решение:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Ясно, что число членов четно, и два числа, разделяющие все множество 5 и 6.
Медиана = (5+6) / 2
= 11/ 2
= 5,5
Следовательно, медиана ряда равна 5,5.
Решено Пример: Верно или неверно: число 673 четное.
Решение: 673 не делится на 2. Значит, 673 не четное число. Итак, приведенное выше утверждение неверно.
Значит, 673 не четное число. Итак, приведенное выше утверждение неверно.
Решено Пример: Выберите правильный ответ. Сумма двух нечетных чисел
- всегда четное число
- всегда нечетное число
- иногда нечетное и иногда четное
- может быть ни нечетным, ни четным
Решение:
5 Сложение двух нечетных чисел утверждает, что
Когда мы складываем два нечетных числа, результатом всегда будет четное число.
Например,
7 + 3 = 10
Следовательно, правильный ответ — вариант 1. Нечетное число + нечетное число = четное число
Решено Пример: Найдите четыре последовательных нечетных числа, сумма которых равна 152.
Решение:
Если мы начнем с нечетного числа и каждое число в последовательности на 2 больше, чем предыдущее число, то мы получим последовательные нечетные целые числа. Пусть первое нечетное число равно n. Следующие три последовательных нечетных числа: (n + 2), (n + 4) и (n + 6) 9.0005
Пусть первое нечетное число равно n. Следующие три последовательных нечетных числа: (n + 2), (n + 4) и (n + 6) 9.0005
Следовательно,
n + (n + 2) + (n + 4) + (n + 6) = 152
n + n + 2 + n + 4 + n + 6 = 152
4n + 12 = 152
4n = 140
n = 35.
Остальные числа
(n + 2) = 35 + 2 = 37
(n + 4) = 35 + 4 = 39
5 и (9 n + 6) = 35 + 6 = 41
Следовательно, последовательные нечетные числа равны 35, 37, 39 и 41.
Решено Пример: Длины сторон треугольника являются последовательными нечетными числами. Какова длина наибольшей стороны, если периметр равен 45?
Решение: Будучи последовательными нечетными числами, нам нужно добавить 2 к предыдущему числу. Пусть первое нечетное число будет х. Следующие два последовательных нечетных числа равны (x + 2) и (x + 4).
Периметр треугольника = сумма трех сторон
45 = x + x + 2 + x + 4
45 = 3x + 6
3x = 45 – 6
3x = 39
x = 13
Длина самого длинного = 13 + 4 = 17
Надеюсь, что эта статья о четных и нечетных числах была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о четных и нечетных числах
В.1 Что такое нечетные числа от 1 до 100?
Ответ 1 Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. В результате 13 — необычное число. Меньше 100 50 нечетных чисел. Четные числа от 1 до 100: 1, 3, 5, 7, 9., 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59 , 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97 и 99.
Q.2 Один нечетное или четное число?
Ответ 2 Учитывая определения четных и нечетных чисел, единица является нечетным числом, поскольку не может делиться на два целых числа. Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..
Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..
В.3 Как объяснить четные и нечетные числа первоклассникам?
Ответ 3 Числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными. Таким образом, нечетные числа оканчиваются на 1, 3, 5, 7 и 9. Четное число — это целое число, которое можно разделить на два на два равных целых числа. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом. Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9., 11, 13, 15,……, 51, 53,…… и так далее.
Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9., 11, 13, 15,……, 51, 53,…… и так далее.
В.4 Как решать четные и нечетные числа?
Ответ 4 Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. Нечетные числа — это те, которые заканчиваются цифрами 1, 3, 5, 7 и 9. 7, 11, 283, 5735, 9859 и так далее. Предоставленное число является нечетным, так как число 2835 заканчивается цифрой 5 (нечетное число). Кроме того, четные числа — это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Предоставленное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число).
В.5 Как найти четные и нечетные числа?
Ответ 5 Есть два способа определить, является ли число четным или нечетным. Они заключаются в следующем: 1. В месте нахождения единицы проверьте цифру числа: Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. количество. Нечетные числа — это те, которые заканчиваются цифрами 1, 3, 5, 7 и 9. 7, 11, 283, 5735, 9859 и так далее. Данное число является нечетным, так как число 2835 оканчивается цифрой 5 (нечетное число). Кроме того, четные числа — это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Данное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число). 2. По группировке: нечетные числа — это те, которые не могут быть объединены в пары. Нечетные числа — это любые числа, которые не делятся точно на два.
Они заключаются в следующем: 1. В месте нахождения единицы проверьте цифру числа: Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. количество. Нечетные числа — это те, которые заканчиваются цифрами 1, 3, 5, 7 и 9. 7, 11, 283, 5735, 9859 и так далее. Данное число является нечетным, так как число 2835 оканчивается цифрой 5 (нечетное число). Кроме того, четные числа — это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Данное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число). 2. По группировке: нечетные числа — это те, которые не могут быть объединены в пары. Нечетные числа — это любые числа, которые не делятся точно на два.
Q.6 Что такое четные простые числа?
Ответ 6 Простые числа — это положительное целое число, которое не делится без остатка ни на какое целое число, кроме самого себя и 1. Простое число нельзя разделить ни на какое другое число без остатка.

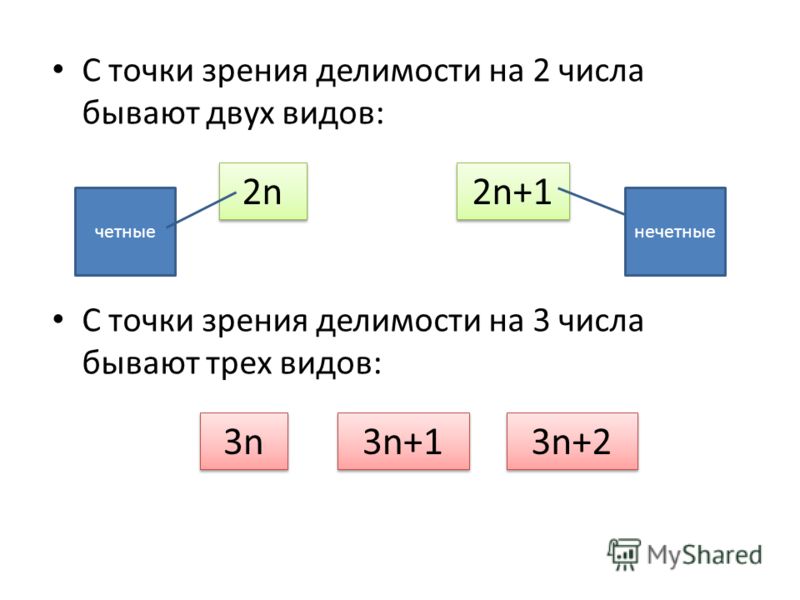 L. (January 1919), «The Number Zero «, The Ohio Educational Monthly Т. 68 (1): 21–22,
. Проверено 11 апреля 2010.
L. (January 1919), «The Number Zero «, The Ohio Educational Monthly Т. 68 (1): 21–22,
. Проверено 11 апреля 2010. ; Grant, Kerry E. & Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rev. ed.), Rowman & Littlefield, ISBN 0-7425-0202-3
; Grant, Kerry E. & Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rev. ed.), Rowman & Littlefield, ISBN 0-7425-0202-3 (2008), The Bluejacket»s Manual: United States Navy (Centennial ed.), Naval Institute Press, ISBN 1-55750-221-8
(2008), The Bluejacket»s Manual: United States Navy (Centennial ed.), Naval Institute Press, ISBN 1-55750-221-8 ), New York: Wiley, ISBN 0-471-36857-1
), New York: Wiley, ISBN 0-471-36857-1 (1975), The Thread of Discourse , Walter de Gruyter, ISBN 90-279-3164-X
(1975), The Thread of Discourse , Walter de Gruyter, ISBN 90-279-3164-X 26 (2): 83–95, DOI 10.1016/j.jmathb.2007.05.004
26 (2): 83–95, DOI 10.1016/j.jmathb.2007.05.004 57 (5): 835–863, DOI 10.1080/02724980343000512
57 (5): 835–863, DOI 10.1080/02724980343000512





 Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное. Эти правила всегда верны, независимо от того, сколько цифр в числе.
Если число оканчивается на $0$, $2$, $4$, $6$ или $8$, то оно четное. Эти правила всегда верны, независимо от того, сколько цифр в числе. Например: 9 + 4 = 13
Например: 9 + 4 = 13 Например: 7 × 5 = 35
Например: 7 × 5 = 35