Двойное неравенство — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
При взвешивании арбуза оказалось, что он тяжелее
одной 5-килограммовой гири, но легче двух таких
гирь. Чему равна масса арбуза?
ОТВЕТ
Обозначим массу арбуза через х.
Тогда, масса арбуза заключена в промежутке от 5 кг до 10 кг.
Вместо двух неравенств 5 < х
и
х < 10 можно записать одно двойное
неравенство: 5 < х < 10.
Его читают так: «х больше пяти и меньше десяти».
Решениями неравенства 5 < х < 10 являются числа 6, 7, 8 и 9, расположенные
между числами 5 и 10:
2. Тема: ДВОЙНОЕ НЕРАВЕНСТВО.
Дата:Date:
Тема: ДВОЙНОЕ НЕРАВЕНСТВО.
3. ЦЕЛИ УРОКА: LESSON OBJECTIVES
Изучить понятие двойного неравенства иусвоить форму его записи
Научиться читать и записывать двойные
неравенства
ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ
5.5.3.6 записывать результат сравнения натуральных чисел с помощью знаков >, <, =;
5.5.3.7 исследовать ситуацию, требующую сравнения и упорядочивания натуральных
чисел.
При счете натуральные числа называют
по порядку: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,…
Из двух натуральных чисел меньше, то
которое при счете называют раньше, и
больше то, которое при счете называют
позже.
Число 4 меньше, чем 7, число 8 больше,
чем 7.
4
В(2)
0
1
2
А(6)
3
6
х
Число 3 меньше, чем 6, и больше чем 2.

Это записывается в виде двойного
неравенства:
2<3<6
5
Запишите с помощью двойного неравенства:
число 11 меньше, чем 20, а число 20 меньше, чем 25.
6
Прочитайте двойные неравенства.
13 17 43
56 57 70
4 5 6
100 200 300
44 45 48
7
Запишите с помощью двойного неравенства:
а) число 10 больше, чем 5, и меньше, чем 15;
б) число 11 меньше, чем 18, и больше, чем 8;
в) число 21 меньше, чем 28, а число 28 меньше,
чем 45.
а) 5 < 10 < 15
б) 8 < 11 < 18
в) 21 < 28 < 45
8
Назовите все натуральные числа, которые
лежат между:
а) 11 и 19;
б) 2089 и 2091.
a) 12; 13; 14; 15; 16; 17; 18;
б) 2090.
9
Отметьте на координатном луче все натуральные
числа, которые:
а) меньше 9;
б) больше 10, но меньше 14.
Ответ:
Ответ:
10
Я задумал число, оканчивающееся
цифрой 5. Оно больше, чем 210, и
меньше, чем 220. Какое это число?
11
12.
 Домашнее задание. Home Task. ЗАДАНИЕ 1.
Домашнее задание. Home Task. ЗАДАНИЕ 1.Выполнить сравнение величин.
3 кг и 3000 г,
34 м и 340 дм,
23 т и 230 кг.
ЗАДАНИЕ 2.
Можно ли заменить данные неравенства двойным неравенством?
Если да, то запиши подходящее двойное неравенство.
а)
б)
в)
г)
2<у
у>2
2<у
у<2
и
и
и
и
у<6
у<6
z<6
у<6
————————————————————————————
R
E
F
L
E
C
T
I
O
N
РЕФЛЕКСИЯ УРОКА
English Русский Правила
Двойное неравенство презентация, доклад
Слайд 1ОТВЕТ
При взвешивании арбуза оказалось, что он тяжелее одной 5-килограммовой гири, но
легче двух таких гирь. Чему равна масса арбуза?
Обозначим массу арбуза через х.
Тогда, масса арбуза заключена в промежутке от 5 кг до 10 кг.

Решениями неравенства 5
Слайд 2Тема: ДВОЙНОЕ НЕРАВЕНСТВО.
Дата:
Date:
Слайд 3ЦЕЛИ УРОКА: LESSON OBJECTIVES
Изучить понятие двойного неравенства и усвоить форму его записи
Научиться
читать и записывать двойные неравенства
ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ
Слайд 4 При счете натуральные числа называют по порядку: 1, 2, 3,
4, 5, 6, 7, 8, 9, 10, 11,…
Из двух натуральных чисел меньше, то которое при счете называют раньше, и больше то, которое при счете называют позже.
Число 4 меньше, чем 7, число 8 больше, чем 7.
Повторение пройденного.
Изучение нового материала.
Число 3 меньше, чем 6, и больше чем 2.
Это записывается в виде двойного неравенства:
2
В(2)
А(6)
2
3
6
Запишите с помощью двойного неравенства:
число 11 меньше, чем 20, а
число 20 меньше, чем 25.
Изучение нового материала.
11
Прочитайте двойные неравенства.
Изучение нового материала.
13 • 17 • 43
56 • 57
• 70
4 • 5 • 6
100 • 200 • 300
44 • 45 • 48
Запишите с помощью двойного неравенства:
меньше, чем 15;
б) число 11 меньше, чем 18, и больше, чем 8;
в) число 21 меньше, чем 28, а число 28 меньше, чем 45.
а) 5
б) 8
в) 21
Решение упражнений
Назовите все натуральные числа, которые лежат между:
а) 11 и 19;
б)
2089 и 2091.
a) 12; 13; 14; 15; 16; 17; 18;
б) 2090.
Решение упражнений
Слайд 10Ответ:
Ответ:
Отметьте на координатном луче все натуральные числа, которые:
а) меньше 9;
б) больше 10, но меньше 14.
Решение упражнений
Я задумал число, оканчивающееся цифрой 5. Оно больше, чем 210, и
меньше, чем 220. Какое это число?
Закрепление нового материала.
Слайд 12Домашнее задание. Home Task.
ЗАДАНИЕ 1.
Выполнить сравнение величин.
3 кг и 3000 г,
34
м и 340 дм,
23 т и 230 кг.
Можно ли заменить данные неравенства двойным неравенством?
Если да, то запиши подходящее двойное неравенство. а) 2 б) у > 2 и у в) 2 г) у
а) 2 б) у > 2 и у в) 2 г) у
ЗАДАНИЕ 2.
Слайд 13REFLECTION
РЕФЛЕКСИЯ УРОКА
1.4: Составные неравенства — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19681
- Дэвид Арнольд
- College of the Redwoods
В этом разделе обсуждается метод, используемый для решения составных неравенств, который представляет собой фразу, которая обычно относится к паре неравенств, соединенных либо словом «и», либо словом «или». Прежде чем мы приступим к расширенной работе по решению этих неравенств, давайте сначала потратим пару слов (в целях повторения) на обсуждение решения простых линейных неравенств.
Простые линейные неравенства
Как и при решении уравнений, вы можете прибавить или вычесть одинаковую сумму из обеих частей неравенства.
Свойство \(\PageIndex{1}\)
Пусть \(a\) и \(b\) — вещественные числа с \(a \[a+c и \[a-c Эта утилита одинаково действительна, если вы замените «меньше чем» с \(>, \leq\) или \(\geq\). Пример \(\PageIndex{1}\) Решить неравенство \(x + 3 < 8\) для \(x.\) Решение Вычесть \(3\) из обеих частей неравенство и упростить. \[\begin{align*} x+3 &<8 \\ x+3-3 &<8-3 \\ x &<5 \end{align*}\] Таким образом, все действительные числа меньше чем \(5\) являются решениями неравенства. Традиционно набор решений неравенств изображается на числовой прямой. Мы можем описать набор решений, используя построитель набора и нотацию интервала. Решение: \[(-\infty, 5)=\{x : x<5\}\nonumber\] Важным понятием является идея эквивалентных неравенств. Эквивалентные неравенства. Два неравенства называются эквивалентными тогда и только тогда, когда они имеют одно и то же множество решений. Обратите внимание, что это определение аналогично определению эквивалентных уравнений. То есть два неравенства эквивалентны, если все решения первого неравенства являются также решениями второго неравенства, и наоборот. Таким образом, в примере \(\PageIndex{1}\) вычитание трех из обеих частей исходного неравенства дает эквивалентное неравенство. То есть неравенства \(x+3 < 8\) и \(x < 5\) имеют одно и то же множество решений, а именно, все действительные числа, меньшие 5. Неслучайно инструменты в Свойстве \( \PageIndex{1}\) производят эквивалентные неравенства. Всякий раз, когда вы добавляете или вычитаете одинаковую сумму из обеих частей неравенства, полученное неравенство эквивалентно исходному (у них один и тот же набор решений). Давайте посмотрим на другой пример. Пример \(\PageIndex{2}\) Решите неравенство \(x-5 \geq 4\) для \(x. Решение Добавьте 5 к обеим частям неравенства и упрощать. \[\begin{align*} x-5 & \geq 4 \\ x-5+5 & \geq 4+5 \\ x & \geq 9 \end{align*}\] Закрасить раствор на числовой строке. В построителе наборов и интервальных обозначениях решение \[[9, \infty)=\{x : x \geq 9\} \nonumber\] Вы также можете умножать или делить обе стороны на одно и то же положительное число. Свойство \(\PageIndex{2}\) Пусть \(a\) и \(b\) – действительные числа с \(a \[a c и \[\frac{a}{c}<\frac{b}{c}\] Опять же, эта утилита одинаково действительна, если вы замените символ «меньше чем» на \(>, \leq, \text{или} \geq.\) Инструменты в свойстве 4 всегда производят эквивалентные неравенства. Пример \(\PageIndex{3}\) Решить неравенство \(3x \leq −18\)для \(x.\) Решение Разделить обе части неравенства на \(3 \) и упростить. \[\begin{align*} 3 x & \leq-18 \\ \frac{3 x}{3} & \leq \frac{-18}{3} \\ x & \leq-6 \end {align*}\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальных обозначениях решение \[(-\infty,-6]=\{x : x \leq-6\} \nonumber\] Пока что нет никакой разницы между техникой решения неравенств и методикой решения уравнений. Однако есть одно важное исключение. Рассмотрим на мгновение истинное утверждение \[-2<6 \label{eq6}\] Если вы умножите обе части неравенства \ref{eq6} на \(3,\), вы все равно получите истинное утверждение; т. е. \[-6<18 \nonumber\] Но если вы умножите обе части неравенства \ref{eq6} на \(−3,\), вам нужно «обратить символ неравенства», чтобы сохранить истинное заявление; то есть \[6>-18 \nonumber\] Это обсуждение приводит к следующему свойству. Свойство \(\PageIndex{3}\) Пусть \(a\) и \(b\) — действительные числа с \(a < b\). Если \(c\) - любое действительное отрицательное число, то \[a c>b c\] и \[\frac{a}{c}>\frac{b}{c}\] Обратите внимание, что вы «переворачиваете знак неравенства», когда умножаете или делите обе части неравенства на отрицательное число. Пример \(\PageIndex{4}\) Решить неравенство \(−5x > 10\) относительно \(x.\) Решение Разделить обе части неравенства на \(−5 \) и перевернуть знак неравенства. Упрощать. \[\begin{array}{r}{-5 x>10} \\ {\dfrac{-5 x}{-5}<\dfrac{10}{-5}} \\ {\quad x <-2}\end{array} \nonumber\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальной нотации решение \[(-\infty,-2)=\{x : x<-2\} \nonumber\] Теперь обратим наше внимание на решение составных неравенств. В предыдущем разделе мы изучили тонкости «и» и «или», пересечения и объединения, а также рассмотрели некоторые простые составные неравенства. В этом разделе мы опираемся на эти основы и обращаем внимание на более сложные примеры. В этом случае лучший способ учиться — это делать. Начнем с примера. Пример \(\PageIndex{5}\) Решите следующее составное неравенство для \(x.\) \[3-2 x<-1 \quad \text { or } \quad 3-2 x >1 \nonumber\] Решение Сначала решим каждое из неравенств независимо. В первом неравенстве прибавьте \(−3\) к обеим частям неравенства, затем разделите на \(−2,\), поменяв знак неравенства на противоположный. \[\begin{align*} 3-2 x &<-1 \\-2 x &<-4 \\ x &>2 \end{align*}\] Заштрихуйте решение на числовой прямой. Точно такую же последовательность операций можно использовать для решения второго неравенства \[\begin{align*} 3-2 x &>1 \\-2 x &>-2 \\ x &<1 \end{align*}\] Хотя вы решаете каждую часть неравенства независимо друг от друга, вам нужно организовать свою работу следующим образом, расположив решение числового ряда для первого неравенства над решением второго неравенства. \[\begin{array}{rllllrll}{3-2 x}&{<}&{-1} & {\text {или}} & {\quad 3-2 x}&{>}&{ 1} \\ {-2 x}&{<}&{-4} & &{-2 x}&{>}&{-2} \\ {x}&{>}&{2} && {x }&{<}&{1}\end{массив} \nonumber\] Решение в интервальных обозначениях и обозначениях построителя множеств имеет вид \[(-\infty, 1) \cup (2, \infty)=\{x : x<1 \text { or } x>2\} \nonumber\] Давайте рассмотрим другой пример. Пример \(\PageIndex{6}\) Решите следующее составное неравенство для \(x.\) \[-1<3-2 x<1 \label{eq12}\] Решение Напомним, что \(a < x < b\) идентично утверждению \(x > \[3-2 x>-1 \quad \text { and } \quad 3-2 x<1 \label{eq13}\] Решите каждое неравенство самостоятельно, организовав работу следующим образом. \[\begin{array}{rllllrll}{3-2 x}&{>}&{-1} & {\text {и}} & {\quad 3-2 x}&{<}&{ 1} \\ {-2 x}&{>}&{-4} & &{-2 x}&{<}&{-2} \\ {x}&{<}&{2} && {x }&{>}&{1}\end{array} \label{eq14}\] Заштрихуйте решение каждого неравенства на отдельных действительных линиях, одну поверх другой Решение, как в интервальных, так и в обозначениях построителя множеств, равно \[(1,2)=\{x : 1 Обратите внимание, что в нашем ответе мы использовали компактную форму составного неравенства. С тем же успехом мы могли бы использовать \[(1,2)=\{x : x>1 \text { and } x<2\} \nonumber\] Обе формы записи построителя наборов одинаково допустимы. . Вы можете использовать любой из них, но вы должны понимать оба. Альтернативный подход. Возможно, вы заметили, что при решении второго неравенства в \ref{eq14} вы повторяете те же операции, что и при решении первого неравенства. То есть вы вычли \(3\) из обеих частей неравенства, а затем разделили обе части неравенства на \(−2,\), поменяв знак неравенства на противоположный. Это повторение раздражает и предлагает возможный короткий путь в данной конкретной ситуации. Вместо того, чтобы разбивать составное неравенство \ref{eq12} на две части (как в \ref{eq13}), давайте сохраним неравенство вместе, как в \[-1<3-2 x<1 \label{eq16}\] Теперь правила работы с этой формой. Свойство \(\PageIndex{4}\) \[a можно прибавлять (или вычитать) ту же сумму к (из) все три части неравенства, как в \[a+c или \[a-c Вы также можете умножить все три части на то же самое положительное число \(c > 0,\) как в \[c a Однако, если вы умножите все три части на одно и то же отрицательное число \(c < 0,\) затем не забудьте поменять местами знаки неравенства, как в \[c a>c x>c b\] Правила деления идентичны правилам умножения. Если \(c > 0\) (положительно), то \[\frac{a}{c}<\frac{x}{c}<\frac{b}{c}\] Если \( c < 0\) (отрицательно), то при делении знаки неравенства меняются местами. \[\frac{a}{c}>\frac{x}{c}>\frac{b}{c}\] Каждый из инструментов в свойстве \(\PageIndex{4}\) всегда производят эквивалентные неравенства. Итак, вернемся к составному неравенству \ref{eq16} и вычтем \(3\) из всех трех членов неравенства. \[\begin{array}{c}{-1<3-2 x<1} \\ {-1-3<3-2 x-3<1-3} \\ {-4<-2 x<-2}\end{array} \nonumber\] Затем разделите все три члена на \(−2,\), меняя при этом знаки неравенства. \[\begin{array}{c}{-4<-2 x<-2} \\ {\dfrac{-4}{-2}>\dfrac{-2 x}{-2}>\ dfrac{-2}{-2}} \\ {2>x>1}\end{array} \nonumber\] Принято менять порядок этого последнего неравенства. Читая неравенство справа налево, мы получаем \[1 , которое описывает действительные числа, большие 1 и меньшие \(2.\). Решение рисуется на следующую реальную строку. Обратите внимание, что это идентично решению, установленному на реальной линии на рисунке \(\PageIndex{2}\). Обратите также внимание, что этот второй альтернативный метод более эффективен, особенно если вы немного поработаете в уме. Рассмотрим следующую последовательность, в которой мы вычитаем три из всех трех членов, затем делим все три члена на \(−2,\), меняя знаки неравенства, а затем, наконец, читаем неравенство в противоположном направлении. \[\begin{array}{c}{-1<3-2 x<1} \\ {-4<-2 x<-2} \\ {\quad 2>x>1} \\ { \quad 1 Давайте посмотрим на другой пример. Пример \(\PageIndex{7}\) Решите следующее составное неравенство для \(x.\) \[-1 Решение Сначала умножим все три члена на \(2,\), чтобы очистить дроби. \[2(-1)<2\left(x-\frac{x+1}{2}\right) \leq 2(2) \nonumber\] \[-2<2(x) -2\left(\frac{x+1}{2}\right) \leq 4 \nonumber\] Отмена. Обратите внимание на использование круглых скобок, что очень важно, когда используется знак минус. \[-2<2 x-\cancel{2}\left(\frac{x+1}{\cancel{2}}\right) \leq 4 \nonnumber\] \[-2<2 x-(x+1) \leq 4 \nonumber\] Распределите знак минус и упростите. \[\begin{align*} -2 &< &&2x-x-1 &&\leq 4 \\ -2 &< &&x-1&& \leq 4\end{align*}\] Добавить \(1\ ) всем трем участникам. \[-1 Это решение описывает действительные числа больше \(-1\) и меньше \(5,\), включая \(5. Ответ, описанный как в нотации интервала, так и в нотации построителя множеств, следует \[(-1,5]=\{x :-1 Давайте посмотрим на другой пример Пример \(\PageIndex{8}\) Решите следующее составное неравенство для \(x.\) \[x \leq 2 x-3 \leq 5 \nonumber\] Решение Предположим, что мы пытаемся изолировать \(x\), как мы это делали в примере \(\PageIndex{7}\). Возможно, мы попытаемся добавить \(−x\) ко всем трем элементам. \[\begin{align*} x &\leq &&2x-3 &&\leq 5 \\ x-x &\leq &&2x-3-x &&\leq 5-x \\ 0 &\leq &&x-3 &&\leq 5-x \end{align*}\] Ну, это мало помогло, просто перенес задачу с \(x\) на другой конец неравенства. Подобные попытки не помогут выделить \(x. Решение: разделим неравенство (со словом «и», разумеется). \[x \leq 2 x-3 \quad \text { и } \quad 2 x-3 \leq 5 \nonumber\] Мы можем решить первое неравенство, вычитая \(2x\) из обеих частей неравенства, затем умножая обе части на \(−1,\), обращая неравенство в процессе \[\begin{align*} x & \leq 2 x-3 \\-x & \leq-3 \\ x & \geq 3 \end{align*}\] Чтобы решить второе неравенство, прибавьте \(3\) к обеим частям, затем разделите обе стороны на \(2\): \[\begin{align*} 2 x-3 & \leq 5 \\ 2 x & \leq 8 \\ x & \leq 4 \end{align*} \] Конечно, вы, вероятно, захотите организовать свою работу следующим образом \[\begin{array}{rllrl} x & \leq 2 x-3 & \text{and} &2 x-3 & \leq 5 \\ -x & \leq-3 && 2 x & \leq 8 \\ x & \geq 3 & & x & \leq 4\end{array} \nonumber\] Таким образом, нам нужно заштриховать на числовой прямой все действительные числа, которые больше или равны \(3\) и меньше или равно \(4,\), как показано на рисунке \(\PageIndex{5}\). Решение, описанное как в нотации интервала, так и в нотации построителя множеств, равно \[[3,4]=\{x : 3 \leq x \leq 4\} \nonumber\] Эта страница под названием 1.4: Составные неравенства распространяется под лицензией CC BY-NC-SA 2.5, автором, ремиксом и/или куратором этой страницы является Дэвид Арнольд. Привет и добро пожаловать в это видео о графических решениях линейных неравенств ! Сегодня мы изучим, что такое линейное неравенство, и узнаем, как изобразить простые и составные неравенства на числовой прямой. Мы также поговорим о том, как строить графики неравенств, включающих абсолютное значение, и неравенств с более чем одной переменной. Прежде чем мы начнем, давайте рассмотрим несколько вещей. Во-первых, неравенство сравнивает два значения и показывает, меньше, больше, меньше или равно, больше или равно друг другу. Например, \(x\lt 15\) означает, что значение \(x\) меньше 15. Решения — это числа, которыми мы можем заменить переменные в неравенствах, которые сделают их истинными. Например, одним из возможных решений \(x\lt 15\) является 5, потому что 5 меньше 15. Решения неравенств графически изображаются на числовых линиях и координатных плоскостях , в зависимости от того, сколько переменных входит в неравенство. Эти графики помогают проиллюстрировать все возможные решения или набора решений для неравенства. Давайте рассмотрим пример: \(x \lt 5\). Если \(x\) меньше 5, то все возможные решения для \(x\) должны быть числами меньше 5. Мы можем проиллюстрировать это на числовой прямой. Сначала найдите 5 на числовой прямой и нарисуйте незакрашенный кружок над 5. Мы оставляем этот кружок открытым, чтобы показать, что 5 не является частью набора решений для этого неравенства. Затем нарисуйте линию на числовой прямой, чтобы указать возможные решения для \(x\). Поскольку \(x\) меньше 5, нам нужно провести линию слева от 5. Обратите внимание, что линия продолжается слева от 5 со стрелкой на конце. Стрелка указывает на то, что хотя числовая линия заканчивается на -10, существует бесконечное число решений (числа меньше -10), которые могут сделать это неравенство верным. Попробуем еще. Постройте график множества решений неравенства \(x>-3\). Если \(x\) больше -3, то все возможные решения для \(x\) должны быть числами больше -3. Приостановите видео здесь, нарисуйте числовую линию и посмотрите, сможете ли вы построить ее самостоятельно. Я знаю ты сможешь! Давайте вместе посмотрим на числовую прямую. Обратите внимание на незакрашенный кружок прямо над -3 на числовой прямой. Помните, это означает, что -3 не является частью набора решений, потому что \(x\neq -3\). Вот еще одно неравенство: \(x\leq 1\). Нарисуем неравенство на числовой прямой. Сначала найдите 1 на числовой прямой и нарисуйте над ней заштрихованный кружок на числовой прямой. Кружок закрыт, чтобы указать, что 1 является частью набора решений для этого неравенства. Затем, начиная с 1, нарисуйте линию, чтобы указать все другие возможные решения для \(x\). Поскольку \(x\) меньше или равно 1, нам нужно провести линию слева от 1. Теперь ваша очередь. Постройте график множества решений неравенства \(x\geq -4\). Приостановите видео здесь, нарисуйте числовую линию и попробуйте сами. Когда закончите, возобновите просмотр видео, и мы вместе пройдемся по графику. Давайте посмотрим на числовую строку для \(x\geq -4\): Как видите, кружок над -4 закрыт, чтобы указать, что -4 является частью набора решений. A составное неравенство — это два или более неравенства, которые соединены вместе либо «и», либо «или». Иногда они пишутся с помощью символов «и» и «или». Например, \(x\leq -1\cup\text{ }x> 5\) — составное неравенство, означающее то же, что и \(x\leq -1\text{ или}\text{ }x > 5\). Возможными решениями являются все числа, которые либо меньше или равны -1, либо больше 5. При построении сложных неравенств на числовой прямой применяются те же правила, что и для простых неравенств. Оба выражения неравенства изображены на одной и той же числовой прямой. Построим графики решений для \(x \leq -1\text{ }\cup x > 5\), начиная с первого неравенства, \(x \leq -1\). Поскольку \(x \leq -1\), в точке \(-1\) есть замкнутый круг с линией, идущей слева от него. Затем изобразите набор решений для второго неравенства \(x > 5\) на той же числовой прямой. Поскольку \(x > 5\), в точке 5 есть незакрашенный круг с линией, идущей справа от него. Числовая строка теперь показывает все решения, если \(x\) меньше или равно -1 или больше 5. Вот как может быть выражен набор решений \(\left ( -\infty ,-1] \cup (5 ,\infty \right )\) с символом бесконечности, круглые скобки обозначают незакрашенные кружки, не являющиеся частью набора решений, и скобки для закрытых кружков, которые являются частью набора решений Рассмотрим составное неравенство \(x > -2\cap x\leq 6\), что также можно записать в виде \(-2 \lt x \leq 6\). Поскольку эти два неравенства связаны «и», на графике должны быть отражены все решения для \(x\) если оно больше \(-2\) и меньше или равно 6. Следуя тем же шагам, что и раньше, давайте изобразим оба решения на одной и той же числовой прямой, начиная с \(x > -2\).0032 Поскольку \(x > -2\), в точке -2 есть открытый круг с линией, идущей справа от него. Затем изобразите решения для \(x \leq 6\) на той же числовой прямой. Поскольку \(x\leq 6\), в точке 6 есть замкнутый круг с линией, идущей слева от него. Однако этот график не точен. Напомним, что эти неравенства соединены «и», что означает, что числовая прямая должна показывать, где пересекаются решения обоих неравенств. В числовой строке теперь отображаются все решения для \(-2\lt x \leq 6\). Этот набор решений может быть выражен следующим образом: \((-2,6]\), где скобка указывает, что -2 не является частью набора решений, а скобка означает, что 6 является частью набора решений. Решения неравенств с абсолютным значением также можно изобразить на числовой прямой. Напомним, что абсолютное значение — это расстояние числа от нуля. Другими словами, это неотрицательное значение числа. Абсолютное значение обозначается как это: \(|x|\). Рассмотрим неравенство \(\left | x \right |> 7\). Решения для \(x\) включают все числа, которые находятся на расстоянии более 7 пробелов от 0 на числовой прямой. Теперь мы готовы построить графики \(x> 7\) и \(x\lt -7\). Следуя тем же шагам, которые мы практиковали, начертите оба неравенства на одной и той же числовой прямой. Первое неравенство утверждает, что \(x > 7\), поэтому на графике показан незакрашенный кружок в точке 7 с линией, идущей вправо. Второе неравенство утверждает, что \(x> -7\), поэтому на графике показан незакрашенный кружок в точке -7 с линией, идущей влево. Попробуем еще: \(\left | 1+b \right |\leq 8\). Полоски абсолютных значений указывают, что возможные решения могут быть положительными или отрицательными. Отсюда выделите переменную \(b\) в обоих неравенствах. Вычтите по 1 с обеих сторон, и мы получим \(b\leq 7\). И то мы будем делать то же самое здесь. Отнимите 1 с обеих сторон, и мы получим: \(1+b\geq-8\) Множество решений этого неравенства включает все значения, которые меньше или равны 7 и больше больше или равно -9. Обратите внимание, что эти неравенства связаны термином «и». Мы ищем решения, которые верны для обоих неравенств, поэтому числовая линия должна показать, где решения обоих неравенств перекрываются. В числовой строке теперь отображаются все решения для \(-9\leq b\leq 7\). Набор решений может быть выражен следующим образом: \([-9,7]\), где скобки указывают, что -9 и 7 являются частью набора решений. Теперь твоя очередь. Следуя тем же шагам, что и мы, нарисуйте график набора решений для \(\left | 2x-3 \right |> 5\). Приостановите видео здесь, нарисуйте числовую линию и попробуйте сами. Когда вы закончите, возобновите просмотр видео, и мы рассмотрим его вместе. Давайте посмотрим. Во-первых, перепишите неравенство в виде двух неравенств без столбцов абсолютного значения. После этого изолируйте переменную \(x\). Итак, у нас есть \(2x-3> 5\) и \(2x-3\lt -5\). \(2x-3> 5\) Отсюда мы собираемся добавить 3 к обеим сторонам. Итак, имеем: \(2x-3+3> 5+3\) И разделите на 2 с обеих сторон. \(2x\div 2> 8\div 2\) Здесь мы собираемся выполнить те же шаги. Мы добавим 3 к обеим сторонам. \(2x-3\lt -5\) И разделить на 2 с обеих сторон. \(2x\div 2\lt -2\div 2\) Теперь мы можем построить график набора решений для \(x>4\) или \(x\lt-1\). Этот набор решений может быть выражен следующим образом \((-\infty , -1)\cup (4,\infty )\) со скобками, обозначающими незакрашенные кружки, не являющиеся частью набора решений. Хорошая работа! До сих пор мы рассматривали неравенства, содержащие одну переменную. Что, если неравенство имеет две переменные? Рассмотрим \(y>3x+1\). Поскольку есть две переменные, нам нужно проиллюстрировать наборы решений на координатной плоскости. Обратите внимание, что \(y> 3x+1\) находится в форме пересечения наклона , \(y=\text{ }mx+b\). Когда неравенство имеет две переменные и находится в форме пересечения наклона, первым шагом является построение линии на координатной плоскости. Поскольку точка пересечения \(y\) (\(b\)) равна 1, линия будет пересекать ось \(y\) в точке 1 или \((0,1)\). Затем нарисуйте линию, чтобы соединить точки. Так как знак неравенства в исходном выражении меньше (и не меньше или равен ), соедините упорядоченные пары пунктирной линией. Пунктирная линия означает, что точки на этой линии не являются возможными решениями. Набор решений для линейного неравенства показан в виде заштрихованной области на координатной плоскости. Эта заштрихованная область охватывает область справа или слева от линии, изображенной на графике. Чтобы выяснить, какую область закрасить, выберите контрольную точку, чтобы подставить ее в неравенство и решить. Простая контрольная точка для работы — это исходная точка \((0, 0)\). Подставьте 0 вместо \(x\) и \(y\) в неравенстве. Итак, если у нас есть наше неравенство \(y> 3x+1\) и мы подставим 0 вместо \(x\) и \(y\), мы получим: \((0)> 3(0)+1\) Получается: \(0>0+1\) \(0 > 1\) \(\times\) Что, как мы знаем, неправда. Так как 0 не больше 1, то эта точка \((0,0)\) не может быть частью множества решений. Это означает, что значения справа от линии графика не являются решениями неравенства. Вместо этого заштрихуйте область слева от линии. Готовый график имеет пунктирную линию с заштрихованной областью слева от нее. Все возможные решения — это точки слева от линии на графике. Попробуем еще. Рассмотрим неравенство \(y\leq \frac{2}{5}x+2\). Сначала начертите линию на координатной плоскости. Поскольку точка пересечения \(y\) (\(b\)) равна 2, линия будет пересекать ось \(y\) в точке 2 или \((0,2)\). Наклон (\(m\)) равен 25. Начиная с \((0,2)\), используйте наклон, чтобы найти другую точку на линии. Поскольку наклон равен \(\frac{\text{rise}}{\text{run}}\), переместитесь на 2 единицы вверх и на 5 единиц вправо, чтобы добраться до точки \((5,4)\). Затем нарисуйте линию, чтобы соединить точки. Так как знак неравенства меньше или равен , соедините упорядоченные пары сплошной линией. Затем подставьте исходную точку \((0,0)\) в неравенство в качестве контрольной точки, чтобы определить, какую часть координатной плоскости нужно заштриховать. Итак, если мы подставим здесь \((0,0)\) вместо наших \(x\) и \(y\), мы получим: \((0)\leq \frac{2} {5}(0)+2\) Что даст нам: \(0\leq 0+2\) \(0\leq 2\)✔ Это верно! Поскольку \(0 \lt 2\), точка \((0,0)\) является частью множества решений. Это означает, что значения справа от линии графика являются решениями неравенства. Готовый график имеет сплошную линию с заштрихованной областью справа от нее. Все возможные решения — это точки справа от линии или на линии, изображенной на графике. Вы готовы к вызову? Рассмотрим составное неравенство, содержащее две переменные: \(y\geq x\text{ }+1\text{ }\cup y\lt x-8\) Помните, что связывает два неравенства и означает «или». Итак, у нас есть линия \(y\geq x+1\) и линия \(y \lt x-8\). \(y\geq x+1\) имеет точку пересечения \(y\) в точке 1 \((0,1)\) и наклон 1. На графике сплошной линией показано, что точки на линия входит в набор решений. \(y\lt x-8\) имеет \(y\)-пересечение в точке -8 \((0,-8)\) и наклон 1. Он показан пунктирной линией, чтобы указать, что точки на линия не входит в набор решений. После того, как две линии будут построены, подставьте начало координат \((0,0)\) в оба неравенства в качестве контрольной точки. Это определит, какую часть координатной плоскости нужно заштриховать. Итак, если мы подставим сюда \((0,0)\), то получим: \(y\geq x+1\) Или: \(0\geq1\)\(\times\) Мы знаем, что это не так. \(y\lt x-8\) Что упрощается до: >\( 0\lt -8\)\(\times\) Поскольку оба утверждения ложны при решении, заштрихуйте обе линии на сторонах, не включающих начало координат. \(y\geq x+1\) имеет сплошную линию с заштрихованной областью слева от нее. \(y\lt x-8\) имеет пунктирную линию с заштрихованной областью справа от нее. Обе заштрихованные части являются частью набора решений. Сегодня мы много узнали о неравенствах, и у меня есть для вас еще одна задача. Это немного сложнее, но я знаю, что ты справишься. Утверждение о неравенстве: \(2x+4\lt y\leq 3x+8\) Помните, что сложные линейные неравенства изображаются на одной и той же координатной плоскости. Ваш первый шаг — начертить две линии. После построения графика используйте контрольную точку \((0,0)\), чтобы определить, где затенить график. Приостановите видео здесь и попробуйте сами. Когда закончите, возобновите просмотр видео, и мы рассмотрим его вместе. Давайте вместе разберемся с этой проблемой. Два неравенства: \(y>2x+4\) и \(y\leq 3x+8\). На графике \(y>2x+4\) отображается пунктирной линией, а \(y\leq 3x+8\) — сплошной линией. Затем подставьте начало координат \((0,0)\) в оба неравенства в качестве контрольной точки, чтобы определить, какую часть координатной плоскости закрасить. Итак, если мы подставим сюда \((0,0)\), то получим: \(y> 2x+4\) Что дает нам: \(0>0+4\) Или: \(0>4\)\(\times\) Мы знаем, что это \(y\leq 3x+8\) Что упрощается до: \(0\leq0+8\ ) Или: \(0\leq 8\)✔ Мы знаем, что это правда.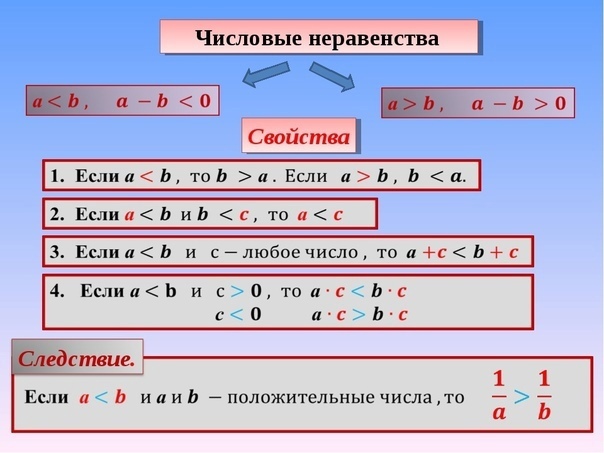
 \)
\)
 Опять же, эта утилита одинаково действительна, если вы замените символ «меньше» на \(>, \leq,\) или \(\geq\). Инструменты в Property \(\PageIndex{3}\) всегда производят эквивалентные неравенства.
Опять же, эта утилита одинаково действительна, если вы замените символ «меньше» на \(>, \leq,\) или \(\geq\). Инструменты в Property \(\PageIndex{3}\) всегда производят эквивалентные неравенства. Составные неравенства


 Решение составного неравенства \(−1 < 3 − 2x < 1.\)
Решение составного неравенства \(−1 < 3 − 2x < 1.\)


 \) Это то есть действительные числа, находящиеся между \(-1\) и \(5,\), включая \(5,\), заштрихованные на вещественной линии на рисунке \(\PageIndex{4}\).
\) Это то есть действительные числа, находящиеся между \(-1\) и \(5,\), включая \(5,\), заштрихованные на вещественной линии на рисунке \(\PageIndex{4}\). \) Итак, что же нам делать?
\) Итак, что же нам делать?
На этой странице нет тегов.

Графические решения линейных неравенств (Видео)
 Аналогично, \(x \geq 6\) означает, что значение \(x\) равно больше или равно 6.
Аналогично, \(x \geq 6\) означает, что значение \(x\) равно больше или равно 6. Значение для \(x\) меньше 5, но не равно ему.
Значение для \(x\) меньше 5, но не равно ему. От -3 вправо идет линия со стрелкой на конце. Эта строка показывает, что все возможные решения для \(x\) — это числа больше -3. Отличная работа!
От -3 вправо идет линия со стрелкой на конце. Эта строка показывает, что все возможные решения для \(x\) — это числа больше -3. Отличная работа! Поскольку \(x\) больше или равно -4, линия продолжается вправо, показывая все возможные решения для \(x\). Хорошая работа!
Поскольку \(x\) больше или равно -4, линия продолжается вправо, показывая все возможные решения для \(x\). Хорошая работа!

 Поскольку возможные решения могут быть положительными или отрицательными, мы можем переписать это неравенство в виде двух неравенств без полос абсолютного значения. \(\left | x \right |> 7\) становится \(x> 7\) и \(x\lt -7\). Обратите внимание, что в неравенстве \(x\lt -7\) поменялся знак. Это связано с тем, что при умножении или делении отрицательного числа в неравенстве его знак меняется.
Поскольку возможные решения могут быть положительными или отрицательными, мы можем переписать это неравенство в виде двух неравенств без полос абсолютного значения. \(\left | x \right |> 7\) становится \(x> 7\) и \(x\lt -7\). Обратите внимание, что в неравенстве \(x\lt -7\) поменялся знак. Это связано с тем, что при умножении или делении отрицательного числа в неравенстве его знак меняется. Поэтому нам нужно переписать неравенство в виде двух неравенств без модуля: \(1+b\leq 8\) и \(1+b\geq -8\). Обратите внимание, что знак во втором неравенстве изменился, так как было введено отрицательное значение.
Поэтому нам нужно переписать неравенство в виде двух неравенств без модуля: \(1+b\leq 8\) и \(1+b\geq -8\). Обратите внимание, что знак во втором неравенстве изменился, так как было введено отрицательное значение.
\( \)
\(1-1+b\geq-8-1\)
\( \ )
\(b\geq-9\)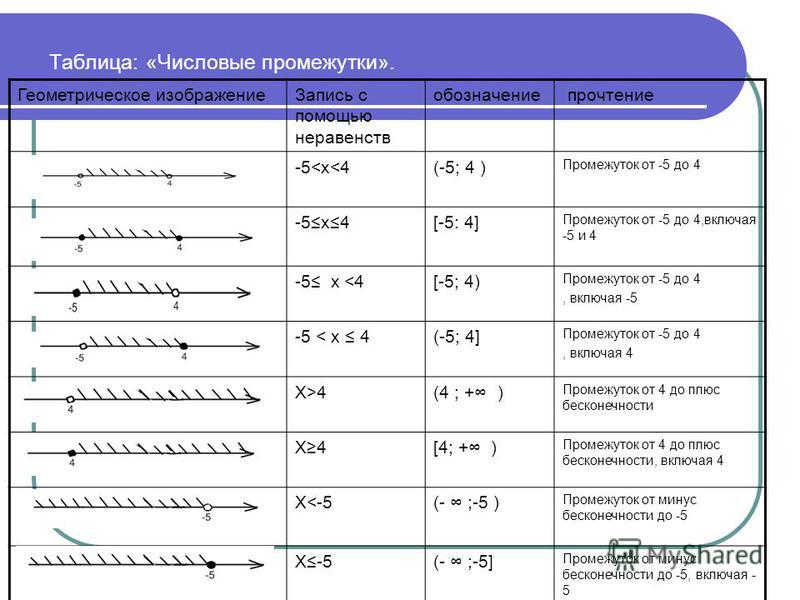
\( \)
\(2x > 8\)
\( \)
\(x> 4\)
\( \)
\(2x-3+3\lt -5+3\)
\( \)
\(2x\lt -2\)
\( \)
\(x\lt -1\) Наклон (\(m\)) равен 3 или \(\frac{3}{1}\). Начиная с \((0,1)\), используйте наклон, чтобы найти другую точку на линии. Поскольку уклон равен \(\frac{\text{rise}}{\text{run}}\), переместитесь на 3 единицы вверх и на 1 единицу вправо до \((1,4)\).
Наклон (\(m\)) равен 3 или \(\frac{3}{1}\). Начиная с \((0,1)\), используйте наклон, чтобы найти другую точку на линии. Поскольку уклон равен \(\frac{\text{rise}}{\text{run}}\), переместитесь на 3 единицы вверх и на 1 единицу вправо до \((1,4)\).
Или:
 Это указывает на то, что точки на этой прямой являются возможными решениями.
Это указывает на то, что точки на этой прямой являются возможными решениями.
Или: Мы можем решить это составное неравенство, выполнив те же действия, что и раньше. Единственное отличие состоит в том, что теперь у нас есть две линии для построения графика на координатной плоскости. Давайте начнем.
Мы можем решить это составное неравенство, выполнив те же действия, что и раньше. Единственное отличие состоит в том, что теперь у нас есть две линии для построения графика на координатной плоскости. Давайте начнем.
\( \)
\((0)\geq ( 0)+1\) Теперь мы подойдем сюда и подключим \((0,0)\). Мы получим:
Теперь мы подойдем сюда и подключим \((0,0)\). Мы получим:
\( \)
\((0)\lt (0)-8\)
Мы знаем, что это тоже неверно.
\( \)
\((0)> 2(0)+4 \)
\( \)
\((0)\leq3(0)+8\)
