На это умножить или сложить: Порядок действий в Математике

alexxlab / / Разное

Как решить один и тот же пример разными способами: китайский метод умножения, египетский, метод решетки — 20 января 2023

Привычные нам способы решения примеров далеко не единственно верные

Поделиться

Складывать, вычитать, умножать и делить мы все научились еще в школьные годы. Многие даже неплохо сохранили эти навыки и до сих пор могут что-нибудь да умножить. В уме. Но что, если приходится умножать многозначные числа? Понятно, что проще всего воспользоваться калькулятором. Но мы не ищем легких путей — вместо них мы нашли несколько способов решить одни и те же примеры. Ими до сих пор пользуются в разных странах, и это не привычное нам умножение столбиком.

В качестве примера, решить который мы попробуем семью разными методами, мы взяли не самый сложный, но и не самый простой: 223 х 304. Произведение этих множителей равняется 67 792. Нам было важно, чтобы числа были не двузначные и чтобы хотя бы в одном из них был ноль (потом объясним зачем). А теперь давайте посчитаем.

Чтобы решить наш пример этим способом, сперва запишем множители. После этого нужно представить число 223 в виде суммы степеней двоек — начинаем с единицы и умножаем на два, пока не получим число, которое будет больше, чем 223. Получится 256. Это уже много. А раз много, значит нам это не нужно. Остается 128.

Поделиться

Дальше нужно число 304 умножить на все получившиеся числа. Но понадобятся нам не все. Из чисел левого столбца нам нужно собрать число 223. Идем снизу вверх. Берем 128, прибавляем к нему 64. Получается 192. Если прибавить к этой сумме 32, получится 224, а это уже перебор. Поэтому 32 пропускаем и прибавляем все остальные. Выйдет наше 223. На те числа, что остались (а это все, кроме 32), мы и будем умножать наше 304. Теперь суммируем всё, что у нас получилось. Сумма этих чисел окажется 67 792.

Поделиться

Если вам кажется, что умножать 304 на 128 в такой ситуации будет полнейшим безумием, воспользуйтесь хитростью и просто умножайте каждое предыдущее число на два — так будет проще.

Всё, что вам понадобится, чтобы решить любой пример с умножением этим крестьянским методом, — это уметь умножать и делить на два.

Для начала будем последовательно делить на два первое число, пока оно не превратится в единицу. Думаете, не получится в случае с числом 223? Только не в древнерусском способе! Если в результате будет получаться число с остатком, отбрасываем эти остатки куда подальше — они нам не пригодятся.

Поделиться

После этой нехитрой процедуры беремся за второй множитель — его будем на два умножать. Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.

Поделиться

Дальше — самая нелегкая задача этого метода: суммировать все числа, что стоят справа (включая 304). Сложно, но у древнерусских счетоводов не было другого выбора, и им приходилось всё считать вручную. У нас, к счастью, есть калькуляторы, так что мы с удовольствием воспользуемся этой возможностью. И калькулятор покажет 67 792. Если вы хотите проверить, действительно ли работает этот метод, можете поменять множители местами и всё пересчитать, но, забегая вперед, мы вам скажем, что от перестановки мест множителей произведение не меняется даже в этом случае.

Первым дело запишем наши числа одно над другим и подведем под ними черту.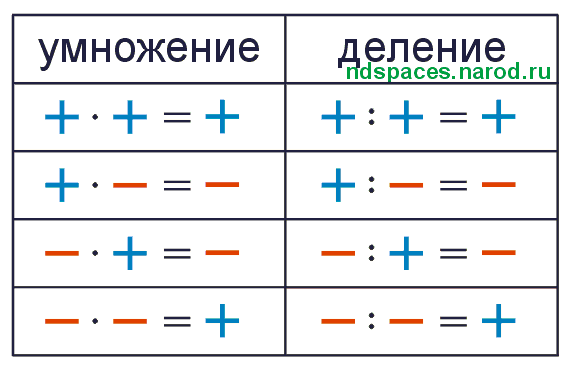 И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.

Поделиться

Получив эту хитрую комбинацию, умножаем соседние цифры (2 на 0, 2 на 4) и в обратную стороны (2 на 3 и 3 на 0). Идем еще дальше и стараемся не запутаться — перемножаем первую верхнюю цифру на третью нижнюю, а третью верхнюю — на первую нижнюю. Умножение закончилось.

Поделиться

Давайте складывать то, что у нас получилось. А получилось у нас 67 792.

Выписываем наших героев и подводим под ними черту, как делали это в методе треугольника. Затем перемножим крайние цифры — 2 и 4. Результат (его мы записываем как 08) будет первой строкой нашего решения. Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.

Поделиться

Ну а дальше умножаем друг на друга цифры из разряда сотен, десятков и единиц и так же записываем их в одну строку. Результат заносим в третью строчку.

Теперь берем вторую цифру во втором множителе и умножаем на первую и третью из первого. Четвертая строка решения готова. Последней, пятой строкой записываем произведение последней цифры первого множителя и первой цифры второго. Наш ромб готов. Осталось только суммировать цифры, расположенные друг над другом. Метод, конечно, красивый, но совсем не простой в применении.

Поделиться

Вот мы и добрались до того момента, где объясним, зачем нам понадобились трехзначные числа, да еще и с нулем. В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.

Поделиться

После этого считаем точки пересечения всех черточек. В зоне единиц их восемь, в зоне десятков — 30, в зоне сотен — 18. Теперь нужно это сложить: 1800+300+8 = 2 108. На калькуляторе, умножая 34 на 62, получится тот же результат.

Переходим к нашему изначальному примеру и умножим 223 на 304. Рисуем две, две и три горизонтальные линии, три вертикальные слева и четыре справа. Место посередине оказывается пустым, поэтому здесь у нас будет воображаемая линия. (Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.

Поделиться

Складываем, начиная с единиц. Там, где получились двузначные числа, оставляем единицы, а десятки перекидываем в соседнюю область. То есть там, где стояли рядом 8 и 12, оказались 9 и 2, а соседство 6 и 17 превратилось в 7 и 7. Считаем, что у нас получилось, справа налево: 67 792.

Чтобы решить наш пример методом решетки (его еще называют древнеиндийским методом), первым делом надо нарисовать таблицу, у которой будет три столбца и три строки — по количеству цифр в умножаемых числах. Потом делим каждую ячейку по диагонали на две части. Решетка готова.

Теперь по горизонтали выписываем цифры числа 223, а по вертикали — числа 304. И перемножаем каждое число сверху на каждое число справа. Результат вписываем в наши ячейки таким образом: сверху — десятки, снизу — единицы (если десятков нет, пишем ноль).

Поделиться

Теперь складываем цифры, которые получились в наших диагоналях. По периметру, начиная с правого нижнего угла и поднимаясь до левого верхнего. Если число вышло двузначным, оставляем только единицу, а десятки плюсуются к единицам числа предыдущего — совсем как в сложении, к которому мы привыкли.

Поделиться

Выписываем ответ, начиная с левой стороны: 67 792. Что и требовалось доказать.

Этот метод похож на метод решетки, но есть отличия. Здесь мы снова рисуем таблицу на три столбца и три строки, но ни на какие ячейки не делим. А наши числа записываем не в виде отдельных цифр, а сотнями, десятками и единицами.

Поделиться

Дальше начинаем умножать те цифры, что сверху, на те, что справа.

Поделиться

Умножили? Осталось только всё сложить: 60 000 + 6000 + 900 + 800 + 80 + 12 = 67 792. Тот результат, который и получится, если умножить 223 на 304.

Разные способы решить один и тот же пример, к слову, далеко не единственная математическая причуда. На днях одна несложная на первый взгляд задачка рассорила весь интернет — скандал разгорелся из-за простого примера для 6-классников. И мы попробовали решить его с математиком.

§ Свойства умножения и деления

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

  • Геометрия: начальная школа
  • Действия в столбик
  • Деление с остатком
  • Законы арифметики
  • Периметр
  • Порядок действий
  • Разряды и классы. Разрядные слагаемые
  • Счет в пределах 10 и 20

Математика 5 класс

  • Взаимно обратные числа и дроби
  • Десятичные дроби
  • Натуральные числа
  • Нахождение НОД и НОК
  • Обыкновенные дроби
  • Округление чисел
  • Перевод обыкновенной дроби в десятичную
  • Площадь
  • Проценты
  • Свойства сложения, вычитания, умножения и деления
  • Среднее арифметическое
  • Упрощение выражений
  • Уравнения 5 класс
  • Числовые и буквенные выражения

Математика 6 класс

  • Масштаб
  • Модуль числа
  • Окружность. Площадь круга
  • Отношение чисел
  • Отрицательные и положительные числа
  • Периодическая дробь
  • Признаки делимости
  • Пропорции
  • Рациональные числа
  • Система координат
  • Целые числа

Алгебра 7 класс

  • Алгебраические дроби
  • Как применять формулы сокращённого умножения
  • Многочлены
  • Одночлены
  • Системы уравнений
  • Степени
  • Уравнения
  • Формулы сокращённого умножения
  • Функция в математике

Геометрия 7 класс

  • Точка, прямая и отрезок
  • Что такое аксиома и теорема

Алгебра 8 класс

  • Квадратичная функция. Парабола
  • Квадратные неравенства
  • Квадратные уравнения
  • Квадратный корень
  • Неравенства
  • Системы неравенств
  • Стандартный вид числа
  • Теорема Виета

Алгебра 9 класс

  • Возрастание и убывание функции
  • Нули функции
  • Область определения функции
  • Отрицательная степень
  • Среднее
    геометрическое
  • Чётные и нечётные функции

Алгебра 10 класс

  • Иррациональные числа

Алгебра 11 класс

  • Факториал

Думать и творить, творить и думать — вот основа всякой мудрости. Иоганн Вольфганг фон Гёте

на главную

Введите тему

Поддержать сайт

Свойства сложения и вычитания Свойства умножения и деления

Свойства умножения

Переместительное свойство умножения

Запомните!

От перестановки множителей произведение не меняется.

a · b = b · a

Сочетательное свойство умножения

Запомните!

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

a · (b · c) = (a · b) · c

Переместительное и сочетательное свойства умножения

позволяют сформулировать правило преобразования произведений.

Запомните!

При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.

Свойство нуля при умножении

Запомните!

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

a · 0 = 0

0 · a · b · c = 0

Распределительное свойство умножения относительно сложения

Запомните!

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

(a + b) · c = a · c + b · c

Это свойство справедливо для любого количества слагаемых.

(a + b + с + d) · k = a · k + b · k + c · k + d · k

Распределительное свойство умножения относительно вычитания

Запомните!

Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.

В буквенном виде свойство записывается так:

(a − b) · c = a · c − b · c

Запомните!

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Свойства деления

  • Ни одно число нельзя делить на ноль.
  • При делении нуля на число получается ноль.

    0 : a = 0

  • При делении любого числа на 1 получается это же число.

    b : 1 = b

Запомните!

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

a : b = (a · k) : (b · k)

, где «k» — любое натуральное число.

Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.

Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.


Свойства сложения и вычитания Свойства умножения и деления

117 Синонимов и антонимов слова MULTIPLY

умножать

1

как в для распространения

производить потомство кролики размножаются с пресловутой быстротой

  • распространять

  • воспроизводить

  • порода

  • производить

  • генерировать

  • производить потомство

  • порождать

  • породить

  • иметь

  • родитель

  • люк

  • мать

  • сир

  • получать

  • порождать

  • пол

  • медведь

2

как в увеличить

сделать больше по размеру, сумме или количеству бурно развивающаяся экономика умножить на богатство инвесторов

  • увеличивать

  • расширять

  • ускорить

  • увеличить

  • способствовать росту

  • поднимать

  • продлевать

  • усиливать

  • усиливать

  • усилить

  • обострять

  • зыбь

  • увеличить

  • максимизировать

  • вверх

  • укреплять

  • сложный

  • укреплять

  • возвеличивать

  • топить

  • накачивать

  • наращивать

  • сверхразмерный

  • взлететь до небес

  • добавить в)

  • шумиха

  • удлинить

  • раздувать

  • увеличить

  • усиливать

  • добавка

  • развивать

  • накапливать

  • удлиняться

  • Прыгать

  • шип

  • раздувать

  • расширяться

  • продлить

  • дополнять

  • вытягивать

  • потягиваться

  • бум

  • накапливать

  • затягивать

  • Взрывать

  • собирать

  • ставить на кон

  • повысить)

  • трещотка (вверх)

  • храповик (вверх)

  • укреплять

  • следовать за

  • плоть (вне)

  • говядина (вверху)

  • уменьшать

  • снижаться

  • уменьшить

  • уменьшить

  • вычитать (из)

  • уменьшить

  • сократить

  • ниже

  • уменьшаться

  • уменьшаться

  • урезать

  • сокращать

  • уменьшить

  • сокращать

  • компресс

  • сжимать

  • конденсировать

  • деэскалация

  • договор

  • экономить

  • сокращать

Подробнее

  • уменьшать

  • снижаться

  • уменьшить

  • уменьшить

  • вычитать (из)

  • уменьшить

  • сократить

  • ниже

  • уменьшаться

  • уменьшаться

  • урезать

  • сокращать

  • уменьшить

  • сокращать

  • компресс

  • сжимать

  • конденсировать

  • деэскалация

  • договор

  • экономить

  • сокращать

Подробнее

3

как в в рост

становиться больше в размерах, объеме, количестве или количестве с каждой попыткой проблемы умножить на

  • увеличивать

  • рост

  • ускорить

  • зыбь

  • расширять

  • накапливать

  • размножаться

  • усилить

  • взбираться

  • распространение

  • обострять

  • воск

  • увеличить

  • прирост

  • свернуть

  • снежный шар

  • устанавливать

  • воздушный шар

  • гриб

  • бум

  • расцветать

  • ценить

  • всплеск

  • наращивать

  • Прыгать

  • взлететь до небес

  • буржуй

  • усиливать

  • удваивать

  • раздувать

  • ракета

  • вершина горы

  • раздувать

  • масса

  • крещендо

  • Взрывать

  • герб

  • затяжка (вверх)

  • снижаться

  • уменьшить

  • отступать

  • уменьшить

  • ослабевать

  • уменьшаться

  • договор

  • снижаться

  • уменьшить

  • отступать

  • уменьшить

  • ослабевать

  • уменьшаться

  • договор

Подробнее

Выбор синонимов

Как глагол умножить отличается от своих синонимов?

Некоторые распространенные синонимы умножить на : увеличить , увеличить и увеличить . Хотя все эти слова означают «сделать или стать больше», умножить на подразумевает увеличение числа за счет естественного зарождения или за счет бесконечного повторения процесса.

с каждой попыткой проблемы умножить

Когда имеет смысл использовать дополнить вместо умножить ?

Значения увеличивают и умножают в значительной степени перекрываются; однако augment подразумевает добавление к тому, что уже хорошо выросло или хорошо развито.

наследство увеличенное его состояние

Когда увеличить будет хорошей заменой умножить ?

Синонимы увеличить и умножить иногда взаимозаменяемы, но увеличить подразумевает расширение или расширение, что увеличивает размер или мощность.

увеличенный кухня

Когда можно использовать увеличить вместо умножить ?

Слова увеличить и умножить могут использоваться в аналогичных контекстах, но увеличение непереходное использование подразумевает прогрессивный рост в размере, количестве или интенсивности; при переходном использовании это может означать простое, не обязательно прогрессивное добавление.

его талия увеличилась с возрастом

увеличилась ее земельные владения

Тезаурус Записи Около

умножить

умножает

умножать

умножение

Посмотреть другие записи поблизости

Процитировать эту запись «Умножить».

Merriam-Webster.com Thesaurus , Merriam-Webster, https://www.merriam-webster.com/thesaurus/multiply. По состоянию на 3 февраля 2023 г. Самый большой словарь Америки и тысячи других определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

хала

См. Определения и примеры »

Получайте ежедневно по электронной почте Слово дня!

Слова, названные в честь людей

  • Тёзка купальника Жюль Леотар какую профессию имел?
  • Врач хирург Пожарный
  • Акробат Судить

Прослушайте слово и напечатайте его. Сколько вы можете получить правильно?

ПРОЙДИТЕ ТЕСТ

Сможете ли вы составить 12 слов из 7 букв?

ИГРАТЬ

Умножить сумматор

{{=loadTemplate(‘KeyMatch’, isTopResult == true) }} {{= titleString }}

{{ если (raw.confmodifieddate) { }}

{{- window.templateHelpers.dateFormatter(raw.confmodifieddate) }}

{{ } }}

{{- window.templateHelpers.videoDescriptionFormatter(raw.description,except) }}

{{=loadTemplate(‘KeyMatch’, isTopResult == true) }} {{= titleString }} {{= fileVersionNumber }}{{= newUpdatedString }} {{ если (ложь == истина) { }} {{= window.templateHelpers.isCurrentVersion(raw.xlnxarchived, raw.language) }} {{ } }}

{{ если (raw.xlnxlastmodifieddate) { }}

{{- window.templateHelpers.dateFormatter(raw.xlnxlastmodifieddate) }}

{{ } }}

{{ если (raw. xlnxdocumenttypes) { }}

Тип документа: {{= raw.xlnxdocumenttypes }}

{{ } }}

{{= необработанное.описание }}

{{ if (raw.xlnxhasmultipleversions == ‘true’ && (false == false)) { }}

Просмотреть все версии

{{ } }} {{ если (raw.xlnxchildipperformance) { }}

Данные о производительности IP и использовании ресурсов:

    {{ _.each(ipPerformanceDocs, функция (элемент) { }}
  • {{= элемент.имя_файла }}
    • {{ }) }}

{{ } }} {{ если (raw.xlnxchilddesignfile) {}}

Файл(ы) дизайна:

    {{ _.each(designFileDocs, функция (элемент) { }}
  • {{= элемент.имя_файла }}
    • {{ }) }}

{{ } }} {{ if (raw.xlnxchildassociatedfile || raw.xlnxrelateddocs) { }}

Связанные файлы:

    {{ _.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *